Nonrandom mating in Drosophila melanogaster laboratory populations derived from closely adjacent ecologically contrasting slopes at “Evolution Canyon”

Abstract

Ecological differentiation of natural populations of Drosophila melanogaster, Drosophila simulans, and another drosophilid, Zaprionus tuberculatus, in “Evolution Canyon,” Mount Carmel, Israel, is well established. The fitness complex of D. melanogaster includes oviposition temperature preferences, tolerance to high temperature, drought stress and starvation, and different longevity patterns. This remarkable differentiation has evolved despite small interslope distances (only 100–400 m), within easy dispersal distance. The differences between populations are those expected from genetic adaptation to local microclimates. How such differentiation could evolve and be maintained despite the likelihood of genetic exchange between populations is a challenging question. We hypothesized that interslope microclimatic differences caused strong differential selection for stress tolerance, accompanied by behavioral differentiation (habitat choice and reduced migration rate), reinforced by sexual isolation. Here we report highly significant mate choice by flies from different slopes of the canyon, with preference for sexual partners originating from the same slope. No preferences were found when the sexual partners belonged to different isofemale lines from the same slope.

The origin of reproductive isolation is the central event in the evolution of biological species (1, 2). Sexual isolation may evolve either in allopatry or sympatry, with and without geographical separation, respectively. It is widely accepted that postmating (postzygotic) isolation results from and completes the evolutionary divergence, whereas premating (prezygotic) isolation is associated with its initial stages (refs. 3–5 and references therein). The selectionist paradigm explains both allopatric and sympatric premating isolation as a result of divergent selection. However, the proposed versions of this selection-induced process vary significantly, especially with respect to sympatry. The main problem of sympatric speciation can be formulated as follows (3, 6–10). Is sexual isolation an incidental by-product of genetic divergence? Or, alternatively, is it selected directly because of its contribution to higher fitness?

No clear answers to these questions are yet available. We are still far from understanding how isolation evolves, mainly because of scarcity of evidence, especially in the sympatric scenario. Understanding how selection works, quantifying its effects, and characterizing its interaction with other factors contributing to the differentiation of natural populations (migration, habitat choice, sexual behavior, etc.) are among the major issues of evolutionary biology. A wide range of genetic organization patterns, from major genes and compact blocks of epistatic (coadapted) genes to multiple loci dispersed over many chromosomes, was revealed in laboratory studies (refs. 11–13; for review, see also ref. 14). Much less is known about the population–genetic basis of adaptation and speciation in nature, despite an abundance of field studies and sophisticated theories. It is not an easy task to distinguish among different models and theories based on field measurement of fitness components (15). Presumably a better understanding could be achieved through elucidation of population genetic processes related to adaptation to stressful environment (16). It would be exciting to address the foregoing problems in the context of incipient sympatric speciation, when ecological–genetic divergence occurs without geographic isolation.

A unique opportunity to consider such a situation is provided by a natural model, “Evolution Canyon” at Lower Nahal Oren, Mount Carmel, Israel (17, 18). The opposite slopes, separated by only 100 m (bottom) and 400 m (top), represent dramatic biotic contrasts because of the higher (up to 600% more) solar radiation on the south-facing slope (SFS) than on the north-facing slope (NFS). The SFS is warmer, drier, microclimatically more fluctuating, and less predictable than the NFS. Our previous studies showed a strong interslope differentiation of Drosophila for a complex of adaptive traits (19, 20). These included changes in viability and longevity caused by short-term and lifetime temperature treatments and changes in fly weight because of desiccation/starvation treatments at different temperatures, different levels in the variation of fluctuating asymmetry, different rates of mutation and recombination, and habitat choice (preferred oviposition temperature). This remarkable differentiation has evolved despite small interslope distance (a few hundred meters), well within the dispersal capability of Drosophila species (21–23).

What prevents the evolving slope-specific adaptive gene complexes from recombinational collapse? We hypothesized that strong differential selection for stress tolerance has also promoted behavioral differentiation: habitat choice, reduced migration rate, and positive assortative mating facilitating further adaptive interslope divergence. The assumption of possible habitat preferences was supported experimentally (19). The direction of the difference in preferred temperatures of oviposition was as expected according to the habitat choice models of polymorphism maintenance in spatially heterogeneous environments. The main goal of the current study was to investigate the possibility of incipient sexual isolation between the subpopulations derived from the opposite slopes of “Evolution Canyon.”

Materials and Methods

Sampling was conducted during 1995 and 1997 at two midstations, 90 m above sea level, on opposite slopes of “Evolution Canyon” (Lower Nahal Oren, Mount Carmel, Israel). A series of isofemale lines was established from samples collected during spring–summer 1995 (“old” collection) and fall 1997 (“new” collection) and maintained in culture under standard conditions (25°C, approximately 40% mean relative humidity, and cornmeal–sugar–agar food medium). The experiments were conducted on specially designed synthetic populations (one per slope for either the old or new collection). Each population was constructed by crossing 25 isofemale lines (25 × 10 = 250 virgin flies of each sex were combined in a population cage). These populations were maintained under random mating for 12 (new collection) and 48 (old collection) generations, before the mate-choice tests were started. We conducted several mate-choice tests to examine mating behavior.

In multiple-choice tests, three anesthesia methods were used (ether, CO₂, and no anesthesia) with two methods of fly marking [pen marking by a dot on the scutellum and marking by black grapes introduced in vials instead of medium, analogous to the technique based on colored food (ref. 24)]. Flies were allowed to recover for 5 days after the pen-marking procedure. Each combination of “collection (two variants) × anesthesia (three variants) × marking (two variants)” was represented by six repeated half-pint milk bottles with 40 flies in each (10 SFS males + 10 SFS females + 10 NFS males + 10 NFS females). Forty flies were simultaneously introduced into the mating chamber and were observed for 60 min. When a pair commenced mating, it was aspirated out, and the mated types were recorded. Marking was alternated between repeats to control its possible effect on the results. A total of 2,880 flies participated in all tests.

Single mate-choice tests were conducted only for the new collection. Bottles in each of the 4 single-choice experiments included 39 flies: 13 tested males (either NFS or SFS) and 13 SFS females + 13 NFS females, and vice versa. Each combination “tested sex × slope × marking” was represented by 6 bottles totaling 1,400 flies. CO₂ anesthesia was used with one variant of fly marking (pen marking by small spot on the scutellum). The tests were conducted on virgin 7-day-old flies. In both multiple- and single-choice experiments, the number of formed pairs was registered.

To test whether intraslope genotypic differences may also result in female choice, a separate series of experiments was conducted. We tested whether females of different isofemale lines within the slope manifest any preferences toward the males of their own line compared with males of other lines from the same slope. The experimental design was analogous to that described above for the single-choice experiments. In each case, females were exposed to males from their own origin vs. males of two other lines from the same slope. Interslope female-choice tests were repeated as a separate control to these intraslope-choice tests.

To test the significance of deviation from panmixia in single- and multiple-choice experiments, logarithm–linear analysis was conducted by means of the statistica package (STATSoft, Tulsa, OK). In addition, an attempt to quantify the mate-choice effects was made based on maximum likelihood analysis of data obtained in single-choice tests.

Results

Multiple-Choice Test.

Significant nonrandom mating was established in all tested variants (Table 1). Remarkably, significant excess of pairs formed by partners of the same slope was observed for both collections and all three types of anesthesia, although the deviation from the expected 50% level was not very high (mean 12.2% and 14.2% for the old and new collections, respectively). To test the significance of other components of variation, the initial six-way table (independent variables: anesthesia, collection (“old” or “new”), female slope origin, male slope origin, slope of marked flies, repeat) of pair formation was subjected to logarithm–linear analysis. Only three factors appeared to be significant with respect to the observed number of pairs: F (female slope origin), interaction A × F (female origin with type of anesthesia), and, especially, interaction F × M (female and male origin) (Table 2). This analysis confirmed the foregoing conclusion of highly significant interaction “female slope” × “male slope” in pair formation: the corresponding χ² components of either partial and marginal associations (79.8 and 73.6, df = 1) by far exceeded any other component. The only two other significant components, factors F and A × F, reflect the fact that receptivity of SFS females was negatively affected by ether anesthesia (in both old and new collections).

Table 1.

Nonrandom mating in multiple-choice tests in flies derived from the opposite slopes of “Evolution Canyon”

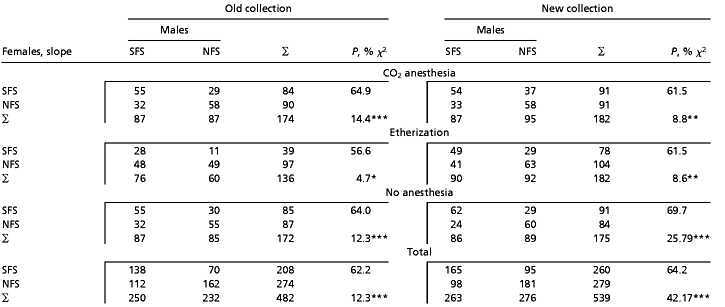The maximum possible number of pairs per each of the six variants is 240. P, % is the proportion of same-slope pairs in the test, and χ² is testing for significance the assumption H₀ = “no mate choice” (with  

^*,  

^**, and  

^** indicating significant deviation from H₀ at P < 0.05, 0.01, and 0.001, respectively). 

Table 2.

The results of logarithm-linear analysis of the multiple-choice tests (χ² components for main effects and two-way interactions)

Factor*	df	Partial association		Marginal association
		χ2	P	χ2	P
A	2	2.339	0.3105	2.339	0.3105
C	1	3.184	0.0743	3.184	0.0744
F	1	7.085	0.0078	7.085	0.0078
M	1	0.025	0.8746	0.025	0.8746
A × C	2	5.052	0.0800	3.700	0.1572
A × F	2	19.690	0.0001	15.543	0.0004
A × M	2	4.423	0.1096	0.776	0.6784
C × F	1	5.240	0.0221	2.652	0.1035
C × M	1	2.782	0.0954	0.961	0.3270
F × M	1	79.848	0.0000	73.584	0.0000

^*The factors are denoted as follows: A, anesthesia; C, collection; F, the slope of female origin; M, the slope of male origin. The pair-wise interactions are denoted as A × C, … F × M. 

Single-Choice Test.

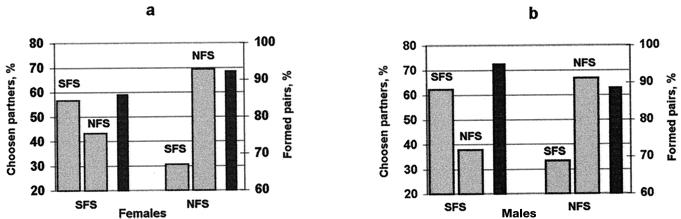
The results presented in Table 3 and Fig. 1 corroborate those of multiple-choice tests. An excess of same-slope pairs is seen in both female-choice and male-choice experiments, i.e., both sexes are selective in choosing a mating partner. Seemingly, SFS flies display a slightly higher deviation from randomness. However, such a conclusion cannot be based only on comparisons of the proportions of same- and different-slope crosses. Other mating parameters, namely male activity and female receptivity, may have affected the results (25). Our experimental design, which included all four possible single-choice variants, allowed quantification of the foregoing parameters and testing the significance of male and female choice in flies derived from both slopes. This was done by maximum likelihood methodology (26).

Table 3.

The results of single-mate choice tests

Choosing flies		Chosen partners		Σ	P, %	χ2	P
Sex	Slope	SFS	NFS
Females	SFS	38	29	67	63.3
	NFS	22	50	72	63.2	8.64	0.0033
Males	SFS	46	28	74	66.7
	NFS	23	46	69	62.2	10.76	0.001

Figure 1.

Single mate-choice tests. (a) Female choice; (b) male choice. Proportions of pairs resulting from same- and other-slope choice are presented. The black column on the right-hand side for each test represents the percent of formed pairs (of a possible 78 pairs total for each test). For a detailed analysis of the results, see Table 3.

In the simplest form, the expected frequencies of different outcomes of the experiment can be presented as in the following scheme:

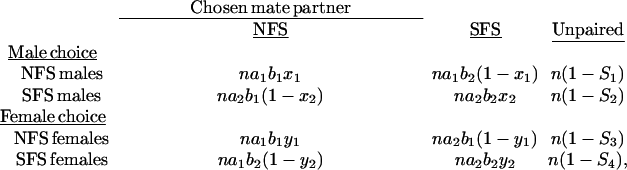where a₁ and a₂ denote the activity of NFS and SFS males, respectively; b₁ and b₂ denote receptivity of NFS and SFS females; x₁ and x₂ denote selectivity of NFS and SFS males; y₁ and y₂ denote selectivity of NFS and SFS females; and S_j (j = 1, … ,4) are the expected frequencies of unpaired flies of the choosing gender (males and females). Clearly, the foregoing model assumes that the observed numbers of forming pairs result from the independent action of three groups of factors: slope-specific activity of males, receptivity of females, and male and female mate choice. Moreover, we assumed that the parameters characterizing male activity and female receptivity remain the same in male- and female-choice experiments.

Using the observed numbers N_ij (i = 1,2,3; j = 1,2,3,4) in each of the four experimental variants, one can evaluate the unknown set of parameters θ = {a₁, b₁, x₁, y₁, a₂, b₂, x₂, y₂} in such a way that it will provide the maximum of the likelihood function L(θ) or (which is equivalent) to its logarithm:

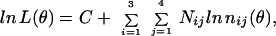where C is some constant and n_ij (θ) are the expected numbers of the classes in the foregoing scheme. The optimum (maximum likelihood) values of the parameters of vector θ can be found by numerical optimization of the function lnL(θ). This approach allows comparison of different hypotheses about the parameters of vector θ.

Let θ̂ = θ̂₁ = {â₁, b̂₁, x̂₁, ŷ₁, â₂, b̂₂, x̂₂, ŷ₂} be a full vector of estimates and θ̂ = θ̂₂ a vector of estimates with some restrictions corresponding to specific assumptions, like “no mate choice in females from SFS ” or “equal receptivity of females from both slopes. ” To compare each such hypothesis represented by a vector θ₂ with a smaller number of parameters, one can use the statistics

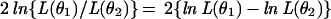distributed asymptotically as χ² with df = k₁ − k₂ degrees of freedom, where k₁ and k₂ are the number of parameters in the compared hypotheses (26).

The results presented in Table 4 indicate some interslope asymmetry in sexual activity: (i) a lower receptivity of SFS females than of NFS females: the maximum likelihood estimate b₂ = 0.912 is significantly lower than 1 (P < 10⁻⁶ when corresponding hypotheses, M₃ and M₂, are compared), whereas b₁ is very close to 1; (ii) reduced activity of NFS but not SFS males: the estimate a₁ = 0.900 is significantly lower than 1 (P < 10⁻⁶ when corresponding hypotheses, M₄ and M₂, are compared), whereas a₂ is very close to 1. An important aspect of the presented analysis is the possibility of quantifying the proportions of same- and different-slope choices in pair formation. NFS but not SFS females appeared to display highly significant (P < 0.0001) positive assortative mating (y₂ = 0.538 is close to 0.5, the level expected at random mating, whereas y₁ = 0.645 differs significantly from 0.5 as found by comparison of hypotheses M₁₀ and M₉ in Table 4). By contrast, males of both slopes showed the same level of mate choice. The hypothesis of no male choice is rejected at P < 0.0004 (comparison of hypotheses M₁₁ and M₉), whereas the assumption of equal level of NFS and SFS male choice fits the data.

Table 4.

Components of sexual behavior of D. melanogaster from “Evolution Canyon” in single-choice tests

Model	â1	b̂1	x̂1	ŷ1	â2	b̂2	x̂2	ŷ2	ln L(θ)	χ2 (df)	H0	P
M1 = general (no restrictions)	0.900	0.999	0.648	0.718	0.999	0.913	0.641	0.538	−121.53
M2 = full receptivity of NFS females and
full activity of SFS males b1 = a2 = 1	0.900	1	0.648	0.718	1	0.912	0.641	0.538	−121.53	0.00 (2)	M1	NS
M3 = M2 and full receptivity of SFS females	0.850	1	0.667	0.718	1	1	0.641	0.487	−152.86	144.28 (1)	M2	<10−6
M4 = M2 and full activity of NFS males	1	1	0.590	0.718	1	0.850	0.641	0.567	−168.75	217.46 (1)	M2	<10−6
M5 = M2 and x1 = x2	0.901	1	0.644	0.718	1	0.912	0.644	0.539	−121.54	0.05 (1)	M2	NS
M6 = M2 and x2 = 0.5 and y2 = 0.5	0.898	1	0.649	0.718	1	0.915	0.5	0.5	−122.98	6.68 (2)	M2	0.035
M7 = M2 and x2 = 0.5	0.900	1	0.648	0.718	1	0.912	0.5	0.539	−122.90	6.31 (1)	M2	0.012
M8 = M2 and y1 = y2	0.906	1	0.646	0.636	1	0.905	0.641	0.636	−122.61	4.97 (1)	M2	0.03
M9 = M5 and y2 = 0.5	0.898	1	0.645	0.718	1	0.915	0.645	0.5	−121.62	0.37 (1)	M5	NS
M10 = M9 and y1 = 0.5	0.898	1	0.645	0.5	1	0.915	0.645	0.5	−124.95	15.34 (1)	M9	0.0001
M11 = M9 and x1 = x2 = 0.5	0.906	1	0.5	0.718	1	0.907	0.5	0.5	−124.31	12.39 (1)	M9	0.0004

a₁ and a₂ denote the activity of NFS and SFS males; b₁ and b₂, receptivity of NFS and SFS females; x₁ and x₂, selectivity of NFS and SFS males; y₁ and y₂, selectivity of NFS and SFS females. M₉ is the main model [with all nonsignificant (NS) parameters taken as constant, either 1 or 0.5]. 

We conducted a special experiment to test whether intraslope sexual selection may affect the results, or more generally, whether any genotypic differences (including those of within slope) may result in female choice. In parallel to the female-choice test repeated for synthetic populations, we also tested whether females of isofemale lines displayed any preferences when subjected to a mixture of males of their own line and other lines from the same slope. The results of intraslope mate-choice tests were negative, namely females did not discriminate against males from the other lines compared with males from their own origin (Table 5). By contrast, the repeated test on interslope mixtures markedly reproduced the results of the initial female mate-choice tests (compare Tables 5 and 3).

Table 5.

Comparison of female choice tests with heterospecific partners taken from the same and opposite slopes

Scale	Slope	Chosen partners		Σ	P, %	χ2	P
		Homo	Hetero
Intraslope	SFS	102	103	205	49.8	0.00	NS
	NFS	73	77	150	48.7	0.11	NS
	Σ	175	180	355	49.3	0.07	NS
Interslope	SFS	54	29	83	65.1	6.91	0.008
	NFS	42	21	63	66.7	6.33	0.012
	Σ	96	50	146	65.8	13.76	0.0002

Note the close similarity of the results of the interslope test to those shown in Table 3. 

Discussion

Evolutionary Origin of Premating Isolation.

Suppressed gene exchange caused by interpopulation geographical isolation (allopatry) may promote the evolution of sexual isolation as a first step of speciation (2, 27). Incipient sexual isolation among geographic races of the same species, including D. melanogaster, has been reported in a number of studies (e.g., refs. 24, 28, 29). Likewise, experiments with laboratory populations clearly showed that artificial selection for different adaptive and behavioral traits may promote a tendency of positive assortative mating (e.g., refs. 30 and 31, and references therein). These results confirm the importance of gene pool separation, but they cannot allow discrimination as to the evolutionary origin of premating isolation: by direct selection (Dobzhansky) or as a by-product of gene pool divergence (Darwin, Muller, Mayr, Carson; see ref. 3). The latter situation may occur, for example, when the trait involved in ecological adaptation (such as body size or wing size) simultaneously affects mate choice (32, 33).

More promising in addressing the latter problem is the sympatric model, even though its relative importance in speciation is far more controversial than the allopatric one (ref. 2, but see ref. 34). Classical experiments by Thoday (35, 36) with D. melanogaster demonstrated that disruptive selection for quantitative traits (such as bristle number) within a population may promote evolution of positive assortative mating. Theoretical modeling shows that selection against migrants in systems with spatially heterogeneous selection can bring about a genetically determined reduction in the migration rate (37). However, as pointed out by Felsenstein (38), in the case of sympatry (without geographical isolation), divergent selection will be opposed by recombination, preventing genetic differentiation. In Felsenstein's model evolution of a modifier allele promoting assortative mating was possible only in the case of tight linkage between the modifier locus and fitness loci. Another consequence of adaptation to spatially varying conditions is evolution of habitat preferences, allowing storage of genetic polymorphism in the population without heavy genetic load (39–41). Habitat choice may facilitate the evolution of mate choice, resulting in sympatric speciation (e.g., 33, 42–44). Therefore, theoretically it seems reasonable that microsite ecological–genetic differences can promote a tendency toward habitat preferences and a reduced mixing of adaptively diverging gene complexes within a population (10). The genetic architecture of fitness-related traits subjected to ecological selection (e.g., additive vs. epistatic effects, correlation between fitness-related and mate-choice traits, etc.) may be an important factor determining the possibility of evolving premating reproductive isolation. However, the major problem is still a dearth of evidence in natural populations confirming this scenario.

The “Evolution Canyon” Model.

Our previous results for D. melanogaster, D. simulans, and Z. tuberculatus indicated that flies from the ecologically contrasting opposite slopes of “Evolution Canyon” differ significantly and reproducibly for stress tolerance (19). The direction of the revealed differences was exactly the one expected according to the microclimatic contrasts. Significant microscale differentiation was also found in Drosophila persimilis population in the Sierra Nevada Mountains of California (39). In that study, the compared subpopulations were scored for inversion frequencies and allozymic variants. The observed differentiation was explained in terms of the habitat-choice mechanism. Likewise, significant microspatial heterogeneity in allozyme allele frequencies was found in cactophilic species Drosophila buzzatii (among flies emerging from different host roots) (45).

The parallel data on differential adaptation of sibling species of Drosophila from the opposite slopes of “Evolution Canyon” called for further experimentation. The basic question we addressed was how this remarkable ecological, or microclimatic, differentiation could evolve and be maintained despite the extremely small interslope distance, which could easily be surpassed by the migration ability characteristic of Drosophila. In other words, what prevents the evolving slope-specific adaptive gene complexes from recombination collapse? A working hypothesis was proposed postulating that the interslope microclimatic contrasts cause strong differential selection for stress tolerance (heat and drought resistance), which in turn and incidentally promotes a complex of behavioral adaptations facilitating reduced gene exchange: habitat choice, reduced migration rate, and nonrandom mating. The foregoing tests (for both D. melanogaster and D. simulans) showed that adaptation to the contrasting conditions of the opposite slopes had indeed resulted in strong genetic divergence for habitat choice (19). In this paper, we have demonstrated a significant tendency of interslope sexual isolation manifested as female and male mate choice. The phenomenon of mating preferences was observed in single and multiple mate-choice tests. Remarkably, the tendency for an excess of same-slope pairs in multiple-choice tests was not affected by the collecting date and the methods of anesthesia (see Tables 1 and 2). Likewise, the time of testing had no effect on the results of female choice (the interslope tests presented in Table 5 were conducted a few months after the tests shown in Table 3). However, the mating-choice parameters are confounded with those of male activity and female receptivity (46). Moreover, the results of multiple-choice experiments may depend on the dynamics of pair formation (46, 47). Therefore, to retrieve the selective mating components, we analyzed single mate-choice data by the maximum likelihood method (Table 4). The obtained estimates point to some asymmetry in patterns of premating isolation: males of both slopes, but only NFS females, displayed positive assortative mating. We hypothesize that this interslope asymmetry in female choice may reflect the fact that SFS is much more stressful (hence the population density there is presumably lower) and heterogeneous. Consequently, this may reduce the chances of getting a sexual partner and simultaneously increase the genetic variation within the SFS population (20).

The Drosophila adaptive syndrome formed by strong microclimatic differences on the opposite slopes of “Evolution Canyon” includes survival and longevity in normal conditions and at elevated temperature, reaction to short-term heat and drought treatments, and starvation stress (19). Before being tested, our lines were raised over 0.5–2.5 years in standard laboratory conditions. The processes of adaptation to laboratory conditions could influence these results only in one direction: reducing the initial genetic differences between flies from the opposite slopes. Despite between- and within-line variation, the maintenance of the material under laboratory standardized conditions did not eliminate the interslope differences. Nor could founder effect be responsible for the positive assortative mating observed in our mate-choice tests, because we used independent collections of different years and 25 isofemale lines in establishing each of the tested synthetic populations. All this allows us to conclude that the observed dissimilarities reflect the slope-specific genetic adaptations to the interslope microclimatic contrasts.

The Genetic Basis of Adaptation and Speciation.

The fact that the divergence in adaptive traits within a population at a microsite is accompanied by nonrandom mating makes this system a promising model to bridge theory and evidence in an in-depth analysis of adaptation under heterogeneous stressful conditions (14, 16), including the interactions among mutation, recombination, selection, migration, and habitat choice. Further experiments should dissect genetically the slope-specific differentiation for stress-resistance traits and behavioral adaptations, including habitat choice and mate choice, causing premating isolation. Important questions are: How many loci are involved in the initial stages of sexual isolation (4)? To what extent do chromosomal locations of behavioral-adaptation loci overlap with stress-adaptation loci (which may affect the dynamics of genetic correlations and gene pool divergence (10)? Is epistasis (coadaptation) a characteristic feature of any of these systems, and how is it related to linkage and recombination (48), especially with respect to postmating isolation loci? Our multivariate quantitative trait loci mapping methodology based on joint analysis of correlated trait complexes (49, 50) is one avenue to a better understanding of the genetic basis of adaptation and speciation.

Abbreviations

SFS

south-facing slope

NFS

north-facing slope