Population pharmacokinetics and pharmacodynamics of enoxaparin in unstable angina and non-ST-segment elevation myocardial infarction

Abstract

Aims

A major concern with any antithrombotic therapy is an increase in the risk of haemorrhage. The aim of this study was to analyse population pharmacokinetics and pharmacokinetic/pharmacodynamic (PK/PD) relationships for enoxaparin in patients with unstable angina (UA) and non-ST-segment elevation myocardial infarction (NSTEMI), which may help predict risk of haemorrhage.

Methods

Anti-factor Xa (anti-Xa) activity was measured as marker of enoxaparin concentration in 448 patients receiving the drug as a single 30-mg intravenous bolus followed by 1.0 or 1.25 mg kg⁻¹ subcutaneously twice a day. A population pharmacokinetic analysis was conducted and individual estimates of enoxaparin clearance and area under the curve were tested as prognostic factors for the occurrence of haemorrhagic episodes.

Results

Basic population PK parameters were an enoxaparin clearance of 0.733 l h⁻¹[95% confidence interval (CI) 0.698, 0.738], a distribution volume of 5.24 l (95% CI 4.20, 6.28) and an elimination half-life of 5.0 h. Enoxaparin clearance was significantly related to patient weight and creatinine clearance, and was the only independent predictor of experiencing both all (10.7%, P = 0.0013) and major (2.2%, P = 0.0004) haemorrhagic events. A creatinine clearance of 30 ml min⁻¹ was associated with a decrease in enoxaparin clearance of 27% compared with that in a patient with a median creatinine clearance of 88 ml min⁻¹, and was related to a 1.5- and 3.8-fold increase in the risk of ‘all’ and ‘major’ haemorrhagic episodes, respectively.

Conclusions

Enoxaparin clearance depends on body weight, and, therefore, weight-adjusted dosing is recommended to minimize interpatient variability in drug exposure and the risk of haemorrhage. The importance of an increased risk of haemorrhage with decreasing renal function must be weighed against the benefit of treatment with enoxaparin in patients with UA and NSTEMI.

Introduction

Enoxaparin is a low-molecular-weight heparin widely used for the prophylaxis and treatment of deep-vein thrombosis, and the treatment of unstable angina (UA) and non-ST-segment elevation myocardial infarction (NSTEMI). A major concern with any antithrombotic therapy is the increased risk of haemorrhage. The Thrombolysis in Myocardial Infarction-11A (TIMI-11A) study demonstrated that an initial 30-mg intravenous bolus of enoxaparin followed by subcutaneous injection of 1 mg kg⁻¹ twice a day was associated with a low rate of haemorrhage (1.9%) [1]. The efficacy of this regimen was established in a subsequent large study (TIMI-11B) [2]. In the TIMI-11A study, anti-factor Xa (anti-Xa) concentrations were measured before administration of enoxaparin and at the approximate predicted time of peak plasma concentration (3–5 h postdose) on several occasions during enoxaparin treatment. Peak anti-Xa concentrations tended to be higher in patients experiencing major haemorrhagic episodes [1].

Enoxaparin is a polysaccharide composed of a wide range of molecular entities, which consist of a number of different saccharide building blocks and with different chain lengths. Thus, it is not possible to evaluate the pharmacokinetics of enoxaparin by a simple physicochemical method. In the present work, the factor Xa enzyme inhibition assay was used, because factor Xa activity is thought to reflect best circulating concentrations of active anticoagulant.

Based on anti-Xa activity measurements obtained in the TIMI-11A study, population pharmacokinetic (PK) and pharmacodynamic (PD) analyses were performed. Their aims were: (i) to estimate typical enoxaparin PK parameters and assess interpatient PK variability in a population representative of UA/NSTEMI patients, (ii) to assess the influence of pathophysiological covariates on PK parameters (primarily enoxaparin clearance, the major determinant of exposure to the drug), and (iii) to investigate clearance and area under the curve (AUC) estimates as prognostic factors for enoxaparin-related haemorrhage.

Methods

Study design

TIMI-11A was an open-label study of the safety and tolerability of two weight-adjusted enoxaparin regimens in patients with UA and NSTEMI. The protocol and results are described in detail by Antman [1]. During the in-hospital phase, patients received a 30-mg intravenous bolus followed by weight-adjusted doses of either 1 mg kg⁻¹ (309 patients) or 1.25 mg kg⁻¹ (321 patients) of enoxaparin subcutaneously every 12 h for a median duration of 3 days. Following hospital discharge, patients received a fixed dose of 60 mg (body weight ≥ 65 kg) or 40 mg (< 65 kg) subcutaneously every 12 h for a median of 10 days. The cohort receiving 1.25 mg kg⁻¹ was started before the 1 mg kg⁻¹ cohort because of a high rate of major haemorrhage in the former. Patients with a creatinine plasma concentration of at least 2.0 mg dl⁻¹ were excluded. The study was performed in accordance with the Declaration of Helsinki, with the approval of the Institutional Review Boards from each of the 45 US and Canadian participating institutions, and with the written, informed consent of each patient.

The primary endpoint of the TIMI-11A study, major haemorrhage occurring within 2 weeks of enrolment, was defined as ‘a clinically overt haemorrhage resulting in a fall of at least 3 mg dl⁻¹ in haemoglobin or a retroperitoneal, intracranial, or intraocular haemorrhage’. All other episodes of bleeding were considered minor haemorrhages. The study design, exclusion criteria and other study endpoints have been described previously [1].

The blood-sampling schedule was not prospectively designed for a population PK analysis. Venous blood samples were obtained before (trough) and 3–5 h after (peak) the third weight-adjusted dose of enoxaparin and again on the last day of weight-adjusted dosing. Additionally, a few samples were collected during fixed-dose administration following hospital discharge. Plasma was frozen and stored at −80 °C until analysis could be performed.

The exact date and time of blood sampling, date and time of administration and actual dose were documented for the following: bolus dose, first, third (PK assessment) and last (PK assessment) weight-adjusted doses, first fixed dose, dose prior to PK assessment (if any) during fixed-dose administration and last fixed dose.

Anti-Xa activity was determined in a single laboratory using a validated amidolytic assay, with excess bovine factor Xa and the chromogenic substrate CBS 3139 (Diagnostica Stago, Asnières, France). The assay was linear over the calibration range of 0.025–0.401 IU anti-Xa ml⁻¹, the lower limit of quantification was 0.025 IU anti-Xa ml⁻¹, within-assay reproducibility was 5% or less, between-assay reproducibility was 12%, and accuracy was in the −14 to +9% range. Linear response to serial dilution was obtained in the 0.4–10 IU anti-Xa ml⁻¹ range.

PK analysis

The analysis was performed using nonlinear mixed effect modelling (NONMEM program double precision, version IV, level 2.0; University of California, San Francisco, CA, USA) [3]. A one-compartment structural kinetic model was used with basic parameters being apparent clearance (CL), apparent volume of distribution (V) and absorption rate (K_a) (ADVAN 2, TRANS 2 subroutines). The first-order estimation method was used. Covariance between parameters was tested using the BLOCK option.

Interindividual and interoccasion variabilities in parameters (P) were implemented as exponential terms according to Karlsson and Sheiner [4], where ω_P and π_P represent approximate coefficients of variation of interindividual and interoccasion variability, respectively. Residual variability was modelled using a proportional error model, where σ is an approximate coefficient of variation (CV) of residual error. Both first order and first order conditional estimation methods were used. The standard errors of estimates (SE) were calculated as the square root of the diagonal elements of the estimation covariance matrix. In each run the 95% confidence interval (CI) of point estimates was determined from the corresponding SE, as follows: CI = point estimate ±1.96 × SE.

The covariate analysis focused on enoxaparin clearance, the most important parameter determining systemic exposure (quantified using AUC). The regression model was written as:

for continuous covariates, and as:

for dichotomous covariates (assigned a value of 0 or 1), with θs representing regression coefficients.

Pathophysiological covariates tested included: age, body size (weight, body surface area, body mass index, ideal body weight), sex, race, white blood cell count, haemoglobin level, haematocrit, creatinine level and creatinine clearance (CRCL).

The likelihood ratio test was used to discriminate between models, and the difference (δ) in objective functions was used to compare models. Covariates were included if individually significant at P < 0.05 (δ > 3.84), and retained if significant at P < 0.005 (δ > 7.88) in the presence of all other included covariates (multivariate analysis). Empirical Bayes estimates of individual clearance values were obtained at various steps in the analysis.

Formal validation is not universal and should depend on the intended use of the model [5, 6]. We used validation approaches that tested the appropriateness of covariate effects retained in the final model. Two different approaches were used:

1. ‘Validation through parameters’[6]. A learning set of patients was used for model building and a test set for model validation. This approach is based on both qualitative and quantitative evaluations of the learning-set population model prediction of CL in the test-set patients [7]. The learning set population model predictions of test set patients’ CL (based on covariate values of the test patients) were compared with individual CL estimates, based on observed concentration and Bayesian estimation after fitting a base model (without covariates) to the test set. The evaluation was based on the prediction error that was plotted against covariates to assess any residual dependence of CL on covariates in the test set (qualitative) and evaluated for bias (median prediction error) and precision (median absolute prediction error) in subpopulation of at-risk patients (e.g. patients with low CRCL).

2. The bootstrap approach [8]. This validation was performed on the refined final model based on the whole population (index plus validation sets). It consisted of repeatedly fitting the final model to 500 bootstrap replicates of the data. The percentage of runs in which the covariate effects were significant was calculated (95% CI of θ_cov for each run not including 0), as were the 95% CI of bootstrapped parameters estimates (taken as the 2.5th to 97.5th interpercentile range of the 500 replicates).

Prediction of haemorrhage risk (PK/PD analysis)

This assessment was limited to the incidence of major haemorrhage (primary endpoint of the study) and the incidence of all haemorrhages. The most severe event score was assigned to patients experiencing several events during treatment so that there was only one event per patient. No attempt was made to account for the possible repetition of bleeding events. In addition, the analysis did not take account of the role of treatment duration on the incidence of events.

A final set of individual clearance and AUC (over a dosage interval of 0–12 h at steady state) data was generated on each occasion by Bayesian estimation, using parameter estimates from the final population model as prior information. When multiple estimates of clearance and AUC were available for an individual patient, mean values were calculated across the study period and used as measures of exposure for this patient. Dose (in mg kg⁻¹) was also considered a measure of exposure. In addition, the following pathophysiological variables were considered potential covariates: sex and baseline weight, age, CRCL, platelet count, haematocrit and haemoglobin.

Univariate and multivariate logistic regression analyses were used to relate first the probability of all haemorrhage and second the probability of major haemorrhage to the covariates. Multivariate model development involved stepwise selection of covariates starting from the null model. Significance levels for variable entry or removal at each step were P < 0.10 and P < 0.05, respectively. Analyses were carried out using SAS software (SAS version 6.12; SAS Institute Inc., Cary, NC, USA). For each significant covariate, odds ratios were computed using the exponent of the estimated parameters of the multivariate logistic regression and their 95% Wald confidence intervals based on the asymptotic standard errors. The bootstrap approach was also used to evaluate the confidence intervals of those odds ratios because it does not require any asymptotic assumption on the distribution of parameters. The number of bootstrapped datasets was fixed to 5000, and the 2.5th and 97.5th percentiles on the set of estimated odds ratios were taken for the confidence intervals. Bootstrap was performed using the Splus function ‘bootstrap’ (Splus 4.5 User's Manual; Insightful Corporation, Seattle, WA, USA).

Simulation of haemorrhage risk using PK and PK/PD models

The two models were combined to predict clearance and haemorrhagic events. The simulation process was implemented in ACSL BioMed (ACSL BioMed version 4.0; Pharsight Corp., Mountain View, CA, USA). Patient characteristics were generated from empirical distribution and covariance observed in the TIMI-11A population (Table 1). In total, 100 simulations of 448 patients were performed. The variability in the outcome came from the PK model (random effects for interindividual variability and covariate effects for enoxaparin clearance) and from the simulation process (generation of haemorrhagic events). Results are reported as median and 5th to 95th interpercentile range of 100 simulations when each simulation only generated one variable (e.g. incidence of haemorrhage) or as median of medians and of 5th and 95th percentiles when each simulation generated a median and a 5th to 95th interpercentile range (e.g. clearance).

Table 1.

Patient characteristics.

					Quantiles
	n	Mean	SD	Median	5%	95%	Symbol
Demographics
Age (years)	448	62.5	11.6	63.0	43.0	81.0	AGE
Weight (kg)	448	84.6	18.2	82.8	58.0	117	WT
Height (leftm)	448	170	10.6	171	152	185	HT
Body surfalefte area (m2)	448	1.95	0.22	1.94	1.58	2.33	BSA
Body mass index	448	29.4	6.53	28.1	21.5	42.6	BMI
Lean body mass (kg)	448	58.7	11.4	59.9	42.0	76.7	LBM
Ideal body weight index	448	1.36	0.40	1.27	0.98	1.96	I_IBW
Sex (M/F)	281/167						SEX
Race: Caucasian/black/oriental/other	364/54/4/26						RACE
Laboratory measurements
White blood cells (mm3)	448	8.11	2.54	7.80	4.80	12.7	WBC
Haemoglobin (g dl−1)	448	13.9	1.53	13.9	11.4	16.3	HB
Haematocrit (%)	448	40.7	4.31	40.8	33.3	47.6	HCT
Platelets (× 1000)	448	232	62.3	223	146	345	PLA
Creatinine (mg dl−1)	448	1.02	0.26	1.00	0.70	1.60	CREA
Creatinine clearance (ml min−1)*	448	90.1	34.8	85.7	41.2	152	CRCL

^*Based on Cockcroft DW, Gault MH. Prediction of creatinine clearance from serum creatinine. Nephron 1976; 16: 31–41.

Results

Database

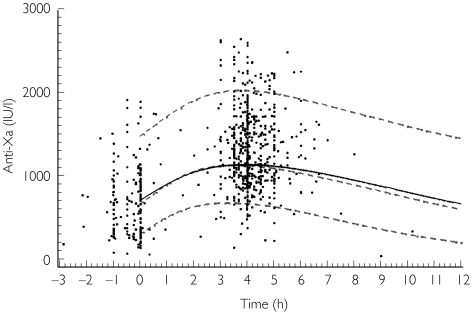
The database for PK analysis contained data from 448 of the 630 patients (71%) entered in the clinical study, who were evaluated over 615 visits and 788 anti-Xa activities (1.3 per visit). Patients were studied during one or two visits. Samples were drawn 1–7 days after the first enoxaparin administration. The anti-Xa activity-time profile of pooled data is illustrated in Figure 1. Although the TIMI-11A study was designed to have samples taken when ‘peak’ and ‘trough’ drug plasma concentrations occurred, samples were actually obtained over a wide range of times. Baseline characteristics of the TIMI-11A patient population are summarized in Table 1. The patient population was predominantly Caucasian (81%) and male (63%).

Figure 1.

Population pharmacokinetic model predictions and observed concentrations of enoxaparin (anti-Xa). ——, Population prediction (typical patient); - - - - -, individual predictions (5th, 50th (median), 95th percentiles of 1000 patients). 0 refers to the time of dosing.

A learning set consisting of two-thirds of the study population was randomly selected from the database (300 patients, 411 visits), to build the population model. The remaining 148 patients (204 visits) were used to validate the model (test set). The final parameter estimates were obtained by fitting the model to the whole dataset. Notably, the covariate model was not rebuilt using the whole dataset. The pathophysiological characteristics of patients in the two datasets were similar (data not shown).

Forty-eight patients (10.7%) experienced 38 minor (8.5%) and 10 major (2.2%) haemorrhagic events during the study.

PK model building

The basic population PK model was best represented by a one-compartment model with interindividual variability in drug clearance. Interindividual variability in absorption constant and distribution volume could not be estimated. Interoccasion variability in drug clearance was not a significant model variable in the basic model.

Several covariates, when introduced into the clearance regression model one by one, significantly improved the fit of the basic model. All measurements of patient size were highly significant factors (δ−9.8 to −98.4, P < 0.005), but weight was by far the most influential (δ = −98.4). The second most important covariate was CRCL (δ = −89.6). Age and sex were also significant (δ = −32.6 and −7.6, respectively). These patient covariates were used to define the following full regression model for clearance (where weight is denoted by WT):

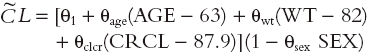All variables measuring patient body size were co-linear, so only one (weight) was retained for the model.

When the full model was tested against restricted models by omitting each covariate in turn, weight and CRCL were the only significant covariates. In this data set, the CV of interindividual variability decreased from 46.0% to 26.9%, which represents a 41% decrease in variance after adding the covariates.

Final PK model

The learning set model was found to predict CL well in test-set patients (1st validation step, not shown).

This model was run on all 448 patients (learning +validation sets) in order to refine the final parameter estimates. In this data set, interpatient variability in volume and interoccasion variability in clearance could be estimated. Parameter estimates of this model, as well as the results of the bootstrap model, are given in Table 2. There was a significant covariance between clearance and volume in this model (correlation: −0.89). Parameter estimates did not change when covariance was accounted for.

Table 2.

NONMEM estimates of population pharmacokinetic parameters (whole data set, 448 patients).

	Final model		Bootstrap (n = 500)
Parameter	Estimates	95% CI	Median	95% CI
Clearance (l h−1)	0.733	0.698–0.738	0.734	0.702–0.766
WT (θ5)	4.32 × 10−3	1.13 × 10−3–7.51 × 10−3	4.47 × 10−3	1.39 × 10−3–7.65 × 10−3
CRCL (θ6)	3.38 × 10−3	1.76 × 10−3–5.00 × 10−3	3.38 × 10−3	1.77 × 10−3–5.01 × 10−3
V (l)	5.24	4.20–6.28	5.19	2.55–6.59
Ka (h−1)	0.235	0.157–0.313	0.232	0.149–0.361
ωCL (%)	26.9	20.9–31.8	26.6	20.3–31.8
πCL (%)	21.7	14.9–26.8	21.7	12.3–27.2
ωV (%)	56.1	36.4–70.6	55.8	34.2–77.2
σ (%)	21.5	16.4–25.6	21.3	16.5–25.6

95% CI, Confidence interval calculated from parameter standard errors (final model) or as 2.5th and 97.5th percentiles of bootstrap estimates; WT, weight; CRCL, creatinine clearance; V, apparent volume of distribution; K_a, absorption rate; ω, coefficient of variation of interindividual variability;π, coefficient of variation of intraindividual variability;σ coefficient of variation of residual error.

The parameter and confidence intervals estimated after 500 bootstrap replications of the database were very close to the NONMEM estimates, particularly for CRCL. The confidence intervals for the estimates of random-effect variance were also very similar. Finally, in the 500 bootstrapped databases, CRCL and weight effects were significant (95% CI excluding 0) in 98.6% and 83% of the runs, respectively, confirming the stability of the covariate effects. According to the final model, a ‘typical’ patient with median weight and median CRCL would have an enoxaparin clearance of 0.733 l h⁻¹, a distribution volume of 5.24 l and a half-life of 5.0 h. Variation in weight within the 5th and 95th percentiles of the database (58–117 kg) would result in a change in clearance of between −14% and 21%. However, using a weight-adjusted dosage regimen, there is no change in exposure (AUC) according to weight (data not shown). Patients with CRCL of 50 ml min⁻¹ (the threshold for moderate renal impairment) or 30 ml min⁻¹ (the threshold for severe renal impairment) would have enoxaparin clearances decreased by 17% and 27%, respectively.

Covariates for risk of haemorrhage

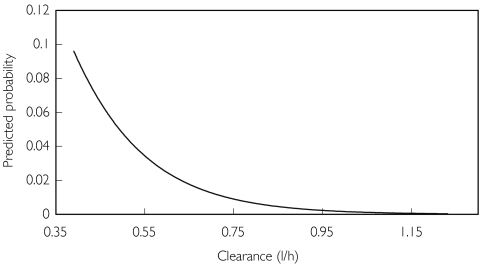
In univariate analyses, enoxaparin clearance, enoxaparin AUC (but not dose), CRCL and age were related to the risk of haemorrhage (P < 0.01). In multivariate regression analyses, enoxaparin clearance was the only significant predictor for both all (P = 0.0013) and major (P = 0.0004) haemorrhage. The effects of CRCL and age seen in the univariate analysis appear to be accounted for by the effect of enoxaparin clearance. The odds ratios for the logistic regression models are given in Table 3. The model-predicted probability of major haemorrhage as a function of enoxaparin clearance is shown in Figure 2. Bootstrapped parameters and confidence intervals were close to the original estimates. Enoxaparin clearance was a significant covariate in 91.0% and 96.9% of the 5000 bootstrap replications of the database for all and major haemorrhage, respectively.

Table 3.

Logistic regression models for the probability of haemorrhage.

		Model		Bootstrap (n = 5000)
Endpoint	Covariate	Odds ratio* (95% CI)	P	Odds ratio* (95% CI)
All haemorrhage†	CL	0.800 (0.702–0.917)	0.0013	0.803 (0.683–0.920)
Major haemorrhage‡	CL	0.505 (0.346–0.735)	0.0004	0.499 (0.275–0.707)

^*Odds ratio for a 0.1 unit change in clearance (i.e. 13% of mean CL), point estimate of the model and median of the 5000 bootstraps.

^†Incidence 10.7% (48/448 patients).

^‡Incidence 2.2% (10/448). CI, Confidence interval; CL, apparent clearance.

Figure 2.

Predicted probability of major haemorrhage as a function of enoxaparin clearance.

Prediction of haemorrhagic events

The population PK model and the logistic regression PK/PD models were used to predict change in the risk of haemorrhage for different values of CRCL and enoxaparin clearance (Table 4). The risk of haemorrhagic side-effects was strongly associated with enoxaparin clearance. Patients with a low enoxaparin clearance (the 5th percentile) had a twofold and 10-fold increased risk of all or major episodes, respectively.

Table 4.

Population pharmacokinetics and logistic regression model predictions.

		Increased odds compared with median
Creatinine clearance (ml min−1)	Clearance (l h−1)	All haemorrhage	Major haemorrhage*
85.7 (median)	0.733† (typical)	1.00	1.00
–	0.390 (5th percentile)	2.14	10.4
50 (upper limit moderate renal impairment)	0.605† (17% decrease)	1.33	2.39
30‡ (upper limit severe renal impairment)	0.537† (27% decrease)	1.54	3.81
42.5 (median of patients with creatinine clearance <50)§	0.581† (21% decrease)	1.40	2.83

^*Prediction for major haemorrhage should be taken with caution due to the small number of events in the database.

^†Population pharmacokinetic model predictions.

^‡Predictions may not be valid because of the small number of patients in the database (n = 4).

^§Median of n = 55 patients in the database.

Patients with impaired renal function are also at risk because of the associated decrease in enoxaparin clearance. In our dataset, 51 patients had moderate renal impairment (50 ml min⁻¹ > CRCL ≥ 30 ml min⁻¹), whereas only four patients had severe renal impairment (CRCL < 30 ml min⁻¹). The median CRCL in these 55 patients was 42.5 ml min⁻¹. According to the models, these patients would have a 21% decrease in enoxaparin clearance and 1.4- and 2.8-fold increased risks of all or major haemorrhagic episodes, respectively, compared with a typical patient with a CRCL of 88 ml min⁻¹. A decrease in enoxaparin clearance of 27%, as predicted in patients with a CRCL of 30 ml min⁻¹, would result in a 1.5- and 3.8-fold increase in the risk of all and major haemorrhagic episodes, respectively.

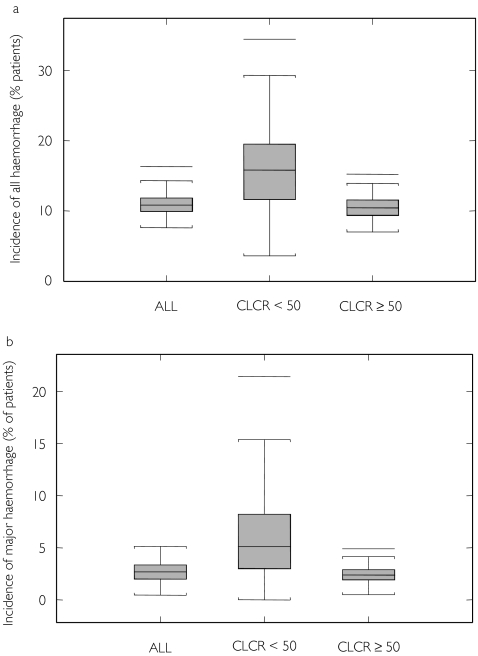
Finally, a simulation of the population PK and logistic regression models was performed to generate 100 replicates of the 448-patient database. The predicted incidence of haemorrhage is illustrated in Figure 3. The median incidence (5th−95th percentiles) of either all or major haemorrhage are close to the data from the original study, namely 11% (8.7–14%) and 2.7% (1.5–4.1%), respectively, further illustrating the accuracy of the models. The median (5th−95th percentile) CRCL and enoxaparin clearance in patients with moderate renal impairment (CRCL < 50 ml min⁻¹) were 40.6 ml min⁻¹ (26.2–49.1 ml min⁻¹) and 0.527 l h⁻¹ (0.272–1.09 l h⁻¹), respectively. The median (5th−95th percentile) simulated incidence of either all or major haemorrhage in these patients was 16% (5.1–27%) and 5.3% (2.3–13.5%), which is 1.5- and 2.2-fold more than other patients. These values compare well with the model-computed odds ratio (Table 4).

Figure 3.

Predicted incidence of haemorrhage in TIMI-11A population from 100 simulations in 448 patients. CRCL, Creatinine clearance.(a) All haemorrhage. (b) Major haemorrhage.

Discussion

The simulation of population PK and exposure-effect models provides a quantitative framework for the assessment of the clinical relevance of PK changes in patient subgroups [9].

The population PK analysis demonstrated that body weight and renal function (CRCL) were significantly related to enoxaparin (anti-Xa) clearance. This finding is consistent with previous results obtained with enoxaparin and other low-molecular-weight heparins in healthy volunteers [10]. Because the dose of enoxaparin was adjusted for weight, the effect of the latter on clearance did not translate into a change in drug exposure. Independent of the effect of weight, the mean decrease in enoxaparin clearance was 21% in patients with a CRCL of <50 ml min⁻¹. The validity of these covariate effects was assessed by two model validation approaches. Interpatient variability in enoxaparin clearance was moderate (CV = 46.0% in the basic model and 26.9% in the final model), as was the intrapatient (day-to-day) variability (CV = 21.7% in the final model).

In the current database, 10.7% of patients experienced at least one haemorrhagic episode during the study, with 38 minor (8.5%) and 10 major (2.2%) episodes. The PK/PD analysis showed that enoxaparin clearance is a major prognostic factor for the risk of haemorrhage (both all and major haemorrhagic episodes). These results confirm and extend previous observations based on anti-Xa activities in this population and those in a previous study where enoxaparin was given at a lower dose for the prevention of deep-vein thrombosis after hip replacement [1, 11].

The simulation study based on the population PK and logistic regression PK/PD models had demonstrable accuracy in predicting the incidence of both all and major haemorrhages. According to these models, in patients with a CRCL < 50 ml min⁻¹ (patients with moderate renal impairment), there was a mean decrease of 21% in enoxaparin clearance and an increase of 1.3- and 2.4-fold in the risk of haemorrhagic events for all and major haemorrhage, respectively. The importance of this increase must be weighed against the low overall risk of bleeding and the positive benefit : risk ratio of enoxaparin treatment in patients with UA/NSTEMI. The large ESSENCE and TIMI-11B trials with enoxaparin, in which the overall benefit : risk ratio of the drug was demonstrated, included patients with mild or moderate renal impairment, but excluded those with severe renal impairment. A further analysis of obese and renally impaired patients included in those two large clinical trials revealed that patients with severe renal impairment had increased rates of haemorrhage, whereas obese patients had a reduced number of both major haemorrhagic and ischaemic events [12]. A further PK study in renally impaired patients found that the AUC of enoxaparin was 20% and 21% higher in patients with mild and moderate renal impairment, respectively, but 65% higher in patients with severe impairment, compared with normal healthy volunteers [13]. The findings in patients with moderate renal impairment are consistent with the present results. In patients with severe renal impairment, the extent of increase in drug exposure suggests that it is advisable to reduce the dose of enoxaparin. Regarding obesity, another PK study found that similar exposure was obtained with enoxaparin 1.5 mg kg⁻¹ daily in obese and non-obese subjects. Our data also show no effect of obesity (other than that due to the increased weight) on enoxaparin pharmacokinetics. It appears that no further dose-adjustment is necessary when weight-adjusted dosing is used in obese patients [14].

In conclusion, we performed a population PK/PD analysis of the TIMI-11A database and constructed a model to estimate enoxaparin PK parameters and covariates, and to determine which factors predicted haemorrhagic incidence best. Enoxaparin clearance was found to be the only independent predictor of haemorrhagic events. Patients with severe renal impairment appeared to be at increased risk of haemorrhage because of decreased enoxaparin clearance. Since the TIMI-11A study, more detailed reports have recommended that enoxaparin dosage should be adjusted in patients with severe renal impairment.