Assessment of the relative in vivo potency of the hydroxylated metabolite of darifenacin in its ability to decrease salivary flow using pooled population pharmacokinetic–pharmacodynamic data

Abstract

Aims

To describe the population pharmacokinetic–pharmacodynamic relationship between darifenacin (UK-88,525) and its hydroxylated metabolite (UK-148,993), and the reduction in salivary flow (SF, a M₃-mediated response). This enabled an estimation of the in vivo potency of the metabolite to decrease SF relative to that of the parent drug.

Methods

A total of 262 individuals were pooled from 11 Phase 1 studies and one Phase 2 study. A comparison was made between a series of pharmacodynamic models (direct-effect, indirect-effect, link and binding model) using NONMEM.

Results

The binding model yielded the best description of the decrease in SF by fully accounting for the time course of the pharmacodynamic effect. An internal validation exercise demonstrated the robustness of this model. Covariate analysis identified a circadian rhythm in SF. This model, with confidence intervals (CI) determined by likelihood profiling, indicated that the relative potency of the metabolite to darifenacin to reduce SF was 11.1% (95% CI 3.8, 19.6). This implied that the metabolite was ninefold less potent than darifenacin in vivo. Accounting for the unbound fraction of darifenacin (2%) and its metabolite (13%), the in vivo protein binding-corrected relative potency was estimated to be 2.1%, indicating that the metabolite was 50-fold less potent than the parent drug. The model supported the assumption that no other metabolites contributing to the impairment of the SF were formed during first-pass, and that the development of sensitization or tolerance was not evident over time. The validation process indicated that the i.v.–oral crossover study was necessary for the estimation of the relative potency.

Conclusions

Population modelling of darifenacin and its hydroxylated metabolite yielded individual pharmacokinetic predictions that could be used to assess the in vivo potency of the metabolite to decrease SF relative to that of the parent drug. The metabolite had a negligible effect on SF.

Introduction

Darifenacin (UK-88,525: (S)-2-{1-[2-(2,3,-dihydrobenzofuran-5yl)ethyl]-3-pyrrolidinyl}-2,2-diphenylacetamide) is a novel antimuscarinic agent, which demonstrated clinical benefit in the treatment of over-active bladder (OAB) [1]. This disorder is common but under-reported in the general population [2] with an estimated prevalence of 17% in patients aged 40 years or more [3]. The muscarinic M₃ receptor is primarily involved in the pathophysiology of OAB [4, 5]. The functional smooth muscle responses induced by cholinergic nerve stimulation of the bladder and gastrointestinal tract are mediated via M₃ receptor activation. A selective antagonist of this receptor has the potential to minimize safety concerns and provide benefits over existing treatments of OAB [5].

Darifenacin is a selective muscarinic M₃ receptor antagonist [6–9], having a 30- to 100-fold higher affinity for M₃ than for M₁ and M₂ receptors [6]. In addition, a clinical study demonstrated a superior risk–benefit ratio for darifenacin over oxybutynin, the former having comparable urodynamic efficacy but with less effect on salivary flow (SF) [10]. Although darifenacin displays a 10-fold less effect on the salivary M₃ receptor compared with gastrointestinal and bladder M₃ receptors, it is anticipated that the drug will still affect SF [5]. The subjective experience of dry mouth is not directly related to the objective measurement of drug-induced SF. The latter is mediated peripherally by M₃-receptors in the salivary glands, whereas dry mouth is mediated by M₁/M₃-receptors in the CNS [1, 11].

The hydroxylated metabolite of darifenacin (UK-148,993) is formed by cytochrome P450-3A4 (CYP3A4) and P450-2D6 (CYP2D6) [12, 13]. Darifenacin is highly bound to plasma proteins (98%) with corresponding value for the hydroxylated metabolite of 87%. During the development of darifenacin several different formulations have been tested [e.g. intravenous (i.v), solution, immediate and extended release]. The population pharmacokinetics of darifenacin and its metabolite are best described by a model that incorporates saturable first-pass metabolism, CYP2D6 genotype and formulation-dependent bioavailability [13].

Since the hydroxylated metabolite of darifenacin may contribute to its pharmacological activity, the aim of this study was to determine the relative in vivo potency of darifenacin and its metabolite with respect to their effects on SF in a large population of subjects.

Methods

Study design

All studies were conducted with ethics committee approval. Informed consent was obtained from all subjects. Patient characteristics are presented in Table 1. Pharmacokinetic and pharmacodynamic data were collected in 262 individuals (214 healthy volunteers and 48 patients) in 11 different Phase 1 studies and one Phase 2 study. A summary of the studies is presented in Table 2.

Table 1.

Characteristics of and selected covariates for the 262 healthy volunteers and patients from 11 Phase 1 studies and one Phase 2 study analysed.

Continuous characteristic	Median	Range	Discrete characteristic	Frequency	Description
Age (years)	29	18–85	Gender	237/25	Males/females
Weight* (kg)	74	50–115	Subject	214/48	Volunteer/patient
Height* (m)	1.76	1.49–1.95	Race	249/9/4	White/Black/other
			Alcohol use	63/177/21/1	0/1–15/16–30/> 30 units/week
			Smoking*	165/89	Nonsmoker/smoker
			Food*†	204/31	Fasted/fed
			Observation time	7169/771	08.00–23.59/00.00–07.59

^*Not assessed in all individuals.

^†Time varying after start in some studies.

Table 2.

Description of the 11 Phase 1 studies and one Phase 2 study analysed.

Study description	Design	Subjects	*Samples	Doses/formulations
Single oral dose escalation	XO	15 ♂HV	32	0, 1–20 mg SOL
SOL-IR, young-elderly	XO	20 ♂/7 ♀HV	10	10 mg IR/SOL
I.v. dose escalation	XO	8 ♂HV	71	0, 0.6, 2, 6 mg i.v.
Multiple dose IR-CR	XO	13 ♂HV	65	7.5 mg IR TID, 20 mg CRS,CRM,CRF OD
Dose escalation IR-CR	XO	26 ♂HV	65	7.5, 15, 30 mg CR OD 2.5, 5, 10 mg IR TID
One tablet CR vs. 2 tablets CR	XO	24 ♂HV	30	45 mg, 15 + 30 mg CR
Relative F IR and CR	XO	24 ♂HV	59	4 mg i.v., 10 mg IR TID, 30 mg CR OD
Ketoconazole interaction	PG	16 ♂HV	19	30 mg CR OD 0, 400 mg ketoconazole
Erythromycin interaction	PG	29 ♂HV	18	30 mg CR OD 0, 400 mg erythromycin
Multiple dose SOL	PG	16 ♂HV	15	0, 10 mg SOL TID
Multiple dose IR	XO	16 ♂HV	36	2.5, 5, 10 mg IR TID
IR-CR in patients	XO	30 ♂/18 ♀PTS	8	2.5 mg IR TID, 15, 30 mg CR OD

^*Median number of samples per subject. XO, Cross-over; HV, healthy volunteer; PTS, patient; PG, parallel group; SOL, solution; IR, immediate release; CR, (continuous) extended release; CRS, CR; CRM, medium CR; CRF, fast CR; OD, once daily; TID, 3×/day.

Plasma samples for the measurement of darifenacin and metabolite were kept on ice after collection and centrifuged within 60 min at 4 °C and at 1500 g for 10 min. Samples were stored at −20 °C pending analysis. Plasma concentrations of darifenacin and its hydroxylated metabolite were determined using atmospheric pressure ionization-mass spectrometry, except in one study which used a comparable method with high-performance liquid chromatography-UV [14]. Consistency in bioanalysis between studies was assured throughout. Limits of quantification for darifenacin and the metabolite were 0.0586 and 0.113 nm, respectively. Accuracy ranged from 0.6 to 4.6% and precision from 3.6 to 18.8% over a concentration range of 0.0586–4.68 nm darifenacin.

Stimulated SF was determined using a method described by Brion et al.[15]. Saliva was collected for 1 min whilst sucking on a preweighed sweet. After 1 min the saliva and the remains of the sweet were collected and the difference in weight was recorded as the amount of saliva produced; 7937 observations of SF were obtained, resulting in a median of 30 observations (range 4–71) for each individual. The studies were selected based on the availability of SF data and their diversity with respect to important covariate information (e.g. dose-range, formulations, single/multiple dose, CYP2D6 genotype and CYP3A4 inhibitors). This diversity increased the within- and between-subject differences in the concentrations of darifenacin and its metabolite. These differences facilitated the estimation of the relative potency of drug and metabolite. One Phase 2 study was added to investigate the similarities between healthy volunteers and patients. In two Phase 1 studies no metabolite concentrations were assessed. For these individuals the population estimates of the metabolite pharmacokinetic parameters were used in the pharmacodynamic analysis.

Data analysis

Initial datasets from each study were constructed with identical formats, and merged prior to the analysis. Pharmacokinetic–pharmacodynamic models were fitted to the data using the software NONMEM (Non-linear Mixed Effects Modelling, version V, double precision) (GloboMax LLC, Hanover, MD, USA) with first-order conditional estimation with interaction (FOCE I) [16, 17]. NONMEM was operated in a UNIX environment (Linux Red-Hat 7.1) using a Fortran compiler (GCC version 2.91.66).

Pharmacokinetic model

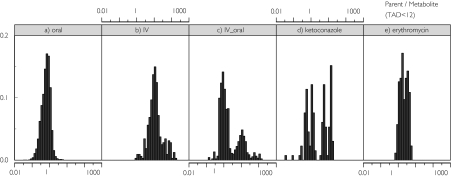
Empirical Bayesian estimated individual pharmacokinetic parameters obtained in a separate analysis yielded adequate individual predictions for the pharmacokinetic profiles of darifenacin and its metabolite [13]. Their population pharmacokinetics were both described by a two-compartment disposition model with first-order absorption. Presystemic formation of the metabolite was simulated in the model by simultaneous oral darifenacin and equimolar metabolite dosing (scaled by the relative bioavailability of the metabolite) using a hypothetical metabolite absorption compartment. The fraction metabolized and the relative bioavailability of the metabolite (Fm) were confounded. Therefore, the fraction metabolized was fixed to one. Fm depended on a typical value for this parameter (TVFm) and the individual empirical Bayes estimate of F for darifenacin [Fm = TVFm × (1 − F)]. The typical value for the metabolite clearance was assumed to decrease if ketoconazole or erythromycin was present. The population pharmacokinetic model for darifenacin included the covariates characterizing the influence of formulation (70–110% higher bioavailability for extended release compared with immediate release following equivalent daily doses), dose (dose nonlinearity 1.1–1.35-fold), CYP2D6 genotype (heterozygote extensive metabolizers and poor metabolizers have 40% and 90%, respectively, higher exposure to the drug than homozygote extensive metabolizers). The presence of ketoconazole or erythromycin increases darifenacin bioavailability to approximately 100%, and ketoconazole additionally decreases clearance by 67.5%. Darifenacin clearance is 31% lower in females and 10% lower at night. Treatment with ketoconazole and erythromycin results in a decrease of 62 and 29% in exposure to the metabolite, respectively. These factors resulted in a wide range of darifenacin : metabolite concentration ratios. The frequency histograms of these ratios from the studies incorporated into this analysis are presented in Figure 1.

Figure 1.

Histograms of frequencies (left to right) of darifenacin : metabolite concentration ratios in (a) oral dosing studies, (b) an i.v. dosing study, (c) an oral–i.v. crossover study, (d) a ketoconazole interaction study, and (e) an erythromycin interaction study.

Pharmacodynamic model

A population pharmacokinetic–pharmacodynamic model describing SF during darifenacin treatment was developed. The model enabled estimation of the relative potency of the hydroxylated metabolite of darifenacin compared with parent drug with respect to their ability to decrease SF. Four structural pharmacodynamic models were tested, namely a direct and indirect-effect model, a link model and a binding model. All models were characterized by a delay in effect, except for the direct-effect model. Each model assumed a different possible cause of this delay. The link model described the distribution to the effect site, the binding model the kinetics of binding to the receptor, and the indirect-effect model the effect on endogenous compounds after receptor binding. By comparing these models, the possible rate-limiting step in the concentration–effect relationship could be identified. The shape of response differed between these models, because of the different assumptions made about the delay. With increasing dose, the time to reach maximum effect/inhibition (PD-T_max) is constant with the link model. In contrast, PD-T_max is achieved later with increasing dose when using an indirect-effect model but earlier with a binding model. Sequential modelling prevented any effect of the model selection on the pharmacokinetics. The decrease in SF was described by an inhibitory E_max model relative to baseline (and placebo) taking into account the contribution of both darifenacin and its metabolite according to:

$${\text{C}}_{\text{e}}={\text{C}}_{\text{d}}+{\text{C}}_{\text{m}}\times \text{Rel}.\text{Pot}.$$

C_e represents the effect-site concentration and was calculated using both darifenacin (C_d) and metabolite (C_m) concentrations. Rel. Pot. represents the estimated relative in vivo potency of the metabolite. It was assumed that ketoconazole and erythromycin did not affect SF. A delay in effect (k) was described for the link model (k_e0), the indirect-effect (k_out) and the binding model (k_off). The latter model described the link between the pharmacokinetics and the pharmacodynamics with the change in the fraction of activated (R*) and inactivated (R) receptors over time according to:

$$\begin{array}{c}\text{d}(\text{R}*)/\text{d}\left(\text{t}\right)=-{\text{k}}_{\text{on}}\times {\text{C}}_{\text{e}}\times \text{R}*+{\text{k}}_{\text{off}}\times \text{R}\\ \text{d}\left(\text{R}\right)/\text{d}\left(\text{t}\right)={\text{k}}_{\text{on}}\times {\text{C}}_{\text{e}}\times \text{R}*-{\text{k}}_{\text{off}}\times \text{R}\end{array}$$

where k_on and k_off represent the rate constants of onset and offset of the activation of the receptor, respectively. K_D = k_off/k_on (nm). The effect on the SF is described by:

$$\text{Effect}=\text{Base}\times (1-{\text{E}}_{\text{m}}\times \text{R)}$$

where Base is the baseline SF (ml min⁻¹) and E_max the maximum decrease in SF (ml min⁻¹). No separate placebo term was included in the model. Data from placebo-treated subjects contributed to the baseline estimation.

Interindividual variability

The mixed-effect model estimates the typical value of parameters, the interindividual variability components and the residual variability magnitude, by combining data from all subjects and identifying the within- and between-individual structure of, and information in, the observed data. The parameter estimates of all individuals, including those who do not receive the same doses, contribute to the population parameter estimates. Exponential models were used to account for interindividual variability, such that the parameter value in an individual (P_i) is a function of the parameter value (Base and EC₅₀ or K_D) in the typical individual (P_pop) and an individual deviation represented by η_i. The η_is in the population are symmetrically distributed, zero-mean random variables with a variance that is estimated as part of the model estimation: P_i = P_pop × exp(η_i).

Residual error model

Since data were obtained from different studies in patients, healthy volunteers and involving different formulations, it was anticipated that the residual error may not be constant across all individuals [18]. The individual contribution to the residual error was accounted for by including an interindividual variability term (η_i) in the residual error model:

$$\text{Y}=\text{IPRED}+\left[\right(\text{IPRED}\times {\varepsilon }_1+{\varepsilon }_2)\times exp({\eta }_{\text{i}}\left)\right]$$

where Y represents the observation (i.e. SF), IPRED the individual prediction and e₁ and e₂ are symmetrically distributed, zero-mean random variables with variance terms that are estimated as part of the population model fitting process. The magnitude of the variability in e₁ can be viewed as the ‘proportional’ component and that of e₂ as the ‘additive’ component of the residual error model. Estimation of the interindividual variability in the residual error required FOCE I.

Model diagnostics

Basic goodness-of-fit plots including population (PRED) and individual predictions (IPRED) vs. observed concentrations (DV), individual weighted residuals (IWRES) vs. individual predictions and the distribution of the weighted residuals (WRES) over time were used for diagnostic purposes. The objective function value (OFV) is proportional to −2 times the log-likelihood, and the difference in OFV between two nested models (the more complex model can be reduced to the simpler one) is approximately χ²-distributed. A difference >3.84 in OFV (one degree of freedom) is significant at the 5% level if nonlinearity and heteroscedasticity in the model is accounted for [19]. Corresponding values (changes in the OFV) for P = 0.01 and P = 0.001 were 6.63 and 10.83, respectively. For non-nested models, the OFV cannot be used for formal testing. However, the differences mentioned above between models of the same number of parameters were considered to represent an improvement in the description of the data.

Covariate analysis

To assess whether additional variables influenced the pharmacodynamic response, individual empirical Bayes estimates of the parameters were generated from the ‘basic’ model (without covariate interactions), and plots of the difference between these and the population estimates vs. covariates were constructed to visualize potential relationships. Generalized additive modelling (GAM) [20], implemented in Xpose 3.0 [21], was used to identify possible influencing variables. To account for time-varying covariates, data from one individual given the drug on different occasions were treated as originating from separate individuals. Covariates identified in the GAM as being important were included in the mixed-effects model applying a stepwise procedure. Covariates were first assessed univariately in the model, and ranked according to the drop in objective function value (ΔOFV) associated with their inclusion. Variables were then stepwise tested in the model, in descending order. Only variables producing a decrease in OFV of more than 3.84 on inclusion were incorporated in the model. When no more covariates could be included based on this criterion, a backwards deletion was carried out. A stricter criterion was then applied, retaining only physiologically plausible covariates associated with an increase in the OFV of more than 10.83 on their exclusion. To be retained in the final model, the 95% confidence interval (CI) of the proportional covariate effect (based on the standard error of the parameter estimate given by NONMEM) should not include a parameter value of zero.

Internal validation

The internal validity of the population pharmacokinetic–pharmacodynamic models was assessed by graphical analysis (goodness-of-fit plots) and a jack-knife procedure (repeated analysis with removal of individual studies per run). The (nonsymmetrical) 95% CI of the estimate of the relative potency was determined using likelihood profiling with linear interpolation.

Simulations

In Phase 3 studies, doses of 7.5, 15 and 30 mg of an extended-release formulation of darifenacin were investigated further. To demonstrate the utility of the pharmacokinetic–pharmacodynamic model, SF–time profiles were simulated following multiple administration of this formulation and these doses. For simulation of the pharmacodynamics the unbound ‘active moiety’ was used, which was the sum of darifenacin and hydroxylated metabolite concentrations corrected for their free fractions and in vivo relative potency.

Results

Model development

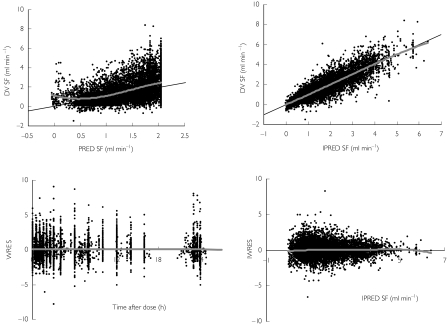
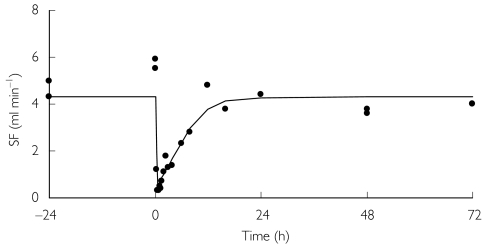
A comparison between the adequacy of the structural pharmacodynamic models is shown in Table 3. Modelling of SF required a term to account for the delay in onset of action. Baseline SF was estimated to be the same for all models. None of the models accommodated different rate constants for the onset of action between darifenacin and its metabolites or an estimation of sigmoidicity. The link, indirect-response and binding models were in close agreement in their estimate of E_max. The binding model was superior to the others as indicated by it giving the lowest OFV. The relative potency using the binding model was estimated at 11.1%. Estimation of interindividual variability was supported for baseline SF and K_D with a proportional interindividual error. The binding model was used for the validation and likelihood profiling of relative potency. The goodness-of-fit plots are presented in Figure 2. Although wide variability is apparent, no trends or biases were discerned. The IWRES vs. time after dose and IPREDs were symmetrically distributed. The upper truncation in the plot of the model PREDs vs. the observations (OBS) is a consequence of the highest model prediction being unable to exceed the population estimate for the baseline (without interindividual variability). The horizontal bands in the plot of IPRED vs. OBS represent placebo-treated individuals (e.g. IPRED =5.5). A plot of SF over time from a typical individual after an i.v. infusion of 4 mg darifenacin is shown in Figure 3. For most individuals multiple baseline measurements were made prior to dosing. After the last dose, a return to baseline was observed. Thus, Base could be estimated accurately (relative SE 4%), because it was derived from information both prior to and after dosing and from placebo-treated individuals. Accommodating interindividual variability in the residual error model resulted in a decrease in OFV of 497 points. In addition to resulting in an improvement in individual fits, this led to a marked decrease in the proportional residual variability of 4.4%.

Table 3.

Comparison between different structural pharmacodynamic models of the inhibitory effect on salivary flow of darifenacin and its hydroxylated metabolite.

Model type	Direct effect	Link	Indirect response	Binding	Binding (final model)
OFV	−305	−857	−738	−920	−981
Base (ml min−1)	1.98	1.99	1.97	2.00	2.05 ± 0.08
IIV (base) (%)	53	52	52	52	52
NTO–base					−0.102 ± 0.017
Emax (ml min−1)	0.909	1.13	1.17	1.09	1.08 ± 0.027
EC50 or KD* (nm)	19.3	33.3	36.6	28.8*	0.557 ± 0.066*
IIV (EC50) (%)	89	82	83	83	82
k (h−1)	NA	1.88	3.89	0.983	0.974 ± 0.060
T1/2k (min)	NA	22	11	42	41
Rel. potency (%)	2.86	15.1	12.8	11.1	2.09 ± 1.36†
Residual error
Additive (ml min−1)	0.332	0.254	0.256	0.248	0.257
Proportional (%)	25.9	29.5	29.7	29.6	28.9
IIV (residual) (%)	25	27	27	27	27

OFV, Objective function value; base, baseline salivary flow (SF); IIV, interindividual variability; NTO, night-time observations–effect on Base; E_max, maximum decrease in SF; EC₅₀, concentration of active moiety associated with 50% of E_max; K_D, ratio of rate constant from active to inactive receptors (k_off) over rate constant of inactive to active receptors (k_on); k, effect–delay rate constant (link-model, k_e0; indirect-effect, k_out; binding-model, k_off); T_1/2k, half-life k; Rel. potency, potency of the metabolite for decreasing SF relative to darifenacin; NA, not applicable.

^*For binding model only.

^†Corrected for free fraction.

Figure 2.

Top panels: Population predictions (PRED) and individual predictions (IPRED) vs. observed (DV) salivary flow (SF) measurements. Bottom panel: The individual weighted residuals (IWRES) vs. IPRED and the distribution of residuals (WRES) over time (grey line: spline).

Figure 3.

Salivary flow (SF) in a representative individual after 4 mg i.v. darifenacin. The data were used by NONMEM to make individual predictions (represented by the line).

Covariate identification

The GAM analysis indicated that food (during drug administration) and gender were correlated with baseline SF. These covariates and time of observation [day time/night time (NTO)] were formally tested in a forward inclusion step. Observation time and gender resulted in ΔOFV of −28 and −61, respectively. Food was not a significant influence, as although ΔOFV was −6.6, a successful minimization could not be obtained and the estimated food effect on baseline was less than 0.2%. During the backwards elimination step from the full model, deletion of gender did not result in an increased OFV. Therefore, only time of observation was found to be a significant covariate for baseline SF (10% lower at night), indicating a circadian rhythm in baseline. The 95% CI of this covariate ranged from 6.0% to 14.4%. A placebo effect on baseline was not found.

Internal validation

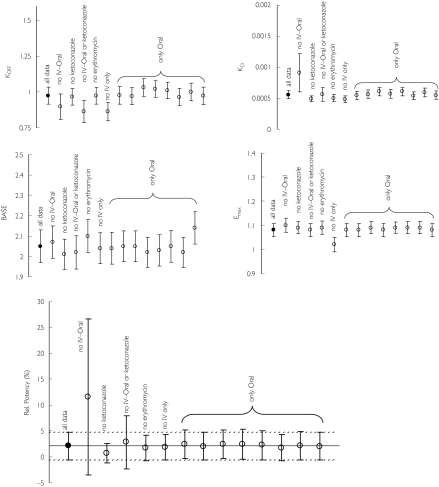
No bias or imprecision were observed in the jack-knife procedure (Figure 4), as all parameter estimates and their 95% CI (1.96 times the SE provided by NONMEM) of the reduced datasets overlapped with the full dataset. The parameter estimates outside the 95% CI indicated decreased model robustness when the data did not contain i.v.–oral or i.v. only data.

Figure 4.

Validation of the final pharmacodynamic model (corrected for the free fractions) using a cross-validation (study-by-study omission). •, Full dataset; ○, reduced dataset (mean + 95% CI) ○.

Likelihood profiling of relative potency

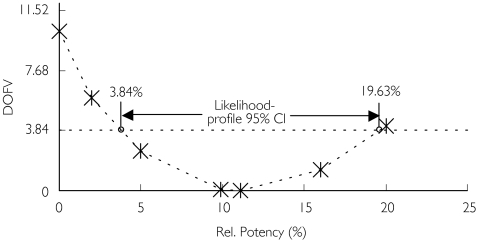
The likelihood profile of the relative potency is depicted in Figure 5. The relative potency of the metabolite for SF was 11.1% or ninefold less potent than that of darifenacin. The 95% CI of the relative potency of the metabolite for SF was 3.8–19.6%. Only minor skewness to the right was observed for the likelihood profile (average 95% CI 11.5%). The interval did not include zero and therefore the metabolite was concluded to have some activity, although this was unlikely (P < 0.05) to exceed 19.6% of that of parent drug.

Figure 5.

The likelihood profile of the relative potency of the metabolite (bound + unbound) with respect to its ability to decrease salivary flow. DOFV, Change in objective function value

Correction for free fraction

The protein binding-corrected relative potency was calculated based on the free fraction of darifenacin (f_u,d = 2%) and its metabolite (f_u,m = 13%) according to:

$${\text{C}}_{\text{e},\text{fu}}={\text{f}}_{\text{u},\text{d}}\times {\text{C}}_{\text{d}}+{\text{f}}_{\text{u},\text{m}}\times {\text{C}}_{\text{m}}\times \text{Rel}\text{. Pot}\text{.}$$

The final model was reparameterized using the free fraction of darifenacin and hydroxylated metabolite. C_e,fu represents the composite unbound concentrations of the ‘active moiety’ of darifenacin. The estimates of the final reparameterized model are presented in Table 3. No major changes (ΔOFV =0) were observed with the basic model except for K_D and relative potency. K_D decreased from 28.8 nm to 0.557 nm and relative potency decreased from 11.1% to 2.1% on the basis of unbound concentrations. This indicated that metabolite was 50-fold less potent than darifenacin.

Simulations

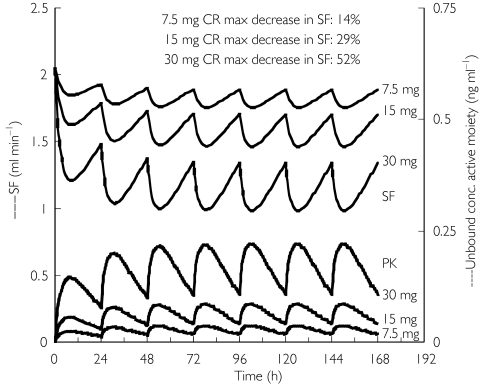
The simulated unbound concentration of the active moiety–time profiles and SF–time profiles following 7.5, 15 and 30 mg extended-release formulation of darifenacin at steady-state dosing are presented in Figure 6. Steady state was reached both in the pharmacokinetics and pharmacodynamics during the first week of therapy. The maximum decrease in SF on day 6 was 14, 29 and 52% following administration of 7.5, 15 and 30 mg darifenacin extended release, respectively.

Figure 6.

Simulation of the effect on salivary flow after dosing with 7.5, 15 and 30 mg darifenacin extended release for six days. The lower set of profiles represents the pharmacokinetic data. The upper set of profiles (black lines) represents the salivary flow

Discussion

The population pharmacokinetic–pharmacodynamic relationship between darifenacin (UK-88,525) and its metabolite (UK-148,993) and the decrease in SF were best described using a binding model to characterize the delayed (but rapid onset) of effect. This enabled accurate estimation of the in vivo potency of the metabolite relative to that of the parent drug from multiple studies. In general, metabolites are not administered in clinical studies. Any in vivo estimations of potency are normally obtained in preclinical studies where parent and metabolite are administered separately [22]. The potency estimate is then applied to all subsequent assessments of the clinical activity of the metabolite. If separate administration is not feasible, another approach is to consider a wide range of parent drug : metabolite concentration ratios [23]. A pharmacokinetic–pharmacodynamic modelling approach is especially suited for combining a wide range of ratios, because it accounts for differences in parent and metabolite pharmacokinetics [24, 25].

The binding model is used less commonly than the link- or indirect-effect model for clinical pharmacokinetic–pharmacodynamic modelling. However, the results from the binding model support the experimental findings that darifenacin acts as a M₃ receptor antagonist. A binding model has been used successfully to describe the slow offset of receptor binding by omeprazole [26]. This indicated that the binding kinetics at the receptor is the rate-limiting step for the observed delay in the concentration–effect relationship. Binding models are characterized by an earlier peaking in effect with increasing dose. With the direct effect model, time to peak effect is unchanged, and with the indirect-effect model, the time to peak effect increases with increasing dose. Another feature of the binding and other models tested is that E_max is greater than 1. The inhibitory E_max-model (relative to baseline) could in theory result in non-positive prediction for SF. However, no negative SF values were observed in the present work, as the relative proportion of inactivated receptors was less than 0.91, and thus E_max × R was less than 1 {link and indirect-effect model: E_max × [C_e/(C_e + EC₅₀)] was less than 1}. No sigmoidicity was observed. Although caution should be used when extrapolation is performed outside the observed range of concentrations of the active moiety of darifenacin treatment with respect to negative SF predictions, the observed concentrations were over a wide range. Thus, an E_max value of greater than 1 is not likely to hamper the general application of this model for other clinical studies.

Inclusion of interindividual variability in the residual error resulted in a large drop in the objective function value (− 497). In addition, the residual error decreased by 4.4%. This indicated that the residual error was not constant across all individuals. Indeed, data were obtained from different studies in both patients and healthy volunteers [18]. This correction for the information content of a subject will minimize the influence of the (few) individuals with poor fits on the overall fit of the pharmacodynamic profiles.

No placebo effect was supported by the modelling. Covariate analysis indicated that night-time observations (00.00–08.00 h) of SF were associated with a 10% lower baseline value, consistent with a circadian rhythm. The decrease is not likely to be clinically relevant. Diurnal variation in SF was also described by Ionescu et al.[27], who reported minimum values for SF in the morning (07.30–08.00 h) and maximum ones in the afternoon (17.30–18.00 h) in both diabetic patients and a nondiabetic control group.

The likelihood profiling of the relative potency estimate demonstrated minor skewness in the 95% CI. The latter based on the SE from NONMEM (− 6.3, 28.5%) was inflated compared with that obtained through likelihood profiling (3.8, 19.6%). The NONMEM-based 95% CI encompassed zero, whereas likelihood profiling demonstrated that a relative potency of 0% is associated with an increase in the objective function of 10.2 (P = 0.0014).

Correction for the free fractions of darifenacin and its metabolite resulted in the relative in vivo potency decreasing from 11.1 to 2.1%. This 5.3-fold change could be explained by the 6.5-fold difference in free fractions of darifenacin (2%) and its metabolite (13%).

No major bias or imprecision were observed in the jack-knife procedure. However, omission of the oral–i.v. crossover study yielded a higher and less accurate estimate of the relative potency [11.5% with 67% relative standard error (r.s.e.)]. In contrast, omission of the ketoconazole interaction study yielded a lower and less accurate estimate of the relative potency (0.68% with 140% r.s.e.). Omitting both these studies also resulted in a biased and less accurate estimate (2.78% with 94% r.s.e.). There was a large within-individual range in drug : metabolite ratios in these studies. Without these information-rich data, relative potency assessments appeared to be less robust. In contrast, omission of the pharmacokinetic interaction study with erythromycin did not decrease the accuracy of the relative potency estimates. This could be explained by less inhibition of metabolism by erythromycin compared with ketoconazole, resulting in less within-individual variability in the drug–metabolite ratios, which is necessary for the accurate estimation of relative potency of this high-extraction drug. Thus, if no metabolite i.v.-dosing studies have been performed, an oral–i.v. study may be the best source for estimating in vivo relative potency of high-extraction drugs.

The model adequately characterized multiple-/single-dose, oral/i.v. and inhibitor study data. These types of data encompass a wide range of within-individual parent : metabolite(s) ratios. Adequate description of oral/i.v. and inhibitor studies by the model is consistent with the assumption that no other metabolites contributing to the inhibition of SF were formed during the first-pass metabolism of darifenacin. No development of sensitization or tolerance was evident over time, because no differences between single- and multiple-dose data were detected.

The simulated SF–time profiles after dosing with extended-release formulations of darifenacin at steady state demonstrated that the largest difference in maximum decrease in SF was observed between the 15- and 30-mg formulations.

In conclusion, population modelling of darifenacin and its metabolite yielded individual pharmacokinetic predictions that could be used to assess the in vivo potency of the metabolite with respect to its ability to decrease SF relative to that of the parent drug. The metabolite had a negligible effect on SF.