Models for time-varying covariates in population pharmacokinetic-pharmacodynamic analysis

Abstract

Aim

If appropriately accounted for in a pharmacokinetic (PK)–pharmacodynamic (PD) model, time-varying covariates can provide additional information to that obtained from time-constant covariates. The aim was to present and apply two models applicable to time-varying covariates that capture such additional information.

Methods

The first model estimates different covariate–parameter relationships for within- and between-individual variation in covariate values, by splitting the standard covariate model into a baseline covariate (BCOV) effect and a difference from baseline covariate (DCOV) effect. The second model allows the magnitude of the covariate effect to vary between individuals, by inclusion of interindividual variability in the covariate effect. The models were applied to four previously analysed data sets.

Results

The models were applied to 10 covariate–parameter relationships and for three of these the first extended model resulted in a significant improvement of the fit. Even when this model did not improve the fit significantly, it provided useful information because the standard covariate model, which assumes within- and between-patient covariate relationships of the same magnitude, was only supported by the data in four cases. The inclusion of BCOV was not supported in two cases and DCOV was unnecessary in three cases. In one case, significantly different, nonzero, relationships were found for DCOV and BCOV. The second extended model was found to be significant for four of the 10 covariate–parameter relationships.

Conclusions

On the basis of the examples presented, traditionally made simplifications of covariate–parameter relationships are often inadequate. Extensions to the covariate–parameter relationships that include time-varying covariates have been developed, and their appropriateness and benefits have been described.

Introduction

Time-varying covariates are frequently observed in clinical studies. Changes in covariates over time may be particularly important to consider in long-term studies, but may also occur over the short-term. Populations that are particularly likely to show short-term (acute) time-variation are neonates [1–3], patients undergoing organ transplant [4, 5], and other seriously ill (intensive care unit) patients [6], who may have rapidly changing organ functions/health status. Covariates such as postnatal age, weight and renal function will reflect these changes. In some settings, the covariate (and thereby the variation) may be controlled by the study investigator (e.g. concomitant medication in an interaction study). However, the present study focuses on covariates that are not controllable, that is in observational studies. A systematically changing covariate may reflect improvement or worsening of disease, possibly related to the disposition of the drug, whereas random changes in a covariate may reflect natural variability over time, or may be due solely to assay error and may not be indicative of changing pharmacokinetic (PK) or pharmacodynamic (PD) parameters. Thus, information may be linked to the nature of covariate changes. If properly accounted for in the PK-PD model, time-varying covariates may provide more valuable information than time-constant covariates.

Establishing relevant covariate relationships for a drug is one of the main aims of population nonlinear mixed-effects PK-PD modelling. It seeks to explain parameter variability and to facilitate dose adjustment decisions. Normally, modellers do not differentiate between time-varying and time-constant covariates in PK-PD models, i.e. variation within an individual is treated the same way as interindividual variation in a covariate. However, there are instances when it might be of value to consider inter- and intrasubject variation separately, as acknowledged by Taright et al. [7]. An example of this is in a disease progression model for bone mineral density (BMD) in osteoporosis [8], where bodyweight influenced BMD at baseline, whereas changes in bodyweight (reflecting mainly changes in body fat) were not related to BMD.

There is a possibility that the magnitude of the effect of the change in a covariate differs between individuals, for example where one unit change in the covariate causes a substantial change in the parameter in one individual but has no effect on the parameter in another individual. As a consequence, individual dose adjustments based on these covariates may result in larger or smaller changes in the target variable than anticipated from models that do not accommodate such variability. Interindividual variability in covariate relationships can be appropriately accommodated in covariate models, and subsequently used for prediction.

The aim of this study was to show how extra information about covariate relationships can be gained by the use of models accounting for differences in the within- and between-subject covariate model.

Methods

Two extended models applicable to time-varying covariates are described and applied. The first model enables estimation of different relationships for variation within and between subjects in a covariate. The second model allows estimation of interindividual variability in the covariate effect. These models were applied to four previously analysed data sets. The final models from these analyses contained time-varying covariates modelled using the ‘standard’ covariate model (see below).

Modelling was performed with NONMEM [9] version VI (beta), using the first-order conditional estimation method with interaction (FOCE INTER).

Models

Basic nonlinear mixed-effects model

Models included up to three levels of random effects, namely interindividual parameter variability (IIV), interoccasion parameter variability (IOV) and residual variability for which standard notation is used [10]. Exponential models were used for parameter variability and a proportional and/or additive model for the residual variability.

Covariate models

The standard covariate model (Equation 1) assumes that the population parameter, P_pop, is the same for a given covariate value, i.e. P_pop is as different between two individuals with covariate values a and b, as it is within a single individual who at different times has covariate values a and b.

$${\text{P}}_{\text{pop}}{=\Theta }_{\text{p}}*\left[{\text{1}+\Theta }_{\text{COV}}*\left({\text{COV}-\text{COV}}_{\text{median}}\right)\right]$$

where θ_p represents the typical value of P in the population, COV is the covariate value of the individual (at each time-point) and θ_COV is the fractional change in the parameter for each unit change in the covariate from the (baseline or overall) median value of the covariate (COV_median). The centring of the relationship is not necessary, but is often adopted for convenience and relevance.

In the first extended model, different between and within individual covariate effects are estimated, as shown in equation 2.

$${\text{P}}_{\text{pop}}={\Theta }_{\text{p}}*\left[1+{\Theta }_{\text{BCOV}}*\left({\text{BCOV}-\text{BCOV}}_{\text{median}}\right)+{\Theta }_{\text{DCOV}}*\text{DCOV}\right]$$

This extended model represents the full model, of which the standard model is a reduced version. Two additional reduced models will be presented below. In this model, BCOV is the baseline value of the covariate and DCOV is the individual difference (at each time point) in the covariate from baseline (COV–BCOV). θ_BCOV describes the effect of between-individual variation, and corresponds to the fractional change in P_pop with each unit difference in BCOV from the median baseline covariate (BCOV_median). θ_DCOV describes the effect of covariate variation within an individual, and is the fractional change in P_pop with individual changes in COV. If θ_BCOV and θ_DCOV are similar, there is no indication of distinctive inter- and intra-individual covariate models. If θ_BCOV and θ_DCOV are different, the choice of final model will be based on several aspects, as discussed below. Three different extended models were always tried; first the full model including both BCOV and DCOV, and then two reduced models where in the first BCOV, and in the second DCOV, was fixed to zero. Model selection was based on the difference in the objective function value (ΔOFV) between the fits of these models, and the values of the parameters with their associated SEs. The reduced models provide information on whether the data support relationships with BCOV or DCOV or both. Information in the observed data related to the parameter ‘P’, as well as the variability in the values of BCOV and DCOV, determine the precision (SEs) of θ_BCOV and θ_DCOV. When only the standard model is applied, it is not possible to determine the relative contribution from the between- and within-subject variability to the parameter estimate and its precision.

In the second extended model, which can be used independently or in combination with the first, interindividual variability in the covariate effect is estimated, as shown in equation 3.

$${\text{P}}_{\text{i}}={\Theta }_{\text{P}}*\left[1+{\Theta }_{\text{COV}}*{exp}^{\eta \text{COV},\text{Pi}}\left({\text{COV}-\text{COV}}_{\text{median}}\right)\right]*{\text{exp}}^{\eta \text{Pi}}$$

where η^COV,Pi is a (zero mean, variance ω²) random variable, which allows the magnitude of the covariate effect to differ between individuals. A change of one unit in the covariate may accordingly cause substantial alterations in the parameter in some individuals, whereas the effect may be moderate or absent in others. To ensure that P_i remains positive when this model is implemented, the parameters may need to be constrained, e.g. by logit-transformation. In the above model, COV could be replaced by DCOV, and in all cases where DCOV was found to be significant, IIV in DCOV was also tested.

Covariate models were judged to be superior using likelihood ratio tests based on the minimum objective function value (OFV) [9, 11, 12]. The standard errors of the parameter estimates, and visual assessment of goodness of fit graphics, were also used to guide the choice of model.

Example data sets

Gentamicin data

The pharmacokinetic data set originated from 210 cancer patients treated with intravenous doses of gentamicin. Patients were followed for one to five courses (median one), over a maximum of 25 months. On average, data were available for the first 2 days, and one to nine samples per patient and occasion were drawn, resulting in 574 samples in total. The pharmacokinetic analysis has been reported by Rosario et al.[13].

Clearance (CL) was related to creatinine-clearance (CLC), and the central volume of distribution (V₁) to body-surface area (BSA) and albumin concentration (ALB). The following equations describe the model:

$$\text{CL}\left(\text{L}/\text{h}\right)={\Theta }_{\text{CL}}*\left[1+{\Theta }_{\text{CLC}}*\left(\text{CLC}-81\right)\right]$$

$${\text{V}}_{\text{1}}\left(L\right)={\Theta }_{\text{V}}*\text{BSA}*\left[{1-\Theta }_{\text{log}\left(\text{ALB}\right)}*\left(\text{log}\left(\text{ALB}\right)-log\left(34\right)\right)\right]$$

The data set contained no missing covariate records. The covariate data, based on observed values in each individual, are summarized in Table 1.

Table 1. Time-varying covariates gentamicin data set, based on observed values of the covariate within an individual.

Covariate	Symbol	Mean	Median	Range	SD	No. of covariate measurements	No. of patients	No. of associated concentration measurements
Creatinine clearance (ml min−1)	CLC	81.9	76.9	14.8–183	32.2	576	210	574
Baseline	BCLC	77.4	71.7	14.8–180	31.2	210		350
Delta	DCLC	0.4	1.4	−65.8–79.4	18.6	366	132	224
Albumin (g/litre)	ALB	33.5	34.0	14.0–53.0	5.9	439	210	574
Baseline	BALB	33.9	35.0	14.0–47.0	6.1	210		373
Delta	DALB	−2.2	−2.0	−16.0–13.0	5.4	229	97	201
Body surface area (m2)	BSA	1.7	1.7	1.3–2.3	0.2	248	210	574
Baseline	BBSA	1.8	1.7	1.3–2.3	0.2	210		481
Delta	DBSA	0.0	0.0	−0.2–0.1	0.1	38	29	93

Pefloxacin data

The second pharmacokinetic data set was obtained from 74 critically ill patients treated with intravenous 1 h infusions of pefloxacin. The data were gathered over 1–28 days (median 6 days) during one to four treatment periods (separated in time by 2.5–14 days). The analysis has been reported previously [10]. Only a covariate model for CL was investigated. This included CLC, bilirubin (BIL), age (AGE), centre (CEN), systolic blood pressure (SBP) and weight (WT) up to median WT according to the following equation:

$$\begin{array}{c}\text{CL} (\text{L}/\text{h})={\Theta }_{\text{CL}}*\text{exp}[{\Theta }_{\text{CLC}}*(\text{CLC}-100)-{\Theta }_{\text{BIL}}\\ *(\text{BIL}-25)-{\Theta }_{\text{AGE}}*(\text{AGE}-45)+{\Theta }_{\text{CEN}}*\text{CEN}\\ -{\Theta }_{\text{SBP}}*(\text{SBP}-115)+{\Theta }_{\text{WT}}*(\text{WT}-\text{65})]\end{array}$$

All covariates except AGE and CEN varied over time, and no covariate records were missing. The covariate data, based on observed values in each individual, are summarized in Table 2.

Table 2. Time-varying covariates pefloxacin data set, based on observed values of the covariate within an individual.

Covariate	Symbol	Mean	Median	Range	SD	No. of covariate measurements	No. of patients	No. of associated concentration measurements
Creatinine clearance (ml min−1)	CLC	113.2	103.5	0.43–312.0	72.6	114	74	337
Baseline	BCLC	109.7	104.5	0.43–312.0	70.1	74		220
Delta	DCLC	16.5	12.6	−127.5–203.3	62.6	40	37	117
Bilirubin (µmol/litre)	BIL	34.7	21.0	4.0–150.0	35.2	110	74	337
Baseline	BBIL	35.5	21.0	6.0–150.0	35.5	74		229
Delta	DBIL	−3.1	−1.5	−69.0–40.0	23.4	36	34	108
Weight (kg)	WT	69.0	67.0	42.7–125.0	13.6	103	74	337
Baseline	BWT	68.8	67.0	42.7–125.0	12.8	74		247
Delta	DWT	−2.4	−3.0	−16.0–7.6	4.8	29	28	90

Voriconazole data

The third data set came from two paediatric studies of the antifungal agent voriconazole, described in [14]. Children, aged 2–11 years, were treated with intravenous infusions on one to five occasions. In total, 355 voriconazole plasma concentrations were measured (on average 10 per individual) over 0.2–7.6 days. The analysis was performed using log-transformed data with an additive residual error model where the residual error was allowed to vary between individuals [15].

All disposition parameters were normalized to bodyweight and the influence of CYP2C19 genotype on CL was included. In addition to these covariates, the final model included relationships between CL and the two time-varying (log-transformed) covariates alanine amino transferase (ALT) and alkaline phosphatase (ALKP):

$$\text{CL}\left(\text{L}/\text{h}\right){=\Theta }_{\text{CL}}*\text{WT}*\left[{1-\Theta }_{\text{log}\left(\text{ALT}\right)}*\left(\text{log}\left(\text{ALT}\right)-\text{log}\left(25\right)\right)\right]*\left[{1-\Theta }_{\text{log}\left(\text{ALKP}\right)}*\left(\text{log}\left(\text{ALKP}\right)-\text{log}\left(136\right)\right)\right]*\left[\text{PM}*\left({1-\Theta }_{\text{PM}}\right)\right]$$

where PM is an indicator variable that has the value 1 for individuals genotyped as poor or heterozygous extensive CYP2C19 metabolizers and 0 for homozygous extensive metabolizers. One individual had missing covariate records for ALKP, and these were given the median baseline value. The covariate data, based on observed values within individuals, are summarized in Table 3.

Table 3. Time-varying covariates voriconazole data set, based on observed values of the covariate within an individual.

Covariate	Symbol	Mean	Median	Range	SD	No. of covariate measurements	No. of patients	No. of associated concentration measurements
Alanine amino transferase (IU/litre)	ALT	49.3	25	7–535	75.0	77	35	355
Baseline	BALT	34.9	25	7–159	31.9	35		235
Delta	DALT	27.1	2.5	−136–437	87.2	42	25	120
Alkaline phosphatase (IU/litre)	ALKP	161.4	130	47–761	107.9	76	34	355
Baseline	BALKP	148.7	136	47–309	62.3	34		240
Delta	DALKP	−1.5	−13	−101–453	88.3	42	23	115

Paclitaxel pharmacodynamics – myelosuppression

The fourth data set consisted of neutrophil counts monitored in 45 cancer patients receiving paclitaxel. The drug was administered as a 3-h infusion every third week. Data were collected over 196 courses (one to 18 courses per patient, median three), giving a total of 530 observations. The neutrophil-time data were described by a semiphysiological model [16] and the parameters estimated were the baseline cell count (Circ₀), the mean transit time (MTT) of the cells through transit compartments, a feedback parameter (γ) affecting cell proliferation, and the linear drug (paclitaxel) effect (Slope). No covariate–parameter relationships were included in the reference model.

Covariate relationships were tested for Circ₀, MTT and Slope, using the time-varying covariate BIL. Eleven BIL records (from 10 individuals, none at baseline) were missing. These were given the previous observed value when possible, or the median value. The covariate data, based on observed values within individuals, are summarized in Table 4.

Table 4. Time-varying covariates paclitaxel myelosuppression data, based on observed values of the covariate within an individual.

Covariate	Symbol	Mean	Median	Range	SD	No. of covariate measurements	No. of patients	No. of associated PD observations
Bilirubin (µmol/litre)	BIL	8.8	6	2–41	6.3	139	45	530
Baseline	BBIL	9.4	6	4–37	7.5	45		242
Delta	DBIL	−0.7	−1	−24–36	7.5	94	34	288

Results

Gentamicin

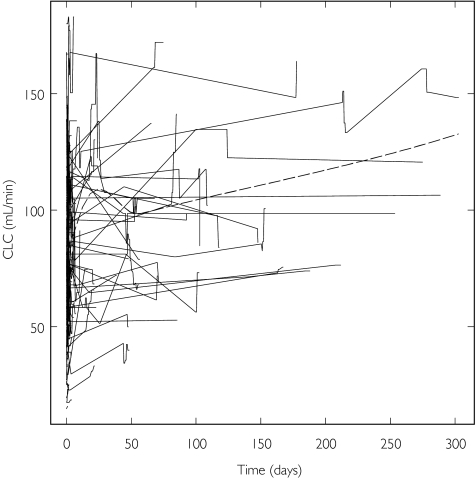
All three covariates in the model for gentamicin varied over time. CLC and ALB were the most variable with individual values both rising and falling (Table 1). A slight trend of increasing CLC (Figure 1) and decreasing ALB (not shown) over time can be seen. BSA was the least variable over time (not shown).

Figure 1.

Creatinine clearance vs. time for gentamicin. Data points from the same individual are joined, and the broken line is a smoothing of the data

When the extended model with separate within- and between-individual relationships for CLC was applied, an improvement in fit was seen (8 unit decrease in OFV). The slope for BCLC was 0.0098 (relative standard error, RSE 5.4%) and that for DCLC 0.0069 (RSE 22%). The higher parameter value and the smaller RSE indicate that BCLC is a relatively better predictor of CL than DCLC. This is further strengthened by a larger increase in OFV on omission of BCLC (+159) compared to DCLC (+40). The adoption of the corresponding models for log(ALB) on V₁ did not improve the fit to the data significantly. When BBSA and DBSA were used in the model for V₁, there was little difference in fit (ΔOFV −0.4). The large imprecision in DBSA (RSE 110%) compared to BBSA (RSE 2.5%) suggests that BBSA is as good a predictor of V₁ as BSA.

No major improvement in fit was obtained by inclusion of IIV in the CLC, BSA or the ALB relationships, and all three parameters were imprecisely estimated. The final model includes BCLC, DCLC and BBSA, and the parameter estimates are shown in Table 5.

Table 5. Reference and final model parameters (RSE) for gentamicin.

	Reference model	Final model
OFV	144.4	135.9
ΔOFV		−8.5
θCL	4.26 (2.3%)	4.1 (2.3%)
θCLC-CL	0.0089 (6.3%)	–
θBCLC-CL	–	0.0098 (5.5%)
θDCLC-CL	–	0.0068 (23%)
θV1/BSA	8.64 (2.7%)	–
θV1/BBSA	–	8.63 (2.6%)
θALBaV1	−0.41 (26%)	−0.41 (26%)
θQ	1.24 (19%)	1.21 (19%)
θV2	8.12 (16%)	8.12 (16%)
ωCL	0.21 (16%)b	0.22 (15%)b
ωQ	0.57 (69%)b	0.61 (56%)b
σprop	0.17 (15%)b	0.17 (16%)b
σadd	0.24 (35%)b	0.22 (40%)b

^aModel for albumin: [ALB/34]^{θ ALB}.

^bThe RSE is relative to the corresponding variance term (ω² or σ²).

Pefloxacin

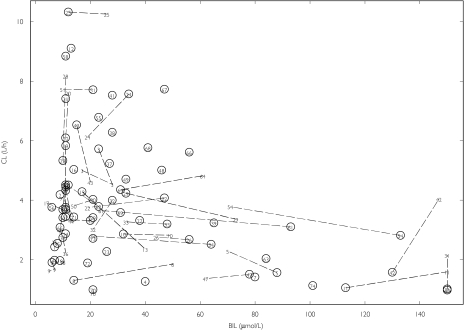
The results focus on the relationships between CL and the covariates CLC, BIL and WT. All three showed considerable variation between individuals in their baseline values, and there were large changes within individuals for CLC and BIL (Table 2). There were no indications of differing models between and within individuals for CLC based on the decrease in OFV (ΔOFV −1.8), however BCLC (RSE 18%) was estimated more precisely than DCLC (RSE 40%), and there was a larger increase in OFV when BCLC was omitted from the model (+36 compared to +14 for omission of DCLC). An improvement in fit was seen when interindividual variability in the CLC relationship was added (ΔOFV −9), and ω_CLC was estimated to be 0.70. For the relationship with BIL, the model improved when different within and between individual models were applied (ΔOFV −6.8), but the estimate of DBIL was imprecise and its removal had little effect on the OFV. Thus, BBIL (θ_BBIL−0.0064, RSE 12%) was a better predictor of CL than BIL (ΔOFV −5.9). It is evident that an increase in BIL within an individual does not always coincide with a decrease in CL (Figure 2). When BWT and DWT were estimated the model fit improved (ΔOFV −5.5), but when DWT was fixed to zero, the increase in OFV was only 0.5 units, indicating that BWT is a better predictor of CL than WT. IIV in the WT and BIL relationships was not supported.

Figure 2.

Pefloxacin occasion specific posthoc CL values (from the model without covariates) vs. BIL. Values are labelled by ID numbers and data points from the same individual are joined. The baseline values are circled

When the effects of BBIL, BWT and ω_CLC were combined in the model, the SBP–CL relationship and the IOV in V were no longer supported. The final model parameter estimates are shown in Table 6.

Table 6. Reference and final model parameters (RSE) for pefloxacin.

	Reference model	Final model
OFV	933.2	913.2
ΔOFV		−20.0
θCL	3.37 (8.2%)	3.74 (7.6%)
θCLC-CL	0.0030 (21%)	0.0029 (17%)
θBIL-CL	−0.0056 (18%)	–
θBBIL-CL	–	−0.0068 (11%)
θAGE-CL	−0.0077 (32%)	−0.0086 (21%)
θCEN-CL	0.21 (38%)	0.19 (41%)
θSBP-CL	0.0017 (67%)	–
θWT-CL	0.028 (29%)	–
θBWT-CL	–	0.039 (24%)
θV	61 (3.3%)	–
θWT-V	0.016 (13%)	0.014 (13%)
θCLC-V	0.0015 (24%)	0.0015 (23%)
θBIL-V	−0.0029 (29%)	−0.0025 (28%)
πCL	0.34 (16%)a	0.32 (16%)a
πV	0.11 (54%)a	–
ωCLC	–	0.61 (36%)a
σ	0.16 (19%)a	0.16 (17%)a

^aThe RSE is relative to the corresponding variance term (ω², π² or σ²).

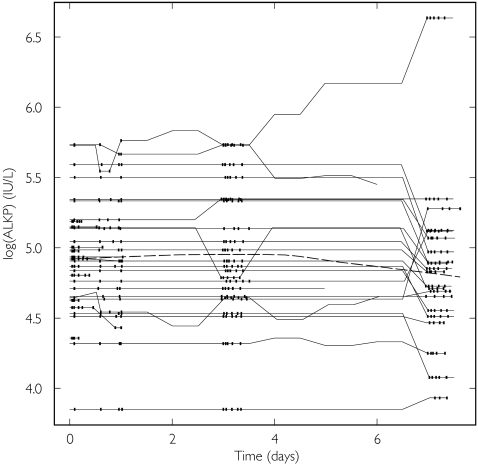
Voriconazole

Large variability was seen at baseline for both ALT and ALKP, which in some individuals changed substantially over time with a trend for decreasing ALKP (Figure 3, Table 3). The implementation of the model with different within and between subject covariate effects for log(ALT) and log(ALKP) did not result in any major improvement in fit. The slopes for log(BALT) and log(DALT) were similar, thus there was no support for the model that allowed differences between and within subjects for log(ALT). The corresponding slopes for log(BALKP) and log(DALKP) were −0.16 (RSE 192%) and 0.56 (RSE 26%), respectively. The removal of log(BALKP) from the model resulted in a small (0.3 unit) increase in OFV, thus the data only supported a relationship between DALKP and CL.

Figure 3.

Log(ALKP) vs. time for voriconazole. Data points from the same individual are joined. The broken line is a smooth of the data, and the time-points where the PK observations were made are indicated by vertical tick marks

The inclusion of interindividual variability in the coefficient of the log(ALT) and log(ALKP), relationships reduced the OFV by 18.4 units. This decrease was entirely due to an estimated variability in the relationship for log(ALT).

The final model included log(DALKP), ω_log(ALT) and ω_log(DALKP), and the parameter estimates are shown in Table 7.

Table 7. Reference and final model parameters (RSE) for voriconazole.

	Reference model	Final model
OFV	141.9	112.1
ΔOFV		−29.8
θCL	0.40 (14%)	0.36 (11%)
θpm-CL	0.46 (32%)	0.46 (31%)
θlog(ALKP)-CL	0.35 (3.4%)	−
θlog(DALKP)-CL	–	0.59 (64%)
θlog(ALT)-CL	0.28 (20%)	0.75a (26%)
θV1	0.80 (20%)	0.78 (23%)
θQ	0.64 (15%)	0.62 (25%)
θV2	1.7 (7.5%)	1.62 (11%)
σ	0.46 (20%)	0.42 (20%)
ωCL	0.67 (10%)	0.61 (11%)
ωlog(ALT)	–	0.30b (61%)
ωlog(DALKP)	–	1.94 (21%)
ωσ	0.77 (32%)	0.77 (33%)

^aConstrained 0.66*θ_log(ALT)-0.33 = 0.23.

^bApproximate SD from logit transformation.

Paclitaxel myelosuppression

BIL demonstrated variation over time, although no overall trends were observed (Table 4). BIL was initially found to influence Circ₀, MTT and Slope. One individual, who showed a large and constant decrease in BIL over time, was found to profoundly influence the BIL relationships [17], and was therefore omitted from subsequent analyses. Without this individual the relationships with MTT and Slope, but not Circ₀, remained significant. An improvement in model fit was seen (ΔOFV −10.5) when separate inter- and intra-individual models were applied to the Slope–BIL relationship; however, the parameter estimates and OFV changes indicated that only DBIL was of importance for predicting the Slope. There was no support for a different within and between individual relationship between BIL and MTT. IIV in the covariate relationship for MTT–BIL did not improve the model fit, however the inclusion of IIV on Slope–DBIL decreased the OFV by 11.8 units.

The final model included the influences of DBIL on Slope, BIL on MTT and ω_Slope-DBIL. The final parameter estimates, obtained by including all individuals, are shown in Table 8.

Table 8. Reference and final model parameters (RSE) for paclitaxel myelosuppression.

	Reference model	Final model
OFV	1062.4	1004.7
ΔOFV		−57.7
θCirc0	5.2 (3.6%)	5.47 (4.4%)
θMTT	127 (2.1%)	131 (3.6%)
θBIL-MTT	–	–0.012 (13%)
θγ	0.23 (2.8%)	0.22 (8.9%)
θSlope	44.2 (4.5%)	48.6 (8%)
θDBIL-Slope	–	–0.034 (25%)
ωCirc0	0.35 (11%)a	0.36 (33%)a
ωMTT	0.18 (30%)a	0.17 (32%)a
ωSlope	0.43 (32%)a	0.38 (27%)a
ωDBIL-slope	–	0.89 (41%)a
σ	0.40 (9.3%)	0.38 (9.9%)

^aThe RSE is relative to the corresponding variance term (ω²).

Discussion

Two new models for time-varying covariates have been investigated, and these (either one or both) provided an improvement in fit for all of the data sets examined. In addition, these models can provide information leading to a better understanding of the covariate relationships. This discussion will focus on the general implications of these models, and will also consider other issues related to time-varying covariates (Table 9).

Table 9. Special considerations for time-varying covariates.

No.	Model/issue	Comment	Reference
1	Separate inter- and intrasubject models		This work Taright et al.[7]
2	Interindividual variability in covariate coefficient		This work
3	Cause or effect	Issue if systematically varying covariate, mechanistic knowledge important.	Bertino et al. [20] Jaresko et al. [21] Fattinger et al. [22]
4	Missing values	Linear interpolation.	Beal & Sheiner [9]
	Modelling of covariate.	Higgins et al. [18] Karlsson et al. [15]
5	Covariate measurement error	Modelling of covariate.	Karlsson et al. [15] Higgins et al. [18]
6	Time-dissociation of covariate influence	Model time-dissociation.	Fattinger et al. [22]
		If covariate change precedes change inparameter – time-delay.
		If parameter change precedes covariate change – reversal of covariate-parameter relationship.
7	Covariate description	Figures of individual levels over time, overlaid smoothes.	This work
		Summaries of BCOV & DCOV (observed values for individuals).	Higgins et al. [18]
8	Diagnostics	Occasion specific parameters vs. covariate.	This work (limited)
		WRES vs. covariate.

In the examples used, the standard covariate models, where only COV (not BCOV/DCOV) were identified, served as reference models for the implementation of the models for time-varying covariates. There might, however, be cases where BCOV (or DCOV) is significant while COV is not, and therefore it might be of value to screen for BCOV (or DCOV) even if COV is not demonstrated to be important. An example of this was the voriconazole data where baseline albumin (but not all albumin) values correlated with CL in the forward model building step (P < 0.05), although it failed to be incorporated into the final model due to the stricter criterion (P < 0.001) in the backward elimination (data not shown).

The standard model implies that the parameter associated with a covariate will vary with every change in the covariate, and that this relationship is the same for all individuals. However, this may not be true in all cases, as shown when the extended covariate models are tested. Possible outcomes of these models are shown in Table 10. An example of a case that leads to improved and more practical therapy is when BCOV is a better predictor than COV (situation 2, Table 10). If the time-variation in the covariate is from a source not related to the change in the parameter (e.g. changes in body fat are not related to BMD [8]), there would be no additional gain in measuring the covariate more than at baseline. There are examples where additional information is needed for therapeutic decisions, e.g. case 5 (Table 10), where the estimate for the relationship between BCOV and a parameter is neither significantly different from zero, nor the corresponding estimate for DCOV. Consequently, decisions on how to treat relationships with BCOV may have to rely on external information.

Table 10. The different consequences of applying models for time-varying covariates, and potential implications for therapy.

Situation	Potential implications for therapy	Examplea
Significant improvementb
1 θBCOV≈0cθDCOV ≠ 0	DCOV superior to COV and BCOV for therapeutic decisions.	Paclitaxel PD, Slope∼BIL
2 θBCOV ≠ 0θDCOV≈0c	BCOV superior to COV and DCOV for therapeutic decisions.	Pefloxacin, CL∼BIL
3 θBCOV ≠ 0θDCOV ≠ 0θBCOV ≠ θDCOV	Both BCOV and DCOV useful, but changes within a patient may require larger (|θBCOV | < |θDCOV|) or smaller (|θBCOV | > |θDCOV|) dosage alterations than between patients.	Gentamicin, CL∼CLC
4 ωCOV, P >0	At baseline, assume no IIV in covariate relationship. Benefit from individualization is related to both ηCOV, P and ηP.At later occasions, DCOV determines therapy, however, changes may have a greater risk of over-/under-dosing therefore more frequent monitoring may be needed.	Pefloxacin, CL∼CLCVoriconazole,CL∼log(ALT)CL∼log(DALKP) Paclitaxel PD, Slope∼DBIL
No significant improvementb
5 θBCOV≈0c	No difference between basing therapy decisions on COV or DCOV, but BCOV is of no value.	Voriconazole, CL∼log(ALKP)
6 θDCOV≈0c	No difference between basing therapy decisions on COV or BCOV, but DCOV is of no value.	Gentamicin, V1∼BSAPefloxacin, CL∼WT
7 θBCOV≈θDCOV	No indication that therapeutic decisions based on BCOV and DCOV should be different.	Gentamicin, V1∼ALBVoriconazole, CL∼ALTPaclitaxel PD, MTT∼BIL
8 ωCOV, P≈0c	Decisions can be based on the assumption that the covariate relationship is the same in all patients.	All examples apart from those in Situation 4

^aExamples from this work, not implying that the models are clinically significant for these drugs.

^bBased on the difference in OFV from the standard covariate model, P < 0.01.

^cThe confidence interval based on the standard error of the parameter estimate encompasses zero.

Large interindividual variability in a covariate-parameter relationship implies that the covariate is not as predictive of the parameter as the standard covariate model suggests. The relationship may be strong in some individuals, such that a small change in the covariate will produce a large change in the parameter, whereas in others the parameter will be unaffected by changes in the covariate. This interindividual variability could possibly be explained by other covariates.

With a time-varying covariate, there is a possibility that the interpretation of its effect is confounded. The covariate may influence drug disposition, but there is also a chance that the drug itself causes the change in the covariate, e.g. a nephrotoxic (hepatotoxic) drug producing a decrease in creatinine clearance (an increase in liver enzyme concentrations) as well as a lowered CL. This may be the case for gentamicin, which is potentially nephrotoxic. Consequently, it may be difficult to distinguish between the cause and the effect, or if the influence is bi-directional. In observational studies some mechanistic understanding is valuable, and probably essential, to postulate or exclude a bi-directional effect.

The variation over time for a covariate can be systematic or random, and can occur in either direction. To summarize the covariate data and capture this variation is more complex than considering a time-constant covariate. Plots of the individuals’ covariates vs. time can be used to visualize the variation [18]. To show to what extent the PK (PD) observations are influenced by the changing covariate, the time-points at which the observations were made can be indicated in the plot (as shown for voriconazole, Figure 3). Numeric summaries of the baseline and difference from baseline covariates, based on observed values within individuals and with the numbers of PK (PD) observations associated with the respective covariates specified, could be informative.

There is need for good, descriptive diagnostics specific to time-varying covariates. To observe whether a change in a covariate is important, a plot of weighted residuals vs. the covariate (identified by subject number) could be useful. If interoccasion variability is part of the model, a plot of individual, occasion-specific, parameter values vs. covariate (using data from all occasions) can also be informative, as is shown for pefloxacin.

Ideally, a covariate should be recorded continuously to capture its full time-course properly. This is never done, however, due to practical and economic limitations, therefore covariate records are routinely incomplete. The easiest way to assign a missing covariate value for an individual is to carry forward (backward) the last (next) measured value. A smoother transition between covariate values could be acquired by using linear interpolation [9]. Another, more sophisticated, way to assign missing values could be to create a model for the covariate [15, 18, 19] and predict the missing value. Any method to reconstruct the full covariate-time profile will rely on assumptions. If it is believed that erroneous assumptions may influence the overall conclusions, a sensitivity analysis may be warranted.

Most laboratory values are measured with error, although modellers usually treat covariate data as error free. Modelling the covariate allows its measurement error to be taken into account [15, 18]. This could either be done sequentially [18] or simultaneously [15], and can be compared to PK-PD modelling (where the PK can be viewed as a covariate in the PD model).

The likelihood to identify these models for time-varying covariates may vary with the level of unexplained variability, although they were identified in all four data sets in this study, i.e. across a range of different magnitudes of IIV, residual error, number of individuals and observations. In the examples used, the strength of the covariate relationship, crudely assessed from the magnitude of θ_COV * (COV_max– COV_min), influenced the finding of significant relationships for the extended models. This is illustrated by the observation that, for the four weakest relationships (gentamicin V₁∼ALB and V₁∼BSA, pefloxacin CL∼WT, paclitaxel PD MTT∼ BIL), neither the first nor the second extended model was supported.

The application of the standard model with time-varying covariates makes the assumption that the same covariate–parameter relationship applies to within- and between-subject covariate variability, and that there is no interindividual variability in the coefficient for a covariate–parameter relationship. The present work demonstrates, as in eight of 10 cases the final covariate model differed from the standard model, that either or both of these assumptions may be inappropriate or not supported by the data. The extended models presented herein will allow the user to test these assumptions and to build more informative models for time-varying covariate–parameter relationships.