Allometric relationships between the pharmacokinetics of propofol in rats, children and adults

Abstract

Aims

Allometric equations have proven useful for the extrapolation of animal data to determine pharmacokinetic parameters in man. It has been proposed that these equations are also applicable over the human size range including the paediatric population. The aim of this work was to study the relationship between various pharmacokinetic parameters for propofol and body weight using data from rats, children and adults. Furthermore, the utility of allometric scaling is evaluated by the prediction of propofol concentrations in humans based on data obtained in the rat.

Methods

The relationship between the pharmacokinetic parameters of propofol obtained in rats, children and adults was analyzed by plotting the logarithmically transformed parameters against the corresponding logarithmically transformed body weights. In addition, based on allometric equations, pharmacokinetic parameters obtained in rats were scaled to humans. These parameters were used to simulate propofol concentrations in long-term sedated critically ill patients using NONMEM. Simulated concentrations were then compared with actually observed concentrations in humans.

Results

The relationship between pharmacokinetic parameters of propofol from rats, children and adults was in good agreement with those from the literature on allometric modelling. For clearance, intercompartmental clearance, central volume of distribution and peripheral volume of distribution, the power parameters were 0.78, 0.73, 0.98 and 1.1, respectively, and r² values for the linear correlations were 0.990, 0.983, 0.977 and 0.994, respectively. On the basis of data obtained after a single bolus injection in the rat, adequate predictions of propofol concentrations in critically ill patients can be made using allometric equations, despite the long-term nature of the use of the drug, the large number of infusion changes per day and/or differences in state of health and age.

Conclusions

For propofol, allometric scaling has proved to be valuable for cross species extrapolation. Furthermore, the use of the allometric equation between adults and children seems to be an adequate tool for the development of rational dosing schemes for children of varying body weights, and requires further study.

Introduction

In recent years, considerable progress has been made in the area of preclinical pharmacokinetic-pharmacodynamic investigations. Chronically instrumented animal models have been developed to allow the study of the relationship between the time course of drug effects and drug concentrations [1, 2]. An important question in this respect is to how data obtained in these animal models can be extrapolated in a quantitative manner to humans.

For the prediction of pharmacokinetics in humans from animal experimental data, two approaches may be used, namely allometric scaling and physiologically based pharmacokinetic modelling. Allometric scaling is a rather empirical approach, whereas physiologically based pharmacokinetic modelling offers a mechanistic solution to extrapolation from one species to another. These latter models allow the integration of more complexities, but their development tends to be resource-demanding and time-consuming.

The allometric model has been used successfully for cross-species scaling, including humans, in pharmacokinetics [3, 4]. Allometric scaling is potentially useful in drug development since it utilizes data that are obtained routinely. Furthermore, the calculations are relatively simple [5]. Briefly, allometric scaling is an empirical examination of the relationships between body function and body size (body weight). Numerous physical and physiological parameters vary according to some mathematical function of body weight, which appears to be reasonably uniform across a broad range of animal species [6–8]. This allows the prediction of the pharmacokinetic parameters in a given species, including humans, based on the values obtained from other mammalian species.

In addition to the successful use of the allometric model for cross-species scaling, it has been suggested that the technique is also applicable for extrapolation within humans with particular reference to the paediatric population [9, 10]. Specifically, it has been proposed that clearances within human beings should be standardized using the general allometric equation, since like many physiological, structural and time related variables, it scales predictably over a very wide range of body weight and species [10]. The allometric equation also has the advantage over a body surface law that it only requires body weight to be known. Surface area is more difficult to determine and verify.

Recently we developed a new formulation of propofol which is intended for special groups such as intensive care patients and children. The new formulation was tested in animals [11] before it was studied in adults [12, 13] and children [14]. In this paper we study the relationships between the various pharmacokinetic parameters for propofol and body weight (varying from 250 g to 100 kg) using data from rats, children and adults. Furthermore, the utility of allometric scaling was evaluated by the prediction of propofol concentrations in individual critically ill patients, based on pharmacokinetic parameters obtained from the rat.

Methods

Animals and patients

Chronically instrumented male Wistar rats received 30 mg kg⁻¹ of propofol over 5 min. Pharmacokinetic parameters for propofol using a two compartment model were obtained based on 19 whole blood samples from each of 22 rats [11].

Six mechanically ventilated children aged 1–5 years received a 6 h continuous infusion of propofol at the rate of 2 or 3 mg kg⁻¹ h⁻¹ for sedation following cardiac surgery. A total of seven arterial blood samples collected at various time points during and after the infusion were used for the estimation of the pharmacokinetic parameters for propofol [14].

Twenty-four male adult patients received a 5 h infusion of propofol at the rate of 1 mg kg⁻¹ h⁻¹ for sedation in the postoperative period following coronary bypass surgery. Pharmacokinetic parameters were estimated based on the 24 blood samples obtained in each patient [12].

Twenty critically ill, mechanically ventilated patients received propofol for 2–5 days in doses as required (1–4 mg kg⁻¹ h⁻¹). Four daily blood samples were collected from each patient [13].

All clinical studies were approved by the local ethics committee (Commissie Toetsing Medische Experimenten) and written informed consent was obtained from the patient or next of kin [12–14].

Analysis of propofol

Whole blood samples were mixed thoroughly and stored at 4 °C until analysis by HPLC with fluorescence detection [15]. Using this method, the coefficients of variation for the intra-assay and interassay precision were less than 3.7 and 9.8%, respectively, over the concentration range 0.05 to 40 mg l⁻¹. The limit of quantification was 0.02 mg l⁻¹.

Allometric equation

The allometric equation allows prediction of pharmacokinetic parameters in any animal species from the product of an allometric coefficient and the body weight to a power function [6–8]. The general allometric power model is represented by the equation:

$$\text{Y}=\text{a}\times {\text{BW}}^{\text{b}}$$ (1)

where Y is the biological characteristic to be predicted, BW is the body weight, and a and b are an empirically derived constant and exponent, respectively [6–8]. The nature of the constant a and exponent b differs, because the former is a drug-dependent variable and the latter varies depending on the type of pharmacokinetic or physiological parameter (i.e. clearance (CL), volume of distribution (V) or half-life (t_1/2)). When applied to drug clearance CL, the exponent b is 0.75, such that:

$${\text{CL}}_{\text{i}}={\text{CL}}_{\text{std}}\times {({\text{BW}}_{\text{i}}/{\text{BW}}_{\text{std}})}^{0.75}$$ (2)

where CL_i is the clearance in the individual i and CL_std is the clearance in a standardized individual with body weight BW_std. BW_std can be of any value in kg, and is often set at 70 kg for adult patients. When applied to physiological volumes, the exponent is 1. For time-related indices such as elimination half-life, the exponent is 0.25 [6–8].

Exploration of the relationship between the individual pharmacokinetic parameters for rats, children and adult patients

The individual estimates for the different pharmacokinetic parameters obtained in rats [11], children [14] and adults [12] were logarithmically transformed and plotted against the corresponding logarithmically transformed body weights. According to the nature of allometric equations, the parameters a and b in the (linear) relationship were calculated using linear regression (Excel 2000, Microsoft Corporation) for each of the parameters clearance (CL) and intercompartmental clearance (Q), volume of the central compartment (V₁) and the volume of the peripheral compartment (V₂).

Scaling pharmacokinetic parameters of propofol from rats to adult patients and simulations in critically ill patients

From the preclinical study [11], values of the population mean of clearance (CL), volume of the central compartment (V₁), intercompartmental clearance (Q) and volume of the peripheral compartment (V₂) in the rat (250 g) were scaled to humans (70 kg) on the basis of the allometric equation using the estimated values of the parameters a and b. In a separate simulation using NONMEM (Version V) [16], these human scaled pharmacokinetic parameters, together with the propofol dosing regimens as given to the long-term sedated critically ill patients [13], were used to simulate propofol concentrations in these individual patients. Concerning interindividual variability in the pharmacokinetic parameters, log-normal distributions of the volumes and clearances in the population were assumed such that:

$${\text{θ}}_{\text{i}}={\text{θ}}_{\text{tv}}={\text{e}}^{\text{η}\text{i}}$$ (3)

in which θ_i is the individual value of the parameter θ, θ_tv is the mean population value of this parameter (‘typical value’) and η is a random variable normally distributed around zero. A constant coefficient of variation model was used for the intraindividual variability such that:

$${\text{c}}_{\text{ij}}={\text{c}}_{\text{pred,ij}}\times \left(1+\text{ε}\right)$$ (4)

in which c_ij is the jth measured concentration in the ith individual, assuming that the residual error is proportional to the propofol concentration. In equation 4, ɛ is a random variable normally distributed around zero.

Simulations were performed using the Onlysimulation (uniform) routine as implemented in the NONMEM software [16]. Pharmacokinetic parameters scaled for humans as well as intra- and interindividual variabilities estimated in the rat were used. Predicted concentrations were then compared with the observed propofol concentrations in these long-term sedated critically ill patients.

Results

The demographic and clinical characteristics of the animals and patients from the four different studies are shown in Table 1.

Table 1.

Characteristics of the animals and patients in the different studies

	Rats [11]	Children [14]	Adults [12]	Critically ill adult patients [13]
Number of animals/patients	24	6	24	20
Age (range)	Adult	1–5 years	37–73 years	52–79 years
Body weight (range)	0.25–0.3 kg	10–21 kg	64–93 kg	70–96 kg
Diagnostic group	Healthy	Surgery for congenital heart malformation	Coronary artery bypass surgery	Long-term sedated critically ill patients
Indication for propofol sedation	Experimental nonventilated	Postoperative mechanical ventilation	Postoperative mechanical ventilation	Nonpostoperative mechanical ventilation
Duration of propofol sedation (fixed or range)	5 min	6 h	5 h	45–120 h
Body temperature (range)	36.5–37.5 °C	35.0–37.5 °C	33.0–37.8 °C	35.3–39.6 °C
Renal function (range)	Normal	Normal	Normal	Normal–need for haemodialysis
Liver function	Normal	Normal	Normal	Normal
Cardiac function (range)	Normal	Cardiac dysfunction (see diagnostic group)	Normal (ejection fraction >40%)	Normal– end-stage cardiac failure

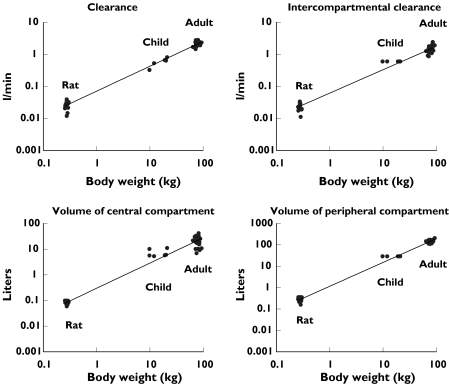
Figure 1 shows the relationship between the pharmacokinetic parameters for propofol after bolus injection in the rat [11], after a 6 h infusion following open-heart surgery in children aged 1–5 years [14] and after a 5 h infusion in adults following coronary artery bypass grafting [12]. According to the nature of allometric equations (Y = a × BW^b or log Y = log a + b × log BW), the regression of the logarithm of the different pharmacokinetic parameters (Y) and the logarithm of the body weight (BW) of the rats, children and adults produce a linear relationship (Figure 1). The values of the constant a and the exponent b for each pharmacokinetic parameter are shown in Table 2.

Figure 1.

Clearance, intercompartmental clearance, volume of the central compartment and volume of the peripheral compartment of propofol vs body weight in rats following bolus injection [11], in children for sedation after a 6 h infusion following open-heart surgery [14] and in adults after a 5 h infusion for sedation following coronary artery bypass grafting [12]

Table 2.

Values for constant a, exponent b and r² for the pharmacokinetic parameters of propofol, based on data from rats [11], children [14] and adults [12] using the allometric equation Y = a × BW^b (see Figure 1)

Parameter	Constant a	Exponent b	r2
CL	0.071	0.78	0.9898
Q	0.062	0.73	0.9832
V1	0.30	0.98	0.9774
V2	1.2	1.1	0.9944

CL = clearance, Q = intercompartmental clearance, V₁ = volume of central compartment and V₂ = volume of peripheral compartment.

Table 3 shows the values of the observed population pharmacokinetic parameters in the rat and the predicted pharmacokinetic parameters in humans based on parameter estimates in the rat, obtained by scaling from a body weight of 250 g to 70 kg on the basis of the allometric equation. A value of 0.75 was used as a power parameter for clearances and a value of 1 was used as the power parameter for volumes [6–8]. The observed pharmacokinetic parameters in critically ill patients following 2–5 days of propofol infusions at different rates [13] are also shown in Table 3.

Table 3.

Observed population pharmacokinetic parameter estimates (value (SE)) of propofol in the rat (250 g), scaled pharmacokinetic parameters of propofol in humans (weighing 70 kg) using the allometric equation and observed pharmacokinetic parameters of propofol in intensive care patients (value (SE))

	Observed in the rat (250 g)		Scaled for humans (70 kg)	Observed in intensive care patients [13]
Pharmacokinetic parameter	Value (SE)	%CV	Value	Value (SE)	%CV
CL (l min−1)	0.0261 (0.00205)	34%	1.63	2.1 (0.066)	17%
V1 (l)	0.0811 (0.00544)	15%	20.6	20.5 (2.4)	47%
Q (l min−1)	0.0227 (0.00325)	26%	1.45	1.4 (0.11)	27%
V2 (l)	0.291 (0.0067)	23%	71.9	150 (17.5)	25%
Intra-individual variability (%CV)	19.9%			36.5%

CL = clearance, Q = intercompartmental clearance, V₁ = volume of central compartment and V₂ = volume of peripheral compartment, intraindividual variability is expressed as %CV and equals the square root of the variance of ɛ, interindividual variability is expressed as %CV and equals the square root of the exponential variance of η minus 1. The pharmacokinetic parameters scaled for humans were obtained using the allometric equation with power parameters according to the literature (0.75 for clearances and 1 for volumes) and the pharmacokinetic parameters observed in the rat (column 2).

The pharmacokinetic parameters that were scaled for humans together with the intra- and interindividual variabilities observed in the rat (Table 3) were used to simulate propofol concentrations based on the propofol dosing regimens used in individual intensive care patients. Figure 2 shows the best, median and worst performances of these simulated propofol concentrations vs observed concentration profiles in critically ill patients. Analysis of observed vs predicted concentrations gave a r² value for the linear correlation of 0.83 and a P value < 0.0001.

Figure 2.

Simulated concentrations using bolus injection data obtained in the rat (line) and observed propofol concentrations (dot) [13]vs time, in critically ill patients. Best, median and worst performances of individual simulations are presented

Discussion

Extrapolation of animal data to determine pharmacokinetic parameters in man is an important tool in drug development, and allometric equations have proven useful for this purpose [6–10]. However, there are very few studies on the utility of allometric relationships for interpolating pharmacokinetics from adults to children and in guiding dosing in this special patient group.

To our knowledge, we have demonstrated for the first time that the relationships between pharmacokinetic parameters in rats, children and adults can be described adequately by the allometric equation. With respect to propofol, the values estimated for exponent b (Figure 1, Table 2) are in very good agreement with literature values for clearance of about 0.75, and for volume parameters about 1 [7].

In theory allometric scaling can be used for both interpolation and extrapolation. Generally the precision of the parameter estimates obtained by interpolation can be quite high. However, upon extrapolation the precision of the predicted parameter estimates may be poor and result in deviation and bias, particularly when extrapolating from relatively small animals (i.e. rodents) to humans. We have illustrated the utility of allometric scaling by predicting concentrations in humans (weighing 70 kg) based on data obtained in the rat. Good agreement with observed values [13] from critically ill patients was obtained. Adequate predictions from rat data to critically ill patients can be made, despite the long-term nature of the use of the drug, the large number of infusion changes per day and/or differences in state of health and age between patients and rats.

The success of allometric scaling from rat to man for propofol can be explained by the fact that propofol is a high extraction ratio drug which is primarily eliminated by the liver and in which clearance is highly dependent on hepatic blood flow. Metabolism of propofol is primarily by conjugation and independent of the mixed-function oxidase system. In addition, propofol exhibits linear pharmacokinetics, which do not change on multiple dosing. Simulations in humans based on information from animal studies may lead to an optimization of trial design and possibly to a decrease in the number of patients needed for clinical trials or a decrease in the number of clinical studies required.

The results from a recent study show that interspecies scaling using an allometric function is applicable to 11 out of a total of 44 veterinary drugs [17]. Other studies have found that it is possbile to use allometry to predict the pharmacokinetics of chinolones [18], thiopentone and ketamine [19] based on body size. In addition, Chiou et al.[20] concluded that the rat may serve as a useful animal model to predict plasma clearance of drugs in humans based on the data from 54 drugs. However, the allometric equation should be employed with caution, particularly when extrapolating between patient groups, because of the small amount of published evidence.

Within the human physiological range, it is known that in children liver perfusion, body composition (percentages of body water and fat), and plasma protein binding change with age. In this context, the American Food and Drug Administration (FDA) has proposed four age groups for study; neonate (birth to 1 month), infant (1 month to 2 years), child (2 to 12 years) and adolescent (12–16 years). Holford [10] has proposed that clearances within human beings should be standardized using this power law, since the general allometric equation is a good predictor of body function over a very wide range of body weights and species. The widely used alternatives, surface area, linear and per kilogram models, are, in his view, inferior in comparison with the power law. However, it should be realized that allometric power models are applicable down to a certain age. From birth to about 12–18 months, there are major changes taking place in systems that affect drug disposition. The allometric scaling method is too simplistic to account for these rapid changes and more complex physiologically based pharmacokinetic modelling is needed in neonates and young infants.

In the present work, data have been gathered from six children varying in age from 1 to 5 years, which is a small sample size with a relatively small range in body weight. Therefore, the objective of future investigations should be to confirm the described allometric relationship in a larger group of children possessing a wider range of body weight. Whereas the use of the allometric power model for cross species scaling is generally accepted, this is not the case within the human size range [9, 10]. Therefore, the allometric scaling approach should be further studied in children, in order to optimize dose selection and provide information for future investigation of drugs in paediatric practice.

In conclusion, for propofol, allometric scaling proved to be most useful for cross species extrapolation. Despite the long-term nature of its use in critically ill patients, the large number of infusion changes per day and differences in state of health and age, human propofol concentrations can be adequately predicted based on data obtained from preclinical studies in the rat. Furthermore, the use of the allometric equation seems an adequate tool to develop rational dosing schemes for children of varying body weights but needs further study for other drugs in different age groups.