Double proton transfer dynamics of model DNA base pairs in the condensed phase

Abstract

The dynamics of excited-state double proton transfer of model DNA base pairs, 7-azaindole dimers, is reported using femtosecond fluorescence spectroscopy. To elucidate the nature of the transfer in the condensed phase, here we examine variation of solvent polarity and viscosity, solute concentration, and isotopic fractionation. The rate of proton transfer is found to be significantly dependent on polarity and on the isotopic composition in the pair. Consistent with a stepwise mechanism, the results support the presence of an ionic intermediate species which forms on the femtosecond time scale and decays to the final tautomeric form on the picosecond time scale. We discuss the results in relation to the molecular motions involved and comment on recent claims of concerted transfer in the condensed phase. The nonconcerted mechanism is in agreement with previous isolated-molecule femtosecond dynamics and is also consistent with the most-recent high-level theoretical study on the same pair.

Since the work by Watson and Crick on the determination of DNA structure in 1953 (1), proton-translocating tautomerization of base pairs has been suggested as a cause of mutations (2). Model systems with similar pair structures can be studied by photoinducing proton transfer (3, 4), and such studies are helpful for understanding the dynamics of mutagenesis (5).

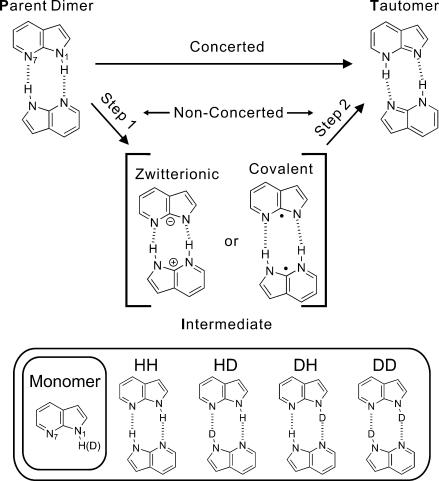
In this regard, the dimers of 7-azaindole (7-AI) molecules are prototypical because they are structurally similar to the H-bonded adenine–thymine (A–T) pair with two bonds; the guanine–cytosine (G–C) base pair has three H-bonds. Following the first observation of excited-state double proton transfer in 7-AI by Taylor et al. in 1969 (6), a number of researchers have studied its characterization in the dimers and also of 7-AI monomers catalyzed by various H-bonded counterparts of protic guest molecules (ref. 7 and references therein). One of the fundamental issues, with important implications, is whether the transfer process (8–17) of the two hydrogens proceeds in a concerted manner with a single transition state, or through a stepwise pathway by forming an intermediate species, as shown in Fig. 1.

Fig. 1.

Molecular structures involved in the stepwise, or concerted, double proton-transfer dynamics of the model base pair, 7-AI dimer. The structures of deuterated species studied are also displayed.

The first report of the dynamics of double proton transfer in 7-AI in the isolated molecule (molecular beam) was published in 1995 (8). The pair was excited with a femtosecond pulse, and another pulse, at different time delays, was invoked to observe the mass spectra. The parent ion showed a biexponential behavior, even near the zero-point energy, and the time constants of both decays changed significantly, by a factor of more than eight, with isotopic substitution. These two time constants (650 fs and 3.3 ps) were found to decrease with the excess excitation energy, as more vibrational modes (18) become involved. Castleman and coworkers, using their novel technique of Coulomb explosion, studied the same isolated 7-AI dimers (ref. 11 and references therein) and arrested the intermediate of mass-119 (7-AI-H⁺) species. They found that this intermediate forms in 660 fs (a very similar time constant to our parent decay; ref. 8) and decays by 5 ps, again in excellent agreement with the observation made in this group (8). These results from two independent groups and techniques support a nonconcerted reaction pathway. However, the results of high-resolution spectra (ref. 12 and references therein) made Sakota et al. conclude that the reaction mechanism is a concerted one. The inference, as discussed below, is not conclusive because of the limited time resolution used in their picosecond experiments.

The mechanism has been discussed in a number of theoretical papers. Ab initio configuration interaction singles calculations showed that the electronic excitation was localized on one moiety in the 7-AI dimer, making the transfer to occur in a stepwise mechanism (ref. 13 and references therein). Guallar et al. (14) have performed a molecular dynamics simulation and showed that the process is sequential through the formation of an intermediate having a covalent character (biradical-type). Catalán et al. have used what they called a hybrid density functional theory and asserted that the excitation is delocalized over the 7-AI dimer and that the process is concerted (ref. 15 and references therein); Douhal et al. critiqued this assertion (ref. 13 and the cited ref. 21 therein). Very recently, in 2006, by performing calculations of the highest level (CASSCF/CASPT2), Serrano-Andrés and Merchán (16) showed the presence of stable intermediate states having zwitterionic and covalent characters. They also found that the concerted pathway has a transition state that is higher in energy than the intermediate stepwise pathway by 3.5 kcal/mol. This difference should be even larger in polar media.

In the condensed phase, experiments were also carried out in this group using both transient absorption (time resolution of 130 fs) and fluorescence upconversion (time resolution of 300 fs); the excitation wavelengths used were 320 and 266 nm, respectively. From these results and the careful analysis (9) it was concluded that the first proton transfer occurs within 130 fs for the undeuterated species (280 fs for the deuterated species), and that the second proton transfer occurs with a time constant of 1.2 ps (5 ps for the deuterated species). Takeuchi and Tahara, using a time resolution of 290 fs (fluorescence upconversion), reported decays with constants of 200 fs and 1.1 ps, but assigned the former to internal conversion (¹L_a/¹L_b states) and the latter to a concerted transfer process (ref. 17 and references therein). The strongest argument provided by the authors was the observation of a small signal change from a biexponential to a single-exponential decay when the excitation wavelength was scanned from 280 to 313 nm (near the 0,0 transition). As it is well known, excitation at high excess energies opens channels of vibrational relaxation and energy redistribution as well as internal conversion. Also experiments, especially those near the origin, require the appropriate time resolution (9) to resolve the first femtosecond step. The weak isotope effect of 1.5 reported by Takeuchi and Tahara (see ref. 17 and the cited reference 5 therein) is caused by moisture. As shown here (and also in ref. 9), the isotope effect is much higher, with a value of 7.4 reported in this work (see Materials and Methods).

Here, we report results of a systematic investigation of the effect of solvent polarity and viscosity, and solute isotopic composition and concentration, all made by exciting the pair near the 0,0 of the transition. An intermediate, which has a large dipole moment, will manifest its presence in changes of the rates with polarity (9, 13, 16). At a given polarity, the determination of kinetic isotope effect (KIE) is also a powerful measure of the degree of concertedness, if truly dominant (19–22). The results of such experiments, “proton inventory” (19–22), are unique for concerted double-proton-transfer reactions. To a good approximation, the rates follow the rule of geometric mean, i.e., k^HD = k^DH = (k^HHk^DD)^1/2, where k^HH, k^HD, k^DH, and k^DD are the corresponding isotopic-species rate constant. The results reported here for the effect of solvent polarity and viscosity and solute isotopic composition and concentration are entirely consistent with the stepwise mechanism.

Results

Steady-State Spectra.

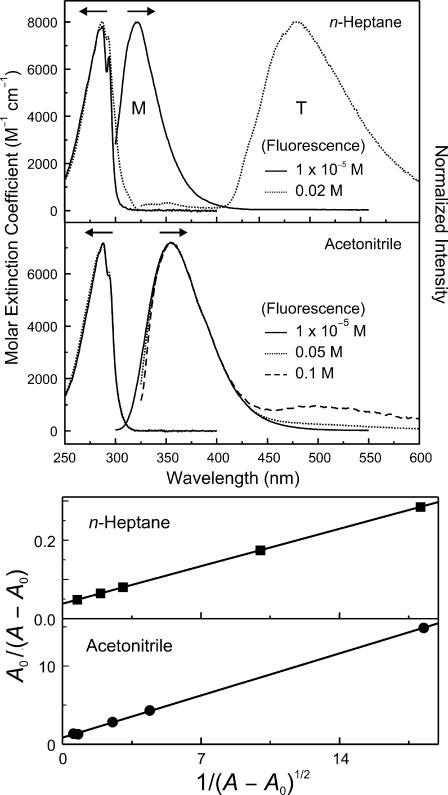
Fig. 2 shows that the lowest absorption band of 7-AI in n-heptane shifts to the red and grows around 310 nm with the increase of 7-AI concentration. The spectral changes reflect the self-association of 7-AI by H-bonding to produce dimers in the nonpolar solvent (n-heptane) as in other nonpolar solvents, 3-methylpentane and n-hexane (9, 17). Only the UV emission around 320 nm from 7-AI monomers appears at the low concentration of [7-AI] = 1.0 × 10⁻⁵ M. However, at the high concentration of [7-AI] = 0.02 M, and for red-tail excitation at 315 nm, the UV fluorescence shifts to ≈350 nm and a new visible fluorescence appears around 480 nm. Because the dimer absorption is more red-shifted, the dimers can be predominantly excited at 315 nm. The visible fluorescence has been shown to arise from the tautomer generated by proton transfer (9, 17). The weak UV band is composite of the fluorescence of monomers having a nanosecond lifetime and possibly some oligomers (9, 17).

Fig. 2.

Steady-state absorption and fluorescence spectra. (Upper) In n-heptane, absorption spectra were obtained with [7-AI] = 1 × 10⁻⁵ (solid) and 1 × 10⁻³ M (dotted). Fluorescence spectra were measured with [7-AI] = 1 × 10⁻⁵ (solid, λ_ex = 290 nm) and 2 × 10⁻² M (dotted, λ_ex = 315 nm). In ACN, absorption spectra were obtained with [7-AI] = 1 × 10⁻⁵ (solid) and 1 × 10⁻² M (dashed). Fluorescence spectra were measured with [7-AI] = 1 × 10⁻⁵ (solid, λ_ex = 290 nm), 0.05 (dotted, λ_ex = 320 nm) and 0.1 M (dashed, λ_ex = 320 nm). The fluorescence was normalized to that of the monomer. Note that at steady state the emission of monomers and tautomers dominate because of their relatively long lifetimes. (Lower) Linear relationships for dimers. Plots of A₀/(A − A₀) versus 1/(A − A₀)^1/2 at 317 nm in n-heptane (squares) and ACN (circles); see text.

The absorption and emission spectra of 7-AI in acetonitirile (ACN) are shown in Fig. 2. In contrast to the spectra obtained in n-heptane, the absorption spectra do not show significant dependence on the concentration of 7-AI. The fluorescence spectra, however, exhibit the concomitant growth of the visible fluorescence around 500 nm relative to the UV fluorescence with the increase of 7-AI concentration. There is no absorption around 380 nm, that is, the 7-AI dimeric tautomer does not exist in the ground state (23). The spectral similarity of the visible fluorescence in ACN to that in n-heptane is consistent with the visible band being the fluorescence of 7-AI tautomers.

The equilibrium constant (K_eq) for the monomer–dimer (M–D) equilibrium, M + M ↔ D, can be expressed as K_eq = [D]/(C − 2[D])², where C is the actual concentration of 7-AI in solution (C = [M] + 2[D]). In the case where the absorption spectrum of the dimer overlaps that of the monomer, a linear relationship, based on Beer–Lambert law, is derived (24) to relate A₀/(A − A₀) to the quantity 1/(A − A₀)^1/2 (see Fig. 2 Lower), where A is the absorbance at a given wavelength, and A₀ is that of the monomer A₀ = ε_MCl [supporting information (SI) Text]. The plot of A₀/(A − A₀) versus 1/(A − A₀)^1/2 at 317 nm in Fig. 2 shows the expected linearity and confirms the formation of dimers in ACN. From the slope, using a linear least-squares fit, we obtained K_eq to be 32 M⁻¹ in ACN. For n-heptane, with a similar plot, the value of K_eq was found to be much higher, 1.8 × 10³ M⁻¹, consistent with the reported values for 3-methylpentane (1.8 × 10³ M⁻¹) and for n-hexane (2.4 × 10³ M⁻¹) solutions (9, 17). We note that dimer formation of 7-AI in ACN has been reported using mass spectrometry (25).

Time-Resolved Fluorescence.

Viscosity and concentration dependence.

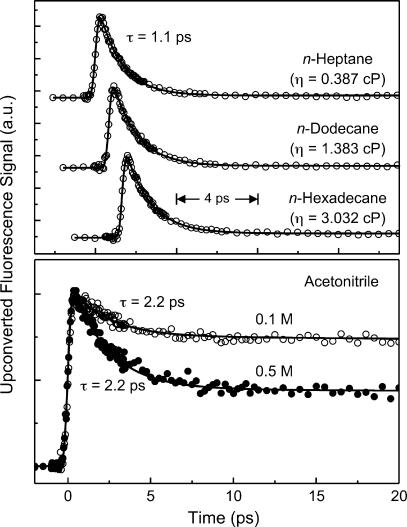
To investigate the role of solvent viscosity, we measured fluorescence transients at 380 nm in a series of n-alkane solvents. The results in Fig. 3Upper show that, within our experimental errors, the femtosecond transients are identical in n-heptane, n-dodecane, and n-hexadecane having viscosity (η at 25°C) of 0.387, 1.383, and 3.032 cP, respectively. The decay time in all solvents is ≈1.1 ps; there is ≈3% of a nanosecond component that is that of the monomer (SI Table 1). In n-hexane (0.300 cP at 25°C), the decay time has been reported to be 1.1 ps (17). Thus, the insensitivity of the observed dynamics to solvent viscosity is established in the viscosity region of 0.3 ≤ η ≤ 3.

Fig. 3.

Viscosity and concentration effects. (Upper) Fluorescence transients, collected at 380 nm, of 7-AI (0.02 M) in n-heptane, n-dodecane, and n-hexadecane. Solid curves are best-fitted exponential decays. (Lower) Fluorescence transients, monitored at 420 nm, of 7-AI in acetonitrile having [7-AI] = 0.1 (open circles) and 0.5 M (filled circles). Solid curves are best-fitted exponential decays.

For the concentration dependence we show the fluorescence transients of 7-AI in ACN (Fig. 3 Lower). The 29% of the fluorescence transient, recorded at 420 nm, of 7-AI in ACN with [7-AI] = 0.1 M decays with a time constant of 2.2 ps. The residual transient (71%) remains flat in the time window shown. At the higher 7-AI concentration of 0.5 M, the fluorescence transient gives a time constant of 2.2 ps (60%) and a constant offset of 40%. The fact that the time constant does not vary with concentration, but the amplitude fraction does, indicates that collision-induced dimer formation (bimolecular excimer) in the excited state does not occur, at least on the time scale of interest. Accordingly, in this study the time constants of proton transfer are independent of the concentration of 7-AI.

Polarity dependence.

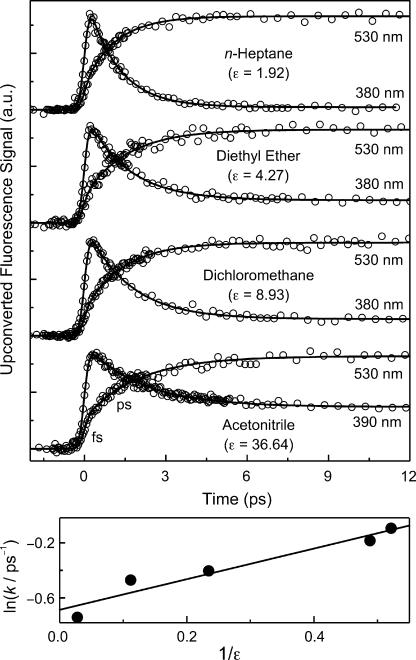
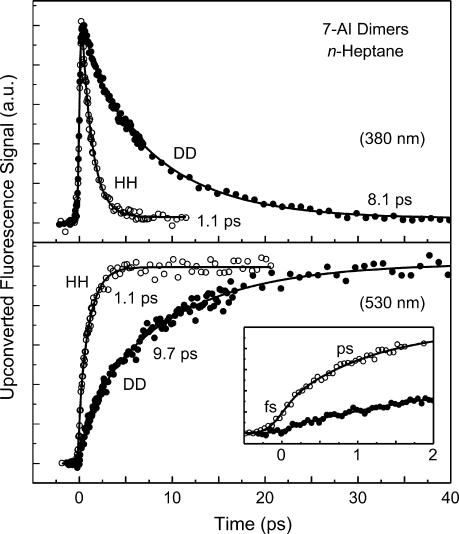
Fig. 4Upper shows a series of fluorescence transients recorded in the UV and green regions and for various polarity. In n-heptane, the tautomeric fluorescence at 530 nm grows with a time constant of 1.1 ps (75%), which is identical, within our experimental errors, to the decay time of 1.1 ps obtained at 380 nm, following the ultrafast rise (25%). In alkane solvents, it has been reported that vibrational cooling of the tautomer has a time constant of 12 ps and appears as a rise when the maximum of tautomeric fluorescence (480 nm) is monitored (9), but as a decay when the red tail of the band (560–600 nm) is detected (ref. 17 and the cited ref. 5 therein). Here, at 480 nm, we did observe the 12 ps component, and it is not detected at the wavelength of 530 nm. For each solution, the decay time obtained in the UV region matches well the rise time of tautomeric green fluorescence (SI Table 1). Hence, the picosecond time constants observed in all of the solutions are related to proton transfer in 7-AI dimers. As mentioned before, the constant offset in our time window, which is more appreciable in polar solvents, is due to the fluorescence of monomers and possibly oligomers (9, 17). The time constants used for the fit of all of the transients in Figs. 3 Upper and 4 Upper are given in SI Table 1.

Fig. 4.

Polarity effects. (Upper) Fluorescence transients of 7-AI in n-heptane ([7AI] = 0.02 M), diethyl ether (0.1 M), dichloromethane (0.1 M), and acetonitrile (0.5 M). Monitored wavelengths for UV and green fluorescence are indicated near transients. Solid curves are best-fitted exponential decays. (Lower) Rate changes with dielectric constant. Plot of the logarithm of the proton-transfer rate (k) against the reciprocal of the medium dielectric constant. A linear fit (line) is also shown (see text).

The rise and decay time constants vary with solvent polarity. The time constant changes from 1.1 to 2.1 ps. We note that the viscosity of the solvent and the concentration of the solute were verified to have no significant effect on the proton-transfer dynamics (see above). To examine polarity correlations, we plot the logarithm of the rate constant of proton transfer, k, i.e., the reciprocal of the time constant, versus the reciprocal of the dielectric constant (Fig. 4 Lower). In general, it is clear that the more polar the medium, the smaller the rate constant. From an electrostatic model of Kirkwood et al. (26), one predicts a linear relationship between ln(k) and 1/ε for reactions of both neutral and charged dipolar molecules. The intercept gave k₀ (ε = 2) of (1.1 ps)⁻¹ which is in good agreement with the value in n-heptane (ε = 1.92); the slope (∝μ²/r³) gives an effective radius of ≈1.4 nm for the intermediate with μ = 12 D.

Isotope dependence.

Fig. 5 shows the effect of deuterium substitution on the fluorescence transients of 7-AI in n-heptane. The transients at 380 and 530 nm are profoundly influenced by deuteration. The fluorescence of the deuterated samples, collected at 380 nm, decays with a time constant of 8.1 (80%) and 1.8 ps (18%). The tautomeric fluorescence at 530 nm rises with a constant of 9.7 (76%) and 1.6 ps (21%), showing close correlation with the decay at 380 nm; the rest (3%) of the transient is observed to build up within our temporal resolution. The observation of a relatively small amount (18%) of the 1.8-ps component indicates that the sample contains some nondeuterated 7-AI (18%), giving the real isotopic enrichment of 82% in the prepared sample (9). The lengthening of the 1.1-ps component to 1.8 ps can be rationalized, as discussed below.

Fig. 5.

Isotope effects. Fluorescence transients of protiated (open circles) and deuterated 7-AI (filled circles) in n-heptane. The fluorescence was collected at 380 nm (Upper) and 530 nm (Lower). (Inset) An enlargement of the early-time rise behavior. Solid curves are best-fitted exponential decays.

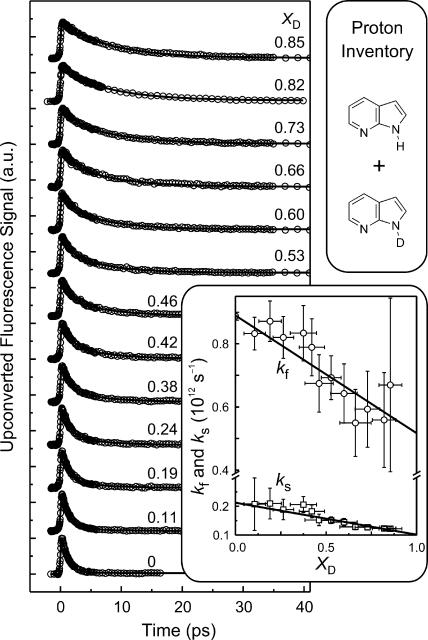
Upon deuteration, the time constant of 1.1 ps in the nondeuterated 7-AI solution changed to 8.1 ps giving rise to a KIE of 7.4. It is worth mentioning that the KIE measured in solutions is very sensitive to the isotopic enrichment in bulk solution (9, 17). The inset of Fig. 5 shows that the initial fractional amplitude of the ultrafast component (within our temporal resolution) in the rise of tautomeric fluorescence decreases from 0.25 to 0.03 upon deuteration of 7-AI samples. Given these changes, we performed a series of “proton inventory” (3, 21, 27, 28) experiments and measured the rates for various isotopic fractions by varying the relative concentration composition of 7-AI, deuterated and undeuterated. This way, equilibration results in dimers with a statistical isotopic mixture. Fig. 6 presents the fluorescence transients, collected at 380 nm, of 7-AI in n-heptane at various deuteration ratios.

Fig. 6.

Proton inventory experiments. Fluorescence transients, monitored at 380 nm, of 7-AI in n-heptane for various isotopic fractionation, X_D. The X_D values are given on each transient. (Inset) Rate changes with isotopic fractionation. Plots of k_f (open circles) and k_s (open squares) versus X_D for 7-AI in n-heptane. k_f and k_s are the fast and the slow component obtained in the decay dynamics. The linear fits for k_f and k_s were performed with proper weighting of the standard deviation for each data point (see text).

In isotopically mixed systems, four different dimeric isotopomers can exist: HH, HD, DH, and DD, where the successive two letters denote the protic hydrogen atom on pyrrolic nitrogen (N₁) and pyridinic nitrogen (N₇) atoms, respectively, in an excited moiety of the dimer. The rate constants for the above isotopomers are k^HH, k^HD, k^DH, and k^DD, respectively. If X_D is the mole fraction of the deuterated 7-AI in the sample, then X_D = [D]/([H] + [D]). The decay of the dimers with one N₁H moiety, i.e., the two species of HH and HD (see Fig. 1), can be expressed (27, 28) in terms of the concentration of [N₁H], and similarly for [N₁D] (SI Text). Because the time scale of isotopic exchange at our concentration in the solvent used is expected to be much longer than picoseconds, no H/D exchange is expected during proton transfer. The normalized fluorescence decay of a statistically equilibrated sample is thus composed of two decays of N₁H and N₁D (27):

where X_H is the mole fraction of the protiated 7-AI in the sample (X_H = 1 − X_D). It follows that k_f = k^HH + (k^HD − k^HH)X_D, and k_s = k^DH + (k^DD − k^DH)X_D. In Fig. 6, each transient fits well to Eq. 1, including the 2–3% long-lived component. Without straining any parameters in Eq. 1, the k_f and k_s values, as well as the real isotopic fractionation (X_D) in the sample, were determined. The extracted k_f and k_s values are linearly dependent on the X_D values. Accordingly, from the linear plots of k_f and k_s with variation of X_D in Fig. 6, the rate constants k^HH, k^HD, k^DH, and k^DD were obtained to be (1.1 ps)⁻¹, (1.9 ± 0.2 ps)⁻¹, (4.7 ± 0.4 ps)⁻¹, and (9.9 ± 2.8 ps)⁻¹, respectively. One should note that the assignment of k^HD and k^DH to (1.9 ps)⁻¹ and (4.7 ps)⁻¹ could also be interchangeable, but the significant point is that k^HD ≠ k^DH ≠ (k^HHk^DD)^1/2 = (3.3 ± 0.8 ps)⁻¹, as discussed below.

Discussion

The above results can be summarized as follows. First, viscosity of the medium (n-alkanes) in the range of 0.3 ≤ η ≤ 3 has no significant effect on proton-transfer rates. Second, the concentration of the solute in polar ACN over the range of 0.1–0.5 M, similarly, has no effect on the rates (but the equilibrium concentration does change). We have determined the equilibrium constant of K_eq to be 32 M⁻¹ and 1800 M⁻¹ in ACN and n-heptane, respectively, indicating difference in the free energy and populations. Third, the effect of polarity is significant as evidenced in the change of the rate from (1.1 ps)⁻¹ in n-heptane to (2.1 ps)⁻¹ in ACN. Fourth, the dependence of the rates on isotopic composition (from proton inventory experiments) over a whole range of mole fraction provides the rate constants for the isotopically different species, k^HH, k^HD, k^DH, and k^DD, and these rates are indicative of the reaction mechanism.

In a full account of our previous work (9), we have discussed the key issues pertinent to proton-transfer dynamics in 7-AI. The experimental observations and theoretical studies made (up to 1999) were discussed. From this detailed discussion of dynamics in the condensed phase, with comparison with that in the gas phase, we pointed out several points regarding barrier crossing and highlighted some misconceptions regarding the meaning of concertedness and reaction trajectories. Basically, in reactions of this type we must consider two types of trajectories (Eqs. 1 and 2 in ref. 9):P → I → T; and P → T, where P, I, and T correspond to the parent initial dimer, an intermediate, and the tautomer, respectively. When the pair has essentially no internal energy (or energy below the barrier), as in molecular beam or low-temperature experiments, then the role of the intermediate becomes prominent. However, at much higher energy above the barrier, it is meaningless to speak of tunneling through the barrier and the associated nonconcerted dynamics. In the case of 7-AI, the barrier is ≈1.3 kcal/mol and at room temperature the thermal (internal) energy is sufficient to induce above-the-barrier crossing. As pointed out in ref. 9, the rates in the beam experiment at a few kcal/mol of internal energy are comparable to those in the condensed phase.

Several remarks are worth emphasizing. First, bifurcation of trajectories is a well known phenomenon in many systems (29, 30). Second, the only experiment with a time resolution sufficient to resolve the initial femtosecond transfer is the one reported using transient absorption (9), giving, following excitation of the pair, a rise of 280 fs (for DD) and ≤130 fs (for HH). This experiment was made at 320-nm excitation, low enough in energy to prevent high-energy state excitation; the excitation is “below” the origin at 310 nm. Third, the isotope effect was observed for both the first and second step (reported in the gas phase in ref. 8) with similar range and it is not conceivable that internal conversion and proton transfer have similar isotope effects. Finally, essentially all high-level theoretical studies (ref. 16 and references therein) have pointed out the presence of the intermediate along the reaction path, and that the concerted path is at higher energy than the nonconcerted one by 3.5 kcal (16). Consistent with our view of a reduced two-coordinate landscape (8), molecular dynamics simulations (14) have shown that the motion of the wave packet occurs in the N···N and N—H space, and on the observed time scale.

Our results not only support the above picture but also identify the intermediate as ionic in character, consistent with the results of a recent high-level theoretical study (16). The effect of solvent polarity on the dynamics of proton transfer is the result of changes in the energetics of P, I, and T and/or the variation of H-bond distance along the proton-transfer coordinate. In general, the rate constant of a reaction is sensitive to polarity (26, 31) if the reactant and product have different dipole moments; the more polar the state the lower its energy becomes. The reaction rate is expected to increase in polar solvents if the product is more polar than the reactant. On the other hand, if an ionic intermediate is present, polarity of the medium is expected to further stabilize its energy, resulting in an acceleration of the first transfer and deceleration of the subsequent proton transfer. The solvent polarity could also change the distances involved in proton transfer, and there exists a correlation between the increase in polarity and decrease in heavy-atom distances (in this case the N···N) if the species is nearly neutral (32, 33); if the species is strongly ionic, then the reverse could occur. It follows that time-resolved experiments of solutions of different polarity can elucidate the presence/absence of the intermediate and its nature (ionic vs. covalent).

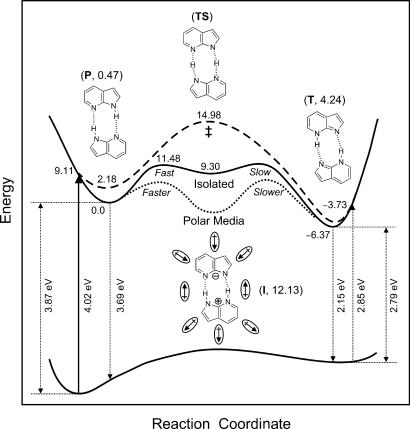
In the present study of polarity effect, which requires special care because of the lower value of K_eq, the rate constant (k^HH) decreases with increasing solvent polarity (Fig. 4). In ACN, the rate becomes slower by a factor of two than that obtained in the nonpolar solvent of n-heptane. One should note that the solvation time (260 fs) of ACN (34) is much shorter than the reported proton-transfer time (2.1 ps). In the work of Serrano-Andrés and Merchán (16), the dipole moments of all (isolated) excited-state species have been calculated to be 0.47, 12.13, 17.29, and 4.24 D for the initial dimer, the zwitterionic intermediate, the covalent (biradical-type) intermediate, and the tautomeric dimer, respectively. If proton transfer occurs by a concerted mechanism conserving center of symmetry (ref. 15 and references therein), then no change of the rates is expected in polar solvents, because the dipole moment remains zero (the same as the ground state). Because the tautomeric dimer is more dipolar (4.24 D) than that of the normal dimer (0.47 D), the rate constant is expected to increase with increasing of polarity. Moreover, for the centrosymmetric reaction path, the polar solvent can shorten the N···N distance, but this will result, if any, in an increase in the rate. We note that the barrier decreases as the N₁···N₇ decreases (9). For the reaction path with ionic intermediate (the zwitterion of ref. 16), as mentioned above, the first transfer will have a larger rate, whereas the second one will experience a decrease of its rate constant.

The behavior observed here for the reaction-rate change with solvent polarity is consistent with the noncentrosymmetric pathway (16). Considering the zwitterionic intermediate, the experimental results indicate a stepwise mechanism with the first transfer being on the femtosecond time scale and the second one on the picosecond time scale, again consistent with our previous picture (9). We note that the first step (≤130 fs for HH and 280 fs for DD) observed using transient absorption (9) in nonpolar solvents would become even faster in polar media, considering both aspects of solvation free energy change and H-bonding geometry effect. We also note that the magnitude of the change of the rate with polarity will depend on the exposure to the solvent and on the entropic difference due to more solvent ordering around the solute in polar media (35). For example, the change in the rate of double proton transfer in oxalamidine derivatives has been reported to be 5 times larger in ACN than in the nonpolar solvent of methylcyclohexane; in this case the first step is the rate determining step (35), and the two H-bonding centers are exposed to the solvent (in 7-AI the network is “hydrophobic-like”).

Further elucidation of the mechanism comes from the proton inventory experiments. From the results in Fig. 6 we obtained k^HH, k^HD, k^DH, and k^DD to be (1.1 ps)⁻¹, (1.9 ± 0.2 ps)⁻¹, (4.7 ± 0.4 ps)⁻¹, and (9.9 ± 2.8 ps)⁻¹, respectively. If the transfer of 7-AI dimers occurs concertedly, then, the rates should follow the prediction of the rule of geometric mean. However, our results show that k^HD ≠ k^DH ≠ (k^HHk^DD)^1/2 and this geometric mean is (3.3 ± 0.8 ps)⁻¹, supporting a stepwise pathway where one of two transition states determines the rate (20, 28, 36). Given that the first step is on the femtosecond time scale, one would like to know the KIE for the second proton transfer. The total rate change from HH to DD is a factor of 9. Considering the two rates for HD and DH, we conclude (3, 36) that the primary KIE is 4.7 ± 1.6 and the secondary is 1.9 ± 0.6. The large value for the primary KIE (4.7) is rationalized by using the tunneling process (9) of the second step of the reaction. The secondary KIE of 1.9 is likely to originate from cooperativity. The N···N distance of the deuterated bridge is generally longer than that of the protonated bridge (32, 37, 38), and for cyclically H-bonded dimeric complexes it has been reported that the lengthening of a H-bond by deuteration also lengthens cooperatively the coupled H-bond (37, 38). Accordingly, the barrier for N···N motion increases and the rate decreases by a factor of 1.9. Typically, a small change in the distance between heavy atoms results in a pronounced change of the rates in distance-sensitive tunneling processes. The dramatic KIE of k^HH/k^DD = 9 for the second proton-transfer step is smaller than that observed [15 = (1.7 ps)⁻¹/(25 ps)⁻¹] in the isolated pair (molecular beam) with the excess energy of 1.0 kcal/mol (8). The lower limit of the activation barrier for the second transfer is estimated to be 2.6 kcal/mol from the analysis of rates using a tunneling model (8). With low energy of excitation at 313 nm near the 0,0 transition (310 nm), there also exists a thermal excitation at room temperature in the condensed phase. KIE in solution should be less than that in the beam experiment because of the thermal averaging and some change in barrier height.

Theoretical ab initio studies are consistent with these observations. The recent CASSCF/CASPT2 study (16), with the highest reliability, as well as other previous studies at the configuration interactions singles level of theory (ref. 13 and references therein), has shown that proton transfer occurs by the two-step mechanism. Also, the barrier for the concerted motion is being higher in energy by ≈3.5 kcal/mol. The calculations indicate that there is a substantial heavy-atom motion in the first step compared with that in the second step. Limbach et al. have suggested that the observation of smaller KIE in the first step (8) is correlated to a larger heavy-atom motion, which increases the tunneling mass and decreases the KIE, in the first step as compared with the second step (39). In their study of double and multiple proton-transfer reactions a pronounced KIE was found (39, 40) for intermediates with shorter heavy-atom distances. Molecular dynamics studies (14) have revealed the motion of the wave packet in the N···N and N—H coordinates and given time scales for nuclear relaxation (≤100 fs) and for the first proton transfer (200 fs step) on the time scale covered (1.5 ps). Given all of these experimental and theoretical findings, we depict in Fig. 7 the reaction coordinates and structures involved, and highlight the energetics (from ref. 16) and the effect of polarity.

Fig. 7.

A potential energy profile. For the proton transfer processes of 7-AI dimers, we adapt the potential energy curves calculated in ref. 16, and include influence of polar solvents. Energy differences of involved species in kcal/mol are also given near reaction paths; the values are taken relative to that of the lowest excited state of the parent dimer. The numbers in parentheses give the dipole moment in Debyes. The effect of polarity is schematically superimposed on the calculated curves to illustrate the observed changes with dielectric constant.

Concluding Remarks

From studies made in the isolated molecule (molecular beam) by different groups and techniques and in the condensed phase (different polarity and isotopic composition) using both transient absorption (time resolution of 130 fs) and fluorescence upconversion (time resolution of 300 fs), and also from recent high-level and previous theoretical calculations, the evidence is overwhelming that double proton transfer proceeds nonconcertedly. If the reaction path is truly centrosymmetric (ref. 15 and references therein) the polarity effect would be absent and the isotope effect would follow a statistical geometric mean, contrary to experimental findings. It is important to understand that in reactions with low-energy barriers, bifurcation of trajectories is common and if the internal energy is sufficiently high, the reaction would appear as so called “concerted.” Moreover, the time scale for the asymmetric molecular motions are certainly on the time scale of the reaction and has no relation to the electronic transition moment of the monomer (41). Elsewhere, we have detailed concepts pertinent to the meaning of concertedness and family of trajectories (29) and the same description applies to the problem addressed here. While this manuscript was in the review process, a paper appeared in PNAS with the title “The answer to concerted versus step-wise controversy for the double proton transfer mechanism of 7-azaindole dimer in solution” (42). The basic argument is the same as discussed before (17), however in the conclusion it is stated that “The concerted mechanism, by its definition, does not require such a strict simultaneity, but it only means that the motions of the two protons are correlated.” It seems to us that the initial strict definition of concertedness (with C_2h symmetry path) is now softened toward a breakage of C_2h symmetry and asynchronous motions. Of course, the motions of the two hydrogens must be correlated as discussed above and elsewhere (8, 9, 14).

Materials and Methods

The 7-AI (98%) was purchased from Sigma-Aldrich and was purified by recrystallization twice from cyclohexane. Subsequently, it was dried in vacuo before use. N₁-Deuterated 7-AI (isotopic purity ≥95%) from Cambridge Isotope Laboratories was used as purchased. A major and serious problem in the study of the deuterated species in solution is the exchange of deuterium with hydrogen in residual water moisture in the environment (glassware, optical cell, solvent, atmosphere etc.). Here, we obtained the KIE of 7.4, whereas that reported by Takeuchi and Tahara (ref. 17 and the cited ref. 5 therein) was 1.5; unfortunately, this low value of KIE, presumably due to moisture, was used to suggest a “small isotope effect” on the rates. Thus, all of the preparations of samples containing deuterated 7-AI were carried out using well-dried glassware in a glove bag (Sigma-Aldrich) filled with a dry nitrogen gas so as to protect the samples from environmental moisture. All of the solvents (anhydrous), purchased from Sigma-Aldrich, were used as received. The experimental apparatus is detailed in SI Text. All fluorescence transients were obtained by the excitation of samples at 313 nm, near the 0,0 transition (310 nm).

Abbreviations

7-AI

7-azaindole

KIE

kinetic isotope effect.