Cultural hitchhiking on the wave of advance of beneficial technologies

Abstract

The wave-of-advance model was introduced to describe the spread of advantageous genes in a population. It can be adapted to model the uptake of any advantageous technology through a population, such as the arrival of neolithic farmers in Europe, the domestication of the horse, and the development of the wheel, iron tools, political organization, or advanced weaponry. Any trait that preexists alongside the advantageous one could be carried along with it, such as genetics or language, regardless of any intrinsic superiority. Decoupling of the advantageous trait from other “hitchhiking” traits depends on its adoption by the preexisting population. Here, we adopt a similar wave-of-advance model based on food production on a heterogeneous landscape with multiple populations. Two key results arise from geographic inhomogeneity: the “subsistence boundary,” land so poor that the wave of advance is halted, and the temporary “diffusion boundary” where the wave cannot move into poorer areas until its gradient becomes sufficiently large. At diffusion boundaries, farming technology may pass to indigenous people already in those poorer lands, allowing their population to grow and resist encroachment by farmers. Ultimately, this adoption of technology leads to the halt in spread of the hitchhiking trait and establishment of a permanent “cultural boundary” between distinct cultures with equivalent technology.

In a seminal work, Ammerman and Cavalli-Sforza (1) analyzed the spread of farming technology through Europe in terms of a diffusive flow or displacement of population that they termed a demic flow. Earlier work (2) had considered “cultural” diffusion where technology was passed without significant movement of population. A quantitative model (3) of this “wave-of-advance” theory made use of the Fisher equation (4) with a wave speed of ≈1 km per year.

Demic flow (5, 6) raises the possibility that cultural, genetic (7, 8), and linguistic traits (6, 9) with no intrinsic advantage may “hitchhike,” i.e., spread with the advancing farmers. The Indo-European languages and the genetic distribution of European people (10) have been advanced as prime examples. Other processes, such as contact-induced language evolution (6) and other advancing technologies, such as horse husbandry, the wheel, and iron, are also claimed to be examples. A quantitative model of cultural hitchhiking is therefore of interest for determining how much common understanding of the general phenomenon can be gained by such a simple mechanism.

Hitchhiking is well studied in the genetic literature (11, 12), and loss of genetic diversity through culture is known in whales (13); however, little has been done with continuous geography. Here, we incorporate inhomogeneous geography and the competing mechanisms of demic and cultural diffusion into a model (14) that can give either wave of advance or diffusion and growth scenarios.

Although a deterministic model ignores crucial rare events, it should be regarded as a historical null hypothesis. Its predictions can be taken as requiring no special explanation, and its failures can be taken as evidence of rare events that had significant and long-lived consequences.

Results and Discussion

We consider four different scenarios: Europe, India, South Africa, and a simple test geography. Figs. 1–4 provide a limited visualization of each case, and animated movies are available as supporting information (SI) Movies 1–3. The parameters of the model are derived from estimable quantities such as birth rates, death rates, population densities, and land fertility. In the farming scenario, a 5-year birth interval is assumed for the hunter–gatherer lifestyle, where it is convenient for a women to carry only one small child at a time. For farming cultures, the birth interval is 2 years (5). We assume a lifespan of 50 years. The higher density of food production permitted by farming leads to population densities of neolithic farmers (F) and converts (X), which are a factor of 50 higher than for indigenous hunter-gatherers (H). The most fertile land supports a farming population density of 50 people per km², declining with altitude and mean temperature.

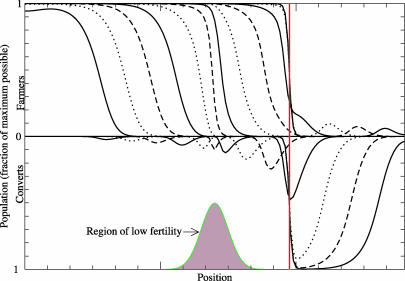
Fig. 1.

Results from test area for population density at a series of times (alternating solid/dotted/dashed lines). The red line shows the final cultural boundary. The wave speed is ≈1.1 km/yr (see SI Applet, with which the reader can explore parameter sensitivity).

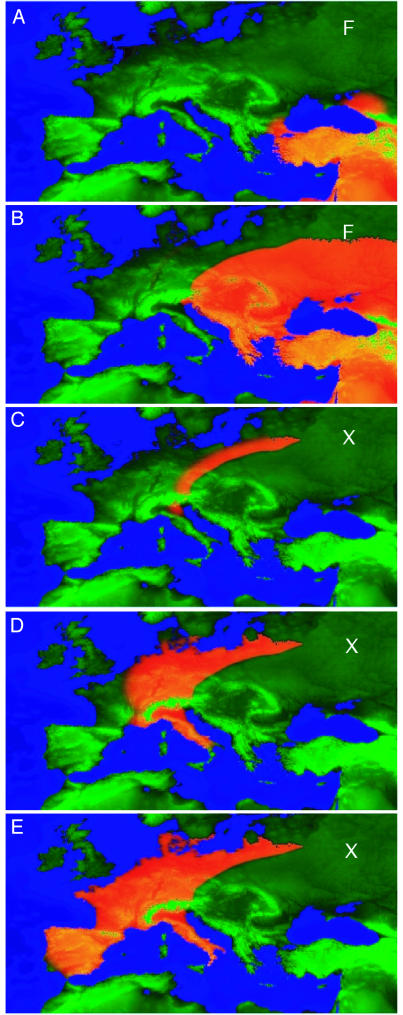
Fig. 2.

Snapshots from our European scenario: fertile areas are bright green, and infertile areas are dark green. Altitude is adjusted for sea-level rise to create an evolving map of Europe since 11,000 B.P. Population density is shown in orange. The first F snapshot shows the bottlenecks around the Black Sea, which act as secondary sources for F (9,500 B.P.), and the second F snapshot shows the final distribution of F. The snapshots labeled X show the evolving distribution of X from 8,000 B.P.).

Fig. 3.

India. The four F snapshots show an F wave spreading from the fertile crescent along the coast into India (11000 B.P.–6,000 B.P.). The fourth F snapshot represents the final distribution of F. The snapshots labeled X show the early (6,000 B.P.) and final distribution of X, respectively.

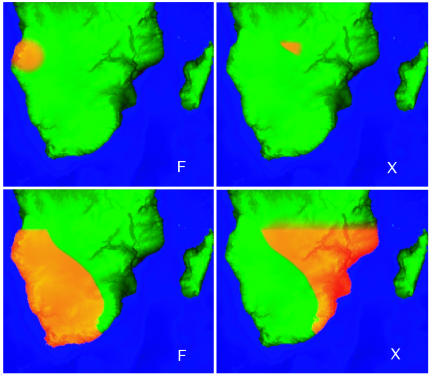
Fig. 4.

Early and final distributions of Europeans (F) (Left) and postcontact and final populations of converts (Right). Above 12.5° south latitude, there is a saturated population of Bantu farmers (H), which cannot be invaded. Below this 12.5° south latitude, the H population represents Khosians who do not convert to farming. We use the same numerical parameters as before, but because transport is considerably more modern, and population grows by immigration as well as birth, time is rescaled to give a 300-year time scale. If only the diffusion time scale is altered (D = 120 km²/yr) no wave is formed. Europeans colonize the whole area at low population, but after a period of coexistence, they are eliminated by Bantu converts (X) advancing from the north.

Test Geography.

The test geography was developed to investigate parameterization, measure wave speed, and examine various boundaries. It comprises an artificial map, symmetric in latitude, with a Gaussian-shaped mountain range of low fertility and diffusion.

Fig. 1 shows a situation where F is initiated at a single position within a preexisting saturation population of H. F expands and spread as a wave, with a halo of X in the transition region. The wave front is slowed at the mountains where diffusivity (D) is lower. If the mountains are high enough to form a subsistence boundary, the wave stops. If lower, but sufficiently steep, a diffusion boundary occurs, and the F-wavefront steepens until the boundary is crossed. Meanwhile, technology diffusion continues, and the halo of X develops a pronounced skew as conversion of H to X becomes significant. The trailing converts are displaced by the advancing F, but the X peak grows steadily in strength from further conversion. Ultimately, the convert population is strong enough to stop the F advance, and a cultural boundary is formed that steadily sharpens. Cultural boundary formation is accelerated by the mountain range, but does not necessarily coincide with it.

We also used the test area to examine including a time delay (15–17) to account for childhood: this time delay slows the wave, but the behavior can be exactly replicated by using a larger time scale (τ) or smaller D. Similarly, for small population sizes the wave advances more slowly (18). This effect is more important, because it means that delays at bottlenecks will be more pronounced than the model suggests; these areas also are most sensitive to specific historical events and discretization of geographic data. Rather than attempt ad hoc adjustments, we simply note that the model is sensitive to behavior at bottlenecks and emphasize when these occur.

Having established the behavior of the model in separating the beneficial trait (farming) from the neutral one (F or X culture), we apply the model to real historical events. We reiterate that some outcomes of simulations may be sensitive to the choice of different parameters. Owing to parameter uncertainty, we cannot claim to have definitive answers; however, we can show plausible locations of cultural/genetic boundaries, which, in turn, can help determine the origin of the technological wave of advance. The model does not necessarily form a wave: if diffusion is faster than growth, coexistence and slow replacement occurs. See the SI Applet, which allows the reader to test parameter sensitivities in the test area.

Europe.

Europe is the locale for which most evidence of the arrival of neolithic farming is available. However, there is still debate about how the neolithic transition happened and how relevant it is for potential hitchhiking traits of archaeology, linguistics, and genetics.

Fig. 2 shows our European scenario. It is based on a point source of F in the fertile crescent at 11,000 B.P. and a saturation population of H elsewhere. Parameterization gives a wave solution reaching the Bosphorus by 9,600 B.P., consistent with the wavefront speed of 1 km/yr observed for the neolithic advance (19). The wave slows at bottlenecks there and in the Caucasus. In a different scenario, these bottlenecks may also explain the late arrival of Homo sapiens into Europe, a similar wave that swept the Neanderthal population to extinction, probably in southern Spain (20, 21). The bottlenecks act as secondary sources, so the history of spread through the Middle East has no effect on the final cultural boundaries.

Hence the arrival into Europe appears to come from two sources: north and south of the Black Sea. Herein lies an uncertainty in the model: it is entirely possible that crossing these bottlenecks could be delayed by historical events. There is strong evidence that farming spread through the Ukraine from the West (contrary to Fig. 2), implying that the bottleneck effect is important.

As the wave reaches central Europe, the twin halo of “converts” becomes the dominant population. Henceforth the converts bring farming into Europe. The location of this boundary is sensitive to the choice of parameters and detailed events at the bottlenecks. If the population increase is slow, converts take over immediately (and repeatedly). If migration is faster the F occupy all of Europe.

Work by Zvelebil (22) and radiocarbon evidence (23) suggests a corridor of F stretching from Turkey along the Danube and Rhine/Elbe watersheds to the North Sea. This rapid migration has been explained by a “leap frog” model in which small isolated enclaves of farming were formed by small-scale, long-distance migration. Those small farming enclaves acted as sources, quickly overwhelmed by converts who spread farming to the rest of Europe. However, we find that the same distribution can be reproduced assuming no F-wave via the Caucasus bottleneck and enhanced migration rates along major rivers (24, 25). Further evidence for water-borne travel is the settlement of Crete by 8,000 B.P. and the fact that in our model, farming fails to reach the British Isles before the land bridge across the channel vanishes ≈8,500 B.P., regardless of whether the F–X transition occurs.

A final feature of the European model is the existence of “mountain kingdoms” of converts surrounded by F. This phenomenon happens if the F-wave passes around a farming subsistence boundary, trapping an H population, which become X as warming makes the land more viable for farming. Mountain kingdom formation requires that the hunter–gatherer population is able to sustain itself in areas inaccessible to farming. Survival of such mountain kingdoms would require continuous strong defenses to avoid subsequent invasion, but may be a possible explanation for the Basque isolate language.

We note that the cultural boundary may be different for genetic and linguistic traits and over time will be broadened by interbreeding/mixing. Thus, although Indo-European languages completely dominate Europe, genetic traits appear as a gradient (10). The LinearBandKeramik (LBK) style has a boundary close to that shown in Fig. 2 with two exceptions: it does not extend east into the region occupied via the Caucasus route, and it extends further along the Rhine–Danube corridor (6). This finding suggests LBK first arose after the wave reached southern Europe and traveled faster along rivers than elsewhere.

India.

India has four language families, the largest of which are Indo-European and Dravidian. There is debate about whether the Indo-European language was introduced alongside farming, horse riding, or iron technology. Our model is applicable to any such waves of advance, if the appropriate parameters and starting conditions are used.

For consistency of notation we continue to refer to the culture bringing new technology as F, the preexisting culture as H, and the converts as X.

The starting position of F is the same as in the European scenario. The F population spreads evenly across the fertile crescent and along the coast toward India. As the wave reaches the northwest of the subcontinent, the switch from F to X occurs, creating a cultural boundary (Fig. 3). The exact location of this transition is strongly parameter-dependent, but the existence of a boundary is not. An intriguing result is the splitting of the X population into two groups, one in southern India and an enclave in Pakistan. This distribution is remarkably similar to the distribution of Dravidian speakers today, suggesting that the Dravidian language group predates Indo-European in India and was split into two groups by the advancing Indo-Europeans. Simulations with the new technology that started in southern Russia or the Far East do not give the enclave, supporting the idea that Indo-European came from the Middle East. Genetic evidence (26) also supports this invasion from the west.

Bottlenecks around Afghanistan act as secondary sources, making the initial starting point less important and specific events promoting or inhibiting the wave in these areas crucial to subsequent history.

It thus seems possible that Middle Eastern farmers are responsible for establishing Indo-European language in India. However, an alternate scenario is possible in which farming arrived from the east, where rice and buffalo were domesticated, introducing the Dravidian language throughout India. A subsequent wave of advance, as simulated, based perhaps on horses or iron age, introduced Indo-European language and genes. Yet another theory is that Dravidian arrived with farming from the west and the language was adopted throughout India. It may seem odd that the same people who carried the Indo-European language to Europe should speak a different language on their journey east, although the Iran–Afghan bottleneck may have induced an F–X transition. Still others (3) speculate that Indo-European may not have been the language of the farmers at all, as some linguistic evidence points to a Caucasian origin of the language. This theory suggests that Indo-European hitchhiked alongside horse and iron in both Europe and India. All of these theories can be modeled with different parameters and starting conditions. Although details vary with parameterization, only the wave of advance from the fertile crescent yields the splitting into disjoint Dravidian-speaking populations.

Southern Africa.

Southern Africa provides a more recent example of a wave of advance with a totally different set of boundary conditions. It is likely that a previous wave of advance swept farming and the Bantu language group through Central Africa. However, the crops used (e.g., sorghum and millet) were not suitable for the Mediterranean climate of South Africa. When the first European settlers arrived in 1652, farming had yet to reach the southern tip of Africa, despite the large population of Bantu-speaking farmers to the north. When the European settlers came in contact with the African farmers, the latter adopted wheat and barley, which enabled them to expand southward (27).

To investigate this hypothesis within our model, we set initially one H population (Bantu) at F saturation in the north, able to convert to X and another at H densities elsewhere (Khoisan) unable to convert to X on the time scales of this simulation. Bantu farmers without European cereals are unable to migrate below 12.5° south.

As soon as the European F make contact with the large Bantu population, converts are formed (Fig. 4Upper Right) and compete successfully with the F. Both ultimately take control of about half the land mass available (Fig. 4 Lower). The X region correlates well with the present-day distribution of Bantu speakers.

Although the starting conditions are a rough approximation to real historical events, the model shows that the passing of new technology, which allows an already well established population to access new territory, leads to strong competition and that converts from the large population (Bantu) can overwhelm the indigenous small population (Khoisan) before they can adopt the new technology themselves. If the diffusion constant is increased by a factor of three without increasing the birth rate, a different scenario appears: the F population colonizes the area, but is then wiped out by advancing X. Obviously, a full model should also include immigration (changed boundary condition) and warfare technologies (different interpopulation competition) from Europe.

Conclusions

We have rederived a Fisher-type equation to incorporate both real geography and multiple populations characterized by either advantageous or neutral traits. It may be used to investigate putative cases where spread of technological advances may be associated with spread of cultural traits.

With neolithic-era migration rates, the model forms a singular wave, which can be halted permanently by subsistence boundaries and temporarily by diffusion boundaries and is ultimately terminated by a cultural boundary. The subsistence boundaries can ultimately be overcome by further technological development. More rapid modern migration rates do not permit the establishment of a wave solution, and cultural boundaries are not observed.

We have shown that a trait that has no intrinsic benefit can hitchhike along with an advancing advantageous trait, but that at some point the hitchhiking trait can be dropped as the technology is adopted by the preexisting population. If the hitchhiking trait does not mix with the preexisting population, a sharp cultural boundary is formed. Although features such as mountains affect the position of the boundary, it is not usually coincident with them. Although the model may reach a final steady state with sharp boundaries, these boundaries are unlikely to remain sharp over time: the model assumes a limiting case with no mixing of genes or culture. Hence, where current-day genetics shows a gradient across Europe, this mixing may have arisen from subsequent intermarriage.

Case studies highlight crucial geographic barriers and bottlenecks, which act as secondary sources of the wave. We reemphasize that bottlenecks coincide with small populations: we assume smooth population variation, but the wave speed may fluctuate significantly because of stochasticity for small populations (18).

The “beneficial” population traits are not necessarily beneficial at an individual level: the F and X populations typically have lower food intake per person and shorter lifespans than the H population.

By making a quantitative model incorporating both demic and cultural diffusion, we enable arguments previously made verbally to be investigated computationally. Although the exact choice of parameters is scenario-dependent, the model enables us to determine which results are generally stable and historically inevitable and which are more sensitive to specific events.

Model and Methods

Cohen (14) generalized the Fisher equation for a single population to account for varying environment. His model was defined by four culture-, biology-, and technology-dependent parameters (birth rate, death rate, food consumption, and area required per person) and two geographical parameters (land fertility and ease of travel). Details are given in SI Appendix.

To investigate the hitchhiking effect of neutral cultural traits, we consider three populations: the bearers of the new technology, the preexisting population, and members of the preexisting population who adopt the new technology. For notational convenience we refer to them by analogy with Ammerman and Cavalli-Sforza (1) as: neolithic farmers (F), indigenous hunter–gatherers (H), and converts (X). Converts are hunter–gatherers who have adopted farming culture but retain other cultural traits such as language or genetics. The three cultures coexist, competing for territory, but do not mix.

In addition to demic diffusion, we introduce two further interactions. Hunter–gatherers (H) become convert farmers (X) by technology transfer on contact with other farmers (F or X). There is also direct competition between F and X. Depending on the trait that distinguishes the populations, this competition may represent ethnic conflicts between groups, dominance of a particular language, or adoption of artistic style. In the genetic context this competition is equivalent to assortative mating, which is unlikely to be true for the farming transition. For genetic maps, mixing is more appropriate (28), which leads to a gradient of genetic markers rather than a cultural boundary, similar to a geographically homogeneous model (29). The female lineage may also differ from the male (30).

The implementation of these two interactions into Cohen's (14) equation gives a set of coupled logistic population equations (see Eqs. 1–43 in SI Appendix):

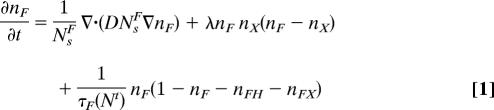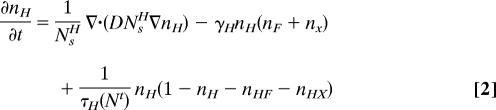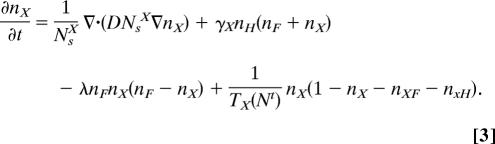Here D is a diffusivity, τ_i is the time scale for increase of population i, and N_sⁱ is the maximum population possible (“saturation”). The n_i are the fractions of maximum population currently attained by population i, and N^t is the total population of all types. γ is the rate of technology transfer, and λ is the rate at which the stronger population eliminates the weaker n_ij = n_jN_s^j/N_sⁱ; numerical values for these parameters are given in Table 1 in SI Appendix.

The actual behavior depends on the parameterization of how superior the F and X technology is to that of H and on the initial conditions. If the F population starts at a single location, a demic diffusion wave forms; however, the wave halts at (or is diffracted by) subsistence boundaries, permanent features such as oceans and mountains where living and/or farming is impossible. More subtly the wavefront can also stop if the land quality decreases steeply enough relative to the population gradient, forming a diffusion boundary, restarting once the population in the more fertile region has grown. If enough converts are created, the advancing wave may continue based on the X population rather than F. Thus cultural boundaries are formed across which the beneficial trait is transmitted, but the hitchhiking traits are not.

Having developed the mathematical framework for a multitrait wave of advance, we apply it to specific cases. We use geographic data from the U.S. National Geophysical Data Center (www.ngdc.noaa.gov/mgg/gdas/gd-designagrid.html) to build a realistic, inhomogeneous land model. The topographic data array was discretized to 6 min of arc, and the altitude data were modified for rising sea level to create an evolving map. The land fertility is modeled as a function of temperature and altitude. The parameters were first adjusted to fit present-day conditions, then uniformly cooled to simulate the postglacial period. The appropriate coordinate transformation of the diffusion equation was implemented to describe the unequal area grid on a spherical earth.