DNA condensation in two dimensions

Abstract

We have found that divalent electrolyte counterions common in biological cells (Ca²⁺, Mg²⁺, and Mn²⁺ ) can condense anionic DNA molecules confined to two-dimensional cationic surfaces. DNA-condensing agents in vivo include cationic histones and polyamines spermidine and spermine with sufficiently high valence (Z) 3 or larger. In vitro studies show that electrostatic forces between DNA chains in bulk aqueous solution containing divalent counterions remain purely repulsive, and DNA condensation requires counterion valence Z ≥ 3. In striking contrast to bulk behavior, synchrotron x-ray diffraction and optical absorption experiments show that above a critical divalent counterion concentration the electrostatic forces between DNA chains adsorbed on surfaces of cationic membranes reverse from repulsive to attractive and lead to a chain collapse transition into a condensed phase of DNA tethered by divalent counterions. This demonstrates the importance of spatial dimensionality to intermolecular interactions where nonspecific counterion-induced electrostatic attractions between the like-charged polyelectrolytes overwhelm the electrostatic repulsions on a surface for Z = 2. This new phase, with a one-dimensional counterion liquid trapped between DNA chains at a density of 0.63 counterions per DNA bp, represents the most compact state of DNA on a surface in vitro and suggests applications in high-density storage of genetic information and organo-metallic materials processing.

The existence of distinct states of DNA compaction is vital to the functions of viruses, bacteria, and eukaryotic cells (1). The more compact states lead to the efficient packing of colossal genomic DNA molecules within the small confines of the cell nucleus, the bacterial cytoplasm, and viral capsids. Equally important are the less compact states of DNA required during much of the cell life cycle to allow proteins access to the DNA template for a multitude of biological tasks (e.g., gene regulation, transcription, replication). The biologically relevant DNA-condensing agents in vivo include cationic proteins (e.g., histones) and polyamines such as spermidine and spermine with sufficiently high counterion valence (Z ≥ 3) (1–5). In bacteria, polyamine molecules such as spermine (4⁺) and spermidine (3⁺) are known to be critical for DNA compaction (1). Polyamines also are required in DNA catenation (interlocking) by topoisomerases, presumably for locally condensing neighboring DNA segments (1, 6).

There have been a number of theoretical (7–11) and experimental studies aimed at elucidating the fundamental physical mechanisms responsible for DNA condensation. Experimental studies done in vitro have found that DNA condensation from bulk solution critically depends on the valence of the counterions and that a valence of 3 or larger is required to overcome the inherently large electrostatic repulsive barrier between the like-charged polyelectrolytes (2–5). Furthermore, experiments show that counterions with Z = 2 simply provide screening of the electrostatic repulsions but do not lead to DNA collapse. It has been suggested that interactions between like-charged particles in electrolyte solutions may be affected in confined geometries near macroscopic surfaces. In particular, anionic colloidal spheres were found to attract each other in weak monovalent salt solutions near a surface (12, 13).

In this paper we show that the spatial dimension available to DNA plays a key role in the intermolecular interactions. Specifically, DNA chains adsorbed between cationic membranes within the lamellar (L_α^c) phase of cationic lipid (CL)-DNA complexes (14–17) are found to undergo a collapse transition in the presence of simple divalent cationic biological salts, namely Ca²⁺, Mg²⁺, and Mn²⁺. Co²⁺ also was used because its absorption peak in the visible at 512 nm allowed a direct measurement of binding to DNA in the collapsed phase. Synchrotron x-ray diffraction (XRD) and absorption measurements show that the collapsed phase consists of DNA chains electrostatically tethered by divalent counterions in two dimensions (2D). The trapped counterions form a novel one-dimensional (1D) liquid between the molecular chains at a density of 0.63 ions/DNA base pair. Thus, these simple divalent ions may play a critical role in controlling the compaction state of genomic nucleic acid, for example, in rod-shaped viruses where the genome is adsorbed onto a curved cationic protein surface. Furthermore, the observed enhanced counterion mediated attractive forces, leading to the DNA condensation for Z = 2 in 2D, may act between any like-charged polyelectrolyte macromolecules, such as cytoskeletal fibers or charged polypeptides adsorbed onto or near surfaces in vivo.

Materials and Methods

Materials.

The CLs consisted of binary mixtures of cationic monovalent lipid DOTAP (dioleoyl trimethylammonium propane) and the neutral colipid DOPC (dioleoyl phosphatidyl choline), both lipids having two 18- carbon (C₁₈) aliphatic chains per molecule. All lipids were purchased from Avanti Polar Lipids. We used highly purified linear λ-phage DNA (48,502 bp, contour length of 16.5 μm) from New England Biolabs.

X-Ray Samples.

CL-DNA-salt complexes were prepared by mixing deionized water solutions of linear λ-phage DNA (5 mg/ml) and CLs of mixed lipids (25 mg/ml) directly in 1.5-mm diameter quartz x-ray capillaries with ρ = DOTAP/DNA = 2.2 (wt/wt), which yielded isoelectric (charge-neutral) complexes and adding an appropriate amount of the salt solution to achieve a final salt concentration. The CLs consisting of binary DOPC/DOTAP mixtures were prepared by sonication and had an average size of 0.06 μm. During the CL-DNA complex formation CLs replace DNA counterions, releasing >95% of the Na⁺ and Cl^- (from DNA and lipids, respectively) ions into solution with a very large entropic free energy gain (of order k_BT per released counterion). The result is a close association between DNA and lipid in a compact complex with an average size of 0.2 μm. We previously have established that the complex structure does not change with the overall DNA and lipid concentration of the samples (14, 17).

Samples for Optical Density Measurements.

CL-DNA complexes were prepared in 1.5-ml microcentrifuge tubes at the same lipid and DNA concentrations as for x-ray measurements with a known total amount of CoCl₂ added to a final salt concentration M. After equilibrating for several days, the condensed complexes were separated from the supernatant and unbound Co²⁺ ions by centrifugation (10,000 rpm) and subsequent ultrafiltration through 10,000 MWCO filters (Millipore). The Co²⁺ ions were quantified in the supernatant by measuring the optical density at 512 nm. The difference of the Co²⁺ concentrations in supernatant and the original salt solution gave the amount of Co²⁺ retained within the complexes. We have confirmed that no DNA or lipid was lost into the supernatant during the procedure.

XRD.

The XRD experiments were carried out at the Stanford Synchrotron Radiation Laboratory at 10 keV. The unoriented (powder) samples sealed in 1.5-mm quartz x-ray capillaries were mounted on a standard four-circle diffractometer. We used a double bounce Si (111) monochromator crystal and a series of slits before and after the sample to obtain a longitudinal resolution of 0.001 Å^-1 [(half-width-at-half-maximum (HWHM)] and an out-of-plane resolution of 0.004 Å^-1 (HWHM).

Results and Discussion

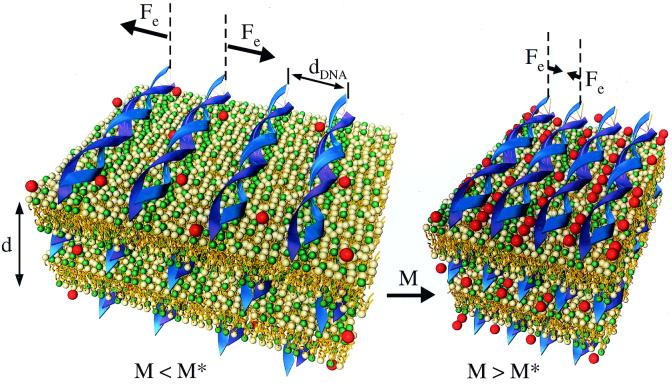
To explore the nature of DNA compaction on a surface we have used the lamellar (L_α^c) phase of CL-DNA complexes (14–18) in the presence of multivalent cations as an ideal in vitro model system. CL-DNA complexes are one of the most promising synthetic vehicles for gene delivery applications (19–22). It has been demonstrated that CL-DNA complexes are comprised of liquid crystalline self-assemblies with well-defined structures (14–17, 23, 24). The structure and thermodynamic stability of these CL-DNA complexes also has been the subject of much recent theoretical work (25–30). The L_α^c complexes consist of locally ordered 1D arrays of DNA chains intercalated between oppositely charged membrane bilayers with the chains uncorrelated between different layers (Fig. 1 Left) (14–16). The nanoscale parameters of these complexes can be precisely controlled. In the absence of added salt the interactions between DNA chains in L_α^c complexes are dominated by long-range repulsive forces extending to near 60 Å (14–16), consistent with recent theory (25, 26). Thus, the 2D arrays of DNA molecules occupy all of the available membrane area and the average interaxial spacing between DNA chains (d_DNA, Fig. 1 Left) for isoelectric (ρ = DOTAP/DNA weight ratio = 2.2) CL-DNA complexes is fixed between 24.55 Å < d_DNA < 57.1 Å by the membrane charge density. Here, d_DNA is experimentally controlled by changing the mole fraction of neutral lipid DOPC (Φ_DOPC) in the bilayers between 0 < Φ_DOPC < 0.75 (14–16).

Figure 1.

Schematic illustration of the force reversal between DNA chains adsorbed on cationic membrane surfaces within the lamellar L_α^c phase. For divalent counterion concentrations M < M* the electrostatic forces (F_e) are repulsive. For M > M* the forces become attractive, which leads to the DNA condensation transition on a surface. In contrast, the electrostatic forces between DNA chains in bulk aqueous solution with divalent counterions are purely repulsive. During the transition, the spacing between the DNA double helices rapidly decreases to a separation of order the diameter of the condensing ions (shown as red spheres). In the condensed state (M > M*) there are ≈0.63 ions/base pair along the DNA.

We note that the repulsive interactions between DNA chains adsorbed on cationic membranes is analogous to other charged systems where the spacing between the objects is set by a constraint. For example, the spacing between charged membranes (31, 32), charged colloids (33), and DNA chains (34), suspended in salt-free water, is set by the constraint of the finite volume occupied by the objects and not a result of a balance of attractive and repulsive forces. In the CL-DNA system the membrane charge density is the constraint that sets d_DNA. In each of these systems, the total charge within a unit cell is on average zero because of the presence of the counterions. However, in the absence of any added salt, in each case the interactions between the objects is long-ranged and repulsive and, for example, falling off with a power of the distance between the objects in the case of membrane sheets and DNA rods (31, 32, 34). The principal difference between these systems and the DNA-CL system is that the counterions are in solution in the former systems, whereas in the present case, the main counterions of interest are the CLs, which are confined to the 2D lipid membrane.

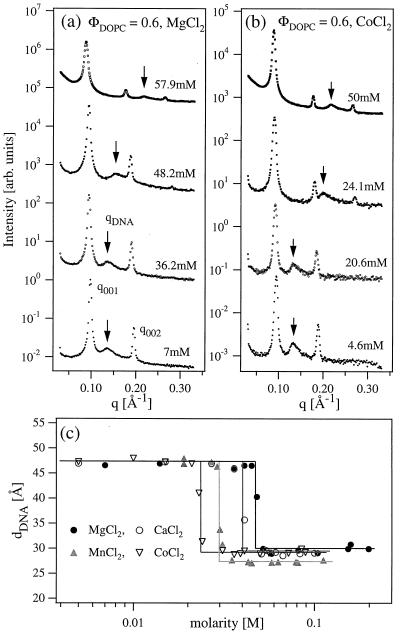
The XRD scans of isoelectric CL-DNA complexes at Φ_DOPC = 0.6 are shown in Fig. 2a as a function of increasing divalent MgCl₂ salt concentration (M). The x-ray profile at M = 7 mM is typical of the L_α^c complexes described previously (14–16) and shown schematically in Fig. 1 Left. The sharp lamellar peaks at q₀₀₁ and q₀₀₂ are caused by the alternating bilayer lipid-monolayer DNA structure with periodicity d = 2π/q₀₀₁ = 67 ± 1 Å equal to the combined thickness of lipid bilayer (δ_m = 42 Å) and DNA monolayer (hydrated DNA diameter ≈25 Å). The additional broad peak (arrow in Fig. 2) results from the 1D lattice of DNA chains with the peak position inversely proportional to the interaxial distance of d_DNA = 2π/q_DNA = 47 ± 0.5 Å determined by the total membrane area of the Φ_DOPC = 0.6 isoelectric complexes (14–16).

Figure 2.

(a) Synchrotron XRD measurements of the powder isoelectric [ρ = (weight lipid)/(weight DNA) = 2.2, Φ_DOPC = (weight DOPC)/(weight lipid) = mole fraction of DOPC = 0.6] CL-DNA complex samples in the presence of MgCl₂. d_DNA abruptly changes from 47 Å (set by Φ_DOPC) at low MgCl₂ concentrations (M) to 28.9 Å above M = M* = 48.2 mM. Also, the complex periodicity d increases to 70 ± 1 Å for M > M*. (b) Similar XRD measurements in the presence of CoCl₂ show that Co²⁺ ions also cause a condensation transition of the 2D DNA arrays but at smaller M* ≈ 24 mM. The (003) peak appears for M > M* in a and b, while the (004) is visible below and above M*. This is because the (003) peak in the lipid-DNA lamellar structure factor is near a zero crossing of the form factor. For M > M*, the screening of the head groups in the presence of the trapped counterions leads to a decrease in the area per charged head group. To match the change in the area per head, the area per tail decreases through chain stretching, which leads to a different position for the zero-crossing of the form factor. (c) Variation of the d_DNA with the concentrations of four different divalent salts.

As the MgCl₂ concentration is increased, the DNA spacing remains constant (36.2 mM scan), until a sharp transition is observed just above M = M* = 48.2 mM into a phase comprised of a condensed 1D lattice of DNA chains with d_DNA = 28.9 ± 0.5 Å at 57.9 mM (Fig. 2a, top profile). This is manifested in the small-angle x-ray-scattering (SAXS) by the abrupt and significant shift of the DNA peak position to higher q_DNA for M > M*. The observation of the sharp lamellar peaks at all salt concentrations indicates that the overall lamellar structure of the complex remains unchanged. In this highly condensed state the surfaces of neighboring DNA helices are separated by a distance ≈ 4 Å similar to the ionic diameter of the hydrated divalent ions (35). The condensation transition occurs over a remarkably narrow range of salt concentration ΔM ≈ 3 mM.

We emphasize that divalent cations do not cause DNA condensation in aqueous solution. The absence of bulk DNA condensation was confirmed with microscopic observations, light scattering, and XRD measurements up to 1 M salt concentrations for all of the divalent salts considered in this study. Furthermore, a sharp condensation transition of 2D DNA chains is not observed with monovalent salts (NaCl), which instead gradually modify the complex structure at higher (≈300 mM) salt concentrations (36).

Divalent metal salts other then Mg²⁺ also cause DNA condensation in 2D. The XRD scan sequence for the Φ_DOPC = 0.6, ρ = 2.2 complexes in the presence of CoCl₂ (Fig. 2b) is essentially similar to that with MgCl₂, with the d_DNA rapidly decreasing from 47.4 ± 0.5 Å at low salt to 29 ± 0.2 Å at high CoCl₂ concentration. However, the salt concentration M* of the condensation transition decreases with the increasing atomic number of the divalent ion: DNA is condensed with 24.1 mM CoCl₂, but is still uncondensed in the presence of 36.2 mM MgCl₂ (Fig. 2 a and b). The sharpness of the condensation transition and the dependence of M* on the divalent ion species is further demonstrated in Fig. 2c, which shows the variation d_DNA(M) for four different divalent cations. In the uncondensed phase the DNA spacing is fixed at d_DNA = 47 ± 0.5 Å by Φ_DOPC = 0.6 and remains constant independent of the ion type until a critical salt concentration M*. Above M* the 1D lattice of DNA chains condenses to a state where the surfaces of DNA molecules are separated by a distance of order the divalent cation diameter. This distance, d_DNA = 29 ± 0.4 Å, is independent of the ionic species with the exception of Mn²⁺, which causes condensation to a d_DNA = 27.3 Å about 2 Å smaller than the other divalent ions. The complex structure remains unchanged at higher salt concentrations M > M*, until the complexes dissociate because of the electrostatic ionic screening at M ≈ 300 mM, independent of the ion species. A recent atomic force microscopy (AFM) study of DNA chains adsorbed on cationic membranes in the transient presence of Mg²⁺ and Mn²⁺ does not find the collapse transition described here (37). To enhance contrast, the AFM imaging is carried out after the divalent ions are removed through rinsing. Thus, the actual divalent concentrations are more likely much less than that required for condensation.

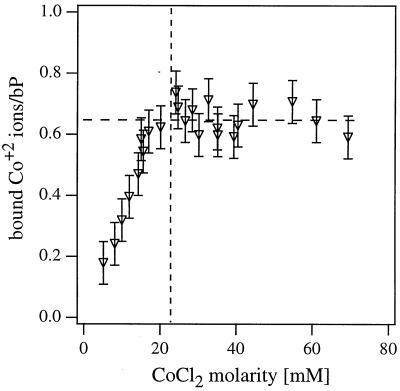
To further investigate the condensation transition we have measured the number of divalent Co²⁺ ions trapped within the L_α^c complexes. Co²⁺ absorbs visible light (with absorption peak at 512 nm), whereas lipids and DNA have measurable absorption in the UV part of the spectrum. Therefore, it is possible to quantify the ionic concentration within the complexes by separating them from the supernatant and measuring the supernatant optical density at 512 nm. The measured ionic content of the complex as a function of increasing CoCl₂ concentration is shown in Fig. 3. The ion concentration increases linearly with the solution salt concentration up to a value M* = 24 mM at which the DNA condensation transition is observed with the XRD measurements (Fig. 2b). For M > M* the concentration of Co²⁺ ions within the complex remains constant at ≈0.63 bound divalent metal ions/DNA base pair.

Figure 3.

The number of bound Co²⁺ counterions per DNA base pair as a function of the divalent salt CoCl₂ concentration. The counterion concentration within the isoelectric Φ_DOPC = 0.6 CL-DNA complexes with CoCl₂ was quantified directly by measuring the supernatant optical density at 512 nm.

The XRD and absorption data lead us to conclude that with increasing divalent salt concentration the L_α^c complexes undergo a transition between the two states depicted in Fig. 1. At low salt concentrations M < M* the DNA spacing is set by the membrane charge density and the divalent salt ions diffuse freely within the complex (Fig. 1 Left, M < M*). At a critical salt concentration M = M* the 2D-confined DNA undergoes a sharp transition into a state with DNA helices separated by the ionic diameter of the divalent ions. Thus, the condensed phase consists of DNA chains electrostatically tethered with short divalent linkers in 2D shown schematically in Fig. 1 Right (M > M*). The absence of a diffraction peak from the divalent counterions trapped between DNA chains, which we have measured to be at a density of ≈0.63 ions/DNA base pair, leads us to conclude that the divalent linkers must form a disordered 1D liquid between the DNA chains. This is also consistent with our observation for M > M* (57.9 mM in Fig. 2a and 50 mM in Fig. 2b), of a large SAXS that is absent for M < M*. The observed SAXS for M > M* is consistent with highly disordered trapped counterions between DNA chains, which lead to concentration fluctuations and the observed SAXS.

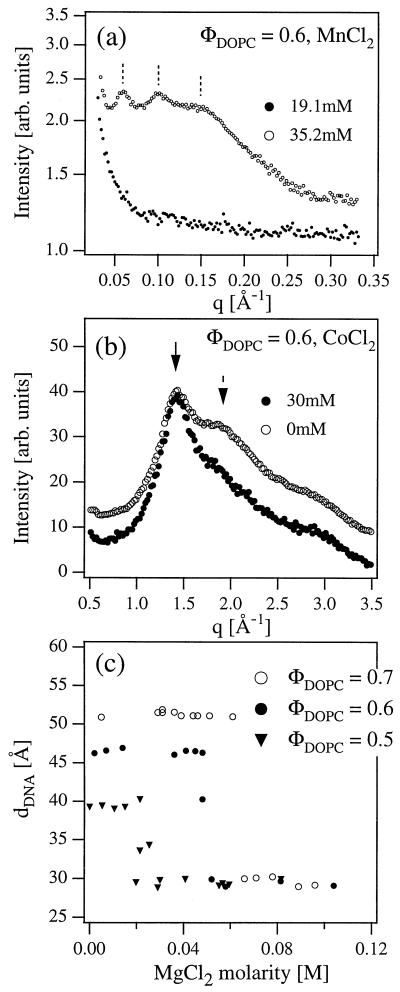
The overall charge neutrality of the CL-DNA-divalent ion complexes indicates that the transition should be accompanied by an expulsion of a fraction of CLs from the L_α^c stack. The lipid expulsion is observed directly by SAXS scans in the complex-free supernatant region of the samples (Fig. 4a). For M < M* at 19.1 mM MnCl₂ the supernatant scattering has no peak-like features, consistent with all lipid and DNA contained within the isoelectric complexes and no excess material present in solution. However, for M > M* at 35.2 mM MnCl₂ the XRD scan, showing three harmonics of a layering peak, indicates that a dilute lamellar lipid phase with periodicity d_l ≈ 100 Å coexists with the complexes. The large d_l indicates that this excess lipid phase consists of highly charged membranes and confirms that the DNA condensation transition is accompanied by an expulsion of CLs from the complexes, leading to coexistence with charged multilamellar vesicles in the supernatant.

Figure 4.

(a) Synchrotron XRD measurements of the complex supernatant below (●) and above (○) the condensation transition in the presence of MnCl₂. For M > M* the XRD pattern shows the existence of a multilamellar lipid phase of highly charged lipids expelled from the complexes during the 2D DNA condensation. (b) Wide-angle x-ray measurements of the complexes with CoCl₂. Solid arrow indicates the peak caused by the fluid lipid chain packing and dashed arrow indicates the peak of water. (c) The onset of condensation occurs at lower values of MgCl₂ concentration M* as the initial DNA interaxial spacing d_DNA is decreased from 50.3 Å to 47.0 Å to 39.5 Å for Φ_DOPC = 0.7, 0.6, and 0.5, respectively.

The x-ray data show unambiguously that the remaining lipids within the CL-DNA complex remain globally mixed and that there are no coexisting lamellar regions with a high and low density of cationic DOTAP in the complex. Such coexistence and global demixing would manifest themselves in the XRD pattern as two sets of lamellar diffraction peaks. Indeed, global lipid demixing does occur at very low volume fractions of CL (Φ_DOPC > 0.8), resulting in a coexistence of two lamellar phases with different average lipid compositions and, of course, a different d_DNA, determined by the average lipid charge density (15, 16, 36). All of the data reported here are for CL-DNA complexes in a single-phase lamellar region of the lipid composition phase diagram. Furthermore, global lipid demixing would lead to a d_DNA matching the lipid charge density, whereas the observed single d_DNA in the condensed 2D DNA phase matches the hydrated radius of the divalent ions. Therefore, global lipid demixing does not play a role in the observed attractive forces between the DNA chains for M > M*.

Within the single lamellar phase, we have local demixing with a higher concentration of CLs near the chains both for the uncondensed M < M* and condensed M > M* regions. Indeed, within mean-field theory, the local lipid distribution is determined self-consistently by the Poisson-Boltzmann equation between DNA chains sandwiched between cationic membranes (25, 26). Our data show that if DNA is confined to a 2D cationic membrane, then attractions caused by trapped divalent ions within the complex are sufficient to overcome the DNA chain-chain repulsions. The repulsions result from a combination of the osmotic pressure of the CL counterions and the pure Coulomb part. Except for a change in dimensionality from two to three, and interchanging CLs with counterions, the physics is similar for DNA chains in solution where one has local demixing (i.e., a nonuniform distribution) of counterions in solution between the chains both before and after DNA condensation; however, condensation requires counterions with Z ≥ 3.

The nature of the DNA condensation transition in 2D is further elucidated by measurements of the wide-angle x-ray diffraction scans of the complexes (Fig. 4b). The dominant features of this data are a peak at 1.43 Å^-1 because of the average chain packing density of the bilayer lipids and a pair of broad peaks at 1.9 Å^-1 and 2.8 Å^-1 because of the water liquid structure factor. Therefore, the ratio of the intensities of lipid and water peaks gives an indication of the relative amount of water within the L_α^c complex stack. For M < M* (Φ_DOPC = 0.6, 0 mM CoCl₂) the ratio of the 1.9 Å^-1 water peak and lipid peak intensities is 0.81, whereas it is 0.57 for M > M* (30 mM CoCl₂). Hence, there is substantially less water present within the condensed CL-DNA complexes than in the uncondensed ones. This is consistent with Fig. 1 because within the L_α^c complexes water is contained between the DNA strands, and this space is reduced and occupied by metal ions for M > M*.

The sharp condensation transition indicates a presence of a divalent ion-mediated attractive interaction between the DNA strands, whose strength increases with the salt concentration and at M = M* overcomes the electrostatic repulsion between the DNA helices that is present in L_α^c complexes without bound counterions (15, 16, 36). The experiments also show that the relative strengths of attractive to repulsive interactions increases as d_DNA decreases, indicating that the attractive interactions are shorter-ranged than the electrostatic repulsions. This is shown in Fig. 4c, which shows that the onset of condensation M* decreases as the uncondensed spacing d_DNA is decreased from d_DNA = 50.3 Å to 47.0 Å to 39.5 Å for Φ_DOPC = 0.7 to 0.6 to 0.5 for isoelectric complexes as a function of increasing MgCl₂. We note that for all Φ_DOPC, d_DNA exhibits exactly the same value in the condensed phase. This is strong evidence that the condensation by divalent counterions occurs because of a dimensionality effect rather than a lipid effect (where one would expect different d_DNA in the condensed phase at different Φ_DOPC).

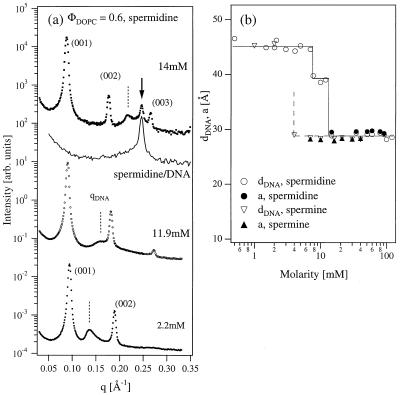
The ion-mediated interactions and condensation transition in 2D also were found to exist in complexes in the presence of higher valency ions, such as trivalent cationic polyamine spermidine. The XRD data for Φ_DOPC = 0.6 complexes with spermidine is shown in Fig. 5a. The 2D condensation transition takes place at M* ≈ 12 mM smaller than for any divalent cation. However, spermidine with Z = 3 also can condense DNA in the bulk with local hexagonal symmetry (5), which resulted in the observation of a coexistence between the 2D and 3D condensed DNA states at M ≥ 14 mM. In both phases the DNA strands are separated by a distance of order the spermidine molecular diameter (d_DNA = a = 28.9Å, Fig. 5b). Interestingly, in the presence of spermidine we have observed an intermediate DNA packing regime where the 2D DNA is only partially condensed with d_DNA = 39.1Å (Fig. 5b, 12 mM > M > 8 mM) before the onset of a tighter DNA packing phase and a 3D DNA condensation. Similar behavior is observed in complexes with higher (4⁺) valency spermine, which, as expected, causes the condensation transition at a lower M* ≈ 4 mM (Fig. 5b).

Figure 5.

(a) Synchrotron XRD measurements of the isoelectric Φ_DOPC = 0.6 complexes with trivalent polyamine spermidine chloride. Spermidine causes DNA condensation in 2D (DNA correlation peak indicated with dashed lines) at 11.9 mM, and at higher concentration also removes DNA out of the complexes into a coexisting phase of spermidine-condensed 3D DNA with hexagonal symmetry (solid arrow at 14 mM). Solid line shows a SAXS scan of pure bulk DNA condensed with ≈14 mM of spermidine (without lipids) and proves that the extra peak in 14 mM complex scan is caused by the coexisting spermidine-DNA phase. (b) Variation of d_DNA in complexes with spermidine and spermine. Also shown is the DNA spacing a in the bulk spermidine and spermine condensed DNA phase.

A number of theoretical papers have described different mechanisms leading to attractive forces between like-charged polyelectrolytes in bulk solution. The origin of attractive forces between polyelectrolytes lies in a phenomenon known as Manning condensation where counterions are bound to the polyelectrolyte backbone when the Manning parameter ξ = l_B/b (= 4.17 for DNA) > 1. Here, l_B = e²/ɛk_BT = 7.1 Å for water is the Bjerrum length and b = 1.7 Å for DNA is the distance between the negative charges on the polyelectrolyte backbone (38). Counterion condensation strongly suppresses the repulsive electrostatic interactions between the polymers with increasing Z by reducing the effective charge per unit length to a fraction 1/Zξ of its bare charge per unit length e^-/b. Oosawa (7) has shown that fluctuations in the bound counterion charge density of neighboring chains are correlated over large distances, producing a long-range attractive force f₁(d_DNA) similar to an effective van der Waals attraction and falling off as 1/d_DNA²,

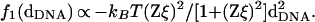1

In more recent theories bound counterions on adjacent DNA chains develop positional correlations (like a Wigner crystal lattice at T = 0), resulting in a short-range exponentially decaying force f₂(d_DNA) with both strength and range increasing with the ion valence Z as Z² and Z, respectively (8–10),

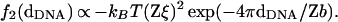2

This latter interaction is consistent with the results of computer simulations of DNA-like charged rods in bulk solutions (8). Because counterion condensation is entropically more favored as Z increases, attractive interactions become larger and electrostatic repulsions are suppressed with increasing Z (2–5, 7). This trend is indeed observed in experiments where monovalent and divalent salts do not cause DNA condensation from bulk aqueous solution and condensation in 3D requires Z = 3 or larger (2–5).

Although there are currently no models of attractions between rods confined to surfaces, both counterion-mediated forces described by Eqs. 1 and 2 are expected to be larger when DNA is confined in 2D. Manning condensation should be enhanced because there is a smaller entropy penalty with the free (unbound) counterions having only a 2D surface to explore. Also, the electric fields may be longer-ranged in these lower dimensional conditions, which would favor condensation (39). We also note that the observed DNA condensation on a surface occurs with only 63% of DNA charges neutralized with divalent ions. In contrast, bulk condensation occurs when nearly 90% of DNA charges are neutralized by the condensing counterions, which is only possible for Z ≥ 3 for bulk DNA (2–5). The observed onset M* of the condensation decreases with Z, indicating the increase of attractive force magnitude consistent with both Eqs. 1 and 2. Moreover, Fig. 4c shows that the attractive force decays faster than the counteracting repulsion of the DNA strands. The latter was found to decay as 1/d_DNA² in salt-free complexes (15, 16). Therefore, it is likely that the shorter-range attraction f₂(d_DNA) at least gives a large contribution to the forces observed in the present experiments. This is supported by the stronger dependence of magnitude and range of f₂(d_DNA) on Z and the possibility that f₂(d_DNA) may vary with the species of the divalent counterion (through e.g., the counterion diameter).

Conclusions

The data presented demonstrate that reduced spatial dimensionality from three to two in a polyelectrolyte system enhances counterion-mediated attractive forces. For DNA confined to a surface, these attractive forces are found to overcome repulsive forces, leading to a chain collapse transition into a condensed phase of DNA tethered by divalent (Z = 2) counterions. In contrast, condensation in bulk aqueous solution requires Z to be equal to or larger than 3. Significantly, all of the studied divalent salts cause condensation with M* decreasing monotonically with the ion atomic number. This shows unambiguously that the ion-mediated DNA attraction driving the condensation in 2D is not ion species-specific. This is in contrast to bulk DNA attraction where ion-specific effects have been suggested to modify inter-DNA forces (40): alkaline metals, such as Mg²⁺ and Ca²⁺, bind primarily to phosphates on the DNA backbone, whereas transition metals like Mn²⁺ also can bind to base oxygens and nitrogens exposed in grooves, therefore causing bulk DNA condensation in poor solvents or at high temperatures. The finding that the condensed d_DNA is smaller for Mn²⁺ than for alkaline metals substantiates that Mn²⁺ indeed fits within the DNA grooves.

Higher valency ions spermidine and spermine not only condense the 2D DNA arrays within the complexes, but also remove DNA from the complexes to form hexagonally packed polyamine-condensed DNA in bulk solution. This suggests a possible mechanism for intracellular DNA release from the CL-DNA complexes used in cell transfection experiments (19–24). Once removed from the CL-DNA complex, the DNA can easily dissociate from the short polyamine molecules, because the probability of the DNA dissociation from an oppositely charged oligo-electrolyte (i.e., a short polyelectrolyte) increases with decreasing oligo-electrolyte length.

The condensed phase of DNA chains tethered by divalent counterions in 2D may have interesting potential applications. The hybrid DNA-lipid-metal ion phase, with trapped metal ions forming a 1D liquid between the DNA chains at a density of 0.63 ions/DNA base pair, can be a precursor to novel organo-metallic materials (41). Different reaction routes may lead to the simultaneous large-scale synthesis of nanoscale wires. The extreme packing state for the DNA chains attached to surfaces within these lamellar L_α^c complexes renders these materials ideal for the high-density storage and straightforward retrieval of genetic information.

Abbreviations

2D

two-dimensional

CL

cationic lipid

Z

counterion valence

XRD

x-ray diffraction

1D

one-dimensional

DOTAP

dioleoyl trimethylammonium propane

DOPC

dioleoyl phosphatidyl choline

SAXS

small-angle x-ray-scattering