Algebraic orbifold conformal field theories

Abstract

The unitary rational orbifold conformal field theories in the algebraic quantum field theory and subfactor theory framework are formulated. Under general conditions, it is shown that the orbifold of a given unitary rational conformal field theory generates a unitary modular category. Many new unitary modular categories are obtained. It is also shown that the irreducible representations of orbifolds of rank one lattice vertex operator algebras give rise to unitary modular categories and determine the corresponding modular matrices, which has been conjectured for some time.

1. Introduction

Cosets and orbifolds are two methods of producing new two-dimensional conformal field theories from given ones (1). In refs. 2–5, unitary coset conformal field theories are formulated in the algebraic quantum field theory and subfactor theory (6) framework, and such a formulation is used to solve many questions beyond the reach of other approaches. The main purpose of this paper is to formulate unitary orbifold conformal field theories in the same framework and to give some applications of this formulation.

There is another approach to conformal field theories by using the theory of vertex operator algebras (cf. refs. 7 and 8). In the case of orbifolds, this has been studied, for example, in refs. 9 and 10. Although there are various advantages to these different approaches, our main results, Theorems 4.3 and 5.4, have not been obtained previously by other methods.

Under general conditions, as specified in Theorem 4.3, it is shown that the orbifold of given unitary rational conformal field theories generates a unitary modular category. Theorem 4.3 gives a large family of new unitary modular categories, which can be found in Sections 5 and 6. As an application of this general theory, it is shown in Theorem 5.4 that the irreducible representations of orbifolds of rank one lattice vertex operator algebras give rise to unitary modular categories [hence a unitary three-dimensional topological quantum field theory, cf. ref. 11] and the corresponding modular matrices are determined. More precisely, the simple objects of the modular categories are in one-to-one correspondence with the irreducible representations of these vertex operator algebras, which were classified in ref. 10. These simple objects and the modular matrices first appeared as examples in ref. 12 on the basis of certain heuristic arguments, and these examples can be clearly interpreted as a conjecture on the existence of certain unitary modular categories with the same modular matrices. Theorem 5.4 thus confirms this conjecture.

2. Preliminaries

First, the notion of irreducible conformal precosheaf and its covariant representations is recalled, as described in ref. 13.

By an interval, I shall always mean an open connected subset I of S¹ such that I and the interior I′ of its complement are nonempty. I shall denote by ℐ the set of intervals in S¹. I shall denote by PSL(2, R) the group of conformal transformations on the complex plane that preserve the orientation and leave the unit circle S¹ globally invariant. Denote by G the universal covering group of PSL(2, R). Notice that G is a simple Lie group and has a natural action on the unit circle S¹.

Denote by R(ϑ) the (lifting to G of the) rotation by an angle ϑ. This one-parameter subgroup of G will be referred to as rotation group (denoted by Rot) in the following. An irreducible conformal precosheaf 𝒜 of von Neumann algebras on the intervals of S¹ is a map

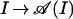from ℐ to the von Neumann algebras on a separable Hilbert space ℋ that satisfies the following properties:

• A.  Isotony. If I₁, I₂ are intervals and I₁ ⊂ I₂, then

  

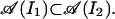
• B.  Conformal invariance. There is a nontrivial unitary representation U of G on ℋ such that

  

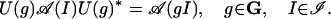
• C.  Positivity of the energy. The generator of the rotation subgroup U(R(ϑ)) is positive.

• D.  Locality. If I₀, I are disjoint intervals, then 𝒜(I₀) and A(I) commute. The lattice symbol ∨ will denote “the von Neumann algebra generated by.”

• E.  Existence of the vacuum. There exists a unit vector Ω (vacuum vector), which is U(G) invariant and cyclic for ∨_I∈ℐ𝒜(I).

• F.  Irreducibility. The only U(G)-invariant vectors are the scalar multiples of Ω.

The term irreducibility refers to the fact (cf. Proposition 1.2 of ref. 13) that under the assumption F ∨_I∈ℐ𝒜(I) = B(ℋ).

A covariant representation π of 𝒜 is a family of representations π_I of the von Neumann algebras 𝒜(I), I ∈ ℐ on a separable Hilbert space ℋ_π and a unitary representation U_π of the covering group G of PSL(2, R), such that the following properties hold:

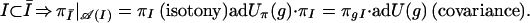A covariant representation π is called irreducible if ∨_I∈ℐπ(𝒜(I)) = B(ℋ_π). By our definition, the irreducible conformal precosheaf is in fact an irreducible representation of itself, and we will call this representation the vacuum representation.

Let H be a simply connected simply-laced compact Lie group. By Theorem 3.2 of ref. 14, the vacuum positive energy representation of the loop group LH (cf. refs. 15 or 16) at level k gives rise to an irreducible conformal precosheaf denoted by 𝒜_Hk. By Theorem 3.3 of ref. 14, every irreducible positive energy representation of the loop group LH at level k gives rise to an irreducible covariant representation of 𝒜_Hk. When H_k ⊂ G_l is a connected subgroup of a simply connected Lie group, Proposition 2.2 in ref. 2 gives an irreducible conformal precosheaf, which will be denoted by 𝒜_Gl/Hk, and this is referred to as the coset conformal precosheaf. We will see such examples in Section 4.

Next we will recall some of the results of ref. 17 and introduce notations.

Let {[ρ_i], i ∈ I} be a finite set of equivalence classes of irreducible covariant representations of an irreducible conformal precosheaf with finite index. For the definitions of the conjugation and composition of covariant representations, see Section 4 of ref. 14 or Section 2 of ref. 13.

Suppose this set is closed under conjugation and composition. We will denote the conjugate of [ρ_i] by [ρ_ı̄] and the identity sector by [1] if no confusion arises and let N_ij^k = 〈[ρ_i][ρ_j], [ρ_k]〉. Here 〈x, y〉 denotes the dimension of the space of intertwinners from x to y [denoted by Hom(x, y)] for any representations x and y (by Theorem 2.3 of ref. 13, we do not have to distinguish between local and global intertwinners here). We will denote by {T_e} a basis of isometries in Hom(ρ_k, ρ_iρ_j). The univalence of ρ_i and the statistical dimension of (cf. Section 2 of ref. 13) will be denoted by ω_ρi and d_ρi respectively.

Let φ_i be the unique minimal left inverse of ρ_i; define:

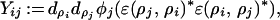where ɛ(ρ_j, ρ_i) is the unitary braiding operator (cf. ref. 13).

Define σ̃ := Σ_id_ρi²ω_ρi⁻¹. If the matrix (Y_ij) is invertible, by Proposition on p. 351 of ref. 17, σ̃ satisfies |σ̃|² = Σ_id_ρi². Suppose σ̃ = |σ̃|exp(ix), x ∈ ℝ. Define matrices

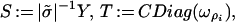where C := exp(i(x/3)). Then these matrices satisfy the algebraic relations:

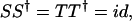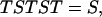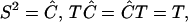where Ĉ_ij = δ_i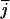 is the conjugation matrix. Moreover,

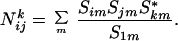1

Eq. 1 is known as the Verlinde formula, which determines the fusion rules N_ij^k from the S matrix.

3. The Orbifolds

Let 𝒜 be an irreducible conformal precosheaf on a Hilbert space ℋ, and let G be a finite group. Let V : G → U(ℋ) be a faithful§ unitary representation of G on ℋ.

Definition 3.1:

We say that G acts properly on 𝒜 if the following conditions are satisfied:

• (i)  For each fixed interval I and each g ∈ G, α_g(a) := V(g)aV(g*) ∈ 𝒜(I), ∀a ∈ 𝒜(I);

• (ii)  For each g ∈ G, V(g)Ω = Ω, ∀g ∈ G.

Remark 3.1:

As pointed out to us by Roberto Longo, conditions i and ii above imply that for each g ∈ G and h ∈ G, [V(g), U(h)] = 0 (cf. ref. 18), which is a condition we initially added in Definition 3.1. However, in all known examples, all three conditions above are easily checked.

Suppose a finite group G acts properly on 𝒜 as above. For each interval I, define ℬ(I) := {a ∈ 𝒜(I)|V(g)aV(g*) = a, ∀g ∈ G}. Let ℋ₀ = {x ∈ ℋ|V(g)x = x, ∀g ∈ G} and P₀, the projection from ℋ to ℋ₀. Notice that P₀ commutes with every element of ℬ(I) and U(g), ∀g ∈ G.

Define 𝒜^G(I) := ℬ(I)P₀ on ℋ₀. The unitary representation U of G on ℋ restricts to an unitary representation (still denoted by U) of G on ℋ₀. Then by using the definitions, one can check the following:

 Proposition 3.2. The map I ∈ ℐ → 𝒜^G(I) on ℋ₀ together with the unitary representation (still denoted by U) of G on ℋ₀ is an irreducible conformal precosheaf.

The irreducible conformal precosheaf in Proposition 3.2 will be denoted by 𝒜^G and will be called the orbifold of 𝒜 with respect to G.

Remark 3.3:

The net ℬ(I) ⊂ 𝒜(I) is a standard net of inclusions (cf. ref. 19) with conditional expectation ɛ defined by

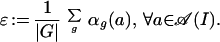Note that ɛ has finite index. We can therefore apply the theory in ref. 20 (also cf. refs. 21 and 22) to this setting. It follows, for example, that if G acts properly on 𝒜 as in Definition 3.1, then for each I, the action of G on 𝒜(I) is outer, i.e., ℬ(I)′ ∩ 𝒜(I) ≃ ℂ, where ℬ(I) is the fixed point subalgebra of 𝒜(I) under the action of G.

4. Complete Rationality

As in ref. 13, by an interval of the circle, we mean an open connected proper subset of the circle. If I is such an interval, then I′ will denote the interior of the complement of I in the circle. We will denote by ℐ the set of such intervals. Let I₁, I₂ ∈ ℐ. We say that I₁, I₂ are disjoint if Ī₁ ∩ Ī₂ = ∅, where Ī is the closure of I in S¹. When a I₁, I₂ are disjoint, I₁ ∪ I₂ is called a 1-disconnected interval in ref. 23. Denote by ℐ₂ the set of unions of disjoint 2 elements in ℐ. Let 𝒜 be an irreducible conformal precosheaf, as in Section 2.1. For E = I₁ ∪ I₂ ∈ ℐ₂, let I₃ ∪ I₄ be the interior of the complement of I₁ ∪ I₂ in S¹, where I₃, I₄ are disjoint intervals. Let

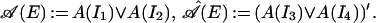Note that 𝒜(E) ⊂ 𝒜̂(E). Recall that a net 𝒜 is split if 𝒜(I₁) ∨ 𝒜(I₂) is naturally isomorphic to the tensor product of von Neumann algebras 𝒜(I₁) ⊗ 𝒜(I₂) for any disjoint intervals I₁, I₂ ∈ ℐ. 𝒜 is strongly additive if 𝒜(I₁) ∨ 𝒜(I₂) = 𝒜(I), where I₁ ∪ I₂ is obtained by removing an interior point from I.

Definition 4.1:

(complete rationality of ref. 24). 𝒜 is said to be completely rational, or μ rational, if 𝒜 is split, strongly additive, and the index [𝒜̂(E) : 𝒜(E)] is finite for some E ∈ ℐ₂. The value of the index [𝒜̂(E) : 𝒜(E)] (it is independent of E by Proposition 5 of ref. 24) is denoted by μ_𝒜 and is called the μ index of 𝒜.

Proposition 4.2. Let 𝒜 be an irreducible conformal precosheaf, and let G be a finite group acting properly on 𝒜. Suppose that 𝒜 is split and strongly additive. Then 𝒜^G is also split and strongly additive.

Proof:

It follows from the definitions that 𝒜^G is split.

Let I be an interval and I₁, I₂ be the connected components of a set obtained from I by removing an interior point of I. To show that 𝒜^G is strongly additive, it is sufficient to show that 𝒜(I₁) ∨ ℬ(I₂) = 𝒜(I). Let us show that 𝒜(I₁) ∨ ℬ(I₂) = 𝒜(I). First note that [𝒜(I) : 𝒜(I₁) ∨ ℬ(I₂)] < ∞. In fact, let I₂⁽ⁿ⁾ ⊂ I₂ be an increasing sequence of intervals such that I₂⁽ⁿ⁾ have one boundary point in common with I₂, Ī₁ ∩ Ī₂⁽ⁿ⁾ = ∅, and ∪_nI₂⁽ⁿ⁾ = I₂. By the additivity of the conformal net 𝒜 (cf. ref. 13), we have that 𝒜(I₁) ∨ ℬ(I₂⁽ⁿ⁾) [respectively 𝒜(I₁) ∨ 𝒜(I₂⁽ⁿ⁾)] are increasing sequences of von Neumann algebras such that

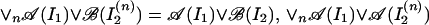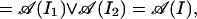where we have used the assumption that 𝒜 is strongly additive. By the splitting property, we have

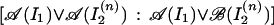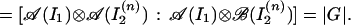It follows (cf. Proposition 3 of ref. 24) that [𝒜(I₁) : 𝒜(I₁) ∨ ℬ(I₂)] ≤ |G|.

So there exists a faithful normal conditional expectation ɛ̃ : 𝒜(I) → 𝒜(I₁) ∨ ℬ(I₂). Note that

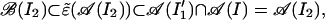and so ɛ̃(𝒜(I₂)) in an intermediate von Neumann algebra between ℬ(I₂) and 𝒜(I₂). So (cf. ref. 25 or refs. therein) there exists a subgroup K of G such that ɛ̃(𝒜(I₂)) is the pointwise fixed subalgebra of 𝒜(I₂) under the action of K. Because ℬ(I₂) ⊂ 𝒜(I₂) is irreducible by Remark 3.3, ɛ̃(𝒜(I₂)) ⊂ 𝒜(I₂) is also irreducible, and it follows that there exists a unique conditional expectation from 𝒜(I₂) to ɛ̃(𝒜(I₂)), given by

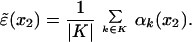Let us show that K is the trivial subgroup, i.e., if k ∈ K, then k is the identity element of G.

Let v ∈ 𝒜(I₂) be the isometry (cf. Section 2 of ref. 19) such that

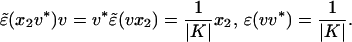Define a map γ̃ : 𝒜(I) → 𝒜(I₁) ∨ ℬ(I₂) by:

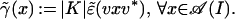One checks easily that

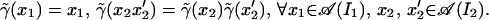It follows that γ̃(xy) = γ̃(x)γ̃(xy) for any x, y ∈ 𝒜(I), because 𝒜(I) is generated by two commuting subalgebras A(I₁) and A(I₂).

For any k ∈ K, define v_k = α_k(v) and

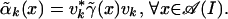Then one checks that

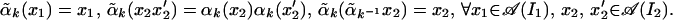It follows that

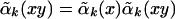for any x, y ∈ 𝒜(I), because 𝒜(I) is generated by two commuting subalgebras A(I₁) and A(I₂). One can also check similarly α̃_k(α̃_k⁻¹(x)) = x, ∀x ∈ 𝒜(I). So α̃_k is an automorphism of 𝒜(I). Because 𝒜(I) is a type III factor, there exists a unitary operator U_k ∈ B(H₀) such that α̃_k(x) = U_kxU*_k, ∀x ∈ 𝒜(I). Because α̃_k(x₁) = x₁, ∀x₁ ∈ 𝒜(I₁), we have U_k ∈ 𝒜(I₁)′ = 𝒜(I′₁) by Haag duality (cf. Section 2 of ref. 13).

If for all unitary U′ ∈ 𝒜(I′), (U_kU′Ω, Ω) = 0, then (U′Ω, U*_kΩ) = 0, and it follows that (𝒜(I′)Ω, U*_kΩ) = 0. Because 𝒜(I′)Ω is dense in ℋ by the Reeh–Schlieder theorem (cf. ref. 13), it follows that U*_kΩ = 0, which implies U*_k = 0 by using the Reeh–Schlieder theorem again because U*_k ∈ 𝒜(I′₁). Hence there exists a unitary U′ ∈ 𝒜(I′) such that (U_kU′Ω, Ω) ≠ 0. Note that 𝒜(I′) ⊂ 𝒜(I′₁). Replacing U_k by U_kU′ if necessary, we may assume that (U_kΩ, Ω) ≠ 0.

Let g_n ∈ G be a sequence of elements, such that g_nI′₁ = I′₁, and g_nI₂ is an increasing sequence of intervals containing I₂, i.e., I₂ ⊂ g_nI₂ ⊂ g_n+1I₂, and ∪_ng_nI₂ = I′₁ (one may take g_n to be a sequence of dilations). By applying Ad(U(g_n)) to the equation

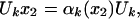and by using α_k(Ad(U(g_n))x₂) = Ad(U(g_n))(α_k(x₂)), we get

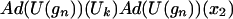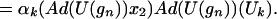It follows that

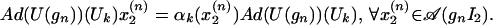Let U be a weak limit of Ad(U(g_n))(U_k). Note that

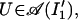because Ad(U(g_n))(U_k) ∈ 𝒜(I′₁) by our choice of g_n. Because (Ad(U(g_n))(U_k)Ω, Ω) = (U_kΩ, Ω) ≠ 0, where we use the fact that Ω is invariant under the action of U(g_n), it follows that

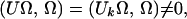so U ≠ 0, and we have

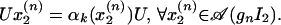Because ∪_ng_nI₂ = I′₁, ∨_n𝒜(g_nI₂) = A(I′₁) by the additivity of the conformal net 𝒜 (cf. ref. 13), it follows that

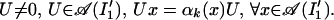Recalling that α_k is an automorphism of 𝒜(I′₁) and 𝒜(I′₁) is a factor, it follows that

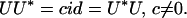Changing U into (1/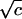)U if necessary, we may assume that U is unitary, and so we have

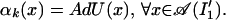So U ∈ B(I′₁)′ ∩ 𝒜(I′₁), and by Remark 3.3, AdU(x) = x = α_k(x), ∀x ∈ 𝒜(I′₁). It follows that V_kxΩ = xΩ, ∀x ∈ 𝒜(I′₁), and by the Reeh–Schlieder theorem, V_k = id, so k is the identity element in G. Because k ∈ K is arbitary, we have shown that K is the trivial group.

So 𝒜(I₁) ∨ ℬ(I₂) = 𝒜(I), and

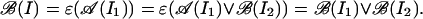 Theorem 4.3. Let 𝒜 be an irreducible conformal precosheaf, and let G be a finite group acting properly on 𝒜. Suppose 𝒜 is completely rational or μ rational as in Definition 4.1. Then there are only a finite number of irreducible covariant representations of 𝒜^G and they give rise to a unitary modular category as defined in II.5 of ref. 11 by the construction as given in Section 1.7 of ref. 5.

Proof:

This follows immediately from Proposition 4.2, Correlation 32 of ref. 24 and (2) of Correlation 1.7.3 of ref. 5.

Remark 4.3:

An irreducible covariant representation of 𝒜^G is called an untwisted representation if it appears as a summand in the restriction to 𝒜^G of a covariant representation of 𝒜. A representation is called twisted if it is not untwisted. By computing the μ indices, we can show that the set of twisted representations of 𝒜^G is not empty. This fact is first noticed in ref. 24 under the assumption that 𝒜^G is strongly additive. Note that this is very different from the case of cosets (cf. ref. 4, Correlation 3.2, where it was shown that under certain conditions there are no twisted representations for the coset).

5. A Class of Orbifolds

The irreducible conformal precosheaf 𝒜_U(1)2l associated with LU(1) at level 2l is studied in Section 3.5 of ref. 5. We have μ_𝒜U(1)2l = 2l, and there are exactly 2l irreducible representations of 𝒜_U(1)2l which is labeled by integer k, 0 ≤ k ≤ 2l − 1. By identifying ℝ^2M = (x, y) → x + iy ∈ ℂ^M, where x, y are column vectors with M real entries, we have the following natural inclusion LSU(M)₁ × LU(1)_M ⊂ LSpin(2M)₁, where U(1) acts on ℂ^M as a complex scalar, and the subscripts are the levels of the representations. Also note that we have natural inclusions LSpin(M)₂ ⊂ LSU(M)₁ ⊂ LSpin(2M)₁. Define J := (Id_M, −Id_M) ∈ SO(2M) and lift it to Spin(2M). Note that for A ∈ SU(M), JAJ = Ā, and JAJ = A if A ∈ Spin(M). From the definition, one can check that AdJ generates a proper ℤ₂ action on 𝒜_SU(M)1, and by using the branching rules for the inclusion LSpin(M)₂ ⊂ LSU(M)₁ in Section 4 of ref. 26, we can prove the following:

Lemma 5.1.

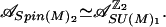Similarly, by using branching rules, we can prove the following:

Lemma 5.2.

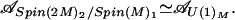One can use Lemmas 5.1, 5.2, Theorem 4.3, and the ideas of Section 4 of ref. 4 to determine the modular matrices as defined in Section 2 for 𝒜_Spin(M)2 and the net

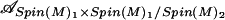associated to the diagonal coset LSpin(M)₂ ⊂ LSU(M)₁ × LSpin(M)₁. Details will appear elsewhere.

To state the results for the net 𝒜_{Spin(M)1×Spin(M)1/Spin(M)2}, recall the set of integrable weights of irreducible positive energy representations of LSpin(2l) at level k is given by:

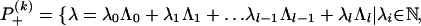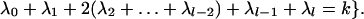When l is even, this set admits a ℤ₂ × ℤ₂ automorphism generated by A_s, A_v, where A_s, A_v are given by:

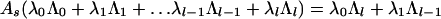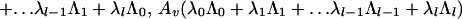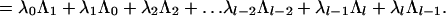When l is odd, this set admits a ℤ₄ automorphism generated by A_s, where A_s is given by

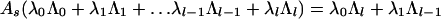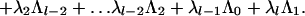These automorphisms will be called diagram automorphisms. Note that the set of diagram automorphisms is ℤ₂ × ℤ₂ when l is even and ℤ₄ when l is odd.

Theorem 4.6 of ref. 2, which concerns the ring structure of general diagonal cosets of type A, now holds for our diagonal coset, with the action of ℤ_N there replaced by ℤ₂ × ℤ₂ when l is even and by ℤ₄ when l is odd, because the proof of ref. 2 applies verbatim. As in Section 4.3 of ref. 2, I denote by [Λ̇, Λ̈; Λ] the orbit of (Λ̇, Λ̈; Λ) under the diagonal action of the diagram automorphisms, where (Λ̇, Λ̈) are the integrable weights (both at level 1) of LSpin(M) × LSpin(M). The following is a complete list of irreducible representations of 𝒜_{Spin(M)1×Spin(M)1/Spin(M)2}.

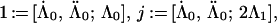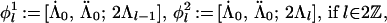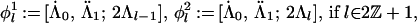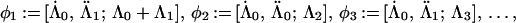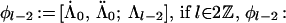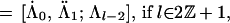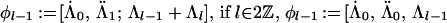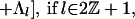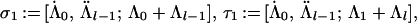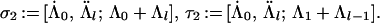2

I have also chosen the notations to make the comparisons with the notations of ref. 12 easy (l corresponds to N on pp. 517 and 518 of ref. 12).

The univalences of the above representations are given by:

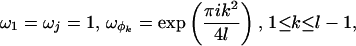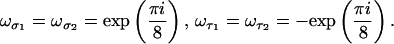By using the remark after Proposition 3.1 of ref. 4, the T matrix can be chosen to be

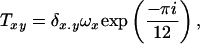3

where ω_x is given as above. One can then determine the S matrix [cf. (2) of Lemma 2.2 in ref. 3] for 𝒜_{Spin(M)1×Spin(M)1/Spin(M)2}. The notations in (7) have been chosen so that the S matrix is given by Table 1.

Table 1.

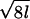× S matrix

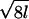× S	1	j	φlj	φk′	σj	τj
1	1	1	1	2
j	1	1	1	2	−	−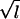
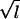
φli	1	1	(−1)l	2(−1)k′	bij	bij
φk	2	2	2(−1)k	4 cos	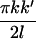0	0
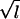
σi		−	bij	0	aij	−aij
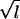
τi		−	bij	0	−aij	aij

Here a_ij = 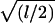(1 + (2δ_i,j − 1)exp(−(πil/2))), b_ij = (−1)^l+δ_i,j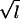 exp (πil/2), δ_i,j is the usual Delta function, and 1 ≤ i, j ≤ 2. 

Note that the ℤ₂ action on 𝒜_U(1)2l given by AdJ as defined before Lemma 5.1 is a proper action on 𝒜_U(1)2l. The reader familiar with ref. 8 may notice that the action given by AdJ corresponds to −1 isometry of rank one lattice vertex operator algebras (cf. refs. 8 and 10). By using the branching rules in Section 4 of ref. 26, we can show:

Lemma 5.3.

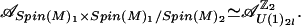By Lemma 5.3 and Theorem 4.3, we have proved the following theorem:

 Theorem 5.4. All irreducible representations of 𝒜_U(1)2l^ℤ₂ are given by (2) for l ≥ 3. These irreducible representations give rise to a unitary modular category whose S and T matrices are given by Table 1 and (3).

When l = 2, Spin(4) = SU(2) × SU(2), one checks that Theorem 5.4 still holds in this case, where the integrable weights of LSpin(4) should be replaced by the integrable weights of LSU(2) × LSU(2). When l = 1, by using the fact that 𝒜_U(1)2 ≃ 𝒜_SU(2)1, one can check that

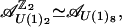and 𝒜_U(1)8 has already been studied in Section 3.5 of ref. 5.

Remark 5.5:

The reader may wonder why we identify the orbifold of 𝒜_U(1)2l with respect to the natural ℤ₂ action as a coset in Lemma 5.3 instead of considering such an orbifold directly as in ref. 10. The reason is that the “twisted representations” in ref. 10 are defined only algebraically. To show that these “twisted representations” in ref. 10 give rise to covariant representations of our orbifold, one needs to study the analytical properties of the twisted vertex operators in ref. 10, which are not trivial if one tries this directly. On the other hand, there are no such problems for cosets (cf. Remark 4.3). As noted before in Lemma 5.3, the ℤ₂ action on 𝒜_U(1)2l given by AdJ corresponds to the −1 isometry of rank one lattice vertex operator algebras (cf. refs. 8 and 10). The classification of irreducible representations of the orbifold rank one lattice vertex operator algebras is given in ref. 10, which corresponds to the first part of Theorem 5.4. We note that the S matrix can be identified with the S matrix on Proofs 517 and 518 of ref. 12. However, there are mistakes in the S matrix on Proofs 517 and 518 of ref. 12 corresponding to the entries of a_ij, b_ij in Table 1. Table 1 gives the correct S matrix.

6. More Examples and Questions

The lattice vertex operator algebras and their automorphism groups provide a rich source of examples of orbifolds (cf. refs. 8, 10, and 27). I have determined the S, T matrices and hence the fusion rules for the orbifold of rank 1 lattice Vertex Operator Algebras in Theorem 5.4. It would be interesting to generalize this theorem to higher-rank cases.

Let 𝒜_SU(N)k be the irreducible conformal precosheaf, and let G be a finite subgroup of SU(N). Then there is a natural action of G on 𝒜_SU(N)k, and it is easy to check that this action is proper (if the action of G is not faithful, one can replace G by a quotient G′ as explained in the footnote of Definition 3.1). By the results of refs. 28 and 23, 𝒜_SU(N)k is completely rational. Hence Theorem 4.3 applies in this case, and we have a family of unitary modular categories. It would be interesting to study these modular categories in general.

Finally, let me mention that permutation orbifolds (cf. ref. 29 and refs. therein) provide another interesting class of orbifolds. Let us formulate these orbifolds in our setting. Let 𝒜 be an irreducible conformal precosheaf. Then the tensor product of 𝒜 with itself n times 𝒜^⊗n := 𝒜 ⊗ 𝒜 ⊗ … ⊗ 𝒜 is also an irreducible conformal precosheaf. Let G ⊂ S_n be a finite subgroup of S_n, the permutation group on n letters. Note that any finite group is embedded in a permutation group by Cayley's theorem. There is an obvious action of G on 𝒜^⊗n by permuting the n tensors, and one checks directly by definitions that this action of G on 𝒜^⊗n is proper as defined in Section 3. Note that if 𝒜 is μ rational, so is 𝒜^⊗n by definition. If 𝒜 is μ rational, by Theorem 2.6, we obtain a large family of unitary modular categories from the orbifold (𝒜^⊗n)^G. The modular matrices of the unitary modular categories associated with the permutation orbifolds above have been written down on the basis of heuristic physics arguments in ref. 30. It would be interesting to do the computations in our framework as in Section 4 and compare them with the results of ref. 30.