A new paradigm for electrostatic catalysis of radical reactions in vitamin B₁₂ enzymes

Abstract

The catalytic power of enzymes containing coenzyme B₁₂ cofactor has been, in some respects, the “last bastion” for the strain hypothesis. The present work explores the origin of this effect by using simulation methods that overcome the sampling difficulties of previous energy minimization studies. It is found that the major part of the catalytic effect is due to the electrostatic interaction between the ribose and the protein, and that the strain contribution is very small. Remarkably, enzymes can use electrostatic effects even in a radical process, when the charge distribution of the reacting fragments does not change significantly during the reaction. Electrostatic catalysis can, in such cases, be obtained by attaching a polar group to the leaving fragment and designing an active site that interacts more strongly with this group in the product state than in the reactant state. The finding that evolution had to use this trick provides further evidence to the observation that it is extremely hard to catalyze enzymatic reactions by nonelectrostatic factors. The trick used by B₁₂ enzymes may, in fact, be a very powerful new strategy in enzyme design.

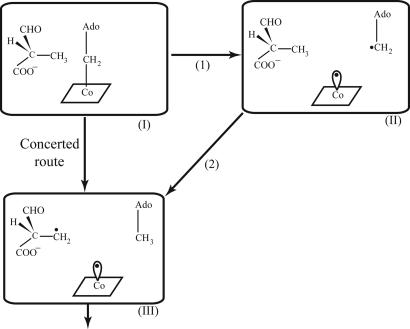
The origin of enzyme catalysis is a problem of great importance and significant interest (e.g., refs. 1–8). There are currently compelling evidences that electrostatic effects give the largest catalytic contributions (e.g., refs. 1 and 2). However, some workers believe that various effects have been exploited in the evolution of enzyme catalysis (e.g., ref. 9). One of the most prominent proposals for nonelectrostatic catalytic effects involves the strain hypothesis (e.g., refs. 9 and 10), where it is assumed that the enzyme destabilizes the ground state of the reacting system and thus reduces the activation barrier for the chemical step. Although enzymes appear to be too flexible to allow for significant strain effects (e.g., refs. 11 and 12), the catalytic power of enzymes containing coenzyme B₁₂ cofactor (for review, see ref. 13) has been taken as major support for the strain hypothesis. More specifically, during the reaction of B₁₂ enzymes the Co-C bond of B₁₂ is cleaved, leading to the formation of 5′-deoxadenosyl radical and Cob(II)alamin, and to a subsequent (or concerted) radical-based rearrangement of the substrate (the reacting system is shown in Fig. 1, and a typical reaction mechanism is depicted in Fig. 2). The rate of the nonenzymatic reaction of the Co-C bond cleavage is >10 orders of magnitude slower than the reaction of B₁₂ enzymes (a more quantitative analysis will be given below). The problem in rationalizing this enormous rate acceleration is the fact that we are dealing with a radical reaction, which would not provide a simple way for the enzyme to exert electrostatic effects for stabilizing the transition state (TS). This presents a major problem to the view that enzymes catalyze reactions mainly by electrostatic effects, and that other factors cannot give large contributions (2). In fact, B₁₂ enzymes have been originally assumed to present what is perhaps the best support for the popular idea (e.g., refs. 9 and 10) that strain energy contributes in a major way to enzyme catalysis. This idea emerged from the pioneering work of Halpern and coworkers (14) and, to some extent, from subsequent works that modified this view (see below) but still kept the notion that strain energy plays a major role in the catalysis of such enzymes, in contradiction to studies in other enzymes (e.g., refs. 1, 2, 11, and 12), where it was concluded that enzymes cannot exert significant strain. Thus, it is still hard to determine the origin of the catalytic power of B₁₂-containing enzymes.

Fig. 1.

The reacting system of mutase and similar B₁₂ enzymes.

Fig. 2.

The first steps of the reaction catalyzed by mutase.

At this point it should be useful to expand the discussion of the current view about the catalytic effect of B₁₂ enzymes, where we will restrict ourselves for simplicity to the extensively studied case of B₁₂ mutase. As stated above, the question is this: How can mutase achieve a catalytic effect of >10 orders of magnitude? Early attempts to resolve this problem proposed the so-called mechanochemical strain idea, where it was suggested (14, 15) that the enzyme compresses the Co-N_Im bond, and that this leads to upward folding of the corrin ring and to strain in the Co-C bond. However, more recent theoretical (e.g., refs. 16 and 17) and spectroscopic studies (e.g., ref. 18) have indicated that this proposal is not justified. Thus, despite the great progress in structural (e.g., refs. 19 and 20), biochemical, and chemical studies (for review, see ref. 13), it is very hard to determine the origin of the catalytic effect by the available experimental information. The main problem is the need to determine the relative importance of different energy contributions, and it is not clear how to obtain unique energy decomposition from experimental studies.

In principle, it is possible to explore the catalytic effect by quantum mechanics–molecular mechanics (QM/MM) approaches (e.g., refs. 3, 5, and 12). Major hints about the origin of the catalytic effect have been provided by Jensen and Ryde (21), who used a QM/MM-type approach. Their study reproduced a very large catalytic effect of ≈24 kcal/mol (evaluated relative to the vacuum Co-C bond cleavage) and ≈32 kcal/mol reduction in the bond dissociation energy. These calculated catalytic contributions were assigned to ≈10 kcal/mol stabilization of the dissociative state (by electrostatic and van der Waals interactions), ≈14 kcal/mol deformation energy, which was found to be stored in the ribose moiety and ≈7 kcal/mol from other factors. These calculations most probably present an overestimate and also involve energy minimization calculations rather than free energy calculations. Furthermore, the finding of a very large deformation energy probably reflects problems in obtaining free energy contributions in proteins and accounting for the full protein flexibility, which will be one of the main issues addressed in the present work. However, the finding that the interactions between the ribose group and the enzyme polar groups constitute a major catalytic factor is very significant (regardless of whether the analysis that attributed the main catalytic effect to the resulting deformation is reliable). A related instructive study (22) used a cluster model and observed an electrostatic stabilization effect of ≈4 kcal/mol. However, this model could not quantify the steric proposal, because it does not include a model of the protein matrix.

Another recent theoretical study (23) used the ONIOM QM/MM approach and obtained a barrier of ≈18 kcal/mol for stretching the Co-C bond in the enzyme up to 3.2 Å. It was then argued that the Co-C is not a good reaction coordinate. Another set of calculations found a conformational transition of the substrate at a very small stretch of the Co-C bond (at ≈2.2 Å) and that, at these conformations, one can presumably reach an intermediate, where the Co-C bond length is ≈2.7 Å and the energy is only 7 kcal/mol, and then a TS with an energy of 10 kcal/mol. Unfortunately, the surface for the transition to the crucial intermediate was not evaluated (the reported energy profile has discontinuity). It was then argued that the catalysis is due to the conformational changes. It seems to us that a proper analysis of the energetics should provide the surface as a function of the Co-C bond length and any other chosen reaction coordinate without discontinuity. This would have allowed for an examination of the validity of the conformational change idea. Most likely, the reported result reflects the use of an energy minimization approach on a very complex surface where it is hard to obtain the total energy of the system (it is not clear whether the discontinuous transition reflects the same protein structure). In general, it is extremely difficult to monitor the energy of conformational changes in proteins without using free energy perturbation (FEP) approaches. It is possible, of course, to hold the protein fixed and to obtain an upper limit for the proposed effect, but this was not reported in ref. 23.

Despite the insight provided by the above calculations, they have not determined conclusively the relative importance of the different catalytic factors. That is, as stated above, calculation of strain energy by energy minimization of a many-atom protein system is extremely problematic [unless it involves a careful constraint treatment that can provide an upper limit in some cases (11, 12)]. The problem is associated with the large dimensionality and the interplay between the protein deformation and the substrate assumed strain. Proper analysis must involve extensive sampling (see ref. 24 for a related problem) and cannot be based on QM/MM energy minimization studies (see ref. 25). The best way is to ask how much it will cost to change the substrate from the presumed strained form to the unstrained form by FEP calculations (see figure 6.4 in ref. 1). Alternatively, one can try to use very extensive free energy calculations of the reaction profile and then attempt to estimate the energy contributions by the linear response approximation (LRA) or related approaches (see below).

In our view, the contribution of strain or other factors to the catalysis of B₁₂ enzymes cannot be determined and quantified by energy minimization-type studies regardless of whether they are done classically or by QM/MM methods. Thus, our challenge is to use an approach that properly describes the chemical reaction of mutase and still allows us to perform the extensive sampling needed for the elucidation of the origin of the catalytic power of B₁₂ enzymes. This challenge is overcome in the present work, which resolves the long-standing problem of the origin of the catalytic power of B₁₂ enzymes. It is found that the catalytic power of these enzymes is due to electrostatic effects despite the fact that we are dealing with a radical reaction where the charge distribution of the broken bond does not change significantly during the reaction. The unique strategy used by the enzyme is discussed and analyzed.

Prelimenary Analysis

To estimate the catalytic effect of mutase (or related B₁₂-containing enzymes), we have to consider the corresponding reference reaction in solution. As explained in detail elsewhere (e.g., ref. 2), the most meaningful reference reaction (as much as the effect of the enzyme environment is concerned) is a solution reaction that involves the same mechanism as the one used by the enzyme (namely the reaction described in Fig. 2). Now, what is known from experimental studies is the enthalpy of the Co-C bond cleavage; the bond dissociation energy (BDE) is ≈30 kcal/mol (26), and the equilibrium constant for the bond breaking of the AdoCbl is ≈8 × 10⁻¹⁸ M (13), which corresponds to reaction free energy of ≈23 kcal/mol (unlike the BDE, this contribution includes a significant entropic component). The rate constant for homolysis of AdoCbl in solution has been estimated to be ≈10⁻⁹ s⁻¹ (see references in refs. 13 and 21), which corresponds to ≈31 kcal/mol activation barrier. On the other hand, the activation barrier of the chemical step in B₁₂ enzymes is estimated from the corresponding k_cat to be ≈2–300 s⁻¹ (Δg^# = 17–16 kcal/mol) (see references in ref. 13), and the reaction free energy is estimated by some to be close to zero (13). Because the BDE and the activation barrier for the solution reaction are ≈30 kcal/mol, we will assume that this represents a reasonable estimate of the activation barrier for the bond-breaking process. Unfortunately, it is not clear whether the bond-breaking reaction is the proper reference reaction. That is, if the reaction in the enzyme is concerted, then it should be compared with a similar concerted reaction in solution; at present, there is no clear information about such a reaction. However, the recent ab initio study of Kozlowski and coworkers (27) has shown that the concerted reaction has ≈4 kcal/mol lower activation barriers than the stepwise reaction. This study also indicated that the reaction enthalpy of the solution reaction is ≈22 kcal/mol (see also ref. 28).

If we estimate the reaction entropy to be ≈30 cal/K·mol (a very reasonable estimate of typical translational and rotational effects), we get reaction free energy of ≈22–10 ≅ 12 kcal/mol for the solution reaction. Comparing the above values to the corresponding values in the enzyme, we get ΔΔg^# ≅ 31 − 4 − 17 ≅ 10 kcal/mol and ΔΔG ≅ 10 kcal/mol. If we take the bond-breaking process as the reference reaction, we obtain ΔΔg^# ≅ 31 − 17 ≅ 14 kcal/mol. The key question, however, is this: What is the origin of this catalytic effect? This issue will be addressed below.

Results and Discussion

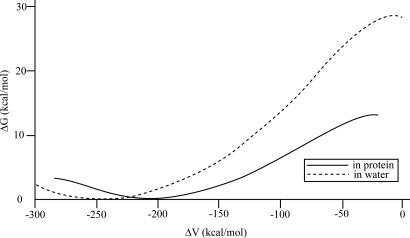
The first step of our study involved empirical valence bond (EVB) simulations of the Co-C bond-breaking process in solution and in the active site of methylmalonyl CoA mutase from Propionibacterium freudenreich subsp. shermanii (19) (PDB entry 4REQ), which is depicted in Fig. 3. The calculated EVB free energy profiles (Fig. 4) reproduce ≈16 kcal/mol reductions in the activation barrier for the bond-breaking step (Δg_enz^# = 13 kcal/mol, Δg_wat^# = 29 kcal/mol). This accounts for almost all of the observed catalytic effect (for the bond-breaking step). It also accounts for ≈50% of the reduction in the reaction free energy (ΔG₀^p ≈ 13 kcal/mol instead of ≈0 kcal/mol). The missing contribution will be accounted for below, by considering a concerted path, but we will start here by focusing on the bond-breaking step, because it provides the most insightful picture.

Fig. 3.

The reacting system in the active site of mutase.

Fig. 4.

Free energy profile for the reaction in mutase and in the protein and in solution.

As a first step in the analysis of the origin of the catalytic effect, we run the same EVB calculations but now with, and without, the residual charges on the reacting region. In this case (see Fig. 5), the entire catalytic effect disappeared. This means that the effect of the enzyme is associated with the interaction between the active-site groups and the substrate residual charges. Now, this type of conclusion was also reached by QM/MM calculations (21), but it was then deduced that most of the catalytic energy is manifested as changes in the van der Waals interactions and deformation energies. However, as recognized in ref. 21, it is difficult to perform meaningful analysis of the catalytic energy contributions in the B₁₂ system. Thus, we have to establish here where the catalytic energy is actually stored.

Fig. 5.

Reaction profile for the reaction in the protein and in solution in the situation where the reacting system is without any residual charges. In this case, we see that the catalytic effect disappears, indicating that this effect is electrostatic in nature.

Unfortunately, the calculations of the overall catalytic effect do not tell us whether we have here a reactant state destabilization (RSD) or TS stabilization, nor can they tell us what the origin of the overall electrostatic effect is. To explore these aspects of the problem, we used the LRA (e.g., ref. 29). This approach approximates the free energy of “charging” the given system in a specific environment by

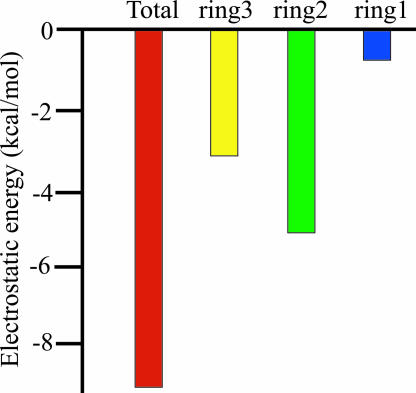
where U_Q and U₀ are, respectively, the potential energies of the nonpolar and the polar (charged) form of the system, and 〈 〉_Q designates an average over the indicated charged form. This expression provides a very good approximation for the results of the corresponding FEP charging calculations. The results of the LRA calculations are summarized in Table 1 and Fig. 6[also see supporting information (SI) Table 2]. As seen from the table, the catalytic effect is due to electrostatic TS stabilization rather than to RSD. That is, the LRA estimate of the binding energy of the reactant state is (−12.8 − 26.9 + 5.0 =) −34.7 kcal/mol. Although this may be an overestimate, it is clear that if we had RSD, the binding energy should have been positive and led to destabilization of the bound “chemical” part.

Table 1.

LRA electrostatic contributions

System	ΔΔGelec(2Å)w→p	ΔΔGelec(4Å)w→p	ΔΔGelec(2Å→4Å)w→p
Ring1	−12.8	−13.3	−0.5
Ring2	−26.9	−32.0	−5.1
Ring3	5.0	1.9	−3.1

Energies are in kcal/mol. The calculated values were obtained by using Eq. 1 to evaluate the free energy of charging the indicated system. The Co-C bond distance (in Å) is given in brackets with the given charge state [e.g., Q(2Å) for 2-Å distance]. Ring₁, ring₂, and ring₃ represent, respectively, Co + corrin + Im, ribose, and adenine.

Fig. 6.

The difference between the LRA electrostatic contributions in the protein (relative to the corresponding contributions in water) [ΔΔG(r₁ = 4.0 Å) and ΔΔG(r₁ = 2.0 Å)] upon moving from the reacting state to the transition state in the bond-breaking step (see Table 1 for more details).

Apparently, the most straightforward rationalization of the catalytic effect is that it is almost entirely due to electrostatic effects, because the electrostatic LRA analysis more or less reproduced the total effect obtained from the EVB profiles. Interestingly, performing a full FEP charging process for the reacting system (which is more accurate than the LRA estimate) gave ΔΔG_elec of ≈12 kcal/mol, which is even closer to the EVB catalytic effect. We also provide, in SI Fig. 9, the largest contribution of the protein residues to the overall electrostatic effect. Note, however, that these contributions do not represent the more relevant effect of mutating each residue (see legend of SI Fig. 9).

One may argue at this point that we have not evaluated the actual strain contribution (we have only shown that the electrostatic effect accounts for all of the calculated catalytic effect in the bond-breaking step); thus, we will now focus on this issue.

Consistent calculations of strain effects are extremely challenging and cannot be accomplished by energy minimization or related approaches. Here, we explored the strain effect by two complementary approaches. First, we “mutated” ring 2 and 3 (the ribose and the adenine, respectively) from the nonpolar form of the substrate (the end point of the LRA unchanging procedure) to dummy atoms of a very small size. Performing this analysis in water and in the protein (SI Table 3) indicated that the strain effect is very small for the nonpolar form of the substrate. We also examined the possibility that the strain effect is coupled to the electrostatic effect by performing linear interaction energy-type analysis (30) and evaluating the average van der Waals interaction for trajectories where the substrate is in its polar form. The results of these calculations (SI Table 4) also indicated that the strain effect is small, because we have similar average van der Waals contribution for the substrate in water and in the protein. It is also useful to point out that the evaluation of the free energy of moving from dummy atoms to the fully polar substrate in the protein and in solution at 2 and 4 Å gives us a complete thermodynamic cycle (see ref. 31). Thus, if we combine the FEP process of mutating the rings with the process of charging the rings, we should account for the entire energetics of the EVB profiles in Figs. 4 and 5 or, in other words, for the entire catalytic effects. Now, because the mutation step provides a very small steric contribution (it will probably be smaller with longer runs) and because the charging step accounts for the catalytic energy, we proved our overall point that the catalysis is due to electrostatic effects.

To clarify the difficulties of obtaining the present results by QM/MM energy minimization approaches, we provide in SI Fig. 10 the convergence of the FEP estimate of the steric effect as a function of time. Apparently, it is essential to run at least 20 ps or 20,000 time steps to obtain converged results. Thus, we conclude that the existence of strain effect cannot be obtained by QM/MM energy minimization. Here, one may argue that our findings are based on semiempirical or classical calculations rather than on ab initio QM/MM calculations, but the fact is that the same convergence problems are expected regardless of the origin of the potential surface.

Taking into consideration all of the above findings, it appears that the catalytic effect of the bond-breaking step is associated with electrostatic TS stabilization. However, the study of the Co-C bond-breaking step has not accounted for the reaction free energy, which is estimated to be close to zero, instead of the calculated value of >10 kcal/mol.

To resolve this discrepancy, we have to explore the catalytic effect along the concerted path. This is done here by using the EVB surface calibrated on the ab initio-based surface of SI Fig. 11b. The resulting EVB surfaces for the protein and solution reactions are given in Fig. 7. Evidently, we obtained a catalytic effect of ≈11 kcal/mol (Δg_p^≠ = 16 kcal/mol and Δg_w^≠ = 27 kcal/mol). Furthermore, we also reproduced the large reduction in the reaction free energy (ΔG_p = 3 kcal/mol and ΔG_w = 22 kcal/mol as compared with ΔG_p ≅ 11 kcal/mol for the stepwise bond-breaking process).

Fig. 7.

Describing the free energy surface on the complete concerted space for the reaction in mutase and in solution.

The nature of the electrostatic effect that allows B₁₂ enzymes to catalyze radical reaction will be considered in the next section.

Concluding Remarks

Although there are growing evidences that the main catalytic factor in enzymatic reactions is associated with electrostatic effects (see ref. 2 for a review), it is hard to exclude other effects by direct experimental studies, and a combination of experimental and theoretical studies are essential to reach unique conclusions on the validity of different proposals. The idea that ground state provides major catalytic effects has been found to be problematic (2). However, the catalytic effect of B₁₂ enzymes has been, in some respects, the last bastion of the strain theory.

This work explored, quantified, and elucidated the origin of the catalytic power of B₁₂ by using the EVB and LRA simulation methods that allow us to overcome the convergence difficulties of previous QM/MM approaches. It was found, in agreement with previous studies, that the catalytic power is associated with the interaction between the ribose and the protein [in particular, Glu-370, which is equivalent to Glu-330 in the mutase from Clostridium cochlearium (20)]. However, in contrast to previous studies, it was determined that the interaction between the active site and the reacting substrate is associated with electrostatic interactions rather than strain effects. This finding was established by several approaches, ranging from showing that the catalytic effect disappears once we study the reaction without the electrostatic effects, to FEP calculations of the steric effect. It was also shown that the assessment of the steric effect cannot be done without using converging free energy calculations rather than energy minimization approaches.

It is useful to comment here about our conclusion that the strain effect does not play a major role in B₁₂ enzymes. We have established (SI Table 3) that the strain effect is small when the reacting system is fully nonpolar. However, one may wonder about the coupling between electrostatic and steric effects. Here, it is important to realize that if the gain in electrostatic interaction leads to strain, then the resulting strain must always be less rather than more than the electrostatic effect (usually less than half). Thus, it is hard to see how the electrostatic interaction with the active site can lead to major steric effects.

Our study has found, in agreement with a recent work (27), that the reference reaction involves a concerted path, and thus that the estimated catalytic effect should be smaller than what was previously assumed. Furthermore, it is found that, with the concerted path, it is possible to reproduce the very large change in the reaction free energy, where the stabilization of the radical on the substrate adds to the significant reduction of the overall reaction energy relative to the free energy of breaking a Co-C bond in solution.

Another interesting point is related to the repeated implication that B₁₂ enzymes work by RSD (e.g., ref. 32), where the binding energy is used to destabilize the reacting fragments in their ground state (9) (for a clear definition of the RSD proposal, see ref. 2). Here, we show by LRA calculations that the ground state is stabilized rather than destabilized by the enzyme (see Table 1 and 2).

The important finding that the interactions between the 2′- and 3′-OH groups of the ribose with Glu-370 play major role is supported by the reduced activity found upon removal of the 2′-OH (33) and the loss of activity upon mutation of the equivalent Glu-330 in glutamate mutase (E. N. G. Marsh, personal communication).

In considering the electrostatic TS stabilization, one may wonder how a charge–dipole (Asp-370–ribose OH group) interaction can lead to a large effect upon moving of the dipole by ≈2 Å, because the dielectric in proteins is relatively large. The reason is that when we deal with preorganized environment the charge–dipole interactions can be quite large, and the corresponding effective dielectric is small. One can also view this effect as having a large electric field in the preorganized region.

Now, we can come back to our original question: How can B₁₂ enzymes catalyze their reactions without strain effects and by electrostatic factors, where the reaction involves a radical bond-breaking process, without a significant change in the charge distribution of the reacting fragments? In most cases with large catalytic effects, it is possible to show that this effect is due to the interaction between the preorganized electrostatic environments of the active site and the change in charges of the reacting fragments (1, 2). Here, however, the charge change is negligible, and it has been difficult to see what the origin of the catalytic effect is. Now, as shown here, B₁₂ enzymes use an elegant new electrostatic trick in the absence of simpler electrostatic options. That is, as shown in Fig. 8, the enzyme stabilizes the TS by attaching to the leaving carbon the very polar Ado group that is more stabilized when the bond length increases. In other words, once it was “realized” by evolution that it is hard to stabilize the broken nonpolar bond (because no dipole is being formed by separating the bonded atoms), it was found that the catalysis can be obtained by attaching a polar group to the leaving group. The fact that evolution had to use this trick provides further evidence to the observation that it is extremely hard to catalyze enzymatic reaction by nonelectrostatic factors. The trick used by B₁₂ enzymes may, in fact, be a very powerful new strategy in enzyme design.

Fig. 8.

Schematic description of the catalytic effect of B₁₂ enzymes. This figure describes the corrin as a disk and the Ado group as a polar group attached to the leaving carbon. With the addition of a polar group (the polarity is designated by a dipole) to the leaving carbon and with an active suite that is preorganized to stabilize the polar group at a large bond separation distance, we obtain a way to catalyze radical reactions by electrostatic effects.

Computational Methods

The elucidation of the free energy contributions to the catalytic effect of B₁₂ enzymes presents a major challenge that is hard to accomplish with molecular orbital QM/MM approaches because of the need of a very extensive simulation time for sufficient convergence of the free energy profile. Separating between electrostatic and other contributions may present major problems even for FEP approaches. In our view, at present the most effective way of addressing the B₁₂ problem is the use of the EVB method (1, 34), which will be used here. We would like to clarify that the EVB does not especially focus on electrostatic contributions (although it evaluates them more reliably than most other methods do), and it can capture any possible catalytic effect as has been demonstrated elsewhere (e.g., refs. 1 and 2). Thus, we will only consider crucial points here.

The EVB model considered as quantum system the atoms that are labeled in Fig. 1 as EVB atoms. The bonding and charges of theses atoms was assigned according to the following resonance:

where the energy of each of the above resonance structures (the diabatic energy) was described by a “force field” type set of functions and the mixture of these diabatic energies by off diagonal terms gave the actual potential surface for the reaction. The reaction free energy was then evaluated by the FEP umbrella sampling (FEP/US) procedure described elsewhere (e.g., ref. 34).

The charges of the reacting system were taken as the ab initio ESP (35) charges evaluated at the B3LYP/6–31+G* level with the Gaussian 03 (36) program package for the given system in a COSMO solvent model (37). The relevant charges are given in SI Table 5 (and see SI Fig. 12). The FEP adiabatic charging (FEP/AC) calculations were performed with 30 frames (i.e., 30 values of λ_m in Eq. 2), each of 20 ps with time steps of 1 fs. These calculations were then repeated 10 times with different initial conditions, and the average value of all these calculations was taken as the calculated free energy. Before performing the above simulations, we relaxed and equilibrated the simulation system by a 100-ps run. The EVB free energy profile (FEP/US) was evaluated in the same way as the FEP/AC calculations. The FEP/AC and FEP/US simulations were performed by using the MOLARIS program (29) with an explicit simulation sphere of 18 Å completed to 21 Å by Langevin dipoles surface and then extended to infinity by a macroscopic sphere. This system was subjected to the surface constraint all atom solvent (SCAAS) model (29) with its spherical polarization and distance constraints. The long-range electrostatic effects were treated by the local reaction field treatment (29) and described by the ENZYMIX (29) force field. The ESP charges were taken as the EVB charges of SI Table 5. It is important to point out that other charge sets (e.g., LANL2DZ) gave similar catalytic effect, because we used the same set in solution and in protein, and the difference between the corresponding “solvation” is much less sensitive to the charge set used than the absolute energies. Similarly, the results of the calculations did not appear to be sensitive to the force field used for the corrin ring (we examined different sets of force field parameters). Apparently, although some features changed, the overall catalytic effect stayed the same. The EVB parameters taken were the standard ENZYMIX parameters, except for the atoms involved in bond-making and bond-breaking processes. These parameters were calibrated on the ab initio surface described below and are given in SI Table 6.

An important issue of the present study is the analysis of the nature of the solution surface. This is done in SI Fig. 11, where we start by constructing the relevant generic 2D surface. This surface reflects a combination of the results from our ab initio calculations and from those of ref. 27 and experimental constraints. More specifically obtaining accurate surface for the B₁₂ system is very challenging, and even the recent calculations of ref. 27 have not reproduced quantitatively the gas-phase bond energy. However, the trend in such calculations is expected to be reasonable. Thus, we first performed RB3LYP/LANL2DZ calculations and then forced the energy along the r₁(R_C0−C6) axis to reproduce the observed bond energy. We also forced the hydrogen transfer axis for r₂(R_C6−H9) = 4.0 Å to reproduce the observed difference in radical energy (38); namely, −10 kcal/mol for transfer from A to B. Basically, we introduced a linear interpolation to correct the gas phase calculations and then add the same correction to the solution surfaces that was obtained by using the COSMO solvent model. The solution surface also includes the entropic corrections associated with the solute entropy, which were estimated by using a restraint release approach (39). This generic solution surface (SI Fig. 11) was then used to generate the corresponding EVB surface, and the same EVB parameters were used in the protein calculations.

Abbreviations

EVB

empirical valence bond

FEP

free energy perturbation

LRA

linear response approximation

QM/MM

quantum mechanics–molecular mechanics

RRA

restraint release approach

RSD

reactant state destabilization

TS

transition state.