Abstract
Displaced intra-articular distal radius fractures are difficult to treat, with numerous associated complications. The potential onset of post-traumatic osteoarthritis (OA) is a major concern. The relationship between malreduced intra-articular fracture of the distal radius and subsequent early onset of radiocarpal OA is clinically important, yet poorly understood. To better understand this presumed mechanical relationship, detailed information regarding joint loading, kinematics and associated stress distributions must be obtained. Toward this end, a three-dimensional finite element (3D FE) contact model of the radiocarpal joint has been developed, including the radius, lunate, scaphoid, articulations between these bones and selected soft tissues near the joint. FE model geometry was derived from cryomicrotome sections of a cadaver wrist. Radiocarpal contact stress distributions in the intact and simulated malreduced fracture conditions, previously collected using a cadaveric intra-articular fracture model, are used to establish validity of the computational model. Finally, a section of the distal radius constituting the entire lunate fossa was displaced 1, 2 and 3 mm to represent a depressed lunate die-punch fracture.
INTRODUCTION
Intra-articular fractures of the distal radius are a significant clinical problem. In a large number of such fractures, the normally smooth articular surface is greatly disrupted (Figure 1). The frequency of post-traumatic OA of the wrist after this injury has been reported to be as high as 40 to 65%,1 and the clinical result is often a painful stiff wrist. It has been suggested that this is of particular concern in the younger patient with an incongruity of greater than 2 mm.1 The development of OA following displaced intra-articular fractures has been attributed to a variety of factors, including the initial trauma to cartilage, elevated contact stresses and joint instability.2 Although this is a current area of intense research, there remains little that can be done to reverse the initial cartilage trauma, and its influence on subsequent joint loading is poorly understood. With operative intervention, an incongruous joint can be restored to its original anatomical position. Joint instability can be addressed surgically, as well, but has received little attention overall in the management of intra-articular fractures.
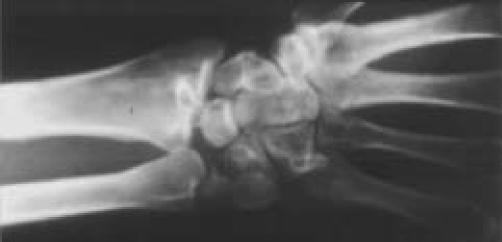
Figure 1.
Natural history radiographic appearance of the wrist following healing of lunate die-punch-type fracture of the distal radius.
Several authors have shown in clinical studies that radiographically-evident "step-offs" that persist following wrist fracture are highly correlated with the onset of early OA. Knirk and Jupiter found that OA developed in 91% of distal radius fractures that healed with any articular incongruity, and in 100% of those that healed with a step-off of 2 mm or more.1 In contrast, they found a poor correlation for the extent of initial intra-articular disruption with the subsequent development of arthritis. Over half of their patients with arthritic changes had a fair or poor clinical result. Fernandez and Geissler confirmed that operative reduction of displaced intra-articular fractures reduced the incidence of OA to approximately 5%.3 Bradway et al. found radiographic evidence of OA in only 9% of patients with a step-off of less than 2 mm, but in 100% of those with a step-off of 2 mm or more.4 While they found that the worst results in their series tended to be in patients who had the most comminuted fractures, they noted that the prognosis was most directly related to a surgeon's ability to reconstruct a congruent distal radial articular surface. This belief represents the current clinical consensus,5 and these findings in the wrist are generally consistent with clinical experience in other articular joints.6,7
The heterogeneity of injuries involved in clinical studies makes it difficult to arrive at specific conclusions regarding clinical outcome, especially since such series normally include only a relatively small number of patients at any one institution. The compilation of relevant clinical information regarding the management of these fractures has been complicated by patient-to-patient variability, and by the great range of fracture fixation devices used to treat them. The fractures are seldom contained within a single plane, and it is not uncommon for multiple fracture fragments to be present. Thus, the use of plain radiographs to assess the degree of fracture malreduction can be misleading, with their appearance sensitive to the obliquity at which radiographs are obtained.8 The extent of concomitant ligamentous injury associated with these fractures has only recently begun to be appreciated. In most clinical studies, little attention has been given to the presence of these ligamentous injuries, and their potential influence upon post-injury mechanics has not been studied.
Finally, while clinical study may help to identify general relationships between fracture management and clinical outcome, it provides little information regarding relationships between the details of fracture management, the resulting alterations in joint loading and the eventual clinical outcome. Without this information, there is little rigorous guidance toward further improvement and refinement in intra-articular fracture management techniques. In order to begin to understand these relationships in the wrist, more information must be obtained regarding, first, the nature of stress distributions in the vicinity of the articular surfaces, and second, the associated kinematics of the carpal bones.
Laboratory research into the biomechanics of these intra-articular fractures offers an alternative means of investigating the mechanical implications of residual incongruity.9–13 Although most agree that both mechanical and biological processes cause OA, the factors contributing to its onset are believed to be primarily mechanical in the specific clinical situation of post-traumatic OA. Altered juxta-articular geometry associated with the presence of residual surface incongruities is a logical mechanism by which the details of stress transfer across the joint could be changed following distal radius fracture. Any resulting abnormal stresses would likely be implicated in subsequent disease pathology. Trauma-related injury to the osteochondral zone beneath the articular surface is another potential contributing factor.14 Our experience with a cadaver model of a simple intra-articular fracture suggests that changes in the proximal carpal row kinematics probably accompany irregularities in articular surface geometry, as well.11
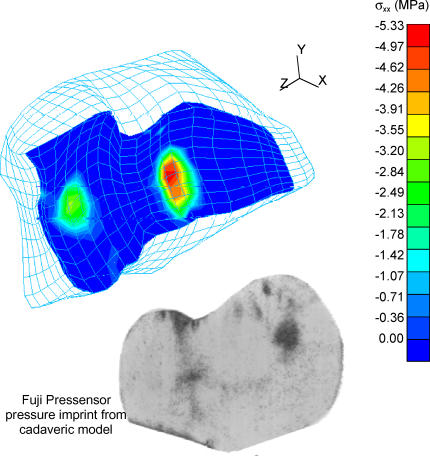
The presumed mechanical relationship between residual surface incongruity and subsequent OA is poorly understood, in part because alterations in radiocarpal stresses accompanying fracture step-off are unknown. Cadaveric models (Figure 2) have demonstrated increased contact stresses (measured using pressure-sensitive film inserted into the joint space)9,10,13 and altered kinematics (measured using electromagnetic sensors affixed to the bones)11 associated with 1-, 2- and 3-mm step-offs simulating a depressed lunate fossa fracture. While useful in terms of establishing the details of surface loading, these data provide only limited insight into potential initiating factors in the degenerative sequence of events, since they yield little direct information regarding the full juxta-articular stress distribution. Analytical15 or computational16,17,18 modeling of articular joints can greatly complement experimental methods, especially when the two methodologies are tightly coupled.
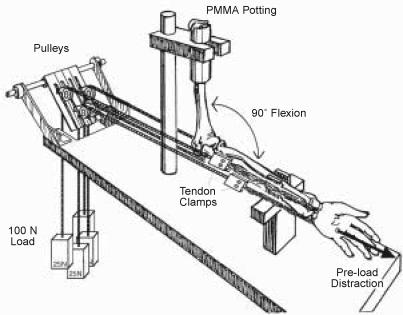
Figure 2.
Schematic of cadaveric model previously used to study the effect of intra-articular distal radius fracture step-off on radiocarpal contact stresses, measured using Fuji Pressensor pressure-sensitive film (modified from Baratz et al. 1996).
A. Loading fixture.
B. Simulated distal radius fracture step-off.
C. Pressure transducer placement and orientation relative to distal radius articular surface.
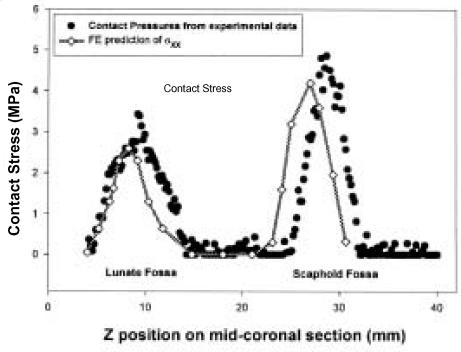
A computational model of the radiocarpal joint permits parametric study of relationships between surgically relevant parameters and alterations in the radiocarpal stress distributions. A two-dimensional FE model of the radiocarpal joint was previously developed to investigate precisely this problem (Figure 3).16 While providing reasonable agreement with measured contact stress distributions, it was limited to a single plane of analysis. In the case of the radiocarpal joint, in which out-of-plane motions are substantial, two-dimensional analyses are clearly of limited utility. Previous three-dimensional FE models of the wrist have been described in the literature; one restricted to the radiocarpal joint17 and the other including the entire wrist.18 Both models relied on CT for source geometry, thus the inclusion of articular cartilage was restricted to uniform thickness regions layered on the ends of the bones. Both also modeled contact in a fairly constrained and arbitrary fashion—Ulrich et al.17 did not explicitly solve the radiocarpal contact problem, while Carrigan et al.18 constrained articulating bodies to small displacements.
Figure 3 .
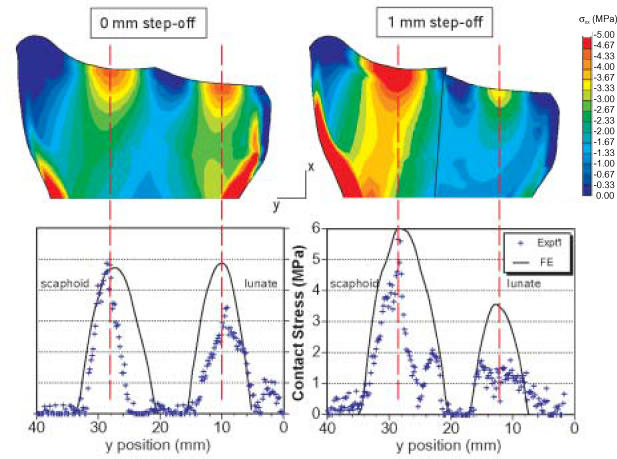
Contour plots of FE-computed stress distribution and graphs comparing computed contact stresses to those measured experimentally (NOTE: The symbols in the graphs are from a single experimental specimen).
Maximum Contact Stress (MPa).
| Step-off (mm) |
Experimental*
(mean±SD) |
FE |
|---|---|---|
| 0 | 4.79 ± 0.97 | 4.87 |
| 1 | 5.66 ± 0.98 | 6.07 |
| 2 | 7.22 ± 1.19 | 6.93 |
| 3 | 8.36 ± 2.15 | 7.73 |
n = 8 specimens
In this paper, we briefly describe the development of a computational model of the radiocarpal joint that, in concert with our previously developed experimental models, provides insight that might one day lead to improvements in intra-articular fracture management techniques. FE-predicted stresses are compared with previously available experimental data reflecting radiocarpal stress distributions in order to validate the model. Finally, a step-off incongruity is introduced into the FE mesh.
METHODS
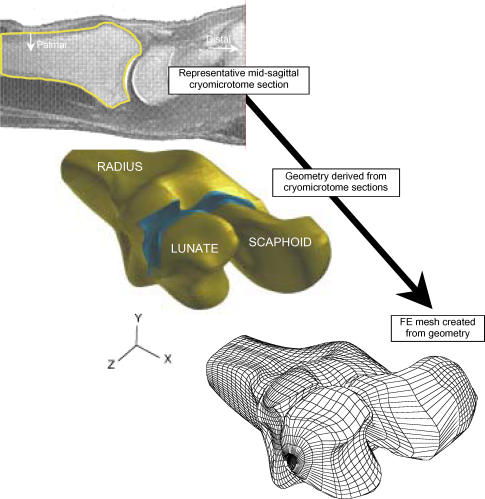
Radiocarpal geometry was obtained from cryomicrotome sections of a cadaver wrist. This procedure (performed at the Medical College of Wisconsin) involved freezing a cadaver forearm to a very low temperature, then sectioning it at specific intervals (0.5 mm) sagittally with a microtome. A total of 144 tissue slices were cut at 0.5 mm intervals from the mid-forearm through the fingers and photographed. Tissue boundaries were digitized and slices were subsequently registered. One such image is shown in Figure 4, allowing clear identification of boundaries for the radius, lunate, and the associated cartilage surface layers.
Figure 4.
This schematic highlights the procedure for generating a 3D FE model of the radiocarpal joint from cryomicrotome source image data.
These image data were then processed to yield full three-dimensional reconstruction of relevant bone and cartilage geometry (Figure 4). Starting from the digitized boundary point data, solid modeling software (PATRAN, MSC Software) was used to create geometric entities (parametric bicubic surfaces) bounding the bone and cartilage regions. A volumetric mesh, consisting of eight noded hexahedral elements, was created on the geometry using mesh generation capability within PATRAN.
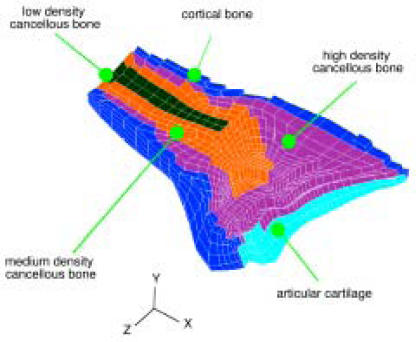
Linear elastic isotropic material regions representing cortical bone (E=13.8 GPa), three different densities of cancellous bone (1400 MPa, 690 MPa, and 345 MPa) and subchondral bone (2800 MPa) were defined. The Poisson's ratio of all bone elements was prescribed to be 0.3. Elements were assigned bone modulus values according to their distance from the outer cortical shell, with progressively less dense cancellous regions from the cortex to the center of the bones. After a mesh was created, material property distribution was assigned to the mesh based on the proximity of element centroid locations to the cortex using custom-written PATRAN subroutines. The resulting mesh is depicted (Figure 5) in a mid-coronal view of the radius.
Figure 5.
This cut-away view of the distal radius FE mesh shows the prescribed material property distribution.
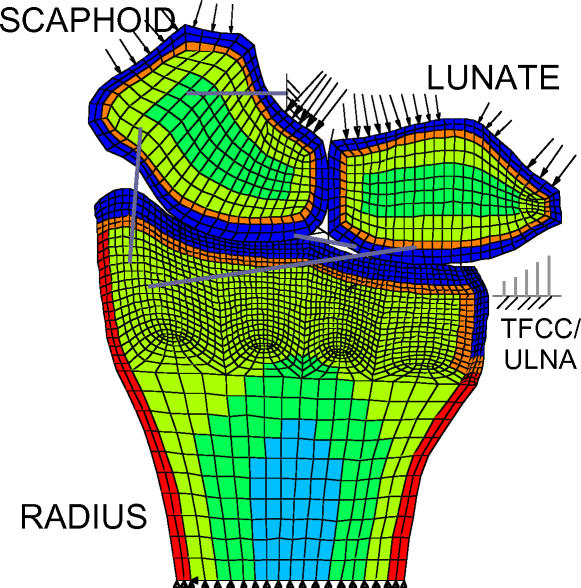
Cartilage elements were meshed across the articular surfaces of the radius, scaphoid, and lunate. These elements were assigned a modulus of 10 MPa, and a Poisson's ratio of 0.45. Relevant wrist ligaments were modeled as piecewise linear spring elements. These included the radiolunate, radioscaphoid, scapholunate and scaphotriquetral ligaments. The spring constants assigned for all ligaments were taken from the literature.15 While the ulna contributes structurally to support the wrist joint, it was not explicitly modeled as a continuum. The structural support provided by the ulna through the triangular fibrocartilage complex (TFCC) was included by modeling TFCC/ulnar support as a parallel array of compressive springs attached from fixed nodes to the lunate.
Contact elements (3D slidelines) were defined on the articulations between the radius and lunate, radius and scaphoid, and scaphoid and lunate. These elements allowed for finite sliding between the contacting bodies and accommodated a non-zero frictional coefficient of 0.01. The entire proximal end of the radius was fixed, and two different mid-carpal load/displacement driving conditions were studied. In one case, mid-carpal loads were applied on the distal surfaces of the lunate and scaphoid (force control). These loads were obtained from a previously reported analysis.15 In another case, experimentally recorded carpal bone motions were used to drive the FE model via applied displacements (displacement control). The source kinematic data reflecting carpal bone motion was recorded by rigidly attaching electromagnetic sensors19 (3Space Tracker, Polhemus, Inc.) to the lunate and scaphoid during application of a 100 N load across the radiocarpal joint.11 These displacement data were scaled and applied to the carpal bone FE models.
The FE solutions were obtained using a large displacement static analysis in ABAQUS FE software (ABAQUS, Inc.) on a Cray C90 at the Pittsburgh Supercomputing Center. The average analysis time for the models (nominally 13,000 degrees of freedom) was about 700 CPU seconds.
One of the objectives of the FE modeling undertaken was to study the effect of articular incongruities on the stress distribution in the joint. Toward this end, the FE mesh was modified to reflect the depressed lunate die-punch fracture simulated experimentally. A section of the distal radius mesh constituting the entire lunate fossa was freed from its neighboring elements, and displaced 1, 2 and 3 mm along the long axis of the radius. This was accomplished by removing elements at the base of the fragment, and then tying the nodal degrees of freedom at the fragment base to their nearest neighboring nodes on the remainder of the radius using tied multi-point constraints (MPC's). The model was driven using carpal kinematic data obtained for the corresponding step-off case. Computed contact stresses were then compared to previous experimental recordings of contact stress obtained in the cadaveric fracture step-off studies.
RESULTS
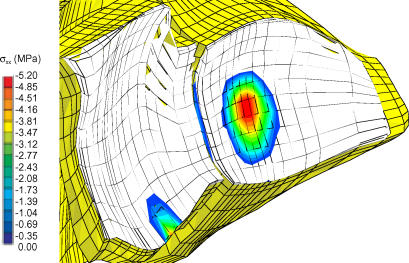
The results from the FE simulations reflect two distinct zones of contact on the distal radius, one each for the scaphoid and the lunate (Figure 6). Large displacements of the lunate and scaphoid were computed in the course of the solution. Adequate mesh refinement was established by performing a mesh convergence study considering three distinct levels of mesh sizes. The coarsest mesh had 3229 elements and the most refined mesh had 8980 elements. For the force control case, applied loads corresponded to a force of 100 N distributed over the distal surfaces of the lunate and the scaphoid. The maximum contact stress predicted in force control was 4.6 MPa on the scaphoid fossa. The resulting loads were distributed as 53 N through the scaphoid fossa and 49 N through the lunate fossa, consistent with previously reported results. The mesh convergence study showed that as mesh refinement was increased, the computed maximum contact stress approached the experimentally reported maximum contact stress value of 4.8 MPa (averaged over eight forearms tested).10
Figure 6.
Computed contact stress distribution on the distal radius articular surface, with inset of contact stress imprint from cadaveric model for comparison.
In displacement control, the resulting radiocarpal contact stress distribution also showed two distinct zones of contact (one each on the lunate and scaphoid fossa). The maximum predicted contact stress value was 5.3 MPa and it occurred on the scaphoid fossa in a more dorsal location than computed with the force control condition.
Figure 7a shows a close-up of the radiocarpal articulation including a 1-mm step-off. In the presence of a 1- mm step-off of the lunate fossa, the computed contact stress distributions shifted ulnarly (Figure 7b), as was observed experimentally. As the magnitude of step-off increased, there was a continued trend toward unloading of the lunate fossa, increased loading in the scaphoid fossa and a shift in location of maximum stress on the scaphoid fossa toward the fracture line. These findings are all consistent with our previously published results obtained in a cadaveric step-off model.10
Figure 7.
Simulated distal radius without step-off (A) and with 1-mm step-off (B) on the FE mesh of the distal radius articular surface with computed contact stress distribution shown.
Figure 7A.
Figure 7B.
DISCUSSION
One of the motivations for this research was the need for a more accurate three-dimensional representation of multibody contact in the radiocarpal joint with which to study juxta-articular stress distributions following imprecise fracture reduction. A high-fidelity 3D FE mesh was generated from cryomicrotome sections of a cadaver forearm. The resulting 3D model incorporated finite sliding large deformation contact modeling capabilities not previously used in articular joint simulation. The model was run under force and displacement control in independent simulations. The force control analysis was performed to establish the utility of this general FE approach. The very close agreement of FE predictions to experimental results obtained with force control was highly encouraging, even if the kinematics of the carpal bones were somewhat circumscribed. Displacement control of the FE model was then implemented to allow simulation of intra-articular fracture step-off utilizing previously collected experimental data reflecting radiocarpal kinematics in a cadaver forearm subjected to static loading.
The 3D radiocarpal FE model exhibited behavior consistent with findings from earlier models of joint contact. The predicted compressive strains (εxx) on the cartilage were on the order of 25-30%, reaffirming the function of cartilage as a load-distributing layer. The role of the subchondral plate in transferring the load applied on the joint surface to the cortical shell was also affirmed.
The load carried by the springs representing the TFCC was around 20% of the total applied load that agreed well with prior analytical models,15 in which the TFCC/ulnar component of the total load on the wrist was calculated to be 22%. In previous experimental studies, this component was determined to be around 18% in an intact forearm when the wrist was in a neutral position,20 and around 8% with ulnar deviation of the wrist.15 In reality, the ulna is a complex structure, and its shape and position with respect to the carpus influences the load transfer at the wrist.
Another important finding relates to the maximum shear stress at the interface between the cartilage and subchondral bone on the radius. Maximum shear stress levels at the deepest (fourth layer of elements) level of cartilage were higher than those seen in more superficial layers. The location of this maximum shear corresponded to the rim of the contact area. Cartilage is a nearly incompressible material (υ=0.45), and the high compressive contact stresses on the surface generate large transverse (shear) deformations. Immediately beneath the cartilage, the subchondral plate, by virtue of its much smaller Poisson's ratio (υ=0.3) and much higher elastic modulus, resists this transverse deformation leading to high stresses at the cartilage-subchondral bone interface. This shear stress is proportional to the longitudinal (compressive) stresses in more superficial layers. Any aberrant behavior in the joint that gives rise to abnormal local contact stresses would directly influence the maximum shear at the deeper levels of cartilage. Elevated levels of shear stress at the osteochondral junction have been suggested to be initiators of fissures in the deeper zones of cartilage as observed in clinical OA.2
The success of any type of modeling technique depends upon its being validated using previously established methods. In the present situation, experimental methods employing pressure-sensitive film have been successful in measuring the contact pressures on the articulating surfaces of the radiocarpal joint.9,10,12 Comparing the FE-predicted stress distribution on the articular surface to the experimental measurements forms a sound basis for validating the FE model. However, a number of important guidelines need to be followed before such comparisons can be made. Most importantly, it is necessary to ensure that the FE model accurately represents the experimental loading conditions. Large deformation FE contact simulations are sensitive to small changes in initial appositions of the contacting bodies, making it critical to ensure that the carpal bones are in the same relative positions and orientations in the computational model in comparison with the experimental cadaver specimen.
For the present model, a number of unique situations confounded validation efforts. The specific cadaver specimen used to generate the base geometry for the FE model was not first tested in our experimental protocol. This implied that, before applying the experimental boundary conditions to the FE model, a one-to-one correspondence had to be established between the bones of the model and of the cadaver specimen used in the experiments. To make this comparison, data representing the boundary of the bones of the experimental cadaver specimen were necessary. Although available, the data points were few in number (compared to the cryomicrotome-based data). These data were collected by manually digitizing the outer surfaces of the bones using an electromagnetic digitizing stylus. The combination of these two factors resulted in a less-than-ideal situation for establishing correspondence. In addition, no contact pressure measurements were made for this particular cadaver specimen. Contact stress distributions were available for a number of other specimens, but for which no bone boundary information was available for establishing post hoc correspondence. The cadaver specimen, which was used for establishing correspondence with the FE model, provided the kinematic data of the carpal bones when the wrist was taken from an unloaded to a fully loaded state.
Another limitation relates to constitutive treatment of articular cartilage. Prior FE models of joint contact that have placed emphasis on accurate description of cartilage constitutive behavior have tended to be geometrically simple.21–24 In real joints, as demonstrated by the present model, articular surfaces tend to be highly irregular and cartilage thickness varies as a function of location. Such variations cannot be adequately represented with simplistic geometric representations of articular joints. The advantage that the present model offers is thus obvious. It can couple the sophistication of material models with true geometric representation of the joint. The ABAQUS FE code utilized in this study has a poroelastic material capability, which can emulate the biphasic behavior of cartilage. Poroelastic modeling provides capabilities for representing coupled pore fluid diffusion/stress analysis involving partially or fully saturated fluid flow. Incorporating more complex material definitions would be a straightforward extension of the present FE model.
Despite the previously mentioned limitations, the present three-dimensional FE model of the radiocarpal joint is the first attempt at accurately characterizing articular joint contact stresses using existing modeling techniques. The utility of the model lies in the fact that it can now be used as the baseline for making any modifications that would potentially increase model sophistication and applicability. The model has potential to provide a clinician with rigorously established guidelines for treatment of intra-articular fractures. Clinical series have recognized the relationship between the degree of residual articular incongruities and eventual degenerative changes.1 The FE-predicted results provide quantitative descriptions of the load transfer mechanism through the joint, and therefore potentially reinforce the decision-making process by detailing the efficacy of a treatment procedure. Additionally, the model has capability to incorporate the structural contributions of fracture fixation devices that are conventionally employed to promote faster healing. In this scenario, the clinician, with the help of the model, can decide which type of fixation technique/device is the most suitable one for a specific wrist. This means that the models have to be more patient-specific, and present advancements in the field of musculoskeletal imaging, combined with the availability of faster computers, make such a scenario possible in the foreseeable future.
ACKNOWLEDGMENTS
The financial support of the Whitaker Foundation (DDA) is gratefully acknowledged. This research was also supported in part by grant number MSS950003P from the Pittsburgh Supercomputing Center, sponsored by the National Science Foundation.
References
- 1.Knirk JL, Jupiter JB. Intra-articular fractures of the distal end of the radius in young adults. J Bone Joint Surg. 1986;68A:647–659. [PubMed] [Google Scholar]
- 2.Radin EL, Martin RB, Burr DB, Caterson B, Boyd RD, Goodwin C. Mechanical factors influencing cartilage damage. In: Peyron JG, editor. Osteoarthritis, Current Clinical and Fundamental Problems. France: CIBA-Geigy; 1985. pp. 90–99. [Google Scholar]
- 3.Fernandez DL, Geissler WB. Treatment of displaced articular fractures of the radius. J Hand Surg. 1991;16A:375–384. doi: 10.1016/0363-5023(91)90001-r. [DOI] [PubMed] [Google Scholar]
- 4.Bradway JP, Amadio PC, Cooney WP. Open reduction and internal fixation of displaced, comminuted, intra-articular fractures of the distal end of the radius. J Bone Joint Surg. 1989;71A:839–847. [PubMed] [Google Scholar]
- 5.Trumble TE, Culp RW, Hanel DP, Geissler WB, Berger RA. Intra-articular fractures of the distal aspect of the radius [review] Instr Course Lect. 1999;48:465–480. [PubMed] [Google Scholar]
- 6.Lansinger O, Bergman B, Korner L, Anderson GBJ. Tibial condylar fractures—A twenty year follow-up. J Bone Joint Surgery. 1986;68A:13–19. [PubMed] [Google Scholar]
- 7.Waddell JP, Johnston DWC, Neidre A. Fractures of the tibial plateau: A review of ninety-five patients and comparison of treatment methods. J Orthop Trauma. 1981;21:376–381. doi: 10.1097/00005373-198105000-00007. [DOI] [PubMed] [Google Scholar]
- 8.McCallister WV, Smith JM, Knight J, Trumble TE. A cadaver model to evaluate the accuracy and reproducibility of plain radiograph step and gap measurements for intra-articular fracture of the distal radius. J Hand Surg. 2004;29(5):841–847. doi: 10.1016/j.jhsa.2004.04.019. [DOI] [PubMed] [Google Scholar]
- 9.Anderson DD, Bell AL, Gaffney MB, Imbriglia JE. Contact stress distributions in malreduced intra-articular distal radius fractures. J Orthop Trauma. 1996;10(5):331–337. doi: 10.1097/00005131-199607000-00007. [DOI] [PubMed] [Google Scholar]
- 10.Baratz ME, DesJardins JD, Daniel TE, Anderson DD, Imbriglia JE. Displaced Intra-articular Fractures of the Distal Radius: The Effects of Fracture Displacement on Contact Stresses in a Cadaver Model. J Hand Surg. 1996;21A:183–188. doi: 10.1016/s0363-5023(96)80098-0. [DOI] [PubMed] [Google Scholar]
- 11.DesJardins JD, Daniel TE, Anderson DD, Baratz ME, Imbriglia JE. Changes in Carpal Kinematics with Displaced Intra-articular Fractures of the Distal Radius. Advances in Bioengineering. 1994;28:357–358. [Google Scholar]
- 12.Viegas SF, Tencer AF, Cantrell J, Chang M, Clegg P, Hicks C, O'Meara C, Williamson JB. Load transfer characteristics of the wrist. Part I. The normal joint. J Hand Surg. 1987;12A(6):971–978. doi: 10.1016/s0363-5023(87)80093-x. [DOI] [PubMed] [Google Scholar]
- 13.Wagner WF, Jr, Tencer AF, Kiser P, Trumble TE. Effects of intra-articular distal radius depression on wrist joint contact characteristics. J Hand Surg. 1996;21A(4):554–560. doi: 10.1016/S0363-5023(96)80003-7. [DOI] [PubMed] [Google Scholar]
- 14.Thompson RC, Jr, Oegema TR, Jr, Lewis JL, Wallace L. Osteoarthrotic changes after acute transarticular load: An animal model. J Bone Joint Surg. 1991;73A(7):990–1001. [PubMed] [Google Scholar]
- 15.Horii E, Garcia-Elias M, An KN, Bishop AT, Cooney WP, Linscheid RL, Chao EYS. Effect on force transmission across the carpus in procedures used to treat Kienböck's disease. J Hand Surg. 1990;15A(3):393–400. doi: 10.1016/0363-5023(90)90049-w. [DOI] [PubMed] [Google Scholar]
- 16.Anderson DD, Daniel TE. A Contact-Coupled Finite Element Analysis of the Radiocarpal Joint. Seminars in Arthroplasty. 1995;6(1):30–36. [PubMed] [Google Scholar]
- 17.Ulrich D, van Rietbergen B, Laib A, Rüegsegger P. Load transfer analysis of the distal radius from in-vivo high-resolution CT-imaging. J Biomechanics. 1999;32:821–828. doi: 10.1016/s0021-9290(99)00062-7. [DOI] [PubMed] [Google Scholar]
- 18.Carrigan SD, Whiteside RA, Pichora DR, Small CF. Development of a Three-Dimensional Finite Element Model for Carpal Load Transmission in a Static Neutral Posture. Annals of Biomedical Engineering. 2003;31:718–725. doi: 10.1114/1.1574027. [DOI] [PubMed] [Google Scholar]
- 19.An KN, Jacobsen MC, Berglund LJ, Chao EYS. Application of a magnetic tracking device to kinesiologic studies. J Biomechanics. 1988;21(7):613–620. doi: 10.1016/0021-9290(88)90225-4. [DOI] [PubMed] [Google Scholar]
- 20.Short WH, Palmer AK, Werner FW, Murphy DJ. A biomechanical study of distal radius fractures. J Hand Surg. 1987;12A:529–534. doi: 10.1016/s0363-5023(87)80202-2. [DOI] [PubMed] [Google Scholar]
- 21.Ateshian GA, Lai WM, Zhu WB, Mow VC. An asymptotic solution for two contacting biphasic cartilage layers. J Biomechanics. 1994;27(11):1347–1360. doi: 10.1016/0021-9290(94)90044-2. [DOI] [PubMed] [Google Scholar]
- 22.Donzelli P. Troy, NY: Renssalear Polytechnic Institute; 1995. A mixed penalty contact finite element formulation for biphasic soft tissues. PhD Thesis. [Google Scholar]
- 23.Spilker RL, Maxian TA. A mixed-penalty finite element formulation of the linear biphasic theory for soft tissues. Int J Numer Methods Eng. 1993;30:1063–1082. [Google Scholar]
- 24.Wu JZ, Herzog W, Epstein M. Articular joint mechanics with biphasic cartilage layers under dynamic loading. J Biomech Eng. 1998;120(1):77–84. doi: 10.1115/1.2834310. [DOI] [PubMed] [Google Scholar]