Use of a novel Förster resonance energy transfer method to identify locations of site-bound metal ions in the U2–U6 snRNA complex

Abstract

U2 and U6 snRNAs pair to form a phylogenetically conserved complex at the catalytic core of the spliceosome. Interactions with divalent metal ions, particularly Mg(II), at specific sites are essential for its folding and catalytic activity. We used a novel Förster resonance energy transfer (FRET) method between site-bound luminescent lanthanide ions and a covalently attached fluorescent dye, combined with supporting stoichiometric and mutational studies, to determine locations of site-bound Tb(III) within the human U2–U6 complex. At pH 7.2, we detected three metal-ion-binding sites in: (1) the consensus ACACAGA sequence, which forms the internal loop between helices I and III; (2) the four-way junction, which contains the conserved AGC triad; and (3) the internal loop of the U6 intra-molecular stem loop (ISL). Binding at each of these sites is supported by previous phosphorothioate substitution studies and, in the case of the ISL site, by NMR. Binding of Tb(III) at the four-way junction and the ISL sites was found to be pH-dependent, with no ion binding observed below pH 6 and 7, respectively. This pH dependence of metal ion binding suggests that the local environment may play a role in the binding of metal ions, which may impact on splicing activity.

INTRODUCTION

The removal of non-coding sequences, or introns, and the ligation of coding regions, or exons, is an integral step in the maturation of eukaryotic precursor (pre-)mRNA. Pre-mRNA splicing in the eukaryotic nucleus is carried out by the spliceosome, a dynamic assembly of five small nuclear snRNAs and at least 100 proteins. Existence of an extensive network of RNA–RNA and RNA–protein interactions in the spliceosome is supported by in vivo and in vitro biochemical assays, data from cross-linking experiments and computational calculations (1).

U2 and U6 snRNAs are the only two snRNAs that are required in both steps of splicing and their sequences are the most conserved of all five snRNAs. In the assembled spliceosome, they form regions of base pairing through several helices (2–6). The U2–U6 snRNA complex has been shown to catalyze an intramolecular reaction similar to the first step of splicing in the presence of branch site region of the intron (7,8). This evidence strongly suggests these RNA components comprise the core of the active spliceosome.

Metal ions play a significant role in RNA folding and ribozyme catalysis (9). Bound metal ions assist in folding and stabilization of RNA stem-loop structures by increasing the number of favorable intra- and inter-strand interactions. Divalent metal ions, particularly Mg(II), are essential for spliceosomal assembly and activity. Several lines of evidence support the obligatory role of divalent metal ions in the activity of the U2–U6 snRNA complex. Replacement of phosphate groups with phosphorothioate groups, which do not strongly bind hard metal ions such as Mg(II), at specific sites on the U6 snRNA backbone resulted in obliteration of splicing activity. These sites include the backbone at U74 of U6 snRNA, which forms part of an internal loop within the intra-molecular stem loop (ISL) (10), the two G residues in the invariant ACAGAGA segment between helices I and III (11), and the A residue of the invariant AGC triad near the four-way junction (12). Splicing activity was rescued by Mn(II), a softer metal ion, which coordinates more readily with sulfur atoms. Moreover, UV-induced cross-linking experiments demonstrated metal-ion-dependent interaction between these regions (13). In vitro RNA-only splicing activity was also shown to be dependent upon Mg(II), resulting in the formation of a covalent product between the branch site and the ACG triad (7,8).

Evidence for pH-dependent metal ion binding of a bulged uridine of the U6 ISL (U80 in the yeast sequence, which corresponds to U74 in the human sequence) comes from NMR studies (14). Protonation of the neighboring C–A base pair and binding of metal ions were found to be mutually antagonistic. At higher pH, the C–A pair was deprotonated; U80 was stacked in the helix and formed an ion-binding site. The authors suggested the possibility of a pH-dependent mechanism for the regulation of spliceosomal activity (14). Although it is possible that other sites exhibit pH dependent ion coordination behavior, the pH-dependence has not been examined.

The goal of this research is to identify the locations of site-bound multivalent ions within the U2–U6 complex and ascertain the pH dependence of ion-binding behavior. To accomplish this, we have used Förster resonance energy transfer (FRET) between site-bound luminescent lanthanide ions and a covalently attached organic dye. The novelty of this study is that the lanthanide ions are coordinated to the sites in the RNA complex without the use of chelates.

THEORY

The alkaline earth metals most commonly bound to RNA under physiological conditions, e.g. Mg(II), are spectroscopically uninformative. Use of ions with useful spectroscopic properties permits more direct observation of metal-ion-binding properties of these sites. Terbium(III) is a lanthanide ion which is an open shell, paramagnetic species and is luminescent in solution under favorable conditions (15,16). Hydroxyl (-OH) vibrations of water molecules provide a channel for internal conversion of the lanthanide excitation energy; thus the luminescence of lanthanide ions is strongly quenched in aqueous solution (17). Upon binding to RNA molecules, however, water molecules are removed from the coordination sphere, and the relaxation channel is decreased, thereby increasing luminescence considerably. Moreover, nucleic acid bases absorb strongly at 280 nm. Thus, RNA acts like an antenna to transfer energy to RNA-bound Tb(III) ion. This phenomenon further enhances its luminescence significantly. Like Mg(II), Tb(III) is a ‘hard’ acid, and prefers ‘hard’ base ligands, and it has been shown to occupy the identical or similar site as Mg(II) in some X-ray structures of RNA (18). Luminescence studies of lanthanide ions bound to native tRNA and the hammerhead ribozyme have probed metal-binding properties of these molecules (19–21).

FRET is commonly used as a ‘molecular ruler’ in biomolecular structural studies. Initially the acronym FRET referred specifically to fluorescence resonance energy transfer because the donor and acceptor pairs were both fluorophores. In a variant experiment, the luminescence energy of chelated lanthanide ions was transferred directly to an acceptor molecule (22), in which case the approach was called LRET (luminescence resonance energy transfer). Lanthanide luminescence is formally neither fluorescence (singlet-to-singlet transition) nor phosphorescence (triplet-to-singlet transition), but as a result of atomic configuration where emission arises predominantly from electric dipole transitions (23). For this reason, both forms of energy transfer obey the same fundamental principles, and it has been suggested that the acronym FRET applies both to the specific (fluorescence) and general (Förster) resonance energy transfers (24).

FRET originates from non-radiative interaction between a donor and an acceptor exhibiting a spectral overlap between donor emission and acceptor excitation spectra. The energy transfer efficiencies can be calculated by several methods (25). In this article, two equations were used:

1

where E is the energy transfer efficiency, τ_DA and τ_D are lifetimes of the donor in the presence and absence of the acceptor, respectively; and

2

where I_AD is the intensity of acceptor in the presence of donor and I_AD,100% is the intensity of acceptor in the presence of donor when the energy transfer efficiency is 100%.

In previous FRET studies, donor–acceptor (D–A) pairs were covalently bound to target molecules directly or indirectly. In the case where luminescent metal ions have been used as donor, EDTA-like chelates were always covalently bound to the target molecules; the metal ions were bound indirectly to the targets through the organic ligands (26). In this work, we used Tb(III), a lanthanide ion, non-covalently bound through inner sphere coordination to sites within the folded RNA as FRET donors. The acceptor Cy3 was an organic dye covalently bound to the RNA molecules.

The Förster radius R₀ is defined as the distance between donor and acceptor when E = 50%. For a particular D–A pair, its Förster radius is constant in a particular environment. In this article, two D–A pairs are used. Cy3/Cy5 has a Förster radius R₀ of 54 Å adapted from Ha et al. (27) because we used similar environments. Selvin reported R₀ of 61 Å for Tb(III)/Cy3 with a chelated Tb(III) with quantum yield of 0.48 (23). However, the quantum yield of Tb(III) bound directly to RNA was measured as 0.2 by the method described by Xiao and Selvin (28). Based upon the difference in quantum yield, we calculated that R₀ for transfer between RNA-bound Tb(III) and Cy3 equals to 61/(0.48/0.2)^1/6 Å ∼54 Å (23). The distance R between two probes is then calculated by:

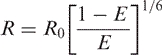3

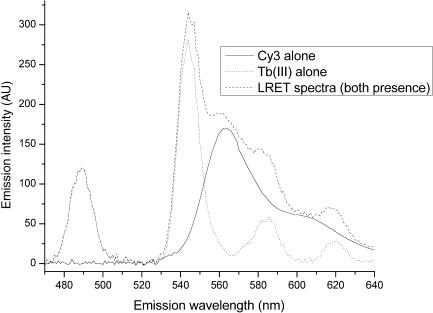
In the presence of Cy3 within an appropriate distance, lifetimes of Tb(III) luminescence decrease as a result of resonance energy transfer. Because the lifetimes of Cy3 (in nanoseconds) and Tb(III) (in milliseconds) are very different, self-fluorescence of Cy3 was eliminated in detected luminescence signals by use of a long delay time (100 μs) prior to data acquisition. As shown in Figure 1, the luminescence of RNA-bound Tb(III) at 565 nm directly excited at 280 nm by a Xenon flash lamp pulse is essentially nonexistent. Thus, the detected luminescence signal at 565 nm is only from Cy3 as a result of energy transfer from Tb(III). The recorded decay is therefore the result of the FRET-mediated Cy3 excitation, the lifetimes of which are identical to the donor lifetimes. Distances between the donor and acceptor are obtained according to Equations (1) and (3). FRET involving more than one site-bound Tb(III) to Cy3 produces a decay curve containing components corresponding to each transfer. In this study, we were able to resolve up to three individual lifetimes, corresponding to three independent Tb(III)-binding sites.

Figure 1.

Emission spectra of Tb(III) and Cy3. With a delay time of 100 μs, all signal from the Cy3–Tb(III) sample at 565 nm was attributable to energy transfer from Tb(III) to Cy3 because Tb(III) does not emit at this wavelength. The lifetimes of the contributing components were the lifetimes of the Tb(III) emission in the presence of acceptors. Multiple D–A (donor–acceptor) distances resulted in multiple lifetimes. When recording the emission of Cy3, we did not incorporate the delay time of 0.1 ms used for Tb(III) measurements.

In order to ensure the reliability of analysis of multiple lifetimes, the results were further supported by separate stoichiometric and mutational studies.

MATERIALS AND METHODS

RNA design and synthesis

All experiments were carried out on RNA sequences of human U2–U6 snRNA (Figure 2) (8). For measurements with single 5′-Cy3 and double 5′-Cy3, 3′-Cy5 labels, the top strand was purchased from Dharmacon (Lafayette, CO). Otherwise, unlabeled RNA strands were made by in vitro transcription under standard conditions using T7 RNA polymerase with synthesized DNA templates from IDTDNA (Coralville, IA). DNA templates were designed with a standard T7 promoter sequence. T7 RNA polymerase for transcription reactions was expressed and isolated according to a published protocol (29). Transcripts were purified by electrophoresis on a denaturing polyacrylamide gel and eluted with an electro-eluter (Schleicher and Schuell, Whatman, Inc.). RNA concentrations were determined from the absorbance at 260 nm, and the integrity of the final RNA samples was confirmed by the appearance of a single band on a 15% denaturing polyacrylamide gel.

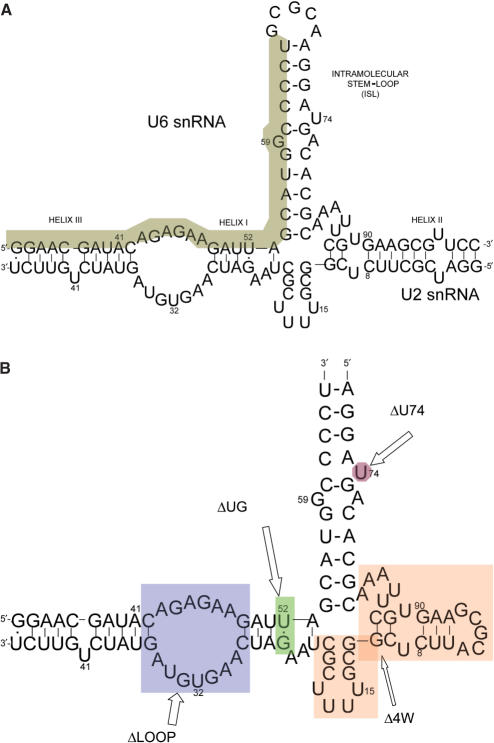
Figure 2.

Sequences of RNA oligomers used in this work. (A) Proposed complex formation between the central domains of human U2 and U6 snRNA. Previously established helices I, II, III and U6 intra-molecular stem loop (ISL) are labeled. The invariant top strand 32-mer area is shaded. (B) The simplified construct and its mutations used in the FRET study. The sequence represents the simplified original construct (called WT), which includes an invariant 32-nt top strand and a 69-nt bottom strand. Fluorescent dyes are attached at the 3′ or 5′ end of the 32-nt strand. The four mutation areas are shaded. All mutations were created by variations of segments of the bottom strand. ΔLOOP eliminates the ACAGAGA loop by mutating the bottom sequence to result in a complementary stem. ΔUG mutates the U–G base pair to U–A. Δ4W eliminates the four-way junction by replacing the shaded area with three adenosines. ΔU74 deletes the shaded uridine from the U6 ISL sequence.

Non-denaturing gel electrophoresis

RNA samples were loaded on a 10% non-denaturing gel in Tris-HEPES buffer. 0.01 nmol (∼1 µg) each of top and bottom strand were combined, heated at 80°C for 45 s and cooled at room temperature for 10 min prior to loading to the gel. The gel was run in a 4°C cold room under 100 V. The gel was stained with ethidium bromide for UV visualization.

Measurement of Tb(III) luminescence

Tb(III) stock solution was made by dissolving Tb₂O₃ in HClO₄ (both purchased from Sigma Aldridge). Concentration was measured by titration with EDTA as described previously (19). The excitation wavelength was 280 nm. Tb(III) has minimal luminescence in water solution. Upon binding to RNA, its luminescence is greatly enhanced by the two phenomena described above.

Lanthanide ions can hydrolyze RNA polymers nonspecifically at high concentrations, pH and temperatures (30). In the study, 7 µM Tb(III) did not hydrolyze the RNA samples under the described conditions for days (data not shown). Also, high buffer pH could change the binding properties of lanthanide ions by converting them to lanthanide hydroxides or changing hydration status (31). However, we observed no difference in lifetimes of Tb(III) bound to RNA at pH 5.6–7.2, suggesting its overall hydration/binding status was not altered significantly.

RNA samples (1 µM) were titrated with Tb(III) until the luminescence did not increase further. The dissociation constant of Tb(III) binding to U2–U6 snRNA complex was calculated by fitting the plot of the saturation plot with a standard binding isotherm for three equivalent sites yielded a mean K_d of ∼3 µM. The moderate binding affinity allows us to use the stoichiometry measurements in the next section with minimal assumptions. The Tb(III) could be competed off the RNA by Mg(II), resulting in decreasing luminescence to zero. This showed that Mg(II) occupied the same or similar sites as Tb(III). However, Mg(II) had ∼200 times weaker affinity to U2–U6 complex than Tb(III).

Measurement of metal-ion-binding stoichiometry to RNA constructs

The continuous titration approach of measuring Tb(III):RNA binding stoichiometry, or Job Plot method, was used (32), employing a repetitive dilution approach for the titration. In a 200-μl cuvette, the total [RNA + Tb (III)] concentration was 2.0 μM. For an RNA fraction of 0.9, 180 μl 2 μM RNA and 20 μl 2 μM Tb(III), both in buffer, were mixed; for an RNA fraction of (0.9)², 20 μl of the previous mixture was removed and 20 μl 2.0 μM Tb(III) in buffer was added to the cuvette. The RNA fraction of (0.9)ⁿ can be achieved using this approach. Measurement of Tb(III) emission was performed on a Cary Eclipse spectrophotometer (Varian, Inc.), with excitation at 280 nm. The emission intensity at 545 nm was plotted against the corresponding RNA mole fraction and fit to a Gaussian function in SigmaPlot 8.0 (Systat Software, Inc.). The number of ion-binding sites is equivalent to (1 − x)/x, where x is the RNA fraction at the peak of the Gaussian curve (19).

Measurements of Tb(III) luminescence decay

RNA concentration in all assays was kept low at 0.7 μM; Tb(III) concentration was 3.5–7 μM. The concentration of Tb(III) was kept at or below 7 μM in order to minimize diffusional energy transfer, which dominates the decay signals at high [Tb(III)] (33). Buffers contained 150 mM NaCl and 10 mM MES for pH 5.6, 6.1, 6.6 or 10 mM MOPS for pH 7.2. The pH was adjusted by NaOH and HCl. A high concentration of NaCl (150 mM) was used to minimize nonspecific binding of Tb(III).

Lifetime measurements were carried out on a Cary Eclipse fluorophotometer. Photomultiplier tube (PMT) power was 800 V, if not specified otherwise. Excitation pulses had a width of 2–3 μs at 280 nm and excitation/emission slits were 10 nm. With unlabeled RNA, Tb(III) luminescence decay (τ_D) at 545 nm was recorded. Tb(III) luminescence decay (τ_DA) was measured at 565 nm when Cy3-labeled RNA was used. The reason for the use of different detection wavelengths is that luminescence of Tb(III) bound to unlabeled RNA has maximal signal at 545 nm, with essentially no signal at 565 nm (Figure 1), whereas Cy3 has a maximum emission at 565 nm. Because we incorporate a detection delay of 0.1 ms, the signal at Cy3 (which has a lifetime in the nanosecond range) is fully attributable to energy transfer from Tb(III). Decay curves were fit with OriginLab using built-in least-square-goodness-of-fit Levenberg–Marquardt algorithm (LMA). OriginLab software reports results of χ² in reduced (normalized) χ² format; we have therefore used reduced χ² values in this article. A maximum of three independent decay components could be accurately obtained. The exponential decay equation is as follows:

4

where I₀ is the system background, A_is are the amplitudes for each exponential decay that can be used to identify the population ratio of different decays and t_is are the individual decay lifetimes.

FRET experiments using the Cy3–Cy5 pair

Measurements were performed on the Cary Eclipse. Excitation of Cy3 was at 520 nm with excitation/emission slits of 5 nm and the temperature set at 22°C. The emission scan was collected from 540 to 700 nm. Equal molar amounts (0.7 μM each) of top (labeled) and bottom strands were annealed prior to measurements. RNA samples labeled with Cy3 only, Cy5 only and both dyes were measured.

RESULTS

Design of RNA samples and confirmation of base pairing

The proposed secondary structure of human U2–U6 snRNA complex is shown in Figure 2A. It contains three intermolecular helices and a U6 intramolecular stem loop (ISL) (8). In order to simplify construction of samples suitable for our studies, a model pairing was designed in which the invariant top strand (shaded in Figure 2A) and a variable bottom strand represented the native U2–U6 RNA pairing and variants thereof. In order to make this change, the five-base loop within the ISL was omitted and a terminal loop was added to helix II. This pentaloop was demonstrated in separate experiments not to bind metal ions (data not shown). Variations of the bottom strand were designed so that when paired with top strand, suspected ion-binding sites were deleted by the formation of complementary base-paired segments (Figure 2B). The top strand included nucleotides 33–64 of the U6 sequence. The bottom strand was a chimera of fragments of U2 and U6 snRNAs.

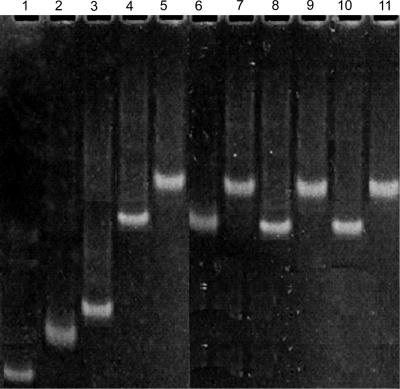
In order to confirm that the bottom strands formed base pairs with the invariant top strand, we monitored migration of each paired RNA sample on a non-denaturing gel. In each case, the disappearance of both single-stranded top and bottom bands and the appearance of a new band which migrated slower than either of the single bands (Figure 3) suggested that the constructs formed complexes by pairing of top and bottom strands.

Figure 3.

Demonstration of base pairing between top and bottom strands by a non-denaturing gel electrophoresis. Lane 1: the invariant top 32 mer. Lane 2: Δ4W bottom strand (40 nt) alone; Lane 3: Δ4W bottom with top strand. Both the brightest bands in lanes 1 and 2 disappeared in lane 3, indicating pairing of the strands. Lanes 4 and 5: WT bottom (69 nt) alone and with top strand. Lanes 6 and 7: ΔLOOP bottom (68 nt) alone and with top strand. Lanes 8 and 9: ΔU74 bottom (68 nt) alone and with top strand. Lanes 10 and 11: ΔUG bottom (68 nt) alone and with top 32 strand. The retardation of paired strands indicated the formation of base-paired complexes.

Stoichiometry of site-bound ions

In order to estimate the number of site-bound terbium ions per RNA complex, Tb(III) luminescence for different ratios of [Tb(III)]:[RNA] was recorded and plotted using a Job plot (32). In this context, ‘site-bound’ denotes the residence of the metal ion at a specific site accompanied by loss of one or more water molecules. In the case of Tb(III), it is associated with increased luminescence. The luminescence intensity represents the amount of RNA-Tb(III) complex by assuming a linear relationship between binding and the luminescence intensity. The principle of this method is that when the combined Tb(III) and RNA concentration is kept constant, at the maximum luminescence intensity, the metal-ion-binding site number corresponds to the mole ratio of [Tb(III)]:[RNA].

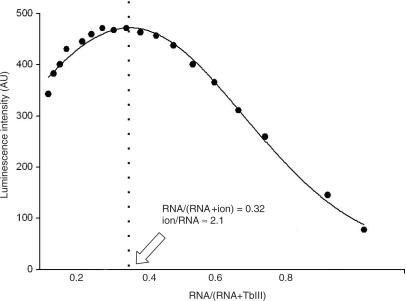
Figure 4 shows the fit process of Tb(III) binding to the ΔU74 mutant complex at pH 7.2 as an example. The luminescence intensity at 545 nm versus RNA fraction for each measurement was plotted. The data were fit by a Gaussian distribution. The peak of the curve was at the RNA fraction of 0.32. The stoichiometry of ions bound to RNA was calculated as n = (1 − x)/x, where x = 0.32 for ΔU74 at pH 7.2. This fraction corresponds to 2.1 binding sites, or approximately two site-bound ions per RNA complex.

Figure 4.

Measurement of RNA metal-ion-binding stoichiometry by Job plot. By way of example, the Job plot for determination of ion-binding stoichiometry of the ΔU74 mutant complex (from which U74 had been deleted from the ISL) at pH 7.2 is shown. Luminescence was recorded for samples with a range of RNA/Tb(III) ratios, with total [RNA + Tb(III)] = 2 µM (see Materials and methods section for details), and was plotted versus RNA/(RNA + ion). Gaussian curve was fit to the data points and the peak of the curve was at RNA/[RNA + Tb(III)] = 0.32. The binding site number (ion/RNA) was n = (1–0.32)/(0.32) ∼2.1. The stoichiometry for other constructs was calculated with the same method (19).

Using the same process, we found 3.0 binding sites in the construct WT at pH 7.2. The stoichiometry was the same as that of the native U2–U6 construct (3.1) (sequence in Figure 2A), which validated that moving the loop did not affect the number of its site-bound ions. Compared to the native construct (U2–U6) and construct WT, ΔLOOP (1.8) and ΔU74 (2.1) each had one less binding site, Δ4W (2.9) and ΔUG (3.3) both had three binding sites (Table 1).

Table 1.

Tb(III) binding stoichiometry of RNA constructs at pH 7.2

Construct	Tb(III)–RNA
U2–U6	3.1 ± 0.1
WT	3.0 ± 0.2
Δ4W	2.9 ± 0.1
ΔLOOP	1.8 ± 0.2
ΔU74	2.1 ± 0.1
ΔUG	3.3 ± 0.3

Construct ‘U2–U6’ includes the original U2 and U6 sequences shown in Figure 2A. Abbreviations for other constructs and experimental details are provided in the Materials and methods section.

The loss of one binding site in the ΔLOOP construct as compared with the original three sites occurred upon replacement of the loop between helices I and III by Watson–Crick base pairs. This suggested that this loop had one Tb(III)-binding site. Similarly, deletion of the U74 nucleotide from the ISL (ΔU74 mutant) resulted in the loss of one binding site, suggesting that U74 of U6 ISL participated in the formation of one binding site. We could not determine the location of the other binding site from these experiments alone because the Δ4W and ΔUG mutations did not eliminate any binding sites.

We note that the use of this approach includes certain assumptions, such as fairly tight binding and a linear relationship between luminescence intensity and the amount of RNA–metal complex, and that measurements derived from them are therefore only approximate. However, our results are likely to be reasonable estimates of Tb(III)-binding behavior in the system because they were internally consistent. Our spectroscopic data on the native and mutant segments thus support the tentative conclusion that there are three metal-ion-binding sites on U2–U6 complex at pH 7.2: one in the ACAGAGA loop, one in the vicinity of U74 in the U6 ISL and one was not determined.

Lifetime measurements of Tb(III) site bound to unlabeled RNA

For measurement of Tb(III) lifetime without acceptor, τ_D, luminescence decay of Tb(III) was monitored at 545 nm following a 280-nm flash. RNA concentration was 0.7 µM. Essentially no luminescence was detected for Tb(III) solution without RNA concentrations up to 1 mM. Therefore, all signals were from the RNA-bound ions. Tb(III) luminescence decay with each of the unlabeled RNA constructs was measured. Analysis of each of the decays revealed a single exponential lifetime. The lifetime was relatively constant at τ_D = 0.77 ± 0.05 ms, regardless of construct or pH (in the range of 5.6–7.2). The observation of a single population of lifetimes suggests that the metal ions were in similar environments (hydration, etc.) in each of the constructs.

Determination of the angle between helix I and U6 ISL

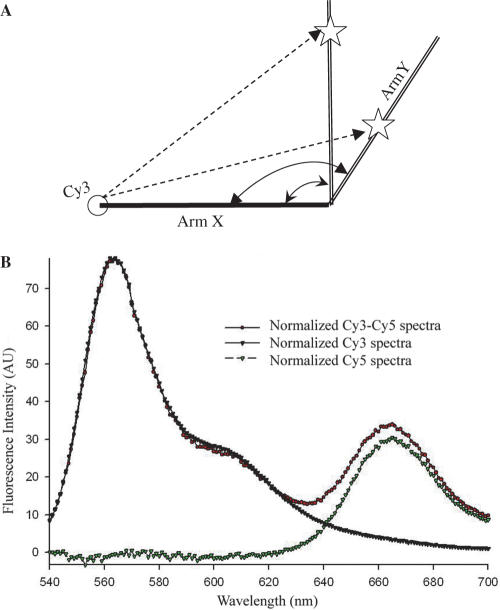
In order to formulate distances obtained from LRET measurements into ion residency locations, the lengths of ‘arms’ X and Y, and the angle between them, are needed (Figure 5A). As an approximation, we make the assumption that helices I and III form a continuous arm between Cy3 and the four-way-junction structure (arm X in Figure 5A); the U6 ISL from the four-way-junction to Cy5 is arm Y. Cy3 and Cy5 were attached to the ends of the X and Y arms by means of covalent bonding (Figure 2B, 5′ and 3′ ends of invariant top strand). In order to find the angle between the two arms, we measured FRET between the two dyes. The samples were excited at 520 nm and emission scans were collected from 520 to 700 nm. The acceptor normalization method was used to determine the distance between the two dye molecules (25). A scheme of the normalization process is shown in Figure 5B.

Figure 5.

Calculation of the angle between helix I and U6 ISL using the acceptor normalization method. (A) The metal-ion-binding site on arm Y cannot be determined without knowing the angle between arms X and Y. As shown, the distance between Cy3 and a site-bound Tb(III) ion (dashed line from Cy3 to star) will correspond to different sites on arm Y if the angle between arms X and Y is unknown. (B) ‘Acceptor normalization method’ normalization process. Normalized Cy5 fluorescence, which is the acceptor intensity, is calculated from normalized Cy3–Cy5 emission spectra minus normalized Cy3 scan.

The distances between Cy3 and Cy5 in different constructs were summarized in Table 2. ΔLOOP complex was examined first because it has a complementary paired X arm. There was a distance of 79±2Å between the two dyes in ΔLOOP. When covalently bound to RNA helix, the fluorophores Cy3 was stacked onto the end of helix like an extra base (34). We assume Cy5 has the same behavior as Cy3 due to their structural similarities. The X arm of ΔLOOP has 21 continuous base pairs and the Y arm has 11 bp. Assuming each forms a regular A-type helix, with an average rise of 2.6 Å/bp, the length of the X arm is 2.6 Å(21 + 1) ∼57 Å, and the Y arm is 2.6 Å(11 + 1) ∼31 Å. The distance between the ends of X and Y arms was 79 Å. The angle between the X and Y arms was triangulated to be 124 ± 5, i.e. essentially tetrahedral. There are several assumptions made in these calculations that may contribute to some inaccuracy in the overall measurement, e.g. linear A-type helix throughout the X and Y arms; and random orientation of the dyes on their linkers. Assumption of randomness in the orientation of dye linkers was generally made, and was considered in the κ² measurement as well as the distance measurement. The X arm of the ΔLOOP construct comprises all Watson–Crick or GU base pairs, which are anticipated to obey standard A-type helical geometry; similarly, the NMR-derived structural model of the ISL indicates an essentially collinear A-type helix for this stem loop (14) (the Y arm).

Table 2.

Distances between Cy3 and Cy5 in different constructs

Construct	% Efficiency	Cy3–Cy5 distance (Å)
WT	14 ± 1	73 ± 1
Δ4W	13 ± 1	74 ± 1
ΔLOOP	9.4 ± 1	79 ± 2
ΔU74	13 ± 1	74 ± 1
ΔUG	12 ± 1	75 ± 1

The invariant top strand was labeled with Cy3 and Cy5 on 5′ end and 3′ end respectively. In each construct, by paring the 32-nt labeled oligomer with its bottom strand, the distance between the two dyes was measured by the acceptor normalization method described in the text and shown in Figure 5B.

We then used the same FRET technique to measure the Cy3–Cy5 distance in each of the complexes that contained the native ACAGAGA loop sequence in the X arm. FRET measurements yielded a mean Cy3–Cy5 distance of 74 ± 2 Å. Assuming that the angle between the two arms remained constant in all constructs in which the four-way junction was not altered, and using the same values for the triangulation (31 Å for the Y arm, 124° between the X and Y arms and Cy3–Cy5 distance of 74 Å), the mean length of the X arm with the native internal loop was calculated as 52 ± 1 Å, as compared with 57 Å in the construct with the complementary base-paired ACAGAGA region. These data suggest that presence of the internal loop shortens the overall length of the stem. Although it is possible that presence of the highly flexible internal loop in the helix I–III regions may induce some deviation from pure A-type helix or perfect collinearity in the X arm, we note that addition of a fragment representing the intron (which pairs with the bottom strand opposing the ACAGAGA sequence) did not alter the measurement (data not shown).

Lifetime measurements with Cy3-labeled RNA constructs at pH 7.2

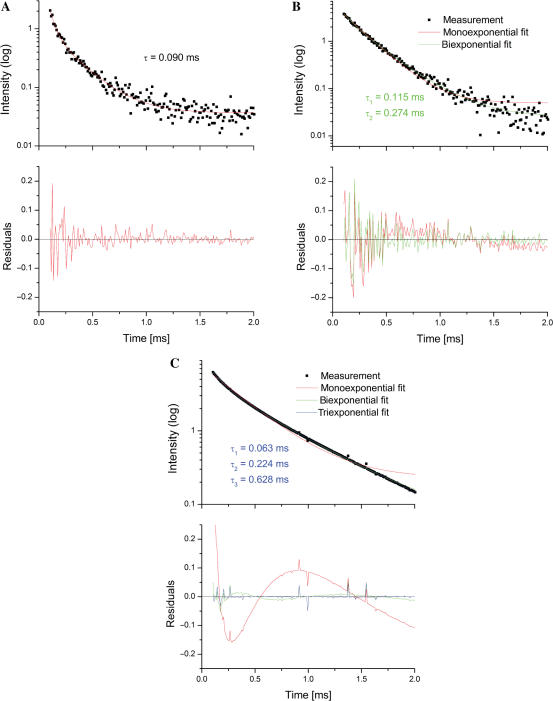
We next measured the distances between Cy3 and Tb(III) at pH 7.2. In order to accomplish this, we analyzed decay curves following FRET from site-bound Tb(III) ions to Cy3. FRET contributions from individual Tb(III) ions to Cy3 yield distance information between the organic dye and each of the luminescent metal ions. The resultant emission decay curve was analyzed for the best fit by one, two or three (the maximal number of curves that could be reliably evaluated) components. For data acquired at pH 7.2, the luminescence decay curve was best fit by the sum of three independent decay curves with lifetimes τ_DA1–3 of τ_DA1 = 0.06 ± 0.005 ms; τ_DA2 = 0.22 ± 0.019 ms and τ_DA3 = 0.63 ± 0.031 ms, with an overall χ² = 0.00021 (Figure 6C). To estimate the quality of the fit, apart from the χ² value, the residuals (difference between expected and experimental data) were considered. The three-exponential fit is consistent with three independent decay curves, corresponding to three independent ion-binding sites, the location of which can be mapped from their distance from Cy3.

Figure 6.

The exponential decay fitting process used in the study. The exponential decay data were fitted with mono, bi- or tri-exponential decay curves. An example of the best fit in each category (1, 2 or 3 lifetimes) was presented. (A) WT construct at pH 5.6 best fitted to one-lifetime decay. τ ≈ 0.09 ms. (B) Construct ΔU74 at pH 7.2 best fit to two-lifetime exponential decay. τ₁ ≈ 0.12 ms; τ₂ ≈ 0.27 ms. (C) Construct WT at pH 7.2 best fitted to three-lifetime exponential decay. τ₁ ≈ 0.06 ms; τ₂ ≈ 0.22 ms; τ₃ ≈ 0.63 ms. The residuals represented the differences between experimental data and fitting curves, which showed the goodness of fit. The choice of the number of lifetimes is based on the R² and χ² values. The improvement of the fit was shown by comparing other fits and the residue figures. Residuals refer to the difference between theoretical and experimental data.

As further support for the finding of three discrete site-bound Tb(III) ions at pH 7.2, the stoichiometry measurements acquired under steady-state conditions, also yielded approximately three Tb(III) ions for the WT construct under the same conditions (Table 1).

Calculation of Cy3-Tb(III) distances and localization of ion-binding sites

From the measured values for τ_DA1, τ_DA2 and τ_DA3 and the relationships in Equation (1), transfer efficiencies E₁, E₂ and E₃ were calculated as 92 ± 1, 71 ± 1 and 18 ± 1%, respectively, from which [using Equation (3)] we calculated distances (R₁, R₂ and R₃) corresponding to 36, 46 and 69 Å from the Cy3 dye. Using the three distances, the approximate length of the X and Y arms, and the calculated X–Y angle of ∼124°, we estimated the locations of the three binding sites within the WT construct. Again, using the value of ∼2.6 Å rise per base pair in an A-type helix and for Cy3, the first site, measured as 36 Å from Cy3, corresponds to a site located (36 − 2.6)/2.6 ∼ 12.8 bp away from Cy3. This approximate measurement places the ion within the center part of the ACAGAGA loop, i.e. in the vicinity of the first G if helical geometry is maintained, or in the GAG sequence if the unpaired helix is compacted. The second site, ∼46 Å from the dye, is near the end of the X arm (length of X arm ∼52 Å with Cy3); therefore the ion is located in the vicinity of the four-way-junction structure, which includes the AGC triad. In order to place the third ion, which was at a distance of 69 Å from the Cy3 dye, we exploited the angle between the X and Y arms (estimated by FRET methods to be ∼124°) as well as the length of the X arm (52 Å with Cy3) to solve for the length of the third side of the triangle, which was 25 Å from the X–Y junction (Figure 5A). Arm Y, corresponding to the U6 ISL, has already been shown to adopt essentially A-type helical geometry throughout (14), which (assuming the human ISL adopts similar overall structure to that of yeast) allows us to place the third ion ∼25/2.6 ≈ 9.6 bp away from the four-way junction. This placed the site in the vicinity of U74 within the ISL.

Confirmation of ion-binding locations by use of mutations

In order to confirm the validity of the three-lifetime fit of the luminescence data and to assist with determination of precise ion-binding locations, we repeated the Tb(III)-Cy3 FRET studies on variant U2–U6 complexes. As a means to test for the presence of each independent site (which would have a corresponding luminescence transfer process), we designed a specific U2–U6 pair in which the suspected site was mutated or deleted by the formation of Watson–Crick base pairs in place of the bulge, loop or non-canonical pairing.

We first probed binding with the U6 ISL. The proposed site in the vicinity of U74 has been shown to bind metal ions (14). ΔU74 has the deletion of U74. Samples were excited at 280 nm, started recording with a gate of 0.1 ms at 565 nm. The ΔU74 decay data were analyzed and two lifetimes were found (Figure 6B), 0.12 and 0.27 ms, with χ² = 0.00056. These two lifetimes and calculated distances were very similar to the ones resulted from the ACAGAGA loop site and four-way-junction site of the WT construct. The disappearance of the longest luminescence lifetime with the modification suggested that the structure caused by U6 ISL U74 was responsible for the metal-ion-binding on the Y arm.

To test the hypothesis that the loop between helices I and III is responsible for binding, we performed lifetime FRET on ΔLOOP in which the bottom strand was mutated to form Watson–Crick base pairs in place of ACAGAGA loop. The decay data were recorded and analyzed as described. In comparison with the WT construct, two lifetimes were found, 0.35 and 0.60 ms (χ² = 0.0008). These lifetimes and the calculated distances corresponded to those in the four-way-junction site and the ISL site of WT. The disappearance of the first site suggested that the loop was responsible for binding at the first site.

Finally, we attempted to determine which region was responsible for ion binding in the proximity of the four-way junction. We first replaced the four-way junction (shaded area in Figure 2B) with a 3-nt ‘hinge’ in Δ4W. The FRET decay curve of Δ4W was similar to that of WT (best fit with lifetimes of 0.05, 0.32, 0.60 ms, χ² = 0.00064), implying similar ion-binding sites as that of WT. These results suggested that either the four-way junction itself was not responsible for the second binding site, or that binding was replaced by three adenosine residues at the hinge.

It has been shown that the U–G non-Watson–Crick base pair has many important biological functions including the potential to bind metal ions (35,36). To test whether U–G was responsible for binding metal ions, a U–G to U–A base pair mutation was made in ΔUG. The exponential decay analysis suggested it still had three binding sites, and its binding properties were similar to WT (best fit with lifetimes of 0.05, 0.32, 0.60 ms, χ² = 0.00017). From which we concluded that mutating the U–G base pair did not change the second binding site.

In summary, we have identified three binding sites on the U2–U6 complex at pH 7.2. Using mutations, we have defined the regions responsible for the first and third binding sites. However, the second binding site, in the region of four-way junction, remains poorly characterized.

PH dependence of ion binding

We evaluated the pH dependence of Tb(III)-binding behavior at each of these sites by performing the lifetime FRET at different pH environments. We excited the Tb(III)–RNA sample at 280 nm and recorded the resulting emission at 565 nm as described previously. All results are listed in Table 3.

Table 3.

Summary of Tb(III) lifetimes (in milliseconds) in the presence of acceptor (τ_DA) at different pH values

	pH 5.6				pH 6.1				pH 6.6				pH 7.2
	τ1	τ2	τ3	χ2	τ1	τ2	τ3	χ2	τ1	τ2	τ3	χ2	τ1	τ2	τ3	χ2
WT	0.09	–	–	0.00024	0.07	0.27	–	0.00073	0.13	0.32	–	0.00092	0.06	0.22	0.63	0.00021
Δ4W	0.14	0.34	–	0.00078	0.14	0.34	–	0.00065	0.05	0.24	–	0.00108	0.05	0.32	0.60	0.00064
ΔLOOP	–	–	–	–	–	0.30	–	0.00074		0.30	–	0.00083	–	0.35	0.60	0.0008
ΔU74	0.06	–	–	0.00033	0.10	0.26	–	0.00075	0.10	0.26	–	0.00085	0.12	0.27	–	0.00056
ΔUG	0.09	–	–	0.0005	0.08	0.29	–	0.00047	0.08	0.29	–	0.00089	0.05	0.32	0.60	0.00017

The fitting process was described in the text and examples were shown in Figure 6. τ₁, τ₂ and τ₃ are three lifetimes (±SD included in text). The Cy3–Tb(III) distances corresponding to the three lifetimes are ∼32, ∼50 and ∼67 Å, respectively. χ² values (reported as reduced χ² values) from deconvolution of compound curves are listed with the lifetimes.

pH 5.6

The resulting decay of construct WT was best fit with one lifetime (τ = 0.09 ± 0.005 ms, χ² = 0.00024, Figure 6A), which corresponds to a distance of ∼39 Å between Tb(III) and Cy3. This distance from Cy3 also places the Tb(III) in the ACAGAGA loop. The absence of emission components corresponding to the other two sites suggests that terbium ion is binding only at the ACAGAGA loop, i.e. binding at other locations is pH dependent. Similarly, the decay curves following the excitation of Tb(III) bound to the ΔU74 or ΔUG constructs were best fit with a single lifetime (τ = 0.06 ± 0.03 ms, χ² = 0.00033; τ = 0.09 ± 0.004 ms, χ² = 0.00050, respectively). Interestingly, decay data for Δ4W were best fit by two lifetimes (τ₁ = 0.14 ± 0.005 ms, τ₂ = 0.34 ± 0.0015 ms, χ² = 0.00078), which corresponded to the ACAGAGA and junction regions. These data suggested that replacing the junction for the hinge may create a non-pH-dependent ion-binding site, whether by creating a new U–G base pair or by changing the binding property of the AGC triad. It has been shown that U–G non-Watson–Crick base pairs have the potential to bind metal ion (35,36). Excitation of ΔLOOP did not yield signal and suggested no ions were bound to this construct at this pH, thus reinforcing the conclusion that the one site at pH 5.6 was the ACAGAGA loop.

pH 6.1 and pH 6.6

At pH 6.1, the decay curves of construct WT were best fit with two lifetime (τ₁ = 0.07 ± 0.003 ms, τ₂ = 0.27 ± 0.02 ms, χ² = 0.00073). The calculated distances between Tb(III) and Cy3 suggested the locations of the ion sites on the ACAGAGA loop and the junction. Similarly, the decay curves of the Δ4W, ΔU74 or ΔUG constructs were best fit with similar double lifetimes (τ₁ = 0.14 ± 0.01 ms, τ₂ = 0.34 ± 0.02 ms, χ² = 0.00065; τ₁ = 0.10 ± 0.004 ms, τ₂ = 0.26 ± 0.01 ms, χ² = 0.00075; τ₁ = 0.08 ± 0.003 ms, τ₂ = 0.29 ± 0.01 ms, χ² = 0.00047; respectively), suggesting same two ion-bound locations. The decay curve of ΔLOOP has one lifetime (τ = 0.30 ± 0.01 ms, χ² = 0.00074), indicating the ACAGAGA loop site was disrupted. At pH 6.6, the two pH environments yielded similar lifetime results. The lifetime results of different constructs at different pH values were summarized in Table 3.

We also measured Tb(III) luminescence decay at greater Tb(III) concentration (>7 μM), and found that the decay was dominated by a component with a very short lifetime (<0.01 ms). This additional component is consistent with energy transfer between Tb(III) and Cy3 over a very short distance, presumably as a result of Tb(III) diffusion during the Tb(III) luminescence lifetime (33). However, in samples for which [Tb(III)] was maintained <7 μM, we found no contribution for this decay component. Moreover, we obtained identical results from [Tb(III)] in the range of 3.5–7 µM. We therefore concluded that diffusional energy transfer does not contribute significantly to our data.

In summary, we have identified three regions of site binding by Tb(III) in the U2–U6 snRNA complex, all of which can be competed by Mg(II). One is located at the ACAGAGA loop; it is not pH dependent in the pH range of 5.6–7.2. The second is located in the vicinity of the four-way-junction structure, possibly associated with the AGC triad in the context of the intact junction structure; it binds metal ions at pH > 6 only. The third ion-binding site is located in the vicinity of U74 of U6 ISL; it binds metal ions at pH > 7 and does not bind at pH lower than 7.

DISCUSSION

FRET techniques have long been used as a valuable tool in structural biology. As an extension of traditional FRET experiments in which one monitors the fluorescence energy transfer between two organic dyes, experiments using lanthanide ions as donors (22) have several advantages over regular FRET: (1) large difference in lifetimes between donor and accepter minimizes inaccuracies stemming from incomplete incorporation of an organic dye; (2) the orientation factor of the site-bound metal ion becomes unimportant, as compared to organic dyes, which are more dependent on the rotational mobility of the fluorophores (23); (3) the millisecond lifetimes of lanthanide luminescence, as compared with nanoseconds for organic dyes, allow for ease of time-resolved data acquisition by a standard fluorophotometer; and (4) the R₀ values of the Ln(III)–organic dye pairs are generally larger than for dye–dye pairs, enabling measurements over a longer distance (23).

In contrast with previous lanthanide FRET experiments, which used chelated ions as exogenous probes (22), we have now taken advantage of the relative similarity in binding properties between Mg(II), the spectroscopically uninformative native ion, and Tb(III), a luminescent lanthanide ion, to exploit energy transfer between excited site-bound Tb(III) and a covalently attached fluorophore to target locations where Tb(III) is situated in RNA complexes. Mg(II) and Ln(III) ions have been shown to occupy overlapping sites in a number of RNAs (37–39). In the U2–U6 snRNA construct used in these studies, competition of Tb(III) luminescence by Mg(II) implied that each of the ions was capable of occupying a site in the same vicinity, although detailed properties of binding may be different (40,41).

This is the first time a site-bound metal ion has been used as a FRET probe. Misra and Draper have described three general modes of multivalent ion binding to RNA: ‘diffuse binding’ that screens charges between RNA backbone segments, ‘outer sphere site binding’ involving specific coordination of anionic ligands to hydrated Mg(II), and ‘inner sphere site binding’, involving one or more direct contacts between the ion and a ligand without intervening water molecules (42). All modes are important for the stabilization of RNA structure. However, a key feature that makes this measurement possible is that emission of Ln(III) is largely quenched by the -OH oscillations of water (17), so that luminescence is only observed for those ions bound via some degree of inner sphere coordination.

Use of Tb(III) in a FRET study allows us to map binding sites directly without altering its native structure or mutating chemical groups. As a result of the relatively large R₀ of the Tb(III)–dye pair, long lifetime and high signal-to-noise ratio, ion-binding site can be probed over a wide range of distances and multiple populations could be resolved from the measurements with greater confidence. The number of sites is limited to the fitting process of the luminescence decay curve; in this case, we found that deconvolution into three independent curves was the limit of resolution. However, the fact that there were only three site-bound Tb(III) ions contributing to energy transfer to Cy3 was supported by separate stoichiometry measurements of each of the U2–U6 complex. Measurements for each construct in which a suspected binding region was replaced by a complementary paired stem resulted in one less site-bound Tb(III) ion.

LRET was first used as a technique to measure rapid-diffusion energy transfer (33). The lifetime of lanthanide luminescence is so long (in the millisecond range) that the decay signal is dominated by the shortest distance between donor and acceptor if the concentration of donor and/or acceptor is high because there is ample time for D–A distance to change as a result of diffusion. Because a metal ion site bound to RNA is likely to have residence times in the nanosecond range (43), we must consider the possibility that in the presence of a large excess of metal ions, the relatively rapid exchange rate of the ion may create the appearance of a small lifetime component. We attempted to minimize contribution from diffusional conformational change by working with as low a concentration of RNA and Tb(III) as possible.

An additional diffusional effect may be contributed by conformational change within the RNA at a rate more rapid than the lifetime of the Tb(III) luminescence. In this case, closer distances will dominate a particular measurement. Measurements of time-dependent conformational change of this RNA structure are beyond the scope of this study. However, we note that we included measurements in mutants that allowed for limited conformational change (e.g. deletion of the flexible ACAGAGA loop and the four-way junction), and back-calculations from sites of ion binding determined by other methods as well as those inferred from our LRET results were in excellent agreement with our primary determinations. Taken together, we have found that our data do not appear to be biased by short-distance components that would reflect the effects of conformational change during the acquisition time.

From Tb(III)–Cy3 FRET data, we found that lifetimes of the three curves (whether calculated by deconvolution or measured individually in mutant constructs) fell into three groups at pH 7.2: τ_DA1 ∼ 0.07 ms; τ_DA2 ∼ 0.31 ms and τ_DA3 ∼ 0.61 ms, corresponding to distances from Cy3 (at the 5′ terminus of the U6 snRNA strand) of 36, 46 and 69 Å, respectively. Using the angle of 124° determined between the two arms, calculated from FRET between Cy3 and Cy5 on termini, we translated these distances into locations corresponding to Tb(III)-binding sites in the central part of the ACAGAGA sequence, the four-way junction, and the internal loop (including U74) of the U6 ISL.

The fact that we observed the same patterns in the native and mutant sequences supports the robustness of the fitting process. Lifetime measurements on each mutation resulted in a decay curve missing the specific component corresponding to the mutation without perturbing the remaining components. The one exception was the slightly longer distance between Cy3 and the four-way-junction site in the ΔLOOP construct (35 Å, as compared with ∼28 Å), which is consistent with the longer continuous stem created by the complementary pairing between helices I and III in place of the flexible ACAGAGA loop.

We point out that the initial assumption of a rigid A-helix for each of the stems is only an approximation, but that there is experimental validity to this approximation. The NMR-derived structure of the U6 ISL indicates the generally helical conformation of this stem loop (14). Of greater concern is the helix I–III stem formed between U2–U6 snRNA, which contains the asymmetric internal ACAGAGA loop, as the loop is likely to impact on length and flexibility of the helix. We conducted FRET and LRET measurements on both the native U2–U6 pairing and a mutant pairing in which the ACAGAGA loop was replaced by a complementary stem. These measurements indicated that presence of the loop shortens helix I–III by ∼4 Å. Direct measurements of the degree of flexibility conferred by the loop are beyond the scope of this study; nonetheless, back-calculations from the ion-binding site within the ISL identified from NMR measurements (14) results in the same angle of ∼120° as we determined from our triangulation, which provides convincing evidence that any flexibility in the stem does not compromise the accuracy of our measurements.

Divalent cations play both catalytic and structural roles in ribozymes (9). U2 and U6 snRNAs are the only RNAs required for both splicing reactions and their sequences are conserved phylogenetically. A protein-free U2–U6 complex has been shown to catalyze an intramolecular reaction similar to the first step of splicing (8). This evidence strongly suggests that the spliceosome is a ribozyme. The obliteration of splicing activities following substitution of phosphorothioate for phosphate in the backbone at U74, the two G residues in the invariant ACAGAGA segments, or the A of the invariant AGC triad, and the rescue of activity with Mn(II), support the model that binding of Mg(II) or other hard metal ion in these regions is essential for structural or chemical activities associated with RNA splicing (10–12,44). NMR experiments displayed changes in proton chemical shifts for U80, the yeast equivalent of U74, upon addition of Mg(II) to an RNA stem loop representing the ISL from S.cerevisiae (14), implying that this was a region of ion interaction. Our results obtained by FRET from site-bound Tb(III) are entirely consistent with the conclusions of these other investigations.

Using the same Tb(III)-Cy3 FRET technique, we also evaluated the pH dependence of each of the luminescence contributions to the total decay signal. First, we found that the signal with the shortest lifetime, that associated with binding of Tb(III) in the ACAGAGA loop, exhibited no pH dependence, i.e. we observed a luminescence component from this site at all pH values examined. It is important to note that, however, under in situ conditions, behavior at this site may be modulated by increased structure associated with formation of the branch site motif upon pairing of the intron strand with U2 snRNA (45).

The luminescence component with the longest lifetime, corresponding to the site within the ISL disappeared at pH below 7, suggesting that Tb(III) does not bind to this site below pH 7. The remaining compound luminescence decay curve was identical to that of the ΔU74 mutant. This conclusion is completely consistent with findings of Huppler et al. on the ISL sequence of yeast (14), who had observed changes in NMR chemical shifts to show the pH-dependent metal ion binding of the U6 ISL. Similarity (but not identity) of yeast and human sequences is no guarantee of equivalent ion-binding behavior. Therefore, the current demonstration of pH dependent site-binding in the human sequence via a new method, at a location identified by phosphorothioate substitution experiments to require interaction with hard metal ions to achieve splicing activity (10), is of biological, as well as technical, importance. Similarity of behavior with the yeast construct (46) suggests that the ion-binding behavior at this site is conserved phylogenetically.

The ion-bound site located in the vicinity of the four-way-junction structure has previously been suggested (12), but the pH dependence of the site has not been analyzed. Our stoichiometry data suggest only one binding site in the vicinity of the four-way junction (Table 1). At pH 5.6, the Δ4W mutant (in which the four-way junction was replaced by a three-adenosine bulge) contributed luminescence to the compound signal, implying that there was a Tb(III) ion bound at this site. In contrast, any of the constructs containing the native four-way junction exhibited evidence of binding the ion only at higher pH values. NMR studies of the four-way junction have shown that it is flexible (46); although it is possible that pH-dependent site in the junction has been replaced by a pH-independent site in the adenosine bulge, we consider it more likely that the lesser flexibility or perturbation of local structure induced by the bulge modifies metal-ion-binding properties by a native site in the area. The most likely candidate is the AGC triad, whose backbone was implicated in the binding of hard metal ions essential for splicing by phosphorothioate substitution experiments (12). We speculate under native conditions, a pK shift in the adenosine of the triad allows it to be protonated at pH < 6, preventing ion binding. If so, removal of the flexible junction perturbs specific structural or electrostatic features surrounding the triad by artificially stabilizing other non-canonical interactions.

Although the environment in cells is maintained at relatively constant pH, shifted nucleotide pK_a in small ribozymes have been found to be surprisingly frequent, and have been associated with various ion-binding and catalytic mechanisms (47). The two pH-dependent metal-ion-binding sites we identified here may contribute to such mechanisms in the regulation of spliceosomal activity.