The afterhyperpolarization conductance exerts the same control over the gain and variability of motoneurone firing in anaesthetized cats

Abstract

Does the afterhyperpolarization current control the gain and discharge variability of motoneurones according to the same law? We investigated this issue in lumbar motoneurones of anaesthetized cats. Using dynamic clamp, we measured the conductance, time constant and driving force of the AHP current in a sample of motoneurones and studied how the gain was correlated to these quantities. To study the action of the AHP on the discharge variability and to compare it to its action on the gain, we injected an artificial AHP-like current in motoneurones. This increased the natural AHP. In three motoneurones, we abolished most of the natural AHP with the calcium chelator BAPTA to investigate the condition where the discharge was essentially controlled by the artificial AHP. Our results demonstrate that both the gain and the coefficient of variation of the firing rate are inversely proportional to the magnitude and to the time constant of the artificial AHP conductance. This indicates that the AHP exerts the same control over the gain and the variability. This mechanism ensures that the variability of the discharge is modulated with the gain. This guarantees a great regularity of the discharge when the motoneurone is in a low excitability state and hence good control of the force produced.

In many types of neurones, action potentials trigger a slow calcium-dependent potassium current that provokes an afterhyperpolarization (AHP) (Llinas & Yarom, 1981; Lancaster & Adams, 1986; Schwindt et al. 1988; Wilson et al. 2004). This current plays a major role in shaping the discharge properties. In spinal motoneurones, it keeps the slope of the stationary current–frequency curve (I–f curve) at low values (typically 1 Hz nA⁻¹ in anaesthetized cats), thus confining the stationary firing rate to the 10–50 Hz range (Kernell, 1999), and it limits the discharge variability (Person & Kudina, 1972; Powers & Binder, 2000). Reducing the AHP current with apamin or serotonin was shown to increase the firing frequency and to steepen the I–f curve. The discharge also becomes more irregular (Zhang & Krnjevic, 1987; Hounsgaard & Kiehn, 1989; Chandler et al. 1994; Lape & Nistri, 2000). During episodes of fictive locomotion in decerebrate cats, AHP is reduced by neuromodulation, and both the slope of the I–f curve and the discharge variability increase (Brownstone et al. 1992).

Controlling both the gain, i.e. the slope of the I–f curve, and the discharge variability of motoneurones is indeed a requirement of motor unit physiology. A low gain entails that motoneurones discharge at frequencies well below the tetanic fusion frequency of their motor unit. At these frequencies, the force developed is particularly sensitive to irregularities in the motoneurone discharge (see Burke, 1981). Moderate shortening of a single interspike interval can produce remarkably long lasting enhancement of the force (catch property) (Burke et al. 1970; Stein & Parmiggiani, 1979). Conversely, lengthening of a single interspike interval can dramatically reduce the force. This suggests that the steady discharge must be all the more regular as the gain is low. Therefore, we hypothesise that the AHP current controls the gain and the variability of motoneurons according to the same law.

The aim of the present paper is to verify this hypothesis. This requires determining how the gain and the variability are related to the magnitude and kinetics of the AHP conductance. This was achieved by using dynamic clamp. Exploiting the method developed in Manuel et al. (2005) we measured the parameters of the AHP current (conductance, time constant, reversal potential) in a sample of lumbar motoneurones of anaesthetized cats. A correlation analysis then enabled us to unravel the combination of parameters that determined the gain. We also relied on dynamic clamp to study how the AHP current affects the discharge variability. We injected an artificial AHP-like current that increased the natural AHP. We could vary separately the magnitude of the artificial conductance and its decay time, and we studied how these two parameters affected the steady-state discharge. Abolishing most of the natural AHP in a few motoneurones with the calcium chelator BAPTA allowed us to investigate a simpler condition where the discharge was controlled by the artificial AHP current. We found that, like the gain, the coefficient of variation of the discharge was inversely proportional to the magnitude of the artificial AHP conductance and to its decay time, which validates our hypothesis. The relationship we established between the AHP conductance and the gain agrees with the predictions of integrate-and-fire models incorporating a slow AHP current (Kernell, 1968; Ermentrout, 1998; Wilson et al. 2004; Meunier & Borejsza, 2005). In sharp contrast, such models cannot explain our results on the variability of the discharge because they do not take into account the fast currents involved in spiking.

Methods

Animal preparation

Experiments were carried out on 11 adult cats (3.25–4.25 kg) deeply anaesthetized with sodium pentobarbitone (Pentobarbital, Sanofi, Paris, France). In accordance with French legislation, the investigators had valid licenses to perform experiments on live vertebrates delivered by the Direction des Services Vétérinaires (Préfecture de Police, Paris). The animal house and the experimental room had received the agreement of the same authority. Anaesthesia was induced with an i.p. injection (45 mg kg⁻¹), supplemented whenever necessary (usually every 2 h) by i.v. injections (3–6 mg kg⁻¹). This kind of anaesthesia strongly depresses the L-type nifedipine-dependent calcium current in motoneurones (Guertin & Hounsgaard, 1999) and prevents spontaneous activation of monoaminergic descending pathways. Therefore, the discharge pattern of motoneurones in our experiments was mainly controlled by the AHP. Animals were paralysed with pancuronium bromide (Pavulon, Organon SA, Puteaux, France) at a rate of 0.4 mg h⁻¹ and artificially ventilated (end tidal P_CO2 maintained around 4%). A bilateral pneumothorax prevented movements of the rib cage. The adequacy of anaesthesia was primarily assessed on myotic pupils. The induction of paralysis with pancuronium bromide did not elicit any change in the blood pressure (measured in the carotid artery) and heart rate. The stability of blood pressure and heart rate throughout experiment provided us with a second criterion for the adequacy of anaesthesia. At the onset of the experiments that lasted more than 20 h, amoxicillin (500 mg; Clamoxyl, Merieux, Marcy1-Etoile, France) was injected subcutaneously to prevent the risk of infection. Amoxicillin provoked neither convulsions (before neuromuscular blockade) nor bursting activity in motoneurones. In addition, methylprenidsolone (5 mg; Solu-Medrol, Pharmacia, Uppsala, Sweeden) was given subcutaneously to prevent oedema. The central temperature was kept at 38°C. Blood pressure was maintained above 90 mmHg by perfusion of a 4% glucose solution containing NaHCO₃ (1%) and gelatine (14%; Plasmagel, Roger Bellon, Neuilly sur-Seine, France) at a rate of 3–12 ml h⁻¹. A catheter allowed evacuation of urine from the bladder. At the end of the experiments, animals were killed with a lethal intravenous injection of pentobarbitone (250 mg).

The following nerves were cut, dissected and mounted on a pair of stimulating electrodes to identify recorded motoneurones: anterior biceps and semimenbranosus taken together (ABSm), posterior biceps and semitendinosus taken together (PBSt), gastrocnemius medialis together with gastrocnemius lateralis and soleus (Triceps surae, TS), the remaining part of the tibialis nerve (Tib) and the common peroneal nerve (CP). The lumbosacral spinal segments were exposed by laminectomy, and the tissues in hind limb and spinal cord were covered with pools of mineral oil kept at 38°C.

Recordings

Intracellular recordings of motoneurones were made in the Discontinuous Current Clamp mode (DCC, 9 kHz) of the Axoclamp2B (Molecular Devices, Chatillon, France). This is the recommended mode for dynamic clamp experiments (Brizzi et al. 2004; Prinz et al. 2004) because it allows for reliable measurements of the membrane potential, even when large currents are injected. In most cases, we used micropipettes (tip diameter 2–2.5 μm) filled with 3 m KCl (resistance 2–4 MΩ). Identification of motoneurones rested on the observation of an antidromic action potential following the electrical stimulation of their axon in a peripheral nerve.

In most motoneurones the recording session ran as follows. Firstly, a series of at least 15 action potentials, elicited by brief depolarizing pulses (duration 1 ms, 5–25 nA) applied at the soma and repeated at a rate of 1 or 2 Hz, were recorded and averaged. This allowed us to measure the amplitude and duration of the natural AHP. Secondly, in order to measure the input conductance, the voltage responses to a series of current pulses (intensity −5 to +5 nA increasing by steps of 1 nA; 1 s duration, repeated at the rate of 0.5 Hz) were recorded. At least five successive traces were recorded and averaged for each intensity of the current. Thirdly, we investigated the impact of an AHP-like current (I_dc) imposed by dynamic clamp (see below) on the firing properties. Trains of action potentials were elicited by injecting depolarizing current pulses (1 s duration, repeated at 0.5 Hz) of increasing amplitude (5–40 nA, by steps of 2–3 nA). We never observed windup during the successive trains. At least five control pulses were used for each amplitude of the current. Then, the dynamic clamp current was added, and we recorded at least five voltage responses for each intensity of the depolarizing pulse and for each set of parameters of the artificial AHP that was tested.

In a sample of motoneurones, we accurately measured the conductance, time constant and reversal potential of the natural AHP current that followed a single spike elicited by a brief depolarizing pulse (duration 1 ms, 5–25 nA). This was done using the method that was fully described in Manuel et al. (2005). Briefly, we injected, using dynamic clamp, an artificial current that increased the AHP amplitude. Using the current balance equation, we then computed for each value of the artificial conductance the intensity of the natural AHP current at the voltage trough and plotted it versus the AHP amplitude. The intensity of the AHP current was linearly related to the AHP amplitude. Exploiting this linear relationship, we determined both the conductance and the reversal potential of the natural AHP current.

In some motoneurones, we reduced the natural AHP with BAPTA. This calcium chelator was preferred to EGTA (Krnjevic et al. 1978) because it is believed to be more efficient due to the much faster kinetics of its binding with calcium ions (Markram et al. 1998). We used intracellular micropipettes filled with a mixture of 0.1 m BAPTA and 3 m KCl (resistance 2.5–6.5 MΩ). At this high concentration, BAPTA was found to reduce the calcium-dependent afterhyperpolarization in neocortical neurones (Schwindt et al. 1992). In the present experiments, BAPTA was iontophoretically injected into the cell with a negative current of 20 nA for a duration of at least 2 min. During BAPTA injection, which affects all calcium-dependent phenomena, we monitored the resting potential and the voltage amplitude of the natural AHP following single action potentials elicited by brief depolarizing pulses (1 ms; 2 Hz). Once the resting potential and the AHP amplitude were stabilized, we analysed the effects of the artificial AHP on the repetitive discharge. Because it was difficult to keep the motoneurone stable over a long period of time, we varied only the artificial conductance and did not investigate the effects of the time constant. In addition, we did not measure what remained of the natural AHP conductance.

Dynamic clamp induced AHP-like current

The AHP current is activated through a cascade of intracellular events starting with the spike-triggered influx of calcium (Krnjevic et al. 1975, 1978). In most theoretical works (Baldissera et al. 1976; Powers, 1993; Meunier & Borejsza, 2005), these complex processes were not modelled in details, and only the effective voltage dependence of the AHP current was taken into account. We did likewise for the artificial AHP current imposed via the dynamic clamp. This current was applied through the same micropipette used for intracellular recordings. It was given by the formula:

where $G_{\text{dc}}^{\text{max}}$ was the maximal conductance, z(t) the voltage-dependent activation variable, V_dc the reversal potential and V the membrane potential. The variable z(t) represented the proportion of the maximal conductance that was recruited at a given time. We incorporated AHP summation in our model using the same formalism as Baldissera et al. (1976, 1978) and Meunier & Borejsza (2005). During each spike, we instantaneously increased the activation variable z(t) from z_before to z_after = αz_before + (1 − α), where 0 ≤ α ≤ 1, when the membrane voltage crossed the value 0 mV. We then let the activation variable z(t) relax exponentially with the time constant τ_dc (i.e. z(t) = z_after e^−t/τ_dc) until the next spike occurred. In our experiments, α was fixed at 0.5, which entailed that the first spike already recruited half of the maximal artificial conductance, $G_{\text{dc}}^{\text{max}}$. The artificial conductance steadily increased, spike after spike, until a steady-state regime was obtained. The discharge displayed an initial frequency adaptation over the first 2–4 spikes. Increasing the artificial conductance decreased this initial adaptation, in keeping with the results of Miles et al. (2005). The reversal potential (V_dc) was always set to −100 mV. This value was chosen to ensure that the reversal potential of the artificial current was below the reversal potential of the natural AHP current (ranging from −68 to −95 mV according to Manuel et al. (2005)). The maximal artificial conductance ranged between 0.1 and 1 μS (in the control condition $G_{\text{dc}}^{\text{max}}$ = 0), and the relaxation time constant (τ_dc) was in the range 20–80 ms. These values were chosen in view of the measurements we made in a previous study (Manuel et al. 2005). The conductance was in the range of the natural AHP conductance. In contrast, the time constant was longer than the time constant of the natural AHP to make the artificial AHP prevail.

The dynamic clamp current was calculated using the sequencer of the Power1401 ADC/DAC unit (CED, Cambridge, UK). The CPU embedded in this unit executes one instruction every 10 μs. It took 11 steps to complete the whole loop, from membrane potential sampling to current injection, i.e. 110 μs. This time was the same as the sampling period, which guaranteed a real time feedback loop. The Power1401 unit was under the control of a PC computer running the Spike2 software (CED, Cambridge, UK). Recordings were stored for off-line analysis.

Data analysis

Motoneurone classification

The averaged voltage trace after the emission of an action potential was used to measure the amplitude, duration and half-decay time of the natural AHP. The input resistance was the slope of the linear relationship between the intensity of subthreshold current pulses and the peak voltage response. We classified motoneurones into physiological types as Zengel et al. (1985). We used the ratio of the AHP half-decay time to the motoneurone input conductance because it was shown to correctly predict the type of 90% of the motor units. Motoneurones with a ratio smaller than 6 were classified as FF type, i.e. innervating fast twitch, fatigable motor units. Those with a ratio greater than 33.3 were classified as S type, i.e. innervating slow twitch, fatigue resistant motor units. Those in between were FR type, i.e. innervating fast twitch, fatigue resistant motor units.

Current–frequency relationship and coefficient of variation of the discharge frequency

Stationary current–frequency (I–f) curves were drawn using the responses to the suprathreshold depolarizing pulses. Several responses were recorded for each condition tested (i.e. for given values of the current pulse intensity I, of $G_{\text{dc}}^{\text{max}}$ and of τ_dc). In each response, the first three to five spikes were discarded to consider only steady-state firing. For each remaining spike, we measured the instantaneous firing frequency, defined as the inverse of the time elapsed since the previous spike. We pooled the different responses and computed the mean firing frequency and its standard deviation. Plotting the mean firing frequency (± s.d.) against the current intensity, we obtained a family of I–f curves, one corresponding to control ($G_{\text{dc}}^{\text{max}}$ = 0) and the others to different test conditions (i.e. different values of $G_{\text{dc}}^{\text{max}}$ or τ_dc). All stationary I–f plots were linear over the whole range of current intensities explored. The slope of the linear regression determined the stationary gain. At each intensity of the current pulse, we measured the variability of the discharge by computing the coefficient of variation (CV) of the instantaneous firing rate, that is, the ratio of the standard deviation of the firing frequency to its mean. This coefficient of variation is very close to the coefficient of variation of interspike intervals because the discharge of motoneurones is quite regular. For the sample of motoneurones shown in Fig. 1, we also computed the gain for the first interval interspike in the control case ($G_{\text{dc}}^{\text{max}}$ = 0).

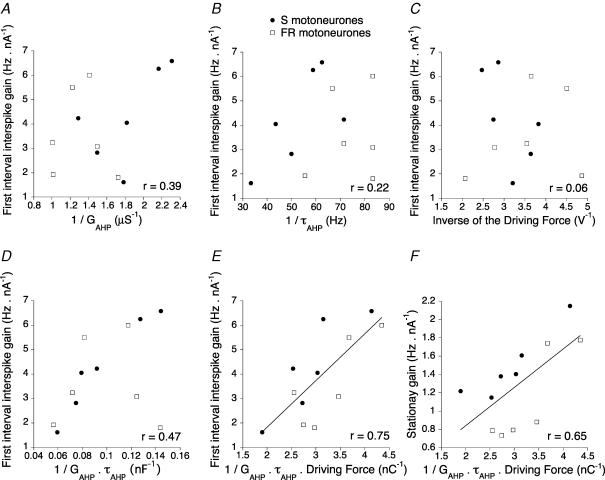
Figure 1. Correlations between the gain and the parameters of the AHP.

In all plots, the filled circles correspond to the 6 motoneurones classified as S type and the open squares to the 6 motoneurons classified as FR types. The gain for the first interspike interval is plotted against the inverse of the AHP conductance (A), the inverse of the AHP decay time constant (B), and the inverse of the AHP driving force (C). The driving force is the spike voltage threshold minus the reversal potential. The criterion used for determining the spike threshold was that the voltage derivative reached 10 mV ms⁻¹ (Brownstone et al. 1992; Sekerli et al. 2004). D, gain for the first interspike interval against the inverse of the product of the AHP conductance and the decay time constant. E, gain for the first interspike interval against the inverse of the product of the AHP conductance, the decay time constant and the driving force. The continuous line is the best linear fit computed with the least squares method. F, stationary gain against the inverse of the product of the AHP conductance, the decay time constant and the driving force. The continuous line is the best linear fit. The coefficient of correlation is given in each panel.

Results

The data reported here were obtained from 32 motoneurones (15 CP, 6 ABSm, 5 Tib, 4 PBSt, 2 TS). These motoneurones had a resting membrane potential more hyperpolarized than −60 mV and antidromic spikes of more than 70 mV in amplitude. These conditions remained stable for the whole duration of the recording.

How the gain depends on the parameters of the AHP current

We studied the correlations between the gain and the parameters of the AHP current (conductance, time constant and driving force, i.e. the difference between the spike voltage threshold and the AHP reversal potential). This population analysis was carried out on a sample of 12 motoneurones in which we measured the parameters of the AHP current elicited by a single spike (Manuel et al. 2005). This sample included six S type, six FR, and no FF motoneurones. S and FR motoneurones did not display significant differences in their first interval gain (4.3 ± 1.9 versus 3.6 ± 1.8 Hz nA⁻¹, Student's unpaired t test, P = 0.55) and stationary gain (1.5 ± 0.4 versus 1.1 ± 0.5 Hz nA⁻¹, P = 0.18). In simple models of motoneurones (Meunier & Borejsza, 2005), the gain is proportional to the inverse of the product of the conductance, decay time and driving force of the AHP current. We investigated whether such reciprocal relationships could be disclosed in our sample.

We focused on the first interspike interval because our method allowed us to measure with a good accuracy (5–10%) the parameters of the AHP current elicited by the first spike. The gain was not correlated with the inverse of any individual parameter of the AHP current as shown in Fig. 1A for the AHP conductance (r = 0.39, P = 0.1, single sided t test), in Fig. 1B for the decay time constant (r = 0.22, P = 0.2), and in Fig. 1C for the driving force (r = 0.06, P = 0.4). We also tested whether the gain was correlated with the inverse of the product of two parameters of the AHP current. No correlation was found for the conductance and driving force (r = 0.39, P = 0.1), and for the time constant and driving force (r = 0.22, P = 0.2). Some correlation was found with the conductance and time constant (r = 0.47, P = 0.06) as shown in Fig. 1D. However, less than one-quarter of the variance was accounted for (r² = 0.22). In contrast, a good linear correlation was observed between the gain and the inverse of the product of the three parameters as shown in Fig. 1E. This product has the dimension of an electric charge. The correlation coefficient was 0.75 (P = 0.003), and the (dimensionless) slope of the best fit was 1.9 (continuous line in Fig. 1E).

We also analysed the correlations between the stationary gain and the AHP parameters. As before, no correlation was found between the gain and individual parameters of the AHP current, nor between the gain and the product of any two parameters. The correlation between the stationary gain and the inverse of the product of the three parameters is shown in Fig. 1F. The slope of the best linear fit was 0.32. The linear correlation coefficient was slightly smaller (r = 0.65, P = 0.01) than for the first interspike interval. This is probably because the stationary gain depends not only on the conductance, time constant and driving force of the AHP current but also on the rate of AHP summation (Meunier & Borejsza, 2005), which is likely to vary from one motoneurone to the other. We could not determine this quantity with our method, which measures the parameters of the AHP current only after the first spike. Alternative methods (Ito & Oshima, 1962; Baldissera & Gustafsson, 1971, 1974) were not used because they were prone to large errors.

Altogether, we showed that the gain was not correlated with any single parameter of the AHP but with the product of the conductance, time constant and driving force. The gain tended to be inversely proportional to this product. These results imply that the gain is not set by a single parameter of the AHP. This is why the gains of S and F type motoneurones are not statistically different although the AHP time constant is smaller for F motoneurones. However, if one could alter a single parameter, the others remaining fixed, the gain would vary as the inverse of this parameter. This was verified as described below using dynamic clamp.

How the AHP conductance affects the variability of the discharge

Using the same sample and a similar correlation analysis, we attempted to investigate how the variability of the stationary discharge was related to the parameters of the AHP current. However, the coefficient of variation of the instantaneous firing rate was not the same for the different points of a given I–f curve and no systematic trend was observed as the injected current increased. For each motoneurone, we estimated the coefficient of variation by averaging the measures made at different currents. No clear correlation was found between this average coefficient and any combination of the AHP parameters in the sample of motoneurones used.

We then relied on dynamic-clamp experiments to investigate whether modifying a single parameter of the AHP current had a systematic effect on the coefficient of variation. We also compared the changes in the coefficient of variation with those observed on the gain. In 25 motoneurones (8 also used in the population analysis presented above and 17 others), we imposed an artificial AHP-like conductance that added to the natural one and increased the AHP. Figure 2 illustrates how the discharge of a motoneurone was modified when an artificial AHP conductance was imposed. A 19 nA depolarizing pulse made the neurone fire tonically. When the artificial AHP was added ($G_{\text{dc}}^{\text{max}}$ = 0.1 μS, τ_dc = 23 ms), the hyperpolarization after each action potential increased and the emission of action potentials was delayed (Fig. 2Aa, thick trace). The artificial AHP conductance was 0.05 μS just after the first spike and increased to 0.065 μS just after the second spike (Fig. 2Aa). When the artificial AHP was increased ($G_{\text{dc}}^{\text{max}}$ = 0.9 μS, τ_dc = 23 ms, Fig. 2Ab), the action potentials were further delayed and less summation of the AHP conductance occurred.

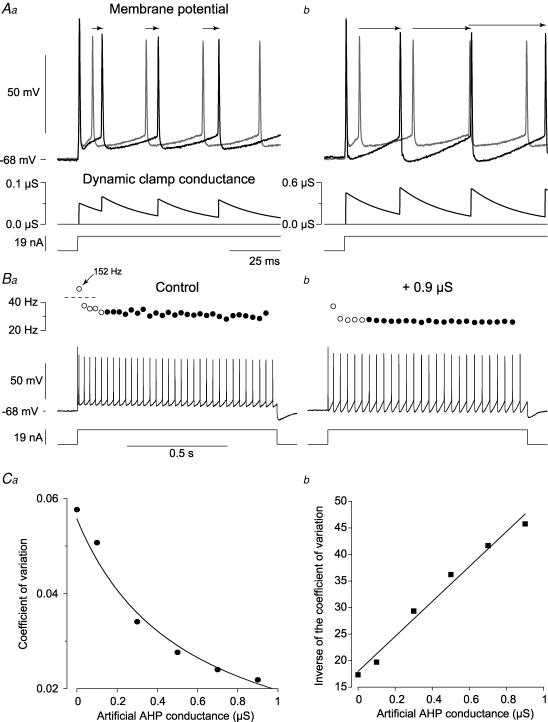
Figure 2. Increasing the AHP with dynamic clamp decreased the mean firing rate and the discharge variability.

Aa, response of a Slow type ABSm motoneurone to a 19 nA pulse (bottom trace) in control condition (thin trace) and when an artificial AHP was added (thick trace, $G_{\text{dc}}^{\max }$ = 0.1 μS and τ_dc = 23 ms). The arrows indicate the time shift of each spike compared to control. The middle trace shows the temporal summation of the AHP-like conductance imposed via dynamic clamp. b, response of the motoneurone when the artificial AHP conductance was increased to $G_{\text{dc}}^{\max }$ = 0.9 μS (thick trace). The thin trace is again the control condition (same trace as in Aa). Same arrangement as in Aa. The artificial conductance was 0.45 μS after the first spike, and increased to 0.52 μS after the second. Ba, control response displayed in full (time scale 10 times slower than in Aa). The lower trace shows the depolarizing pulse, the middle trace shows the intracellular recording of the voltage and the circles above the intracellular recording indicate the instantaneous discharge frequency. Note that the open circle corresponding to the instantaneous frequency for the first interspike interval (152 Hz, arrow) is out of scale as indicated by the dashed line. The filled circles are the instantaneous frequencies of the spikes that were used for computation of the coefficient of variation of the stationary discharge. b, response of the motoneurone when an artificial conductance ($G_{\text{dc}}^{\max }$ = 0.9 μS and τ_dc = 23 ms) was added. Same arrangement as in Ba. Ca, coefficient of variation during the stationary discharge plotted against $G_{\text{dc}}^{\max }$, which we increased from 0.1 to 0.9 μS. b, inverse of the coefficient of variation plotted against $G_{\text{dc}}^{\max }$. The continuous line is the best linear fit computed with the least squares method (r = 0.99, P = 0.0001).

The instantaneous discharge frequency during the whole pulse is shown in Fig. 2B. In the control case (Fig. 2Ba), the initial frequency at the onset of the pulse was 152 Hz, and after a brief period of adaptation it decreased to a mean frequency of 32 Hz. The variability of the frequency was low during the stationary discharge (CV 0.058; the spikes used for this computation corresponded to the black circles in the figure). When an artificial AHP conductance of 0.9 μS was added (Fig. 2Bb), the initial frequency dropped to 39 Hz, and the discharge frequency settled at 26 Hz after the initial adaptation phase. The adaptation ratio, i.e. the ratio of the instantaneous frequency computed on the first interspike interval to the mean frequency of the stationary discharge, was about three times smaller than in the control case. This indicates that the artificial AHP conductance decreased the initial adaptation (Miles et al. 2005). In addition, the stationary discharge was even more regular (CV = 0.022) than in the control case.

Figure 2Ca shows how increasing the artificial conductance affected the coefficient of variation of the stationary discharge. The coefficient of variation steadily decreased as the conductance of the artificial AHP was increased, but the relationship was not linear. In contrast, the inverse of the coefficient was linearly correlated to the conductance as shown in Fig. 2Cb (r = 0.99, P = 0.0001). This indicates, that the variability of the discharge is inversely proportional to the magnitude of the AHP conductance.

The gain also was inversely proportional to the AHP conductance. This is illustrated in Fig. 3 for the same motoneurone. Figure 3A shows the stationary I–f curve in the control case and when the artificial AHP current was added. The slope was reduced from 1.6 Hz nA⁻¹ in control condition to 1.4 and 1.2 Hz nA⁻¹ when artificial AHP currents of maximal conductance ($G_{\text{dc}}^{\max }$) 0.5 and 0.9 μS, respectively, were added (τ_dc = 23 ms). Figure 3B shows that the relationship between the inverse of the gain and the artificial conductance was linear (filled squares, r = 0.97, P = 0.0007). The slope of this relationship was 0.22 nC μS⁻¹. We may then conclude that the variability of the discharge and the gain are both inversely proportional to the AHP conductance.

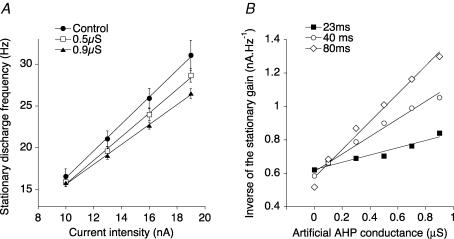
Figure 3. The gain of the stationary I–f curve decreased when the artificial AHP conductance was increased.

A, I–f curves in control condition ($G_{\text{dc}}^{\max }$ = 0 μS, •), when $G_{\text{dc}}^{\max }$ = 0.5 μS (□) and $G_{\text{dc}}^{\max }$ = 0.9 μS (▴). The decay time constant of the artificial AHP was 23 ms. Data points correspond to the mean stationary discharge frequency for a given current intensity, and the vertical bars show the standard deviation. The oblique lines are the best linear fits of the I–f curves, computed using the least squares method. B, inverse of the stationary gain plotted against the artificial conductance $G_{\text{dc}}^{\max }$ for three values of the AHP decay time constant: 23 ms (▪), 40 ms (○) and 80 ms (⋄). Note that the control gain ($G_{\text{dc}}^{\max }$ = 0 μS) fluctuated from one determination to the other. The oblique lines are the best linear fits. Same motoneurone as in Fig. 2.

The same experiment was repeated with an AHP time constant set to 40 ms or to 80 ms. When we increased the decay time constant of the artificial AHP, the relationship between the inverse of the gain and the conductance was again linear (Fig. 3B). However, the slope was steeper. The slope increased to 0.52 nC μS⁻¹ for 40 ms (open circles, r = 0.99, P = 0.0001), and to 0.83 nC μS⁻¹ for 80 ms (Fig. 3B, open diamonds, r = 0.99, P = 0.0001). Three time constants were tested in another motoneurone. In six others, only two time constants were tested (23 and 40 ms in 4 motoneurones, 40 and 80 ms in 2 motoneurones). In all cases, the relationship between the inverse of the gain and the AHP conductance was linear, and it steepened as the decay time increased.

How the decay time constant of AHP affects the discharge variability and the gain

Figure 4 illustrates how the decay time constant affected the discharge variability and the gain. In the motoneurone shown, we fixed $G_{\text{dc}}^{\text{max}}$ to 0.4 μS and let τ_dc vary from 23 to 80 ms. As long as the time constant of the artificial AHP was smaller than the time constant of the natural AHP (30 ms in this motoneurone), the artificial AHP only changed the slope of the I–f curve (Fig. 4A). When the time constant of the artificial AHP exceeded 30 ms, the gain was further reduced and the I–f curve was also shifted towards smaller discharge frequencies (Fig. 4A, 50 ms). Increasing the AHP time constant consistently reduced the discharge variability. The coefficient of variation decreased as the AHP decay time was increased. It was equal to 0.05 in control condition (without artificial AHP) when a current of 4 nA was injected. It dropped to 0.025 for the same value of the injected current when an artificial AHP with a 30 ms decay time constant was added (Fig. 4B). It further diminished to 0.02 when the decay time constant of the artificial AHP conductance was increased to 80 ms. The dependence of the gain and of the coefficient of variation on the time constant of the artificial AHP are compared in Fig. 4B. The slope of the I–f curve varied as the inverse of the time constant (filled squares, r = 0.99, P = 0.01). Like the gain, the coefficient of variation decreased as the inverse of the time constant (open triangles, r = 0.99, P = 0.01). Performing the same experiment in six other motoneurones yielded similar results on the gain and the variability. Altogether, we may conclude that the variability of the discharge and the gain decrease according to the same law when the AHP time constant increases.

Figure 4. The stationary gain and the coefficient of variation decreased similarly when the decay time constant of the artificial AHP was increased.

A, I–f curves in control condition (•), and when adding an artificial AHP conductance ($G_{\text{dc}}^{\max }$ = 0.4 μS) with a decay time constant of 30 ms (□) or 50 ms (▴). The curves obtained for time constants of 23, 40 and 80 ms are not shown. Data points indicate the mean frequency of the stationary discharge and vertical bars show the standard deviation. The oblique lines are the best linear fits of the I–f curves, computed with the least squares method. B, stationary gain (▪) and coefficient of variation for I = 4 nA (▵) plotted against the inverse of the decay time constant. Numbers next to the data points indicate the time constant. The oblique line is the best linear fit for the stationary gain. CP motoneurone of slow type.

Impact of an artificial AHP conductance on a motoneurone deprived of its natural AHP

In all motoneurons recorded in our dynamic clamp experiments, the artificial AHP reduced the discharge frequency, the discharge variability and the stationary gain. However, these effects were small because the artificial AHP was superimposed on the natural AHP, which was already sufficient to make the neurones fire regularly at low rate and with a low gain. To allow the artificial AHP to take nearly full control of the discharge, we attempted to remove the natural AHP by using the free calcium chelator BAPTA. We obtained good and stable recording conditions (resting membrane potential below −60 mV) in two CP motoneurones and in one Tib motoneurone. Similar observations were made on these three neurones.

The results obtained in the motoneurone in which the natural AHP was the most depressed by BAPTA are shown in Figs 5 and 6. After a 2 min iontophoretic injection of BAPTA, the AHP amplitude after a single action potential was reduced by as much as 60% (insert in Fig. 5). Subsequent injections of BAPTA did not reduce further the AHP. In response to a 20 nA depolarizing pulse, the motoneurone discharged at higher frequencies than usual. At the onset of the pulse, the firing frequency reached 210 Hz (see grey traces in Fig. 5D and E), and after a brief phase of adaptation, the discharge remained highly variable around a mean frequency of 66 Hz (±15 Hz, Fig. 5A). The coefficient of variation (0.36) was about eight times larger than the mean coefficient of variation in the sample of motoneurons used in the population analysis presented above.

Figure 5. The artificial AHP strongly reduced the mean firing frequency and the discharge variability of a motoneurone in which the natural AHP was depressed by BAPTA.

A, response of the motoneurone to a depolarizing current step of 20 nA lasting 1 s (lower trace). The dots above the intracellular recording indicate the instantaneous discharge frequency. Note that only the stationary discharge is shown. The insert below A shows the reduction of the AHP amplitude following injection of BAPTA. The action potentials were elicited by intrasomatic pulses (1 ms, 10 nA) repeated at 2 Hz. The thick trace shows the afterhyperpolarization remaining after BAPTA injection (average of 10 successive responses). The thin trace is the average of 20 control responses recorded before BAPTA injection. B and C, response of the motoneurone when the conductance $G_{\text{dc}}^{\max }$ of the artificial AHP current was set to 0.1 μS and to 0.7 μS. Same arrangement as in A. The decay time constant of the artificial AHP was 23 ms in both cases. D, the responses in control condition (grey trace) and when an artificial AHP was added (black trace, $G_{\text{dc}}^{\max }$ = 0.1 μS and τ_dc = 23 ms) are expanded and superimposed. The middle trace shows the temporal summation of the dynamic clamp AHP-like conductance. E, the response when the artificial AHP conductance was increased to $G_{\text{dc}}^{\max }$ = 0.7 μS (black trace) is expanded and superimposed to the control response (grey trace, same as in D). Note that more summation of the artificial conductance occurred in D than in E. The ratio of the AHP conductance just after the third spike to the conductance after the first spike was 1.44 in D and 1.20 in E. This is because the initial conductance was lower (0.05 μS in D compared to 0.35 μS in E) and reduced less the firing frequency. CP motoneurone of unknown physiological type.

Figure 6. The coefficient of variation and the gain of the stationary discharge were inversely proportional to the artificial AHP conductance in a motoneurone in which the natural AHP was strongly depressed.

A, I–f curves in the control case (•), when $G_{\text{dc}}^{\max }$ = 0.1 μS (□) and $G_{\text{dc}}^{\max }$ = 0.7 μS (▴). The decay time constant of the artificial AHP was 23 ms. Each data point shows the mean stationary discharge for a given current intensity. The half error bars indicate the standard deviation. The oblique lines are the best linear fits to the I–f curves. B, coefficient of variation (•, measured for a 20 nA current intensity) and stationary gain (□) plotted against the artificial conductance $G_{\text{dc}}^{\text{max}}$. C, inverse of the gain plotted against the artificial conductance $G_{\text{dc}}^{\text{max}}$. The oblique line is the best linear fit. D, inverse of the coefficient of variation plotted against the artificial AHP conductance for the three current intensities investigated (▴: 17 nA; •: 20 nA; ○: 23 nA). The lines are the best linear fits for I = 17 nA (dotted), 20 nA (continuous), 23 nA (dashed). Same motoneurone as in Fig. 5.

When an artificial AHP was added, the motoneurone discharged at a lower rate, with less adaptation and less variability. When the maximal artificial conductance ($G_{\text{dc}}^{\max }$) was set to 0.1 μS, a small afterhyperpolarization was visible after each spike (Fig. 5D, compare black and grey traces). The initial firing frequency dropped to 174 Hz (see Fig. 5D, black trace), the mean firing frequency of the steady discharge decreased to 53 Hz (Fig. 5B) and the coefficient of variation went down to 0.14. Therefore, although small, the artificial conductance substantially modified the discharge. This was due to the fact that this motoneurone was essentially deprived of its natural AHP and was therefore highly sensitive to the artificial AHP conductance. When the artificial conductance ($G_{\text{dc}}^{\max }$) was set to 0.7 μS, the AHP amplitude increased (Fig. 5E), the initial firing frequency dropped to 50 Hz, the mean stationary frequency to 34 Hz (Fig. 5C) and the coefficient of variation decreased to 0.05. These values were similar to the control values observed in motoneurones in which the natural AHP was not depressed by BAPTA. Note that adding an artificial AHP decreased the spike voltage threshold (measured as explained in the legend of Fig. 1C). It was equal to −39.6 ± 0.9 mV without the dynamic clamp and decreased to −44.5 ± 0.6 mV when an artificial conductance of 0.7 μS was added (see Fig. 5E). Notice also that the AHP that followed the spike train (arrows in Fig 5B and C) increased with the artificial AHP conductance imposed on the motoneurone.

As expected, adding the artificial AHP reduced the gain of the motoneurone. Before imposing the artificial AHP conductance (BAPTA alone), the slope of the I–f curve (filled circles in Fig. 6A) was 9.7 Hz nA⁻¹. For $G_{\text{dc}}^{\text{max}}$ = 0.1 μS (open squares), the gain decreased to 5.9 Hz nA⁻¹, i.e. only 60% of the control. For $G_{\text{dc}}^{\text{max}}$ = 0.7 μS (filled triangles), the gain dropped to 1.8 Hz nA⁻¹ (20% of the control). Figure 6B shows that the gain and the coefficient of variation decreased nonlinearly as the artificial conductance increased. In contrast, the inverse of the gain (Fig. 6C, r = 0.99, P = 0.0001) and the inverse of the coefficient of variation (Fig. 6D) were proportional to the artificial AHP conductance. Figure 6D shows that the inverse of the coefficient of correlation was linearly correlated to the conductance for all three values of the injected current tested with slopes 18 μS⁻¹ for I = 17 nA (r = 0.99, P = 0.0006, dotted line), 25 μS⁻¹ for I = 20 nA (r = 0.99, P = 0.006, continuous line) and 22 μS⁻¹ for I = 23 nA (r = 0.99, P = 0.002, dashed line). This suggests that the coefficient of variation of the stationary discharge is inversely proportional to the AHP conductance, whatever the amount of current injected.

Discussion

The present study is the first experimental work establishing relationships between the AHP conductance, and the gain and variability of the neuronal discharge. A population analysis suggested that the gain was inversely proportional to the product of the conductance, time constant and driving force of the AHP current. We then performed dynamic clamp experiments in which we varied only one parameter of the AHP current (either the conductance or the decay time) while keeping the two other parameters fixed. These experiments allowed us to investigate how the AHP conductance acts on the variability of the discharge and to compare its effects on the variability and on the gain. We found that the coefficient of variation of the instantaneous firing frequency, which characterizes the variability, was inversely proportional to the conductance of the artificial AHP, and also to its decay time. Similar results were obtained for the gain. Altogether, our study indicates that the AHP conductance exerts the same control over the gain and the variability. This mechanism ensures that the variability of the discharge is adjusted to the firing frequency. This guarantees a great regularity of the discharge when the motoneurone is firing at low frequency and a good control of the force produced.

Relationship between the gain and the parameters of the AHP conductance

Theoretical studies (Wilson et al. 2004; Meunier & Borejsza, 2005) have shown that in integrate-and-fire models with an AHP conductance the gain is inversely proportional to the product of the conductance, decay time and driving force of the AHP current. These studies also predicted the value of the proportionality factor between the gain and the inverse of this product. In the case of the first interspike interval, this proportionality coefficient is equal to e²/4 (Wilson et al. 2004; Meunier & Borejsza, 2005). Our experimental results agree very well with these modelling studies. We found the same reciprocal relationship between the gain and the product of the three parameters of the AHP current as in the models (see Fig. 1E and F). Moreover, the slope of this relationship (1.9 for the first interspike interval) is close to the theoretical prediction (e²/4). However, the data points in Fig. 1E and F are quite spread out, and the best fits account for only half of the variance of the sample (the coefficient of determination r² was equal to 0.56 and 0.42 for the first interspike interval and for the steady state discharge, respectively). Part of the dispersion is accounted for by errors in the measurements of the AHP current parameters (5–10% typically in each of the three parameters, Manuel et al. 2005). Moreover, the gain displayed some fluctuations from one determination to another (see Fig. 3B).

This agreement between our experimental results and models was not warranted in view of the numerous simplifications made to obtain solvable models of motoneurones. In spinal motoneurones, other subthreshold currents than the AHP current are present that were not incorporated in models. An I_h current substantially contributes to the resting potential (Schwindt & Crill, 1984; see also Kiehn et al. 2000). A persistent calcium current was demonstrated (Schwindt & Crill, 1980; see Hultborn et al. 2004). Recently, it was suggested that the persistent sodium current played an essential role in the rhythmic firing of motoneurones (Lee & Heckman, 2001). The good agreement of our data with the models indicates that none of these currents plays a substantial role in controlling the gain of motoneurones in anaesthetized animals.

In awake animals, the balance between the AHP and persistent inward currents may be drastically altered when neuromodulation occurs. Serotonin release due to the activation of descending pathways decreases the amplitude of AHP (see Hultborn et al. 2004). On the opposite, serotoninergic neuromodulation enhances the persistent calcium current (Perrier & Delgado-Lezama, 2005). Noradrenergic α1-agonists (Lee & Heckman, 1999), and acetylcholine (Chevallier et al. 2006) also neuromodulate subthreshold currents. During neuromodulation, the gain then becomes determined by the interplay between the various inward and outward currents active in the subthreshold voltage range.

Relationship between the AHP conductance and the discharge variability

We found that the coefficient of variation of the instantaneous firing frequency was inversely proportional to the conductance and the relaxation time constant of the artificial AHP current added with dynamic clamp. How the AHP conductance acted to reduce the CV could be investigated in a motoneurone deprived from most of its natural AHP by BAPTA because the artificial AHP had a large effect on the discharge in this condition. The reduction of CV was associated with a shortening of the time window in which the spike could be emitted. This decreased variability was not due to a reduction of voltage fluctuations. Indeed, the residual conductance of the artificial AHP current at the end of the interspike interval was always small compared to the passive input conductance of the motoneurone and did not significantly affect the size of voltage fluctuations.

Two reasons may be advanced to explain the reduced variability. Firstly, the voltage trajectory before the spike became steeper as the artificial AHP conductance was increased. This made it more difficult for voltage fluctuations to trigger a spike. Secondly, the voltage threshold itself became less variable. This is likely to have been due to the de-inactivation of the transient sodium current following from the increased hyperpolarization. This de-inactivation would also explain why increasing the AHP conductance reduced the mean value of the voltage threshold (see Fig. 5). The dual origin of the variability reduction is in agreement with the study of Powers & Binder (2000), who suggested that the discharge variability arose from fluctuations of both the membrane potential and the voltage threshold.

Recently, Bacci & Huguenard (2006) demonstrated in fast spiking cortical interneurones that inhibitory autapses reduced the discharge variability and enhanced spike-timing precision. They ascribed this effect to the hyperpolarization elicited by autapses rather than to the conductance increase. Whatever its origin (AHP, autapses, recurrent inhibition …), negative feedback triggered by spikes appears essential to control spike timing in neurones.

Integrate-and-fire models cannot account for the effects of the AHP on discharge variability

The similar dependence of the gain and of the coefficient of variation on the parameters of the AHP current may reflect the fact that both measure the sensitivity of the discharge to fluctuating inputs. The gain, defined as the slope in the stationary I–f curve, indicates how slow variations of the input current modulate the firing rate. It quantifies the static sensitivity of the motoneurone. In contrast, the CV measures how the firing frequency is affected by synaptic and intrinsic noise, which displays fast fluctuations. Therefore, the CV is related to the dynamic sensitivity of the motoneurone.

The static properties of motoneurones are expected to depend mostly on slow ionic currents like the AHP current, and little on currents with fast kinetics. This is why the gain of motoneurones is well predicted by an integrate-and-fire model that incorporates the AHP current but not the fast currents involved in spike generation. In contrast, the integrate-and-fire model cannot explain the dynamic sensitivity of the motoneurone discharge. It does not display voltage threshold fluctuations. Moreover, numerical simulations, where a small white noise was added to the constant current input, revealed a very different dependence of the coefficient of variation on the AHP conductance compared to real motoneurones (see online Supplemental material). In these simulations, the CV was not inversely proportional to the AHP conductance and decreased much less than in dynamic clamp experiments when the AHP conductance was increased (see supplemental Fig. 1A). The AHP time constant had even less impact on the CV (see supplemental Fig. 1B), which decreased linearly over the range of time constants explored in dynamic clamp experiments.

Integrate-and-fire models cannot account for the transient features of the discharge of motoneurones. They explain neither the variability of the discharge nor the initial frequency adaptation, which both involve the inactivation of the transient sodium currents (Miles et al. 2005). Theoretical studies of the dynamical features of the motoneurone discharge require the use of conductance-based models incorporating the fast currents involved in spike generation.