Abstract
Slow relaxation from an isometric contraction is characteristic of acutely fatigued muscle and is associated with a decrease in the maximum velocity of unloaded shortening (Vmax) and both these phenomena might be due to a decreased rate of cross bridge detachment. We have compared the change in relaxation rate with that of various parameters of the force–velocity relationship over the course of an ischaemic series of fatiguing contractions and subsequent recovery using the human adductor pollicis muscle working in vivo at approximately 37°C in nine healthy young subjects. Maximal isometric force (F0) decreased from 91.0 ± 1.9 to 58.3 ± 3.5 N (mean ± s.e.m.). Maximum power decreased from 53.6 ± 4.0 to 17.7 ± 1.2 (arbitrary units) while relaxation rate declined from −10.3 ± 0.38 to −2.56 ± 0.29 s−1. Vmax showed a smaller relative change from 673 ± 20 to 560 ± 46 deg s−1 and with a time course that differed markedly from that of slowing of relaxation, showing very little change until late in the series of contractions. Curvature of the force–velocity relationship increased (a/F0 decreasing from 0.22 ± 0.02 to 0.11 ± 0.02) with fatigue and with a time course that was similar to that of the loss of power and the slowing of relaxation. It is concluded that for human muscle working at a normal physiological temperature the change in curvature of the force–velocity relationship with fatigue is a major cause of loss of power and may share a common underlying mechanism with the slowing of relaxation from an isometric contraction.
Slow relaxation from an isometric contraction is a characteristic feature of muscle that has been fatigued by metabolically demanding contractile activity (e.g. Edwards et al. 1972, 1975a; Cady et al. 1989; Westerblad & Lännergren, 1991). Despite the familiarity of these observations the reasons for this behaviour of muscle are still not fully understood. The relaxation phase is electrically silent, distinguishing it from the slow relaxation of myotonia, so there are two broad possible mechanisms. Either the process of removing calcium could be slowed or, alternatively, the rate at which myosin cross bridges detach from the thin actin filaments could be reduced. Direct measurements of intracellular calcium in Xenopus fibres (Allen et al. 1989) suggested that slow relaxation was due to slow re-accumulation of calcium into the sarcoplasmic reticulum but subsequent work on single mouse skeletal muscle fibres came to the opposite conclusion (Westerblad & Allen, 1993, 1994a), implicating a change in the kinetics of cross bridge detachment as the likely cause of contractile slowing associated with fatigue.
A change in cross bridge kinetics will be reflected in the force–velocity relationship of the muscle and can be investigated with whole human muscles working in situ. The maximum velocity of unloaded shortening (Vmax) is determined by the detachment rate of cross bridges pulled into positions opposing movement (Huxley, 1957). If slow relaxation is due to slow cross bridge detachment then it might be associated with a decrease in unloaded shortening velocity. Several studies have shown Vmax to be reduced by fatigue (Edman & Mattiazzi, 1981; de Haan et al. 1989; Curtin & Edman, 1994; de Ruiter et al. 1999a, 2000a) and this contractile slowing has been suggested to play a major part in the loss of power associated with acute fatigue (James et al. 1995). These studies add weight to the suggestion that it is reduced cross bridge detachment that is responsible for slow relaxation rather than it being a consequence of changes in calcium handling. In all these investigations, however, the measurements made in the fresh state have been compared with a single measure in the fatigued state. Consequently, although the results are consistent with slow relaxation being due to slow cross bridge detachment there is insufficient data to establish a clear relationship. Showing that changes in relaxation and Vmax have a similar time course would be evidence for a common underlying mechanism but such observations have not been made either during the development of fatigue or subsequent recovery.
The purpose of the work described here was therefore to see if the time course of changes in relaxation and various measures of the shape of the force–velocity relationship correlate with one another during fatiguing exercise and recovery in human muscle working at a normal physiological temperature. Our hypothesis was that loss of power and slowing of relaxation with fatigue would correlate with a slowing of the maximum velocity of unloaded shortening, thus indicating a common underlying mechanism.
Methods
Subjects
Seven healthy subjects (22–55 years of age, four male) took part after giving their written informed consent. The subjects were all right-handed, did not undertake any specific exercise of the hand muscles and were familiar with fatiguing electrical stimulation under ischaemic conditions. The study was approved by the local ethics committee and was carried out in accordance with the Declaration of Helsinki.
Force recording and stimulation
Methods for stimulating the adductor pollicis and recording force are given in detail elsewhere (de Ruiter et al. 1998, 1999a). Briefly, the subject sat in an adjustable chair with the left forearm supinated and the hand held horizontally with the thumb abducted and in contact with a vertical pin. The pin was attached to a strain gauge, mounted below the plane of the hand, which rotated about the same axis as the thumb, the movement being controlled by a linear motor. The smallest thumb angle at which force could be measured was 36 deg and the largest 74 deg (maximal abduction) before anatomical limits were approached, but in the present study the shortening contractions never started at angles greater than 71 deg, allowing a maximal thumb rotation of 35 deg. Timing, duration and frequency of stimulation, the onset and speed of motor movement and data sampling frequency (1000 Hz) of the force and angle signals, were all computer controlled.
The adductor pollicis muscle was activated by percutaneous electrical stimulation of the ulnar nerve at the wrist with constant current unidirectional square wave pulses of 200 μs duration (Digitimer Ltd, model DS7, Welwyn Garden City, UK) at different frequencies. The current was set 30% above the stimulus that produced maximal isometric tetanic force during 1.0 s, 80 Hz stimulation. Force records of contractions were filtered (fourth order low pass digital Butterworth filter, 50 Hz cut-off frequency).
Temperature
Variations in muscle temperature affect relaxation rate, maximal shortening velocity and power production (de Ruiter et al. 1999b; de Ruiter & de Haan, 2000) and consequently care was taken to establish and maintain a constant muscle temperature. The subject's hand and forearm were first immersed in a water bath at 45°C for 20 min and during the experiment an infusion bag was placed over the lower arm and circulated with warm water. These precautions have been shown to result in a constant muscle temperature of 37°C (de Ruiter et al. 1999b).
Experimental protocol
Force–velocity curves were constructed using short duration (1000–90 ms) isovelocity contractions at seven different angular velocities (0, 76, 153, 229, 306, 382 and 458 deg s−1) applied in random order as described in detail elsewhere (de Ruiter et al. 1999a,b). With this method the contraction started at a length greater than the optimum length for force production. The muscle was stimulated and shortly thereafter the thumb allowed to adduct at a constant angular velocity imposed by the motor. Thus the muscle started shortening during the rise phase of force development. The timing of the start of shortening relative to the start of stimulation was chosen so that force remained constant during the thumb movement, resulting in isovelocity shortening with an isotonic phase during which forces were measured. Small adjustments to the timing were necessary to obtain constant forces during shortening at the different velocities for each subject. With increasing shortening speed (lower forces) the shortening started sooner after the beginning of stimulation, e.g. for the contractions at 76 deg s−1 the delay was about 100 ms while for the highest speed of 458 deg s−1 shortening and stimulation started almost simultaneously. Therefore, particularly at the highest speeds, it was important that the muscle reached its maximum active state as soon as possible. To achieve this, two other adjustments were made. First the stimulation frequency was increased with increasing velocity (range: 80–180 Hz). Secondly, contractions started at greater thumb angles with increasing shortening speeds (range: 56–71 deg). Pilot experiments showed that applying a stimulation frequency of 180 Hz during the fastest contractions at 458 deg s−1 resulted in near maximal (> 95%) forces in the unfatigued muscle and maximal forces during fatigue. A similar rationale was used for the choice of stimulation frequencies during the contractions at the other velocities.
After the appropriate stimulation current was established, one to three ‘trial and error’ contractions at each speed (with 1 min rest between) were used to make the small adjustments to the timing of the movement, as described above. Thereafter the test measurements began. Fatigue was caused by repetitive stimulation with the set of contractions (see below) that, at the same time, was used to obtain the force–velocity relationship of the muscle.
The blood supply was occluded by inflating a pneumatic cuff (> 220 mmHg) around the upper arm and the muscle was then fatigued using a set of seven isovelocity shortening contractions at different angular velocities (0, 76, 153, 229, 306, 382 and 458 deg s−1). The total duration of this set was 9 s, with sufficient time between contractions to allow complete muscle relaxation. The muscle was fatigued by applying nine of these sets with 6 s rest between (total duration 129 s). The order of the contraction velocities was the same within each set for one subject, but was randomized between subjects. Following the last set, the cuff was deflated and recovery monitored by applying the same set of seven contractions at 10 s, 45 s, 90 s 180 s and 360 s recovery.
In addition, three ‘passive’ sets were imposed to measure the passive forces: the thumb made all the abduction (induced by the motor) and adduction movements but with the stimulator switched off. A ‘passive’ set was imposed immediately prior to the first stimulated set of contractions, immediately after the ninth set (with blood flow still occluded) and following the last set during recovery. Passive forces were found not to change (P > 0.05) over the course of the experiment. The appropriate passive force at each velocity was subtracted from the total force trace to determine the active force at each velocity.
Data analysis
All forces were measured at a thumb angle of 51 deg, which was optimum for force production, although the angle–force relationship is very flat over the range (38–71 deg) of thumb angles (de Ruiter et al. 1998).
Relaxation rate was taken as the highest value of the differentiated force signal during relaxation from an isometric contraction. This value was subsequently expressed relative to the isometric force at the end of stimulation to calculate maximal relaxation rate, hence the units N s−1 N−1, or s−1.
Forces measured at the 51 deg thumb angle were used to construct the force–velocity relationship of the muscle. Data points were fitted (least squares, without constraining the curve to pass through F0) to the Hill (1938) equation and a/F0 was used to quantify the curvature of the relationship. Force values from the fitted Hill curves were multiplied by the angular velocity to obtain power–velocity curves, expressed in arbitrary units (N deg s−1). Optimal shortening velocity (Vopt) was defined as the velocity of shortening giving the highest power output (Pmax). Maximal shortening velocity (Vmax) was determined as the intercept of the Hill curve with the velocity axis.
Statistics
The results are presented as means ± s.e.m. ANOVA for repeated measures was used to test for significant (P < 0.05) changes over time, followed by Bonferroni post hoc tests. Pearson's correlation coefficient was calculated to establish significance of correlations (P < 0.05).
Results
Effects of fatigue on relaxation rate and contractile properties
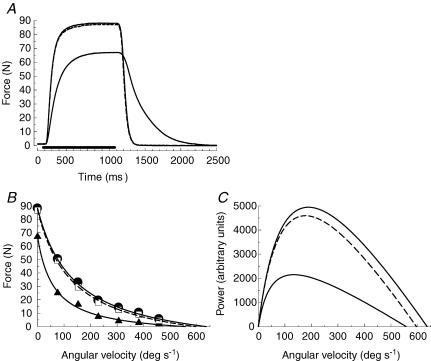
Figure 1A shows the loss of force and slowing of relaxation of an isometric tetanus as a result of the full protocol of nine sets of contractions under ischaemic conditions. The slowing of relaxation was associated with changes in the force–velocity relationship (Fig. 1B) such that there was a decrease in the estimated maximum velocity of shortening (Vmax) and an increased curvature of the relationship (a/F0). Calculating the power (Fig. 1C) it can be seen that there was a decrease in the maximum power (Pmax) and that this was shifted to a lower velocity (optimum velocity; Vopt). Absolute values for these measures are given in Table 1, both for the changes occurring as a result of fatigue under ischaemic conditions and for measurements made after 6 min of recovery with an intact circulation. In subsequent figures the data are reported as percentages of the initial values to help compare the different time courses.
Figure 1. Effects of fatigue on the contractile characteristics of the adductor pollicis.
A, original records of an isometric tetanus (80 Hz) in the initial, fresh, state (upper continuous line), after the ninth series of fatiguing contractions (lower continuous line) and following 360 s recovery (dashed line, almost completely superimposed on the fresh trace). B, force–velocity curves for the same subject in the initial (•, continuous line), fatigued (▴, continuous line) and recovered state (□, dashed line). C, the relationship between power (derived from data in Fig. 1B) and velocity for the same subject in the fresh (upper continuous line), fatigued (lower continuous line) and recovered (dashed line) state.
Table 1.
Parameters of the force–velocity relationship during ischaemic contractions of in vivo human adductor pollicis muscle in nine healthy young subjects
| F0 (N) | Relaxation (s−1) | Vmax (deg s−1) | Vopt (deg s−1) | Pmax (arbitrary) | a/F0 | |
|---|---|---|---|---|---|---|
| Initial | 91.0 ± 1.9 | −10.3 ± 0.38 | 673 ± 20 | 201 ± 10 | 53.6 ± 4.0 | 0.22 ± 0.02 |
| Fatigued | 58.3 ± 3.5 | −2.56 ± 0.29 | 560 ± 46 | 132 ± 7 | 17.7 ± 1.2 | 0.11 ± 0.02 |
| Recovered | 87.8 ± 1.6 | −10.2 ± 0.25 | 619 ± 23 | 186 ± 10 | 48.5 ± 3.6 | 0.22 ± 0.02 |
Absolute values for isometric force (F0), relaxation rate, estimated velocity of unloaded shortening (Vmax), maximum power (Pmax), velocity for maximum power (Vopt) and the constant a/F0 indicating the curvature of the force–velocity relationship. Values are for the initial set of contractions at the start of the fatiguing series (Initial), after 9 sets of contractions under ischaemic conditions (Fatigued) and after 360 s of aerobic recovery (Recovered). Data are given as mean ± s.e.m.
Clearly there are a number of changes in contractile properties associated with fatigue which may share common cellular mechanisms; the question is which, if any, of these changes correlate with the changes in power and relaxation rate of the muscle during the development of fatigue and subsequent recovery?
Time course of changes in contractile properties during fatigue and recovery
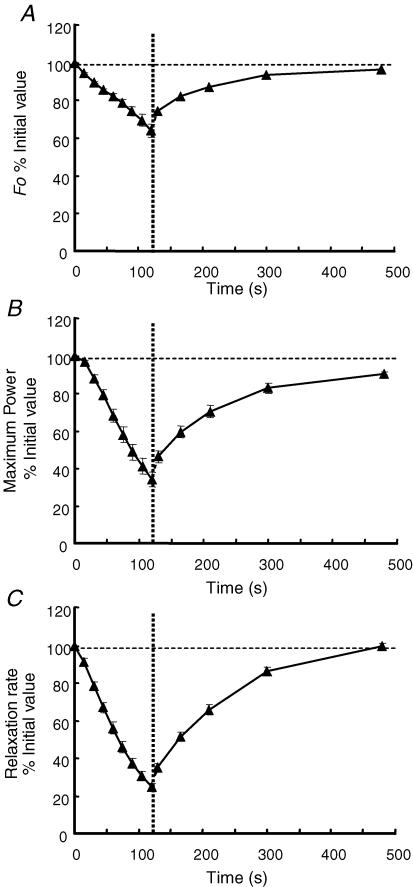
Figure 2 shows the changes in maximum isometric force, peak power and relaxation rate. Isometric force declined in an approximately linear fashion to 64% of the initial value during the fatiguing sequence (Fig. 2A). There was a small rapid increase in force during the first 10 s of aerobic recovery which thereafter recovered to 96% of the initial value with a half-time of about 80 s. Peak power was maintained following the second series of contractions (Fig. 2B) but then declined in an approximately linear fashion to 33% of the initial value. After a small but rapid recovery in the first 10 s, peak power returned to 90% of the initial value by 6 min with a half-time of approximately 80 s. The fact that the loss of peak power as a result of fatigue was far greater than the loss of isometric force clearly indicates that the speed of the muscle was affected and this is also evident in the change in relaxation rate (Fig. 2C). Relaxation rate declined from the start of the fatiguing sequence to reach 25% of the initial value by the ninth series of contractions. There was a complete recovery over 6 min with a half-time of, again, approximately 80 s.
Figure 2. Changes in muscle contractile properties during fatigue and recovery.
A, changes in isometric force (80 Hz) during the nine fatiguing series of contractions under ischaemic conditions and the subsequent 6 min of recovery with an intact circulation, beginning at the vertical dotted line. B, changes in maximum power during fatigue and recovery. C, changes in relaxation rate from an isometric tetanus during fatigue and recovery. Data are the mean ± s.e.m. and are expressed as a percentage of the initial values (100% indicated by the horizontal dashed line).
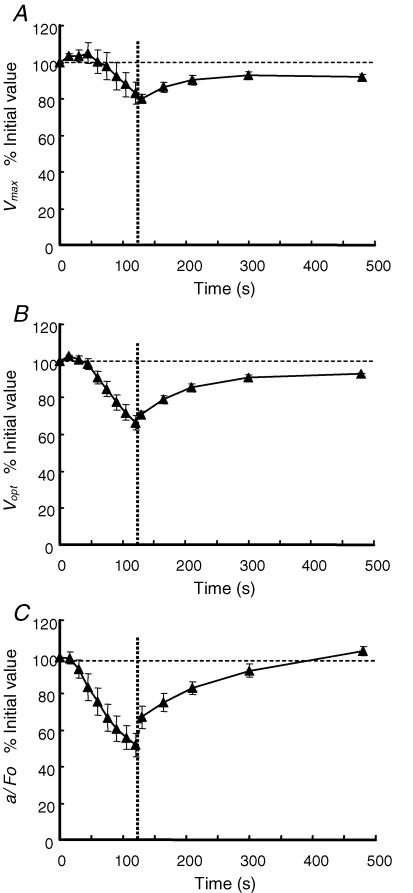
Different measures of the force–velocity relationship and how they change during fatigue and recovery are shown in Fig. 3. Vmax (Fig. 3A) was well maintained for the first four series of contractions following the initial test and there is a suggestion that the values even increased slightly. Thereafter, Vmax declined in a linear fashion to 83% of the initial value. During the first 10 s of recovery there was a further slight decline and then a recovery to 92% of the initial value by 6 min, with a half-time of approximately 60 s. Vmax was estimated by extrapolation of the force–velocity relationship to the intercept on the velocity axis, and the values are very dependent on forces recorded at the higher velocities of movement, which are inevitably small and subject to some uncertainty. Consequently we also report values of Vopt (Fig. 3B) which is estimated largely from the higher forces obtained at intermediate velocities. Nevertheless, Vopt behaved in a very similar way to Vmax being maintained during the first four series of contractions before declining to 66% of the initial value. Vopt recovered to 93% of the initial value by 6 min with a half-time of about 60 s. Neither Vmax nor Vopt changed sufficiently or with the appropriate time course to explain the major loss of power observed as a result of the fatiguing series of contractions (compare Fig. 3A and B with Fig. 2B). However, the curvature of the force–velocity relationship increased (decreasing a/F0) (Fig. 3C) with a time course that was closer to that of peak power. Values for a/F0 were maintained after the first series of contractions but then declined to 50% of the initial value. Full recovery was achieved somewhat before the full six minutes.
Figure 3. Time course of changes in the force–velocity relationship during fatigue and recovery.
A, changes in the maximum velocity of unloaded shortening (Vmax) during the nine fatiguing series of contractions under ischaemic conditions and the subsequent recovery with an intact circulation, beginning at the vertical dotted line. B, changes in the optimum velocity to generate power (Vopt) during fatigue and recovery. C, changes in the curvature of the force–velocity relationship (a/F0) during fatigue and recovery. Data are the mean ± s.e.m. and are expressed as a percentage of the initial values (100% indicated by the horizontal dashed line).
Relationships between rate of relaxation and parameters of the force–velocity curve
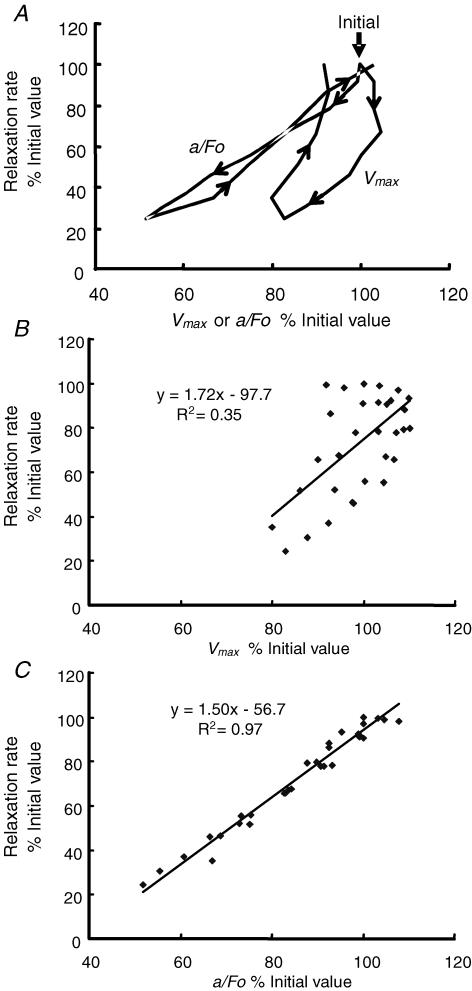
Figure 4A shows the changes in rate of relaxation during fatigue and subsequent recovery as a function of change in either Vmax or a/F0. Only the mean values are shown for clarity and illustrate the fact that as relaxation slowed during the early part of the fatiguing protocol there was no change in Vmax and that during the recovery phase there was incomplete recovery of shortening speed so that the curve describes an open loop. Only a weak linear relationship is seen between Vmax and relaxation when individual data are plotted (Fig. 4B). In contrast, changes in relaxation rate are closer to those of a/F0. The mean data in Fig. 4A suggest there is some fluctuation around a strictly linear relationship that may differ between fatigue and recovery but plotting individual data points (Fig. 4C) reveals a very tight relationship (R2 = 0.97).
Figure 4. Relaxation rate in relation to changes in Vmax and a/F0.
A, mean data taken from Figs 2 and 3 showing the relationship between relaxation rate and Vmax and a/F0 during fatigue and recovery. Vertical arrow indicates the initial values (100%) and the arrowheads indicate the direction of change, first during fatigue and then recovery; note the marked hysteresis of the Vmax curve which is much less evident with the relationship between relaxation and a/F0. B, the relationship between relaxation rate and Vmax during fatigue and recovery; individual data points and linear regression are shown. C, the relationship between relaxation rate and a/F0 during fatigue and recovery; individual data points and linear regression are shown.
Discussion
The present results provide some new insights into two features of fatiguing human muscle working in situ at 37°C. The first is that an increased curvature of the force–velocity relationship makes a significant contribution to the overall loss of power in acutely fatigued muscle. Secondly, we suggest that the slowing of relaxation is associated with an increased curvature of the force–velocity relationship and consider some of the metabolite changes in fatigued muscle that might be responsible for these two phenomena.
Our initial hypothesis, that a decrease in Vmax would underlie both the slowing of relaxation and loss of power, which are characteristics of acutely fatigued muscle, has proved not to be the case. The time course of changes in Vmax did not correlate with either the decreases in power or relaxation rate of the muscle during the development of fatigue or the recovery phase. The estimation of Vmax by extrapolation is always a matter of some concern but we believe the conclusions drawn here are reliable since the same pattern, namely a relatively late decrease in shortening velocity during the course of fatigue, can also be seen in the data for Vopt, which is less susceptible to the errors inherent in measuring small forces at the higher velocities.
Changes in Vmax and power
The extent of the change in Vmax, declining by about 17% at the end of the ninth series of contractions, is similar to the changes we have previously reported (de Ruiter et al. 1999a, 2000a) and to the slowing seen in isolated preparations (Edman & Mattiazzi, 1981; Curtin & Edman, 1994; Barclay, 1996; Westerblad et al. 1998). The time course quite clearly shows that slowing of Vmax and Vopt are relatively late events in the fatiguing protocol and there is even a suggestion that after two or three series of contractions there were small increases in velocity before Vmax began to decline (Fig. 3A). The reason for this increase is not known but it is unlikely to be due to warming of the muscle since metabolic heat production during a maximal isometric contraction is approximately 1.0°C per minute (Edwards et al. 1975b) so 14 short contractions with a total duration of about 5 s are unlikely to have affected Vmax, which has a Q10 of approximately 2.0 (de Ruiter & de Haan, 2000). Another possibility is a mechanism similar to that described by Maréchal & Beckers-Bleukx (1998) and Zhu et al. (2003), associated with the production of NO.
Loss of force-generating capacity, as reflected by the decrease in isometric force (Fig. 2A), accounts for about half the loss of peak power shown in Fig. 2B while a decrease in Vmax of the order reported here makes very little difference to the peak power developed, as estimated from the Hill equation. In contrast, the increase in curvature (decreasing a/F0) seen as the muscle fatigues shows a similar time course to the loss of power, decreasing steadily from the second series of contractions (Fig. 3C), and accounts for most of the other half of the decrement of power.
The contribution that the curvature of the force–velocity relationship makes to the power output of a muscle is well recognized and in isolated preparations, working at lower temperatures than used here, the curvature of the relationship has generally been found to become flatter with fatigue, which has the effect of preserving muscle power (Curtin & Edman, 1994; Barclay, 1996). Our findings contrast with those for the isolated preparations in that a/F0 decreased from 0.22 to 0.11 with fatigue, a change which is very similar to our previous observations (0.23 to 0.14, de Ruiter et al. 2000a). The difference between the isolated and in situ preparations may well be that of temperature since we have seen that the decrease in curvature does not occur with human muscle when fatigued at lower temperatures (de Ruiter & de Haan, 2000; and see discussion of relaxation rate below).
Changes in relaxation rate and curvature of the force–velocity relationship
The second unexpected finding of the present study was that the time course of slowing of relaxation did not correspond with measures of Vmax or Vopt. Relaxation began to slow from the start of the fatiguing series while changes in Vmax and Vopt were late events. Westerblad & Lännergren (1994) have also reported, for Xenopus fibres at 20°C, that relaxation rate decreases more rapidly than shortening velocity and with a different time course. Unlike the findings of Westerblad & Lännergren (1994) who report a flattening of the force–velocity curve, we found there was a distinct similarity between the time courses of change in relaxation rate and the decrease in a/F0, suggesting some connection between these two events. The value a/F0 is not much affected by the precise intercept on either the force or velocity axis of the force–velocity curve and we are therefore confident of the relationships demonstrated in Fig. 4A and C. Although the data in Fig. 4C indicate a tight linear relationship between relaxation and a/F0, there are small deviations in that a/F0 did not decrease until the third series of contractions (20 s in Fig. 3C) while relaxation changed after the second series (Fig. 2C), and this can be seen in the mean data plotted in Fig. 4A. Otherwise there was a good relationship, including the small, rapid, recovery that occurred within 10 s of the circulation being restored.
The fact that there was not a linear relationship between relaxation rate and Vmax does not, in itself, rule out a causative relationship since there is no reason why any such relationship should be linear. However, the difference in the relationship between Vmax and relaxation rate during fatigue and recovery argues against any common underlying mechanism; this is in contrast to the relationships between relaxation and a/F0 which appear to be similar during both fatigue and recovery.
Possible cross bridge mechanisms giving rise to a decrease in curvature of the force–velocity relationship
Finding that changes in relaxation rate are related to changes in a/F0 suggests that slowing of relaxation is a reflection of changes in cross bridge function. It is interesting therefore, to consider what aspect of function might be affected. In the Huxley (1957) treatment of cross bridge kinetics, the curvature of the force–velocity relationship is determined by the sum of the rate constants for attachment (f) and detachment (g1) of the myosin head in the range of possible cross bridge attachments where force can be developed. Consequently a decrease in either f or g1 could explain the observed decrease in a/F0. For a reasonable proportion of cross bridges to be attached in the isometric state f has to be greater than g1 in the ratio of about 4, or 3, to 1. The change in a/F0 we have observed is large, halving from 0.22 to 0.11. To cause such a change the value of f + g1 would have to change proportionately and this can only happen if there is a substantial reduction in f. For instance, halving g1 would decrease f + g1 by about 10–12%, while halving the value of f would decrease f + g1 by around 40%.
Possible causes and consequences of change in a/F0
In the relatively simple model of cross bridge kinetics used here f, the rate constant for attachment, combines two steps, the initial binding of myosin to actin and the subsequent release of inorganic phosphate that leads to the development of force. This second process is known to be slowed in the presence of high intracellular inorganic phosphate with a greater proportion of cross bridges remaining in the low force state (Cooke et al. 1988; Godt & Nosek, 1989; Stienen et al. 1990; Dantzig et al. 1992). Consequently, where f appears to change, as in the present observations, it could be a consequence of slower release of bound inorganic phosphate (Pi) and, in this situation, muscle stiffness should be better preserved than the force in the fatigued state. This is what has been observed (Curtin & Edman, 1994).
Relaxation from an isometric contraction in single fibres is characterized by an initial relatively slow linear phase of force decline, a shoulder and a subsequent more rapid exponential decay of force. The shoulder, and subsequent loss of force, is associated with relative movements of different elements of the fibre, generally with the end sarcomeres being stretched (Huxley & Simmons, 1970). Curtin & Edman (1989) showed that these differential movements are reduced in the fatigued state and this was associated with an increased resistance of the fibre to stretch. Subsequently Curtin & Edman (1994) confirmed the increased resistance to stretch and showed that muscle stiffness was increased relative to force in the fatigued state and suggest that this may act to stabilize the fibre. Human muscle working in situ does not show the two phases of relaxation but it does become more resistant to stretch when fatigued (de Ruiter et al. 2000a). An increased proportion of cross bridges in a low force state could reduce force during shortening, thus increasing the curvature of the force–velocity relationship; they would also provide an additional resistance during stretch.
An increased curvature of the force–velocity relationship as a consequence of a decrease in f with fatigue would seem to explain the present observations but may not be the explanation for slow relaxation in every fatigued muscle. There is a marked slowing of relaxation during moderate fatigue of frog muscle fibres maintained at 1–2°C (Curtin & Edman, 1989) but, in contrast to the findings presented here, Curtin & Edman (1994) found a decrease in the curvature of the force–velocity relationship as a result of fatigue with a/F0 increasing by about 30%. Westerblad & Lännergren (1994) mention that the force–velocity relationship ‘seemed less curved’ in the fatigue state which is not consistent with the present observations. Our own previous work has shown responses which vary with conditions. de Ruiter et al. (2000a) reported a change in a/F0 from 0.23 to 0.14 with fatigue, which is almost identical to the present observations. However, inspection of the data presented in Fig. 5A of de Ruiter & de Haan (2000) suggests that a change in curvature of the relationship as a result of fatigue only occurs at the highest temperature. Subsequent calculations from their data reveal that, at 36.8°C, a/F0 decreased from 0.24 to 0.15, consistent with the present observations. However, at the lower temperatures there was no change in curvature. It is notable that in that series the extent of fatigue was far greater at the higher temperature where a change in a/F0 was observed and this may apply to other observations. For instance, Curtin & Edman (1994), who found a decrease in curvature as a result of fatigue, were concerned with only ‘moderate’ fatigue and were also working at a low temperature.
It seems likely therefore that the differences between our present observations, where a/F0 decreased with fatigue, and the various findings with isolated preparations, where a/F0 either did not change or even increased, may be a consequence of the different temperatures of the muscles. The isolated preparations were working between 1 and 25°C, while the in situ human muscle was maintained close to 37°C and we have previously found that human muscle at lower temperatures does not show the decrease in a/F0 with fatigue (de Ruiter & de Haan, 2000). In this respect, and in light of the discussion about the possible role of Pi, it may be relevant that Debold et al. (2004) found 30 mm Pi to decrease a/F0 in skinned rat muscle fibres maintained at 30°C but this had no effect, or even increased a/F0, when the fibres were at 15°C.
Cross bridge cycling and calcium pumping
Finally, we return to the question of whether slow relaxation is a consequence of slow calcium reuptake or change in cross bridge kinetics. The results presented here and the subsequent discussion indicate that slowing of relaxation is accompanied by a change in cross bridge kinetics; this does not, however, exclude change in calcium reuptake from playing some role. Although Westerblad & Allen (1993, 1994a) concluded that calcium movements did not play a role in slow relaxation, slow relaxation is seen when the sarcoplasmic reticulum calcium pump is inhibited with 2,5-di(tert-butyl)-1,4-benzohydroquinone (TBQ) in mouse muscles (Westerblad & Allen, 1994b) and in human muscle lacking the fast twitch isoform of the sarcoplasmic reticulum Ca2+-ATPase (Brody's disease; de Ruiter et al. 1999c).
It is possible that with fatigue there are a number of changes affecting both cross bridge kinetics and SR calcium transport. These changes may occur to different extents and with different time courses in mammalian and amphibian muscles and in different fibre types: they may depend on the fatiguing conditions and temperature and are probably the consequence of different metabolic events. Cady et al. (1989) found evidence of both pH-dependent and pH-independent causes of slow relaxation in human muscle. This might explain why slow relaxation is seen in different circumstances sometimes without (e.g. Curtin & Edman, 1994; Barclay, 1996), and sometimes with, a decreased curvature of the force–velocity relationships (e.g. the present results).
In conclusion, our original hypothesis that the development of slow relaxation would be mirrored by the time course of changes in Vmax has not been substantiated and it is apparent that change in Vmax is a late event in the development of fatigue and plays a relatively small part in the loss of power and virtually none in the slowing of relaxation. Instead we have shown that a decrease in curvature of the force–velocity relationship has a close relationship with slowing of relaxation and we speculate that this may be due to a decrease in the rate constant which combines the attachment of myosin and actin and the development of the high force state. It is likely that these conclusions are specific to muscle experiencing considerable fatigue and working at normal mammalian physiological temperatures.
References
- Allen DG, Lee JA, Westerblad H. Intracellular calcium and tension during fatigue in isolated single mouse fibres from Xenopus laevis. J Physiol. 1989;415:433–458. doi: 10.1113/jphysiol.1989.sp017730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barclay CJ. Mechanical efficiency and fatigue of fast and slow muscles of the mouse. J Physiol. 1996;497:871–894. doi: 10.1113/jphysiol.1996.sp021809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cady EB, Elshove H, Jones DA, Moll A. The metabolic causes of slow relaxation in fatigued human skeletal muscle. J Physiol. 1989b;418:327–337. doi: 10.1113/jphysiol.1989.sp017843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooke R, Franks K, Luciani GB, Pate D. The inhibition of rabbit skeletal muscle contraction by hydrogen ions and phosphate. J Physiol. 1988;395:77–97. doi: 10.1113/jphysiol.1988.sp016909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curtin NA, Edman KA. Effects of fatigue and reduced intracellular pH on segment dynamics in ‘isometric’ relaxation of frog muscle fibres. J Physiol. 1989;413:159–174. doi: 10.1113/jphysiol.1989.sp017647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curtin NA, Edman KAP. Force–velocity relation for frog muscle fibres: effects of moderate fatigue and intracellular acidification. J Physiol. 1994;475:483–494. doi: 10.1113/jphysiol.1994.sp020087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dantzig JA, Goldman YE, Millar NC, Lacktis J, Homsher E. Reversal of the cross-bridge force-generating transition by photogeneration of phosphate in rabbit psoas muscle fibres. J Physiol. 1992;451:247–278. doi: 10.1113/jphysiol.1992.sp019163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Haan A, Jones DA, Sargeant AJ. Changes in velocity of shortening, power output and relaxation rate during fatigue of rat medial gastrocnemius muscle. Pflugers Arch. 1989;413:422–428. doi: 10.1007/BF00584493. [DOI] [PubMed] [Google Scholar]
- de Ruiter CJ, de Haan A. Temperature effect on the force/velocity relationship of the fresh and fatigued human adductor pollicis muscle. Pflugers Arch. 2000;440:163–170. doi: 10.1007/s004240000284. [DOI] [PubMed] [Google Scholar]
- de Ruiter CJ, de Haan A, Jones DA, Sargeant AJ. Shortening induced force depression in human adductor pollicis muscle. J Physiol. 1998;507:583–591. doi: 10.1111/j.1469-7793.1998.583bt.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Ruiter CJ, Didden WJM, Jones DA, de Haan A. The force–velocity relationship of human adductor pollicis muscle during stretch and the effects of fatigue. J Physiol. 2000a;526:671–681. doi: 10.1111/j.1469-7793.2000.00671.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Ruiter CJ, Jones DA, Sargeant AJ, de Haan A. The measurement of force/velocity relationships of fresh and fatigued human adductor pollicis muscle. Eur J Appl Physiol. 1999a;80:386–393. doi: 10.1007/s004210050608. [DOI] [PubMed] [Google Scholar]
- de Ruiter CJ, Jones DA, Sargeant AJ, de Haan A. Temperature effects on the rates of isometric force development and relaxation in the fresh and fatigued human adductor pollicis muscle. Exp Physiol. 1999b;84:1137–1150. doi: 10.1017/s0958067099018953. [DOI] [PubMed] [Google Scholar]
- de Ruiter CJ, Wevers RA, van Engelen BGM, Verdjik PWL, de Haan A. Muscle function in a patient with Brody's disease. Muscle Nerve. 1999c;22:704–711. doi: 10.1002/(sici)1097-4598(199906)22:6<704::aid-mus6>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- Debold EP, Dave H, Fitts RH. Fiber type and temperature dependence of inorganic phosphate: implications for fatigue. Am J Physiol Cell Physiol. 2004;287:C673–C681. doi: 10.1152/ajpcell.00044.2004. [DOI] [PubMed] [Google Scholar]
- Edman KAP, Mattiazzi AR. Effects of fatigue and altered pH on isometric force and velocity of shortening at zero load in frog muscle fibres. J Muscle Res Cell Motil. 1981;2:321–334. doi: 10.1007/BF00713270. [DOI] [PubMed] [Google Scholar]
- Edwards RHT, Hill DK, Jones DA. Effect of fatigue on the time course of relaxation from isometric contractions of skeletal muscle in man. J Physiol. 1972;227:26–27P. [PubMed] [Google Scholar]
- Edwards RHT, Hill DK, Jones DA. Metabolic changes associated with the slowing of relaxation in fatigued mouse muscle. J Physiol. 1975a;251:287–301. doi: 10.1113/jphysiol.1975.sp011093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards RHT, Hill DK, Jones DA. Heat production and chemical changes during isometric contractions of the human quadriceps muscle. J Physiol. 1975b;251:303–315. doi: 10.1113/jphysiol.1975.sp011094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Godt RE, Nosek TM. Changes in intracellular milieu with fatigue or hypoxia depress contraction of skinned rabbit skeletal and cardiac muscle. J Physiol. 1989;412:155–180. doi: 10.1113/jphysiol.1989.sp017609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill AV. The heat of shortening and the dynamic constants of muscle. Proc R Soc Lond B Biol Sci. 1938;126:136–195. doi: 10.1098/rspb.1949.0019. [DOI] [PubMed] [Google Scholar]
- Huxley AF. Muscle structure and theories of contraction. Prog Biophys Biophys Chem. 1957;7:255–318. [PubMed] [Google Scholar]
- Huxley AF, Simmons RM. Rapid ‘give’ and the tension ‘shoulder’ in the relaxation of frog muscle fibres. J Physiol. 1970;210:32P. [PubMed] [Google Scholar]
- James C, Sacco P, Jones DA. Loss of power during fatigue of human leg muscles. J Physiol. 1995;484:237–246. doi: 10.1113/jphysiol.1995.sp020661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maréchal G, Beckers-Bleukx G. Effect of nitric oxide on the maximal velocity of shortening of a mouse skeletal muscle. Pflugers Arch. 1998;436:906–913. doi: 10.1007/s004240050722. [DOI] [PubMed] [Google Scholar]
- Stienen GJM, Roosemalen MCM, Wilson MGA, Elzinga G. Depression of force by phosphate in skinned skeletal muscle fibres of the frog. Am J Physiol. 1990;259:C349–C357. doi: 10.1152/ajpcell.1990.259.2.C349. [DOI] [PubMed] [Google Scholar]
- Westerblad H, Allen DG. The contribution of [Ca2+]i to the slowing of relaxation in fatigued single fibres from mouse skeletal muscle. J Physiol. 1993;468:729–740. doi: 10.1113/jphysiol.1993.sp019797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerblad H, Allen DG. Relaxation, [Ca2+]i and [Mg2+]i during prolonged tetanic stimulation of intact, single fibres from mouse skeletal muscle. J Physiol. 1994a;480:31–43. doi: 10.1113/jphysiol.1994.sp020338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerblad H, Allen DG. The role of sarcoplasmic reticulum in relaxation of mouse muscle; effects of 2,5-di(tert-butyl)-1,4-benzohydroquinone. J Physiol. 1994b;474:291–301. doi: 10.1113/jphysiol.1994.sp020022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerblad H, Dahlstedt AJ, Lännergren J. Mechanisms underlying reduced maximum shortening velocity during fatigue of intact, single fibres of mouse muscle. J Physiol. 1998;510:269–277. doi: 10.1111/j.1469-7793.1998.269bz.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerblad H, Lännergren J. Slowing of relaxation during fatigue in single mouse muscle fibres. J Physiol. 1991;434:323–336. doi: 10.1113/jphysiol.1991.sp018472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerblad H, Lännergren J. Changes of the force-velocity relation, isometric tension and relaxation rate during fatigue in intact, single fibres of Xenopus skeletal muscle. J Muscle Res Cell Motil. 1994;15:287–298. doi: 10.1007/BF00123481. [DOI] [PubMed] [Google Scholar]
- Zhu X, Heunks LM, Ennen L, Machiels HA, Dekhuijzen PN. Role of nitric oxide in isometric contraction properties of rat diaphragm during hypoxia. Eur J Appl Physiol. 2003;88:417–426. doi: 10.1007/s00421-002-0719-9. [DOI] [PubMed] [Google Scholar]