What simple and complex cells compute

Visual neuroscientists seek to answer two related questions. First, what does the visual system do? Second, how does it do it? While an answer to the second question is a description based on anatomy and biophysics, an answer to the first question is a description of computations performed on images. Important steps in providing this description were made with the publication of two classical studies on primary visual cortex by Movshon et al. (1978a,b). These studies have not aged in their readability, and do not require an interpretive key to be enjoyed by the contemporary reader. As an introduction, however, this Perspectives article briefly reviews the state of the art at the time of their appearance, their main findings, and their influence on three decades of subsequent investigations.

The 1960s brought important advances in the understanding of the computations performed by the retina. An influential view emerged that described retinal ganglion cells as linear filters, i.e. as processes that compute a weighted sum of the intensities in the stimulus, with weights given by the receptive field (Enroth-Cugell & Robson, 1966). This simple ‘linear model’ applied to the majority of ganglion cells in the cat retina (those of the X type, corresponding to P cells in primates). It was quite powerful, as it promised to predict the responses of X ganglion cells to arbitrary stimuli, on the basis of the simple knowledge of the receptive field.

This purely linear view was complemented by the discovery that another kind of ganglion cells, those of Y type (which correspond to M cells in primates), perform non-linear operations, suggesting that they sum the distorted output of subunits that in turn have linear receptive fields (Enroth-Cugell & Robson, 1966; Hochstein & Shapley, 1976). This arrangement confers position invariance: for stimuli of high spatial frequency, Y cells respond equally regardless of position within the receptive field.

These advances suggested new ways of looking at simple and complex cells in primary visual cortex. Hubel & Wiesel (1962) had defined simple cells as having distinct antagonistic regions in their receptive fields, and had suggested that knowing those regions, one could predict ‘the responses to any shape of stimulus, stationary or moving’. They had defined complex cells as any cell that was not simple, and had reported that complex cells achieved position invariance within their receptive field: they would respond to a stimulus of the appropriate orientation regardless of position within the receptive field. These attributes of simple and complex cells resembled those of X and Y ganglion cells. Some authors proposed that the correspondence could be anatomical, i.e. that it reflected predominance of X inputs to simple cells and of Y inputs to complex cells (Stone, 1972; Movshon, 1975), a suggestion that was not later confirmed. More generally, however, the linear and non-linear models and the stimulation procedures that had been so useful to analyse X and Y cells (Enroth-Cugell & Robson, 1966; Hochstein & Shapley, 1976) constituted promising starting points for a concise and precise characterization of simple and complex cells.

In addition to the breakthroughs in retinal physiology, another force was pushing towards the use of quantitative engineering techniques in primary visual cortex: such techniques were proving successful to study human perception. In particular, the University of Cambridge – where Movshon, Thompson and Tolhurst operated – was a hotbed of research into the relations between single neuron responses and perceptual phenomena. These phenomena were investigated with rigorous psychophysical measures, and described with quantitative models based on image filtering (Graham, 1989; Wandell, 1995). Much of this research rested on the concept of ‘channels’, which are linear filters. Simple cells in the cortex seemed to be good candidates for such a role. Did they exhibit linear summation? The time had come to apply the power of linear systems analysis and related techniques to primary visual cortex.

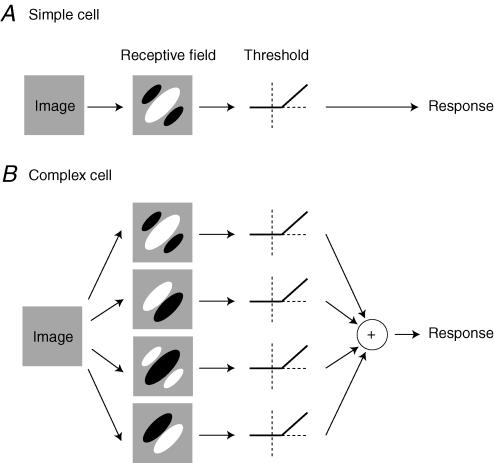
In their first article, Movshon et al. (1978a) applied linear systems analysis to the responses of simple cells. They measured responses of simple cells to gratings and bars, and asked if such responses were consistent with the output of a linear receptive field (Fig. 1A).

Figure 1. The models of simple and complex cells proposed by Movshon, Thompson and Tolhurst (Movshon et al. 1978a,b).

A, linear model of simple cells. The first stage is linear filtering, i. e. aweighted sum of the image intensities, with weights given by the receptive field. The second stage isrectification: only the part of the responses that is larger than a threshold is seen in the firing rate response. B, subunit model of complex cells. The first stage is linear filtering by a number of receptive fields such asthose of simple cells (here we show four of them with spatial phases offset by 90 deg). The subsequent stages involve rectification, and then summation.

Much as Enroth-Cugell & Robson (1966) had done for X retinal cells, they asked if the responses to drifting sinusoidal stimuli were sinusoidal, as one would expect from a linear filter. The results supported this view, provided that the responses were rectified by the spike threshold, which shows only the part of the responses that lie above threshold (Fig. 1A).

The authors then asked how the responses depended on the spatial phase of a standing grating whose contrast oscillated sinusoidally in time. This test had been applied to X and Y retinal cells by Hochstein & Shapley (1976). Here the linear model was put to a quantitative test, and the fit was good, provided again that the output of the receptive field was passed through a rectification stage that thresholded it (Fig. 1A). Movshon, Thompson and Tolhurst were even able to suggest how high the threshold should be relative to rest. They expressed this threshold in the units of firing rate responses, spikes s⁻¹. For example, for the cell in their Fig. 4, the estimated threshold was 8 spikes s⁻¹ (if the receptive field were to output 12 spikes s⁻¹, the neuron would output 4 spikes s⁻¹).

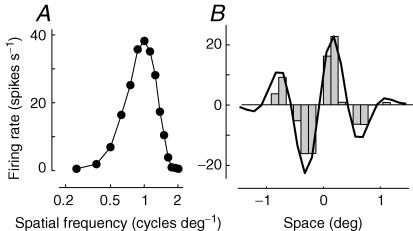
Finally, the authors asked a key question: was the selectivity of simple cells predictable on the basis of the receptive field alone, as had been suggested by Hubel and Wiesel, and as would be expected of a linear filter? To test this hypothesis, they turned again to the approach that had demonstrated the linearity of X retinal cells (Enroth-Cugell & Robson, 1966). First, they measured responses to drifting gratings of various spatial frequencies (Fig. 2A). Then, they measured responses to bars flashed at various positions, thus estimating the profile of the receptive field (Fig. 2B, histograms). According to the linear hypothesis, the first data set could be used to predict the second one. This was indeed the case for the cells (Fig. 2B, curve): just as predicted by the linear model, the selectivity of simple cells for spatial frequency could be predicted on the basis of the receptive field profile.

Figure 2. Linearity of spatial summation in simple cells the experiment in Fig. 9 of the first 1978 article by Movshon, Thompson and Tolhurst (Movshon et al. 1978a).

Responses were simulated from a model simple cell with a linear spatial receptive field that summates strongly distorted thalamic inputs (Carandini et al. 2002). A, spatial frequency tuning of the simple cell. The ordinate marks the amplitude of the sinusoidal modulation caused by drifting sinusoidal gratings, whose spatial frequency is plotted on the abscissa. B, profile of the receptive field of the simple cell. The histogram shows the firing rate elicited by flashing bars in various spatial positions across the receptive field. Negative responses indicate responses elicited when withdrawing the bar. The curve shows the prediction based on linearity, obtained by Fourier transform of the data in A.

For all its success in explaining responses of simple cells, the linear model (Fig. 1A) could not possibly work for complex cells. Complex cells are insensitive to the precise position of a bar within the receptive field, and respond both to the onset and to the offset of the bar. Neither of these properties could arise from a single linear receptive field. Hubel & Wiesel (1962) had therefore described complex cells as summing the output of a number of simple cells with similar orientation preference but different receptive field profiles.

Borrowing from the subunit model proposed for Y ganglion cells by Hochstein & Shapley (1976), such a description could be made quantitative by postulating a number of linear receptive fields orientated in space (subunits), whose outputs are rectified by threshold, and integrated into a single response (Fig. 1B). In their second article, Movshon et al. (1978b) went on to propose such a subunit model for complex cells (Fig. 1B), and to justify each of its components. They started by performing the same three measures that they had performed in simple cells.

First, the authors studied the modulation in firing rate caused by drifting sinusoidal gratings. Complex cells responded phasically only at the lowest spatial frequencies, but as soon as the frequency approached the optimal, the responses became constant in time. This was consistent with a subunit model (Fig. 1B). Each of the subunits would respond with a sinusoid, but the rectified sinusoids would be offset in time, and therefore they would sum to an approximately constant value.

Second, they asked how complex cell responses depended on the spatial phase of a standing grating whose contrast reversed in time. Just as for Y ganglion cells (Hochstein & Shapley, 1976), the cells did not care for spatial phase, giving two responses for each cycle of the stimulus (once for each sign of contrast). These results again were consistent with the subunit model (Fig. 1B): each subunit would give positive responses only once in each cycle, and only at specific spatial phases, but the sum of the positive subunit responses would rise twice in each cycle, irrespective of spatial phase.

Third, they asked whether the selectivity of complex cells was predictable on the basis of the receptive field alone. The answer was a resounding no: as predicted by the subunit model (Fig. 1B), receptive fields of complex cells don't have strong distinct subregions, so it is not possible to predict their selectivity from a receptive field profile.

While all these results seemed consistent with a subunit model (Fig. 1B), a key attribute of that model remained to be verified: are the receptive fields of the subunits really linear? To test this hypothesis, the authors devised an elegant experiment, in which they measured the interaction of dark and light bars in different positions of the receptive field.

To understand this experiment, consider a simplified model of complex cell that includes only four subunits (Fig. 1B), and imagine placing a bright bar over the central positive region in the receptive field of the first subunit. This subunit will give a strong positive response, and will thus operate well above threshold. Conversely, the third subunit, which has the opposite receptive field, will be strongly suppressed, and will operate much below threshold. The second and fourth subunits, in turn, will barely respond, so they will operate (as normally) slightly below threshold. Adding a second bar to the stimulus therefore will mostly reveal the receptive field properties of the first subunit. Indeed, as shown in Fig. 8 of the original article, the interaction profiles between bars resemble receptive fields. If these receptive fields of the subunits operate linearly (and if all subunits are similar in spatial frequency preferences), then it should be possible to predict the spatial frequency selectivity of the neuron based on the receptive field profile of the subunits, just as for simple cells (Fig. 2). The results of this experiment, illustrated in Fig. 9 of the original article, confirm this prediction, providing strong support for the subunit model of complex cells (Fig. 1B).

The results of the two articles therefore can be summarized by two models: the linear model of simple cells (Fig. 1A), and the subunit model of complex cells (Fig. 1B). These models share two key attributes: (1) all the image processing is performed by linear filters; (2) the non-linearities operate on the time-varying signals that are output by the filters.

These models have formed the basis for much that has followed in the subsequent three decades. There is obviously no space here to cover this territory, for which we refer the reader to recent reviews (e.g. Carandini et al. 2005). What might be more useful would be to discuss those aspects that, with 100% hindsight, could have been analysed differently, and would arguably have led to slightly different conclusions.

First, when comparing responses to gratings to the profiles of the receptive field (Fig. 2), whether for simple cells or for the subunits of complex cells, a free scaling factor was allowed to obtain a match. Such a scaling factor should not be necessary for the simple models shown in Fig. 1, but it is necessary for actual cells, whose responsiveness depends very much on the local distribution of contrast. To account for this dependence, the models were later extended to include a divisive stage that controls responsiveness on the basis of the distribution of local contrast (for reviews see Heeger, 1992; Carandini et al. 1999).

Second, the authors were perhaps wise to concentrate on one spatial dimension, and thus to avoid the contentious issue of orientation selectivity. Orientation tuning curves were not measured in this study, arguably because rotating the stimulation device involved placing one's hand within centimetres of electrocution, something that was done only reluctantly, once for each cell (J. A. Movshon, personal communication). Had the authors measured 2-dimensional receptive field profiles they could have asked whether these profiles predicted orientation selectivity. This issue remained open for decades and is not entirely closed to this date (reviewed by Ferster & Miller, 2000).

Finally, perhaps the greatest limitation of these studies is that they concentrated on the spatial domain, and did not test linearity in the temporal domain. On the one hand, as was shown in the subsequent decades, the concept of spatial receptive field can be fruitfully extended to 3-dimensional space–time, to account for phenomena of direction selectivity (in fact, the nascent signs of such an extension can be seen already in the second 1978 article). On the other hand, as demonstrated later by Tolhurst et al. (1980), in primary visual cortex temporal summation is far from linear: responses are much more transient than would be expected from the frequency selectivity curves. This non-linearity is puzzling: how could a receptive field be spatially linear and temporally non-linear?

It is now thought that because a cortical cell sums inputs from a variety of spatially displaced thalamic neurons, even if the individual inputs are grossly distorted by saturating and threshold non-linearities, the overall spatial summation properties of the neuron will remain approximately linear (Carandini et al. 2002; Priebe & Ferster, 2006). Indeed, the simulations shown here (Fig. 2) resulted from a model cell that summates such strongly non-linear inputs. This model cell passes the test of spatial linearity devised by the 1978 papers (Fig. 2), yet it would fail any test of temporal linearity.

If it took three decades to obtain this realization, it is possibly because these 1978 papers made such a compelling case for linearity, and the field took them as evidence that every step in the visual system up to the primary visual cortex had to be linear. The reasoning, partly explicit in these papers and implicit in much of the subsequent literature, was that there could be no non-linear stages from the cones to the cortex because those stages would have prevented the cortical cells from passing the linearity tests.

These are modest limitations, and they are evident only with three decades of hindsight. Overall the impact of these papers on the field was forceful and positive. As is evident from glancing at any recent review (e.g. Carandini et al. 2005) much of what was done to this date to explain responses of primary visual cortex, e.g. to explain properties such as orientation selectivity, direction selectivity and binocular integration, rested on the results of these two classical papers. Moreover, these studies succeeded in providing a foundation for the models of pattern perception based on psychophysical channels (Graham, 1989). Our only hope is that similarly powerful quantitative studies will soon appear for areas beyond the primary visual cortex.