Characterization of actomyosin bond properties in intact skeletal muscle by force spectroscopy

Abstract

Force generation and motion in skeletal muscle result from interaction between actin and myosin myofilaments through the cyclical formation and rupture of the actomyosin bonds, the cross-bridges, in the overlap region of the sarcomeres. Actomyosin bond properties were investigated here in single intact muscle fibers by using dynamic force spectroscopy. The force needed to forcibly detach the cross-bridge ensemble in the half-sarcomere (hs) was measured in a range of stretching velocity between 3.4 × 10³ nm·hs⁻¹·s⁻¹ or 3.3 fiber length per second (l₀s⁻¹) and 6.1 × 10⁴ nm·hs⁻¹·s⁻¹ or 50 l₀·s⁻¹ during tetanic force development. The rupture force of the actomyosin bond increased linearly with the logarithm of the loading rate, in agreement with previous experiments on noncovalent single bond and with Bell theory [Bell GI (1978) Science 200:618–627]. The analysis permitted calculation of the actomyosin interaction length, x_β and the dissociation rate constant for zero external load, k₀. Mean x_β was 1.25 nm, a value similar to that reported for single actomyosin bond under rigor condition. Mean k₀ was 20 s⁻¹, a value about twice as great as that reported in the literature for isometric force relaxation in the same type of muscle fibers. These experiments show, for the first time, that force spectroscopy can be used to reveal the properties of the individual cross-bridge in intact skeletal muscle fibers.

Atomic force microscopy (1–4) and force spectroscopy (5, 6) have been used to reveal the properties of the weak noncovalent bond between receptor molecules and their ligands, and in particular dynamic force spectroscopy has been used to define in detail the properties of the single biotin-avidin bond (1–3, 7). As regarding molecular motors, the optical tweezers technique has allowed the investigation of the properties of an individual actomyosin bond and to measure the force and unitary step displacement generated (8–10). The properties of the single actomyosin bond under rigor conditions were also investigated by measuring the dependence of the bond lifetime on the applied load (11). It was found that bond lifetime was strongly reduced when a load was applied to the bond, in good quantitative agreement with the prediction of Bell theory (12). These results on single actomyosin interaction represent a great step forward in our understanding of molecular mechanism of force generation in muscle; however, they were generally obtained under experimental conditions that differ from those encountered by the same motors in native preparation. In living skeletal muscle, myosin heads (the molecular motors) are distributed over the myosin filament in a very regular fashion, and both actin and myosin filaments are arranged in a quasi-crystalline lattice that maintains a precise geometrical relationship between myosin heads (or fraction S1 of myosin molecule) and the active sites regularly distributed along the actin filament (13). This remarkable order is lost when experiments are made on single molecules, and this may affect the bond properties and force developed. In addition, at physiological ionic strength, actin filaments tend to detach from myosin heads, and it is therefore necessary to perform the above experiments at low ionic strength. However, it is known that molecular motor performance strongly depends on ionic strength (14). The force generated is also strongly affected by myosin S1 orientation, which is not easily controlled in single-molecule experiments (14). This means that the force measured by the recording apparatus, usually along the actin filament axis, may not represent accurately the real capability of the motors when working in a regularly ordered array. The same is true in experiments in which an external load is applied to the single bond, because it is usually difficult to establish the orientation of the load with respect to the bond geometry, and this affects the rupture force. These limitations make it important, for studying the mechanism of force generation in muscle, to investigate the actomyosin bond properties under conditions that preserve the original native bond arrangement and environmental conditions. The experiments reported here satisfy this important requirement being performed, with the force spectroscopy technique, on intact muscle fiber working under full physiological conditions.

It has been shown recently by Seifert (15) that the properties of the individual bond, in an ensemble of parallel bonds, can be revealed by analyzing the rupture force of the ensemble under dynamic loading in analogy to dynamic force spectroscopy applied to a single bond. Based on this consideration, we have analyzed the actomyosin interaction in intact active frog muscle fibers by applying stretches at various velocities and measuring the force needed to produce cross-bridge detachment. It was found that cross-bridge rupture force increased linearly with the logarithm of the loading rate, in agreement with the expectation of the Bell theory for single-molecule interaction.

Model

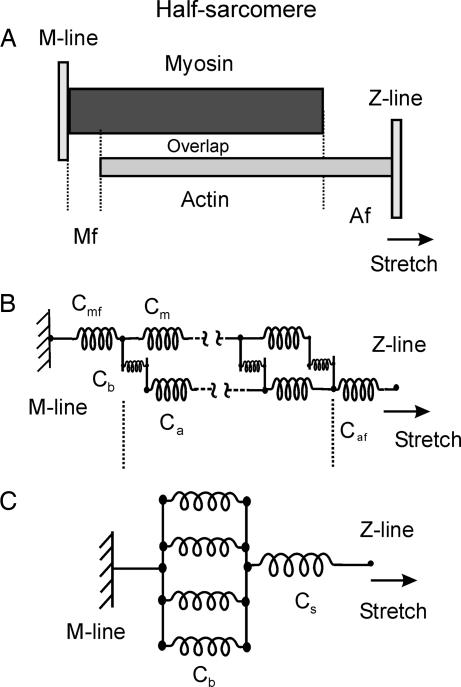
Actin and myosin filament disposition in the half-sarcomere (the functional unit of the striated muscle) of frog muscle fiber at sarcomere length of 2.10 μm is shown in Fig. 1A.

Fig. 1.

Half-sarcomere equivalent models. (A) Arrangement of actin and myosin filament in the half-sarcomere of tibialis anterior frog muscle at 2.10-μm sarcomere length. The actomyosin bonds (cross-bridges) are formed in the central zone where actin and myosin filaments overlap each other. Cross-bridges are mechanically connected to the M-line and Z-line, which delimit the half-sarcomere, through the myosin and actin filaments, respectively. Mf and Af represent the zone of the myosin and actin filament free of cross-bridges, respectively. (B) Distributed model of cross-bridge and myofilament compliances in the half-sarcomere. The model at tetanus plateau includes 45 cross-bridges (C_b compliance) uniformly distributed, 44 actin and myosin segments (C_a and C_m compliances), and the free filament zones with compliances C_mf and C_af. (C) Approximation of the distributed model in B with a lumped model. The series compliance C_s is equal to actin compliance plus myosin compliance. Despite the much simpler structure, the compliance of this model depends on cross-bridge number exactly in the same way as that of the distributed model in B. Only four cross-bridges are shown, for clarity.

The actomyosin bonds, each formed between a myosin head and an actin active site, are uniformly distributed in the central zone where actin and myosin filaments overlap each other. The arrangement of cross-bridge and myofilament compliances in the half-sarcomere is shown in Fig. 1B. To apply Seifert's analysis (15) it is necessary to show that the complex arrangement of Fig. 1B can be reduced to the simple model of Fig. 1C in which an ensemble of parallel bonds is stretched through a series compliance. The response to stretches of the network of Fig. 1B was therefore analyzed as described in Methods. The results showed that cross-bridges are not uniformly strained during a stretch. Nonuniformity, however, was relatively small and decreased with decreasing number of cross-bridges. At plateau of an isometric tetanus, at which the maximum number of heads is attached and the fiber develops the maximum isometric tension (P₀), the difference between minimum and maximum cross-bridge strain was 19.7%. This value decreased to 6.3% at 0.33P₀ while total cross-bridge compliance increased 3 times. Thus, at low isometric tension, at which we made our experiments, cross-bridge strain dispersion is relatively small. Cross-bridges in the half-sarcomere were therefore considered in parallel and in series with myosin and actin filament compliances as in Fig. 1C.

In a model of this kind, stretched at constant velocity v, the time-dependent force F_b acting on the individual bond is

where N is the number of bonds, corresponding to the cross-bridges present in all of the half-sarcomeres in parallel in the whole fiber cross-section. If total cross-bridge compliance, C_b/N is greater than C_s as in our case, the load on the single bond is almost independent of the number of bonds [Seifert's stiff transducer condition (15)] and the rupture force of the cross-bridge ensemble upon stretching, F_t, can be taken as N times the rupture force of the single bond.

Bell's model (12) predicts that loading of a single bond with a force F produces an instantaneous increase of the dissociation rate constant k, according to the equation

where k_B is the Boltzmann constant, T is the absolute temperature, x_β is the bond length or the distance between bound state and transition state, and k₀ is the dissociation rate constant at zero force. For a linear increase of force (constant loading rate) and assuming that bond dissociation is a random process, the most probable rupture force of the bond F* is

where r represents the loading rate of the bond (7, 16). The Bell model thus predicts a linear relationship between the logarithm of loading rate and rupture force of the single bond.

Apart from the scaling factor N, the same kinetics are applicable to the cross-bridge ensemble described above in which F_t = F*N. Eq. 3 was therefore fitted to our data on single fiber to extract the properties of the individual cross-bridge (x_β and k₀).

In the model of Fig. 1C, we approximated all of the sarcomeres in series and in parallel in the selected fiber segment as a single half-sarcomere. This is justified by our previous observations showing very good sarcomere length homogeneity along the fiber (17). In addition, our records (Fig. 2) show that the peak force due to forced cross-bridge detachment is rather sharp, suggesting a good synchronization of the bond rupture. Interestingly, sarcomere length inhomogeneity, accompanying fiber damage, was always associated with a large broadening of the force peak. We also assumed that stretching speed was high enough to avoid cross-bridges cycling during the stretch, and we did not consider the effects of the quick force recovery [caused by the reversal of power stroke and which tends to reduce the speed of the force increase upon stretching (18)]. This is because the reversal of power stroke is assumed to occur without cross-bridge detachment and therefore with no effect on F_t.

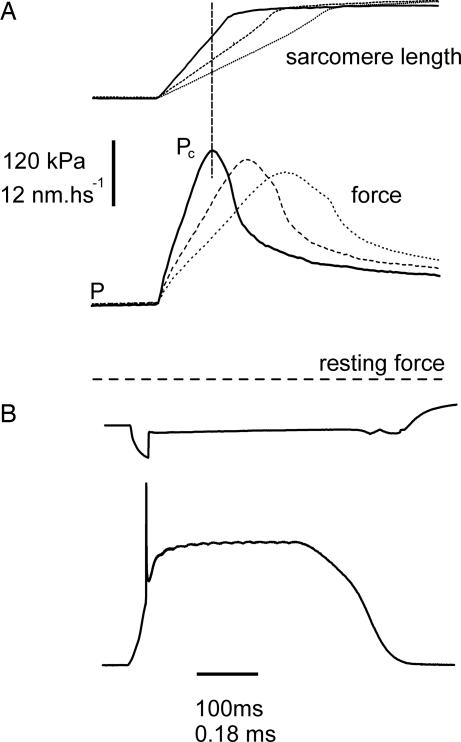
Fig. 2.

Force responses of a single muscle fiber to fast stretches applied during the tetanus rise at a tension P of ≈0.5P₀. (A) Force responses to three stretches at different velocity shown at fast time base. (B) Force response to a single stretch shown at slow time base. Upper traces, sarcomere length; lower traces, force. It can be seen (A) that tension rises almost linearly up to a point at which it stops growing and starts to fall despite continued stretching. Note that tension fall is accelerated after the end of the stretch. This is due to the reversal of power stroke, which releases the tension on the bonds. The intercept of the vertical dashed line with the sarcomere length trace represents the critical length L_c.

Results

Fig. 2 shows the force responses of a single muscle fiber to fast ramp stretches applied on the tetanus rise at tension P of ≈0.5P₀ in an isometric contraction at fast (Fig. 2A) and slow (Fig. 2B) time bases. With the exception of a transient initial fast rise (see Methods), the records in A show that tension rises almost linearly during the stretch reaching a peak P_c and then dropping quickly to a much lower level despite the continuous stretching of the fiber. This means that the fall of force is determined by a sudden increase of fiber compliance due to the forced cross-bridge detachment consequent to loading (19). Therefore, the increment of force upon stretch (P_c − P) represents the total rupture force of the cross-bridge ensemble, F_t.

Tension after the rupture never dropped below the isometric level. This is very likely to be due to the relatively small amplitude of the stretches that were stopped right after the peak force and to cross-bridge reattachment occurring mostly after the end of the stretch with a time constant of ≈11 ms (20). Given the very fast stretches used here, it is unlikely that reattachment could significantly affect the peak force P_c.

Fig. 2A and, in a more complete way, Fig. 3 show that peak incremental force increases with the stretching speed.

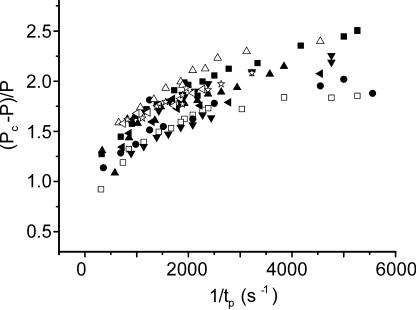
Fig. 3.

Relative force increase upon stretching as a function of reciprocal time to force peak (1/t_p) in 10 fibers. 1/t_p = 4,000 corresponds to a stretching velocity of 5.17 × 10⁴ nm·hs⁻¹·s⁻¹ or 49.2 l₀·s⁻¹. Data were obtained at 0.33P₀ (open symbols) and 0.5P₀ (filled symbols). Different symbols refer to different fibers.

The (P_c − P)/P ratio increased in a nonlinear way as the time to force peak (t_p) was reduced and stretching velocity was correspondingly increased. Note that results at 0.5P₀ and 0.33P₀ do not differ significantly (Fig. 3).

To extract the properties of the individual bond from the data of Fig. 3, it is necessary to know the number N of actin-bound myosin heads at the time of stretch application. This number was calculated for the unitary fiber cross-section by knowing (i) the total number of myosin heads per half-sarcomere (21), (ii) the fraction of them attached (22–24), and (iii) the number of myosin filaments for the unitary cross-section of frog muscle fiber. Assuming 300 myosin heads at tetanus plateau and a fraction of actin-bound of 15%, N was 2.9 × 10¹². At isometric tension of 0.5P₀ and 0.33P₀, at which stretches were applied, N was proportionally reduced. F_t measured at 0.5 and 0.33 P₀ and expressed as force per unit of cross-section was therefore divided by N/2 or N/3, respectively, to find the mean rupture force of the individual bond. This value was successively plotted against the logarithm of the loading rate (rupture force/t_p). The results, reported in Fig. 4, show that in the whole range examined, cross-bridge rupture force increased linearly with the logarithm of loading rate going from 14 pN at 10⁴ pN·s⁻¹ to 22 pN at 10⁵ pN·s⁻¹.

Fig. 4.

Cross-bridge rupture force as a function of the loading rate. Shown are pooled data from 10 experiments (same fibers of Fig. 3) separated in six groups and plotted as mean values ± SEM. The continuous line represents the best fitting of the data.

The mean isometric force developed by the single head, calculated from the ratio of specific force/number of attached heads, was 10.8 pN, a value similar to other reports (24, 25).

Eq. 3 makes it possible to calculate the length of the actomyosin bond x_β (distance from bound position to transition state) from the slope of the straight line fitted to the experimental data in Fig. 4. Once x_β is known, the mean cross-bridge dissociation rate at zero external load k₀ can be calculated from the extrapolated intercept to zero force. The analysis gave mean values of 1.25 ± 0.44 nm for x_β and 33.57 ± 2.84 s⁻¹ for k₀.

For our calculations, we assumed that breaking of a bond in the model of Fig. 1C does not alter the load on the other bonds (15). According to Eq. 1 this condition is strictly valid only when C_b/N ≫ C_s, whereas in our case, C_b/N is 2 (at 0.5P₀) or 3 (at 0.33P₀) times greater than C_s. However, the error associated with this approximation is very likely negligible, as suggested by the results of Fig. 3 showing that data at 0.5P₀ and at 0.33P₀ do not differ significantly despite their different approximation error.

k₀ obtained from Eq. 3 is correct only when considering the most probable bond rupture forces and not the mean rupture forces as in our case. This may lead to an overestimation of k₀ due to the non-Gaussian theoretical distribution of the rupture forces of the single molecule. For high load rates as in our case, k₀ may be overestimated by a factor of ≈1.7 (26). Applying this correction to our result reduces k₀ to 19.74 ± 1.67 s⁻¹.

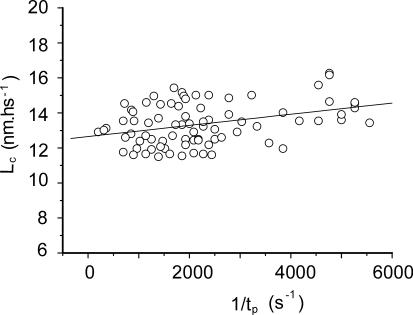
The sarcomere elongation needed to break the cross-bridges (critical length, L_C) was measured at various stretching speeds on the same fibers of Fig. 3, and the results are shown in Fig. 5. It can be seen that L_C increased slightly with stretching velocity. This is due to the increased rupture force, which requires the application of a greater elongation to reach it. Mean L_C was 13.37 ± 0.13 nm·hs⁻¹ (where hs is half-sarcomere).

Fig. 5.

Dependence of L_c from 1/t_p for the same fibers of Fig. 3. The continuous line represents the best fitting of the experimental data. Because L_c was insensitive to the force at which the stretch was applied, data at 0.5P₀ and 0.33P₀ are plotted together with the same symbol.

Only a small fraction of this elongation is absorbed by the actomyosin bond; most of it is absorbed by the filament series elasticity and by the elasticity located in S1 (mainly in the lever arm domain). It is important to note that adding a compliance in series with the bond makes necessary the application of a greater stretch to reach the rupture force (increasing L_C) but does not affect the rupture force itself and therefore has no effect on x_β and k₀.

Discussion

Force response of activated muscles or single muscle fibers to ramp stretches has been extensively studied in the past by a number of authors (27–30), starting from the pioneering experiments of Katz (31). Most of these studies were performed with slow stretching speeds and mainly aimed at investigating the mechanism of the steady force increase occurring during stretching. In this study, we examined the dependence of peak tension on stretching speed systematically by using very high stretching velocities with the aim of deriving the properties of the individual bond. In analogy with previous experiments on dynamic loading of single molecular bond, our data follow the predictions of the Bell theory (12) for the case in which only one energy barrier has to be overcome to break the bond.

Force spectroscopy (5, 6) has been largely used to reveal the properties of the weak noncovalent bond between receptor molecules and their ligands and to define in detail the properties of the individual bimolecular interaction between biotin and avidin (1–3, 7). The interaction of single motor molecules actin and heavy meromyosin or myosin S1, has been investigated under rigor conditions either by studying the relation between loading force and time survival of the bond or by stretching the bond up to the rupture force (11, 32). Calculation based on bond life at various loads gave an interaction distance x_β of ≈2.5 nm, relatively large compared with those found with others bimolecular bonds (5–7) and about twice our value.

With our approach of force spectroscopy, the bond length was calculated from the dependence of cross-bridge rupture force from the loading rate. The mean value of 1.25 ± 0.44 nm we found is significantly larger than that reported for receptor ligand interaction and for antibody–antigen reaction (6). This difference could be due to the different geometry of the bond loading. In our experiments, the load is not applied directly but reaches the bond through the lever arm/converter domain of the myosin head. Recent S1 crystallographic studies (33) suggest that this domain amplifies the very small movement occurring at the active site during the myosin power stroke to a movement of ≈11 nm at the tip of the lever arm along the actin helix. If this mechanism works also in the opposite direction, the rupture force we measured in the fiber, corresponding to the force at the tip of the S1 lever arm, would be much greater at the bond level. Correcting for this amplification would proportionally reduce x_β. An amplification factor of 10, for example, would reduce the bond length to 0.125 nm, similar to single-molecule studies.

Bond length measurements may also be affected by the direction of the applied force compared with the bond geometry. In our experiments, the pulling force was applied along the filament axis in the same direction as the active force developed by the cross-bridges in the muscle fiber. It is not clear, however, through what angle the force is applied to the bond because the lever arm mechanism may also affect the force direction depending on the fulcrum location with respect to the interaction sites.

The relatively great distance of 1.25 nm over which the bond exerts force, due to the lever arm amplifying mechanism, means that the bond appears relatively “compliant,” contributing significantly to the cross-bridge compliance. In particular, because cross-bridges strain at P₀ is ≈2 nm (20), our data show that a significant fraction of cross-bridge compliance may be located in the bond. Such a compliance is consistent with data in literature suggesting that part of working stroke might be caused by a rotation of the motor domain about its contact with actin (34–36).

The detachment rate constant k₀ resulting from our data were 19.74 ± 1.67 s⁻¹. This value refers to unbinding of the strongly bound AM.ADP cross-bridge state that is mostly populated during isometric contraction and forcibly detached by the stretch. Data obtained from force relaxation rate measurements on calcium-activated frog myofibrils and caged-calcium photolysis in skinned fibers from toadfish (37, 38) indicate a detachment rate constant of 8–10 s⁻¹ compared with our value of ≈20 s⁻¹. The reason for this discrepancy is not clear. It is unlikely that the approximations described in Results could be great enough to justify the discrepancy above. Our higher value of k₀ suggests that the cross-bridge detachment rate may not be the rate limiting factor of muscle force relaxation in isometric contractions.

In conclusion, our findings show that force spectroscopy can be successfully applied to the ensemble of cross-bridges present in the half-sarcomere of a skeletal muscle fiber during contraction. In contrast to single-molecule experiments, this procedure allowed us to determine the actomyosin interaction distance and the cross-bridge dissociation rate in muscle in vivo in which physiological environmental conditions and myofilament lattice structure are preserved. Together with single-molecular techniques, this approach can greatly enhance our understanding of the molecular mechanism of force generation in muscle.

Methods

Frogs (Rana esculenta) were killed by decapitation followed by destruction of the spinal cord, according to the procedure suggested by our local ethics committee. Single intact fibers, dissected from the tibialis anterior muscle (4–6 mm long, 60–120 μm in diameter) were mounted by means of aluminum foil clips (18) between the lever arms of a force transducer (natural frequency of 40–60 kHz) and a fast electromagnetic motor (minimum stretch time of 100 μs) in a thermostatically controlled chamber provided with a glass floor for both ordinary and laser light illumination. Stimuli of alternate polarity, 0.5 ms in duration and 1.5 times the threshold strength, were applied transversely to the fiber by means of platinum-plate electrodes, at the minimum frequency necessary to obtain fused tetanic contractions. Sarcomere length was measured by using the striation follower device (39) in a fiber segment (1.2–2.5 mm long) selected for striation uniformity in a region as close as possible to the force transducer. This eliminated the effect of tendon compliance and reduced the effects of mechanical wave propagation on the sarcomere length measurements. Fast ramp shaped stretches (duration between 0.2 and 4 ms, and 16–25 nm·hs⁻¹ amplitude) were applied to one end of the activated fiber while force response was measured at the other end. Because fibers developing maximum tetanic tension were easily damaged by fast stretches, we performed our experiments on the tetanus rise at a tension level of ≈0.5P₀ or 0.33P₀, at which fiber damage was very much reduced. Lowering the tension was also important to reducing cross-bridge strain nonuniformity. Usually, >50 normal contractions could be obtained before the appearance of any sign of fiber damage. Experiments were performed at 14°C at a resting sarcomere length of ≈2.1 μm, so that no change in effective overlap between myofilaments occurred during the stretch.

The linear phase of force increase during the stretch was usually preceded by a small and faster force rise (lasting <0.1 ms) occurring at the start of the stretch, whose amplitude was roughly proportional to the stretching speed. This phase probably arises from the passive properties of the activated fiber such as inertia or viscosity (40), and for this reasons the peak force was corrected for it. To do so, the slower linear part of the force rise was extrapolated back to the starting time of the stretch, and the intercept on the ordinate was considered zero tension. At low stretching speed, the correction was almost negligible, but as the speed increased, the initial fast phase became more and more important, and this effect limited the minimum stretch duration to ≈0.2 ms. Maximum stretch duration was not >4 ms to reduce cross-bridge cycling during the stretch to a negligible level. Stretching velocities ranged from 6.1 × 10⁴ nm·hs⁻¹·s⁻¹ to 3.4 × 10³ nm·hs⁻¹·s⁻¹. Peak force was also corrected for the very small force increase occurring during the stretch due to the rising tetanic force. Passive force response was negligible, and no correction was made for it. Ringer solution had the following composition: 115 mM NaCl/2.5 mM KCl/1.8 mM CaCl₂/0.85 mM NaH₂PO₄/2.15 mM Na₂HPO₄. Force, fiber length, and sarcomere length signals were measured with 5-μs resolution with a digital oscilloscope (Nicolet 4094) and transferred to a personal computer for further analysis.

The equivalence of the distributed model of Fig. 1B, with the lumped model of Fig. 1C, was evaluated by analyzing the response of the distributed model with the method described by Forcinito (41). For calculation, the following values were used for the half-sarcomere: length of overlap region, 695 nm; free actin length, 250 nm; myosin bare zone length, 80 nm; Z-line, 25 nm. We assumed that at tetanus plateau, the average number of myosin heads bound to actin (n) in the half-sarcomere was 45, corresponding to 15% of the 300 heads present (22–24). Myosin heads were assumed to be homogeneously distributed along the overlap region so that they delimit 44 actin and myosin filament segments 15.8 nm long whose compliances are indicated as C_a and C_m, respectively (Fig. 1B). Because in skeletal muscle for each myosin filament there are two actin filaments, C_a corresponds to the compliance of two parallel actin filaments. For simplicity, it was assumed that C_m = C_a; however, calculations showed that cross-bridge strain nonuniformity was unaffected by the C_m/C_a ratio. C_mf and C_af represent the compliances of myosin and actin zone free of cross-bridges, respectively, and C_b is the individual cross-bridges compliance. On the bases of the filament free zone lengths, it was calculated that C_af = 16 C_a and C_mf = 5 C_m. The ratio C_b/C_a = 2,200 was selected so that at tetanus plateau cross-bridge compliance, C_b/N, was equal to filament compliances (42, 43).

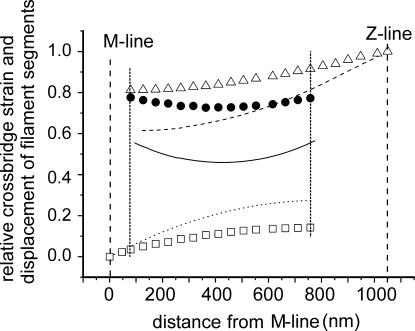
Fig. 6 shows the distribution of the stretch applied to the Z-line among filaments and cross-bridges. With n = 45, corresponding to tetanus plateau, the mean cross-bridge strain was 49.3% of that applied to the Z-line. Cross-bridges were not uniformly strained; however, the difference between maximum and minimum strain is only 19.7%. The maximum strain (and stress) occurs at the extremities of the overlap zone and decreases progressively toward the center. Because the tension developed during the tetanus rise is directly proportional to the number of attached cross-bridges (19) at 0.5 and 0.33 P₀ at which our experiments were performed, cross-bridge number was reduced to 1/2 or 1/3 compared with plateau. This was simulated in the model by assuming that only one cross-bridge every two or three is attached and maintaining the uniform distribution along the myofilaments. At 0.33P₀ the mean fraction of length change absorbed by cross-bridges raised to 74.9%, which means that cross-bridge compliance was 3 times the filament compliance. The difference between maximum and minimum cross-bridge strain decreased to only 6.3%. These results justify the approximation of the distributed model of Fig. 1B to the simple model of Fig. 1C on which Seifert's analysis can be applied.

Fig. 6.

Relative displacement of myosin (squares) and actin (triangles) filament segments and cross-bridge strain distribution (circles) at tension of 0.33P₀ (n = 15) after a length change applied to the Z-line. The same data at P₀ (n = 45) are shown as a dotted line (myosin), a dashed line (actin), and a continuous line (cross-bridge strain). The two vertical dotted lines delimit the overlap region. Note that nonuniformity of cross-bridge and myofilament strain decreases by lowering the number of cross-bridges.