Extreme accumulation of nucleotides in simulated hydrothermal pore systems

Abstract

We simulate molecular transport in elongated hydrothermal pore systems influenced by a thermal gradient. We find extreme accumulation of molecules in a wide variety of plugged pores. The mechanism is able to provide highly concentrated single nucleotides, suitable for operations of an RNA world at the origin of life. It is driven solely by the thermal gradient across a pore. On the one hand, the fluid is shuttled by thermal convection along the pore, whereas on the other hand, the molecules drift across the pore, driven by thermodiffusion. As a result, millimeter-sized pores accumulate even single nucleotides more than 10⁸-fold into micrometer-sized regions. The enhanced concentration of molecules is found in the bulk water near the closed bottom end of the pore. Because the accumulation depends exponentially on the pore length and temperature difference, it is considerably robust with respect to changes in the cleft geometry and the molecular dimensions. Whereas thin pores can concentrate only long polynucleotides, thicker pores accumulate short and long polynucleotides equally well and allow various molecular compositions. This setting also provides a temperature oscillation, shown previously to exponentially replicate DNA in the protein-assisted PCR. Our results indicate that, for life to evolve, complicated active membrane transport is not required for the initial steps. We find that interlinked mineral pores in a thermal gradient provide a compelling high-concentration starting point for the molecular evolution of life.

Starting with Miller and Urey (1), a wide range of studies on the origin of life discuss the chemical synthesis of protobiomolecules (2–4). Concurrently, the studies of replication systems (5–8) culminated in the RNA-world proposal (9). All these approaches require fairly high concentrations of small proto-biotic molecules, whereas geochemical extrapolations indicate a dilute prebiotic ocean with concentrations comparable to contemporary values (10, 11). This discrepancy has been termed the concentration problem of the origin of life (10, 12). In the following, we describe a robust and efficient solution to the concentration problem, based on heat currents in porous mineral precipitates comprising a hydrothermal mound developed over a moderately warm submarine spring.

Living cells are crowded with small molecules which are accumulated as a result of highly evolved active transport mechanisms across the cell membrane (13). A comparably effective transport mechanism is required to solve the concentration problem of the origin of life. However, to accumulate molecules from a highly diluted prebiotic ocean (10, 11), a considerable entropic gap has to be bridged. In a rough estimate, at least a 10⁶-fold accumulation is required for small protobiomolecules to interact. To fulfill the second law of thermodynamics, such states of exceedingly low entropies can only be siphoned from a larger nonequilibrium system. Contemporary life sustains the required high molecular concentration in a dissipative nonequilibrium state by a wide range of highly evolved strategies. For the evolution of life, an already existing protobiological dissipative environment is required (14). The most compelling would refer to an accumulation of molecules into preexisting abundant compartments of cellular dimensions (15). Both requirements are fulfilled by the accumulation mechanism we propose here.

Hydrothermal Setting

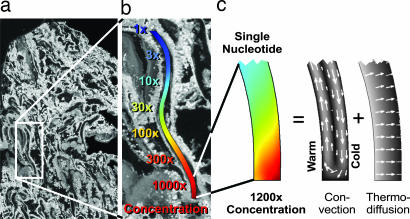
From a geological point of view, thermal gradients are the most abundant dissipative systems on the early earth. They drive convective water flow with a wide variety of geometries. Contemporary hydrothermal vents, both black smokers and “Lost City” type vents, are only extreme cases for heat dissipation. Hydrothermal vents are surrounded by highly porous mineral precipitates. Within these structures, we consider the ubiquitous millimeter to micrometer sized pores and syneresis cracks (Fig. 1a). A temperature gradient, typically along the horizontal direction, exists across such pore systems. We show that these natural settings can easily accumulate single nucleotides >10⁸-fold at the bottom of a plugged pore system. Thus, this accumulation is sufficient to step up from the dilute hydrothermal solution to molar concentrations within the pore.

Fig. 1.

Heat-driven molecular accumulation in hydrothermal pores. (a) Section through aragonite (CaCO₃) from the submarine hydrothermal vent field at Lost City (kindly provided by D. Kelley; ref. 20). (b) Simulation of a part of the pore system. If subjected to a horizontal thermal gradient of 30 K, a 1,200-fold accumulation of single nucleotides is expected (logarithmic concentration color scale). A concatenation of three of these pore sections leads to a 10⁹-fold accumulation. (c) The mechanism of accumulation is driven by heat in a twofold way. Thermal convection shuttles the molecules vertically up and down and thermophoresis pushes the molecules horizontally to the right. The result is a strong molecular accumulation from the top to the bottom (linear concentration color scale).

It is well known that probiotic reactions can be envisaged to foster molecular evolution and favor synthesis over hydrolysis only when concentrations are sufficiently high (16). Submarine hydrothermal environments were previously envisaged as potential sites for the emergence of life, partly because of their contemporary habitability and partly because essential basic materials can be found in such environments (14, 15, 17–20). The concentration mechanism described here considerably strengthens the scenario for a hydrothermal emergence of life.

Robust Exponential Accumulation

The mechanism of accumulation operates as follows. In a hydrothermal vent a plugged pore system is sandwiched between the hot vent interior and the cooling outside ocean (Fig. 1b). A temperature gradient across the pore drives two entangled processes: (i) molecules are shuttled up and down the cleft by laminar thermal convection and (ii) thermophoresis drives the molecules along the temperature gradient, i.e., perpendicular to the convection flow. Both processes are indicated by white arrows in Fig. 1c. In combination, they lead to a strong vertical accumulation toward the closed bottom of the cleft. This geological setting is analogous to a Clusius-tube or thermogravitational column (21). We simulate the behavior of rather rapidly diffusing single nucleotides. Even with conventional biotechnological or microfluidic laboratory methods, such small molecules are hard to concentrate because of their considerable diffusion. The simulation shows a strong 1,200-fold downward accumulation of single nucleotides for the 5 mm short, bent cleft of Fig. 1b. As we will see later, a concatenation of three of these pores leads to a 1,200³ = 1.7 × 10⁹-fold accumulation.

We applied a 30 K temperature difference across the pore and found that maximal accumulation occurred in a pore with a cross-section of 145 μm. The diffusion of molecules in the convection flow was calculated by solving the combined Navier–Stokes, diffusion and heat transfer equations using commercial finite element software (Femlab, Comsol). The simulated pores feature a closed bottom and an open top end. The biomolecule concentration was fixed at the top, whereas the bulk fluid was subjected to gravity and restricted by the pore with nonslip boundary conditions. The heat transfer is barely affected by the slow laminar convection, and the temperature drops linearly across the pore structure.

Previously, we measured the thermophoretic characteristics of nucleotides using microfluidic fluorescence techniques (22). Molecules move along a thermal gradient ∇T with a drift velocity v = −D_T∇T. The ratio between the thermodiffusion coefficient D_T and the mass diffusion coefficent D is termed the Soret coefficient S_T = D_T/D, which typically determines the steady state concentrations. The values for single nucleotides are measured by using the fluorescent molecule 2′,7′-bis(carboxyethyl)-5 (6)-carboxyfluorescein (BCECF) in a 1 mM Tris buffer. BCECF and single nucleotides are of comparable size and charge. We also obtained S_T values for single stranded RNA of 22 bases in sodium chloride-sodium citrate-buffer with a monovalent salt concentration of 1.7 mM as well as double-stranded DNA of 100 and 1,000 bp in 1 mM Tris buffer. All measurements are performed at pH 7.8. In the experiments, the Soret coefficient S_T changes only by a factor of about three when the concentration of monovalent salt is increased from 1.7 to 170 mM. The Soret coefficient of a single nucleotide is comparable to the considerably larger single-stranded RNA of 22 bases. This is typical for thermodiffusion of charged particles smaller than the debye length and is due to reduced ionic shielding (22). Notably, single stranded RNA with 22 bases shows an ≈3-fold smaller thermodiffusion than single-stranded DNA of the same length. The experimental results are presented in Table 1.

Table 1.

Soret coefficient (S_T) and diffusion coefficient (D) for different molecules

Coefficient	Single nucleotide	ssRNA, 22 bases	ssDNA, 22 bases	dsDNA, 100 bp	dsDNA, 1,000 bp
ST 1.7 mM salt, per K	0.015	0.014	0.044	0.075	0.3
ST 170 mM salt, per K	0.006	0.003	0.01	0.019	0.09
D, μm2/s	400	100	115	45	8

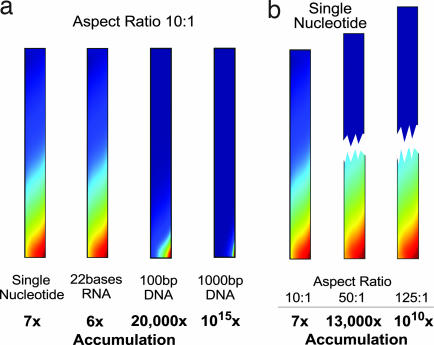
A short pore with an aspect ratio of 10:1 accumulates single nucleotides 7-fold (Fig. 2a). A pore with the same aspect ratio accumulates a 22-bases-long single-stranded RNA to 6-fold, a 100-bases-long double-stranded DNA to 20,000-fold, and a 1,000-bases-long DNA to 10¹⁵-fold levels. For these larger molecules, the short pore behaves like a molecule trap: once molecules enter the top of the pore, they are transported to the pore base and are accumulated to molar-level concentrations in a micrometer-sized spot in bulk water. As a result, the accumulated molecules diffuse freely and would find chemical reaction partners comparable to the situation within prokaryotic cells (13).

Fig. 2.

Predicted effects of the molecule size and pore length on the accumulation level. The simulation results are based on the experimentally measured Soret coefficients and diffusion coefficients for DNA and RNA (see Table 1). (a) The accumulation increases exponentially with the size of the molecule. Whereas single nucleotides are accumulated 7-fold in a short cleft of aspect ratio 10:1, double-stranded DNA comprising 1,000 base pairs accumulates 10¹⁵-fold. The equilibration takes 9 min for single nucleotides and 14 min for single stranded RNA comprising 22 bases. For DNA polynucleotides of 100 and 1,000 bp it takes 18 or 33 min, respectively. (b) Elongation of the cleft exponentially increases the accumulation. For example, the accumulation of single nucleotides is raised to a 10¹⁰-fold level in a pore with an aspect ratio of 125:1. A linear concentration scale is used in both plots, scaled to the respective maximal concentration. The time to reach steady state is 9 min for r = 10, 4 h for r = 50 and 23 h for r = 125.

Pertinent to our argument is the fact that accumulation grows exponentially both with the size of the molecule and the length of a concatenated pore system. In concatenated pores accumulation of molecules increases exponentially, a result of the considerable concentration independence of thermophoresis below molar concentrations (23–25). Thus, although single nucleotides accumulate merely 7-fold in the short pore of Fig. 2a, concatenating 12 of these pores using a wide variety of orientation angles exponentiate the accumulation to an extreme 7¹² = 10¹⁰-fold level. Elongation of the pore has exactly the same effect. As shown in Fig. 2b, a pore system with a total aspect ratio of r = 125:1 accumulates single nucleotides 10¹⁰-fold. Notably, the length of this pore system is only 18 mm, below the typical lengths of pore systems in hydrothermal settings. A compilation of the simulated accumulation values is given in Table 2.

Table 2.

Predicted accumulation depends on the type of molecule and pore aspect ratio

Aspect ratio	Single nucleotide	ssRNA 22 bases	dsDNA
			100 bp	1,000 bp
10:1	7	6	2 × 104	1015
25:1	120	89	1010	(1037)
50:1	13,000	8,000	(1021)	(1075)
125:1	1010	6 × 109	(1052)	(10187)

Accumulation levels that cannot be reached because of steric hindrance are denoted in brackets.

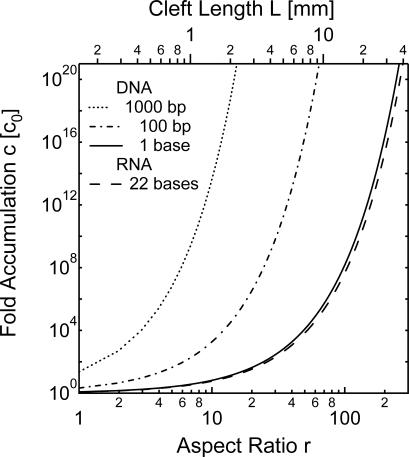
The analytical solution for the accumulation in a rectangular cleft geometry confirms the above numerical findings. The analytical theory (26, 27) was originally developed for gas separation columns (21). The accumulation is found to be an exponential function given by

with the Soret coefficient S_T, the temperature difference ΔT and the aspect ratio r. For 0.42 × S_T × ΔT × r ≫ 1, the molecular accumulation is large and rises exponentially with temperature difference ΔT or pore length. In pores with a sufficient aspect ratio r, substantial accumulation is reached even for small molecules with tiny Soret coefficients (Table 1). The exponential characteristic of Eq. 1 makes the accumulation robust because a small elongation of the pore leads to a large increase in molecular accumulation. Every linear decrease in the temperature difference ΔT can be compensated by a linear increase in pore aspect ratio r. For example, to achieve the same accumulation at just one tenth of the temperature difference, a 10-fold longer pore is needed. To illustrate this the accumulation versus the aspect ratio, r is plotted in Fig. 3 for single nucleotides, polynucleotides of 22 single stranded RNA bases, and double-stranded DNA comprising 100 and 1,000 base pairs.

Fig. 3.

Exponential accumulation. The accumulation depends exponentially on the aspect ratio r and the temperature difference ΔT, according to the analytical theory (Eq. 1). Even for single nucleotides, it is remarkably easy to reach exceedingly large molecular accumulations. The accumulation is calculated for ΔT = 30 K.

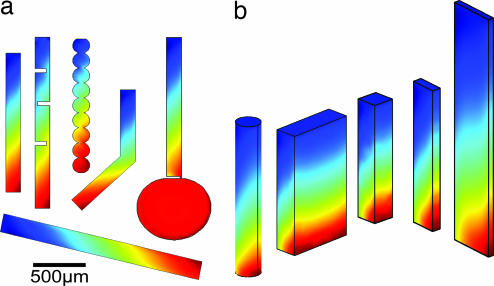
The accumulation is highly robust with respect to the changes in the geometry of the pore. Fig. 4a shows various geometries that yield equal accumulations. We start with a rectangular pore with an aspect ratio of r = 10:1. The accumulation remains at the same level even if the pore is heavily dented, bent, incised, opened toward a bottom molecule repository, or strongly inclined. This insensitivity to geometric variation has two main reasons. First, mass diffusion bridges regions with inferior accumulation. This diffusion between the pores does not require any special geometries between the pore sections. Second, the slowing down of convection resulting from a tilt of the pore section can be easily compensated by a small increase in the pore width, because of the exponent 1/3 in Eq. 2. For example, a tilt from 90° (vertical) to 1° (basically horizontal) enlarges the optimal cleft width only by a factor of four. Therefore, a wide variety of pore systems accumulate molecules with equal efficiency.

Fig. 4.

Robustness of the accumulation. (a) Equally efficient accumulation is found for a large variety of geometries. Regions of reduced accumulation are bridged vertically by mass diffusion. Strongly inclined pores accumulate molecules equally well. A linear concentration scale is used in both plots. (b) Likewise, a wide range of pore cross-sections yields identical accumulations. As for two dimensional clefts, optimal accumulation is achieved if the convection speed balances the diffusion time across the pore.

So far, we have discussed only two-dimensional pores with cleft-like geometries. We simulated the cross-section and assumed that the pore extends considerably further into the third dimension. However, equal accumulation is also found for pores with only limited extension in the third dimension. Fig. 4b shows results for various pore cross-sections with comparable accumulation levels. Also, molecular accumulation is not seen to be significantly lowered over a variety of depths. As noted before, all of the geometries shown in Fig. 4 can be concatenated ad libitum, yielding a wide range of pore system geometries that are capable of an efficient molecular accumulation.

A critical parameter is the width of the pore. For an extended rectangular cleft (26, 27), the largest accumulation is found for an optimal width d₀ given by

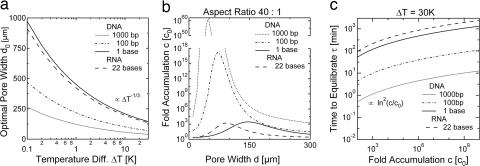
with the viscosity of the fluid μ, the diffusion coefficient of the molecule D, the fluid volume expansion coefficient α, the fluid density ρ, the gravitational acceleration g₀, the inclination angle θ to the horizontal plane, and the temperature difference ΔT. As the result of the exponent 1/3 in Eq. 2, values for d₀ fall between 40 and 400 μm for an extensive range of parameters D, θ, and ΔT, as shown in Fig. 5a.

Fig. 5.

Pore width and equilibration time. (a) The optimal cleft width depends moderately on the molecular size and temperature difference. The optimal cleft width is proportional to D^1/3 and ΔT^−1/3 with the diffusion coefficient D and temperature difference ΔT. As a result, much longer nucleotides require only slightly narrower pores. (b) Accumulation drops considerably for pores with a nonoptimal width. Nucleotides are selectively accumulated in particularly narrow chambers. For a wider pore width d ≈ 150 μm, the accumulation of molecules with different sizes reaches comparable levels. (c) The equilibration toward a 10⁸-fold accumulation takes 14 h for single nucleotides and 25 h for single-stranded RNA comprising 22 bases. For DNA polynucleotides of 100 and 1,000 bp. it takes 70 or 8 min, respectively. This might be counterintuitive, but larger molecules accumulate faster because a considerably shorter cleft is sufficient to achieve the same level of accumulation.

Fig. 5b illustrates the pore size dependence of the accumulation in more detail. DNA molecules of different length are selectively partitioned depending on the pore width. For an equivalent value of ΔT (30 K), single nucleotides accumulate best for a pore width of 145 μm, whereas a 1,000-bp DNA fragment accumulates best for a width of 40 μm. Therefore, the geometry determines the size of the preferentially accumulated molecules. On the other hand, the accumulation of longer polynucleotides is much more efficient, and pore widths ≈150 μm accumulate a wide range of different DNA lengths equally well. Monomers and polymers accumulate to similar levels under all these various pore conditions (Fig. 5b).

The time τ to reach a steady state concentration profile is given by the diffusion time along the pore

As a result, a 10⁸-fold accumulation of single nucleotides is achieved after τ = 14 h, and for a 22-base single-stranded RNA, a 10⁸-fold accumulation is achieved after τ = 25 h. However, the time to reach a comparable accumulation for larger molecules drops to 70 min for 100-bp DNA and 8 min for 1,000-bp DNA (Fig. 5c), the reason being the much shorter cleft length required for longer DNA.

Notably, all these times are extremely short compared with the lifetime of a typical vent chimney, or even the Lost City vent system, which operates at least for 30,000 years (20, 28).

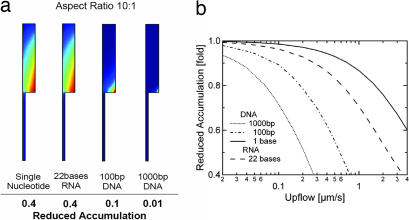
We also tested the robustness of accumulation against diffusive leakage from the pore. In general, a leak of molecules into an attached closed pore space does not inhibit accumulation. An example is shown in Fig. 4a, where a large extension is filled to the same high concentration at the pore base. Only the equilibration time slightly increases as a result of such an extension of the pore. However, leaks into permeable chambers can reduce the accumulation, depending on the concentration gradient ∇c and the resulting diffusive molecular flux, j = −D∇c. The distance between the leak and the surrounding background concentration c = 1 is crucial. This distance is expected to be relatively large for a hydrothermal mound. To characterize the effects of diffusive leaks, we simulated a worst case scenario. A wide diffusive leak is placed at the base of a pore and is connected to the outside over a distance of the pore length itself (Fig. 6a). Otherwise the same geometrical condition as illustrated in Fig. 2 a is used, namely an aspect ratio of r = 10:1 with an optimal width d₀. Thus, we effectively simulate a tube which is open to both sides. Compared with a nonleaking pore, the resulting accumulation is reduced from 7 to 3 for single nucleotides, from 6 to 2.6 for single-stranded RNA, from 20,000 to 2,000 for 100-bp DNA and from 10¹⁵ to 10¹³ for 1,000-bp DNA. These reductions in accumulation that stem from leakage are quite easily compensated for by extending the length of the pore. We conclude that, even if the pore leaks through diffusion, accumulation is maintained at a high level.

Fig. 6.

Reduction of the accumulation by diffusive leakage and upflow. (a) A diffusive leak is introduced at the bottom of the pore over 1/5 of the pore width. The numbers beneath indicate the reduction of accumulation relative to the nonleaking pore in Fig. 2a. (b) Upflow is introduced into the cleft shown on the left side. For longer polynucleotides, the accumulation drops considerably faster with increasing upflow. Short molecules are less affected. The drop in accumulation for both diffusive leaks and upflow drift is readily compensated by a slight elongation of the pore.

In addition to diffusion, slow water flow through pore leakages might hinder accumulation. We focus on an upward flow because this direction is most probable in a hydrothermal mound. We use the same geometry as before (see Fig. 6a), but now add an upward flow at the lower end of the leak. This flow is fed with molecules from the outside concentration of c = 1. Obviously, such an upward flow through the pore directly competes with the downward accumulation. The accumulation versus flow rate is plotted in Fig. 6b. For comparison, the typical convection flow inside the pore is on the 1–10 μm/s scale. Fig. 6b shows that the accumulation of single nucleotides is quite robust against the upflow, probably because of the rapid diffusion of these molecules. Slower diffusing molecules are more vulnerable to pore flow drift, as can be seen from Fig. 6b. For a 22-base single-stranded RNA, the accumulation drops by a factor of two for an upflow of ≈2.5 μm/s. For 100-bp DNA and 1,000-bp DNA, accumulation drops by the same factor for an upflow of 0.6 and 0.2 μm/s, respectively. These flow rates are comparable with the thermal convection speed in the pore. Flow rates in pores of hydrothermal mounds are hard to estimate but are probably slower than these values. As expected, strongest accumulation is found in pores that are well sealed at the bottom. According to our assessment, drift and diffusion in microscopic pore systems in hydrothermal precipitates do not, or only weakly, affect the proposed accumulation mechanism.

Discussion

We compare the assumptions on pore geometry with the geological record. As seen from the representative cross-section in Fig. 1a, an aspect ratio between 25 and 50 can be estimated for single elongated pore spaces in the mounds at the Lost City vent site (≈20–100 μm across and ≤1 mm long). Although, at Lost City, pore shapes may be governed by filamentous bacterial growth, chemical garden-like growth with even higher aspect ratios is likely to occur in comparable hydrothermal systems with moderate temperatures. For example, the 500-mm-long hydrothermal pyrite spires from the 352-million-year-old Tynagh zinc-lead sulfide deposit, Ireland, have central cavities that are ≈100 μm in diameter (aspect ratio r ≤ 5,000:1) (ref. 29 and Fig. 3b). Similar structures have been realized in laboratory simulations (30). Thus, the projected extreme accumulation should be easily reached in natural settings. In any case, the accumulation is exponentiated when low aspect ratio clefts are interconnected. Note that pore concatenation is an especially interesting feature from a geological point of view. During hydrothermal dissolution pores enlarge, become more interconnected (i.e., the value of the aspect ratio increases), and can substantially promote the accumulation of molecules. Based on these results, and given the large number of clefts in any one of multitudinous submarine hydrothermal mounds on the early earth (29), the opportunities would have been manifold for a critical accumulation of organic monomers and polymers synthesized in the same milieu.

In the above calculations, we have assumed a temperature difference of ΔT = 30 K. We anticipate that this is a realistic assumption, because temperature gradients are focused inside the clefts due to the considerably lower thermal conductivity of water (0.6 W/mK) as compared with the surrounding rock (>3 W/mK). The thermal conductivity measured for a hydrothermal pyrite–silica precipitate (31) is 14 W/mK, but the isolated pyrite and quartz minerals yield ≈20 W/mK and 3–4 W/mK, respectively, in laboratory tests (32). The resulting enhancement of the temperature gradient in the liquid part of the pores is 5- to 200-fold. Thus, to obtain the temperature difference of 30 K assumed in the above simulations, the required overall temperature gradient is of the order of 1–40 K/mm, well within reported values of ΔT for natural hydrothermal settings. However, focusing of the temperature gradient in the pores is not essential for the accumulation process. For lower thermal gradients, the same accumulation can be achieved if the pore system is elongated linearly for a decreased temperature difference.

The presented accumulation geometry surpasses previous approaches. Experiments with a circular, laser-heated geometry demonstrated that thermal convection could drive the DNA replicating PCR (33). In the same setting, we observed a considerable accumulation of long DNA (34). Although both of those experiments pointed toward the potential for convection to contribute to the emergence of life (35), no accumulation of short molecules was found or theoretically expected. We now know that this was due to the low aspect ratio of the chamber geometry (r ≈ 0.1). The pore geometries studied here, however, demonstrate a strong accumulation of small molecules, such as single nucleotides, in a highly plausible geological setting on the early earth.

As we have seen, large molecules accumulate more efficiently. One may ask whether the strong accumulation of solvated organic molecules would lead to the tarring of the pore. This is not expected because thermophoretic coefficients become small for concentrations in the molar range (23–25). As a result, accumulation will level out at similar concentrations and will not lead to tarring. Also, a closing of the pore by microscopic solid particles is unlikely, based on our recent experimental findings (36). It was shown that, for low aspect ratio chambers (r ≈ 0.1), 2-μm polystyrene spheres became highly concentrated, but still only formed two or three layers of a colloidal crystal. Further accumulation into the volume of the chamber was disrupted by flow interactions of the solid particles with the thermal convection current (36). As a result, convective flow itself is likely to prevent tarring of the pore by larger particles. On the other hand, a minor accumulation of sticky particles at the pore bottom could contribute to the sealing of the leaks (see Fig. 6). Moreover, in this process, any pore shortening would be negligible.

The mechanism provides concentrated molecules in bulk water without requiring molecules to adsorb onto surfaces. Surface-assisted accumulation is often thought to solve the concentration problem, either via drying or specific adsorption. However, biological systems complex enough to evolve a replicating machinery would most likely need to disconnect, at least temporarily, from such restricting adsorbing surfaces (37). During this desorption or wetting process, there is a high risk of losing the replicated molecules into the bulk water (38). In the present scenario, where they would simply be reaccumulated from the pore solution and the catalytic activity of surfaces can be efficiently used. Our approach has the advantage of offering an active concentration mechanism in an already existing, robust enclosure. Because thermophoretic drift is common for molecules, the accumulation scheme applies similarly to nucleic acids, amino acids, and lipids.

The described accumulation in semiclosed microscopic pores has several synergistic advantages that pertain to the molecular evolution of early life. The enclosure of pore space by mineral precipitates frees life from the need to build a semipermeable organic membrane in its very first evolutionary steps. Microbiological evidence indicates that membrane synthesis appears to be a rather late development (15, 18). Moreover, active transport across a membrane to accumulate molecules in a cell is well known to be a highly evolved process, requiring complex proteins to form vesicles and to actively pump molecules across the membrane.

Notably, the mineral pores that we propose as accumulation centers for the emergence of life are presently populated with thermophilic prokaryotes, and it is speculated that these sites could have been inhabited by the last common ancestor and its biochemical precursors (15, 39). Rapid thermal quenching was demonstrated to be able to polymerize both nucleic (40) and amino (16) acids in a setting in which hydrothermal fluids were injected into cooled (4°C) water. The discussed setting of thermal convection provides comparable temperature interfaces, but now within a single pore. Therefore, both the temperature drop and the needed molecule concentration could be found in an enclosure instead of an open flow reactor.

The water inside the pore network is permanently shuttled by laminar thermal convection. Molecules that stochastically escape the accumulation at the bottom of the pore by diffusion are subjected to a rapid periodic temperature variation within a wide range of temperature amplitudes and cycle times inside a single pore. Equally, freshly precipitated mesoscopic mineral grains are subjected to thermal cycling by the convection. Their catalytic surfaces might generate nucleic acid multimers by thermally triggered periodic condensation (4) and unbinding reactions. In this context, we note that, in a comparable thermal convection setting, DNA was shown to replicate exponentially by using the, albeit protein-catalyzed, PCR (33, 41).

In conclusion, we propose a type of mechanism, driven solely by a temperature gradient, which strongly accumulates even small protobiological molecules in semiclosed hydrothermal pore systems. This setting provides a compelling, dissipative microenvironment to promote the first steps in the molecular evolution of life.

Materials and Methods

Combined solutions of the Navier-Stokes equation (velocity u⃗, pressure p, density ρ, viscosity η), molecule diffusion (concentration c, diffusion coefficient D), and heat transfer (temperature T, heat conductivity k) were simulated in two dimensions by a finite element solver (Comsol, Femlab). Cross terms induce the thermal convection with the expansion coefficient α and the gravitational acceleration g₀, trigger thermophoresis with the thermodiffusion coefficient D_T and consider the flow-induced heating with the heat capacity c_P. Boundary conditions were nonslip for u⃗, neutral for c except for fixing the concentration to c = 1 at the top opening of the column and a horizontal temperature difference of ΔT across the cleft. Material parameters were as follows: density of water 1,000 kg/m³, viscosity 0.0012 (N × s)/m², heat capacity 4,200 J/(kg × K), heat conductivity 0.6 W/(m × K), volume expansion 3.2 × 10⁻⁴, cold temperature 293 K, temperature difference 30 K, and gravitational acceleration 9.8 m/s². The temperature dependence of the above parameters is not significant in the simulations. The Femlab simulation files can be obtained from the authors.