Ultrasensitive magnetic biosensor for homogeneous immunoassay

Abstract

A technique is described for specific, sensitive, quantitative, and rapid detection of biological targets by using superparamagnetic nanoparticles and a “microscope” based on a high-transition temperature dc superconducting quantum interference device (SQUID). In this technique, a mylar film to which the targets have been bound is placed on the microscope. The film, at room temperature and atmospheric pressure, is typically 40 μm from the SQUID, which is at 77 K in a vacuum. A suspension of magnetic nanoparticles carrying antibodies directed against the target is added to the mixture in the well, and 1-s pulses of magnetic field are applied parallel to the SQUID. In the presence of this aligning field the nanoparticles develop a net magnetization, which relaxes when the field is turned off. Unbound nanoparticles relax rapidly by Brownian rotation and contribute no measurable signal. Nanoparticles that are bound to the target on the film are immobilized and undergo Néel relaxation, producing a slowly decaying magnetic flux, which is detected by the SQUID. The ability to distinguish between bound and unbound labels allows one to run homogeneous assays, which do not require separation and removal of unbound magnetic particles. The technique has been demonstrated with a model system of liposomes carrying the FLAG epitope. The SQUID microscope requires no more than (5 ± 2) × 10⁴ magnetic nanoparticles to register a reproducible signal.

Magnetic nanoparticles are a powerful and versatile diagnostic tool in biology and medicine. Bound to a suitable antibody, they are used to label specific molecules, structures, or microorganisms (1). Established techniques such as magnetic cell separation use magnetic field gradients to manipulate and isolate magnetically labeled cells (2). More recently, magnetic immunoassay techniques have been developed in which the magnetic field generated by the magnetically labeled targets is detected directly with a sensitive magnetometer (3, 4).

Weitschies et al. (3) have proposed a novel magnetic relaxation/remanence immunoassay (MARIA) using a superconducting quantum interference device (SQUID) (5) as a magnetic field sensor. In this technique, an immobilized target is immersed in a suspension of superparamagnetic nanoparticles bound to antibodies specific to that target. A pulsed external magnetic field is applied to align the dipole moments of the particles. The SQUID detects the magnetic field from the particles bound to the target. In the current work, we present a more sensitive realization of this technique using a high-transition temperature (T_c) “SQUID microscope” (6).

The basis for the assay is the nature of the relaxation of the particles after magnetization. In contrast to ferromagnetic or ferrimagnetic particles, superparamagnetic particles do not possess a permanent magnetic dipole moment. Rather, their dipole moments may spontaneously rotate toward an “easy direction” via Néel relaxation. The anisotropy energy barrier of the particle, E, which is proportional to its volume, inhibits the dipole moment from rotating but may be overcome with sufficient thermal energy k_BT (T is the temperature and k_B is Boltzmann's constant). Thus, Néel relaxation occurs on a time scale τ_N = 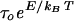, which depends exponentially on the particle volume (7). In addition to Néel relaxation, nanoparticles in suspension undergo Brownian rotation, which randomizes the orientation of the dipole moments. These fluctuations occur on a time scale τ_B, which depends linearly on the particle volume (8). By choosing suitably sized nanoparticles, one may achieve τ_N ≫ τ_B; for example, for an ideal single-domain, 20-nm magnetite particle τ_N ∼1 s and τ_B ∼1 μs. The effective relaxation process is the faster of the two. As a result, when the field is turned off, the free magnetic labels randomize by Brownian rotation in a few microseconds—a time scale shorter than the response time of the SQUID electronics—and they are not observed. In contrast, bound labels cannot rotate and thus relax slowly by the Néel mechanism, producing a measurable field for a period of several seconds. As a result, the SQUID detects the decaying magnetic field produced only by the bound superparamagnetic nanoparticles.

Materials and Methods

SQUID Microscope.

The SQUID microscope detects the magnetic flux (product of magnetic field and area) produced by nearby samples. The cooled superconducting device must be thermally isolated from the room-temperature sample, yet, because the magnetic field of a magnetic dipole falls off as 1/r³, the SQUID must be positioned as close to it as possible for maximum sensitivity. In our microscope, the dc SQUID is mounted on the end of a sapphire rod inside a vacuum enclosure and is cooled to 77 K by a liquid nitrogen reservoir (6). The sensor was fabricated from a thin film of the high-T_c superconductor YBa₂Cu₃O_7−x.

Using standard microfabrication techniques, we pattern a well with a silicon nitride base in a silicon chip. This 440 × 440 μm², 3-μm thick window separates the cold SQUID in the vacuum enclosure from the sample at room temperature and pressure (see Fig. 1). A SQUID-to-sample separation as small as 15 μm has been achieved (9). The entire microscope is placed inside three layers of high-permeability material, which screen out environmental magnetic fields. The SQUID has a flux noise of 15 μΦ_o/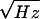 at frequencies down to 1 Hz; Φ_o ≈2 × 10⁻¹⁵ Tm² is the superconducting flux quantum.

Figure 1.

Cross section of the SQUID microscope sample cell (not to scale). The base of the well is a silicon nitride window located above the SQUID sensor (typically ≈40 μm away). A 6-μm thick mylar substrate is cut and placed in the cell, and the suspension of magnetic particles is added. A coil (not shown) applies an aligning magnetic field parallel to the plane of the SQUID. The SQUID is offset laterally to measure the perpendicular component of the field from the nanoparticles as their magnetization rotates. (Inset) Shown is the SQUID geometry viewed from the top; the outer dimension is 370 μm.

In a previous study, we used the SQUID microscope to investigate the dynamics of magnetotactic bacteria, which have a permanent magnetic dipole produced by a chain of single-domain, ferrimagnetic magnetite (Fe₃O₄) nanoparticles (10). Our instrument was able to detect the rotation of a single bacterium, which had a dipole moment of 2 × 10⁻¹⁶ A⋅m². In principle, it is possible to resolve the rotation of a dipole moment of magnitude 10⁻¹⁷ A⋅m², or, equivalently, one single-domain, 35-nm magnetite particle 30 μm away in a 1-Hz bandwidth (11).

This high sensitivity to magnetic dipoles implies that a SQUID should be able to detect a very small number of labeled targets, provided they are sufficiently close. In this paper, we describe the application of our SQUID microscope to the magnetic immunoassay described above.

Antigen and Antibody.

The goal of this study is to develop a sensor for the detection of molecules, structures, and microorganisms. The present investigation involves a model of such a system.

The target consists of a liposome carrying the human CCR5 receptor, which has been altered to carry the FLAG epitope, a unique antigenic surface feature made up of 8 aa. Its use enables us to eliminate cross-reactivity to our controls. Antibodies against this epitope were attached to superparamagnetic particles.

Yeast Strains, Plasmids, and Media.

Saccharomyces cerevisiae strain BJ2168 (MATa prc1–407 prb1–1122 pep4–3 leu2 trp1 ura3–52) into which the CCR5 gene was cloned was used as a source of CCR5-containing membrane fragments (12). The p5 vector carrying the CCR5 gene was constructed by using the progenitor plasmid pNED1 (13). The human CCR5 gene was amplified by using the PCR. The DYKDDDDK (FLAG tag) sequence was introduced at the C terminus of CCR5 for the purpose of serving as the antigenic site. BJ2168 [p5] was grown to A₆₀₀ ≈4 in a tryptophan-deficient synthetic medium at 26°C.

Preparation of Membrane Fragment Containing CCR5.

All steps were carried out at 4°C and all solutions were supplemented with protease inhibitors. Sixty grams of cell paste was resuspended in 50 mM Hepes (pH 7.5), 10% (wt/vol) sucrose, 5 mM EDTA and lysed by using a Braun Scientific (Allentown, PA) glass bead cell homogenizer. Unlysed cells were removed by ultracentrifugation at 750 × g. The membrane fragments containing CCR5 subsequently were collected by ultracentrifugation at 186,000 × g.

Reconstitution of Membrane Fragments Containing CCR5 into Liposomes.

This method is a modified version of the Ste2p reconstitution previously reported (13). Modifications were as follows: N-decyl-β-d-maltoside-solubilized CCR5 membranes were mixed in proportions with 10 ml of Bio-Beads SM-2 (Bio-Rad) at 4°C overnight. The resulting liposomes were collected by ultracentrifugation at 229,000 × g for 2 h. The pellet then was resuspended in 1 ml of 50 mM Hepes (pH 7.5), 150 mM NaCl, and 5 mM EDTA.

Magnetic Nanoparticles.

The superparamagnetic nanoparticles (Quantum Magnetics, Madison, CT) contained two or three 10- to 15-nm magnetite crystals fused together. The vendor specified an average core size of 35 ± 5 nm, as measured by electron microscopy. The nanoparticles were coated with BSA and coupled to the anti-FLAG antibody with a proprietary linker. The average coated particle size, measured with light scattering, was 56 nm. The particles were stored suspended in 10 mM sodium phosphate, pH 7.5 with 5% isopropanol preservative. We estimated the particle concentration to be 40 nM. Over time the particles may settle out or form aggregates, but they are easily redispersed by light sonication or vortexing. Using a low-T_c SQUID susceptometer (Magnetic Property Measurement System by Quantum Design, San Diego), we measured the average dipole moment of the nanoparticles to be m ≈3 × 10⁻¹⁸ A⋅m².

Liposome Detection.

To immobilize the target, we immersed a 6-μm thick mylar film for up to 1 h in a suspension of liposomes with BSA; the BSA blocks nonspecific binding of magnetic particles to the mylar. The most concentrated liposome suspension contained 7.4 mM of lipid. The film was rinsed with a solution of PBS and 0.05% Tween and cut into squares approximately 440 μm on a side. A mylar square was placed in the microscope sample cell flush against the SiN vacuum window (see Fig. 1). The SQUID-to-sample distance was adjusted by 3 micrometers and was typically ≈40 μm, limited by the angular misalignment between the SQUID chip and the SiN window.

Usually, 30 μl of the suspension of antibody-linked magnetic particles was added to the film in the sample cell, of which only ≈1 μl was directly above the SQUID. We allowed up to 2 h to elapse before taking data, to ensure that significant binding occured. In selected experiments, the mylar samples were mixed with the magnetic particles in a separate container before transferring them to the microscope. In this case, we added 30 μl PBS to the mylar in the sample cell to resuspend any unbound nanoparticles.

A coil built into the microscope applied a magnetizing field B_mag = 0.3 mT. The SQUID detects only components of the field perpendicular to its plane. Thus, to minimize the field coupled into the sensor directly from the coil, we applied B_mag in a direction parallel to the plane of the SQUID to within 0.1°. Less than 0.2% of B_mag coupled to the sensor. To maximize the coupling of the SQUID to the field generated by the sample (which is magnetized in-plane), the SQUID was offset laterally by ≈200 μm from the center, to the position where the perpendicular component of the field from the sample is largest (see Fig. 1). The magnetizing field B_mag was pulsed on for 1 s and off for 1 s; data were collected during the latter period. The time for the field to turn off, about 60 μs, was negligible. One hundred averages were typical.

Results

Néel Relaxation Signal.

Fig. 2 shows a typical plot of the magnetic flux measured by the SQUID for the 1-s data collection time interval for different samples. Because large transients generated by switching the field off obscured the relaxation signals during the first 25 ms, this time interval has been excluded. Trace A shows the signal from a substrate coated with liposomes containing the FLAG epitope placed in a 0.4 nM suspension of anti-FLAG labeled nanoparticles. The decaying magnetic flux is generated by the Néel relaxation of the nanoparticles bound to the sample. The large response indicates that a significant number of nanoparticles bind to the sample, as expected from the known, high binding affinity of anti-FLAG antibody to FLAG. On the other hand, if a sample of liposomes containing no FLAG epitopes is placed in the same nanoparticle suspension, only a very small signal is produced, as seen in trace B in Fig. 2 (also in the Inset, offset for clarity). A comparable response is produced by the nanoparticle suspension alone (trace C, almost superimposed over trace B in Fig. 2, and Inset, offset for clarity). We believe these signals are caused by a small fraction of particles binding nonspecifically to the substrate or to the sample cell. Clearly the method can distinguish magnetic labels that are bound from those that are not.

Figure 2.

Néel relaxation. A mylar substrate with liposomes containing the FLAG epitope generates a large relaxation signal (trace A) in the presence of anti-FLAG labeled nanoparticles. Liposomes with no FLAG (trace B), and nanoparticles alone (trace C) generate very little response. A small exponential background decay (trace D) caused by eddy currents in the microscope is present when there is no sample. (Inset) An expanded view of the lower three traces. Fits are in dotted lines. The background decay (trace D) was subtracted from traces A, B, and C before fitting.

The decays in the above traces are not exponential, because the ensemble of magnetic nanoparticles has a wide distribution of particle and core sizes, and the Néel time depends exponentially on the volume. Rather, it can be shown that for small magnetizing fields B_mag ≪ k_BT/m, the flux from the bound magnetic nanoparticles decays logarithmically as Φ(t)∝ln(1 + τ_mag/t) (14), where τ_mag is the magnetization time, here 1 s. The data in Fig. 2 are fitted to

1

with fitting parameters Φ_s and t_o (τ_mag is held constant at 1 s). The quantity Φ_s is the Néel relaxation signal amplitude, and t_o is a time offset, typically ≈ 1 ms. As shown in Fig. 2, the fits (dotted lines) are uniformly excellent.

As shown in trace D in Fig. 2, we detect a small signal even in the absence of liposomes and nanoparticles. The signal is unchanged when we move the cell further away from the SQUID, demonstrating that it is not caused by particles adhering to the SiN window. The decay of the signal is exponential with a time constant of ≈30 ms (Fig. 2 Inset, fit to bottom trace). We believe that this background flux is produced by eddy currents induced in nearby metal objects in the microscope in response to the magnetic pulses. Currently, this background sets our detection limit, because Néel relaxation signals of comparable or lower amplitude cannot be resolved accurately. We conservatively estimate that the smallest amplitude signal we can detect is Φ_s ≈0.2 mΦ_o.

Generally, the noise on the decay curves is determined by the SQUID, and thus is identical to that observed in the absence of a sample and a magnetic field pulse. However, the noise on trace B in Fig. 2 is somewhat higher; it is likely that this increase was caused by magnetic flux trapped in the SQUID.

Dependence of Signal on Nanoparticle and Liposome Concentrations.

Figs. 3 and 4 display the dependence of the signal amplitude, Φ_s in Eq. 1, on the nanoparticle and liposome concentrations, respectively. In both figures, the background contribution in the absence of a sample is subtracted from the data before determining Φ_s. The error bars are determined from the fit to Eq. 1 and do not account for systematic and experimental errors such as sample variability. In Fig. 3, the detection limit of ≈ 0.2 mΦ_o, caused by the background decay, is indicated by the horizontal dotted line. The data point at the lowest concentration is below this line and has a large error because the background has been subtracted from it.

Figure 3.

Φ_s vs. nanoparticle concentration. The amplitude of the Néel relaxation signal is measured as a function of the concentration of nanoparticles in the suspension. The number of liposomes per mylar sample is kept constant. The data are fitted to a line of slope 0.97 ± 0.11. The horizontal dotted line indicates our detection limit.

Figure 4.

Φ_s vs. lipid concentration. Here, the Néel relaxation amplitude is measured as a function of the concentration of the liposome suspension in which the mylar samples are incubated. The concentration of nanoparticles is kept constant. At the highest concentration, the data may be rolling off because of saturation. The line fitted to the data excluding the highest two points has a slope of 0.97 ± 0.09.

To vary the nanoparticle concentration, mylar films with identical liposome densities were prepared. The mylar was incubated for 1 h in a liposome suspension containing 1.5 mM lipid. The films then were soaked for 2 h in suspensions of magnetic nanoparticles diluted to different extents with PBS and 0.05% Tween. As seen in Fig. 3, Φ_s scales approximately linearly with the concentration of suspended particles. This result is expected because the number of particles bound to FLAG should be linear in the particle concentration, so long as the FLAG binding sites are not saturated.

To vary the liposome concentration, mylar films were incubated in various concentrations of liposomes for 1 h, then in the same 0.4 nM suspension of nanoparticles for 2 h. As seen is Fig. 4, Φ_s is approximately linear in the liposome concentration, as expected because the number of FLAG epitopes on the mylar, and hence the number of bound nanoparticles (assuming a sufficient quantity are present) should scale linearly with the liposome concentration. The values of Φ_s for the highest two liposome concentrations may indicate that saturation occurs.

Calibration.

The results thus far have expressed the signal amplitude as magnetic flux. However, the appropriate figure of merit for sensitivity is the number of bound nanoparticles.

The most direct calibration procedure is to count the particles directly by using transmission electron microscopy (TEM). A drop of diluted nanoparticle suspension was placed on a SiO₂-coated Cu TEM grid and allowed to evaporate, depositing particles across the grid. We imaged sections by TEM, counting the number of particles per unit area. Subsequently, several pieces of grid were cut (from the imaged area), and their relaxation signals were measured by the SQUID. This procedure yields a flux of 4 ± 1 nΦ_o per particle, corresponding to a detection limit of (5 ± 2) × 10⁴.

It is instructive to compare this value to that which we expect from theory. An order-of-magnitude estimate for the Néel relaxation amplitude, Φ_s, may be obtained with some theoretical modeling. A detailed analysis yields, for small magnetizing fields (14),

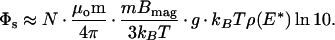2

Here, μ_o is the permeability of free space and N is the number of bound nanoparticles with an average magnetic dipole moment m = 3 × 10⁻¹⁸ A⋅m². The factor mB_mag/3 k_BT arises from the polarization of the dipole moments by the aligning field. For B_mag = 0.3 mT, it is equal to 0.07. The factor of ln10 arises because the data are fitted to a logarithm base 10 rather than a natural logarithm.

The geometrical factor g represents the magnetic coupling between the sample and the SQUID for a given separation, sample size, and sensor geometry. To find g we calculate the magnetic flux through the effective sensing area of the SQUID (0.0163 mm²) from a 440 × 440 μm² sample. The sample is 40 μm away from the SQUID, offset laterally by 200 μm, and magnetized in-plane. We assume the nanoparticles to be distributed uniformly across the substrate and to be sufficiently dilute that magnetic interactions between them are negligible. We calculate g = 2.6 mm⁻¹.

The factor ρ(E*) is the anisotropy energy distribution density for the ensemble of nanoparticles, evaluated at some “mean” anisotropy energy E* (14). Although we cannot know the exact distribution, we know that its integral over energy must be unity, and that the range of energy must be much greater than k_BT. Assuming for simplicity that ρ(E) is constant from the minimum energy E_min = k_BTln(τ_N^min/τ_o) to the maximum energy E_max = k_BTln(τ_N^max/τ_o), we find ρ(E*) = 1/[k_BTln(τ_N^max/τ_N^min)] ∼ 1/10 k_BT for reasonable values of the relaxation times corresponding to our measurement window.

Substituting the above values into Eq. 2, we obtain Φ_s/N ∼ 6 nΦ_o. Thus, our detection limit of 0.2 mΦ_o corresponds to ≈3 × 10⁴ particles, in good agreement with the value from the transmission electron microscopy calibration.

Discussion

We have shown that we can detect magnetic particles selectively bound to a suitably chosen target and that unbound particles contribute little or no signal. The experimentally determined detection limit is currently 5 × 10⁴ magnetic particles. This corresponds to 5 × 10⁴ targets if each is bound to a single magnetic particle, or fewer if multiple particles label each target. For instance, bacteria have thousands to millions of copies of their antigenic sites.

This detection limit is perhaps the best sensitivity yet achieved with this type of magnetic immunoassay. In comparison, similar magnetic immunoassays quote detection limits of more than 10⁶ magnetic labels (3, 4). In addition, the sensitivity and rapidity of the test compare favorably with other, more established methods. The most sensitive enzyme-linked immunosorbent assays (ELISA) are not capable of detecting fewer than 10⁵ labeled antigens.

A substantial advantage of the magnetic relaxation/remanence immunoassay is that it can distinguish between bound and unbound magnetic labels (3). As demonstrated in our experiments, we are able to perform homogeneous assays, in which the labels are left in suspension together with the targets. This method obviates the need for time-consuming wash steps, which are necessary in most other techniques. Furthermore, only extremely small sample volumes are required. Although we used 30 μl of nanoparticles in these experiments, the sample cell is so small that as little as 1 μl of antibody-labeled nanoparticle suspension is sufficient. The sample film itself is only 0.2 mm² in area. Small sample volumes are important in applications where materials are scarce or expensive and allow one to concentrate target samples to a greater extent. The magnetic assay also may have advantages in its speed. Competing techniques often require days to grow cultures of the target organism or time for amplification by other methods. In our technique, the rate-limiting steps are the binding of targets to the substrate and antibody-linked nanoparticles to the target. In the future, we expect to reduce the time required for these steps significantly. The measurement itself takes only 200 s, although for sufficiently large signals (where no averaging is necessary) the measurement time could in principle be as short as 2 s. In addition, the microscope can be configured to scan samples over the SQUID (6), allowing multiple samples to be measured and compared in one run.

Four factors have been identified as limiting the sensitivity to the level achieved here. As mentioned, we believe that eddy currents generate the background exponential decay in Fig. 2. Although this contribution sets our detection limit at 0.2 mΦ_o, the ultimate limit as determined by the noise in the SQUID is only ≈2 μΦ_o for 100 averages (the SQUID flux noise is 15 μΦ_o/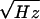 and the effective measurement bandwidth, given by the spectral width of the decay signal, is ≈2 Hz). Thus, by eliminating the background decay, we would gain a factor of 100 in our detection limit for 100 averages. Our next-generation microscope will have less metal near the SQUID and thus will have lower eddy currents. It also will incorporate a cancellation scheme to subtract background contributions.

As seen in Eq. 2, sensitivity also is limited by the dipole moment of the nanoparticles. Advances in production techniques may yield superparamagnetic particles with larger moments for comparable or smaller sizes.

Furthermore, the value of the magnetizing field B_mag is important. As discussed before, the factor mB_mag/3 k_BT in Eq. 2 is only 0.07 for a magnetizing field of 0.3 mT. An aligning coil being fabricated will increase the polarization—and thus our sensitivity—by an order of magnitude.

Finally, the magnetic coupling factor g can be significantly increased. In the current configuration, a large fraction of the nanoparticles do not efficiently couple their magnetic flux to the SQUID. This is evident in the fact that the sensing area of the SQUID is an order of magnitude smaller than the area of the sample. For optimum coupling one needs the sensor area to be comparable with or greater than that of the sample. With a new, more optimal SQUID design, we hope to improve the coupling g by an order of magnitude.

The technique described here matches the versatility of existing immunoassay methods, while offering the potential to greatly improve on their sensitivity. With the modifications outlined above, we expect to improve our detection limit to 50–500 magnetic particles. This can translate, perhaps, to the detection of a single target, if that target can, as expected, bind multiple labels.

Abbreviation

SQUID

superconducting quantum interference device