The proton to electron stoichiometry of steady-state photosynthesis in living plants: A proton-pumping Q cycle is continuously engaged

Abstract

A noninvasive technique is introduced with which relative proton to electron stoichiometries (H⁺/e⁻ ratios) for photosynthetic electron transfer can be obtained from leaves of living plants under steady-state illumination. Both electron and proton transfer fluxes were estimated by a modification of our previously reported dark-interval relaxation kinetics (DIRK) analysis, in which processes that occur upon rapid shuttering of the actinic light are analyzed. Rates of turnover of linear electron transfer through the cytochrome (cyt) b₆f complex were estimated by measuring the DIRK signals associated with reduction of cyt f and P₇₀₀. The rates of proton pumping through the electron transfer chain and the CF_O-CF₁ ATP synthase (ATPase) were estimated by measuring the DIRK signals associated with the electrochromic shifting of pigments in the light-harvesting complexes. Electron transfer fluxes were also estimated by analysis of saturation pulse-induced changes in chlorophyll a fluorescence yield. It was shown that the H⁺/e⁻ ratio, with respect to both cyt b₆f complex and photosystem (PS) II turnover, was constant under low to saturating illumination in intact tobacco leaves. Because a H⁺/e⁻ ratio of 3 at a low light is generally accepted, we infer that this ratio is maintained under conditions of normal (unstressed) photosynthesis, implying a continuously engaged, proton-pumping Q cycle at the cyt b₆f complex.

The energy budget of a plant depends upon the ratio of protons pumped across the thylakoid membrane to electrons passed through photosynthetic electron transfer complexes (the H⁺/e⁻ ratio), which sets the stoichiometries of ATP and NADPH production for use in the Calvin–Benson cycle and other biochemical pathways (reviewed in refs. 1 and 2). There has been a long-standing debate about the magnitude of H⁺/e⁻ for green plant photosynthesis, particularly regarding the proton pumping reactions of the cytochrome (cyt) b₆f complex. It is generally accepted (see review in ref. 3) that for each electron transferred through the linear pathway, one proton is released into the lumen at the level of water splitting; another is transported across the thylakoid membrane by the reduction and reoxidation of plastoquinone (PQ) at the photosystem II (PSII) Q_B site and the cyt b₆f complex Q_o site, respectively; and a third proton is pumped, at least under some conditions, by the turnover of a Q cycle associated with the oxidation of plastoquinol at the cyt b₆f complex (see refs. 4–7 for reviews).

However, in vitro measurements of H⁺/e⁻ ratios for linear electron transport in isolated thylakoids range from 2 (e.g., refs. 8–10) to 3 (e.g., refs. 11 and 12), and several groups have suggested that it changes from 3 to 2 with increasing light intensity (1, 11, 13–17). Such indications of variable coupling ratios have led several groups to suggest that the Q cycle or its proton pumping reactions only operate under certain conditions (e.g., 1, 10, 16–18). On the other hand, several authors have raised doubts about the variability of the H⁺/e⁻ ratios. Rich (19) repeated many of the crucial experiments supporting a variable H⁺/e⁻ ratio and found results consistent with a constant H⁺/e⁻ ratio of 3. Furthermore, Kramer and Crofts (20) tested for the operation of specific electron transfer reactions within cyt b₆f complex necessary for most bypass-type mechanisms and concluded that any such reactions were far too slow to be of physiological consequence. More recently, Kobayashi et al. (21) estimated rates of proton deposition into the lumen of isolated chloroplasts by comparing the extents of light-induced 9-amino acridine fluorescence in the presence of concentrations of uncoupler that support known rates of proton leakage. They then compared the rate of proton deposition with the rates of electron transfer to various electron acceptors in intact and broken chloroplasts to estimate the H⁺/e⁻ coupling ratio. With methyl viologen and nitrate as electron acceptors, they estimated an H⁺/e⁻ ratio of 3 and concluded that this ratio is likely to hold during CO₂ fixation. On the other hand, Cornic et al. (22) argued that because antimycin A, a putative inhibitor of PSI-cyclic electron transfer, inhibits CO₂ fixation in isolated chloroplasts at high, but not low light, cyclic electron transfer is required to supplement the production of ATP at high CO₂ fixation rates. By extension, they argue that this indicates that H⁺/e⁻ is diminished at high light, implying a variable H⁺/e⁻ ratio.

In addition to the ambiguity in the H⁺/e⁻ ratio for linear electron transfer, various cyclic electron transfer pathways have been proposed to operate in chloroplasts (23–27). Because turnover of these pathways does not result in stable reduction of NADPH, they increase the ratio of ATP to NADPH produced by the chloroplast. It has been suggested that these pathways function to tune the output of ATP and NADPH, or to acidify the thylakoid lumen, thus initiating down-regulatory processes (reviewed in ref. 28).

To assess the roles of H⁺/e⁻ variability and cyclic electron transfer pathways, we have developed an assay for proton and electron fluxes that is independent of the subsequent consumptive processes. The assay is based on our recently introduced dark interval relaxation kinetic (DIRK) analysis, for quantifying the steady-state fluxes of electrons through photosynthesis (29). In principle, DIRK can be used to measure fluxes through a wide range of intermediates of photosynthesis. We have demonstrated that, when used to measure electron transfer through the high potential chain (hpc), consisting of cyt f, plastocyanin, and P₇₀₀ (a measurement we refer to as DIRK_hpc), a quantitative estimate of electron transfer in vivo in the steady state is obtained (29). In this work we show that DIRK analysis of the electrochromic shift (ECS) (DIRK_ECS) allows us to estimate the fluxes of protons pumped by the photosynthetic apparatus. The two DIRK techniques, together with the established procedure for estimating PSII electron transfer using saturation pulse fluorescence changes (e.g., 30), make possible in vivo comparisons of proton and electron fluxes through the photosynthetic apparatus over a wide range of light intensities.

Materials and Methods

Plants and Growth Conditions.

Nicotiana tabacum (tobacco) was grown in a greenhouse with a midday light intensity of about 900 μmol photons⋅m⁻²⋅s⁻¹, as described previously (29).

Measurements of Absorbance Changes in the Steady State.

Steady-state rates of photosynthetic electron transfer and proton flux through the ATPase were estimated by following the absorbance changes upon rapid light-to-dark transitions, using our newly developed “diffused optics flash spectrophotometer” (DOFS) (31). This instrument significantly attenuates the interfering light scattering changes in the 500- to 560-nm range, allowing observation of changes in the redox states of cyt f and P₇₀₀ as well as changes in the extent of the ECS. Wavelength selection was provided by a wheel of 2- or 3-nm bandpass interference filters (Omega Optical, Brattleboro, VT) under computer control. Actinic light was provided by a 500-W xenon arc lamp, collimated with quartz lenses. A series of three aluminum discs for holding optical filters were mounted on computer-controlled servo motors and placed in the light path of the high xenon actinic light. One of these filter discs held a series of two dichroic filters (passing light from 640 to 730 nm; Omega Optical), while the other two held a series of neutral density filters (New Focus, Santa Clara, CA). A heat reflecting filter (57401; Oriel, Stamford, CT) was kept in place at all times to remove excess heat from the actinic beam and to prevent saturation of the detectors. The control computer automatically selected actinic light intensities from about 15 to >2010 μmol photons⋅m⁻²⋅s⁻¹ by switching the neutral density filter combinations.

Young, fully expanded, intact leaves were gently clamped into the leaf chamber of the DOFS instrument, which was perforated with two 5-mm-diameter air holes to allow free exchange of gases. At least 3 min was allowed to establish steady-state conditions after each change in illumination intensity. After steady-state conditions were established, the actinic beam was shuttered for approximately 40-ms periods at 15-s intervals to allow the decay of photoactivated processes, and the associated absorbance changes were measured at a range of wavelengths. The actinic light timing was controlled (half-time for closure of approximately 3.4 ms) with an electromechanical shutter (Uniblitz; Vincent and Associates, Rochester, NY). Selected measurements were also performed with a smaller shutter that closed with a half-time of about 0.5 ms, but allowing for less light throughput, with nearly identical results (not shown). During measurements in the 500- to 575-nm range, the detectors were protected from actinic light and fluorescence with Schott BG-18 filters, whereas in the case of infrared measurements, protection was provided by Schott RG730 filters. The blocking filters were mounted on metal discs and positioned by computer control via servo motors. The detector circuit was AC-filtered and thus was sensitive to the pulsed measuring beam but not to offsets due to changes in chlorophyll fluorescence or to leakage of actinic light through the filters. The temperature of the leaves, measured by a thermocouple, deviated from room temperature by less than 1°C during the experiments.

Deconvolution of Redox and Electrochromic Signals.

To measure relative changes in the transthylakoid electric field, Δψ, generated by movement of protons through the ATPase (see below), we measured changes in the ECS that followed rapid shuttering of the actinic light. To ensure that interfering signals did not affect the results, several different estimates of the electrochromic shift were compared, including the straight −ΔI/I₀ changes at 520 or 515 nm, and −ΔI/I₀ differences between the following wavelength pairs: 515–545 nm, 520–530 nm, 520–510 nm, and 510–500 nm. For the relatively rapid changes we report in this work, all estimates were found to be proportional within the noise levels, and changes at 520 nm were used throughout. Cytochrome f redox changes were deconvoluted from the electrochromic shift and other background signals by a previously described method (31, 32). The rereduction kinetics of P₇₀₀⁺ were followed by observing the absorbance changes at 820 nm (33) as previously described (29).

Saturation Pulse Fluorescence Changes.

The DOFS instrument was modified to measure saturation pulse fluorescence changes during the DIRK assays. Saturation pulses of either 9,000 or 5,500 μmol photons⋅m⁻²⋅s⁻¹ white light lasting for about 2 s were achieved by removing, by computer control, both the red and neutral density filters from the actinic light path. Full saturation was assumed because the two pulse intensities gave essentially identical results. The time required to switch all filters was between 100 and 200 ms, depending upon starting and ending servo positions. Chlorophyll a fluorescence yield changes were measured essentially as previously described (34), but with the DOFS optics and detectors. The pulsed measuring beam, which struck the adaxial side of the leaf where the actinic beam struck, consisted of the DOFS xenon measuring flash blocked with a 425-nm (5-nm bandpass) interference filter (Omega Optical) and an infrared rejecting filter (51962; Oriel). Fluorescence was measured on the abaxial side of the leaf with the DOFS sample detector. To minimize the effects of fluorescence reabsorption, the detector was blocked with a color glass filter that transmitted above 750 nm, where chlorophyll absorption is minimal (35). A linear relationship between CO₂ fixation rates (under nonphotorespiratory conditions) and F_V/F_M′ was found with the instrument used in the present study (not shown). Steady-state fluorescence yields, F_s, were taken just before the application of saturation pulses, whereas fluorescence yields with all PSII centers closed, F′_M, were taken during the saturation pulse. The parameter φ_II was calculated as (F′_M − F_s)/F′_M (36).

Results

Saturation Pulse Fluorescence Assays of PSII Electron Transfer Rates.

Electron transfer flux through PSII was estimated by the saturation pulse fluorescence rise technique introduced by Genty et al. (36). The application of supersaturating pulses of light saturates all photochemical reaction centers, and changes in chlorophyll a fluorescence yield reflect the photochemical quantum efficiency of PSII-associated antenna (φ_II; e.g., ref. 30). Multiplying φ_II by the absorbed actinic light intensity has been shown to yield a good estimate of photosynthetic electron transfer rates (see e.g., refs. 30, 36–46). In the present work, we multiplied φ_II by the incident light intensity (the product being denoted i⋅φ_II), which provides, in arbitrary units, a measure of PSII electron flux.

It is noteworthy that, under extreme conditions, estimates of electron flux derived from φ_II have sometimes deviated from those derived from alternative techniques, e.g., CO₂ measurements (reviewed in refs. 46–48). It has been argued that, in some cases, these deviations may be due to secondary effects of high-intensity light pulses on other properties of the system (49–54) or from the operation of alternative electron acceptors or cycles around one or the other photosystem (e.g., 2, 22, 26, 47, 55–62). All experiments in this work were performed under permissive, nonstressed conditions, and we thus do not expect interference from such phenomena.

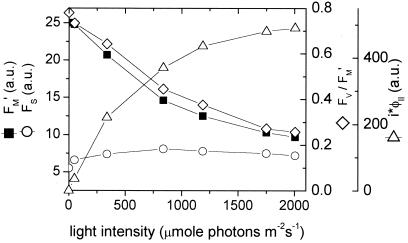
Fig. 1 shows typical light dependencies of fluorescence parameters used in this work. The amplitude of F′_M decreased steadily as the light intensity was increased, reflecting the progressive engagement of nonphotochemical quenching mechanisms (e.g., 63). The steady-state fluorescence, F_s, rose from light intensities between 17 and 800 μmol photons⋅m⁻²⋅s⁻¹, reflecting a net steady-state reduction of Q_A. It then fell between 800 and 2000 μmol photons⋅m⁻²⋅s⁻¹, reflecting the onset of strong nonphotochemical quenching (reviewed in refs. 30, 42, 64). Under dark-adapted conditions, the photochemical quantum efficiency of PSII and associated antenna, estimated by φ_II, was between 0.75 and 0.81 for all leaves measured. The value of φ_II decreased as the light intensity was increased, reaching between 0.15 and 0.22 at about 2000 μmol photons⋅m⁻²⋅s⁻¹. The flux of electrons through PSII, as estimated by i⋅φ_II, showed a typical light saturation curve, reaching its half-maximal value at about 450 μmol photons⋅m⁻²⋅s⁻¹.

Figure 1.

Typical chlorophyll a fluorescence yield parameters during steady-state photosynthesis in intact tobacco leaves. Fluorescence yields in the steady-state, F_s (open circles), and during saturation pulses, F′_M (closed squares), were obtained at varying light intensities, with the use of a diffused optics flash spectrophotometer as described in the text. The quantum yield of photosystem II and associated light-harvesting complexes (F_V/F′_M or φ_II, open diamonds) and an estimate of photosystem II electron flux (i⋅φ_II) were calculated as described in the text.

Dark Interval Relaxation Kinetics.

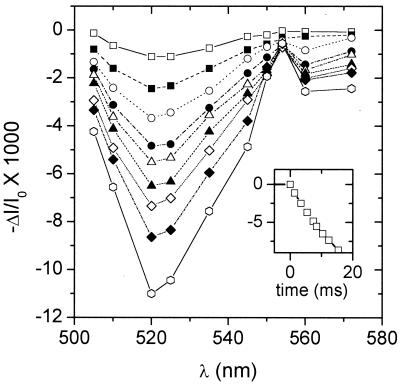
Typical −ΔI/I₀ changes that occurred during DIRK experiments are shown in Fig. 2 and were essentially as described previously (cf. figures 2 and 5 in ref. 31). The pronounced signature of the ECS was observed between 500 and 545 nm (65), whereas contributions from redox changes in the cyt b₆f complex occurred in the 545- to 570-nm region, most notably an absorbance increase due to the reduction of cyt f (α-band peak at 554 nm). Moreover, the spectral changes were consistent with major contributions from ECS and cyt f over the entire time course of the decay, from 1 to 40 ms after shutter closure, indicating that our deconvolution procedures yielded good representations of cyt f and ECS signals. Absorbance changes at 830 nm, associated with P₇₀₀ reduction, were similar to those reported earlier (e.g., 59, 66–68). The half-times for the relaxation ranged from approximately from 10 to 6 ms for P₇₀₀ and 17 to 12 ms for cyt f as the light intensity was changed from 10 to 1600 μmol⋅m⁻²⋅s⁻¹, in line with data presented by several groups (29, 66, 69–72). The half-times for the decay of the ECS remained in a narrow range from 18 to 20 ms over the entire range of light intensities. This range of decay half-times implies that neither electron transfer nor ATP synthesis was hindered by product inhibition, substrate depletion, or feedback processes. The initial rates of relaxation for the electrochromic shift, i.e., DIRK_ECS, were estimated by fitting a line through the 520-nm data 2–8 ms after closure of the shutter.

Figure 2.

Typical spectral and kinetic changes that occur upon rapid shuttering of actinic light. Changes in absorbance, estimated by (−ΔI/I₀)/2.3, were obtained in an intact tobacco, with the use of a diffused optics flash spectrophotometer at a series of wavelengths as described in the text. The background actinic light was set at 900 μmol photons⋅m⁻²⋅s⁻¹ and shuttered for approximately 40 ms every 15 s. Data were averaged over eight traces at each wavelength. Measurements were made at 1.4, 3.4, 5.4, 7.4, 8.4, 10.4, 12.4, 15.4, and 25.4 ms after half-shutter closure for curves represented by open squares, closed squares, open circles, closed circles, open triangles, closed triangles, open diamonds, closed diamonds, and open hexagons, respectively. (Inset) Dark interval relaxation kinetics at 520 nm under the same conditions. The shutter was half-closed at time 0. The full extent of the 520-nm change was 0.0215 ΔI/I₀ units.

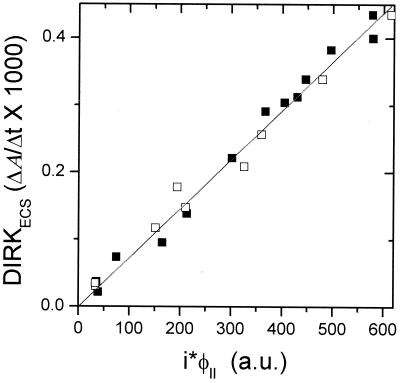
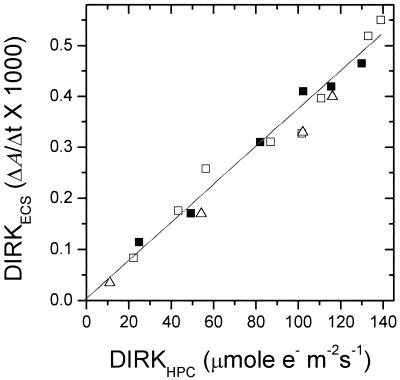
Within the noise level, the magnitudes of DIRK_ECS and DIRK_hpc initial rates were proportional to PSII electron flux as measured by i⋅φ_II (Fig. 3 and 4). Moreover, the relationship remained linear when the initial rate for DIRK_ESC was taken at a wide range of time intervals (from 10 to 60 ms), or when the full extent of ECS signal at about 200 ms was used. This linear relationship indicated that (i) residual cyt b₆f complex turnover did not have an impact on the DIRK_ECS signal and (ii) the conductivity of the ATP synthase to protons remained constant over the experimental range of proton-motive force (pmf), resulting in essentially ohmic proton flux. These relationships are further substantiated in a preliminary report (73), in which a linear relationship was found between O₂ evolution and DIRK_ECS under conditions similar to those reported here. Experiments performed with longer preillumination times, as well as in the reverse light-intensity order, gave nearly identical results, indicating that induction phenomena did not have a significant impact on the results.

Figure 3.

Comparison of DIRK_ECS, estimating proton pumping, and i⋅φ_II, estimating electron flux through PSII. Values were calculated as described in the text. The open and closed symbols represent data taken from two separate plants. The r value of the best-fit line was 0.995.

Figure 4.

Comparison of DIRK_ECS, estimating proton pumping, and DIRK_hpc., estimating electron flux through the cyt b₆f complex and PSI. Values were calculated as described in the text and previously (29). The different symbols represent data taken from three separate plants. The r value of the best-fit line was 0.992.

Discussion

This work had two goals: (i) to introduce a noninvasive technique to estimate H⁺/e⁻ ratios for steady-state photosynthetic electron transfer in intact plants and (ii) to test whether this ratio is variable in a healthy plant under normal conditions. We chose two measurements of electron transfer flux, i⋅φ_II, which is linearly related to flux through PSII, and DIRK_hpc, which is linearly related to flux through PSI. In this way, we should have been able to detect any decrease in the H⁺/e⁻ ratio for linear electron transfer (as a diminution of the slope of DIRK_ECS versus DIRK_hpc), as well as the onset of PSI cyclic electron transfer (as an increase in DIRK_hpc versus i⋅φ_II).

A Technique for Estimating Steady-State Proton Fluxes in Vivo.

We have previously shown that DIRK_hpc is quantitatively related to gross CO₂ fixation (A_G) under nonphotorespiratory conditions (29). In this work, we use an application of the DIRK technique, DIRK_ECS, with which relative fluxes of protons through the ATPase during steady-state photosynthesis can be estimated.

The basis of DIRK analysis is the rapid and selective inhibition of light-driven reactions (by shuttering of the actinic light), allowing relaxation processes whose initial rates reflect steady-state fluxes. When thylakoids are illuminated, protons are continuously pumped from the stroma to the lumen by the photosynthetic electron transfer chain. In addition, water oxidation deposits protons in the lumen. The pmf established by these reactions is dissipated predominantly by the movement of protons through the ATPase, driving the synthesis of ATP. In a steady state, the light-driven flux of protons into the lumen is precisely balanced by counterflux through the ATPase. An abrupt cessation of illumination would result in an essentially instantaneous blockage of light-driven proton deposition in the lumen. On the other hand, proton efflux will continue for as long as the pmf is greater than 0. For a short time interval after shuttering, the changes in efflux will be negligible, and thus its initial rate should reflect steady-state proton flux.

Because protons are charged, net transthylakoid proton movements will affect the membrane potential and thus can be followed by electrodes (15, 74) or by the ECS (65, 75). The ECS is readily measured in higher plants (65, 75) and green algae (76) and has been shown to be a linear indicator of transthylakoid electric field or Δψ (75). It follows that the initial rate of change of the ECS upon shutter closure, i.e., DIRK_ECS, should be a good indicator of steady-state proton flux. We note that this should be true even if the steady-state transthylakoid Δψ is completely dissipated by counterion movements (74, 77). As long as the rate of counterion movements is significantly slower than proton movement through the ATPase, the transmembrane Δψ, and thus DIRK_ECS, will be linearly affected by the initial proton efflux upon shutter closure. In the cases where the steady-state Δψ is dissipated by counterion movements, the initial proton efflux (driven by the proton diffusion potential) will establish a “field inversion,” where Δψ will be positive on the stromal side of the membrane, as has been documented in microelectrode experiments (15, 74) and in our own measurements of ECS in intact leaves (31). Thus the initial rate of change of Δψ should still be proportional to the steady-state proton flux. Computer simulations supporting this line of argument have yet to be presented (J. Cruz, A.K., C.A.S., and D.M.K., unpublished observations).

One potential concern for analysis of the ECS decay is that electron transfer through the cyt b₆f complex will continue for a short time after shutter closure, as the hpc components are reduced in the dark. If the electrogenicity of postillumination hpc reduction represents a significant fraction of the total pmf, its kinetics would overlap and interfere with the decay of the ECS due to ATPase turnover. On the other hand, the pmf stored as ΔpH and Δψ are expected to be well buffered by weak acids (78–81) and by counterion gradients (15), respectively, and thus the fractional contribution of the small number of turnovers that occur in the dark is expected to be small. This is clear from our previous data, in which the initial decay of the ECS occurs on a time scale of tens of milliseconds, but the field inversion, representing the collapse of the total pmf, decays 1,000-fold more slowly (31, 74). Moreover, if interference from postillumination hpc reduction were significant, we would have expected a lag phase in the ECS decay kinetics. In contrast, the decay of the ECS was clearly monotonic, with no lag phase, under all conditions studied, indicating that such interference was negligible (example kinetics are shown in the Inset to Fig. 2). Furthermore, since the halftime for decay of ECS was constant, any residual interference was also constant.

The principle of our DIRK_ECS approach is very similar to that used earlier to estimate H⁺/e⁻ ratios, using pH electrodes or pH-sensitive dyes in isolated thylakoids (1, 8–10, 16, 17). This “pH assay” relies on two assumptions. First, steady-state electron transfer results in water oxidation and stoichiometric release of protons, which eventually escape the lumen. Thus, the net changes in extralumenal pH should reflect steady-state linear electron transfer. Second, in a steady state, proton pumping into the lumen is counterbalanced by proton efflux, and thus, as above, the net efflux of protons upon shuttering should reflect the transthylakoid pH gradient. Comparing the slopes of Δ[H⁺]/Δt during and just after illumination will yield an estimate of H⁺/e⁻. In these experiments, care must be taken to dissipate the transthylakoid Δψ, e.g., with valinomycin or nonactin and KCl, to prevent back pressure from Δψ, whereas in DIRK_ECS, changes in Δψ are required to probe proton flux. One of the most significant advantages of the DIRK_ECS approach over the pH assay is that measurements can be made noninvasively in vivo, as well as in isolated material without the addition of chemicals.

The H⁺/e⁻ Ratio for Steady-State Photosynthesis in Intact C3 Plants.

The relationships between relative fluxes of electrons transferred through PSII and protons passed through the ATPase were found to be linear within the noise level (Figs. 3 and 4). These linear relationships indicate that H⁺/e⁻ remained constant over the entire light saturation curve. Most recent measurements agree that the H⁺/e⁻ ratio for linear electron flow is 3 at low light intensities (1, 72, 82). From our data, we infer that the H⁺/e⁻ ratio remains at 3 in healthy, unstressed plants.

The results presented here are direct estimates of H⁺/e⁻ for steady-state electron transfer in intact leaves and thus have broad consequences for the energy budget of the plant. Our results are consistent with an obligatory, proton-pumping Q cycle for the cyt b₆f complex (19, 20) and contrary to “bypass”-type models with variable coupling stoichiometries (10, 83). In this regard, our interpretation is in agreement with that of Kobayashi et al. (21), that the normal coupling ratio during CO₂ fixation is H⁺/e⁻ = 3. Our results do not necessarily disagree with the data of Berry and Rumberg (1), as these experiments were performed on isolated thylakoids in the presence of ionophores that collapse the Δψ component of pmf, where a ΔpH approaching 3 units is generated. Such low lumen pH significantly slows the rate of linear electron flux, possibly allowing alternative electron transfer pathways to effectively compete, lowering the measured H⁺/e⁻ ratios (1, 11, 72). Likewise, it is possible to reconcile our results with those of Cornic et al. (22) if we allow for additional ATP consumption pathways or other slippage reactions to occur at low [O₂] under saturating light. These additional pathways and reactions would skew the requirements for ATP and NADPH, necessitating additional proton pumping and perhaps triggering cyclic electron transfer.

As pointed out earlier (21, 72), a constant H⁺/e⁻ ratio of 3, and assuming H⁺/ATP of 4 (21, 84–86) will result in the correct overall ratio of ATP:NADPH for the Calvin cycle. We emphasize, though, that H⁺/ATP is still controversial. Under the conditions of our assays, no changes were observed in the slopes of i⋅φ_II vs. DIRK_ECS or in DIRK_hpc vs. DIRK_ECS (Figs. 3 and 4). This lack of change implies that cyclic electron transfer is negligible or is a constant fraction of linear electron transfer, as previously suggested (48). The demands for ATP and NADPH may change under adverse environmental conditions or under altered metabolite demands (e.g., in young leaves, where nitrite reduction is expected to be large). In these cases, we suggest that cyclic electron transfer (87, 88), mitochondria (89), or dissipative processes (e.g., NADPH oxidases, ATPases) may balance these requirements.

Finally, it is worth noting that the linear relationships between the DIRK techniques and the i⋅φ_II parameter (41) as well as gas exchange (29, 73) tend to validate the use of these measurements as linear indicators of flux. The DIRK approach should be particularly useful as an independent test of fluorescence estimates under extreme conditions where the validity of the more commonly used technique has not been fully established.

Abbreviations

ATPase

(C)F_O-(C)F₁ ATP synthase

cyt

cytochrome

hpc

high potential chain

ECS

electrochromic shifting of light-harvesting pigments in response to delocalized transthylakoid electric field

DIRK

dark interval relaxation kinetics

DIRK_hpc

DIRK analysis of absorbance changes associated with reduction of cyt f and P₇₀₀ yielding an estimate of electron flux through the high potential chain of photosynthesis

DIRK_ECS

DIRK analysis of absorbance changes associated with ECS yielding an estimate of light-induced proton fluxes through the ATPase

DOFS

diffused optics flash spectrophotometer

F_s

steady-state chlorophyll a fluorescence yield

F_M

maximal chlorophyll a fluorescence yield obtained under conditions in which nonphotochemical fluorescence quenching is minimal

F′_M

yield of chlorophyll a fluorescence obtained during steady-state illumination, during application of light pulses that saturate PSII photochemistry

H⁺/e⁻

stoichiometry of protons to electrons passed through the photosynthetic apparatus

pmf

proton-motive force

PS

photosystem

φ_II

quantum efficiency of PSII and associated antenna