Automated reverse engineering of nonlinear dynamical systems

Abstract

Complex nonlinear dynamics arise in many fields of science and engineering, but uncovering the underlying differential equations directly from observations poses a challenging task. The ability to symbolically model complex networked systems is key to understanding them, an open problem in many disciplines. Here we introduce for the first time a method that can automatically generate symbolic equations for a nonlinear coupled dynamical system directly from time series data. This method is applicable to any system that can be described using sets of ordinary nonlinear differential equations, and assumes that the (possibly noisy) time series of all variables are observable. Previous automated symbolic modeling approaches of coupled physical systems produced linear models or required a nonlinear model to be provided manually. The advance presented here is made possible by allowing the method to model each (possibly coupled) variable separately, intelligently perturbing and destabilizing the system to extract its less observable characteristics, and automatically simplifying the equations during modeling. We demonstrate this method on four simulated and two real systems spanning mechanics, ecology, and systems biology. Unlike numerical models, symbolic models have explanatory value, suggesting that automated “reverse engineering” approaches for model-free symbolic nonlinear system identification may play an increasing role in our ability to understand progressively more complex systems in the future.

Many branches of science and engineering represent systems that change over time as sets of differential equations, in which each equation describes the rate of change of a single variable as a function of the state of other variables. The structures of these equations are usually determined by hand from first principles, and in some cases regression methods (1–3) are used to identify the parameters of these equations. Nonparametric methods that assume linearity (4) or produce numerical models (5, 6) fail to reveal the full internal structure of complex systems. A key challenge, however, is to uncover the governing equations automatically merely by perturbing and then observing the system in intelligent ways, just as a scientist would do in the presence of an experimental system. Obstacles to achieving this lay in the lack of efficient methods to search the space of symbolic equations and in assuming that precollected data are supplied to the modeling process.

Determining the symbolic structure of the governing dynamics of an unknown system is especially challenging when rare yet informative behavior can go unnoticed unless the system is perturbed in very specific ways. Coarse parameter sweeps or random samplings are unlikely to catch these subtleties, and so passive machine learning methods that rely on offline analysis of precollected data may be ineffective. Instead, active learning (7) processes that are able to generate new perturbations or seek out informative parts of a data set based on internally generated hypotheses may be able to better track down these important hidden system characteristics.

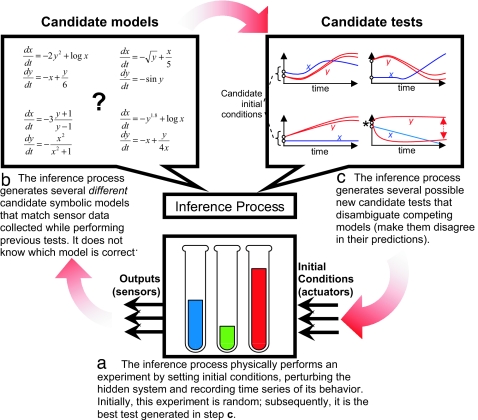
Here we introduce a method for automatically synthesizing both the structure and the parameters of ordinary differential equations from a hidden coupled nonlinear system, given either the ability to selectively perturb the system or selectively sample from noisy data produced by it. The method is composed of two processes: The first synthesizes multiple models from basic operators and operands to explain observed behavior (Fig. 1, step b). The second process synthesizes new sets of initial conditions (new “tests”) that induce maximal disagreement in the predictions of the candidate models (Fig. 1, step c). The best of these tests is then used to extract new behavior from the hidden system (Fig. 1, step a). This alternating cycle continues until some termination criterion is met.

Fig. 1.

A concept diagram showing flow of the interrogation algorithm. The cycle (a, b, c) is repeated until a fixed period has elapsed. The dotted arrow in c represents the divergence between two models' predictions about the future behavior of state variable y. The best test from c that is executed on the physical system is the set of initial conditions that causes the models to disagree the most in their predictions (marked by an asterisk). The framework converges on accurate models by gradually accumulating information about the system from a series of internally generated, intelligent tests. By periodically discarding older tests and replacing them with newer ones, the algorithm cannot only model static systems, but continuously track changing systems by producing models of its current state.

Partitioning, Automated Probing and Snipping

A number of methods have been previously proposed for symbolic regression of nonlinear systems, but were limited to producing linear models (4) or were applied to systems composed of one or a few interacting variables (8–16). Here we introduce a scalable approach for automated symbolic regression, made possible by three advances introduced here: partitioning, in which equations describing each variable of the system can be synthesized separately, thereby significantly reducing the search space; automated probing, which automates experimentation in addition to modeling, leading to an automated “scientific process” (17–20); and snipping, an “Occam's Razor” process that automatically simplifies and restructures models as they are synthesized to increase their accuracy, to accelerate their evaluation, and to render them more parsimonious and human-comprehensible. We describe these three components and validate their performance on a number of simulated and real dynamical systems.

Partitioning.

Partitioning allows the algorithm to synthesize equations describing each variable separately, even though their behaviors may be coupled. Stochastic optimization (21–24) is used for synthesizing the equations, as it is well suited for searching open-ended spaces composed of building blocks. Bayesian networks, although popular, cannot model mutual dependencies (cycles) between variables (25), a pattern often encountered in biological and other regulation (feedback) networks and fundamental to their operation (26). Indeed, modeling of networks with many interdependencies has been identified as a research priority across the sciences (27, 28). When using partitioning, rather than integrate candidate equations for all variables together, a candidate equation for a single variable is integrated by substituting references to other variables with data from the system's observed behavior (see Methods). This allows us to infer the structure of systems comprising more variables and higher degree of coupling than were inferred by other methods (4, 8–16) [see supporting information (SI) Table 4].

Automated Probing.

Automated probing transforms a passive modeling algorithm into an active participant in the discovery process. Rather than passively accepting data from the system under study, the automatically synthesized models are used to create a test tailored to disprove as many of the models as possible. In this work, a test is considered to be a set of initial values for all of the variables comprising the system: For example, when inferring equations describing the single pendulum (Tables 1 and 3), a test is a set of desired initial values of the pendulum arm's angle and angular velocity. Because a new, information-extracting test cannot be derived from this model set or from the system's behavior analytically, candidate tests are optimized to maximize disagreement across the predictions of the models when supplied with these initial conditions. The best test, after a fixed period of optimization, is then either executed on the system and the resulting behavior recorded, or previously provided data are scanned to find the time step at which the variable values most closely match this test. The following time interval is then extracted and provided to the modeling process. The additional results tend to induce reoptimization of the current model set into a new set. This alternating cycle of modeling and testing continues for a fixed period (Fig. 1).

Table 1.

Inference of noisy, synthetic systems

Synthetic system
Single pendulum
Target	dθ/dt = ω
	dω/dt = −9.8sin(θ)
Best model	dθ/dt = ω
	dω/dt = −9.79987sin(θ)
Median model	dθ/dt = ω
	dω/dt = −9.8682sin(θ)
Lotka–Volterra interspecific competition between two species
Target	dx/dt = 3x − 2xy −x2
	dy/dt = 2y −xy − y2
Best model	dx/dt = 3.0014x − 2xy − x2
	dy/dt = 2.0001y − xy − y2
Median model	dx/dt = 2.9979x − 2.0016xy−x2
	dy/dt = 1.999y − 0.917xy−1.005y2
High degree decay
Target	dx/dt = −x9y11
	dy/dt = −x11y9
Best model	dx/dt = −0.925x9y11
	dy/dt = −1.0585x11y9
Median model	dx/dt = 0.77x6y7−0.7x7y9−0.7x7y8
	dy/dt = −5.47x5y7 + 2.69x4y7 +2.33x5y6 + 2.03x4y6 −1.58x3y6 − 1.36x4y5 +0.68x3y5
The lac operon from E. coli
Target	dG/dt = A2/(A2+1)−0.01G+0.001
	dA/dt = G(L/(L+1)−A/(A+1))
	dL/dt = −GL/(L+1)
Best model	dG/dt = 0.96A2/(0.96A2+1)
	dA/dt = G(L/(L+1)−A/(A+1))
	dL/dt = −GL/(L+1)
Median model	dG/dt = (A2−0.05A)/(A2−0.05A+1)
	dA/dt = (G+0.02)(L/(L+1)−A/(A+1))
	dL/dt = −0.65(1.97G−G/(G+1) +0.08L2)L/(L+1)

Thirty independent trials were conducted against each of the four synthetic systems shown above (with ±0.08 noise). The target system itself is shown along with the final model produced by the best and median trial. θ, angle between pendulum arm and vertical; ω, angular velocity; x, population of species 1; y, population of species 2; G, concentration of β-galactosidase; A, allolactose; L, lactose.

Table 3.

Inference of a physical pendulum

	Box is flat	Box is rotated −1.57rad	Box is rotated −2.6rad
General form	dθ/dt = αω + β
	dω/dt = γsin(δθ + ϕ) + f(θ, ω)
Fraction of models matching
Control experiment	4 of 30 (13%)	26 of 30 (87%)	6 of 30 (20%)
Full algorithm	21 of 30 (70%)	29 of 30 (97%)	20 of 30 (67%)
Means and standard deviations	α = 1.0040 ± 0.0009	α = 1.0008 ± 0.0014	α = 1.0039 ± 0.0011
	β = 0.0001 ± 0.0001	β = 0.0028 ± 0.0035	β = −0.0003 ± 0.0007
	γ = −19.43 ± 2.67	γ = −20.45 ± 1.06	γ = −22.61 ± 0.69
	δ = 1.104 ± 0.047	δ = 1.0009 ± 0.0032	δ = 1.0110 ± 0.0492
	ϕ = 0 ± 0	ϕ = −1.575 ± 0.026	ϕ = −2.6730 ± 0.1149
Residual functions	f(θ,ω)={−0.2080, −0.29(ω+1.45), −0.05ω(ω+5.48), −0.24(ω+0.98), −0.26(ω+1.4), …}	f(θ,ω)={1.98sin(θ), cos(1.35θ), −0.204( ω−2.57), sin(−4.02θ), cos(−2.11θ), …}	f(θ,ω)={cos(1.21θ), cos(−5.05θ), 0, sin(θ), cos(1.12θ), …}

A control algorithm (which fully samples the data set) and the full algorithm (which samples the data set using automated probing) were both presented with the same behavior from three hidden physical systems (SI Fig. 6 a–c). The systems differ only in the rotation of the box (angle offset), which changes the relationship between the variables (angle and angular velocity). Each system was perturbed to produce time series data (SI Fig. 6 d–f). Both algorithms were run against each data set 30 times; each trial was conducted for 2 min. For each trial, the model with lowest error against all observed system data was output. These resulting models were often found to fit a general form. The mean parameter estimation for the full algorithm is also shown, along with the residual functions many of the models possessed.

Snipping.

Snipping automatically simplifies and restructures models during optimization. Model optimization occurs by starting the algorithm with a random set of models; calculating the errors of the models against all of the system data observed so far; creating copies of each of the existing models and introducing small, random changes into the copies; evaluating the new models; and replacing those models that are less accurate with their modified, more accurate copies. In this work, models are represented as sets of equations, and equations are represented as nested subexpressions. In many trials, it was observed that these expressions grow very large, but that many of the subexpressions would return values within narrow ranges during evaluation. This is a symptom of overfitting (29, 30), often referred to as bloat (31) in the literature dealing with nested expression-based methods (22): models specialize to explain the observed data, but explain additional unseen data poorly. With snipping enabled, when a new model is created from an older one, subexpressions in the new model are occasionally replaced by a constant chosen uniformly from the range formed by the minimum and maximum values output by the corresponding subexpression in the original model. This process tends to yield more accurate and simpler models, making them more human-readable.

Results

The algorithm was applied to four synthetic systems, and two physical systems.

Application to Synthetic Systems.

To apply the algorithm to a hidden system, the experimenter must specify: (i) the components (i.e., variables) of the system and how they can be observed; (ii) possible operators (algebraic, analytic and/or other domain-specific functions) and operands (variables and parameter ranges) that can be used to describe the behavior and relationships between these variables; (iii) the maximum allowed model complexity (in this work, determined as the maximum allowed depth of subexpressions); (iv) the space of possible tests (in this case, sets of initial conditions of the variables); and (v) the termination criteria (here, minutes of allowed computation time).

The method was applied to four synthetic systems (Table 1) and two real systems (Tables 2 and 3). Synthetic systems (Table 1) are sets of differential equations hidden from the algorithm in which proposed tests (initial conditions) are input, and noisy time series data are output. For all synthetic systems, observation noise was simulated by adding random values chosen uniformly from the range [−0.08, 0.08] to each variable value at each time step in the time series data, after the data had been generated. Uniform rather than Gaussian noise was added due to implementation convenience. Fig. 2 shows two sample trials of the algorithm against one synthetic system (the single frictionless pendulum).

Table 2.

Inference of a biological network from real data

	Algorithm 1	Algorithm 2
Common form	dh/dt = α+βh+γl	dl/dt=δ+εh+ζl
Means and standard deviations
Control	α = 1.85×106±6.49×105	δ = 1.51×105 ± 1.65×105
Full algorithm	β = −46.31 ± 12.55	ε = 26.48 ± 3.27
	γ = −11.18 ± 17.48	ζ = −50.53 ± 7.02
Means and standard deviations	α = 3.42×106±1.56×106	δ = 3.10×105 ± 2.34 × 105
Control	β = −67.82 ± 45.62	ε = 32.66 ± 4.06
Full algorithm	γ = −10.97 ± 52.24	ζ = −63.16 ± 5.63

A control algorithm (which fully samples the data set) and the full algorithm (which uses automated sampling of the data set) were both run on historical data reporting approximated populations of snowshoe hare (h) and Canadian lynx (l) (36). Thirty independent trials of both algorithms were performed, and the best model (with lowest error against all observed system data) was output.

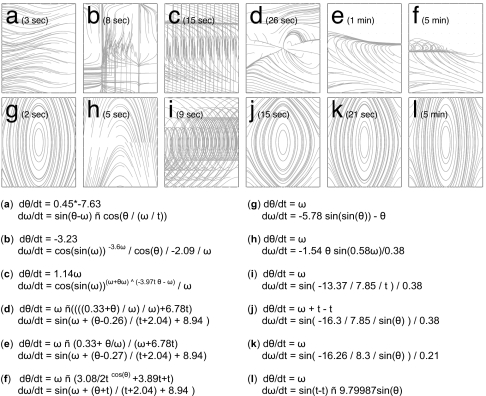
Fig. 2.

A typical unsuccessful and successful trial against the single synthetic pendulum (with ± 0.08 noise). (a–f) Six successive models generated by the algorithm without partitioning, automated probing or snipping, and the phase diagrams produced by those models. (g–l) The behavior of successive models from another typical trial in which all three were used, and the corresponding phase diagrams.

Table 1 reports sample models inferred by the algorithm when applied to four dynamical systems taken from mechanics (the nonlinear single pendulum), ecology (the Lotka–Volterra equations describing interspecific competition for a common resource), an artificially created system with high degree, and genetics (a model of the lac operon from Escherichia coli). For each system, 30 independent trials were performed, and the final model produced by each trial was evaluated on a corpus of previously unseen system behavior. For each system, the models that achieved the lowest and the median error on this data (known as the model's objective error) are reported to convey the algorithm's consistency. All four systems were inferred by the same algorithm, with only minor changes: for the pendulum, trigonometric operators were provided in addition to the basic algebraic operators; for the lac operon, the Hill function x/(x + 1) was provided as a possible equation building block.

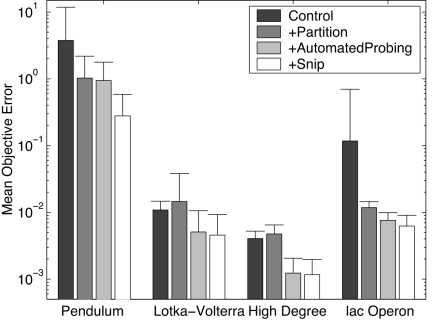
To determine the importance of partitioning, automated probing, and snipping, three control experiments were also run against these systems. The first control experiment uses random tests rather than those proposed by automated probing (the testing phase outputs a random set of initial conditions, rather than searching for an informative set), and does not employ partitioning or snipping. The second control experiment is the same as the first, but employs partitioning. The third control experiment uses both partitioning and automated probing but no snipping. Thirty trials of each control experiment were performed, and the mean errors and sizes of the final models was computed and compared against the models output by the actual algorithm (partitioning, automated probing and snipping). Fig. 3 and SI Fig. 4 report the mean model errors and sizes, respectively. As can be seen, partitioning improves model accuracy for the pendulum and lac operon systems; automated probing improves model accuracy for all systems (although improvement is slight for the pendulum); snipping improves model accuracy for the pendulum and somewhat for the lac operon systems; and snipping reduces mean model size for all systems except the system with high degree. The remaining four control algorithms, in which one or more of the proposed algorithmic components is disabled, are not shown: The reported algorithms are sufficient to show a trend, suggesting that using all three components provides significant modeling improvement across different application domains compared with when only two, one, or none of the components are used.

Fig. 3.

Mean model errors obtained by the four algorithm variants applied to the four synthetic systems (with ± 0.08 noise). Thirty independent trials of each algorithm variant were performed. The best model from each trial was output. The best model was determined as the one with the least error against observed noisy system behavior. That model was then evaluated on previously unseen system behavior without noise, giving its objective error. In this way, a model that achieves the correct equation structure and parameter values should achieve zero objective error. [Objective error cannot be calculated for physical systems, as non-noisy behavior is not possible. Objective error is only used to determine the relative performances of the algorithm variants against synthetic systems.] Each bar reports the mean objective errors of these best models. Shading indicates algorithm variant (dark gray, no partitioning, automated probing, or snipping; medium gray, only partitioning; light gray, partitioning and automated probing; white, partitioning, automated probing, and snipping). Error bars indicate one unit of standard deviation (n = 30).

Fig. 2 reports the performance of a typical trial without and with the three algorithmic enhancements (Fig. 2 a–f and g–l, respectively) against the synthetic pendulum system. As can be seen, partitioning allows the algorithm to quickly identify the first variable, and automated probing invalidates an initially approximate yet structurally incorrect model (Fig. 2g). Finally, snipping eventually produces a compact, human-readable result (Fig. 2l), whereas the control experiment never does.

Partitioning improves modeling because without it, inaccuracies in one equation cause discrepancies in the behavior of other coupled variables, making it difficult to localize where the inaccuracies in a candidate model lie. It is well known that interdependencies between model components hinder gradient-based search methods (32–34). Partitioning allows for the localization of inaccuracies, but it also makes search more tractable: Without partitioning, the space of models increases exponentially with the number of variables; with partitioning, the space grows polynomially (see Materials and Methods for a brief derivation). Finally, partitioning allows for parallel modeling of each variable, further accelerating the modeling process.

Automated probing also improves modeling because it has been shown to be theoretically optimal (35) and practically useful in other domains (18, 19). More specifically, when applied to dynamical systems, tests locate boundaries between the basins of attraction (bifurcation regions) of the system (SI Fig. 5 a, b, and d), and/or elicit extremal behavior from it (SI Fig. 5c), thereby accelerating modeling. This follows from the observation that increasingly accurate models will have bifurcation regions close to one another and to that of the system, so will disagree in behavior given a set of initial conditions chosen from within those regions. Also, by proposing similar tests from the same region, the algorithm can effectively cancel out observation noise from those tests. Similarly, in the case of the system with very high degree (Table 1 and SI Fig. 5c), the system only produces changes in its variables when one or both variables are set close to their maximal allowed values; automated probing tends to autonomously focus tests within that region.

Application to Physical Systems.

The full algorithm and a control algorithm were also applied to two physical systems: an ecological data set describing changes in hare and lynx populations (Table 2) and three variants of a physical pendulum (SI Fig. 6 a–f and Table 3). The algorithms were applied to the two systems with only one change: when applied to the pendulum, trigonometric functions were supplied in addition to the standard algebraic ones. Unlike the simulated system, time series data were collected before modeling began. For the ecological application, historical data were used (36); the physical pendulum was manually swung to generate data.

For the ecological application, the full algorithm requested 10-year spans of data from this 91-year data set according to automated probing: The algorithm optimizes a set of initial conditions, and then locates the year in the data set when the populations most closely match these conditions; the following ten years of data are then extracted and used for further modeling. The control algorithm is the same as the full algorithm except that it was given 10-year spans that progressively cover the entire data set: the first cycle through provides system behavior from 1845 to 1855, the second cycle provides behavior from 1855 to 1865, and so on. For the pendulum, the full algorithm requested 0.2-s spans of data from this set according to automated probing. The control algorithm is the same as the full algorithm except that it was given 0.2-s spans that progressively cover the entire data set: the first cycle through provides system behavior from 0 to 0.2 s, the second cycle provides behavior from 0.2 to 0.4 s, and so on.

It was found that, for the physical systems, the models tended to converge on a common structure; the means and standard deviations of the inferred parameter values indicate the consistency of the algorithm against these real systems (on average 82% of trials converge on a common structure, see Tables 2 and 3). Although, in the case of the ecological data set (Table 2), the control algorithm produced higher parametric consistency due to the uniform sampling of the data set, it was found that the control algorithm had much lower structural consistency than the full algorithm when applied to two rotations of the physical pendulum (Table 3): many of the trials produced linear approximations [for example γsin(δθ + ϕ) would be approximated by γ(δθ + ϕ)]. This can be explained by the observation that automated probing tends to focus on time spans that exhibit nonlinear behavior, such as the transition from over-the-top rotation of the pendulum to rocking motion (SI Fig. 6e). This observation could be tested by applying the algorithm (both without and with automated probing) against a system that exhibits periods of linear and increasingly nonlinear behavior, such as during the transition to a chaotic regime. It is hypothesized that automated probing would focus data collection on the transitional behavior and therefore capture the nonlinearities of the system better than the same algorithm without automated probing.

For both systems, the common model structure that was found had explanatory value. In the case of the ecological data set, the model indicates that the prey species increases at a constant rate but that rate of increase lessens as its population increases, a common feature seen in population growth (37); the prey species decreases in response to increased predators; the predators decrease proportionally to their numbers; and the predators increase proportionally to the number of prey. Although the model proposed by the system is linear (possibly because of the simplifying effects of snipping), in contrast with a more complex nonlinear model typically used to explain these phenomena (38), the meaning extracted from the inferred equations is similar.

In the case of the pendulum, the algorithm produces consistent and accurate models in response to changes in the underlying system. Also, residual functions for the first system (Table 3) are quite consistent, and as they are functions of velocity may indicate modeling of the friction inherent to the system.

Scalability.

To test scalability, both the full algorithm and a control algorithm without partitioning were applied to 18 randomly created stable nonlinear systems, with increasing numbers of variables. As summarized in SI Table 4, the proposed method found exact solutions most of the time (on average, 71% of trials, see SI Table 4) for all systems up to six variables. In contrast, only one of the 18 systems was ever identified without partitioning. As a comparison, structural identification methods reported in the literature (8–16) so far have not modeled systems with more than four variables. For the system with four variables, only a linear model was reported (4).

Discussion

Here we have demonstrated a unified computational framework for automatically inferring models of nonlinear, coupled dynamical systems, with possibly high degree, from direct system interrogation or noisy time series data. The method was validated on data from real systems for which the underlying equations are not known: the method consistently produces models that are similar in structure and meaning to the currently known best models of such systems. The scalability of this method has been demonstrated as systems with many variables, interdependencies and nonlinearities have been successfully identified.

Despite the demonstrated scalability of the described framework, the number of state variables considered here remains orders of magnitude less than the hundreds or thousands of components found in systems biology applications. In future work, existing methods for identifying separable components, such as clustering and correlation methods to identify a subset of the proteins involved in a specific metabolic pathway (39), could complement this framework. In this way, components will first be identified using existing methods; the proposed framework could then automatically synthesize models of these interconnected components separately.

The current limitation of the proposed framework is that it is restricted to systems in which all variables are observable. However, in future the framework could also be applied to systems in which some of the variables are unobservable. With partitioning enabled, parts of the system unaffected by the unobservable variables may gradually be modeled correctly while the model error of variables influenced by the unobservable variables would remain high. This dichotomy could be automatically detected and exploited to localize the influence of unobserved parts of the system: Variables could be classified based on changes in their model error over time. Other techniques could then be brought to bear for clarifying the relationship between the unobserved parts of the system and the isolated variables.

It is possible that the discrete time series used in this work biases the structure of the synthesized models. In future work, the modeling component could be expanded to generate models against different subsets of the time series data, sampled at different frequencies. Commonalities across these models could then be integrated into a single model, ensuring a final model that is insensitive to the sampling frequency of the system data.

Finally, by discarding older results and continuously replacing them with fresh data, the system may track a changing system by constantly generating models of its recent state. By adopting techniques from chaotic modeling in which the changing system is constantly tracked but not explicitly modeled (40), it may be possible to extend the framework to synthesize explicit models of chaotic systems with constantly changing internal structure.

Conclusions

One of the areas where there is a growing need for automated modeling is systems biology. Biological networks tend to be heavily interdependent, and the demonstrated ability of partitioning to separately model the components of a network may be of increasing value when applied to larger networks, and those in which not all variables are observable. Also, the ability to continuously request new data rather than digest precollected data opens the way toward continuous rather than static modeling. The recent finding that organisms exhibit topological changes in gene expression under different conditions (41) indicates the future need for such dynamic modeling paradigms. Our results suggest that the proposed method could be used to automatically generate detailed, testable hypotheses of such complex and changing systems: not just inferring correlations between variables in large coupled biological networks (42, 43) such as genetic regulatory or metabolic networks, but also automatically inferring causal relationships including cyclical dependencies and feedback circuits through active interrogation. Indeed, active interrogation has been identified as a new way forward for understanding biological systems (44). Such automation may prove critical in our quest to model increasingly complex coupled phenomena, identified as a major frontier in 21st century science (27, 28).

Materials and Methods

Here, we describe the three main tools used to make the automated inference of coupled, nonlinear dynamical systems tractable, as well as descriptions of the systems used in this study.

Partitioning.

Partitioning relaxes the constraint that a model must approximate equations for all variables at once. Without partitioning, we used the standard fourth-order Runge–Kutta method (45) to integrate the differential equations of both the hidden system and candidate models. In partitioning, when the differential equation of variable i is integrated, references to other variables are substituted by real data. For more details regarding partitioning, please refer to SI Text.

Modeling.

Candidate models are represented as a set of ordinary differential equations dx₁/dt = f_m⁽¹⁾, …, dx_k/dt = f_m^(k). The equations are encoded as a hierarchy of nested symbolic subexpressions. A model is then composed of a set of nested expressions in which each expression i encodes the equations describing the time evolution of variable i. When performing inference, the user provides a set of possible operators and operands that could be used to compose equations. During the first time step of integration, each operand in each equation is set to the initial conditions, and the expression is evaluated. The return value of each expression then represents the derivative computed for that variable. At subsequent time steps, the variables are updated to their current values and the expression is re-evaluated. The output of a candidate model is then a set of time series for the k variables. When partitioning is used, a candidate model only encodes a single expression, determining the evolution of the current variable under investigation.

Models are optimized against all of the time series observed from the system so far. In the modeling phase of the algorithm (Fig. 1b), each model is therefore integrated p times, where p is the number of times that the system has been supplied with initial conditions, and the resulting behavior observed. Model error then becomes the mean error over all observed time series.

We used a hill climber (46) for model optimization. After evaluation, each model undergoes a random perturbation. If the perturbed model has lower error than the original model, the original model is replaced with the perturbed model; otherwise, the perturbed model is discarded. To create the perturbation, a randomly selected node in the expression is replaced by a new random operator or operand. If the node is changed from an operand into an operator, new random subexpressions are created, according to the arity of the new operator. If it is changed from an operator into an operand, the subexpressions supplying the parameters of the old operator are deleted. If the operand is a variable, a new variable is chosen uniformly from the range [x₁, …, x_k]. If the operand is a constant, a new constant is chosen uniformly from the floating-point range [−10, 10] with probability 0.5, or a small value chosen from a Gaussian distribution (μ = current value; σ = |0.5 current value|) is added to the current constant.

During the first pass through the modeling phase, five random models are created, and optimized for 1,000 iterations. During the second and subsequent passes through this phase, estimation begins with the models optimized during the previous pass. If partitioning is used, the optimization process is broken into k epochs: during each epoch, five candidate equations describing the ith variable are optimized for 1,000/k iterations. The 5k equations are then repackaged into five candidate models comprised of k equations each. The model with the lowest error is output at the end of the last pass through the modeling phase.

Automated Probing.

The key concept behind automated probing is that the most informative perturbation of a hidden system is the one that causes the most disagreement among predictions of candidate models of that system (35). As Fig. 1 illustrates, modeling alternates with testing: new sets of initial conditions (“tests”) are optimized, and the best one is either directly executed on the system to extract new behavior from it (Fig. 1a) or used to select a new sample from time series data. At the beginning of each testing phase (Fig. 1c), a set of five tests are created randomly, in which initial conditions are chosen uniformly from a range specified by the user. Each test is then evaluated for how much variance it can induce in the current set of models. For details regarding computing the quality of a test, see SI Text.

We used a hill climber for test optimization. After the qualities of all five candidate tests are computed, each candidate test is randomly perturbed. If the perturbed test creates more disagreement in model predictions than the original test, the original test is replaced with the perturbed test. To create the perturbation, a variable is selected at random, and a small amount of Gaussian noise (μ = current value; σ = |0.5 current Value|) is added to its initial value. This process is continued for 100 iterations, at which point the test with the highest quality is supplied to the system, or used to locate a new sample from the data set.

Snipping.

When snipping is used, the minimum and maximum values that pass through each operator and operand during integration are recorded. During model perturbation, a subexpression may be replaced with a constant value chosen uniformly from the range defined by the minimum and maximum values previously produced by that node. This allows for the introduction of a small change in expression value while reducing the size of the expression.

The Hidden Systems.

The single pendulum system describes a single, nondriven, nondamped pendulum with no limits on its rotation. The Lotka–Volterra equations are a specific instance of a system describing interspecies competition for a common resource (38). The synthetic system of high degree was generated at random, constrained to contain only a single term for each variable, and each term must have degree 20. Equations were generated until a pair was found that was numerically stable. The lac operon system describing lactose metabolism in E. coli was adapted from Keener and Sneyd (47). Initial conditions for this system assume that the starting concentrations for beta-galactosidase, allolactose and lactose can be externally set, and the resulting behavior observed: Dekel and Alon (48) describe such an experimental setup. Indeed, modern systems biology technology is increasingly able to automatically perturb systems and measure their dynamic output on a genomic scale (49). The predator–prey data, which produced the models reported in Table 2, indicate changes in snowshoe hare and Canadian lynx populations collected by the Hudson's Bay Company and are summarized in ref. 36. The 57.2 × 5.1 cm physical pendulum arm weighed 438 g, and angle was recorded by a Novotechnik RFC 4800–600 noncontacting rotary sensor between the arm and the pendulum base. The synthetic systems reported in SI Table 4 were generated to follow the general form of the Lotka–Volterra competition equations (38). Each equation in each system was generated randomly to contain two terms, to be of second degree, and each term is parameterized by an integer chosen uniformly from the range [−3, 3]. Each system was tested for numerical stability.