Influence of base stacking on excited-state behavior of polyadenine in water, based on time-dependent density functional calculations

Abstract

A thorough study of the excited-state properties of the stacked dimers and trimers of 9-methyladenine in B-DNA conformation has been performed in aqueous solution by using time-dependent density functional calculations and the solvent polarizable continuum model, and results were compared with experimental results on polyadenine oligomers. The effect of base stacking on the absorption and emission spectra is fully reproduced by our calculations. Although light absorption leads to a state (S_B) delocalized over several nucleobases, excited-state geometry optimization indicates that S_B subsequently evolves into a state in which the excitation is localized on a single base. Analysis of the excited-state potential energy surfaces shows that S_B can easily decay into the lowest energy excited state, S_CT, which is a dark excimer produced by intermonomer charge transfer between two stacked bases. The subpicosecond features of the time-resolved experiments are interpreted in terms of ultrafast decay from S_B. After localization, two easy, radiationless decay channels are indeed open for S_B: (i) ground-state recovery, according to the same mechanisms proposed for isolated adenine and/or (ii) decay to S_CT. Our calculations suggest that the slowest part of the excited-state dynamics detected experimentally involves the S_CT state.

The absorption of UV light by nucleic acids is a process of primary biophysical interest because it can start a cascade of photochemical reactions leading to base damage and genetic modifications. The photostability of nucleic acids is thus fundamental for the development of life, and its microscopic origin has been the object of several experimental and computational studies (1). Even if a number of important aspects have not yet been convincingly assessed, there is general consensus regarding the mechanisms that explain the photostability of isolated nucleobases. Indeed, time-resolved spectroscopic studies (1) and quantum mechanical calculations (1–11) agree in suggesting the existence of an ultrafast nonradiative pathway between the bright excited state and the ground electronic state for both pyrimidine and purine nucleobases, which can explain their extremely short (≤1-ps) excited-state lifetimes. However, the excited-state behavior of DNA and nucleobase multimers (the systems of actual interest in vivo) appears much more complex, showing multiexponential decays with very different time constants (12–18). Recent experimental studies on single-stranded polyadenine (polyA) oligomers [(dA)_n] and double-stranded thymine adenine oligonucleotides [(dT)_n/(dA)_n] provide deeper insight into the behavior of the multimer excited states and the factors tuning their decay (12–18). In (dA)₁₈ single-strand and (dA)₁₈·(dT)₁₈ double-strand, a fast initial decay, in the subpicosecond time range, is indeed followed by slower relaxations (lifetimes of ≈0.8 and ≈126 ps, respectively) (12, 13).

Additional time-resolved studies on (dA)₂₀ provide evidence for temporal evolution from three distinct states, the first characterized by ultrafast decay (lifetime ≈0.39 ps) and the other two by significantly longer lifetimes (≈4.3 and ≈182 ps, respectively) (15). It has been suggested (12, 13, 15) that the slower excited-state decay is due to the presence of “excimers” related to the formation of interbase stacking. The existence of excimers has already been noted in dinucleotides (19), and also in several different oligo- and polynucleotides (12–15, 20, 21), and its signature is an emission maximum red-shifted with respect to that of the parent monomers. It is thus clear that base stacking tunes energy delocalization after photoexcitation and influences the excited-state deactivation pathway. However, a number of fundamental questions remain. First, the mechanism of excitation must be more firmly established, especially in regard to its delocalization. Two scenarios appear plausible: either the excitation is delocalized over different nucleobases (22, 23) or it is localized on individual nucleobases and the base stacking merely modulates the temporal evolution of the system on the excited-state potential energy surface (PES), providing additional decay pathways through excimer states. A detailed molecular description of the excimers and their time evolution would also allow a clearcut analysis of the possible role of charge transfer (CT) states (as suggested by refs. 12–14 and 16) and, eventually, an explication of the puzzling difference between the behavior of excimers in various stacked nucleobases. Indeed, experiments suggest that excimers influence the dynamics of polyA, whereas this is not the case for polythymine (12–14).

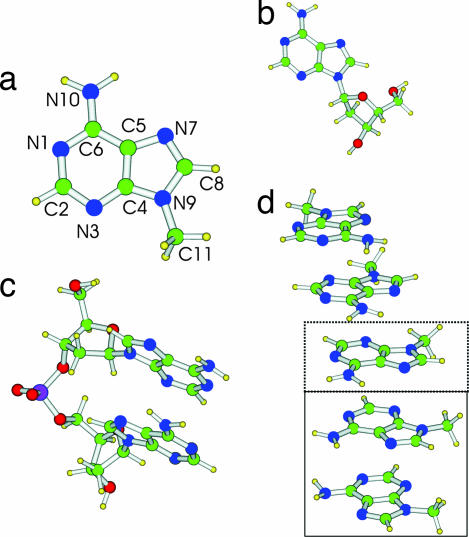
The objective of the present article is to analyze the above questions on the basis of refined quantum mechanical computations that include solvent effects, in order to attain a deeper understanding of the mechanisms underlying the influence of stacking on the excited-state dynamics in nucleic acids. We study, in particular, the ground and lowest excited electronic states of adenosine (Ado), of the dimer of 2′-deoxyadenosine (dA)₂, of 9-methyladenine (9-MA), and of its stacked dimer (9-MA)₂ and trimer (9-MA)₃ (see Fig. 1). To the best of our knowledge, this is the first study on the behavior of excited electronic states performed for stacked multimers of nucleobases by using accurate quantum mechanical methods that include solvent effects (24–26).

Fig. 1.

Schematic drawing and atom labeling of the systems investigated in this study. (a) 9-MA. (b) Adenine nucleoside (Ado). (c) (dA)₂. (d) 9-MA pentamer (9-MA)₅. (The dimer is shown enclosed in a solid-rule box, and the trimer is indicated by the added dotted box).

Results

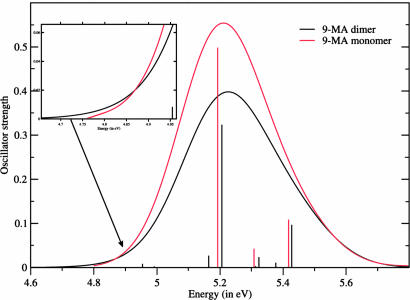
First, we checked the reliability of polarizable continuum model (PCM)/time-dependent density functional theory (TD-DFT) calculations for describing the excited states of 9-MA itself. A detailed analysis is given in supporting information (SI) Text. Briefly, our computations predict the presence of two strong absorption peaks at ≈5 and ≈6 eV, which is in good agreement with the experimental spectra (15, 27) except for a small overestimation of the energy of the red-side peak (see Fig. 2 and SI Table 2). In agreement with previous CASPT2 studies on adenine (7–11), three electronic transitions contribute to the lowest energy absorption band: two with π/π* character (usually labeled π*L_a and π*L_b, respectively) and one with n/π* character. Most of the absorption intensity is carried by the spectroscopic π*L_a state, which corresponds essentially to a HOMO→LUMO transition (we refer to the HOMO and LUMO orbitals as H and L, respectively), as shown in SI Fig. 6. In contrast, the π*L_b state is mainly an H→L + 1 transition. Replacement of the 9-methyl substituent by the deoxyribose ring and inclusion of four water molecules from the first solvation shell do not significantly change the computed vertical excitation energies (VEEs) (see SI Figs. 7 and 8 and SI Table 2).

Fig. 2.

Computed absorption spectra of 9-MA monomer and dimer. Each transition is convoluted by a Gaussian with a FWMH of 0.30 eV.

The above considerations, together with our previous work on pyrimidine nucleobases (4, 5), support the reliability of the proposed computational approach and provide a basis for the subsequent analysis of 9-MA oligomers.

(9-MA)₂ and (dA)₂ Absorption Spectra.

We have performed partial geometry optimizations (see Materials and Methods) in aqueous solution for the ground electronic state (S₀) of a supermolecule formed by two 9-MA stacked as in B-DNA (see Fig. 1d and SI Fig. 9). Stacking interaction induces small but not negligible intramolecular distortions with respect to the geometry of the isolated monomer in aqueous solution. Furthermore, in B-DNA conformation the mutual arrangement of the two monomers is not symmetric, and thus their minimum energy geometries are not perfectly equivalent. The dimer VEEs computed at the PCM/TD-PBE0 level in water are reported in Table 1, and the absorption spectrum is shown in Fig. 2. The picture issuing from a comparison between the spectra computed for the monomer and those for the dimer is very similar to its experimental counterpart. Experiments and computations agree, indicating that passage from the monomer to the multimer induces (i) a slight blue-shift of the maximum of the absorption, (ii) a slight red-shift of the low-energy side, and (iii) a significant decrease in oscillator strength.

Table 1.

VEEs and oscillator strengths issuing from PCM/TD-PBE0/6-31G8(d)//PCM/PBE0/6-31G(d) optimizations in aqueous solution of 9-MA dimer and trimer

Transition	VEE, eV	Oscillator strength	Assignment	Monomer charge	Dipole moment, D
(9-MA)2†
S1	4.96	0.008	H→L	0.05; −0.05	5.74
S2	4.99	0.002	H − 1→L (−) H→L + 1	−0.06; 0.06	6.35
S3	5.16	0.03	H − 1→L + 1	0.03; −0.03	5.76
S4	5.21	0.32	H − 1→L (+) H→L + 1	0.06; −0.06	5.88
S5	5.31	0.03	H − 2→L (+) H − 3→L + 1	0.003; −0.003	4.73
S6	5.32	0.023	H − 3→L (+) H − 2→L + 1	0.002; −0.002	4.91
S7	5.39	0.007	MIxed π/π*	−0.01; 0.01	6.70
S8	5.43	0.10	Mixed π/π*	−0.008; 0.008	6.41
(9-MA)3‡
S1	4.77	0.004	H→L	−0.91; 0.89; 0.02	15.85
S2	4.80	0.000	H→L + 1	0.02; 0.89; −0.91	19.33
S3	5.04	0.002	H→L + 2	0.06; −0.30; 0.24	7.48
S4	5.11	0.045	Mixed	0.23; −0.55; 0.32	7.33
S5	5.17	0.031	Mixed	0.02; −0.35; 0.33	8.47
S6	5.19	0.067	Mixed	0.43; −0.39; −0.04	12.1
S7	5.21	0.336	Mixed	−0.001; 0.001; 0.000	7.69
S8	5.31	0.024	Mixed	0.02; 0.00; −0.02	7.41
S9	5.34	0.005	Mixed	−0.22; 0.00; 0.22	9.10

D, debye (unit of dipole moment): 10⁻¹⁸ esu·cm [0.358 × 10⁻³⁰ m·C (meter coulomb)].

^†Monomer charge in the ground state: 0.0009; −0.0009. Dipole moment = 6.15 D.

^‡Monomer charge in the ground state: −0.003; 0.005; −0.002. Dipole moment = 8.34 D.

The most intense transition in the dimer spectrum arises from the symmetric combination of H − 1→L and H→L + 1 transitions. The orbitals involved in this transition (see SI Fig. 10) derive from the symmetric and antisymmetric combinations of the monomers H and L. The combination of two Hs and two Ls gives rises to the four transitions collected in Table 1. The interbase distance of ≈3.6 Å leads to a small but not vanishing overlap (and coupling) between the orbitals of the two 9-MA moieties. As a consequence, the energy of the orbitals involved in the bright electronic transition changes only slightly, accounting for the small blue-shift of the most intense transition [S₄ at the PMC/TD-PBE0/6-31G(d) level] with respect to the monomer spectra. Three additional weak transitions (responsible for the red-shift of the low-energy side) explain the hypsochromic effect caused by the base stacking. Excited states S₅ and S₆ are reminiscent of the n→π* electronic transitions of the monomer. The S₇ and S₈ transitions receive contributions from excitations involving several molecular orbitals, with a predominant weight of excitations from H and H − 1 toward L + 2 and L + 3. These transitions are thus the counterparts of the π*L_b electronic transition of the monomer.

To verify the influence of the deoxyribose/phosphate backbone on the excited-state properties of the nucleobases, we have optimized the ground-state geometry in aqueous solution for the (dA)₂ system (see Fig. 1c) and computed its absorption spectrum (see SI Fig. 7). The results on (dA)₂ fully reproduce the effect of base stacking on nucleobase absorption. Furthermore, both the VEE and the character of the excited states are very similar to those of (9-MA)₂ (with the single exception discussed below), thus indicating that 9-MA multimers should be suitable models for the study of polyA behavior. The only significant difference between the excited states of (9-MA)₂ and (dA)₂ is the clear CT character of the dark S₁ state in (dA)₂. This is the result of a more pronounced asymmetry in (dA)₂, which localizes the H and L orbitals mainly on two different nucleobases. As soon as the Franck–Condon (FC) region is exited, S₁ acquires a clear CT character in (9-MA)₂ as well (see below).

The effect of asymmetry has been further analyzed by partial geometry optimizations in aqueous solution on a pentamer of 9-MA molecules in the B-DNA conformation (see Fig. 1d), extracting the four possible proximal dimers. The results of the subsequent TD/PBE0 excited-state calculations are reported in SI Fig. 11. It is noteworthy that the overall absorption spectra are very similar to those shown in Fig. 2. The most striking difference with respect to the optimized dimer is the clear CT character of the weak transitions on the red side of the absorption band. In the pentamer, the presence of multiple base stacking interactions leads indeed to small variations in the equilibrium geometry of each 9-MA molecule. For example, the amino groups exhibit different degrees of pyramidalization because of the formation of weak NH₂···NH₂ hydrogen bonds. These small structural modifications increase the energy difference between the frontier orbitals of the two monomers, accounting for the CT character of some of the lowest energy transitions.

(9-MA)₂ Excited-State Geometry Optimizations.

Full geometry optimizations of the three lowest energy excited states of (9-MA)₂ with a fully equilibrated solvent were performed next (see SI Text: Computational Details). Note that, in this limit at the FC point, the bright state is the third excited state (S₃).

PCM/TD-PBE0 geometry optimization of the S₁ state leads to a global minimum, minS_CT, with a nuclear structure typical of a 9-MA⁻·9-MA⁺ stacked pair (see SI Fig. 9). In fact, the geometries of two monomers are strongly different and closely resemble those of the 9-MA radical cation and anion, respectively (see SI Fig. 12). Not surprisingly, the H→L transition induces the intermolecular transfer of a net electronic charge, so that in this region S₁ has a clear CT character and can be labeled S_CT. The minS_CT energy is 0.51 eV below the FC point, and the vertical emission energy is 3.82 eV. The above results are confirmed by PCM/TD-PBE0/6-31+G(d,p) optimizations that individuate a minimum structure with an emission energy of 3.86 eV, whose stabilization with respect to the FC point is 0.43 eV.

We also located the global minimum of the S₂ second excited adiabatic surface (hereafter S_DEL, described in SI Text). Unlike with S₁, S₂ keeps in its minimum an electronic character very similar to that exhibited in the FC region, with the electronic excitation always nearly equally delocalized over the two monomers.

Geometry optimization starting at the FC point on S₃ (the bright state) and following the adiabatic state that has the largest oscillator strength with S₀ leads to another excited-state minimum (see SI Fig. 9). In this region of the coordinate space, the bright-state minimum corresponds to the lowest energy excited state, S₁. Two different minima (corresponding to two different diabatic states) thus exist on the S₁ adiabatic PES: minS_CT and minS_B (the minimum of the bright state, S_B).

At minS_B, the S₀→S₁ electronic transition is a “localized excitation” because both H and L reside on the same monomer. Indeed, although the geometry of one monomer is very close to that of S₀, the other monomer shows a structure similar to that obtained by optimizing the π*L_a state of an isolated 9-MA molecule. The emission energy is 4.37 eV at the 6-31G(d) level and 4.22 eV at the 6-31+G(d,p) level, whereas the energy of minS_B is ≈0.25 eV above minS_CT [≈0.15 eV at the 6-31+G(d,p) level]. Geometry optimization of S_B is rather troublesome because a second state with CT character always remains close to the S_B state, so that optimization can easily collapse into minS_CT where S₁ has a CT character (vide infra).

Because TD-DFT calculations may poorly describe long-range CT transitions (28), it is important to check the reliability of the present TD-DFT calculations in predicting that the lowest energy transition in the stacked dimers and trimers (vide infra) has a CT character. In SI Text, we support in detail the reliability of our results. Here, we note that our results are in good agreement with the experimental absorption and emission spectra and that test calculations at the CASSCF(8,8)/PCM level confirm the conclusions of TD-DFT calculations. Furthermore, the values of ionization potential and electron affinity of 9-MA in aqueous solution indicate that the estimate of the S_CT transition energy is correct (see SI Text). Finally, when applied to the study of stacked cytosine dimer, our computational approach provides a picture extremely similar to that of very recent CASPT2 calculations (23), confirming that TD-PBE0 can accurately describe the excited-state behavior of stacked nucleobases.

9-MA Trimer.

We have optimized in aqueous solution the geometry of (9-MA)₃, a trimer of 9-MA molecules in the B-DNA stacking geometry. The VEEs for the lowest energy excited states are collected in Table 1 and the computed absorption spectra in SI Fig. 13. As already found for (9-MA)₂, the absorption maximum of the spectra is slightly blue-shifted and less intense than that of the monomer, thus confirming that base stacking causes significant hypochromic effects. The bright electronic transition S_B (corresponding to the seventh excited state in the solvent nonequilibrium regime) is delocalized over the three monomers and does not exhibit any CT character, as shown in Table 1 by the Mulliken population analysis. On the other hand, the two lowest energy excitations, S₁ and S₂, have a significant CT character and are very similar to the S_CT state of (9-MA)₂. They correspond indeed to the transfer of a net electronic charge from the “central” monomer toward a lateral monomer. Interestingly, the CT transition is always localized on a dimer, i.e., there is one monomer that is not affected by the electronic transition. Indeed, geometry optimization of the lowest energy excited state leads to a structure analogous to the S_CT minimum of (9-MA)₂. The central, and one of the lateral, monomers exhibit a geometry similar to that of 9-MA in its cationic and anionic form, respectively. The other lateral molecule does not show any significant deviation from the S₀ geometry. The emission energy of this transition (3.87 eV) is very close to that of S_CT in (9-MA)₂ (3.82 eV).

Scans of the (9-MA)₂ Excited-State PES.

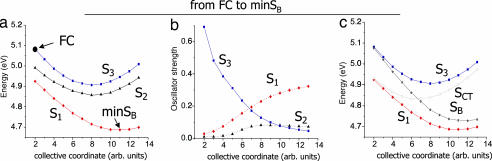
Preliminary insights into the dynamical behavior of (9-MA)₂ can be gained by examining selected energy scans of the lowest energy excited states in the region connecting the FC point to the excited-state minima. Fig. 3a reports the energy of the three lowest energy states in the path between the FC point and minS_B. The S₁ and S₃ adiabatic states along this path (see Fig. 3b) drastically change their electronic character (interchanging their oscillator strengths with S₀, hereafter F_n0). Thus, it has been convenient to define at each point of the path the two diabatic states S_B and S_CT (bright and dark, respectively) introduced in the previous section (see Fig. 3c and SI Text for technical details). At the FC point, the optical excitation drives the system essentially on the S₃ state that, as shown by Fig. 3b, brings most of the F_n0. In contrast, S₁ is nearly dark. At this point, therefore, the two adiabatic states S₃ and S₁ correspond to the diabatic states S_B and S_CT. Subsequently, the electronic character of S₁ changes strongly along the path and acquires oscillator strength at the expense of S₃, transforming progressively into the bright S_B state, even if some residual difference among the diabatic and adiabatic states persists at the minS_B point because S₃ also retains a little oscillator strength (see SI Text for further details).

Fig. 3.

Energy plots of the lowest energy adiabatic excited state of (9-MA)₂ (a), their oscillator strength (b), and the corresponding diabatic states (c) in the region of the coordinate space connecting the FC region and the S_B minimum.

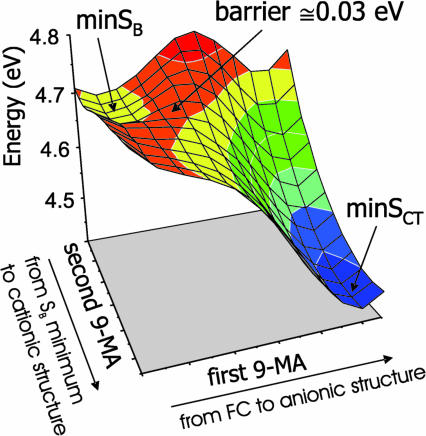
In Fig. 4, we show a two-dimensional (2D) scan of the S₁ adiabatic excited PES from the local minimum minS_B to the global minimum minS_CT. As indicated on the axes, each coordinate describes the motion of a single monomer. The PES shows that the two minima are separated by a very low energy barrier (≈0.03 eV). Furthermore, along this path (see SI Fig. 14) S₁ soon changes its electronic character, losing all oscillator strength with respect to S₀, indicating that the diabatic bright S_B and dark S_CT states cross very close to minS_B.

Fig. 4.

PES of the lowest energy adiabatic excited state of (9-MA)₂ in the region of the coordinate space connecting the S_B and S_CT minima.

Finally, we repeated the scans from FC to minS_B, and from minS_B to minS_CT, for different intermonomer distances, checking that our conclusions are not significantly altered by the inclusion of this degree of freedom, whose variation in any case would be limited by the deoxyribose/phosphate backbone (see SI Text for a more detailed discussion of this point).

Discussion

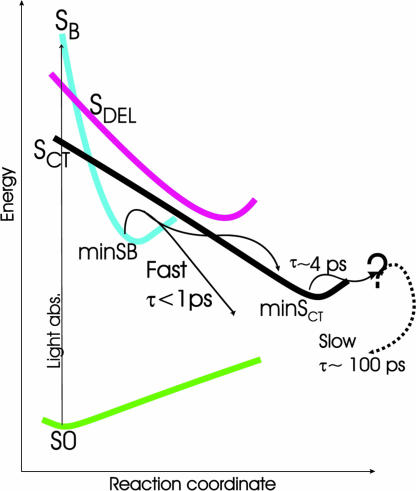
On the basis of the results analyzed in the previous sections, Fig. 5 shows a consistent explanation of the time-resolved spectroscopic studies on adenine oligomers. It is convenient to discuss the short- and long-time behaviors separately.

Fig. 5.

Schematic description of the possible time-evolution of the excited states of the adenine oligomer.

Short-Time Dynamics.

In polyA, the shortest excited-state lifetimes are in the subpicosecond range [≈0.39 ps (15) or ≈0.8 ps (12, 13)], similar to those of Ado. The state involved in these decay channels is characterized by a fluorescence maximum at ≈310 nm (4.0 eV) very close to that of the monomer (≈309 nm) and with a comparable emission intensity (15). Our computations indicate that the system is initially excited essentially onto the bright S_B state, which therefore is expected to be involved in the measured ultrafast process. We have shown that the S_B state is the “multimer” counterpart of the π*L_a bright excited state of the monomer, and that, although in the FC region S_B is delocalized over different monomers, excited-state geometry optimization localizes the excitation on a single monomer. Furthermore, S_B exhibits an emission energy of 4.37 eV [4.22 eV at the 6-31+G(d,p) level] that can be related to the experimental emission maximum of the “fastest state” in polyA (4.0 eV). Two considerations can account for the residual discrepancy between computed and experimental values. First, the computed VEE of the bright S_B state is also overestimated with respect to the absorption maximum by ≈0.25 eV. Second, the mutual arrangement of the dimer has been frozen to that adopted in B-DNA ground state, so that fully relaxed geometry optimizations of the intermolecular degrees of freedom would favor the excited state and decrease the computed/experimental difference.

Always bearing in mind that the details of the ground-state recovery depend on the dynamics of the stacking interactions and on the presence of nonstacked bases, our calculations suggest two possible radiationless ultrafast deactivation pathways for S_B.

Monomer-like decay pathway.

After localization on a single monomer, S_B state can follow the same decay pathways highlighted for π*L_a in the monomer. Indeed, theoretical studies on adenine (7–11) indicate that two paths characterized by small or vanishing energy barriers lead from the bright excited π*L_a state to conical intersections with the ground state, S₀. These two paths could be responsible for the two different excited-state lifetimes (≈0.13 and ≈0.45 ps) shown by Ado (15). In this scenario, one must conclude that the fastest excited-state decay pathway of the monomer is absent, or slowed, in the polymer. Several effects could, in principle, explain this. First, base stacking could make more difficult the out-of-plane deformation of the ring needed to reach the conical intersection with S₀ (7–11). Alternatively, one of the two paths (probably the one involving the π*L_b state) may not be accessible in the polymer. Finally, the nuclear rearrangement leading from an excitation delocalized on two or more bases to one localized on a single base could require a nonvanishing time.

Additional decay pathway due to stacking.

The scans of the excited-state PES for (9-MA)₂ suggest an additional decay mechanism for S_B in the multimers, leading the system into the S_CT state. In fact, S_B interacts with S_CT along the path from the FC point to the S_B minimum and, furthermore, a very small barrier separates the minima of the S_B and S_CT states. These features suggest that, in the polymer, the decay to S_CT is competitive with the monomer-like decay to S₀.

A final remark concerns the lively debate about the delocalized (17, 18, 22, 23) or localized (12–15, 19) nature of the bright state in nucleic acids. We have shown that an excitation delocalized over multiple bases in the FC region can lead to a “local” excited state. In other words, the fact that a state exhibits decay and emission properties typical of a localized excitation does not necessarily imply that the excitation is also localized during the absorption process. On the other hand, our results suggest that the possible delocalization/localization of the bright state in the FC region is ruled by the degree of asymmetry of the various monomers in the multimer.

It is noteworthy that, according to our calculations, n→π* transitions should not play any relevant role in the polyA excited-state dynamics, at least in aqueous solution (see SI Text).

Long-Time Dynamics.

In regard to the long-lifetime (>4 ps) component of the excited-state population, experiments on polyA indicate the existence of two “excimer-like” states: one with a lifetime of ≈4.3 ps (15) and another with a lifetime > 100 ps (≈182 ps according to ref. 15 and ≈126 ps according to refs. 12 and 13). In (dA)₂₀, the former state is characterized by a very weak fluorescence maximum at 348 nm (3.56 eV) (15). According to our analysis, the S_CT excited state resulting from the CT between two stacked monomers is the best candidate for this state. Indeed, the computed emission maximum of S_CT has a very small oscillator strength and its energy (3.86 eV) correlates well with that of the excimer (3.56 eV), bearing in mind that, as reported above, our calculations overestimate the emission energy of the bright state as well (by 0.20 eV). Furthermore, besides its small fluorescence quantum yield, several experimental results suggest that this excimer has a significant CT character (12, 13, 15). Finally, several features of S_CT are fully consistent with the experimental findings. First, according to our computations, the formation of S_CT does not require any substantial conformational rearrangement or modification of the stacking geometry and is thus compatible with a fast conversion of the bright state. Second, the excited-state PES indicates that the bright S_B state has a significant tendency to decay to S_CT. The two diabatic states cross along the path between the FC and minS_B structures and, although a reliable evaluation of the transition probability is beyond the scope of our study, additional 1D scans reported in SI Text suggest that if the system passes on the dark S_CT state it is irreversibly accelerated toward its minimum minS_CT, reaching a region where it is no longer coupled to S_B and cannot therefore jump back onto S_B. Furthermore, after reaching minS_B, the system can easily decay to S_CT by moving adiabatically on S₁. The above finding fully agrees with the experimental indications that the large majority of the excited population in polyA decays to excimer-like states (12, 13, 15).

The minimum energy structure of S_CT proves the existence of an anion-like 9-MA monomer stacked with a cation-like 9-MA monomer. On a longer time scale, this would likely lead to a significant geometry rearrangement within the single strand, which would lose its regular and symmetric stacking geometry. Our calculations do not provide any definite indication regarding the nature of this geometry rearrangement because, on this time scale, structural fluctuations of the strand should be taken into account. However, the existence of a fully relaxed CT minimum could be related to the excimer-like state characterized by the slowest decay (>100 ps); in (dA)₂₀ this state is characterized by a fluorescence maximum of 390 nm (3.18 eV) (15). Both the slowness of the decay and the large Stokes shift are indeed compatible with a significant conformational rearrangement within the DNA strand.

The CT character of the excimer suggests that another possible decay route can involve an excited-state proton transfer between adjacent bases or, more likely, with solvent molecules. The involvement of a proton transfer in the excited-state deactivation has already been proposed in double-stranded DNA (29). In the presence of anionic and cationic species, interstrand proton transfer could be more favored and its role in the deactivation pathway more important.

In summary, the present study reports a detailed molecular description of the most relevant excited states of polyA oligomers, providing strong evidence in support of a fast transfer from the bright spectroscopic state to an underlying excimer-like state with a clear CT character in a stacked dimer. On this basis, it is possible to suggest a consistent explanation for the most significant experimental results and to identify the states responsible for the different lifetime components. Obviously, the situation in single- and double-strand DNA multimers can be much more complex than that modeled in our calculations. The experimental absorption and emission spectra can receive contributions from multiple states, involving a varying number of stacked pairs and with different stacked geometry, strongly modulated by structural fluctuations of the multimer. In double-strand DNA, hydrogen-bonded pairs could play a relevant role, from both static and dynamic viewpoints. For example, simple thermodynamic considerations suggest that interstrand CT states can be present, because the electron affinity of thymine is larger than that of adenine. All of the above effects are consistent with the multiexponential excited-state decay shown by the latest time-resolved experiments (17). Additional theoretical and experimental efforts are thus necessary to fully assess the behavior of the excited states in nucleic acids. On the other hand, it is encouraging that our calculations are able to reproduce the effect of base stacking on the absorption and emission spectra. This may represent a significant step toward a deeper understanding of the influence of base stacking on the excited-state decay in DNA.

Materials and Methods

The geometry of adenine stacked oligomers in a single-stranded polynucleotide has been extracted from the experimental structure of polydeoxyadenosine·polydeoxythymine (1PLY.pdb), a double-stranded DNA. In the ground- and excited-state geometry optimizations of the 9-MA oligomers, the intramolecular degrees of freedom were fully unconstrained, whereas the interbase distance and mutual orientation were kept frozen to their experimental value. Whenever not explicitly stated, geometry optimizations have been performed in aqueous solution at the PBE0/6-31G(d) (30) and TD-PBE0/6-31G(d) (31) levels, with bulk solvent effects included by using the PCM (32, 33). The effect of basis set extension on the VEEs has been estimated by test computations with more extended 6-31+G(d,p) and 6-311+G(2d,2p) basis sets. We checked, by test calculations using the counterpoise method (see SI Text), that inclusion of basis set superposition errors does not significantly affect our conclusions. Ionization potential and electron affinity values have been computed as the difference of energies of the neutral and charged species. Possible pathways available to the system upon excitation have been characterized by 1D and 2D scans of the excited-state PES. More details regarding the computational procedures, and definition of the relevant diabatic states can be found in SI Text. All of the quantum mechanical calculations were performed by using a development version of the Gaussian 03 software (34).

Abbreviations

9-MA

9-methyladenine

CT

charge transfer

FC

Franck–Condon (region)

TD-DFT

time-dependent density functional theory

PCM

polarizable continuum model

PES

potential energy surface(s)

VEE

vertical excitation energy.