Concentration-Dependent Synergy and Antagonism within a Triple Antifungal Drug Combination against Aspergillus Species: Analysis by a New Response Surface Model

Abstract

Triple antifungal combinations are used against refractory invasive aspergillosis without an adequate understanding of their pharmacodynamic interactions. We initially studied the in vitro triple combination of voriconazole, amphotericin B, and caspofungin against Aspergillus fumigatus, A. flavus, and A. terreus by a spectrophotometric microdilution broth method after 48 h of incubation. We then analyzed these results with a recently described nonlinear mixture response surface E_max-based model modified to assess pharmacodynamic interactions at various growth levels. The new model allows flexibility in all four parameters of the E_max model and is able to describe complex pharmacodynamic interactions. Concentration-dependent pharmacodynamic interactions were found within the triple antifungal combination. At the 50% growth level, synergy (median interaction indices of 0.43 to 0.82) was observed at low concentrations of voriconazole (<0.03 mg/liter) and amphotericin B (≤0.20 mg/liter) and at intermediate concentrations of caspofungin (0.95 to 14.88 mg/liter), whereas antagonism (median interaction indices of 1.17 to 1.80) was found at higher concentrations of voriconazole and amphotericin B. Ternary plot and interaction surface analysis further revealed the complexity of these concentration-dependent interactions. With increasing concentrations of amphotericin B, the synergistic interactions of voriconazole-caspofungin double combination decreased while the antagonistic interactions increased. A similar effect was observed when voriconazole was added to the double combination of amphotericin B and caspofungin. In conclusion, the new nonlinear mixture-amount response surface modeling of the triple antifungal combination demonstrated a net antagonism or synergy against Aspergillus species depending upon drug concentrations and species.

Invasive aspergillosis is an important cause of morbidity and mortality in immunocompromised patients (20). New therapeutic approaches are needed to improve outcome (30). The introduction of newer antifungal agents with different mechanisms of action has made combination therapy a possibility and an area of compelling investigational interest (38). Because of their different mechanisms of action, triazoles, echinocandins, and polyenes are likely candidates for combination therapy. Echinocandins inhibit the synthesis of 1,3-β-d-glucan, a key component of the cell walls of most fungi; triazoles inhibit the synthesis of ergosterol by inhibiting the enzyme lanosterol C-14 demethylase; and polyenes act directly at the fungal cell membrane to alter its integrity (10).

Triple combination therapy using all three classes of antifungal agents may be used in refractory aspergillosis (8, 35, 39). However, this practice has not been well studied, and the in vitro pharmacodynamic interactions are unknown. Preclinical studies are therefore required to understand the pharmacodynamic interactions and appropriately adjust in vivo dosing regimens in order to maximize synergistic effects and minimize the antagonistic ones. In vitro pharmacodynamic interactions within a triple combination can be complex (24); powerful analytical tools are required to accurately describe the effects of the triple combination in a wide range of drug concentrations and to determine the nature and intensity of antifungal pharmacodynamic interactions. Response surface methodologies provide the necessary tools to capture the information present in the full concentration-effect data set for two or more agents and to quantify synergy and antagonism (9).

A new nonlinear mixture-amount response surface model for analyzing three-drug combinations was recently described (40). By contrast with other fully parametric response surface models, the new model is flexible enough to describe complicated response surfaces and to determine complex patterns of synergy and antagonism. With this model, response surfaces are modeled using the sigmoid E_max concentration-effect relationship, and pharmacodynamic interactions are assessed based on the Loewe additivity zero interaction theory. It was previously found that amphotericin B interacts in a concentration-dependent manner with triazoles (26), whereas echinocandins interact synergistically with azoles and polyenes (6, 31). Given the expected complexity of the pharmacodynamic interactions within a triple combination of polyene-triazole-echinocandin, we used the new response surface model to analyze the in vitro triple combination of amphotericin B with voriconazole and caspofungin against three Aspergillus species.

MATERIALS AND METHODS

Isolates.

Three clinical isolates each of Aspergillus fumigatus (4215, 2025, and 2350), Aspergillus flavus (50, 8B, and 10B), and Aspergillus terreus (644, 1290, and 1548) were grown on potato dextrose agar slants at 30°C for 5 to 7 days. Conidia were harvested by scraping agar slants with a sterile pipette to achieve a suspension in sterile normal saline. The densities of the conidial suspensions were measured and adjusted on a spectrophotometer (80 to 82% transmittance for all species) to yield a suspension of 10⁶ conidia/ml of each isolate. Each suspension of conidia was diluted 1:25 in the medium in order to obtain four times the final inoculum size, which ranged from 0.5 ×10⁴ to 4.0 ×10⁴ CFU/ml in each well. Inoculum preparation, broth inoculation, and incubation time were based on the CLSI (formerly NCCLS) M38-A broth microdilution guidelines for mold susceptibility-testing (29). Candida parapsilosis (ATCC 22019), and Candida krusei (ATCC 6258) were used for quality control purposes.

Medium.

RPMI 1640 with l-glutamine but without bicarbonate (BioWhittaker Cambrex Bio Science, Walkersville, MD) buffered at pH 7.0 with 0.165 M 1,3-N-morpholino propane sulfonic acid (MOPS) (Sigma-Aldrich, Saint Louis, MO) was used throughout all experiments.

Antifungal drugs.

Caspofungin, (Merck and Company, Rahway, NJ) was obtained as reagent grade powder from the manufacturer and dissolved in medium in order to obtain an initial solution of 1,024 mg/liter. Voriconazole (Pfizer Pharmaceuticals, New York, NY) was obtained in a 10,000-mg/liter vial for injection. Amphotericin B deoxycholate (Apothecon Ben Venue Laboratories, Inc., Bedford, OH) at a stock concentration of 5,000 mg/liter was prepared in sterile water. The lack of any antifungal effect of the excipients of amphotericin B and voriconazole clinical formulations was verified with the MICs for the quality control strains and by comparing antifungal activities of clinical formulations with those of pure powders used previously in our laboratory. The range of concentrations was chosen in such a way as to include the MICs of the drugs alone and extend to lower drug concentrations that are clinically achievable.

Voriconazole and caspofungin were twofold serially diluted in the medium in order to obtain four times the strength of the final concentrations, which ranged from 0.015 mg/liter to 1.0 mg/liter and from 0.5 mg/liter to 256 mg/liter, respectively. A 50-μl aliquot of each concentration of voriconazole was combined with 50 μl of each concentration of caspofungin, including the drug-free controls, in six 96-well flat-bottom microtitration plates (Corning Inc., Corning, NY) in order to obtain 11-by-8 checkerboards. The wells of last column contained only medium. A 50-μl aliquot of medium containing four times the final concentrations of amphotericin B (0, 0.1, 0.2, 0.3, 0.4, and 0.5 mg/liter) was added to each of the six microtitration plates containing the voriconazole-caspofungin combination. Microtitration plates were stored at −70°C for less than 1 month prior to the start of testing. In separate plates, amphotericin B was serially diluted in medium in order to obtain final concentrations ranging from 0.1 to 2 mg/liter.

Susceptibility testing.

Microtitration plates were thawed on the day of testing and inoculated with 50 μl of conidium inoculum. Plates were incubated without stacking at 37°C in a 95% humidified environment (Steri-Cult 200 incubator; DoveBid Inc., CA) for a total period of 48 h. Fungal growth in each microtitration well of all six plates was assessed spectrophotometrically at 405 nm using a 16-scan point spectrophotometer (Elx808; Bio-Tek Instruments, Winooski, VT) with the following equation: percentage of growth = (optical density at 405 nm [OD₄₀₅] of a well − background OD₄₀₅ of this well)/(OD₄₀₅ of the drug-free well − background OD₅₄₀ of the drug-free well) × 100%, where the background OD₄₀₅s were measured from six voriconazole-caspofungin checkerboard plates containing 0 to 0.5 mg/liter amphotericin B and inoculated with a conidium-free inoculum and were handled in the same way as the inoculated plates with the conidium-containing inocula. All tests were repeated three times on different days, and the percentage of growth was calculated for each day based on the ODs of drug-free control of the same day. Furthermore, the MIC was determined for all three drugs as the lowest concentration showing no visual growth. For caspofungin, the minimal effective concentration (MEC) was determined from previous experiments as the lowest drug concentration showing formation of short, stubby, and highly branched hyphae.

Drug interaction and statistical analysis.

Antifungal drug interactions were analyzed using a new nonlinear mixture-amount response surface model (40), which is based on the Loewe additivity zero interaction theory (9). In Loewe additivity theory, interactions are assessed at a particular effect (e.g., percentage of growth) with the combination index (CI) calculated by the following equation: CI = C_A/EC_A + C_B/EC_B + C_C/EC_C, where C_A, C_B, and C_C are the concentrations of the drugs A, B, and C in the combination which elicits a certain effect and EC_A, EC_B, and EC_C are the isoeffective concentrations of the drugs A, B, and C acting alone. When the CI is 1, >1, or <1, the interaction for that particular effect is additive (no interaction), antagonistic, or synergistic, respectively. In order to apply the new response surface model, concentrations of voriconazole, caspofungin, and amphotericin B were transformed to potency units as described below.

Initially, the E_max model (sigmoidal curve with variable slope) was fitted to individual drug concentration-effect data, and the effective concentrations producing 50% of E_max (EC₅₀) was estimated for voriconazole (EC_50,VOR), caspofungin (EC_50,CAS), and amphotericin B (EC_50,AMB). The E_max model is described by the equation E = (E_max − B) × (C/EC₅₀)^m/[1 + (C/EC₅₀)^m] + B, where E is the percentage of growth (dependent variable) at the drug concentration C (independent variable), E_max is the maximum percentage of growth observed in the drug-free control, B is the minimum percentage of growth observed at infinite drug concentration, EC₅₀ is the drug concentration producing 50% of the E_max, and m is the slope (Hill coefficient). The maximum and the minimum of the E_max model were shared among the three drugs for each Aspergillus isolate. Because the logarithms of EC₅₀ values rather than the EC₅₀ values themselves are normally distributed, regression analysis was performed using the logarithms of the drug concentrations in the E_max model with the modified equation E = (E_max − B)/(1 + 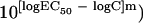+ B, derived from the above standard E_max equation (for more details, see reference 29). Analysis was performed using Prism 4.0 for Mac OSX (GraphPad Prism Inc., San Diego, CA).

Drug concentrations were then transformed to potency units of voriconazole (U_VOR), caspofungin (U_CAS), and amphotericin B (U_AMB) as U_VOR = C_VOR/EC_50,VOR, U_CAS = C_CAS/EC_50,CAS, and U_AMB = C_AMB/EC_50,AMB, where C_VOR, C_CAS, and C_AMB are the actual concentrations of voriconazole, caspofungin, and amphotericin B, respectively. For each combination of the three drugs, the relative potency units x of voriconazole, y of caspofungin, and z of amphotericin B were calculated as U_VOR/U, U_CAS/U, and U_AMB/U, respectively, where U is the total units U_VOR + U_CAS + U_AMB. The relative potency units range from 0 to 1, and by definition x + y + z = 1.

The global response surface model is described by the following set of equations:

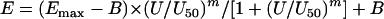(1)

where E is the percentage of growth at any combination of U_VOR, U_CAS, and U_AMB; E_max is the maximum percentage of growth in absence of any drug; B is the minimum percentage of growth in infinite drug concentrations; U is the total potency units and is equal to U_VOR + U_CAS + U_AMB; U₅₀ is the total potency units producing 50% of E_max − B and is given by

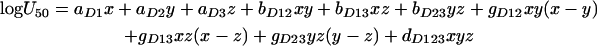(2)

and m is the slope and is given by

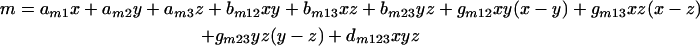(3)

Equations 2 and 3 are full cubic canonical mixture polynomials which describe logU₅₀ and m in function of x, y, and z. The coefficients a, b, g, and d are model parameters estimated from the data with regression analysis. In contrast to m and logU₅₀, B was not modeled in function of x, y, and z because all drugs completely inhibit fungal growth at high concentrations. E_max and B were left free to be fitted using the entire data set. Note that when x, y, or z is 1, the global model collapses to the E_max model of the concentration-effect curves of the drugs alone. In this case, a_D1, a_D2, and a_D3 are the logarithms of U_50,VOR, U_50,CAS, and U_50,AMB (i.e., the potency units of voriconazole, caspofungin, and amphotericin B, respectively, that result in 50% growth) and a_m1, a_m2, and a_m3 are the slopes of the voriconazole, caspofungin, and amphotericin B concentration-effect curves, respectively.

Because the logarithms of the potency units were used, equation 1 is modified to

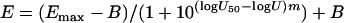(4)

as for the E_max model described above (28). Equation 4 together with equations 2 and 3 were used to fit the global model to the average percentage among the three replicates performed on different days with a weighted (inverse of average variance), nonlinear regression analysis using the nonlinear platform of JMP5.0.1 software (SAS Institute, Cary, NC). The goodness of fit was checked with a variety of diagnostic tests, such as R² values, analysis of variance, lack-of-fit test, residual and leverage plot analysis, correlation matrix, and standard error of parameters. Furthermore, in order to compare the concentration-effect curves of voriconazole, caspofungin, and amphotericin B alone determined with the global model and the E_max model, the a_m1, a_m2, and a_m3 of the global model were compared with the slopes derived from the E_max model, and the deviation of a_D1, a_D2, and a_D3 from 0 was assessed (a significant deviation will indicate that U_50,VOR, U_50,CAS, and U_50,AMB determined by the global model differ from 1 and thus the concentrations that produce 50% of growth will be different than the EC₅₀s determined by the E_max model).

The basic concept of the global response surface model is that the role of each drug is described by its relative potency units in the mixture, which behaves as a new drug with its own sigmoidal concentration-effect relation. The mathematics of the global model are an extension of the E_max model for a single drug to a model that considers each ratio of the three drugs as a drug in its own right. If all coefficients in equation 2 equal 0, then U₅₀ = 1, indicating Loewe additivity. The U₅₀ value is equivalent to the classical combination index of Loewe additivity (9, 40). This derives from Loewe additivity theory. U₅₀ is the sum U_50,VOR + U_50,CAS + U_50,AMB, where U_50,VOR, U_50,CAS, and U_50,AMB are the potency units of voriconazole, caspofungin, and amphotericin B in combination, respectively, that result in 50% growth. Due to transformation of drug concentrations to potency units as described above, U₅₀ = U_50,VOR + U_50,CAS + U_50,AMB = C_50,VOR/EC_50,VOR + C_50,CAS/EC_50,CAS + C_50,AMB/EC_50,AMB, where C_50,VOR, C_50,CAS, and C_50,AMB are the concentrations of voriconazole, caspofungin, and amphotericin B in combination, respectively, that result in 50% growth. However, according to Loewe additivity theory, C_50,VOR/EC_50,VOR + C_50,CAS/EC_50,CAS + C_50,AMB/EC_50,AMB is the combination index for an effect of 50% growth. Thus, U₅₀ is the combination index indicating Loewe additivity, antagonism, and synergy when it is 1, >1, and <1, respectively, for an effect of 50% of growth.

In order to assess interactions at different growth levels than 50%, the U₅₀ was used to calculate the total potency units U_E for any growth level E (e.g., 20% or 80% of the E_max − B) with the following equation:

(5)

Equation 5 can be derived from equation 4 by solving for logU. This equation was not included in the initially published three-drug interaction model, but we used it in order to assess interactions at different growth levels. Interactions at 20% or 80% of growth may differ from interactions at 50% of growth, particularly when the slopes change across the response surface as indicated by equation 3. Thus, in the new modified global model, equation 5 provides the total amount of potency units U_E of the three drugs that results in a particular effect E. Interaction at that particular effect E can be determined by comparing the U_E with the theoretical amount of potency units U_ADD if the drugs were acting additively. U_ADD can be derived from equations 5, 2, and 3 with the interaction terms b_D12, b_D13, b_D23, g_D12, g_D13, g_D23, d_D123, b_m12, b_m13, b_m23, g_m12, g_m13, g_m23, and d_m123 equal to 0. Thus,

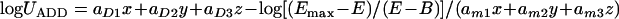(6)

If the interaction index (I) = U_E/U_ADD was higher than 1, then Loewe antagonism was concluded, and if I was lower than 1, then Loewe synergy was claimed. In any other case, Loewe additivity was concluded. The statistically significant deviation of I from 1 was assessed based on the 95% confidence interval of logU_E derived using the covariance matrix calculated based on the standard errors of the global model parameters and the correlation matrix obtained by the JMP5.0.1 program.

Based on equation 2, additivity is indicated when U₅₀ is 1, i.e., when all coefficients of equation 2 are 0. However, even if coefficients b, g, and d are 0, because of the two-stage fitting process a_D1, a_D2, and a_D3 will rarely be exactly 0 (i.e., the individually determined EC₅₀s will be slightly different than the ones determined with the global model), and therefore deviation of U₅₀ from 1 would not always indicate departure from Loewe additivity. In the original model, this was overcome with the introduction of the leading factor (1 − x)(1 − y)(1 − z) into equation 2, which forces the U₅₀ values to 1 for single-drug mixtures. We did not include this factor in equation 2 because preliminary analysis showed that the fit was worse than that of the model without the factor. In our modified global model, this problem was overcome by calculating the interaction index I as described above using equations 5 and 6, which results in indices of 1 for single-drug mixtures.

In addition, without the leading factor, when a_D1, a_D2, and a_D3 are close to 0 and a_m1, a_m2, and a_m3 are close to the Hill slopes determined by the E_max model for each drug alone, the concentration-effect curves predicted by the modified global model for the drugs alone are similar to those predicted by the E_max model. Thus, the a_D1, a_D2, and a_D3 values can serve as internal controls for the fitness of the modified global model. When the leading factor was included, for many data sets, a_D1, a_D2, and a_D3 deviated significantly from 0 (up to six times for some data sets). In addition and more importantly, since the a_D1, a_D2, and a_D3 of the new modified global model without the leading factor correspond to the logarithms of U_50,VOR, U_50,CAS, and U_50,AMB of the concentration-effect curves of each drug, we could determine interactions at any effect (growth) level by using equations 5 and 6. Furthermore, additive effects can be estimated with the modified global model for any drug combination using by equations 2, 3, and 4 without the interaction terms b_D12, b_D13, b_D23yz, g_D12, g_D13, g_D23, d_D123, b_m12, b_m13, b_m23, g_m12, g_m13, g_m23, and d_m123 in equations 2 and 3.

In order to summarize the data, the median and range among the three isolates of the median antagonistic and synergistic interaction indices, the percentages of synergistic and antagonistic combinations among the 327 different fixed-ratio combinations tested in checkerboards, and the corresponding median drug concentrations were determined and are presented for each Aspergillus species. Differences in drug concentrations that produced synergistic and antagonistic interactions were assessed after log transformation with an analysis-of-variance test followed by Bonferroni posttest. P values smaller than 0.05 were considered significant. In order to visualize the percentage of reduction or increase of growth compared to the additive effect in synergistic and antagonistic combinations, respectively, the percentage of growth at each combination of the three drugs was subtracted from the theoretical additive percentage of growth obtained with equations 2, 3, and 4 with elimination of the interaction terms b_D12, b_D13, b_D23, g_D12, g_D13, g_D23, d_D123, b_m12, b_m13, b_m23, g_m12, g_m13, g_m23, and d_m123.

In order to study whether the triple combination is better overall than the double combinations, the sum percentage of all synergistic and antagonistic interactions within the two-drug interaction surfaces was calculated and plotted for each concentration of the third drug. Thus, we analyzed the effects of amphotericin B, voriconazole, and caspofungin concentrations, respectively, on the synergistic and antagonistic volumes of voriconazole-caspofungin (7 × 10 combinations), amphotericin B-caspofungin (5 × 10 combinations), and amphotericin B-voriconazole (5 × 7 combinations) double combinations for all isolates of each Aspergillus species.

RESULTS

Activities of individual antifungal agents.

In order to quantify the antifungal activity of individual agents against each isolate, we report the EC₅₀s determined by the E_max model fitted to concentration-effect data for each compound alone. The median (range) EC₅₀s of voriconazole, caspofungin, and amphotericin B were 0.23 (0.13 to 0.28) mg/liter, 95.54 (71.05 to 473.9) mg/liter, and 0.44 (0.24 to 0.88) mg/liter for all isolates, respectively.

The MICs corresponding to complete growth inhibition were 0.25 to 1 mg/liter of voriconazole, 128 to >256 mg/liter of caspofungin, and 0.5 to 2 mg/liter of amphotericin B for all species. Because MICs are closer to concentrations producing 20% of growth (EC₂₀s) than EC₅₀s, the EC₂₀s were used to assess pharmacodynamic interactions within the triple combination that take place at concentrations close to the MICs of antifungal agents. The MECs of caspofungin were 0.5 to 1 mg/liter for all isolates.

In order to study the steepness of the concentration-effect curves, we also reported the Hill slopes determined by the E_max model fitted to the concentration-effect data for each compound alone. The corresponding median (range) Hill slopes of the concentration-effect curves of voriconazole, caspofungin, and amphotericin B were −2.85 (−6.18 to −1.73), −3.00 (−5.43 to −0.45), and −4.44 (−9.20 to −2.31) for all isolates, respectively.

Goodness of fit of the new modified global model.

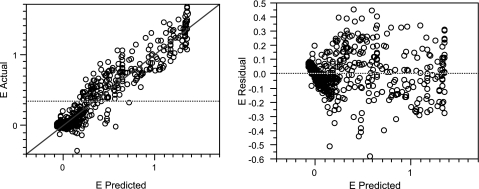
In order to check how well the modified global model described the data, we used several diagnostic tests. The R² values were consistently greater than 0.82 in all fits. There was no statistically significant deviation of the modified global model from the data based on analysis of predicted versus actual data and of the residuals for all isolates, as shown in Fig. 1 for a representative A. fumigatus isolate. Other diagnostic tests, which consisted of analysis of variance, lack-of-fit test, correlation matrix, and standard error of parameters, were consistent with the findings in Fig. 1 for all isolates. None of the 95% confidence intervals of the estimates of the polynomial model parameters included 0 (see, for example, the Fig. 5 legend), which indicates the significance of each of these parameters in the final model.

FIG. 1.

Diagnostic plots used to assess the goodness of fit of the modified global model to the data. Plots of actual versus predicted data (left) and of residuals versus predicted data (right) for the A. fumigatus 4215 isolate are shown (R² = 0.91 for the modified global model).

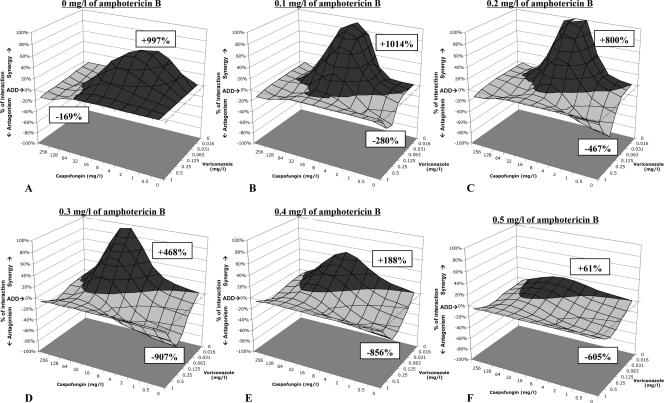
FIG. 5.

Interaction surfaces for the triple combination of voriconazole, caspofungin, and amphotericin B against the A. fumigatus 4215 isolate. The percentages of interaction (additive minus experimental percentage of growth obtained by the modified global model) are plotted for the voriconazole-caspofungin combination in the presence of increasing concentrations of amphotericin B. Volumes above the zero plane (dark gray) indicate synergistic interactions (less growth was observed than the theoretical additive), whereas volumes below the zero plane (light gray) indicate antagonistic interactions (more growth was observed than the theoretical additive). The height or depth of these volumes is proportionally related to the intensity of the synergistic and antagonistic interactions, respectively. The numbers above the synergistic volumes and below the antagonistic ones indicate the sum of all synergistic and antagonistic interactions, respectively, as a measure of both intensity and frequency of these interactions. The double combination of voriconazole plus caspofungin is synergistic at caspofungin concentrations of <32 mg/liter and antagonistic at higher caspofungin concentrations (A). The same holds for the double combination of caspofungin plus amphotericin B (see 0 mg/liter of voriconazole in panels B, C, D, E, and F). The double combination of amphotericin B plus voriconazole is antagonistic (see 0 mg/liter of caspofungin in panels B, C, D, E, and F graphs). Note that synergistic interactions decrease and antagonistic interactions increase with increasing concentrations of amphotericin B. Most of the synergistic interactions were located at low concentrations of amphotericin B (0.1 and 0.2 mg/liter) and voriconazole (0.016 to 0.125 mg/liter) and at 1 to 32 mg/liter of caspofungin. The additive and experimental response surfaces were calculated based on equations 2, 3, and 4 using the following estimates (± standard errors) obtained from the nonlinear regression analysis with the modified global model: B = −0.07 ± 0.02, E_max = 1.35 ± 0.03, a_D1 = −0.17 ± 0.04, a_D2 = −0.12 ± 0.05, a_D3 = −0.03 ± 0.01, b_D12 = −1.78 ± 0.31, b_D13 = 0.92 ± 0.10, b_D23 = −1.38 ± 0.22, g_D12 = −3.46 ± 0.54, g_D13 = 0.24 ± 0.11, g_D23 = 3.39 ± 0.31, d_D123 = −12.0 ± 1.87, a_m1 = −1.58 ± 0.19, a_m2 = −1.75 ± 0.30, a_m3 = −6.66 ± 0.50, b_m12 = 3.95 ± 0.86, b_m13 = 5.15 ± 1.23, b_m23 = 9.88 ± 1.47, g_m12 = 2.61 ± 1.15, g_m13 = −4.36 ± 1.83, g_m23 = −17.3 ± 2.73, and d_m123 = 15.3 ± 5.58. ADD, additivity.

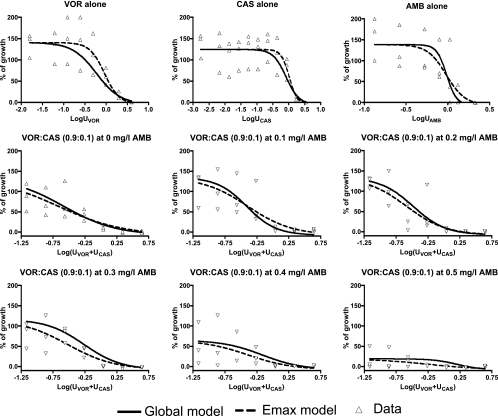
The modified global model parameters associated with the concentration-effect relationships of the drugs alone (a_D and a_m parameters) were close to the individually determined EC₅₀s and Hill slopes. The a_D1, a_D2, and a_D3 were close to 0 (−0.34 to 0.15), which indicates that the U_50,VOR, U_50,CAS, and U_50,AMB determined by the modified global model were close (within one dilution) to the EC₅₀s determined by the E_max model for each drug. The a_m1, a_m2, and a_m3 were not statistically significant different (P > 0.16) from the Hill slopes determined individually with the E_max model. Figure 2 also demonstrates that the concentration-effect curves of each drug alone and in combination determined with the modified global model were similar to the concentration-effect curves fitted individually with the E_max model and close to the raw data. The same holds for the two-drug combination interaction plots in Fig. 3, where the pattern of interaction indices determined by the modified global model was close to that of indices determined individually for different fixed ratios of the two drugs with a previously described isobolographic analysis (26).

FIG. 2.

Concentration-effect data (triangles) for voriconazole (VOR), caspofungin (CAS), and amphotericin B (AMB) alone and for voriconazole-caspofungin combinations at fixed U_VOR/U_CAS ratio of 0.9:0.1 in the presence of increasing amphotericin B concentrations for the A. fumigatus 4215 isolate. The regression curves obtained with the global model fitted to all data (solid lines) and with the E_max model fitted to each concentration-effect data individually (dashed lines) are shown.

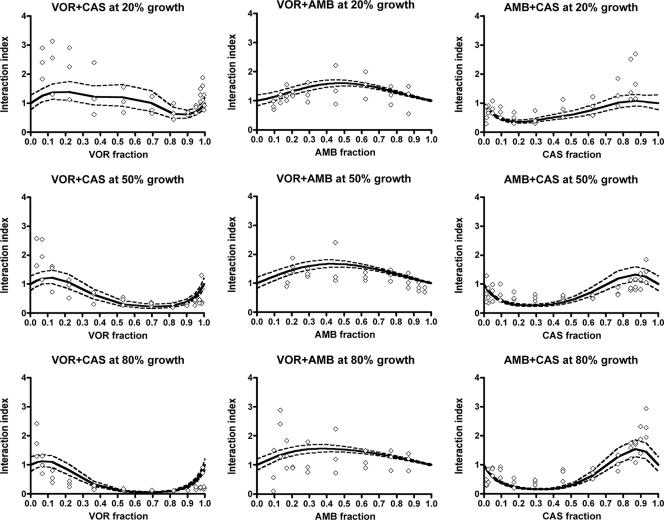
FIG. 3.

Patterns of interaction for the double combinations voriconazole-caspofungin (left graphs), voriconazole-amphotericin B (middle graphs), and amphotericin B-caspofungin (right graphs) for 20% (top graphs), 50% (middle graphs), and 80% (bottom graphs) of growth of the A. fumigatus 4215 isolate. Regression curves (solid lines) and their 95% confidence bands (dashed lines) were derived from the modified global model, where diamonds represent individually determined interaction indices obtained using isobolographic analysis (26). Interaction indices of >1 indicate antagonistic interactions, whereas interaction indices of <1 indicate synergistic interactions. VOR, voriconazole; CAS, caspofungin; AMB, amphotericin B.

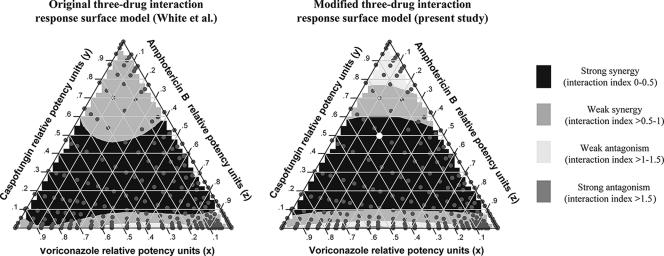
Finally, the modified global response surface model used in the present study yields results similar to those of the original response surface three-drug interaction global model published by White et al. (40). This is illustrated in Fig. 4, where the ternary plots for 50% of growth show similar patterns of pharmacodynamic interactions within the triple combination. Ternary plots are a way of displaying the distribution of three-part composition data such as the interaction indices of the triple drug combinations displayed here (Fig. 4).

FIG. 4.

Ternary plots of the triple combination of voriconazole, caspofungin, and amphotericin B against the A. fumigatus 4215 isolate for 50% of growth, constructed based on the results of the model of White et al. (40) (left plot) and the modified (right plot) global response surface model used in the present study. The model of White et al. was modified in this study by eliminating the leading factor (1 − x)(1 − y)(1 − z). The ternary display is a triangle with sides scaled from 0 to 1. The labels on each side are the relative potency units of each drug. The color inside the triangles indicates the nature and the magnitude of interaction for mixtures with different relative potency units of the three drugs (gray dots). The relative potency units of each drug at a specific mixture can be found by extending the ticks on each side of the triangles towards the point inside the triangle. For example, the white dot in the right triangle represent the combination of 0.2 potency units of AMB (z), 0.5 potency units of CAS (y), and 0.3 potency units of VOR (x), which is synergistic since the interaction index is <0.5 (black area). The color at the x, y, and z sides of triangles represents interactions of the double combinations amphotericin B-voriconazole, voriconazole-caspofungin, and caspofungin-amphotericin B, respectively.

Pharmacodynamic interactions within the double combinations.

Figure 3 also shows that the combinations of voriconazole plus caspofungin and amphotericin B plus caspofungin are antagonistic in the mixtures with a caspofungin proportion of >0.6 and synergistic in the mixtures with a caspofungin proportion of <0.6. Note that interaction indices in Fig. 3 that are >1 are antagonistic and those that <1 are synergistic. Based on the 50% growth level, these antagonistic interactions for most of isolates were observed at combinations with >10 mg/liter of caspofungin. Stronger synergistic interactions were found at higher growth levels for voriconazole plus caspofungin and amphotericin B plus caspofungin. For example, the interaction indices of voriconazole plus caspofungin in Fig. 3 show an overall decline as the percentage of growth increases from 20% to 80%. Similar patterns were found for the other species (data not shown). The combination of amphotericin B plus voriconazole was antagonistic, although some synergistic interactions were observed at low amphotericin B concentrations.

The data points presented in Fig. 3 were obtained with the isobolographic analysis of single fixed-ratio combinations previously described (26). Experimental variation affects the isobolographic analysis, where data are modeled for each fixed-ratio combination, more than the global model, where all data are used for modeling the entire response surface. Discrepancies are more pronounced for fixed-ratio combinations with very high or very low drug proportions because there were fewer data points for these combinations due to the checkerboard experimental design used in the present study. Thus, experimental variation may have a greater impact on the isobolographic analysis of the concentration-effect data of the latter combinations.

Pharmacodynamic interactions within the triple combination.

The interactions observed within the triple combination are summarized in Table 1 for A. fumigatus, A. flavus, and A. terreus isolates. Both synergistic and antagonistic interactions were found for each isolate, with median interaction indices ranging from 0.29 to 2.39. Overall for all three growth levels, the lowest median interaction indices were found for A. fumigatus (0.40 to 0.62) and the highest for A. flavus (1.53 to 1.63). For A. fumigatus and A. flavus isolates, the frequency of synergistic combinations increased with increasing percentage of growth, whereas for A. terreus isolates the synergistic combinations were less frequent than the antagonistic ones at higher percentages of growth (Table 1). Of note, high percentages of growth correspond to low drug concentrations and low percentages of growth correspond to high drug concentrations.

TABLE 1.

Antifungal interactions within the triple combination of voriconazole, caspofungin, and amphotericin B against three isolates each of A. fumigatus, A. flavus, and A. terreus tested in triplicate

Species (no. of isolates)	% of growth	Interaction	Interaction indexa	% of combinationsb	Concn (mg/liter)c of:
					Voriconazole	Caspofungin	Amphotericin B
A. fumigatus (3)	20	Antagonistic	1.39 (1.28-1.45)	46 (43-52)	0.29 (0.27-0.29)	0.49 (0.38-0.92)	0.44 (0.38-0.45)
		Additive	1 (1-1)	11 (7-12)	0.2 (0.11-0.25)	7.07 (3.19-53.83)	0.06 (0.04-0.11)
		Synergistic	0.62 (0.57-0.72)	42 (41-46)	0.03 (0.02-0.03)	8.78 (7.36-9.75)	0.15 (0.15-0.21)
	50	Antagonistic	1.32 (1.31-1.33)	44 (41-45)	0.07 (0.05-0.09)	0.17 (0.10-0.19)	0.23 (0.16-0.24)
		Additive	0.99 (0.99-1)	5 (5-7)	0.02 (0.01-0.03)	0.97 (0.61-1.06)	0.02 (0.02-0.04)
		Synergistic	0.47 (0.43-0.51)	51 (50-52)	0.01 (0-0.01)	1.96 (1.3-2.31)	0.06 (0.04-0.07)
	80	Antagonistic	1.26 (1.25-1.35)	40 (33-43)	0.01 (0.01-0.03)	0.03 (0.02-0.1)	0.11 (0.05-0.13)
		Additive	0.99 (0.99-1.01)	4 (4-9)	0.01 (0-0.02)	0.08 (0.05-0.73)	0.01 (0-0.09)
		Synergistic	0.4 (0.37-0.42)	56 (53-58)	0 (0-0)	0.26 (0.18-0.95)	0.02 (0.01-0.03)
A. flavus (3)	20	Antagonistic	1.63 (1.53-2.39)	60 (59-78)	0.19 (0.12-0.39)	12.7 (5.01-47.51)	0.65 (0.44-2.26)
		Additive	1 (1-1)	11 (7-12)	0.2 (0.11-0.25)	7.07 (3.19-53.83)	0.06 (0.04-0.11)
		Synergistic	0.82 (0.63-0.88)	18 (16-28)	0.15 (0.01-0.2)	23.61 (14.11-31.55)	0.08 (0.07-0.33)
	50	Antagonistic	1.53 (1.46-1.8)	45 (42-69)	0.09 (0.07-0.12)	0.46 (0.38-0.88)	0.41 (0.28-0.68)
		Additive	0.99 (0.98-1)	17 (10-20)	0.1 (0.09-0.13)	0.1 (0.06-1.82)	0.06 (0.03-0.09)
		Synergistic	0.75 (0.49-0.82)	38 (21-39)	0.02 (0.01-0.03)	2.95 (0.95-6.18)	0.07 (0.05-0.17)
	80	Antagonistic	1.53 (1.46-1.7)	42 (38-60)	0.04 (0.03-0.05)	0.03 (0-0.13)	0.25 (0.2-0.28)
		Additive	1 (0.99-1)	15 (13-16)	0.04 (0.04-0.05)	0 (0-0.18)	0.03 (0.02-0.03)
		Synergistic	0.6 (0.29-0.68)	43 (27-47)	0 (0-0.01)	0.16 (0.01-1.43)	0.03 (0.01-0.08)
A. terreus (3)	20	Antagonistic	1.05 (1.04-1.15)	11 (10-47)	0.17 (0.11-0.42)	1.13 (0.4-1.78)	0.32 (0.27-0.32)
		Additive	0.98 (0.98-1)	24 (15-25)	0.26 (0.14-0.6)	0.59 (0.48-1.77)	0.22 (0.1-0.23)
		Synergistic	0.8 (0.76-0.85)	50 (35-64)	0.04 (0.04-0.1)	14.54 (11.61-38.14)	0.26 (0.25-0.37)
	50	Antagonistic	1.18 (1.17-1.29)	56 (32-57)	0.07 (0.07-0.19)	0.47 (0.42-0.63)	0.14 (0.13-0.15)
		Additive	1 (0.99-1)	12 (11-14)	0.07 (0.01-0.11)	0.88 (0.82-1.68)	0.04 (0.03-0.26)
		Synergistic	0.73 (0.66-0.74)	31 (31-57)	0.01 (0.01-0.03)	14.62 (5.12-14.88)	0.13 (0.12-0.2)
	80	Antagonistic	1.39 (1.37-1.52)	58 (36-66)	0.03 (0.02-0.06)	0.16 (0.15-0.23)	0.06 (0.05-0.06)
		Additive	0.99 (0.98-0.99)	8 (6-10)	0.01 (0-0.03)	0.19 (0.14-0.2)	0.08 (0.07-0.08)
		Synergistic	0.59 (0.59-0.65)	32 (27-57)	0 (0-0.01)	3.15 (1.81-5.35)	0.04 (0.04-0.08)

^aMedian (range among the three isolates) of median interaction indices of synergistic, additive, and antagonistic combinations.

^bProportions of 327 different fixed ratio combinations that were significantly antagonistic, additive, or synergistic. The medians (ranges) of percentages among the three isolates are shown, so some groups may not add to 100%.

^cMedian (range among the three isolates) of median drug concentrations of synergistic, additive, and antagonistic combinations.

For each isolate, the synergistic interactions were observed at combinations with low concentrations of voriconazole and amphotericin B and high concentrations of caspofungin (P < 0.05) (Table 1). Based on the 50% growth level, the synergistic interactions were observed for combinations with median concentrations of ≤0.03 mg/liter of voriconazole, ≤0.20 mg/liter of amphotericin B, and 0.95 to 14.88 mg/liter of caspofungin. Conversely, the antagonistic interactions at 50% of growth were observed for combination with higher median concentrations of voriconazole (≥0.05 mg/liter) and amphotericin B (≥0.13 mg/liter) and lower caspofungin concentrations (≤0.88 mg/liter). However, this summary of drug concentrations represents overall patterns of interactions, which do not necessarily reflect the actual patterns of interactions occurring at individual concentrations of the three antifungal agents in combinations.

The concentration-dependent nature of the triple combination of these three agents is better illustrated in the interaction surfaces shown in Fig. 5, where percentages of synergy and antagonism are plotted against the concentrations of voriconazole and caspofungin in the presence of increasing concentrations of amphotericin B. In Fig. 5, it is apparent that the synergistic interactions occurred mostly at low concentrations of amphotericin B (≤0.2 mg/liter) and voriconazole (≤0.125 mg/liter) and at intermediate concentrations of caspofungin (1 to 32 mg/liter) for that particular isolate.

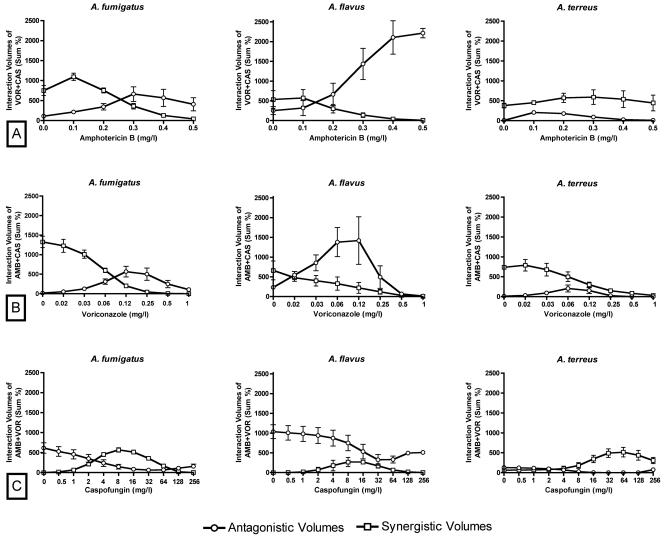
In order to explore whether the triple combination increased the antifungal effects of the double combinations, we also studied the effect of a third drug on two-drug interactions. With increasing concentrations of amphotericin B, the synergistic interactions of the voriconazole-caspofungin double combination decreased while the antagonistic interactions increased (Fig. 6). A similar effect was observed when voriconazole was added to the double combination of amphotericin B plus caspofungin. With increasing caspofungin concentrations, the synergistic volumes of the amphotericin B-voriconazole double combination increased and the antagonistic ones decreased. However, these effects of caspofungin were subtle at concentrations safely achievable in humans (Fig. 6).

FIG. 6.

Synergistic and antagonistic volumes (sum percentage of the interactions presented in Fig. 5) of the double combinations voriconazole-caspofungin (A), amphotericin B-caspofungin (B), and amphotericin B-voriconazole (C) with increasing concentrations of amphotericin B (AMB), voriconazole (VOR), and caspofungin (CAS), respectively. With increasing amphotericin B and voriconazole concentrations, respectively, the synergistic volumes of the voriconazole-caspofungin and amphotericin B-caspofungin double combinations decrease and the antagonistic volumes increase. With increasing caspofungin concentrations, the synergistic volumes of the amphotericin B-voriconazole double combination increase and the antagonistic volumes decrease. Points and error bars represent mean sum percentages and standard errors, respectively, among the three isolates. The squares and circles on the y axis of each graph represent the sum percentages of synergistic and antagonistic volumes, respectively, of only the double combinations voriconazole-caspofungin (A), amphotericin B-caspofungin (B), and amphotericin B-voriconazole (C) in the absence of the third drug.

DISCUSSION

Concentration-dependent pharmacodynamic interactions were found within the triple combination of voriconazole, caspofungin, and amphotericin B. Synergy was observed at low concentrations of voriconazole and amphotericin B and intermediate concentrations of caspofungin, whereas antagonism was found at higher concentrations of voriconazole and amphotericin B. However, the exact pattern of interactions is more complex, as is illustrated in the ternary plots and interaction surfaces. Overall, the synergistic interactions of the voriconazole-caspofungin and amphotericin B-caspofungin double combinations decreased, whereas the antagonistic interactions increased, with increasing concentrations of amphotericin B and voriconazole, respectively.

The complexity of these interactions was well described by an E_max-based mixture-amount response surface model using full cubic canonical mixture polynomials (40). The sigmoid E_max model has been used extensively to successfully describe the concentration-effect relationships of amphotericin B, caspofungin, and azoles (1, 22, 26, 32, 41). In addition, the double combination of polyene-azole was recently analyzed by isobolographic analysis, and the pattern of interactions was dependent on the proportions of antifungal drugs in the mixtures (26), which could be modeled with polynomial regression analysis. These properties enabled us to apply the nonlinear mixture-amount response surface three-drug interaction model developed by White et al. (40). Fully parametric response surface models were previously applied to antifungal drug combinations, but their performance was poor, particularly for complex pharmacodynamic interactions (24). Therefore, nonparametric or semiparametric response surface models were used to better describe complicated antifungal drug combination response surfaces (23). In addition, efforts to develop fully parametric response surface models have continued in areas of anesthesiology, and antineoplastic pharmacology (27, 40). We found that this new model is sufficiently flexible to (i) describe complex response surfaces, (ii) assess pharmacodynamic interactions with statistical confidence based on Loewe additivity zero interaction theory, and (iii) accommodate irregular isobols with local synergy and antagonism for antifungal combinations.

We previously analyzed the triple combination of voriconazole with caspofungin and amphotericin B by using visual determination of drug effects and the fractional inhibitory concentration (FIC) index for the analysis of drug interactions (29a). Concentration-dependent interactions were also found in that study. However, visual assessment of growth limits the analysis for interactions that take place near the complete growth inhibition end point, because subinhibitory effects are difficult to be accurately quantified visually. Although in that study we used two FIC indices to better capture synergistic and antagonistic drug interactions, the exact pattern of pharmacodynamic interactions at the entire concentrations range could not be described with the FIC index analysis. In addition, determining the MECs of caspofungin in combination studies is laborious, is subject to errors, and complicates the drug interaction analysis when MICs are used for the other drugs. Thus, conventional analytical methods of drug interaction analysis may be biased by the MIC end points, subjective inclusion/exclusion criteria in order to account for experimental variability, and investigator bias.

The original three-drug interaction model provides a fine resolution of pharmacodynamic interactions describing the exact pattern or pharmacodynamic interactions within the triple combination (40). Using the modified global model described in this paper, pharmacodynamic interactions can be assessed at any growth level. By using different growth levels, pharmacodynamic interactions can be determined at different drug concentrations, such as the MECs and MICs of antifungal agents. For example, the association of the MICs with the EC₂₀s provides an easy and objective way to assess the pharmacodynamic interactions at concentrations close to the MIC. Finally, using the modified global model described in this paper, additive and interaction surfaces can be constructed and the percentages of synergy and antagonism together with the interaction index can be calculated for each combination.

As drug combination effects can be estimated for any combination of the three drugs, the new response surface global model can be used for pharmacokinetic-pharmacodynamic modeling of combination therapy in order to optimize dosing regimens. Finally, since combination studies with three of more drugs are laborious, time-consuming, and expensive, optimal experimental designs for mixtures can be employed in order to determine the parameters of the new model using the fewest possible data points (21). However, one should acknowledge the complexity of the new model, the use of multiple statistical diagnostic tests to ensure the goodness of fit, and the possibility that some pharmacodynamic interactions may be better described by higher- or lower-order polynomials (27).

Based on the findings of the present study, the double combination of caspofungin with voriconazole was synergistic at combinations with low concentrations of caspofungin and antagonistic at higher caspofungin concentrations. The in vitro combination of caspofungin plus voriconazole against Aspergillus spp. was previously found to be synergistic (6, 31) or additive (7) based upon growth-inhibitory effects, whereas drug combination effects based upon fungal metabolic activity resulted in a range of synergistic (FICi, <1) to antagonistic (FICi, >1) interactions (17). In vivo combination therapy with caspofungin and voriconazole against invasive experimental aspergillosis prolongs survival and reduces fungal burden (14, 16). However, combinations with higher doses of caspofungin (2.5 mg/kg) may result in higher CFU per gram than combinations with lower caspofungin doses (1 mg/kg) (14), consistent with the concentration-dependent interactions that we found in the present study. This apparent increase in fungal burden in vivo may be caused by dosage-dependent hyphal fragmentation (1, 32, 41).

The double combination of caspofungin with amphotericin B was synergistic in combinations where amphotericin B prevailed over caspofungin and antagonistic at higher caspofungin concentrations. In vitro combinations of caspofungin and amphotericin were previously found to be additive to synergistic (2, 6, 7). However, in most of these studies the synergy was weak and was observed mainly for A. fumigatus, as opposed to our studies, where we found synergy with various magnitudes for all three Aspergillus species. Treatment of experimental invasive aspergillosis with caspofungin (0.5 or 1 mg/kg) and amphotericin B reduced fungal burden and prolonged survival compared to monotherapy (5, 36). When higher dosages of caspofungin (3 mg/kg) were combined with amphotericin B lipid complex, the beneficial effects were reduced or reversed (37). In addition, combination therapy with caspofungin plus amphotericin B against murine aspergillosis reduced the fungal burden in the spleen and lung, whereas in kidneys there was no significant reduction compared to monotherapy (36). Notably, caspofungin levels in kidney were previously found to be five times higher than the corresponding levels in lung and spleen (11), reflecting a possible concentration-dependent pharmacodynamic interaction, as we found in the present study.

The double combination of amphotericin B plus voriconazole was antagonistic at the range of concentrations used in the present study. Most of the in vitro studies demonstrated antagonism, while some showed synergy (13). We recently found a concentration-dependent interaction between amphotericin B and itraconazole, with synergy observed for mixtures with an amphotericin B proportion of <0.2 and antagonism observed at higher amphotericin B proportions (26). This is in agreement with the findings of the present study, as most of the drug concentrations used here resulted in mixtures with an amphotericin B proportion of >0.2. In vivo treatment of experimental invasive pulmonary aspergillosis with voriconazole and amphotericin B resulted in worse survival and in similar or higher fungal burdens than with monotherapy (4). However, this antagonism may be associated with higher amphotericin B levels used therapeutically, as we recently found when ravuconazole was combined with liposomal amphotericin B in treatment of invasive pulmonary aspergillosis in rabbits (25). Furthermore, when voriconazole was combined with liposomal amphotericin B against central nervous system aspergillosis in mice, combination therapy prolonged survival and reduced fungal burden compared to monotherapy (5). This synergistic effect may be associated with the low amphotericin B concentrations and high voriconazole concentration in brain tissue (12, 15).

Within the triple combination, the synergistic interactions were observed at combinations with low voriconazole and amphotericin B concentrations. The amphotericin B-voriconazole combination is antagonistic at the entire range of concentrations tested in this study. Therefore, low concentrations of these two drugs will decrease the antagonistic effects of the amphotericin B-voriconazole combination and increase the synergistic effects of the amphotericin B-caspofungin and caspofungin-voriconazole combinations. This was also consistent with the reduction of the synergistic interactions and increase of antagonistic interactions of the voriconazole-caspofungin and amphotericin B-caspofungin double combinations in the presence of increasing concentrations of amphotericin B and voriconazole, respectively. Thus, overall the triple combination is not better that the double combination of voriconazole-caspofungin or amphotericin B-caspofungin, whose benefits are overall reduced in the presence of low concentrations and ultimately reversed at higher concentrations of amphotericin B or voriconazole, respectively.

The mechanism of interactions within the triple combination may be explained by the component two-drug interactions. Caspofungin alters cell wall integrity by inhibiting beta-d-1,3 glucan synthase, whereas amphotericin B disrupts membrane integrity by forming pores and voriconazole alters membrane function by inhibiting ergosterol biosynthesis (10). Thus, voriconazole may antagonize amphotericin B action by inhibiting amphotericin B binding to ergosterol directly, as suggested for lipophilic azoles that are absorbed on cell membranes (34), or indirectly by inhibiting ergosterol biosynthesis (33). On the other hand, the synergistic interaction of the double combinations voriconazole-caspofungin and amphotericin B-caspofungin may be due to the polyene and azole disruption of cell membrane function, possibly resulting in increased susceptibility to caspofungin. This hypothesis is consistent with the observation that deletion of ERG genes increased caspofungin susceptibility (18). The antagonistic effects of the double combinations voriconazole-caspofungin and amphotericin B-caspofungin at high caspofungin concentrations may be associated with the paradoxical increase of fungal growth observed recently with an in vitro colorimetric assay of fungal metabolic activity at high caspofungin concentrations similar to those found in the present study (1). Thus, the antagonistic interactions within the triple combination observed at high amphotericin B and voriconazole concentrations are due to the antagonism between amphotericin B and voriconazole, while the synergistic interactions within the triple combination observed at lower amphotericin B and voriconazole concentrations are due to the synergistic interactions of voriconazole-caspofungin and amphotericin B-caspofungin combinations.

Unfortunately, there are no clinical trials or in vivo studies of triple combination therapy with voriconazole, caspofungin, and amphotericin B against aspergillosis. In a case report of triple combination therapy against invasive pulmonary aspergillosis, addition of voriconazole to a double combination regimen of liposomal amphotericin B plus caspofungin did not resolve fever, and the patient recovered only upon recovering from neutropenia (35). Although in most clinical cases, the three drugs are administered sequentially rather than concomitantly, three-drug interactions may take place in the settings of salvage two-drug combination therapy, since drug levels in primary therapy may persist for long periods during the salvage combination therapy. For example, low plasma drug levels of amphotericin B can be detected for more than a week after therapy (3) and can pharmacodynamically interact with voriconazole and caspofungin during salvage combination therapy (19). However, synergism and antagonism are not necessarily associated with therapeutic benefit and failure, respectively. Pharmacodynamic interactions are defined relative to the effects of the drugs alone, and therefore the absolute effect (e.g., growth inhibition) of a single drug at high concentrations may be greater than the effect of a synergistic combination between low concentrations of two drugs. The therapeutic benefit of a synergistic combination should also be considered in relation to toxicity and tissue penetration.

In conclusion, the new response surface model can adequately describe complex antifungal response surfaces and provide insights into the pharmacodynamic interactions that take place at the entire range of drug concentrations. This information may foster understanding of in vivo pharmacodynamic interactions and optimization of dosing regimens in an attempt to maximize synergistic and minimize antagonistic effects. The concentration-dependent interactions that were found within the triple combination of voriconazole, caspofungin, and amphotericin B underscore the complexity of pharmacodynamic drug interactions, which may not always follow the notion that more drugs at maximally tolerable dosages equal greater efficacy. The triple combination reversed the in vitro positive net effects of voriconazole-caspofungin and amphotericin B-caspofungin double combinations. These findings question prevailing practice and prompt careful consideration of dosing regimens of triple combination therapy.