Dose dependence of mass and microcalcification detection in digital mammography: free response human observer studies

Abstract

The purpose of this study was to evaluate the effect of dose reduction in digital mammography on the detection of two lesion types – malignant masses and clusters of microcalcifications. Two free-response observer studies were performed – one for each lesion type. Ninety screening images were retrospectively selected; each image was originally acquired under automatic exposure conditions, corresponding to an average glandular dose of 1.3 mGy for a standard breast (50 mm compressed breast thickness with 50% glandularity). For each study, one to three simulated lesions were added to each of forty images (abnormals) while fifty were kept without lesions (normals). Two levels of simulated system noise were added to the images yielding two new image sets, corresponding to simulated dose levels of 50% and 30% of the original images (100%). The manufacturer’s standard display processing was subsequently applied to all images. Four radiologists experienced in mammography evaluated the images by searching for lesions and marking and assigning confidence levels to suspicious regions. The search data was analyzed using jackknife free-response (JAFROC) methodology. For the detection of masses, the mean figure-of-merit (FOM) averaged over all readers was 0.74, 0.71, and 0.68 corresponding to dose levels 100%, 50% and 30%, respectively. These values were not statistically different from each other (F = 1.67, p = 0.19) but showed a decreasing trend. In contrast, in the microcalcification study the mean FOM was 0.93, 0.67, and 0.38 for the same dose levels and these values were all significantly different from each other (F = 109.84, p < 0.0001). The results indicate that lowering the present dose level by a factor of two compromised the detection of microcalcifications but had a weaker effect on mass detection.

I. INTRODUCTION

Digital mammography (DM) has been shown to perform at least as well as screen-film mammography (SFM) for overall cancer detection at screening.^1,2 It performs significantly better than SFM for certain subgroups of women such as women aged 40-49, women with dense breasts, and peri- or premenopausal women.¹ However, the overall sensitivity of DM is still only around 70%.¹ The main reason for why lesions are missed is believed to be that anatomical variability of dense breast tissues, rather than system noise (including quantum noise), tends to obscure the lesions.³ This suggests that some increase in quantum noise, or equivalently reduced radiation dose, may be tolerated without significantly compromising detection performance. Since the breast is one of the most radiosensitive organs and mammography is used for screening asymptomatic women,⁴ the radiation dose should be kept as low as possible without compromising image quality.⁵

Two recent phantom studies have suggested that dose reduction in direct DM, may be possible without affecting diagnostic accuracy ^6,7. Using Senographe 2000D (GE) DM systems with similar average glandular dose (AGD) levels – 1.4 mGy⁶ for a standard breast (50 mm compressed breast thickness with 50% glandularity)⁸ – these two studies concluded that dose reduction by 50% did not significantly reduce phantom image quality. A more recent mathematical model observer study of digital images, also acquired from a Senographe 2000D system (AGD not specified), found a slight, but statistically insignificant, drop in detection accuracy for microcalcifications, while no statistically significant effect was observed for masses.⁹

Dose reduction involves an evaluation of cost versus benefit. The benefit of dose reduction is reduced amounts of radiation-induced cancers.⁴ This is particularly relevant in the screening context. The cost is that image quality may be degraded and detection performance thus adversely affected. This implies that fewer cancers may be detected, which may increase mortality. It also implies that more false indicators of cancers may be found at screening, which could lead to unnecessary diagnostic workups including additional dose exposure, biopsies, and patient anxiety. Therefore any proposed dose reduction strategy in DM requires caution and careful evaluation.

None of the previously mentioned studies used clinically realistic images processed according to the manufacturer’s specified protocol. With one exception,⁹ all of the studies have involved subjective evaluations of image quality. In view of these limitations, a more careful examination of the effect of dose reduction on detection performance is needed. The purpose of this work was to investigate the effect of reduced dose on the detection of masses and microcalcifications using objective and higher precision free-response human observer studies.

II. METHOD

The study consisted of the following stages: (1) collection of unprocessed, clinical digital mammograms; (2) insertion of simulated lesions (masses or microcalcifications) into the images; (3) addition of simulated system noise to generate dose-reduced images; (4) processing the images for optimal display using the manufacturer’s algorithm; and (5) two free-response observer performance studies, corresponding to the two lesion types.

A. Collection of unprocessed images

Ninety unprocessed 3328 × 4084 digital mammograms (70 μm pixel size) were selected from the screening department. The unprocessed images included only gain and offset corrections applied to the detector-acquired pixel values. All images were acquired under automatic exposure conditions on a Siemens Mammomat Novation (Erlangen, Germany) unit using a W/Rh anode/filter combination and varying tube potentials (27 to 32 kVp). Under these conditions, the average glandular dose (AGD) was 1.3 mGy for a standard breast.^8,10,11 Only images acquired in the standard medio-lateral oblique projection were used. The inclusion criteria for the images were that they have no visible evidence of disease (as established by a radiologist experienced in mammography). Breasts that were rated as almost completely fatty according to the Breast Imaging Reporting and Data System¹² were excluded from the study to achieve a more uniform detection accuracy by minimizing the case-sampling variability due to different breast-density types, and as it was felt that glandular breasts represent the most clinically challenging cases, and hence the more relevant ones for the purpose of this study.

B. Simulation and insertion of lesions

1. Simulation of masses

Typical characteristics of malignant masses seen in mammography include irregular shaped borders and un-sharp margins.¹² Diameters typically range from around five millimeters up to several centimeters. The mass simulation routine produced simulated breast masses based on the measured anatomical characteristics of real lesions. The simulated masses appeared realistic as verified through an observer performance experiment with expert radiologists.¹³ Five simulated masses were used in this study, as shown in Figure 1. The mean diameter (longest axis at full-width at half maximum, FWHM) of the simulated masses prior to adding them to clinical images was 9.1 mm (range: 8.7 mm – 9.4 mm) at the detector plane. Larger or smaller masses were not included to minimize case-sampling variability, and thereby achieve a more uniform detection accuracy and increase the precision of the observer performance study.

Figure 1.

The five masses used in this study. The longest diameters (measured at FWHM) of the masses ranged from 8.7 mm to 9.4 mm with a mean of 9.1 mm. All size measurements are at the detector plane.

2. Simulation of microcalcifications

Typical characteristics of in-situ malignant lesions involve clusters of sub-millimetre pleomorphic calcifications, commonly referred to as microcalcifications.¹² A simulation technique was used to generate individual microcalcifications¹⁴ as well as their spatial distribution in clusters.¹⁵ For each individual microcalcification, a random-walk algorithm grows an initial shape whose size is pre-defined. The resulting shape is smoothed to remove discontinuities and then a series of dilation operators blur the shape by adding concentric borders with decreasing pixel values. The clusters are formed by randomly selecting 20 to 50 such simulations from a database. They are normally distributed around a central point with a randomized density (number per square millimeter, between 0.5 and 2.0). In this study, five clusters shown in Figure 2 were simulated with an average of 36 microcalcifications in each (range: 28 – 42) in each cluster. The average spread dimension of the clusters (long axis) was 9.8 mm (range: 8.1 – 11.1 mm) at the detector plane. The mean diameter of the individual microcalcifications was 260 μm (FWHM range 100 μm – 550 μm).

Figure 2.

The five clusters of microcalcifications used in this study. There were, on the average, 36 microcalcifications per cluster. The average diameter of the individual microcalcifications was 264 μm. All size measurements are at the detector plane.

3. Insertion of lesions into images

Both lesion types were inserted into the unprocessed images using previously described methods.^11,14 The maximum lesion pixel value difference was adjusted for each image by increasing it until a mammographer could just distinguish the lesion superimposed on an unprocessed but optimally windowed clinical image. Perceptually adjusting visibility to achieve a certain level of detectability is a method often used in detection studies since it is important for statistical power that the lesions be just visible.^16–18 An example of each lesion type inserted into an unprocessed but optimally windowed mammogram is shown in Figure 3.

Figure 3.

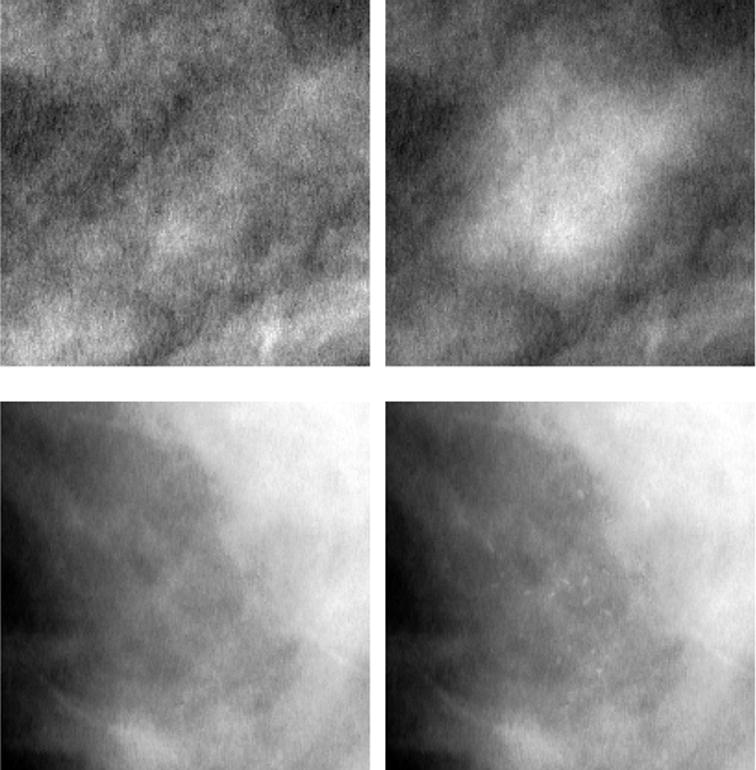
Appearance of lesions inserted into mammographic regions of interest (optimally windowed unprocessed images). The top row, left and right, consists of an image detail with and without a mass inserted, respectively (mass ‘e’ from Figure 1). The bottom row, left and right, consists of an image region with and without a microcalcification cluster inserted, respectively (microcalcification ‘a’ from Figure 2).

For both studies, 40 out of the original 90 full dose images contained lesions (masses or microcalcifications). For the mass study, a total of 65 masses were inserted: 3 masses in 5 images, 2 masses in 15, and 1 mass in 20. For the microcalcifications study, a total of 60 microcalcification clusters were inserted: 3 clusters in 5 images, 2 clusters in 10, and 1 cluster in 25. The coordinates of the lesion centers were generated randomly (but constrained to the glandular region of the breast) and recorded for use in the scoring step of the data analysis (see below). The use of multiple lesions in some images was adopted as it was expected to increase statistical power with little increase evaluation time for the observers.

C. Dose reduction simulation

The original unprocessed images are referred to as full dose or 100% dose images. The method of simulating dose-reduction in digital clinical images has been previously described.^11,19 The method uses information about the noise power spectrum (NPS) at the original and target dose levels, and also takes the local dose variation in the original image into account, to create a noise image which, when added to the original image, results in an image with similar system noise properties as an image actually collected at the target dose level (note the system noise includes quantum, electronic, and other patient-structure independent sources of noise). The NPS of the system was determined for a range of exposure conditions using flat-field images acquired with approximately the same exposure as the clinical images together with flat-field images actually acquired near the 50% and 30% dose levels. This process was performed on all 90 full dose images (normal and abnormal) to yield corresponding sets of images at 50% and 30% of the original dose levels (270 images for each lesion type study). Note that the same lesions and their distributions and locations were used at all three dose levels. This was done to follow the case-matched approach that is known to yield optimal statistical power of the study.²⁰

D. Display Processing

All of the lesion insertions and dose reductions described above were performed on unprocessed images. As the final step before the clinical study, all images underwent Siemens’ standard mammography image display processing, which enhances the visibility of low-contrast objects and of microcalcifications, and allows for simultaneous viewing of the skin-line and center breast region at high image contrast. Figure 4 shows display-processed images corresponding to masses and microcalcifications at the three dose levels used in the studies.

Figure 4.

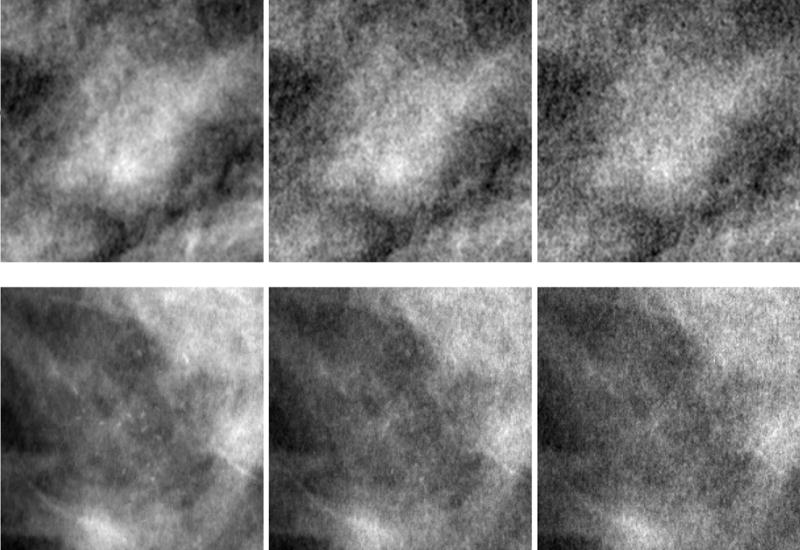
Display-processed regions of interest from two images (top and bottom rows) showing inserted lesions at the three dose levels used in the study. The top row (from left to right) consists of the same mass as in Figure 3 at dose levels 100%, 50% and 30%, respectively. The bottom row (from left to right) consists of the same microcalcification cluster as in Figure 3 at dose levels 100%, 50%, and 30%, respectively. Note the visible increase in noise as the dose is reduced from 100% to 30%.

E. Human observer free-response studies

Starting with the mass study, two sequential free-response studies were conducted. Four radiologists with a range of 12 – 33 years (mean: 16 years) experience in mammography participated in each study, three of which were common to both studies. For each study, the viewing was divided into three sessions held one week apart. Within each viewing session, thirty images were displayed from each dose level (avoiding showing images of the same breast at two dose levels) in random order. The radiologists were informed that there were between zero and three lesions in each image. Each microcalcification cluster was treated as a single lesion and the radiologists were instructed to search for whole clusters rather than isolated microcalcifications. In order to familiarize the radiologists with the study and the display software tools described below, a training session involving 18 images (not used in the actual study) was given at the beginning of each viewing session.

1. Viewing conditions

A dedicated viewing station was set up in a room with low ambient light (<1 lux). The images were displayed on a 5 mega-pixel grayscale mammography monitor (Siemens, model number SMM 21190 P, Erlangen, Germany). The monitor was calibrated according to DICOM part 14²¹ using Verilum software (Image Smith, Inc). The radiologists were free to view the monitor from any distance and viewing-time was unrestricted. The graphical user interface shown in Figure 5 was used to display the images and record the radiologists’ responses.²² The images were displayed at the manufacturer-specified window/level settings contained within each DICOM header. Each 3328 × 4084 image was initially scaled to fit the monitor. The radiologists were allowed to zoom and pan the full-resolution image to search for lesions, as well as adjust the window/level setting. They marked suspicious regions and selected a rating from one (least likely) to four (most likely) for each based on how confident they were that they had found a lesion. The result of the classifications, the confidence ratings and the coordinates of each mark were recorded. The software classified each mark as a lesion localization (when within a 10 mm or 12 mm radius from the centroid of a mass or microcalcification cluster, respectively), or non-lesion localization (all other marks).

Figure 5.

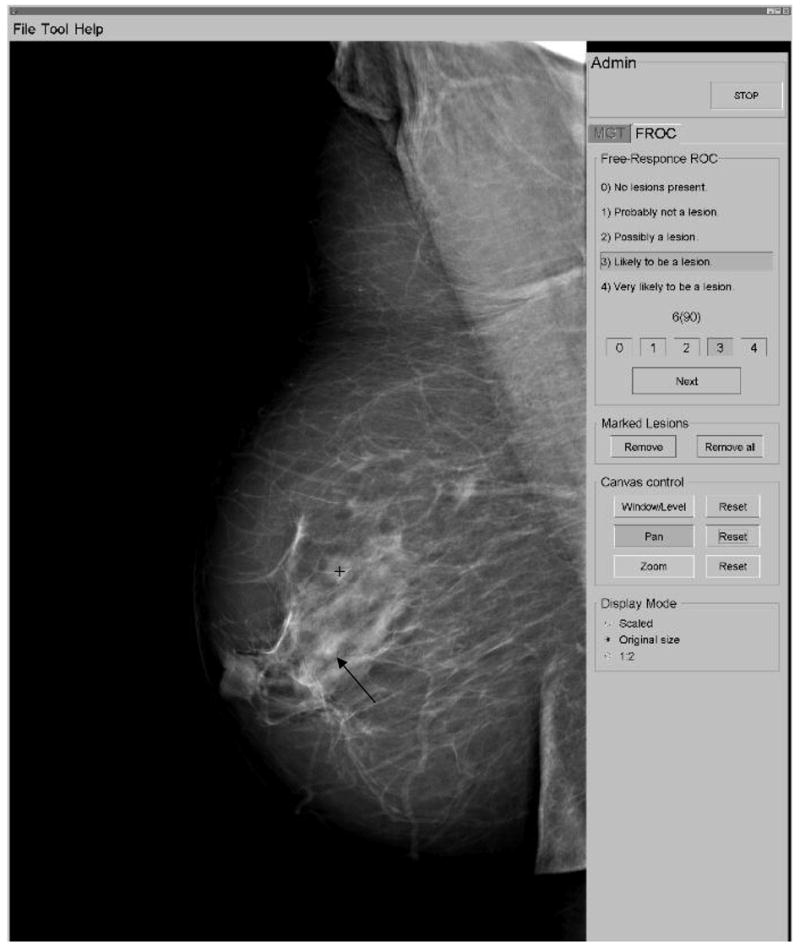
Graphical user interface used in the human observer studies. In this example, there were two masses present in the image: the observer has marked an actual region (mass ‘b’ from Figure 1) with a ‘+’ and ranked it as a ‘3’, i.e. ‘likely to be a lesion’. The second mass in the image, mass ‘e’ from Figure 1, was not marked (actual location indicated with the arrow).

2. Statistical analysis

Free-response data consists of a record of locations (marks) found to be sufficiently suspicious to deserve reporting, and the corresponding confidence-levels (ratings) that they represent lesions. The data for the masses and microcalcifications were analyzed individually with the jackknife free-response receiver operating characteristic (JAFROC) method,^23–25, software version 2.0.^26,27

The essential differences between the well-known receiver operator characteristics and the JAFROC methods are in the data collection step and in the figure of merit (FOM) quantifying observer performance. In the ROC paradigm, localization information is not sought and a single rating is collected for each image. In the free-response paradigm, the data consists of mark-rating pairs that have been scored into non-lesion and lesion localizations.²³ In an ROC study, the FOM is described as the areas under the ROC curve. Calculation of the JAFROC FOM involves creating two lists: a normal-list and a lesion-list. The normal-list is a record of the rating of the highest rated mark (necessarily a non-lesion) for each normal image. The lesion-list is a record of the ratings for each lesion. The number of entries in normal-list is the number of normal images. The corresponding number for the lesion-list is the total number of lesions. The FOM calculation involves making all possible comparisons between the numbers in the two lists. If a rating from the lesion-list exceeds a rating from the normal-list, then a counter is incremented by unity. It the two are equal the counter is incremented by 0.5. The final value of the counter is divided by the total number of comparisons yielding the FOM. The FOM is seen as the probability that lesion ratings exceed all non-lesion localization ratings on normal images (if a lesion rating exceeds the highest rating, it must exceed all ratings on the normal image). This computation may be recognized as calculation of the two sample Wilcoxon test statistic.²⁸

While non-lesion localizations can occur on abnormal images, in JAFROC they are ignored, since otherwise the method has incorrect statistical behavior.^23,25,29 Specifically, it rejects the null hypothesis more frequently than it should, which leads to increased Type I errors and overestimation of the statistical power of the study. Omitting these responses corrects this problem at the expense of some loss in statistical power, since one is discarding potentially important information. In spite of this, it has been shown^23,25 that the statistical power of JAFROC is superior to the ROC method, especially when the lesions are hard to detect, as was true in this study. However, there is need for further refinement to the methodology so that potentially useful information is not discarded.

The JAFROC FOM is a fairly new metric for characterizing free-response performance. Most researchers who have used free-response studies, e.g., in computer aided detection studies, have used lesion localization fraction (LLF) relative to the total number of lesions and non-lesion localization fraction (NLF), relative to the total number of images, to characterize performance (these are commonly referred to in the literature as true positive fraction and mean number of false positives per image, respectively, terminology that can be confused with usage in ROC studies). Therefore, to maintain continuity, in addition to the FOM for each dose level, we also calculated LLF and NLF at each dose level for the most lax criterion used by the observer (i.e. the ‘ones’ and above). We are not aware of any method of assigning significance values to differences in these paired-values, and therefore confine ourselves to statements of trends.

The JAFROC software reports the 95% confidence interval (CI₉₅) for the difference in figures of merit (Δθ). If an effect size (i.e. minimum difference in FOMs that one is interested in detecting) is specified, then the statistical power of the study can be inferred from CI₉₅. Assuming the distribution of Δθ is normal, then CI₉₅ = 2 × (1.96) × σ(Δθ), where σ(Δθ) is the standard deviation of Δθ and the factor 2 × (1.96) is needed to get the 95% coverage interval (roughly, ± two standard deviations). Therefore σ(Δθ) = CI₉₅/3.92. It has been shown²⁴ that if the nominal significance value of the test is 5% (i.e., the type I error probability or p-value is p = 0.05) then for a two sided test a power of 0.8 requires an effect size of 2.802 × σ(Δθ) FOM units, i.e., effect size = 0.715 × CI₉₅.

III. RESULTS

A. Masses

For each radiologist and for each dose level, the FOMs for the mass detection task are shown in Table 1a. The mean (reader averaged) FOMs were 0.74, 0.71, and 0.68 for the 100%, 50% and 30% dose levels, respectively. While there is a decreasing trend, these values were not significantly different from each other (F = 1.67, p = 0.19). Two of the readers showed a decreasing trend of FOM with dose, but the other two showed no consistent trend. The 95% CIs for the difference between each pair of FOMs, shown in Table 1b, all included zero which meant that there was no statistically significant difference between any two dose levels. Table 1a also shows that the mean LLFs and NLFs were approximately the same for all dose levels. In other words, the operating point on the free-response curve did not change appreciably with dose. Note that the FOM can range between 0 and 1, unlike the area under the curve in an ROC study, which lies between 0.5 and 1.0

Table 1a.

Results of JAFROC study for the mass detection task at the three dose levels (100%, 50%, and 30%). FOM = Figure of Merit; LLF = Lesion Localization Fraction; NLF = Non-Lesion Localization Fraction

	100%			50%			30%
Radiologist	FOM	LLF	NLF	FOM	LLF	NLF	FOM	LLF	NLF
1	0.746	0.72	0.48	0.768	0.77	0.26	0.751	0.68	0.38
2	0.771	0.77	0.42	0.753	0.75	0.42	0.705	0.68	0.40
3	0.712	0.71	0.84	0.681	0.83	1.00	0.632	0.82	0.86
4	0.734	0.80	1.02	0.649	0.82	1.10	0.650	0.78	0.82
Means	0.741	0.75	0.69	0.713	0.79	0.70	0.685	0.72	0.62

Table 1b.

Results of statistical analysis of mean FOM values from JAFROC experiment. CI = 95% Confidence Interval

Mean FOMs compared	Difference	95% CI around difference
100% versus 50%	0.028	[−0.033, 0.088]
100% versus 30%	0.056	[−0.004, 0.117]
50% versus 30%	0.028	[−0.032, 0.089]

B. Microcalcifications

For each radiologist and for each dose level, FOMs for the microcalcification detection task are shown in Table 2a. The mean FOMs were 0.93, 0.67, and 0.38 for the 100%, 50% and 30% dose levels, respectively. Since p < 0.0001 (F = 109.84), at least two of the FOMs were significantly different from each other. The 95% CI for the difference between each pair of FOMs are shown in Table 2b, and none of the intervals include zero, indicating that all dose-level pairings were significantly different. All readers showed a strongly decreasing trend of FOM with dose. Table 2a also shows that the mean LLF for the detection of microcalcifications decreased with decreasing dose, while the NLF increased. In other words, the operating point on the free-response curve moved towards poorer performance with decreasing dose.

Table 2a.

Results of JAFROC study for the microcalcification detection task at the three dose levels (100%, 50%, and 30%). FOM = Figure of Merit; LLF = Lesion Localization Fraction; NLF = Non-Lesion Localization Fraction

	100%			50%			30%
Radiologist	FOM	LLF	NLF	FOM	LLF	NLF	FOM	LLF	NLF
1	0.916	0.78	0.06	0.717	0.42	0.22	0.469	0.15	0.36
2	0.902	0.83	0.30	0.648	0.53	0.62	0.362	0.22	0.94
3	0.948	0.85	0.22	0.650	0.53	0.58	0.294	0.17	0.90
4*	0.966	0.85	0.26	0.649	0.56	0.42	0.396	0.15	0.54
Means	0.933	0.83	0.21	0.666	0.51	0.46	0.380	0.17	0.69

^*Radiologist 4 for the microcalcifications was not the same as Radiologist 4 for the masses.

Table 2b.

Results of statistical analysis of mean FOM values from JAFROC experiment. CI = 95% Confidence Interval

Mean FOMs compared	Difference	95% CI around difference
100% versus 50%	0.267	[0.184, 0.350]
100% versus 30%	0.553	[0.470, 0.636]
50% versus 30%	0.286	[0.203, 0.369]

For a side-by-side comparison, the mean FOM for both detection tasks are shown in Figure 6. For the mass detection task an effect size of 0.087 (in FOM units) would result in 80% statistical power, i.e., an effect size of this magnitude would be detected with 80% probability. The corresponding effect size for the microcalcification task is 0.119 (slightly higher than for masses because the sample size was slightly smaller).

Figure 6.

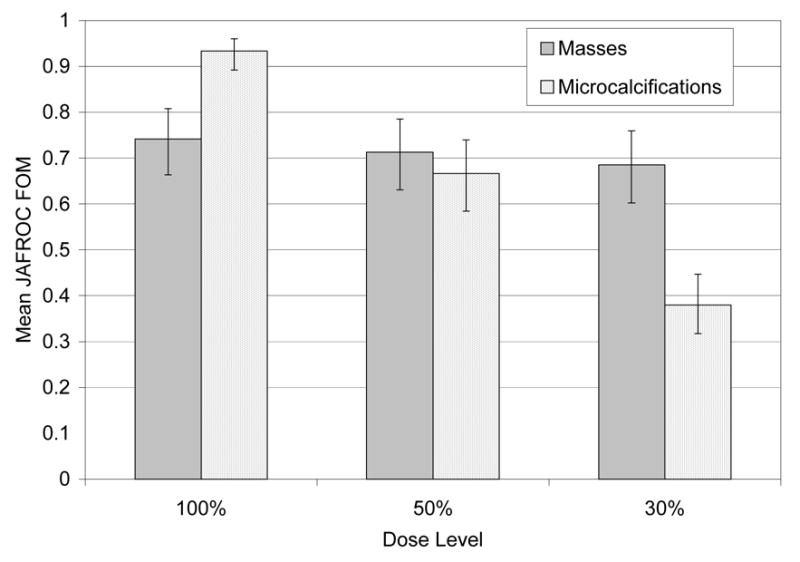
The reader-averaged free-response figure of merit (FOM) at each dose level for masses (gray) and microcalcifications (dotted). Note the steep decline for the microcalcifications as a function of dose and the relative constancy for the masses. The uncertainty bars represent 95% confidence intervals. The microcalcification FOM decline was statistically significant; that for masses was not

IV. DISCUSSION

The principal finding of this study was that mass detection task performance was not significantly affected by dose reduction, although a decreasing trend was observed. In contrast, microcalcification detection task performance degraded significantly as dose was decreased. Therefore, our study suggests that any proposed dose reduction strategy in mammography should be approached with caution and carefully evaluated. Since the 95% confidence-interval is never zero, any conclusions made from the study should include the effect of uncertainty in the measured degradation. The danger is to conclude that since the experiment yielded a non-significant difference, that there is no difference, and the proposed dose reduction method should be adopted. One manifestation of the fallacy of this reasoning is that by using a small enough sample size the experimenter can guarantee a non-significant result. The erroneous conclusion that failure to demonstrate the significance of an effect implies that the effect is zero is fairly common and the correct interpretation of p-values is discussed in depth by Metz.³⁰ The risk of a non-significant but non-zero degradation needs to be carefully balanced against the benefit of dose reduction. In the context of mammography the risk can be assessed if one knows the costs associated with missed cancers (false negatives) and unnecessary diagnostic workups and biopsies (false positives).

Previous studies of the effect of dose reduction have reached different conclusions.^6,7,9 Two studies^6,7 that indicated up to a 50% reduction used homogeneous background mammography phantoms. In these studies, the reported dose reduction factor corresponded to that which maintained sufficient image quality scores. Phantoms are generally not designed to be sensitive to the large range of dose levels that exist in digital mammography.³¹ However, at the relatively low dose levels used in these studies (below 1.5 mGy), that should not be a major problem. Instead, the main limitation may be the homogeneous background of the phantoms used, which mean that these phantom studies do not account for anatomic variation. Phantom studies do no completely control for false-positives and the detection decision criterion variability among observers is expected to decrease statistical power. The effect of criterion variability on degrading the precision of the measurement is one reason for using a criterion-independent objective measure, such as the area under the ROC curve.³² In the present study, a closer match to the clinical task was achieved by using actual mammograms containing realistic masses and microcalcifications as shown in Figures 3 and 4. The findings of a more recent dose reduction study⁹ are closer to those of this work. Simulated microcalcifications and masses were inserted into mammographic backgrounds and mathematical model observers were used to evaluate images at 50% and 25% simulated dose levels. A larger degradation was observed for the microcalcifications than for the masses, though in neither case was this degradation statistically significant.

A possible explanation for the difference in dose effects on masses versus microcalcifications observed in the present study follows from two studies examining the relative effects of anatomical structure and system noise on the detection of lesions in mammographic backgrounds.^17,33 In one study,³³ it was found that anatomical variability was between 30 to 60 times more influential than system noise for mass detection; the corresponding range for microcalcification detection was 0.1 to 3, indicating that system noise was relatively more significant for the detection of microcalcifications than masses. A similar conclusion can be inferred from another study¹⁷ in which it was observed that mammographic backgrounds are dominated by a high magnitude of low spatial frequency components. Lowering dose has a relatively small effect on these low-frequency components compared to at higher frequencies in which system noise is known to dominate. Therefore, dose reduction is expected to have a smaller effect on mass compared with microcalcification detection tasks since masses are in the spectral region that remains relatively unchanging with dose.

An overall limitation of the present work is that it is a simulation study, not a clinical study. However, this limitation needs to be viewed in the perspective of the difficulty of obtaining sufficient numbers of abnormal cases with known truth, and the difficulty of finding masses on the threshold of human perception (the simulation study allowed us to augment statistical power by using just visible lesions). The study used two types of lesions, whereas in practice diverse lesions are seen in mammography.¹² Limiting to two lesion types leads to lower variability within each lesion type, which is expected to increase statistical power. In the present study multiple lesions (1 to 3) were used per abnormal case, whereas in practice abnormal cases with more than one lesion occur infrequently. Larger number of lesion is expected to increase statistical power. The random placement of the lesions cannot simulate the fact that some locations are clinically more likely to contain malignancies than others. Benign versus malignant characterization of lesions was not addressed in this study. Although dose reduction had no statistically significant impact on the detection of masses, it may adversely affect their characterization. Finally, as noted earlier, in order to obtain challenging cases, fatty breasts were under-represented in this study.

V. CONCLUSION

In conclusion, while a statistically significant deleterious effect on detectability of masses with dose reduction was not found, one cannot rule out detectability degradation with dose reduction. In contrast, a strong effect on microcalcification detectability was found. Both of these results suggest that caution should be exercised when considering the use of lower doses.