Direct measurement of force generation by actin filament polymerization using an optical trap

Abstract

Actin filament polymerization generates force for protrusion of the leading edge in motile cells. In protrusive structures, multiple actin filaments are arranged in cross-linked webs (as in lamellipodia or pseudopodia) or parallel bundles (as in filopodia). We have used an optical trap to directly measure the forces generated by elongation of a few parallel-growing actin filaments brought into apposition with a rigid barrier, mimicking the geometry of filopodial protrusion. We find that the growth of approximately eight actin parallel-growing filaments can be stalled by relatively small applied load forces on the order of 1 pN, consistent with the theoretical load required to stall the elongation of a single filament under our conditions. Indeed, large length fluctuations during the stall phase indicate that only the longest actin filament in the bundle is in contact with the barrier at any given time. These results suggest that force generation by small actin bundles is limited by a dynamic instability of single actin filaments, and therefore living cells must use actin-associated factors to suppress this instability to generate substantial forces by elongation of parallel bundles of actin filaments.

Polymerization and depolymerization of either microtubules or actin filaments can generate significant forces for cell movements in the absence of any associated molecular motors (reviewed in refs. 1–4). For cases where protein polymerization generates mechanical force, the energy is provided by the difference in chemical potential between a protein subunit in solution and the same protein subunit embedded in the polymer (5). When actin filaments elongate in close proximity to a biological load, they are believed to generate pushing forces through a ratcheting mechanism where thermal fluctuations allow for periodic insertion of new protein subunits in the polymer despite the presence of a counteracting load force (6, 7). Theoretical treatments of force generation by actin filament polymerization in this geometry (5, 6) predict that filament growth should slow and eventually stall as the applied force on the end of the filament approaches the value determined by Eq. 1:

where k_B is Boltzmann's constant, T is the absolute temperature, δ is the elongation distance for addition of a single protein subunit (2.7 nm for actin), C is the concentration of monomers in solution, and C_crit is the critical concentration for polymerization (equivalent to k_off/k_on for elongation at a single filament end). In living cells, the total concentration of actin is typically ≈100 μM (8), of which 10–100 μM is G-actin (9, 10), but it is not known how much of this actin pool is available for polymerization. The value of C_crit in vivo is also unknown, because the polymerization properties for actin may be strongly influenced by actin-binding proteins. Taking the most generous estimates that all G-actin in a cell is bound to ATP and able to polymerize and that the effective in vivo C_crit is equivalent to the measured C_crit for pure ATP-actin in standard polymerization buffer at the barbed end of a filament (0.12 μM; ref. 11), the maximum theoretical force that could be generated in a living cell by elongation of a single filament is ≈9 pN. For in vitro assays using G-actin concentrations of a few micromolars, the force required to stall the growth of an individual filament is expected to be significantly lower. Starting from this fundamental set of thermodynamic boundary conditions, a wealth of detailed physical and kinetic models have been proposed that predict speed and efficiency of force transduction by this mechanism under a very wide range of biologically relevant conditions and geometries, including large-scale behaviors of complex systems comprising many filaments (reviewed in refs. 12 and 13).

Although the theoretical basis for understanding the origin of forces generated by actin polymerization is well developed, complementary experimental progress has been relatively slow. Recently, direct measurement of forces generated by the growth of densely branched networks comprising thousands of actin filaments has been achieved by using deflection of glass microneedles (14) and silicon cantilevers (15), and network forces have been estimated by using a variety of less direct experimental techniques (16–21), giving values for the force of actin network growth in the range of several nN/μm². It is not possible to extract information from these bulk experiments about the force–velocity relationship for single actin filaments, both because of the difficulty of accurately measuring the number of actin filaments in the networks and because the history of force loading on the network affects the network density (15, 16, 22).

There is only one published measurement of the force generated by a single growing actin filament (23). This experiment relied on microscopic observation of the force-induced bending of growing actin filaments anchored by immobilized myosin heads at one end and a barbed-end binding formin protein at the other end and yielded an estimate that polymerization of a single actin filament can generate at least 1.3 pN of force under conditions where a theoretical maximum of ≈2 pN was expected. The experimental design prevented the investigators from measuring the decrease in filament growth velocity caused by increasing load, from imposing larger forces, or from stalling filament elongation. Because this method relies on filament anchoring by the formin protein, it cannot be used to examine force generation by polymerization of actin filaments with free barbed ends, filaments in bundles, or in the presence of other actin-binding molecules that interfere with formin function.

In this article, we have adapted an optical-trap-based strategy (24, 25) to measure the force generated by actin polymerization. This experimental geometry allows the measurement of stall force and is compatible with the inclusion of a variety of actin-associated proteins. We have successfully measured the stall force for actin filament elongation in the pN range. Surprisingly, we find that the growth of small bundles (approximately eight filaments) stalls at a low load force that would be expected to stall growth of a single actin filament under these conditions, suggesting that the separate filaments in the bundle do not cooperate for force generation.

Results

Observation of Actin Filament Growth Using an Optical Trap.

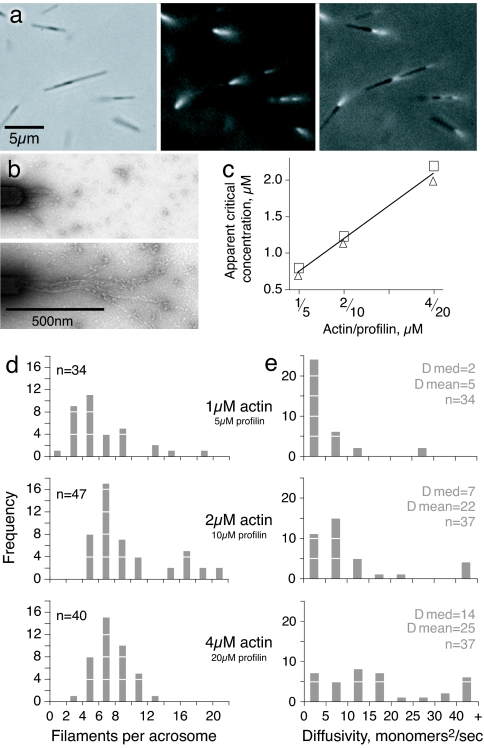
Optical traps are uniquely suited for measuring forces in the pN range under a variety of biochemical conditions. We used the rigid polarized acrosomes from Limulus sperm as nuclei for actin filament growth (11, 26) and as manipulable handles to physically separate the position of the bead in the optical trap from a refractile barrier (Figs. 1 and 2). Before any trapping experiments could be carried out we needed to establish solution conditions where G-actin would not polymerize spontaneously, as filaments in solution would interfere with trapping and disturb our measurements. In the presence of a 5-fold molar excess of profilin and a low-salt, low-magnesium buffer, we found that actin filament elongation occurred exclusively at the barbed ends of acrosomal bundles (Fig. 1 a and b). We determined the apparent critical concentration for barbed end growth on acrosomal bundles under these conditions (Fig. 1c), which under the low-salt, low-magnesium buffer conditions used in our experiments depends linearly on the amount of profilin present (27, 28). The apparent critical concentrations in Fig. 1c include both profilin-bound actin and free actin. Any effects on the actin monomer caused by the profilin, state of the actin (ATP, ADP-Pi, etc.) are measured by this assay and if the role of profilin under our experimental conditions is to alter the critical concentration with no other significant effect on actin polymerization, then the values we measured (Fig. 1c) can substitute for C_crit in Eq. 1 (5). Using the total concentration of actin for C in Eq. 1 we would expect an F_max of 0.5, 0.8, and 1.0 pN for 1, 2, and 4 μM actin, respectively. This calculation is further discussed in supporting information (SI) Fig. 7 and SI Text.

Fig. 1.

Actin filament growth from isolated Limulus acrosomal bundles. (a) Limulus acrosomal bundle fragments (≈5 μm long) were incubated with rhodamine-actin. Small tufts of fluorescent actin filaments are seen growing from the barbed end in this sequence of phase-contrast, rhodamine, and overlay images. Notice that some acrosomes form clusters. (b) Electron micrographs of negatively stained filaments grown from acrosomal bundles with 4 μM monomeric actin and 20 μM profilin. (Upper) Ten seconds of growth. (Lower) Thirty seconds of growth. (c) Apparent actin critical concentration measured for different concentrations of profilin (actin/profilin ratio 1:5 for all experiments). Duplicate points show results of independent experiments. (d) The number of filaments per acrosome, counted during the first 40 s of growth. The difference in the number of filaments per acrosome at different time points was not significant. (e) Diffusivity in length of the actin filaments in the three assay conditions over the first 40 s of growth. The complete set of diffusivity data are presented in SI Fig. 8.

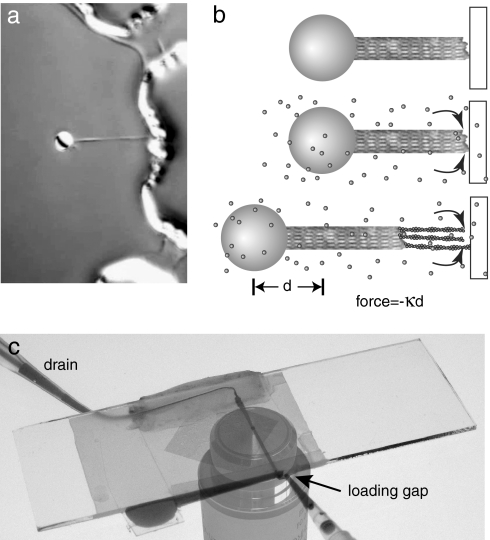
Fig. 2.

Experimental setup. (a) Bead with attached Limulus acrosomal bundle held in keyhole trap and brought next to microfabricated wall structure. Bead is 2 μm in diameter. (b) Schematic showing the sequence of events for an experiment. (Top) The bead-acrosome construct is positioned a few nanometers away from a barrier. (Middle) Actin monomers are introduced into the flow cell. (Bottom) Filaments grow from the barbed end of the acrosomal bundle and force the bead away from the wall. The force is directly proportional to the distance d. (c) Flow cell used in the experiments. The slide is on top and the coverslip (with diamond-shaped patterned area) is at the bottom. Dye shows the fluid path from reservoir to drain. The microscope objective was photographed separately and added for clarity.

We used electron microscopy to characterize the growth of actin filaments on the Limulus acrosomes under the chosen conditions (Fig. 1 d and e). As reported (11), a variable number of individual actin filaments grew from the barbed end of each acrosomal bundle, with a median number of eight filaments per bundle in 4 or 2 μM actin and six filaments per bundle in 1 μM actin (Fig. 1d). By measuring filament lengths as a function of time we estimated the average effective actin elongation rate as 2.6 monomers/μM·s for all three actin concentrations, similar to previously published results (11). The average number of filaments did not increase over time.

Filaments growing from a single acrosomal bundle were highly variable in length. The length fluctuations can be characterized by a “length diffusivity” constant D, which measures the spread of filament lengths around the mean value where the rms fluctuation in filament length over time is (2Dt)^1/2. D can be measured as:

where L is the length of each filament in the group (in monomers) and t is the time in s (29). Average apparent values of D strongly depended on the actin monomer concentration (Fig. 1e) but did not vary with time, indicating that filament breakage cannot be responsible for the observed large values of D.

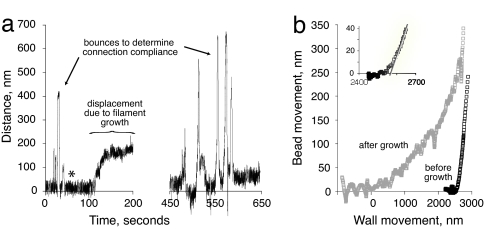
For force measurements using a “keyhole trap” we attached the acrosomal bundle to a 2-μm-diameter polystyrene bead (25). The end of the trapped bundle was brought into close proximity with a microfabricated wall that served as a rigid barrier (Fig. 2 a and b). We then used a piezoelectric stage to bring the wall repeatedly into contact with the bundle tip in a series of bounces, while observing bead displacement (Fig. 3a). This process enabled us to determine the position of the bundle tip relative to the wall and calculate the compliance 1/k_c in the bead-bundle construct. For an infinitely stiff bundle with no compliance in the connection to the bead, the measured position of the bead in the optical trap will remain constant until the wall makes contact with the end of the bundle, and then the bead will be displaced by the exact distance that the wall moves (displacement ratio of 1.0). In any other case, the ratio between the two is given by:

In practice, the displacement ratio was constant, but <1 (indicating a linear spring behavior of the connection). Upon initial contact there was a negligible amount of nonlinear compliance in the linkage between the bundle and the bead, so the transition was not perfectly sharp (Fig. 3b Inset).

Fig. 3.

Displacement of bead in laser trap caused by actin filament growth. (a) Positional data, raw trace. The zero-to-200-s portion shows initial “bounces” to characterize mechanical behavior of the bead and acrosomal bundle construct. Asterisk indicates time when actin was added. After growth reached a plateau, the bead and bundle were pulled away from the wall, and then the series of bounces were repeated. This particular experimental trace was not used for force measurements. (b) Bounce data from a represented as bead displacement as a function of deliberate movement of the wall, before and after actin filament elongation. The zero point was set to coincide with the first contact of the elongated filaments. Using this zero point the stage would have had to move ≈2,530 nm to make contact before the addition of actin.

Next, we introduced actin monomers into the flow cell to initiate the polymerization reaction (Fig. 2). As shown in Figs. 3a and 4, actin filament elongation resulted in displacement of the bead within the optical trap, with the rate of displacement slowing over time until a plateau was reached after filament growth of several hundred nanometers. After the plateau became stable, we could use the piezoelectric stage to pull the wall away from the elongated filament tips, resulting in a recoil of the trapped bead back to the center of the trap. Actin filament elongation was no longer limited by the imposed load force and the filaments presumably continued to grow. A second series of bounces revealed two features consistent with elongation of actin filaments at the end of the acrosomal bundle (Fig. 3b). First, the apparent total length of the bundle was much longer after the addition of actin monomer than before. Second, the apparent compliance between the bead and the bundle became greater (i.e., the curved transition zone became exaggerated), indicating that the filaments that had grown from the bundle tip were deformable, as distinct from the tightly packed and nearly crystalline organization of filaments in the original acrosomal bundle. These two features are consistent with the appearance by light and electron microscopy of actin filaments grown under the same conditions (Fig. 1 a and b).

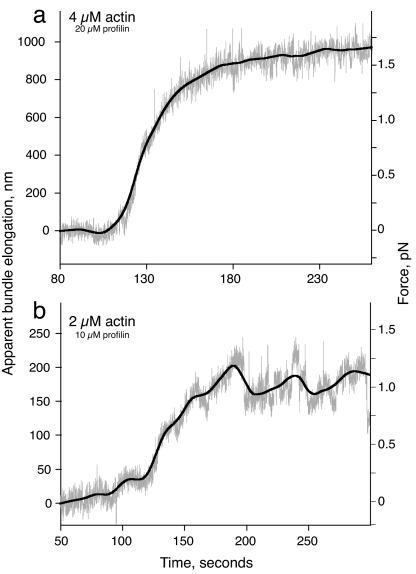
Fig. 4.

Force measurement for actin filament growth with monomeric actin at 2 (b) and 4 (a) μM. Gray trace shows raw data, and the black line is the best-fit curve using the locally weighted least-squares method (46).

Measurement of the Force Plateau.

Because the optical trap was maintained in a steady position during the course of actin filament elongation, the polymerization-driven displacement of the bead within the trap caused the load force to increase over time (Fig. 2b). The net force on the bead caused by the optical trap as a function of position was calibrated by determining the trap stiffness for the 2-μm bead held in the trap before attachment to an acrosomal bundle (24). The elongation length L was determined by dividing the bead displacement (in nm) by the displacement ratio as measured for each bead-acrosome construct before filament growth. Fig. 4a shows a calibrated trace for growth of actin filaments from an acrosomal bundle using actin at a concentration of 4 μM. After the actin reached the acrosome, bead displacement (caused by actin filament growth) continued over ≈100 s. For the relatively weak traps used in these experiments (average k_trap 0.008 pN/nm), the initial forces are small. Consistent with this, the maximum elongation rate observed at the beginning of the growth curves for the optical trap measurements (2.5 ± 1 monomers per μM·s) was the same as the growth rate determined by using electron microscopy under the same solution conditions. As the load force increased, the elongation rate slowed to near-zero, reaching a plateau at a load force of 1.5 pN after apparent bundle elongation of ≈900 nm (Fig. 4a).

Next, we examined the effects of changing actin monomer concentration on force generation by actin polymerization. Fig. 4b shows a trace similar to Fig. 4a but for 2 μM actin (10 μM profilin). Again, displacement of the bead caused by actin polymerization slowed over time until a final plateau was reached at an applied force of ≈1 pN. Strikingly, traces obtained with 2 μM actin were qualitatively as well as quantitatively distinct from those obtained with 4 μM actin. In particular, the 2-μM actin traces typically exhibited large and irregular fluctuations in the bead position at the final force plateau (Fig. 4b).

We performed 11 independent experiments with actin monomer concentrations of 4 and 2 μM, with profilin kept at a constant molar ratio of 5:1 relative to actin. For some experiments, the actin bundling protein α-actinin was added at 1 or 20 μM. Bead displacement caused by actin filament growth and applied force during the final plateau phase for each of these experiments are summarized in Fig. 5.

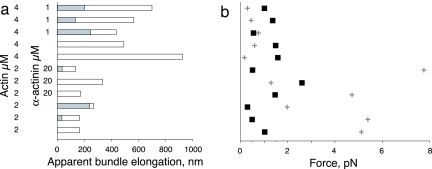
Fig. 5.

Filament lengths and forces necessary to buckle the elongating filaments. (a) Summary of final filament length determined by summing the distance the bundle tip was held away from the wall (shaded regions) and the filament elongation measured from the bead displacement (unshaded region) for 11 experiments. (b) Observed average force at stall (■) determined from bead displacement, compared with the force necessary to buckle a single filament (cross) as determined from the length in a. Vertical axis is as in a.

Force Generation by Actin Filaments in Small Bundles.

Given our experimental geometry, we considered two possible explanations for the origin of the plateau phase. First, applied load forces at the tip of an elongating actin filament are expected to stall filament elongation according to Eq. 1 (5, 6). For small bundles of actin filaments acting in parallel, the total force required to stall elongation in a plateau phase is expected to be the linear sum of the force required to stall each individual filament (6, 7). Alternatively, applied forces at the tip may also cause filaments to buckle (30). After buckling, the filaments may grow unimpeded along the barrier wall and will no longer contribute to bead displacement, although the bent filaments will act as simple springs maintaining a separation between the bead and the wall. In this situation, a plateau phase would be achieved when all of the filaments in the bundle have buckled. Although the force required to stall filament elongation is independent of filament length, the force required for buckling of a filament with one free and one clamped end (31) is given by:

where k_mod is the flexural rigidity of an actin filament, 0.06 pN*μm² (32), and L is the filament length. We can be sure that the plateau is caused by load-dependent stalling of filament elongation rather than by filament buckling if and only if the final applied force during the plateau phase is less than the force that would be required to buckle a single filament at that length.

For all of the measurements using 4 μM actin, and one using 2 μM actin, the final load force during the plateau phase was comparable to or greater than the force required to buckle a single filament at that length (up to 9-fold greater; average 3.5-fold, from Eq. 4). For these conditions, we cannot distinguish whether the plateau was caused by filament buckling, load-induced stall, or a combination of both phenomena. Given that the measured length diffusivity for filaments grown from single acrosomes under this condition results in variable filament lengths on the order of tens of nanometers (Fig. 1e), it seems likely that the efficiency of force generation by these bundles is compromised when the longest filaments reach the wall and start to buckle before the shorter filaments make contact and are able to contribute to resisting the applied load. For the six experiments in which the final load force during the plateau phase was comparable to or greater than the force required to buckle a single filament, the observed plateau force was on average 8.6-fold higher than the average force required to maintain a net 90° bend in a filament at that length. Because the average number of filaments grown from acrosomes under these conditions was also ≈8 (Fig. 1d), it seems likely that the observed plateau force in these cases was generated when each filament in the bundle buckled successively and subsequently acted as a simple spring holding the bead away from the wall. We attempted to limit buckling by adding α-actinin, with no net effect on the plateau phase (Fig. 5b). It is possible that filament buckling was not prevented, because the dissociation rate of α-actinin is fairly high (33).

In contrast to the ambiguous results at 4 μM actin, the experiments using 2 μM actin present clear evidence for load-induced stalling of actin filament growth. Five of six experiments performed at this actin concentration ended in a plateau phase where the applied force was substantially less (by 3- to 21-fold) than the force that would be required to buckle a single filament at that length, and buckling can therefore be ruled out. For these five independent experiments, the net force applied by the optical trap at the plateau phase was in remarkably close agreement with F_max calculated from Eq. 1 for the force expected from growth of a single actin filament: the measured force was 0.76 ± 0.22 pN, as compared with the theoretical F_max of 0.80 pN. However, even at this lower actin concentration, the number of filaments per acrosome is on average ≈8 (Fig. 1d). Therefore, it is clear that the multiple filaments in a small bundle grown under these conditions cannot cooperate in the process of force generation, and the small bundle stalls at the same load as a single filament would stall.

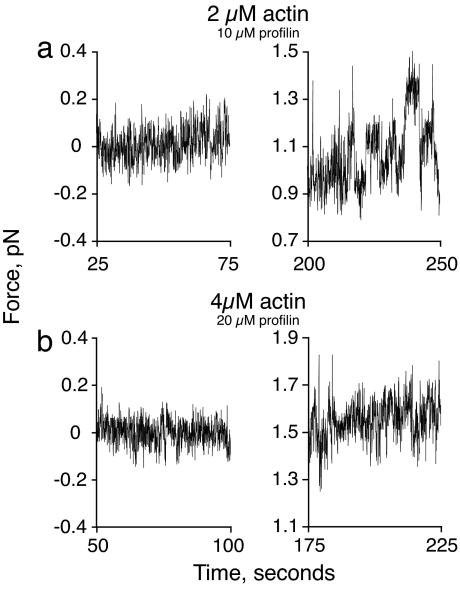
Close examination of the data from force measurements with 2 μM actin provide insight into what might be happening at low actin concentrations as we approach the stall force. In Fig. 6 we compare the noise in the force traces for experiments using 2 and 4 μM actin both before the addition of actin and at the force plateau. Before the addition of actin, the noise traces for both experiments are representing the Brownian motion of the bead in the trap. At the force plateau, the noise in the 4 μM data shows regular random deviations about a median value. The noise in the 2-μM data are quite different. After reaching the force plateau the bead undergoes large force fluctuations that are qualitatively and quantitatively different from those of the 4-μM actin samples. This behavior was observed in three of the five 2-μM actin samples mentioned above and never in the experiments with 4 μM actin. These data are consistent with the bead being pushed away from the wall because of the polymerization of the longest filament in the bundle, and then moving closer to the wall as that filament converts to rapid depolymerization, only to be caught by a new, slightly shorter filament undergoing polymerization, which stalls in turn. We propose that this irregular behavior corresponds to a “dynamic stall” (related to dynamic instability; ref. 34) where the load is borne by only the single longest filament in the small bundle at any given instant in time but the identity of the longest filament is traded off among the individuals in the bundle as each undergoes a load-induced conversion to the depolymerizing state. The fact that this kind of dynamic stall is not observed for experiments performed with 4 μM actin further supports the idea that in these experiments the filaments may be buckled. If buckling occurs significantly before the stall force is reached, then the net filament growth will never be reduced to near-zero and no switching to a depolymerizing state should occur.

Fig. 6.

Noise characteristics of experimental traces before growth (Left) and during the plateau (Right) in the presence of 2 (a) and 4 (b) μM actin.

Discussion

We have used an optical trap-based assay to directly examine force generation by a small bundle of actin filaments by using an experimental geometry that is nearly identical to the idealized case of protein polymerization against a load that has been envisioned in theoretical modeling efforts for >20 years (5–7, 35). An unexpected outcome of our measurements is the observation that the magnitude of the force generated against a rigid barrier by growth of a small bundle of parallel actin filaments (≈8) is close to the predicted maximum force generated by a single actin filament in this geometry (5, 6). For filaments growing slowly at low actin concentrations (≈2 μM), the most likely explanation for this observation is that only the longest filament is in direct contact with the barrier at any given time, and that during the plateau phase the actin filament bundle is engaged in a “dynamic stall” where the load-bearing duty is exchanged among individual filaments undergoing stochastic fluctuations in length (29, 36) (Fig. 6). Theoretical modeling of the dynamics of the actin filament ATP cap supports the idea of dynamic instability-like length fluctuations for actin filaments under conditions where the net filament growth rate is near zero (29, 36). The earlier modeling work predicted this dynamic phenomenon for actin subunit concentrations very close to the critical concentration for growth under unloaded conditions; we propose that a similar explanation may hold when a load force decreases the net filament elongation rate to zero even when the actual actin concentration remains substantially higher than the critical concentration.

Our results imply that small parallel bundles of actin filaments such as those found in filopodia cannot automatically cooperate in a linear manner to increase the amount of force generated at the bundle tip, because the parallel bundle orientation seems to permit force transduction primarily by the longest filament, with a time-sharing of the load-bearing duty among different filaments in the bundle at or near the dynamic stall. Cells may overcome this intrinsic limitation by using specific proteins to protect growing actin filaments from converting to load-induced depolymerization, perhaps including the formin proteins and the “tip complex” observed on the growing ends of filopodia by electron microscopy (37). The flexibility of the membrane surrounding the filopodial actin bundle may also modulate actin elongation and force generation (38).

However, it is also possible that parallel filament bundles are simply relatively inefficient at transducing the energy of actin polymerization into mechanical work against a rigid barrier, compared with other forms of actin filament organization such as the branched dendritic network that is found in lamellipodia (39) and actin “comet tails” associated with intracellular bacterial pathogens (40). In a dendritic network, actin filaments contact the load at a variety of angles, and constant branching nucleation of new filaments near the leading edge ensures that a large number of actively growing filament ends are in direct contact (7, 22), enabling cooperation in generating force against the surface of a load that can result in efficient transduction of several nN/μm² (14, 15). Biologically, the role of filopodia in exploring the environment and forming nascent adhesive structures in response to external signaling cues is well established (41, 42). It is not clear, however, that filopodia can act as powerful generators of protrusive force, a function that may be largely performed in crawling cells by the actin network-filled lamellipodia and pseudopodia (43).

Materials and Methods

Protein Purification.

Actin from rabbit skeletal muscle, profilin from calf thymus, α-actinin from chicken gizzard, and acrosomal processes from Limulus were purified as detailed in SI Text. All protein preparations were assayed by using the appropriate activity assays and SDS/PAGE.

Stock Solutions.

All experiments were carried out with common stock solutions of proteins and buffers. F buffer stock was made up as 100 mM Mops, pH 7.5/500 mM KCl/20 mM MgCl₂/20 mM EGTA/5 mM ATP/5 mM DTT) and stored at −20°C. Buffer 3 was made by mixing 300 μl of F buffer stock with 700 μl of G buffer. BSA was made up as a 10 mg/ml stock in G buffer (2 mM Tris, pH 8.0 at 4°C/0.2 mM CaCl₂/0.5 mM adenosine triphosphate/0.5 mM DTT). All solutions of actin were made by diluting a “40-μM actin” stock solution of 4 μM tetramethylrhodamine-labeled actin (44), 36 μM unlabeled actin, 200 μM profilin in G buffer (made pH 7.4 at room temperature). α-Actinin was made up as a stock solution of five times the desired final concentration in G buffer. All trapping experiments were carried out in 0.1× buffer 3 (3 mM Mops/15 mM KCl/0.6 mM MgCl₂/0.6 mM EGTA/0.3 mM ATP/0.3 mM DTT/1.4 mM Tris/0.14 mM CaCl₂).

Apparent Critical Concentration Assays.

Assays to determine the apparent critical actin concentration under our experimental conditions were performed by diluting the 40-μM actin stock with 5-fold excess profilin down to 1, 2, or 4 μM actin in a final volume of 70 μl made 0.1× in buffer 3 with an excess of washed acrosomes. After incubation at room temperature for 1 h the samples were incubated overnight with gentle agitation. The samples were then spun at 100,000 rpm in a TLA100 rotor (Beckman, Fullerton, CA) for 7 min. The total amount of actin remaining in the supernatant was quantitated by scanning Coomassie-stained SDS/PAGE gels with actin as a standard.

Filament Counting and Elongation Rates by Electron Microscopy.

Carbon Formvar-coated 400-mesh copper grids were made hydrophilic by glow discharge immediately before use. Acrosomes were washed in G buffer before use. For the 4-μM actin experiments, 1/10 volume of 40-μM actin stock was added to a vial containing 1/10 volume buffer 3 and 8/10 volume of acrosomes washed in G buffer. At various times after actin addition the acrosomes were pipetted onto the EM grids and rapidly blotted and fixed with 1% uranyl acetate. Experiments using lower amounts of actin were conducted in a similar manner. Grids were imaged at an accelerating voltage of 80 KV on a TEM1230 electron microscope (JEOL, Tokyo, Japan) equipped with a CCD camera (Gatan, Pleasanton, CA). To calculate filament length and growth rates individual actin filaments were measured by using Metamorph software (Universal Imaging, Dowingtown, PA).

Optical Trap Assays.

Force measurements were performed by using a keyhole trap (24) created with a Nd-YV04, 1,064-nm laser (Spectra Physics, Irvine, CA). Seven-micrometer-high barriers were made of SU-8 photo resist (MicroChem Corp., Newton, MA) on standard 25-mm-square glass coverslips (45). These coverslips were used in a flow cell as described in SI Text. Acrosomes bind nonspecifically to streptavidin-coated beads in F buffer and remain bound when the buffer is changed to 0.1× buffer 3. Trap calibration, video tracking, and attachment of 2-μm microparticles to acrosomes was performed essentially as described for experiments using axonemes and microtubules (25). More details are presented in SI Text.