Internal strain regulates the nucleotide binding site of the kinesin leading head

Abstract

In the presence of ATP, kinesin proceeds along the protofilament of microtubule by alternated binding of two motor domains on the tubulin binding sites. Because the processivity of kinesin is much higher than other motor proteins, it has been speculated that there exists a mechanism for allosteric regulation between the two monomers. Recent experiments suggest that ATP binding to the leading head (L) domain in kinesin is regulated by the rearward strain built on the neck-linker. We test this hypothesis by explicitly modeling a C_α-based kinesin structure whose motor domains are bound on the tubulin binding sites. The equilibrium structures of kinesin on the microtubule show disordered and ordered neck-linker configurations for the L and trailing head, respectively. The comparison of the structures between the two heads shows that several native contacts present at the nucleotide binding site in the L are less intact than those in the binding site of the rear head. The network of native contacts obtained from this comparison provides the internal tension propagation pathway, which leads to the disruption of the nucleotide binding site in the L. Also, using an argument based on polymer theory, we estimate the internal tension built on the neck-linker to be f ≈ 12–15 pN. Both of these conclusions support the experimental hypothesis.

Extensive interest has recently been devoted to the understanding of molecular motors, which play pivotal roles in cellular processes by performing mechanical work using energy-driven conformational changes. Kinesin, myosin, F₁-ATPase, GroEL, RNA polymerase, and ribosome belong to a group of biological machines that undergoes a series of conformational changes during the mechanochemical cycle where the molecular conformation is directly coupled to the chemical state of the ligand. Although substantial progress has been achieved in understanding the underlying physical principles that govern molecular motors during the last decade, major issues still remain to be resolved. Specifically, some of the outstanding questions are as follows. (i) How is the chemical energy converted into mechanical work? (ii) How is the directionality of the molecular movement determined? (iii) How is the molecular movement coordinated or regulated? Several biochemical experiments have quantified the kinetic steps (1, 2), single-molecule experiments using optical tweezers have measured the mechanical response of individual molecular motors (3–5), and an increasing number of crystal structures have provided glimpses into the mechanisms of molecular motors (6–13). These experimental evidences, however, are not sufficient to fully address all of the questions above. For example, little is known not only about the structural details of each chemical state, but also about the kinetic pathways connecting them. Hence, if feasible, a computational strategy using the coordinates from x-ray and/or NMR structures can shed light on the allosteric dynamics of molecular motors. Although some initial numerical studies (14–17) have proceeded toward addressing issue i for a few cases for which both open and closed structures are explicitly known, no previous attempt has been made to answer issue iii. In this paper we investigate this question in the context of the conventional kinesin where the mechanochemical coordination of the motor movement is best manifested among the motor proteins.

One of the experimentally best studied molecular motors is the conventional kinesin (kinesin-1) (18, 19), a relatively small motor protein that transports cellular materials by walking in an unidirectional hand-over-hand manner along the microtubule (MT) filaments. Compared with other motor proteins involved in material transport, such as myosin and dynein, the conventional kinesin has a remarkable processivity and can travel ≈100 steps (≈8.2 nm) without being dissociated from the MT. The mechanochemical cycle conjectured from experiments suggests that there must be a dynamic coordination between the two motor domains to achieve such high processivity. The quest to identify the origin of this dynamic coordination has drawn extensive attention from the kinesin community. Since Hancock and Howard (20) first hypothesized that the “internal strain” was needed for processivity, the strain-dependent mechanochemistry became a popular subject in kinesin studies (21–23). With the aid of optical tweezers, Guydosh and Block (24) recently revisited this issue by monitoring the real-time kinesin dynamics in the presence of ATP and ADP·BeF_x, a tight binding ATP analog (24). They discovered that, when ADP·BeF_x was bound to the kinesin, the pause time of the step increased substantially and that the normal step was restored only after the obligatory backstep. This finding suggests that ADP·BeF_x is released only when the head bound with ADP·BeF_x becomes the leading head (L). Supported by this observation, they advocated a kinetic model in which the rearward strain via the neck-linker facilitates the release of the ligand from the L (24). Stated differently, the binding of the ligand to the L is inhibited because the rearward strain constitutes an unfavorable environment for the ATP binding sites of the L. In the present study, we focus on the elucidation of the structural origin of the coordinated motion in kinesin by adopting a simple computational strategy.

Better straightforward evidence of the regulation on the nucleotide binding site can be obtained when a structure in which both kinesin heads are simultaneously bound to the MT binding site is determined. Such a structure will allow us to identify the structural differences between the L and the trailing head (T). To date, this structure, however, has not yet been reported. The only available structures include an isolated kinesin-1 without the MT (6), an isolated single-headed kinesin-like (KIF1A) with various ligand states (7), and a single KIF1A bound to the tubulin-dimer binding site (25). Therefore, we used existing Protein Data Bank (PDB) structures and manually built a model system of the two-headed kinesin molecule with both heads bound to the tubulin binding sites (see Fig. 2). This model was used to generate an ensemble of structures via simulations. A direct comparison between the L and T equilibrium structures shows that the tension built on the neck-linker induces the disruption of the nucleotide binding site of the L, which directly supports inferences from experimental observations (23–24).

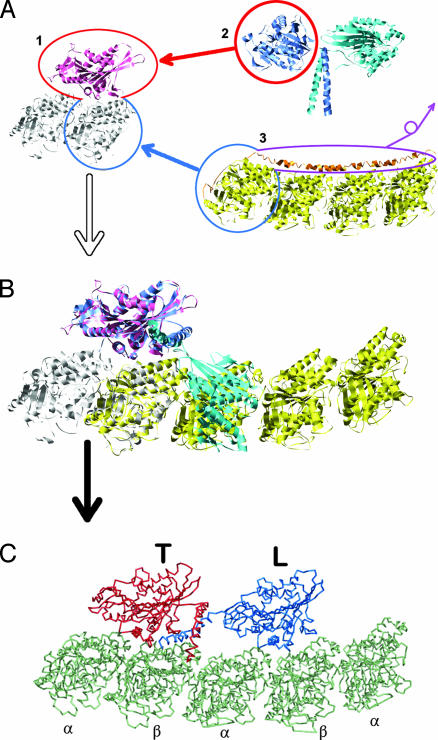
Fig. 2.

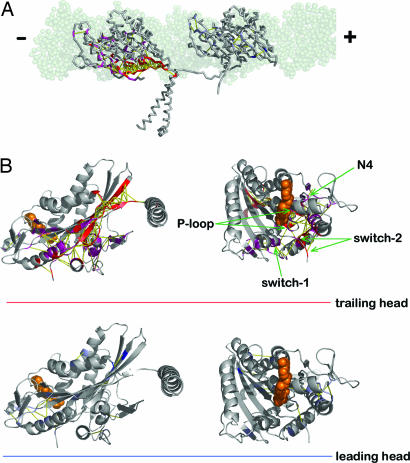
Procedure to construct the two-headed kinesin/MT-protofilament model. (A) Three structures from the PDB are used. 1, Single-headed kinesin (KIF1A) bound on tubulin (PDB ID 1IA0); 2, two-headed kinesin (PDB ID 3KIN); 3, two consecutive tubulin complexed to the stathmin-like domain (PDB ID 1FFX). (B) We overlapped chain A (blue) of 3KIN onto chain K of 1IA0, and we overlapped chains A and B of 1FFX (α-domain) onto chain B of 1IA0, which leads to the structure shown. The structural homology (C_α backbone rmsd = 1.6 Å) between KIF1A and a head of the two-headed kinesin are sufficient that one of the kinesin heads fits to the tubulin binding site. Although the sequence difference between KIF1A and the conventional kinesin (sequence identity, ≈45%) may affect the strength of interactions between kinesin and tubulin, leading to a different binding affinity of conventional kinesin from KIF1A, we assume that the binding orientation of the two-headed kinesin is similar to that of KIF1A on the tubulin. After the structure overlap, chains C and D of 3KIN are internally rotated around a few positions in the neck-linker (324–338) until chains C and D are placed in the vicinity of the binding site of tubulin, which is designed to be identical to the interface between the kinesin T and the tubulin. (C) We performed the simulation to relax the kinesin structure on the MT and obtained the structure shown.

Results and Discussion

Mechanochemical Cycle of Kinesin.

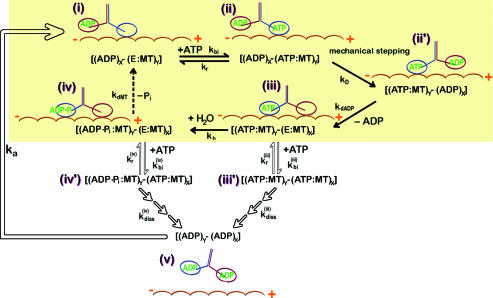
We begin by reviewing the mechanochemical cycle of the kinesin molecule on the MT to clarify the importance of dynamic coordination between the two motor domains for kinesin processivity. Recent experiments using laser optical tweezers, cryoelectron microscopy, electron paramagnetic resonance, and FRET, as well as the crystal structures at various states (7, 26–28) provide glimpses into the structural and dynamical details of how the kinesin molecule walks on the microtubule filaments. Depending on the nucleotide state at the binding site, both the motor domain structure and the binding interface between kinesin and MT are affected. In particular, a minor change of the motor domain coupled to the nucleotide is amplified to a substantial conformational change of the neck-linker between the ordered and disordered state. Experimental studies strongly suggest the mechanochemical cycle shown in Fig. 1 (28). The mechanical stepping cycle of kinesin initiates with the binding of ATP to the empty kinesin head strongly bound to the MT [(i) ⇋ (ii)]. Docking of the neck-linker to the neck-linker binding motif on the L (X in Fig. 1) propels the T (Y in Fig. 1) in the (+)-direction of MT, which leads to an 8 nm mechanical step [(ii) → (ii′)]. The interaction with the MT facilitates the dissociation of ADP from the catalytic core of L [(ii′ → (iii)]. ATP is hydrolyzed and produces ADP·P_i state for the T [(iii) → (iv)]. When P_i is released and the T is unbound from the MT, the half-cycle is completed [(iv) → (i)]. The mechanical step is achieved in a hand-over-hand fashion by alternating the binding of the two motor domains (X and Y in Fig. 1) to the MT (29, 30). High processivity of the kinesin requires this kinetic cycle to be stable (remain within the yellow box in Fig. 1). A premature binding of the ATP to the L in the state of (E:MT) should be prevented, i.e., the condition k_bi⁽ⁱⁱⁱ⁾[ATP]/(k_r⁽ⁱⁱⁱ⁾ + k_diss⁽ⁱⁱⁱ⁾) and k_bi^(iv)[ATP]/(k_r^(iv) + k_diss^(iv)) → 0 should be satisfied in Fig. 1 [see supporting information (SI) Text for the master equation describing the kinetic cycle]. ATP binding to the (iii) or (iv) states can destroy the mechanochemical cycle of the kinesin. The binding of ATP on the L should be suppressed before the γ-P_i is released from the T. Otherwise, both heads become ADP-bound states, which have a weak binding affinity to the MT and lead to dissociation from the MT. Because the kinesin has a high processivity compared with other molecular motors, effective communication is required between the two heads regarding the chemical state of each of the partner motor domains.

Fig. 1.

Mechanochemical cycle of kinesin. The subscripts X and Y refer to each of the kinesin head, E denotes the empty head, and (:MT) is appended if the head is strongly bound to the MT.

Two-Headed Kinesin Bound to the MT.

In the absence of interactions with the MT, the individual kinesin monomers fold into identical conformations. To achieve its biological function, however, folding into the native structure alone is not sufficient. Coupled with the nucleotide and the MT, the two kinesin monomers in the dimeric complex need to alternate the acquisition of the native structure in a time-coordinated fashion for the unidirectional movement. The currently available three-dimensional structure (PDB ID 3KIN; structure 2 in Fig. 2A), in which each monomer is in its native state, does not provide such a dynamic picture because it fails to fulfill the geometrical requirement of simultaneous bindings of both motor domain to the adjacent tubulin binding sites that have an 8-nm gap. The inspection of 3D structure suggests that a substantial increase of the distance between the two motor domains can be gained by breaking a few contacts associated with the neck-linker (β9 and β10) and the neck-linker binding site on the motor domain (β7). To this end, we manipulated the 3D structure of 3KIN around the neck-linker of the L and created a temporary structure whose two heads bind to the MT binding sites simultaneously. Both L and T have energetic biases toward the identical native fold, but the interactions with the tubulin binding sites adapt the dimeric kinesin structure into a different minimum structure, which is not known a priori. We performed simulations (see Methods) to relax this initial structure and to establish the thermal equilibrium ensemble of the kinesin molecule on MT (see Fig. 3A). Transient dimeric kinesin conformations corresponding to the steps (iii) and (iv) during the cycle (Fig. 1) allow us to investigate the structural deviation between L and T of the kinesin molecule. This simple computational exercise can confirm or dismiss the experimental conjecture regarding whether the mechanochemical strain significantly induces regulation on the nucleotide binding site and whether it occurs in the L.

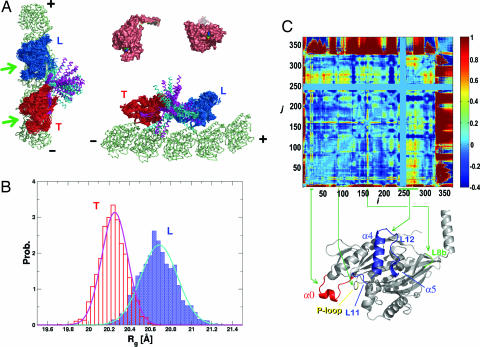
Fig. 3.

The ensemble of structures and structural comparisons between two heads using R_g and X_ij. (A) The thermal ensemble of structures is illustrated by using the multiple structures obtained during the simulations. Different colors are used to distinguish the motor domain (residues 2–323) from the neck-linker and tail part (residues 324–370). Substantial variations of the neck-linker/tail position in ensemble show its flexibility. The nucleotide binding sites in the L and T are indicated by the arrows. In the upper-right corner are two crystal structures of kinesin (3KIN). One is the view from the top (Left) and the other is the view toward the nucleotide binding pocket (Right). When compared with the top view of 3KIN crystal structure, it is visually clear that the nucleotide binding pocket is more intact in the T. (B) Analysis of kinesin motor domains (2–324) using the radius of gyration (R_g). Histograms of R_g collected over the ensemble are fit to a Gaussian distribution. For the T (red), 〈R_g〉_T = 20.3 Å and σ_T = 0.13 Å. For the L (blue), 〈R_g〉_L = 20.7 Å and σ_L = 0.18 Å. (C) Analysis using the structure overlap function. The X_ij value is color-coded on the right (see the text for the definition of X_ij).

Catalytic Core of the L is Less Native-Like on the MT.

Because the nucleotide binding and release dynamics are sensitively controlled by the kinesin structure, we assume that the nucleotide molecule has an optimal binding affinity to the kinesin motor domain in the native structure. For function, there is a need to understand how the native structure of the kinesin motor domain is perturbed under the different topological constraints imposed on the dimeric kinesin configuration by interacting with the MT. The equilibrium ensemble of the structures shows that the neck-linker is in the docked state for the T but undocked for L. In comparison to the native structure, the overall shape of the nucleotide binding pocket in the T is more preserved. As long as the MT constrains the two heads 8 nm apart, this configuration is dominant in the thermal ensemble (see Fig. 3A).

Global shape comparison.

There are in principle multiple ways to quantitatively compare the two motor domain structures. To assess the structural differences, the radius of gyration [R_g² = 1/2N²Σ_{i, j}(R⃗_i − R⃗_j)²] of the two motor domain structures from the equilibrium ensemble are computed (see Fig. 3B). Because the neck-linker and the neck-helix adopt different configurations relative to the motor domain in each monomer, we perform an R_g analysis for the motor domains only (residues 2–324). The R_g distributions show that the L is slightly bigger than the T both in the size {[〈R_g〉(L) − 〈R_g〉(T)] ∼ 0.4 Å} and in the dispersion [(σ_L − σ_T) ∼ 0.05 Å]. Meanwhile, the R_g for the native state (3KIN) is R_g^native = 19.4 Å. Clearly, the sizes of both of the heads in the thermal ensemble are expanded at T = 300 K as compared with the native structure. The size alone does not tell much about the difference between the structures.

The rmsd relative to the native structure and between the two motor domains (residues 2–324) computed over the equilibrium ensemble gives rmsd(T∣native) = 2.0 Å, rmsd(L∣native) = 9.4 Å, rmsd(T∣L) = 9.6 Å, where rmsd(X∣Y) is the rmsd between conformations X and Y. If the α6 helix is excluded from the rmsd calculation of motor domain (residues 2–315), then rmsd(T∣native) ≈ 1.8 Å, rmsd(L∣native) ≈ 3.8 Å, and rmsd(T∣L) ≈ 3.9 Å. The rmsd analysis shows that the α6 helix significantly contributes more for the deviation of the L from its native state than does the T.

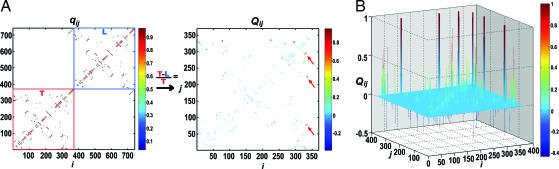
Additional detailed comparisons with respect to the native state can be made by using the structural overlap function of the i − j pair, χ_ij, which is defined as χ_ij = 〈δ(R_ij − R_ij^o)〉 where δ(R_ij − R_ij^o) = 1 if ∣R_ij − R_ij^o∣ < r_tol; otherwise δ(R_ij − R_ij^o) = 0. R_ij^o is the distance of the i − j pair in native state, where r_tol = 1 Å. By setting R_ij^o values identical in both heads (i.e., both heads have the same native state), we compute the χ_ij values for the T and the L, respectively. The relative difference of the χ_ij value between T and L, X_ij, is defined as

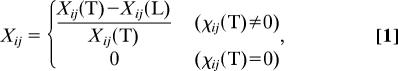which quantitatively measures the structural difference of the two heads. Based on the X_ij value (Fig. 3C), the distances between the MT binding motif of the T (L11, L12, α4, and α5) and other secondary structure units (β1, α0, β2, α1, α2, and α3) are 50% more native-like than in the L.

Conserved native contacts in T reveal the strain propagation pathway in L.

A direct measurement of similarity to the native structure is the fraction of native contacts preserved in the thermal ensemble (31). Because we assume that ATP affinity is optimized in the native state, we can readily assess the quality of the structure by using this measure. We quantify the nativeness of a pair by using q_ij(ξ) = 〈Θ(R_c − R_ij)Δ_ij〉, where Δ_ij = 1 if i, j residues are in contact at the native state (R_ij^o < R_c^K = 8 Å), and Δ_ij = 0 otherwise. q_ij(ξ) (with ξ = T or L) is obtained by averaging over the thermal ensemble. When q_ij(ξ) is averaged over all of the native pairs, the average fraction of native contacts, 〈Q〉, is calculated as 〈Q〉(ξ) = 1/N_QΣ_i<j^N_Q q_ij(ξ), where N_Q is the total number of native pairs. For the T and L conformations, 〈Q〉(T) = 0.86 and 〈Q〉(L) = 0.82, respectively. The relative difference of native contacts between the two kinesin heads at the pair level, Q_ij, is quantified similarly to Eq. 1 as

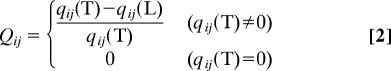In Fig. 4, Q_ij is color-coded based on its value. As expected from the equilibrium ensemble, conspicuous differences are found around the structural motifs having direct contacts with neck-linker, giving Q_ij ≳ 0.5. Quantitative inspection of the other contacts is illustrated in the structure. We color the kinesin head structure based on the Q_ij value. The residue pairs are colored in magenta if 0.2 < Q_ij < 0.5 and red if Q_ij > 0.5, where the positive Q_ij signifies that the native contacts in T are more intact. The residue pairs are colored in light-blue if −0.5 < Q_ij < −0.2 and blue if Q_ij < −0.5. More intact contacts, when the T and the L are compared, are visualized by the yellow line in Fig. 5B. Our analysis not only shows that there is higher probability of the formation of native contacts present in the T in comparison to the L but also suggests how the tension is propagated toward the nucleotide binding site to disrupt the nativeness of the nucleotide binding pocket in the L. As expected, a dense network of intact contacts are found between the neck-linker (β10) and the neck-linker binding motif (β7). This network continues along the α6 helix, perturbing L2, β1, and α4, and finally reaches the nucleotide binding site (see SI Fig. 6 for the nomenclatures of the secondary structures). It is surprising that the disruptions of native contacts are found particularly in the nucleotide binding site, which is believed to be the trigger point for the allosteric transition. All of the important nucleotide binding motifs (P-loop, switch-1, switch-2, and N4) are recognized by our simulational analysis using a nonlinear Hamiltonian (see SI Figs. 7 and 8 and SI Text for the comparison with linear harmonic potential represented as a Gaussian network model).

Fig. 4.

Comparison of two heads using the fraction of native contact. (A) (Left) The average contact map for kinesin. (Right) The relative difference of average contact map between T and L with respect to T. The red arrows mark the set of contact pairs whose Q_ij value is >0.5 (50%). (B) The result of Q_ij in A is redrawn with a 3D plot for clarity.

Fig. 5.

The structure of kinesin on MT shown in colors based on the protocol discussed in the main text. (A) The residues colored in red and magenta on the T (structure on the left) are those maintaining more contact than the residues in the L (structure on the right). Some of the residues in the colored region of the T are involved with the nucleotide binding site. (B) The enlarged view in cartoon representation from the neck-linker docking site (Left) and from the ligand binding site (Right). Sphere representations in orange are ADP molecules. The network of contact pairs is depicted with yellow lines.

Estimate of the Tension in the Neck-Linker.

The deformation of the leading motor domain is caused by the internal tension in the neck-linker. The tension on the neck-linker is estimated by using the force (f) versus extension (x) relationship of a worm-like chain model (32):

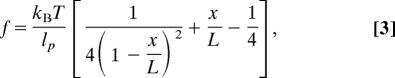where l_p is the persistence length of the polymer and L is the contour length. L ≈ 5.7 nm for the 15-aa neck-linker (residues 324–338) (= 15 × 0.38 nm), and in the equilibrium ensemble of structures, x ≈ 3.1 ± 0.8 nm. Assuming that l_p ≈ 0.4–0.5 nm (33) for this segment, we estimate a tension f = 12–15 pN. By integrating Eq. 3 for 0–3.1 nm, the tensional energy stored in the neck-linker is obtained, which is 17 pN·nm ≈ 4 k_BT. Approximately 20% of the ATP hydrolysis energy (≈25 k_BT) is stored in the neck-linker and directly perturbs the nucleotide binding site of the L, whereas mechanical action to the T is dissipated through the dense network of contacts formed between the neck-linker (β10) and the neck-linker binding site (β7).

For a given extension x when the length of the neck-linker is varied by δL, the variation in the length of the neck-linker can affect the effective tension as f(L + δL) − f(L) ≈ −k_BT/l_p{1/[4(1 − x/L)²] × (2x/L)/(1 − x/L) + x/L}(δL/L). For a given δL/L, the resulting tension change may be significant depending on the value of the extension x. Experimentally, the kinesin dynamics has recently been studied by varying the linker length by introducing a spacer composed of amino acids (34). Because δL = 0.38 nm for the insertion of a single amino acid, the lengthening of the linker leads to a reduction of the tension by Δf ≈ −2 pN. In light of the force values controlling the kinesin dynamics in laser optical tweezers experiments, which are 0–7 pN and because 7 pN is the stall force, a value of Δf ≈ −2 pN can be significant. According to the experimental analysis performed by Hackney et al. (34), the processivity is reduced by ≈2-fold when a single amino acid is inserted or deleted, and 6 or 12 additional amino acids resulted in a 3- to 4-fold reduction in the kinetic processivity.

Conclusions

Because of the size and time scale spanned by a typical molecular motor as well as the lack of crystal structures, theoretical studies based on the structure are not as common an approach as master equation descriptions (35–37) or Brownian ratchet models (38). Knowledge of structural details, however, is the key to understanding the mechanochemistry of molecular motors. In the present study, we propose computational strategies to resolve this problem in kinesin dynamics, particularly the nucleotide binding regulation mechanism between the two motor domains. By building a kinesin model on the tubulin filament, we explicitly identified the effect of internal tension (f = 12–15 pN) on the front kinesin head domain and showed that the tension propagation to the L provokes the switch-related motifs (P-loop, switch-1, and switch-2) in the nucleotide binding pocket. Assuming “the nativeness as a criterion for the optimal nucleotide binding condition,” we concluded that the nucleotide binding pocket in the L is not favorable [or partially unfolded or cracked (39)] for the nucleotide binding while the T is bound to the MT. This conclusion explains the recent real-time single-molecule traces of kinesin generated by Guydosh and Block (24). The reduction of ligand affinity of the L due to the rearward tension benefits the high processivity in two ways. First, premature ATP binding is inhibited before the chemical reaction (ATP hydrolysis, P_i release) in the T is completed, during which the T is tightly bound to the MT and the tension builds on the neck-linker. Second, the release of ADP is facilitated in the L, which accelerates step (ii′) → (iii) in Fig. 1. The latter point is consistent with the experimental observation of Uemura and Ishiwata (21) of a 7-fold increase of the ADP dissociation constant from the monomeric kinesin head in the presence of rearward loading (21).

It is noteworthy that global measures characterizing two-head domains do not distinguish the qualitative differences between the two heads. Major changes in the strained region, such as to the kinesin neck-linker, may be associated to minor global differences in the motor domain. Exactly how these minor global differences that are localized in a small volume are amplified in the process of allosteric transition is another key issue in understanding molecular motors.

Internal tension regulates the interaction between the kinesin and the nucleotide. Conversely, the interaction between kinesin, nucleotide, and MT also switches the internal tension on and off. For conventional kinesin, mechanical and chemical mechanism are closely correlated, producing a remarkable processivity of kinesin movement on the MT.

Methods

The simulations were performed by using two classes of energy function. One is the standard structure-based (SB) potential (40) and the other is the self-organized polymer potential (see SI Text) (16, 41, 42). For these two different topology-based potential functions, we obtained qualitatively identical results. Results from the SB potential are presented in Figs. 3–5, and results from the self-organized polymer potential are in SI Fig. 9. This suggests that the results are robust as long as the information of native topology with a nonlinear form of energy potential is used as an input.

Energy Function–SB Potential.

Using the structure in Fig. 2C as a starting structure, we simulated and sampled an ensemble of two-headed kinesin configurations on the MT. We performed Langevin simulations of the SB model (40), whose equation of the motion of each interaction center is integrated by a Verlet algorithm. The energy potential is given as

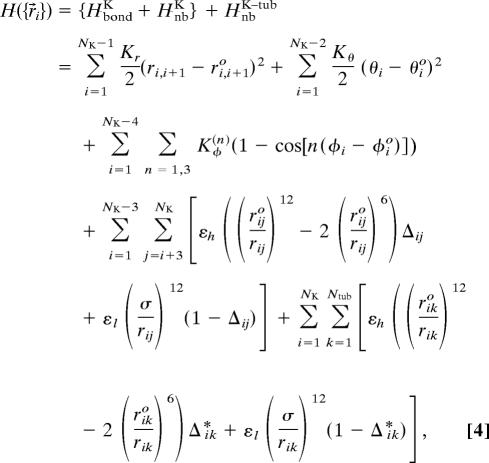where the energy Hamiltonian is divided into intramolecular interactions for the kinesin molecule and intermolecular interactions at the kinesin–MT interface. The superscripts K and tub denote the kinesin and the kinesin–tubulin interaction, respectively. Because our focus is on the kinesin dynamics, we fixed the coordinates of the MT in space. Because the length scale of the kinesin geometry is small (<10 nm) compared with that of MT (diameter, ≈24 nm; persistence length, ≈1 mm), the explicit computation of the dynamics of the entire MT structure, in which the 13 protofilaments constitute the cylindrical geometry, should not qualitatively change our conclusions. The first and the second term define the backbone interactions. The bond distance r_i,i+1 between the neighboring residues i and i + 1 are harmonically constrained with respect to the bond distance in native state r_i,i+1^o with a strength K_r = 20 kcal/(mol·Å²). In the second term, the angle θ is formed between residues i, i + 1, and i + 2, with K_θ = 20 kcal/(mol·rad²). θ_i^o is the angle of the native state. The third term is the dihedral angle potential with K_φ⁽¹⁾ = 1.0 kcal/mol and K_φ⁽³⁾ = 0.5 kcal/mol that describes the ease of rotation around the angle formed between successive residues from i to i + 3 to along the backbone. The Lennard–Jones potential is used to account for the interactions that stabilize the native topology. A native contact is defined from the pair of interaction centers whose distance is R_c^K ≤ 8 Å in native state for ∣i − j∣ > 2. If i and j residues are in contact in the native state, Δ_ij = 1; otherwise Δ_ij = 0. Aided by Δ_ij we assign stabilizing potential for native pairs and repulsive potential for nonnative pairs. We assign ε_h = 1.8 kcal/mol for the intraneck and interneck helix (residue > 338) interactions to secure the coiled-coil association between the neck-helices. For other kinesin residue–residue interactions, we set ε_h = ε_l = 1.0 kcal/mol regardless of the sequence identity. The parameters determining the native topology θ_i^o, φ_i^o, r_ij^o, and Δ_ij are determined from the crystal structure of human kinesin (PDB ID 3KIN) and incorporated to the T kinesin and the coiled-coil whose structure is shown in Fig. 2C. To constitute an identical fold condition, we transferred topological information in T to the L by substituting θ_i^o, φ_i^o, r_ij^o, and Δ_ij from T to L; i.e., θ_i^o(L) = θ_i^o(T), φ_i^o(L) = φ_i^o(T), r_ij^o(L) = r_ij^o(T), and Δ_ij(L) = Δ_ij(T) for all i and j. The kinesin–tubulin interaction parameters (ε_h, ε_l, r_ik^o, and Δ_ik) are similarly defined as kinesin intramolecular interaction parameters except for the slightly larger native contact distance (R_c^K–tub = 10 Å). The parameters r_ik^o and _ik* defining the interface topology between the T kinesin and the tubulin also are transferred to the interface topology between the L and the next tubulin binding site.

Simulations.

The initial structure, whose two heads are constrained to be oriented on the tubulin binding sites, is relaxed under the SB or self-organized polymer Hamiltonian, and subsequently the equilibrium ensemble of the structures is collected from the low-friction Langevin dynamics simulations at T = 300 K. The position of the interaction center is integrated by using

where ζ is friction coefficient,−∂H/∂r⇑ is the conformation force, and Γ⃗ is the random force satisfying 〈Γ⃗(t)·Γ⃗(t′)〉 = (6ζk_BT/h)δ(t − t′) where the integration time (h) is discretized. In low-friction Langevin dynamics, natural time is given by τ_L = (ma²/ε_h)^1/2. We chose ζ = 0.05τ_L⁻¹ and h = 0.0025τ_L. Low friction is deliberately chosen for the purpose of effectively sampling the conformational space (43). Under such conditions, the resulting dynamics as a function of time step should not be taken parallel to the real-time dynamics. To produce an overdamped dynamics, it is essential to integrate the motion by neglecting the inertial term as well as choosing a high-friction coefficient that amounts to the water viscosity (≈1cP).

Abbreviations

L

leading head

MT

microtubule

T

trailing head

SB

structure-based.