Kinetic models of redox-coupled proton pumping

Abstract

Cytochrome c oxidase, the terminal enzyme of the respiratory chain, pumps protons across the inner mitochondrial membrane against an opposing electrochemical gradient by reducing oxygen to water. To explore the fundamental mechanisms of such redox-coupled proton pumps, we develop kinetic models at the single-molecule level consistent with basic physical principles. We demonstrate that pumping against potentials >150 mV can be achieved purely through electrostatic couplings, given an asymmetric arrangement of charge centers; however, nonlinear gates are essential for highly efficient real enzymes. The fundamental requirements for proton pumping identified here highlight a possible evolutionary origin of cytochrome c oxidase pumping. The general design principles are relevant also for other molecular machines and suggest future applications in biology-inspired fuel cells.

In aerobic life, the reduction of oxygen to water drives the generation of the electrochemical gradient across the inner mitochondrial (or bacterial) membrane that powers the production of ATP. Cytochrome c oxidase (CcO), the enzyme catalyzing oxygen reduction, takes up four electrons from the outside of the membrane and four protons from the inside (1–7). In addition, roughly half of the redox energy is used for translocation of four additional protons across the membrane. Even though many models have been proposed to explain this proton pumping (5, 7–17), the central question remains unanswered: How can redox chemistry be harnessed to move protons against both chemical and potential gradients?

In the celebrated Lundegårdh–Mitchell redox loop model (18), the consumption of every electron leads to the net translocation of one electrical charge across a perfectly sealed membrane. In contrast, CcO translocates two (proton) charges per electron (1–7) despite being vulnerable to proton leakage (Fig. 1), a detrimental effect enhanced by membrane potential. However, the directional proton motion is coupled to an exergonic reaction, the reduction of oxygen to water, that makes pumping thermodynamically possible in principle. The objective thus becomes to build the simplest model of a redox-coupled proton pump that is consistent with the overall architecture of CcO and operates through a well defined physical mechanism.

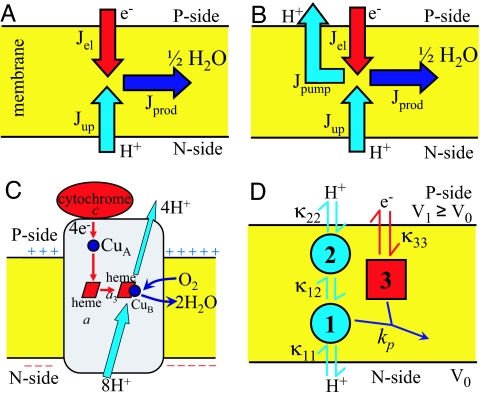
Fig. 1.

Schematic of CcO function. (A) Flux diagram of a Lundegårdh–Mitchell loop in which an electric potential across a protonically sealed membrane is created by taking up protons and electrons from opposite sides. (B) Flux diagram of a true proton pump. J_el is the electron flux, J_up is the proton uptake flux from the N side, J_pump is the net proton pumping flux to the P side, and J_prod is the product flux. Flux conservation requires that J_prod = J_el = J_up − J_pump. (C) CcO proton pump. Electron transfer from cytochrome c via Cu_A and heme a to the binuclear center (heme a₃ and Cu_B) is indicated in red. Light blue arrows indicate proton translocation, including uptake of both chemical and pumped protons from the negatively charged N side and release of pumped protons on the positively charged P side. Blue arrows indicate uptake of dioxygen and release of water. (D) Kinetic scheme of the three-site model. Circles and squares show proton and electron sites, respectively. Arrows indicate proton (light blue) and electron (red) transfer reactions with intrinsic rate coefficients κ_μν. The blue arrow denotes the irreversible product formation.

To build such a model of microscopic proton pumping, we first realize that biological systems are effectively open, that is subject to an influx of reactants and an outflux of products. For a closed system with a fixed number of protons, electrons, oxygen molecules, etc., the second law of thermodynamics would dictate that the enzymatic reaction eventually approaches equilibrium without pumping. However, cells continuously take up “food” and oxygen, and produce water, carbon dioxide, etc., that are then effectively removed. As the simplest approximation to this nonequilibrium system, we thus consider a steady state with a constant supply of reactants and irreversible removal of product.

As the second key element of our model, we impose detailed balance for microscopic reactions (i.e., uptake and transfer of electrons and protons), which is the requirement of the second law of thermodynamics. To achieve a steady state with constant nonzero flux, we assume, for simplicity, irreversible product formation and removal. We note, however, that both this and the above assumption of an open system in steady state can be relaxed by studying the approach to equilibrium of a closed system, with all major results unchanged.

The outline of the paper is as follows. We first introduce the kinetic models of redox-coupled proton pumping based on the above key elements consistent with thermodynamic requirements. We then demonstrate that redox-coupled pumping of protons is possible through purely electrostatic couplings. The simplest three-site model allows us to identify the essential requirements of proton pumping and establishes a connection to molecular motors. By introducing additional protonation sites into an already optimized model, we explore the qualitative effects of certain mutations in the D-channel of CcO. We then show that adding additional redox sites dramatically increases the pumping efficiency, resulting in models that pump against membrane potentials of >150 mV. Finally, we demonstrate that adding “gates” can further enhance the pumping efficiency. In conclusion, we discuss the question how proton pumping might have originated.

Results and Discussion

Kinetic Models.

In building kinetic models of proton pumping, we adapt the formalisms used to study nonequilibrium processes in enzymes and motors (19–21). The models consist of N_p proton sites and N_e electron sites. The resulting microscopic states of the models are specified at the single-molecule level, with protonation and electron-reduction sites either empty or singly occupied. With N = N_p + N_e the total number of proton and electron sites, we thus have 2^N microscopic states that provide a more detailed description than the N “concentrations” one would have at the ensemble level. The states i are defined by the occupancy of the proton and electron sites μ = 1,…, N. Two states i and j are kinetically connected if they are related through a single proton or electron uptake/release or transfer event. Detailed balance then requires that the ratio of rates for transitions from microscopic state i to j and from j to i satisfies k_ji/k_ij = exp[−(G_j − G_i)/k_BT], where k_B is Boltzmann's constant, and T the absolute temperature. In our model, the free energies G_i of states i are determined purely by electrostatic couplings (see Methods). While detailed balance guarantees that the second law of thermodynamics is satisfied, it also greatly increases the challenge to building a pump because every proton pumping path from the negatively charged N side of the membrane to the positively charged P side necessarily constitutes a possible proton leak in the opposite direction.

Fig. 1D presents a kinetic model with N = 3 sites. Consistent with the rough architecture of CcO (Fig. 1C), sites 1 and 3 carry protons from the N side and electrons from the P side into the active site, respectively. Product “water” is formed with a rate coefficient k_p only when the two sites 1 and 3 are occupied simultaneously. The proton site 2 represents the “pumping site” and provides the essential asymmetry in the model. It is connected to both site 1 and the P side of the membrane.

The first objective is to find the simplest kinetic model that produces redox-coupled proton pumping. It is straightforward to show that a two-site model with one proton and one electron site cannot pump protons. However, three-site models of the type shown in Fig. 1D can pump protons while reducing oxygen to water. One readily finds parameter regimes consistent with pumping by using a Monte Carlo search in parameter space to optimize the pumping efficiency η (defined as the number of protons pumped per electron consumed; see Methods). Table 1 lists two sets of parameters with pumping efficiencies of about η = 0.18 and 0.11. Interestingly, we find that the intrinsic free energies of the proton sites can be both positive (model a) and negative (model b), corresponding to low and high-pK_a systems, respectively [see supporting information (SI) Fig. 4]. In exploring the parameter space of our model, we consistently find that for pumping the uptake of protons from the N side has to be favored over proton uptake from the P side. Specifically, the intrinsic rate κ₁₁ of proton uptake from the N side has to be much faster than the intrinsic rates of proton uptake from the P side as well as the rates of electron uptake and of proton transfer. Otherwise, a significant fraction of protons will be taken up from the P side, resulting in loss of pumping.

Table 1.

Parameter values and pumping efficiencies for two three-site pump models (without membrane potential)

	a	b
G10*	3.83	−5.48
G20	8.90	−5.73
G30	15.0	7.78
ε12	12.4	14.5
ε13	−15.0	−6.74
ε23	−22.5	−7.78
κ11†	7.58 × 106	9.98 × 105
κ22	2.84 × 104	1.73 × 104
κ33	2.77 × 104	1.03 × 102
κ12	5.61 × 104	2.92 × 103
kp	105	104
η	0.18	0.11

*G_μ⁰ and ε_μν are in units of k_BT.

^†k_p and κ_μν are in units of s⁻¹.

Our three-site model shows that pumping of protons is possible through purely electrostatic couplings between reversibly connected redox and protonation sites. As a corollary, nonlinear elements such as “gates” and “locks” are not essential for redox-coupled proton pumping. Below, we discuss the basic principles of pumping and the possible implications of the results obtained from this simplest model.

Requirements for Proton Pumping.

The main goal of this article is to understand how an enzyme can pump protons against an electrochemical potential gradient in principle, despite being vulnerable to a possible proton leakage from the P side. In doing so, we aim to identify the basic principles for proton pumping. In this respect, the simplest model, although not immediately comparable to a real system, should nevertheless be helpful to gain insight into the function of the much more complex CcO. It is then appropriate to ask how the redox-coupled proton pumping can be accomplished. The essential feature of our minimal model is that site 2 breaks the symmetry of the proton path. This “kinetic asymmetry” as a prerequisite of vectorial proton translocation is of historical interest. It fully conforms to the Curie principle that “effects cannot be less symmetric than their causes,” as stressed by Mitchell, even though he then defended the case of Lundegårdh–Mitchell redox loop mechanisms (22). In effect, an occupied pumping site 2 serves to prevent protons from leaking into the active site 1 from the P side. If site 2 is eliminated, protons from both sides flow into the membrane to form product, and no pumping can be achieved. Also, symmetrizing the proton path by adding an extra proton site between the site 1 and the N side can disable the pumping ability (see below). Secondly, the electrostatic interactions turn out to be crucial. When the couplings ε_μν (see Methods and Eq. 1) are set to zero, pumping is impossible. In fact, one can argue that our model is analogous to Brownian ratchet models (23), which have been used widely to describe the motility of molecular motors (24). In our model, the energy landscape along the proton pathway depends on the state of the electron site 3 (Fig. 2): upon electron transfer, the energy landscape switches from a “left-leaning” state that favors proton uptake from the N side to a “right-leaning” state that favors release of the pumped proton to the P side. Here, the switching between the asymmetric landscapes is intrinsic to the model and controlled by a microscopic variable, the presence of an electron in site 3. Free energy minima (and, indirectly, barriers) along the proton path respond to redox changes, resulting in “Coulombic gating” of the proton flux.

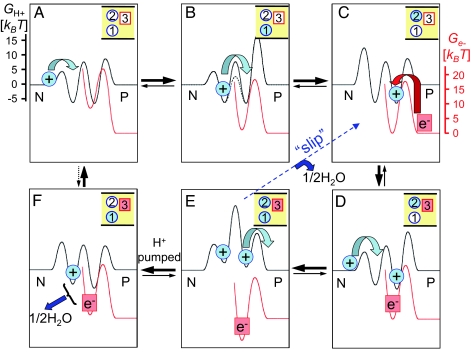
Fig. 2.

Energy landscape representation of electron-coupled proton pumping. Electron reduction induces “ratcheting” between left-leaning energy landscapes for protons (black) by lowering the barriers for proton uptake from the N side (states A, B, and D) and right-leaning landscapes favoring proton release to the P side (states C, E, and F). Proton and electron free energy surfaces (red; shifted vertically) are drawn to scale for model b of Table 1 (including barriers for an attempt frequency of 10⁹ s⁻¹). (A) Initial proton uptake from the N side. (B) Proton translocation to the pump site 2. (C) Electron transfer. (D) Uptake of the second proton from the N side. (E) Release of the pumped proton to the P side. (F) Formation of product “1/2H₂O.” Thick black arrows indicate the dominant steady state flux. The dashed blue arrow indicates “slip,” i.e., product formation without pumping. The dashed black arrow between F and A indicates that the reaction is reversible in principle, halting the pump eventually in a closed system together with depletion of substrates and buildup of product water. Only the six states with significant population are shown. With a “water gate,” internal proton transfer is accelerated, as indicated by the dashed barrier in B, thus increasing the pumping efficiency.

Reduced Kinetic Models Overestimate the Efficiency.

Although the three-site model is the simplest model that pumps protons, solving the corresponding full master equation produces long expressions in terms of the large number of parameters. It is then interesting to ask whether such a complicated model can be reduced to a simpler one without loss of the general picture. Fig. 2 presents the dominant pumping cycle (together with a “futile” slip cycle) of model b in Table 1. Is this simplified kinetic scheme (ignoring all other transitions) adequate to represent the full model? It is straightforward to obtain the pumping efficiency η exactly for this simplified kinetic cycle either via the approach by Hill (19) or via the periodic sequential kinetic models (25). It turns out, however, that the resulting efficiency becomes η ≈ 0.56, much higher than that of the full model (see Table 1). Some of the “slip” cycles ignored in the reduced model of Fig. 2 thus lower the overall efficiency. Reduced kinetic cycles may thus not be appropriate here to represent the full system quantitatively.

Thermodynamics of Proton Pumping.

Are the model properties comparable to real CcO, as characterized by experiment? First, one should note that the parameters in the kinetic models are microscopic in character, making it difficult to compare their values directly to experimental observations. Nevertheless, the thermodynamic properties of the pump models a and b allow us to relate the simple three-site models to CcO (see Table 1). If one identifies site 1 with Glu 242/286 (bovine/Rhodobacter sphaeroides numbering; subunit I), model b appears to reflect CcO more closely, with an apparent pK_a above 9 in both the reduced and the oxidized state (SI Fig. 4). However, it is important to keep in mind that on one hand our models lack the complexity of CcO, and on the other hand only limited experimental information is available for pK_as of proton uptake and release sites, transfer rates, etc.

Mutation of the Proton Entrance from the N-Side.

How sensitive is the pump to mutations? To explore this question, we have added a protonation site between site 1 and the N side. This modification qualitatively mimics mutations in which an ionizable residue is introduced (26, 27) between the highly conserved Asp-91/132 at the opening of the D-pathway and Glu-242/286 at its end by changing Asn-98/139 to an aspartic acid (or aspartate). We find that adding such a fourth site to the already optimized model results in loss of pumping but retains product formation at a high rate. This behavior is qualitatively consistent with the experimentally observed phenotype of the N98/139D mutation of CcO (26, 27). Depending on the parameter regime chosen for this site, the main effect of the extra proton site is either that the proton used in product formation is more likely taken up from the P side (if the pump site is more likely protonated) or that the proton transfer rate from the N side to the pump site is decreased. However, the experimental data exclude the first possibility (26, 27). Hence, our model suggests that the detrimental effect of the N98/139D mutation may stem from an effective slowdown of the rate of proton transfer from the N side.

Efficiency of Pumping Against Membrane Potential.

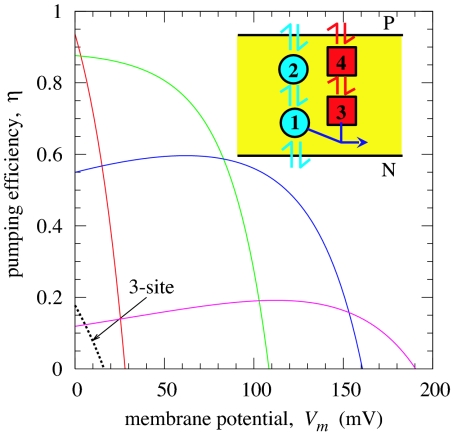
How efficient is oxidase? Experiments suggest that nearly one proton is pumped per electron consumed (i.e., two charges are translocated per electron), which turns out to be a strict upper limit that follows from a graph-theoretic analysis of our network thermodynamic models (19). We found that adding protonation sites to an already optimized pump did not improve the efficiency of our model. In contrast, adding an additional electron site dramatically improved the efficiency. Specifically, when a second electron site is added between the electron site 3 and the P side, the pumping efficiency increases by more than a factor of two (η ∼ 0.5) for a wide range of parameters of the new site. Fully optimized four-site models achieve efficiencies of η >0.9 and can pump protons against membrane potentials V_m > 150 mV, thus approaching the efficiency of CcO (Fig. 3). By adding an extra electron site, it becomes easier to control the proton transfer via electrostatic couplings. For example, if the electron uptake from the P side to site 4 is strongly coupled to the proton transfer from site 1 to the pump site 2, then by adjusting the couplings and intrinsic rates, one can enhance greatly the proton transfer rate to the pump site before the proton is consumed in the active site. Remarkably, in models optimized under load, the efficiency is fairly insensitive to voltage over a broad range before eventually dropping below zero. Breaking up the electron transfer pathway into a series of redox centers (Cu_A, hemes a and a₃, and Cu_B in CcO) thus not only increases the electron transfer rates but is also essential for a high proton pumping efficiency.

Fig. 3.

Pumping efficiency η as a function of membrane potential V_m for a three-site model (dashed line), and different four-site models (solid lines and Inset) that were optimized in different V_m regimes. The voltage drops linearly across the membrane. To mimic CcO, the net thermodynamic driving force of the redox reaction was set to 0.5 V by making product formation reversible. The thermodynamic efficiency of the model shown in purple, (1 + η)V_m/(0.5 V), reaches ≈40% at ≈150 mV.

We notice that pumping efficiencies for some of the four-site models (see Fig. 3) exhibit nonmonotonic behavior. In fact, these models become more efficient as the opposing voltage increases, which seems counterintuitive. When an assisting voltage (V_m < 0) is applied, the efficiency for these models initially drops and then eventually increases, taken over by the high driving force (data not shown). The increase in the efficiency under a positive voltage is attributed to the locations of the charge centers. When either site 2 or site 4 or both are located slightly closer to the N side than the site 1 or site 3, the proton/electron transfer is enhanced by such a positive voltage. Indeed, hemes a and a₃ in CcO are at essentially the same dielectric depth. The important electron transfer between them is thus largely unaffected by the membrane potential, which based on our model is key for a low voltage sensitivity of an optimized pump. By measuring the voltage dependence of the pumping efficiency on real enzymes, one may identify the locations of other charge centers involved in pumping. We note further that analogous behavior has been observed in an optical trap experiment on the motor protein kinesin, where the motor was slowed down under an assisting force (28).

Nonlinear Gates Improve Pumping Efficiency.

Substantial improvements in efficiency can also be achieved by adding “nonlinear” elements to couple proton transfer more tightly to electron transfer. In the water-gated model (13), a linear water chain formed inside a hydrophobic cavity next to the binuclear center (29, 30) serves not only as an efficient proton conducting wire (13, 31), but also as the switch between proton transfer for pumping and water formation (13). To incorporate the water-gate mechanism into our model, we scale the intrinsic proton transfer rate coefficient κ₁₂ by a constant w in states with electron site 3 occupied. This gating lowers the free energy barrier between sites 1 and 2 as shown in Fig. 2B, thus considerably increasing the proton transfer rate to the pump site. After optimizing the model parameters, the pumping efficiency increases dramatically from η < 0.2 to η > 0.6.

Concluding Remarks

Our observation that even a simple three-site model can produce proton pumping against an external potential (Fig. 3), albeit at a low efficiency because of proton leakage, has possible evolutionary implications. Evidence is mounting that the entire family of heme-copper oxidases present in archaea, bacteria, and eukarya has true proton pumping functionality (32). The question then arises as to how proton pumping originated. A natural starting point is the Lundegårdh–Mitchell mechanism of Fig. 1A, in which positive and negative charges are taken up from opposite sides of an otherwise impermeable membrane. However, adding the transmembrane proton connectivity necessary for pumping (Fig. 1B) would appear to reduce the efficiency because of proton leakage. Nevertheless, as we show here, pumping solutions exist for a remarkably broad range of site-2 parameters, for both high and low intrinsic proton affinities (Table 1). The relative simplicity of finding a parameter regime with proton pumping suggests that pumping could have arisen by random mutations that simply added the necessary N- to P-side proton connectivity. As we show, the relatively low pumping efficiency of such an enzyme can easily be improved by adding additional redox sites (Fig. 3) and nonlinear elements such as a water gate (13). By breaking up the electron transfer chain into multiple redox sites, the electron motion can be coupled more tightly to the proton motion. As a comparison of our three- and four-site models shows, this tighter coupling can produce substantial gains in overall pumping efficiency. This efficiency gain may explain the relative complexity of the electron transfer pathway with multiple sites (two hemes, two copper centers) that do not appear to be required for electron transfer alone on the time scales of product formation, and may be relevant for the design of biology-inspired fuel cells.

Methods

Rate Coefficients.

To construct the transition rate coefficients, k_ij, let us consider the simplest model with N = 3 sites (Fig. 1D). This model has a total of 2³ = 8 possible kinetic states. Now, consider two states i and j that are connected by a single proton or electron uptake/release or transfer step between sites μ and ν. The corresponding rate coefficient in the absence of a thermodynamic driving force, G_i = G_j, is defined as κ_μν. Here, we assume, for simplicity, that this intrinsic rate κ_μν for a proton or electron transfer between sites μ and ν is independent of the status of other sites. Relaxing this assumption can enhance the pumping efficiency as shown above. Thus, κ₁₁ and κ₂₂ are the intrinsic rates for proton uptake from the N and P sides, respectively; κ₃₃ is the intrinsic rate for electron uptake; and κ₁₂ is the intrinsic rate for proton transfer between sites 1 and 2 (Fig. 1D). We then write the transition rate coefficients from i to j and from j to i as

respectively. For simplicity, here we assume that the effects of a free energy change are balanced between the forward and reverse rate coefficients corresponding to the factor 1/2 in the exponent both in Eqs. 1 and 2. Models without this restriction could potentially achieve higher pumping efficiencies, but that would increase the number of free parameters. In the absence of a membrane potential (V₀ = V₁), the relative free energy G_i of state i is given by

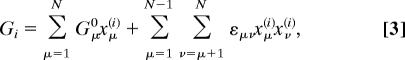where G_μ⁰ is the intrinsic relative free energy of site μ, and ε_μν is the thermodynamic coupling between two sites μ and ν, while x_μ⁽ⁱ⁾ is 0 when site μ is empty in state i and 1 when it is occupied. The intrinsic free energy Gμ0 of occupying site μ with all other sites empty depends on the electrochemical properties, such as pK_a or pH; for many residues involved in CcO proton pumping, these properties have been studied experimentally and theoretically (17, 33, 34). As an example, the rate coefficient for proton uptake from the N side into an otherwise empty enzyme, (000) → (+00), is given by κ₁₁exp(−G₁⁰/2k_BT); and for subsequent proton transfer between sites 1 and 2, (+00) → (0+0), we have a rate coefficient κ₁₂exp[−(G₂⁰ − G₁⁰)/2k_BT].

Electrostatic Coupling.

For simplicity, we restrict our model to purely electrostatic coupling, i.e., ε_μν = q_μq_ν/Dr_μν, where q_μ is the charge of site μ (+e for a proton site, and −e for an electron site), and D is a uniform dielectric constant. Moreover, the Euclidian distances r_μν are determined from the Cartesian coordinates of the sites μ and ν, such that triangle inequalities (r₁₂ + r₂₃ > r₁₃, etc.) are satisfied, imposing |ε₁₂|⁻¹ + |ε₂₃|⁻¹ > |ε ₁₃|⁻¹, etc. Relaxing these requirements, for instance by using a nonuniform dielectric, should improve the efficiency of proton pumping.

Master Equation.

The probability of state i, P_i(t), as a function of time t satisfies the master equation

In the absence of product formation (i.e., k_p = 0), the probabilities would approach equilibrium without proton flux, P_i^eq/P_j^eq = exp[−(G_i − G_j)/k_BT]. For finite product formation rates, k_p > 0, the system approaches a steady state (dP_i^ss/dt ≡ 0) with nonzero fluxes, J_ij = k_ijP_j^ss − k_jiP_i^ss ≠ 0.

Monte Carlo Search for Pumping Solutions.

Even though one can formally write the analytical steady state solution, analyzing it is impractical even for a simple three-site model because of the many degrees of freedom and the large number of parameters. Thus, to explore the parameter space of the model, we numerically determine the steady state of the rate equations for a given set of parameters. We define the pumping efficiency η as the number of protons pumped per electron consumed (Fig. 1B),

The net number of (proton) charges translocated per electron consumed is thus 1 + η, such that the conventional Lundegårdh–Mitchell mechanism (18) corresponds to η = 0, and a perfect pump would have efficiency η = 1. To explore the space of parameters, we perform Monte Carlo simulations in which the model parameters (intrinsic free energies, electrostatic couplings, and intrinsic rate coefficients) are randomly varied. In refining the model parameters, we put limits on the magnitude of the intrinsic free energies (<20 k_BT), electrostatic couplings (<100 k_BT), and rate coefficients (10² to 10⁹ s⁻¹) to keep them within certain physical ranges. For each parameter combination, the proton pumping efficiency η is calculated numerically for finite product formation rates, k_p > 0. By performing simulated annealing (35), we can locate optimal parameter combinations with maximal efficiency η. By repeating the search from different starting points and stopping it before the global optimum is reached, we obtain a distribution of models. By grouping these different solutions, we identify two main classes of models that pump protons, as summarized in Table 1.

Pumping Against Membrane Potential.

In the presence of a membrane potential, V_m = V₁ − V₀ > 0, we assume that the potential drops linearly across the membrane. The contribution ΔG_i(V_m) to the free energy G_i of state i in Eq. 1 is then given by

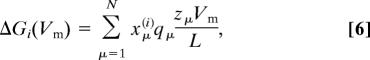where L is the membrane width, and z_μ is the distance from the N side to site μ. Note, however, that care must be taken in specifying the voltage-dependent rate coefficients for proton or electron uptake, because of the broken symmetry of the two sides of the membrane. In the Monte Carlo parameter search, the Cartesian coordinates (and thereby z_μ) of the charge sites are varied.

Protonation Equilibria.

To calculate the probability of a proton site μ to be occupied, we note that the thermodynamic average of the proton (or electron) population, 〈x_μ〉, at equilibrium (i.e., k_p = 0) is given by

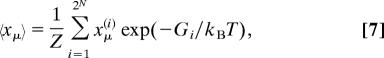where the partition function is

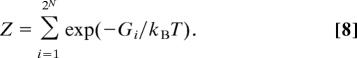For a given pH, the free energy G_i in Eq. 2 can be written as

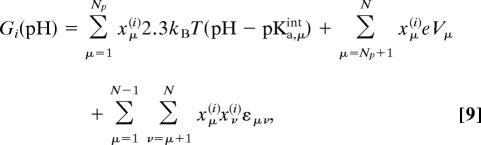where pK_a,μ^intis the intrinsic pK_a of the site μ, which is related to G_μ⁰ via G_μ⁰ = 2.3k_BT (7 − pK_a,μ^int). V_μ = G_μ⁰/e for μ > N_p is the difference in the intrinsic redox potentials between the electron source (cytochrome c for CcO) and site μ. The apparent pK_a of a proton site μ can then be obtained by calculating 〈x_μ〉 over a wide range of pH.

Abbreviation

CcO

cytochrome c oxidase.