Identifying Quantitative Trait Locus by Genetic Background Interactions in Association Studies

Abstract

Association studies are designed to identify main effects of alleles across a potentially wide range of genetic backgrounds. To control for spurious associations, effects of the genetic background itself are often incorporated into the linear model, either in the form of subpopulation effects in the case of structure or in the form of genetic relationship matrices in the case of complex pedigrees. In this context epistatic interactions between loci can be captured as an interaction effect between the associated locus and the genetic background. In this study I developed genetic and statistical models to tie the locus by genetic background interaction idea back to more standard concepts of epistasis when genetic background is modeled using an additive relationship matrix. I also simulated epistatic interactions in four-generation randomly mating pedigrees and evaluated the ability of the statistical models to identify when a biallelic associated locus was epistatic to other loci. Under additive-by-additive epistasis, when interaction effects of the associated locus were quite large (explaining 20% of the phenotypic variance), epistasis was detected in 79% of pedigrees containing 320 individuals. The epistatic model also predicted the genotypic value of progeny better than a standard additive model in 78% of simulations. When interaction effects were smaller (although still fairly large, explaining 5% of the phenotypic variance), epistasis was detected in only 9% of pedigrees containing 320 individuals and the epistatic and additive models were equally effective at predicting the genotypic values of progeny. Epistasis was detected with the same power whether the overall epistatic effect was the result of a single pairwise interaction or the sum of nine pairwise interactions, each generating one ninth of the epistatic variance. The power to detect epistasis was highest (94%) at low QTL minor allele frequency, fell to a minimum (60%) at minor allele frequency of about 0.2, and then plateaued at about 80% as alleles reached intermediate frequencies. The power to detect epistasis declined when the linkage disequilibrium between the DNA marker and the functional polymorphism was not complete.

THE existence of epistasis is supported by classic quantitative genetic studies (e.g., Mather and Jinks 1982; Lamkey et al. 1995) and has also been identified in quantitative trait locus (QTL) studies (e.g., Spickett and Thoday 1966; Lark et al. 1994; Holland et al. 1997; Blanc et al. 2006; Carlborg et al. 2006) and in near-isogenic line studies (Eshed and Zamir 1996; Kroymann and Mitchell-Olds 2005). At the same time, QTL detection methods using population-wide linkage disequilibrium are beginning to demonstrate their potential to identify either mutations causing phenotypic variance or genetic polymorphisms in strong linkage disequilibrium and therefore, presumably, in tight linkage with those mutations. Application of these methods has occurred in large germplasm collections (Thornsberry et al. 2001) and in pedigreed populations (Kraakman et al. 2004; Parisseaux and Bernardo 2004; Arbelbide and Bernardo 2006; Breseghello and Sorrells 2006). Association mapping models to date have assumed additive gene action in the loci analyzed (Kennedy et al. 1992; Yu et al. 2006). Statistical approaches to association mapping that account for epistasis are needed both to detect loci that display little main effect and to discern the extent to which identified additive effect loci also display epistasis.

A typical statistical model to detect association between a DNA marker and the phenotype includes a term for the DNA marker itself and a term for the genetic background of the individual (Kennedy et al. 1992; Thornsberry et al. 2001; Yu et al. 2006). In the absence of the latter term, associations between markers and the phenotype can arise even for markers unlinked to any causal QTL because of correlation between marker allelic states and the genetic background. For example, some marker alleles may be more prevalent in some subpopulations (Knowler et al. 1988; Beer et al. 1997) or in some families (Spielman et al. 1993). In this context, a natural way to test for genetic interactions between the focal DNA marker and other loci in the genome is to add to the statistical model a term for the interaction between the marker and the genetic background. If genetic background is modeled by a fixed effect for classifying individuals into subpopulations, the interpretation for this interaction term would be that the associated effect differs between subpopulations. Alternatively, if the genetic background is modeled as a random polygenic effect with a variance covariance matrix determined by identity-by-descent (IBD) probabilities among individuals, the interpretation for the term would be that allelic effects display resemblance between relatives: the effect of an allele will be more similar if it is carried by, say, two full-sibs than by two unrelated individuals.

The objective of this study was to extend pedigree-based association mapping methods to include epistatic effects by considering an interaction term as described above. The use of observations from complex pedigrees promises to expand the range of data useful for identifying the genetic factors influencing the phenotype and to increase the relevance and cost effectiveness of quantitative trait locus mapping in applied contexts (Jannink et al. 2001; Parisseaux and Bernardo 2004). For this study, I developed a theory to relate the DNA marker by genetic background term back to a more standard concept of additive-by-additive epistasis (Lynch and Walsh 1998). I then formulated statistical models to fit a random effect that accounts for the DNA marker by genetic background interaction. Finally, I simulated random-mating pedigrees with different numbers of individuals, genetic models, magnitudes of epistatic effects, and degree of linkage disequilibrium between the DNA marker and the causal genetic polymorphism. Analysis of these pedigrees served to evaluate the power of the model to identify epistasis and to predict the influence of epistasis on allelic effects in progeny that have not yet been phenotyped.

GENETIC MODEL

For simplicity, consider a two-locus quantitative genetic model that includes only the additive effects at locus Q and the additive-by-additive epistatic effects of the interaction between locus Q and B. In the notation below, the subscripts i and j indicate the maternally and paternally inherited alleles at locus Q, respectively. The corresponding subscripts for locus B are k and l. The genotypic value G is then

(1)

where the α parameters are the additive effects for the alleles at the marked locus Q and the ε parameters are additive-by-additive epistatic parameters for the interaction between locus Q and B. These parameters are defined in the usual way, for example,

These definitions ensure that the parameter expectations are zero and that the covariances between the parameters are zero for a population in Hardy–Weinberg and linkage equilibrium. Given this model,

(2)

where ε is a randomly sampled value among all ε_ik, and 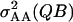is the additive-by-additive genetic variance generated by the interaction between loci Q and B.

The genotypic value conferred to individual x by receiving the Q locus allele Q₁ and considering the genotype of x at locus B is α₁ + ε_1k + ε_1l = α₁ + τ_1x. Similarly, the genotypic value conferred to individual y by receiving allele Q₁ is α₁ + ε_1k′ + ε_1l′ = α₁ + τ_1y. The parameters τ_2x and τ_2y are defined similarly. I derive here the covariance cov(τ_1x, τ_1y),

This covariance of sums decomposes into four simple covariances between single ε parameters. Focusing on one of these simple covariances, we have

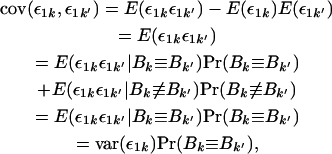where the symbols ≡ and ≢ indicate that the alleles are and are not identical by descent, respectively. The transition from the third to the fourth line of the derivation follows because

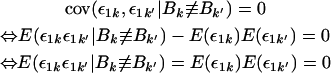The three other simple covariances have the same form, and summing them we obtain

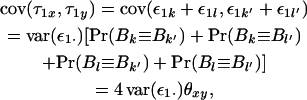(3)

where ε_1· is a randomly sampled value among all ε_1k, and θ_xy is the coefficient of coancestry between x and y. If we assemble all individual-specific τ_1x into a single vector 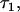result (3) shows that

(4)

where A is the additive genetic relationship matrix, calculated from the known pedigree, and each cell of A, a_xy = 2θ_xy, is the additive relationship between individuals x and y.

A few other developments are useful before moving to the statistical analysis of this genetic model. First, in the biallelic case, 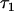and 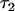are perfectly negatively correlated because of the zero expectation of the ε parameter:

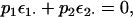(5)

where p₁ and p₂ are the frequencies of the Q locus alleles, with p₁ + p₂ = 1. Consequently, p₁τ_1i + p₂τ_2i = 0 and Second, the allele-specific epistatic variance, var(ε_1·), can be related back to the general epistatic variance, 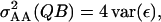defined in (2) by noting that

and, from (5),

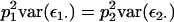such that

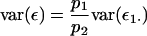Consequently, the 2var(ε_1·) given in (4) is equal to 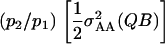Finally, treatment of the interaction between the marked locus Q and a single other locus B can be extended to pairwise interactions between Q and multiple other loci. Assuming linkage equilibrium, effects of pairwise interactions can be summed such that the total variance, denoted 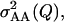is

(6)

where B^c is one of the m loci with which the locus Q interacts. In the statistical model below, therefore, 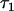is redefined to include all pairwise interactions across loci B^c:

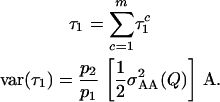(7)

STATISTICAL MODEL

The standard additive model assumes that the effect of a QTL allele is common to all individuals carrying the allele. Denote the marked locus Q with two alleles, Q₁ and Q₂, with effects α₁ and α₂. The linear model for the phenotype Y of an individual is

(8)

where μ is the population mean, X₁ and X₂ are the number of Q₁ and Q₂ alleles carried by the individual (X₁ + X₂ = 2), U is the polygenic effect, and E is a residual (in the notation used here, fixed effects common to all individuals are in lowercase, while random variables sampled for each individual are in uppercase type). In the epistatic model, we decompose the effect of a QTL allele into a component that is common to all individuals carrying the allele and a deviation that represents the interaction of the allele with the genetic background carried by the individual. The linear model then becomes

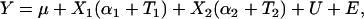(9)

where T₁ and T₂ are deviations from the main effects of alleles Q₁ and Q₂ conditioned by the specific genetic background of the individual. The α effects are considered fixed and the T effects random. Grouping fixed and random effects gives

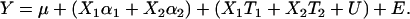Assuming an animal model in which each observation is associated with a unique random effect, the model for the realized vector of observations becomes

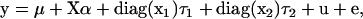(10)

where two columns of the QTL incidence matrix X are the vectors x₁ and x₂ formed from the individual QTL allele incidences, is the vector of the main additive effects of the two QTL alleles, and diag(x₁) and diag(x₂) are diagonal matrices formed from x₁ and x₂, and are vectors of deviation effects caused by epistasis, u is a vector of polygenic effects, and e a vector of residuals. A diagonal matrix Z can be constructed to combine the terms from (10). Using (5), this sum for individual i is

(11)

Substituting 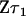into (10) gives

(12)

With respect to the distribution of y, e ∼ N(0, Iσ²), where σ² is the residual variance and I is an identity matrix, and 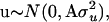where 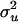is the polygenic additive variance, and

Thus

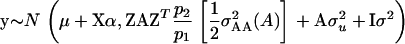(13)

SIMULATIONS AND ANALYSES

In the first simulation setting, I applied the model to analyze a pedigree spanning four generations of 80 individuals for a total of 320 individuals. Founders were simulated to be in Hardy–Weinberg and linkage equilibrium. Mating was random in subsequent generations. The epistatically interacting QTL was biallelic and was assumed to be identified by a functional marker (Shi et al. 2005) such that marker and QTL alleles were in complete linkage disequilibrium (LD) and did not recombine. All alleles had expected frequencies of 0.5 in this setting. The stochasticity of the simulation, however, meant that frequencies deviated from their expectations because of random sampling. Similarly, the genetic model simulated had variances described below that one would obtain if allele frequencies were at their expectations. Deviations from expected allele frequencies also caused deviations in the actual variances simulated from one run to the next.

The simulated trait had a genetic variance of 60 and a phenotypic variance of 100. An epistatic variance of 20 was generated in a compound epistatic network (Cooper et al. 2001): the marked QTL interacted with nine other unlinked loci. Each pairwise interaction generated a variance of 2.2 and effects of each interaction were summed, such that the sum generated a variance of 20. The remaining genetic variance of 40 was generated by 10 unlinked additive-effect QTL, each accounting for a variance of 4. To the genotypic value thus obtained, a normally distributed residual of variance 40 was added to produce each individual's phenotype. In all genetic models, the expected marginal effect of the QTL was zero. All other simulation settings were variants of the first setting (Table 1). Setting 8 involved QTL and interacting loci with low minor allele frequencies. Given the low frequencies, epistatic effects needed to be large to generate the desired variances. In this situation, small stochastic deviations from expected allele and genotype frequencies in the simulation could generate large deviations in the epistatic variance actually simulated. Simulations that generated epistatic variances below 10 or above 40 were excluded from the analysis. Also, for a given simulation run the estimation error was calculated on the basis of the epistatic variance generated in that run, rather than on the basis of the expected variance of 20.

TABLE 1.

Variants from the simulation setting 1 described in the text

Setting	Difference from setting 1
2	Generations consisted of 160 rather than 80 individuals for a total pedigree of 640 individuals.
3	The epistatic variance simulated was 5 rather than 20.
4	The above two variants in combination.
5	The epistatic variance was generated from a simple two-locus interaction rather than a compound epistatic network.
6	The QTL was not in complete LD with the marker. Decay of LD was achieved by simulating 10 generations of random mating with population size 100 for a marker 1 cM from the QTL.
7	The marker was in linkage equilibrium with an additive effect QTL causing a variance of 20.
8	Expected frequency of allele Q1 at the marked QTL was varied continuously from 0.05 to 0.50. Minor allele frequencies of interacting loci were 0.05 for five loci, 0.20 for two loci, and 0.35 for two loci.

Note that for settings 1, 2, and 5–8, the phenotypic variance was 100 while for settings 3 and 4 that variance was 85.

For the base simulation and the first three variants, the analysis was also run with the phenotypes of the fourth (last) generation set as missing data. Genotypic values for the fourth generation individuals were then predicted on the basis of their QTL genotypes and their pedigree relationships using

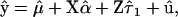(14)

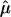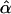where and are best linear unbiased estimates of the fixed effects, and and are best linear unbiased predictors of random effects obtained using variance components estimated by the mixed model analysis. For each simulation, predicted genotypic values were compared to true genotypic values by correlation. The same data were also fit with the standard additive model

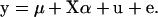(15)

Genotypic values using this model were also predicted using a model corresponding to (14) and correlated to the simulated values. Five hundred randomly generated pedigrees and founders were simulated for each setting, except setting 8, which was replicated 8000 times.

RESULTS

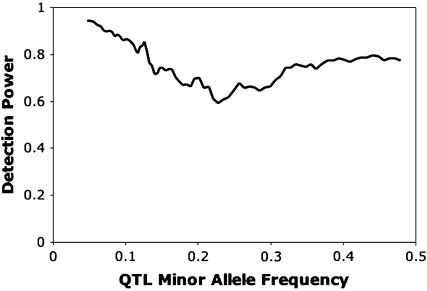
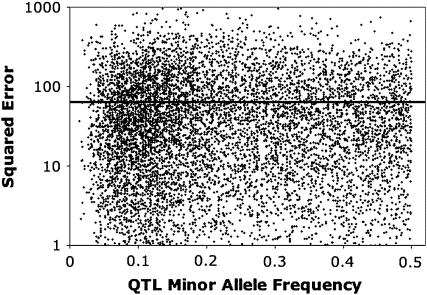
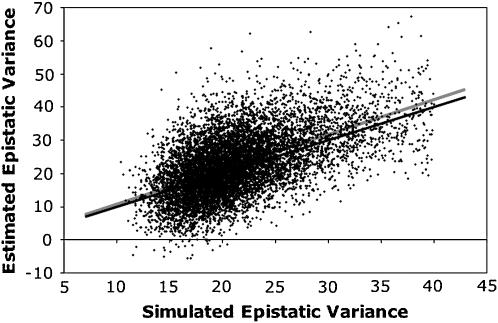
Power to a detect QTL × genetic background interaction depended on the population size and the magnitude of the epistatic interaction (Table 2). In general, the estimated epistatic variance was unbiased (Table 2). Estimates of power and of the QTL × genetic background variance for settings 1 and 5 were similar, indicating that the method was robust to whether the epistatic interaction was simple or compound. Detection power dropped when the associated marker was not in complete linkage disequilibrium with the QTL, as indicated by the contrast between settings 1 and 6. In that case, the estimate of the epistatic variance was also biased downward. When no epistatic variance was simulated, but the focal marker was in linkage equilibrium with an additive effect QTL (setting 7), the QTL × genetic background interaction was rarely significant, and the mean estimate of the epistatic variance was small (Table 2). Average detection power was little affected by the more extreme interacting locus allele frequencies used in setting 8 (Table 2). A plot of detection power against QTL minor allele frequency showed that power was highest (94%) at low QTL minor allele frequency, fell to a minimum (60%) at minor allele frequency of about 0.2, and then plateaued at about 80% as the QTL reached intermediate frequencies (Figure 1). Logistic regression showed that this pattern created a significant quadratic response of power to minor allele frequency (data not shown). There did appear a slight positive bias in the estimate of epistatic variance in setting 8, although the overall mean squared error was not adversely affected (Table 2). The squared error of estimation of the epistatic variance did not appear to depend on the QTL minor allele frequency (Figure 2). A linear regression of estimated epistatic variance on simulated epistatic variance found a slope very slightly greater than 1 (95% confidence interval of 1.02–1.08) and an intercept no different from zero (95% confidence interval of −0.50–0.92; Figure 3).

TABLE 2.

Power to detect QTL × genetic background interaction, mean estimate of the epistatic variance and mean squared error (MSE) of the estimate over 500 simulations for the simulation settings given in the text

Setting	Population		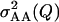Power (%)		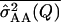MSE	Bias2	Variance
1	320	20	78.8	20.6	68.9	0.4	68.5
2	640	20	97.0	20.2	30.0	0.0	30.0
3	320	5	9.2	5.5	22.9	0.2	22.7
4	640	5	19.0	4.9	11.6	0.0	11.6
5	320	20	74.1	19.5	58.6	0.3	58.4
6	320	20	39.8	13.3	111.8	45.0	66.8
7	320	0	2.2	3.1	24.5	9.3	15.1
8	320	20	76.4	21.2	63.5	1.5	62.0

Figure 1.—

Power to detect epistatic variance plotted against the simulated QTL minor allele frequency. Power was estimated in bins of 400 simulation runs with consecutive QTL minor allele frequencies.

Figure 2.—

Squared error of the estimated epistatic variance 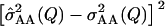plotted against the simulated QTL minor allele frequency. Each point represents one simulation run. The black line is the overall mean squared error.

Figure 3.—

Estimated epistatic variance plotted against simulated epistatic variance 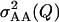for setting 8. Simulated epistatic variance depended on stochastic simulation. The black line shows equal estimated and simulated variances. The gray line is the linear regression of estimated on simulated variance.

Estimates of the additive polygenic and residual variances were close to their simulated values under the epistatic model (Table 3). In contrast, when variances were estimated under the additive model, half of the epistatic variance was absorbed by the additve polygenic variance and half by the residual variance. Slight positive biases in the estimates of the additive polygenic variance were observed in settings 1–4. The bias was greater for the effective population size of N_e = 80 than N_e = 160, and when the epistatic variance was 20 rather than 5 (Table 3). A similar phenomenon was observed for the mean squared error of the estimate of the associated effect, 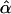: a larger mean squared error (MSE) was observed for the small than the large population size and when the epistatic variance was 20 rather than 5. These observations held when parameters were estimated with either the epistatic or the additive models. The MSE of the associated effect was higher in setting 8 than in other settings (Table 3).

TABLE 3.

Mean estimate of additive polygenic variance and residual variance and mean squared error of main QTL effect, as estimated using the QTL × genetic background interaction model vs. the standard additive model

	QTL × genetic background model			Additive model
Setting		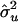	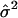MSE()			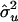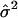MSE()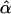
1	40.7	39.7	1.6	50.4	50.6	1.7
2	40.4	39.3	0.8	50.2	49.9	0.9
3	40.2	39.6	1.1	42.7	42.2	1.1
4	40.1	40.0	0.4	42.5	42.4	0.5
5	40.5	40.4	2.2	50.1	50.6	2.5
6	41.4	40.3	2.8	51.3	50.1	3.7
7	57.9	39.4	1.2	59.0	40.0	1.1
8	39.6	39.9	4.0	—	—	—

Standard errors for variance estimates and mean squared errors were less than 0.5 and 0.2, respectively. Setting 8 was not analyzed with the additive model.

When the epistatic variance was high, as in settings 1 and 2, the correlation between the true genotypic values and predicted genotypic values averaged slightly more for the epistatic model than for the additive model (Table 4). Even though the difference in the correlations was small, the correlation was fairly reliably higher using the epistatic model than the additive model (78 and 86% of the time for settings 1 and 2, respectively). When the epistatic variance was smaller, as in settings 3 and 4, the correlations were equal between epistatic and additive models, and the epistatic model outperformed the additive model only slightly more often than half the time (Table 4). When there was no epistatic variance, the epistatic model underperformed the additive model in all respects.

TABLE 4.

Mean correlation between the simulated genotypic value of an individual and its predicted genotypic value for the epistatic and additive models (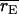 and respectively) and the frequency with which the correlation was higher for the epistatic model than for the additive model [P(r_E > r_A)]

Setting		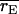	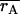P(rE > rA)
1	0.499	0.473	0.78
2	0.508	0.479	0.86
3	0.509	0.510	0.50
4	0.516	0.515	0.58
9	0.516	0.524	0.36
10	0.536	0.540	0.34

Individuals for which the correlation was evaluated were in the fourth generation of the pedigree and had DNA marker data but no phenotypic record. Settings 9 and 10 here have N = 320 and N = 640, respectively, with Standard errors for correlations were less than 0.005.

DISCUSSION

There is general agreement that interaction among loci is important in the causation of complex diseases (Hoh and Ott 2003; Hirschhorn and Daly 2005) and quantitative traits (Blanc et al. 2006; Carlborg et al. 2006). The power of specific statistical models to identify interacting loci will depend on the type of interaction, that is, on the mode of gene action or mode of inheritance of the trait (Dupuis et al. 1995; Hoh and Ott 2003). In terms of detectable modes of inheritance, the statistical model presented here is unique in that it can identify loci that do not interact with just one or two other loci but that engage in many small-effect interactions with other loci. Further, the model can detect loci that have no main effect but influence a trait only through their interactions with other loci. Finally, the model deals parsimoniously with the multiple testing issue inherent in the search for epistasis (Jannink and Jansen 2001; Hoh and Ott 2003) because it does not require testing sets of loci together, but identifies instead the interaction of a single focal locus with the genetic background. In this study, the genetic background has been represented by the additive relationship matrix calculated from the known pedigree of the individuals evaluated. Note, however, that the additive relationship matrix can also be estimated if the pedigree is not known but all individuals have been typed at a sufficient number of markers (Ritland 1996; Yu et al. 2006). The model can therefore also be applied in the absence of a recorded pedigree. Presumably, however, some amount of familial structure is necessary simply to provide a range of genetic backgrounds with which the QTL alleles may interact.

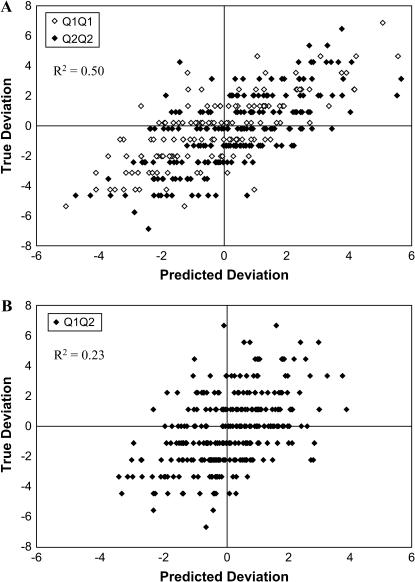
For markers in complete linkage disequilibrium with the causal polymorphism (causal alleles or perfect proxies, sensu de Bakker et al. 2005), simulations showed that the method estimates the epistatic variance associated with a locus in an unbiased way. The coefficient of variation around the estimate will be high, however, at least for pedigrees of the size evaluated here (Table 2). A potential function for the method may be to estimate the extent to which a previously identified QTL interacts with genetic background. This information would then be useful to decide whether to further search the genome for loci that interact with the QTL. If QTL by genetic background interaction is detected, an interesting consequence of the mixed model analysis used here is that a best linear unbiased predictor (BLUP) of the interaction between a QTL allele and the genetic background of an individual can be calculated, even if that QTL allele is not present in the individual (Figure 4). This possibility could help inform decisions about whether to introgress a QTL from the genetic background where it has been detected with a new background. Figure 4 also illustrates a weakness of the statistical method in terms of its use of available data. In particular, the correlation between the true 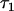deviation and that predicted by the analysis was significantly lower for heterozygous individuals than for homozygous individuals. A possible explanation for this difference is that when the allele frequencies at the marked QTL are intermediate, as they were for most settings evaluated here, the incidences of observations of heterozygous individuals on 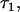as calculated in Equation 11, are close to zero. Thus, all information contributing to the prediction of derives from homozygous individuals. In particular, information contributing to the prediction of the deviation for a heterozygous individual itself can come only from homozygous relatives of the individual, and the most valuable source of information, the individual's own phenotype, cannot contribute. This observation suggests that the method might be more powerful for species that self-fertilize such that individuals are usually inbred.

Figure 4.—

True τ₁ deviation from model (10) plotted against the deviation predicted by the mixed model analysis from a single setting 2 simulation. (A) Plot for individuals homozygous at the marked QTL. To increase graph legibility, τ₁ has been increased and decreased slightly for Q₁Q₁ and Q₂Q₂ individuals, respectively. Note that τ₁ can be predicted even for individuals who do not carry the Q₁ allele. (B) Plot for individuals heterozygous at the marked QTL.

The conversion of additive-by-additive epistasis to additive variance due to drift (Goodnight 1988; Cheverud and Routman 1996), although small, was also observable in these simulations. The conversion in this case will have two effects. First, change of allele frequency at the marked QTL will increase the estimated additive genetic variance. This effect will be stronger as the frequency of the marked QTL deviates from 0.5 due to drift. Second, drift will cause the marked QTL itself to have a positive or negative additive effect depending on the changes in allele frequencies of loci interacting with the QTL. This second effect then does not bias the estimated additive effect but increases its mean squared error. This mean squared error was particularly high in setting 8 when the QTL had low minor allele frequency. When interacting loci have low minor allele frequencies, the absolute effect sizes need to be quite large to generate much variance. These large effects in turn mean that a little drift can cause marginal effects to deviate substantially from their expectations. Given that the marginal effects depend on drift, they are expected to be greater in simulations with N_e = 80 than with N_e = 160. That expectation was borne out (Table 3). The effects should also have been greater when the epistatic variance simulated was 20 than when it was 5, which was also observed. The effects were small, but that was not surprising because drift over four generations with N_e = 80 only increases the inbreeding coefficient to about 0.02. Nevertheless, the conversion of epistasis to additive variance should improve the ability of the additive model to predict genotypic values of progeny without phenotypic records (Table 4).

For the simulation setting 1, the ability of the additive model to predict the genotypic values of unphenotyped progeny was greater than might have been expected on the basis of the simulated narrow-sense heritability of 0.40 alone (Table 4). With that narrow-sense heritability, a correlation of 0.40 between midparent values (which were known) and progeny genotypic value would have been expected. The prediction was greater than that (0.47) because of the conversion of epistatic to additive variance noted above, because relatives other than the parents presumably contributed to the prediction, and because one-fourth of the additive-by-additive epistasis contributes to parent–offspring resemblance. The ability of the epistatic model to predict the genotypic values of unphenotyped progeny, on the other hand, was less than might have been expected on the basis of the broad-sense heritability of 0.60. Thus, for prediction, the epistatic model was not able to take advantage of all variance that was either additive or additive by additive and associated with the marked QTL. Prediction using the epistatic model requires the estimation of two genetic variance components rather than one, and perhaps when these components are poorly estimated the predictions are more rapidly led astray. As noted above also, the method may not be able to fully take advantage of observations from individuals heterozygous at the marked QTL. Finally, it may also be that the power and predictive ability of the epistatic model will increase if the marker QTL is segregating not only within the pedigree as a whole but also within families. Evaluating such circumstances that enhance or detract from the power of the epistatic model could be a topic of further research. In particular, for applied work with self-pollinating crops, determining whether predictions are improved under inbreeding should be explored. Nevertheless, a consequence of the poor prediction under the epistatic model in the simple random-mating situation simulated here is that, even under very strong epistatic gene action, prediction was only marginally better under the epistatic than under the additive model (Table 4).

In linkage analyses where a population is derived from the cross of two inbred lines, allele frequencies will usually be close to 0.5. These intermediate frequencies need not occur, and are indeed unlikely, in association analyses. Simulations under setting 8 covered the likely range of QTL minor allele frequencies wherein the QTL might be detected. Interacting loci in that setting also spanned a range of allele frequencies (Table 1). The performance of the model given these more extreme allele frequencies was not markedly different from its performance with intermediate allele frequencies. Surprisingly, power to detect epistatic variance was highest at low minor allele frequency (Figure 1), presumably because at those frequencies the epistatic effects themselves need to be large to generate perceptible variance. The reason for the nonmonotonic change of power with QTL allele frequency (Figure 1) is unclear. An interaction between the changing size of the epistatic effects and the changing imbalance in QTL allele frequencies could be imagined: large effects favor power at one extreme and greater balance favors power at the other extreme, but at a minor allele frequency around 0.2 neither cause boosts power.

In conclusion, this study lays out the theory for a simple approach to detecting and estimating epistasis affecting loci in association studies. The model has several desirable properties, particularly its ability to detect compound epistasis and to estimate the strength of interaction effects in the absence of knowing the identity of all interactors involved. Given these properties, the model may succeed where others fail. Empirical application will determine its ultimate value.