Abstract
Genomic imprinting is a phenomenon by which the expression of an allele at a locus depends on the parent of origin. Two different two-locus evolutionary models are presented in which a second locus modifies the imprinting status of the primary locus, which is under differential selection in males and females. In the first model, a modifier allele that imprints the primary locus invades the population when the average dominance coefficient among females and males is  and selection is weak. The condition for invasion is always heavily contingent upon the extent of dominance. Imprinting is more likely in the sex experiencing weaker selection only under some parameter regimes, whereas imprinting by either sex is equally likely under other regimes. The second model shows that a modifier allele that induces imprinting will increase when imprinting has a direct selective advantage. The results are not qualitatively dependent on whether the modifier locus is autosomal or X linked.
and selection is weak. The condition for invasion is always heavily contingent upon the extent of dominance. Imprinting is more likely in the sex experiencing weaker selection only under some parameter regimes, whereas imprinting by either sex is equally likely under other regimes. The second model shows that a modifier allele that induces imprinting will increase when imprinting has a direct selective advantage. The results are not qualitatively dependent on whether the modifier locus is autosomal or X linked.
PARENT-OF-ORIGIN-SPECIFIC gene expression, commonly termed genomic imprinting, was first documented in the gnat genus Sciara over 40 years ago (Crouse 1960). Further work has shown genomic imprinting to be widespread among mammals including mice (McGrath and Solter 1984; Surani et al. 1984), humans (Giannoukakis et al. 1993; Bartolomei and Tilghman 1997), sheep (Feil et al. 1998), pigs (de Koning et al. 2000), and opossum (O'Neill et al. 2000), and some studies have reported the phenomenon in flies (Lloyd 2000; Bonduriansky and Rowe 2005) and Arabidopsis thaliana (Alleman and Doctor 2000). Over 80 genes and untranslated RNAs are known to be imprinted in mammals (Morison et al. 2005) and one recent bioinformatic study suggests that the number could be at least 600 (Luedi et al. 2005). Many of these genes are involved in development and defects in their imprinting are central to human diseases including Angelman syndrome and Wilms' tumor (Walter and Paulsen 2003).
Although the exact molecular mechanisms involved in establishing and maintaining genomic imprints remain undetermined, much is known about the basic details. Imprinted genes often occur in clusters that contain one or more imprinting control regions (ICRs) (Delaval and Feil 2004). ICRs often exhibit different patterns of DNA methylation depending on whether the allele is paternally or maternally inherited (Reik and Walter 2001). In the case of Igf2, the first imprinted murine gene to be discovered, methylation of the ICR occurs in spermatogenesis and prevents the DNA binding protein CTCF from associating with the ICR (Delaval and Feil 2004). In the absence of CTCF, a downstream enhancer catalyzes expression of Igf2 from the paternally derived allele. Ooctyes do not undergo methylation at the ICR, which allows CTCF binding and results in expression of a nearby transcript, H19 instead of Igf2, from the maternally derived allele. The establishment of gamete-specific de novo methylation requires the action of DNA methyltransferase 3a (Dnmt3a) and Dnmt3b while the maintenance of methylation patterns in somatic cells requires Dnmt1 (Wilkins 2005). These so-called “imprinting genes” are all autosomal, but the gamete-specific expression of the imprint suggests the existence of an X-linked imprinting gene (Peterson and Sapienza 1993). Indeed, at least one X-linked imprinting gene is known; Xist is required for imprinted X-chromosome inactivation in extraembryonic tissue in mice (Okamoto et al. 2004).
Many theories have attempted to explain the evolution of genomic imprinting, but the most prominent are the kinship theory (Haig 1992) and the sex-specific selection theory (Iwasa and Pomiankowski 2001; Day and Bonduriansky 2004). The kinship theory relies on asymmetries in relatedness between individuals' maternally and paternally derived alleles (Haig 1997). Such asymmetries develop in species with polygamous mating systems. In polyandrous species for example, the maternally derived alleles of half-sibs will have a greater degree of relatedness than the paternally derived ones. In addition, if offspring can obtain maternal resources post-fertilization, paternal inclusive fitness will increase as offspring obtain a higher fraction of those resources. In contrast, maternal inclusive fitness will not increase as greater use of maternal resources for one offspring comes at a cost to the resources obtained by its half-sibs. In this scenario, the kinship theory predicts that genes increasing an offspring's share of maternal resources, such as growth enhancers that act in development, will be expressed from the paternally derived allele and repressed on the maternally derived allele. Polygamous mating systems are common in many taxa including mammals, whereas the opportunity for paternally derived alleles to influence the rate at which an embryo acquires maternal resources is rare outside of mammals and some plants. Models using evolutionary game theory have supported predictions from the kinship theory (Haig 1997), whereas explicit population genetic models exhibited more complex scenarios (Spencer et al. 1998; Spencer and Feldman 2005).
The sex-specific selection hypothesis suggests that genomic imprinting could evolve due to different selection pressure on the sexes. For X-linked loci, inheritance is asymmetric with respect to parental origin, and imprinting allows expression from such loci to be sexually dimorphic (Iwasa and Pomiankowski 2001). Under weak selection, quantitative genetic models of X-linked loci suggest that when selection is stronger against one sex, expression in the offspring of alleles derived from the other sex should be higher (Iwasa and Pomiankowski 2001). For autosomal loci, inheritance is symmetric with respect to parental origin; imprinting can evolve at such loci in response to sex-specific selection as the change in expression level will benefit one sex more than another (Day and Bonduriansky 2004); Autosomal two-locus modifier models have shown that when fitness is additive and selection favors greater expression at a locus in males than in females, modifiers that silence maternally derived alleles can invade the population (Day and Bonduriansky 2004); modifiers that silence paternally derived alleles can invade when the opposite is true. These predictions are more general than those of the kinship theory in that paternal imprinting of growth-enhancing genes can occur when selection favors stronger gene expression in females, regardless of relatedness among kin.
Sex-specific selection is a promising hypothesis to explain the evolution of genomic imprinting because many taxa exhibit traits with sex-dependent expression (Andersson 1994) and such traits are likely targets for sex-specific selection pressures (Rice and Chippindale 2001). Imprinted genes have been found in a taxonomically and phenotypically diverse group of organisms that may not all meet the genetic relatedness and maternal care assumptions of the kinship theory. Although previous models of the sex-specific selection hypothesis have been suggestive of its applicability (Iwasa and Pomiankowski 2001; Day and Bonduriansky 2004), these models have, for the sake of analytical tractability, assumed that fitness is additive. This assumption is particularly problematic because of the close connection between genomic imprinting and dominance between alleles at diploid loci (Sapienza 1989; Anderson and Spencer 1999). Imprinting silences alleles regardless of whether their fitness effect is dominant or recessive in relation to other alleles at the same locus. On average, one would expect imprinting to be advantageous when deleterious alleles are dominant and disadvantageous when deleterious alleles are recessive. Without explicitly considering the coefficient of dominance in an analysis of the evolution of genomic imprinting, this simple expectation cannot be tested. This work presents such an analysis; we build a two-locus modifier model in which the primary locus is under selection and alleles at the modifier locus determine whether or not alleles at the primary locus are imprinted. Selection and dominance coefficients at the primary locus are allowed to have sex-specific values.
Additionally, our model considers both autosomal and X-linked modifier alleles at the secondary locus. Recent empirical research on the molecular mechanisms underlying X-chromosome inactivation (XCI) in mammals has shown that XCI and genomic imprinting share many features (Lee 2003). This similarity has prompted some to suggest that XCI and genomic imprinting coevolved with either XCI evolving first as a form of dosage compensation and imprinting later as a by-product (Lee 2003) or imprinted XCI evolving to replace an older dosage compensation mechanism and then spreading from the X chromosome to the autosomes (Reik and Lewis 2005). In either case, X-linked modifier loci would have been crucial in the evolution of genomic imprinting. It is unknown whether the sex linkage of these modifiers would effect the evolution of imprinting at autosomal loci; this study begins to address this question.
MODELS
Drawing from the work of Spencer and Williams (1997), we consider two different scenarios for how alleles at the modifier locus imprint the primary locus. In the first scenario, we assume that the modifier locus acts late enough in gametogenesis that the imprinting status of an allele at the primary locus depends only on the identity of the modifier allele present in the gamete. Following Spencer and Williams (1997), we call these modifiers cis-acting. In vertebrates, sperm are generated following the completion of meiosis but oocyte development is arrested at metaphase II (Duesbery and Woude 2002), which suggests that both alleles at the modifier locus of the parent could contribute to determining the imprinting status at the primary locus. Such modifiers are called trans-acting. This usage of cis- and trans- is different from that in molecular biology where the terms are used to describe elements involved in gene regulation so we will take care to distinguish the two meanings when necessary. In the context of our model, we define maternal and paternal imprinting narrowly as the silencing of gene expression from alleles inherited via female and male gametes, respectively.
cis-acting autosomal modifiers:
Assuming that modifiers of imprinting are cis-acting, we need only track gamete frequencies and not full genotype frequencies. This allows us to make use of the two-locus fitness modifier framework (Bodmer and Felsenstein 1967) developed by Feldman and Karlin (1971). For the sake of simplicity, we consider only two alleles at each locus, A1 and A2 at the primary locus and M1 and M2 at the modifier locus. The modifier allele M1 will be considered a so-called “Mendelizing” allele and will not imprint alleles at the primary locus. M2 will be an imprinting allele and will silence an allele at the primary locus Ai if M2 and Ai occur in the same gamete and that gamete comes from the imprinting parent. For cis-acting modifiers, we follow the convention (Spencer and Williams 1997) in which imprinting is fully penetrant or in which all M1 gametes contain unimprinted Ai and all M2 gametes contain imprinted Ai. Selection occurs only at the primary locus and individuals that receive an imprinted allele have the same viability as individuals homozygous for the unimprinted allele.
First, we assume that the modifier locus is autosomal and that maternally derived alleles are imprinted. As the model is symmetric with respect to sex, results for paternal imprinting by autosomal modifiers will be analogous. Let the frequencies of gametes A1M1, A2M1, A1M2, and A2M2 produced by females be denoted by x = (x1, x2, x3, x4) and those produced by males by y = (y1, y2, y3, y4). Selection at the primary locus occurs according to the viabilities in Table 1, where  is the viability of an AiAj female (f) or male (m) without a maternally imprinted allele whereas
is the viability of an AiAj female (f) or male (m) without a maternally imprinted allele whereas 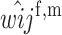 is the viability of the same individual with an imprinted Ai. AiAj individuals who receive a modifier allele from their father have viability
is the viability of the same individual with an imprinted Ai. AiAj individuals who receive a modifier allele from their father have viability  which is equal to
which is equal to  for maternal imprinting, and those who receive modifier alleles from both parents have viability
for maternal imprinting, and those who receive modifier alleles from both parents have viability  which in this case is equal to
which in this case is equal to  (See Table 2 for model parameter definitions.) Recursions for female gamete frequencies after selection and recombination are
(See Table 2 for model parameter definitions.) Recursions for female gamete frequencies after selection and recombination are
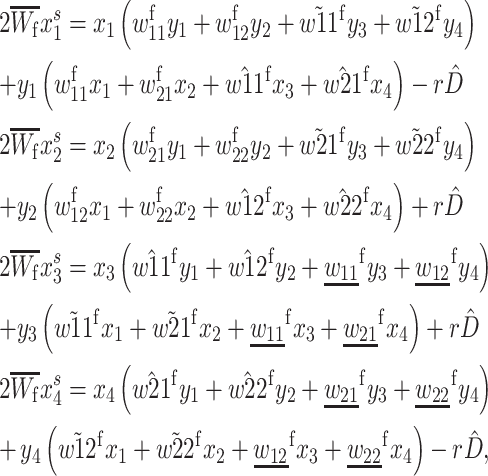 |
(1) |
where the mean fitness in females,  is sum of the right-hand sides and assures that
is sum of the right-hand sides and assures that  r is the recombination rate, and
r is the recombination rate, and 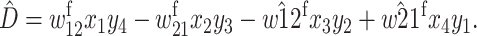 Recursions for males gametes are identical except for the viability parameters, where
Recursions for males gametes are identical except for the viability parameters, where 
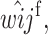
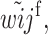 and
and  are replaced by
are replaced by 
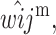
 and
and 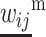 for i, j ∈ (1, 2).
for i, j ∈ (1, 2).
TABLE 1.
Viabilities for the cis- and trans-acting modifier models
| Maternal chromosome | Paternal chromosome |
|||||
|---|---|---|---|---|---|---|
| A1M1 | A2M1 | A1M2 | A2M2 | A1M* | A2M* | |
| A1M1 |  |
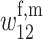 |
 |
 |
 |
 |
| A2M1 |  |
 |
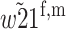 |
 |
 |
 |
| A1M2 |  |
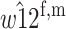 |
 |
 |
 |
 |
| A2M2 |  |
 |
 |
 |
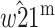 |
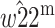 |
TABLE 2.
Model parameter definitions
| Parameter | Definition |
|---|---|
 |
Viability of an AiAj female (f) or male (m) in which neither allele at the primary locus is imprinted or silenced. |
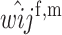 |
Viability of an AiAj female (f) or male (m) in which the maternal allele, Ai, is imprinted. |
 |
Viability of an AiAj female (f) or male (m) in which the paternal allele, Aj, is imprinted. |
 |
Viability of an AiAj female (f) or male (m) in which both alleles at the primary locus are imprinted. |
| μ | Rate at which mutation changes A1 to A2 when A1 is selectively advantageous in both females and males. |
| h, s | Dominance (h) and selection (s) coefficients in females. |
| k, t | Dominance (k) and selection (t) coefficients in males. |
| η, α, γ | Rate at which individuals with M1M1, M1M2, and M2M2 genotypes at the modifier locus imprint gametes in the trans-acting model. |
| ω, ν | Relative viability of females and males, respectively, with an imprinted allele when there is direct selection for imprinted expression in trans-acting model. |
Instead of attempting to fully analyze the above recursion and its male counterpart, a task that has proven difficult even for simpler two-locus models without sex-specific viabilities, we assume that the population is fixed for one modifier allele and look for conditions that permit the frequency of the other allele to increase after it has arisen via spontaneous mutation, a process called invasion. In a population fixed for M1, invasion by M2 means that imprinting at the primary locus in the population will increase when initially rare, while invasion by M1 in a population fixed for M2 means Mendelian expression has returned to the primary locus. To simplify the analysis, r is assumed to be 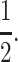 Lower values of r for both autosomal (Spencer and Williams 1997) and sex-linked modifiers (J. Van Cleve and M. W. Feldman, unpublished results) without sex-specific selection tend to inhibit the evolution of genomic imprinting by making the conditions for the invasion of the imprinting modifier M2 more stringent.
Lower values of r for both autosomal (Spencer and Williams 1997) and sex-linked modifiers (J. Van Cleve and M. W. Feldman, unpublished results) without sex-specific selection tend to inhibit the evolution of genomic imprinting by making the conditions for the invasion of the imprinting modifier M2 more stringent.
Selection at the primary locus is assumed to be directional since heterozygote advantage at a primary locus lacking sex-specific selection with either autosomal (Spencer and Williams 1997) or sex-linked modifiers did not permit M2 to invade (and imprinting to evolve) unless imprinting conferred an extra selective advantage. Allowing viability to be sex specific yields two cases of interest: first, selection favors one allele, A1, in both sexes but to differing degrees; second, selection favors different alleles in each sex. Our assumption that AiAj individuals with imprinted Ai have the viability of an AjAj homozygote means that to determine invasion conditions for M1 and M2, genetic variation must be present at the primary locus in the face of directional selection. A polymorphic equilibrium can be the source of such genetic variation, but unlike the classic one-locus two-allele model that has a unique polymorphic equilibrium, the two-sex model has up to three polymorphic equilibria (Owen 1953), two of which can be simultaneously stable (Owen 1953; Kidwell et al. 1977; Karlin and Lessard 1986). By considering only directional selection, we exclude the possibility of two simultaneously stable polymorphic equilibria (Karlin and Lessard 1986, p. 219).
Directional selection favoring A1 in both sexes:
When selection favors A1 in both sexes, the A1 fixation is globally stable (Karlin and Lessard 1986; Selgrade and Ziehe 1987). In females, we assume that the viabilities in Table 1 are 
 and
and  where h, s ∈ (0, 1), and in males
where h, s ∈ (0, 1), and in males 
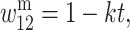 and
and  where k, t ∈ (0, 1). We introduce unidirectional mutation from A1 to A2 at rate μ, where
where k, t ∈ (0, 1). We introduce unidirectional mutation from A1 to A2 at rate μ, where  to generate variation at the primary locus. Mutation from A2 to A1 is ignored because the frequency A2 will be small enough such that the increase in the frequency of A1 will be negligible. Following mutation, the frequencies of gametes produced by females are given by
to generate variation at the primary locus. Mutation from A2 to A1 is ignored because the frequency A2 will be small enough such that the increase in the frequency of A1 will be negligible. Following mutation, the frequencies of gametes produced by females are given by
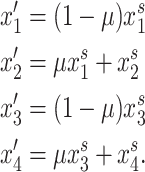 |
(2) |
Recursion (2) generates a mutation–selection balance close to the A1 fixation. When the population is fixed for M1 and there is no imprinting, this equilibrium is given by
 |
and
 |
(Haldane and Jayakar (1972), where subscript I denotes fixation of M1. Following standard modifier theory, we can reduce our recursion to a linear system about (xI, yI) that tracks only the frequencies of gametes that contain M2. The Jacobian of this linearization of (2) is
 |
(3) |
where the entries of J1 are given in the appendix. We were unable to derive simple expressions for the eigenvalues of (3) and instead present a sufficient condition for M2 to invade. An application of the Jury test (Edelstein-Keshet 2005) to Equation 3 shows that P(1) < 0, where P(λ) = Det[λI − J] is the characteristic polynomial, is sufficient to obtain an eigenvalue with magnitude greater than one. By evaluating P(1) when s = t, we can explore the effect of sex-specific dominance at the primary locus and vary the strength of selection symmetrically in both sexes. In this case,
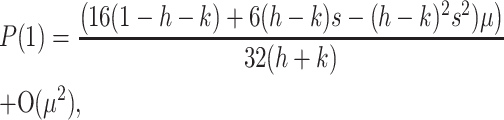 |
and our sufficient condition is, dropping terms of order μ2,
 |
(4) |
Equation 4 is plotted in Figure 1a, where in the white region M2 can invade for all values of s and in the dark gray region the sufficient condition is not met for any value of s. In regions with lighter shades of gray, only a subset of s values allow invasion with the size of that subset proportional to the lightness of the shading. Solid lines denote boundaries between the regions where (4) is met and not met; each line represents a boundary for values of s indicated by the contour labels. When dominance at the primary locus is the same in both sexes, i.e., h = k, the condition for invasion is  which is identical to our initial expectation that imprinting is favored when deleterious alleles are dominant. If both h and k are
which is identical to our initial expectation that imprinting is favored when deleterious alleles are dominant. If both h and k are  invasion is assured. For weak selection, the invasion condition generalizes such that averaged across the sexes, dominant deleterious alleles promote invasion, or h + k > 1. As the strength of selection increases, maternal imprinting distorts this condition. When
invasion is assured. For weak selection, the invasion condition generalizes such that averaged across the sexes, dominant deleterious alleles promote invasion, or h + k > 1. As the strength of selection increases, maternal imprinting distorts this condition. When  the female offspring of mothers who pass their daughters an M2 allele will see a reduction in dominance at their primary locus as imprinting effectively sets
the female offspring of mothers who pass their daughters an M2 allele will see a reduction in dominance at their primary locus as imprinting effectively sets 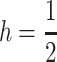 (Pearce and Spencer 1992), which increases their fitness on average. If also
(Pearce and Spencer 1992), which increases their fitness on average. If also 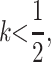 sons who receive an M2 allele from their mother will have dominance increase and may experience a loss of fitness on average; because imprinting is maternal, these males will not pass imprinted alleles to their own daughters who will have dominant deleterious alleles. In this case, for M2 to invade, k must be closer to
sons who receive an M2 allele from their mother will have dominance increase and may experience a loss of fitness on average; because imprinting is maternal, these males will not pass imprinted alleles to their own daughters who will have dominant deleterious alleles. In this case, for M2 to invade, k must be closer to  than h + k > 1 requires, as an increase in k reduces this fitness loss in sons. When
than h + k > 1 requires, as an increase in k reduces this fitness loss in sons. When 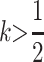 and
and  sons who receive an M2 from their mothers will have reduced dominance of deleterious alleles at the primary locus. Daughters will have increased dominance of deleterious alleles, but this is partially offset by the reduction in dominance in their own sons; the result is that M2 invades for some values of h and k, where h + k < 1. Numerical analysis of the eigenvalues of (3) (data not shown) suggests condition (4) is both necessary and sufficient, provided that the magnitude of the dominant eigenvalue is not equal to one; the eigenvalue with the largest magnitude is called the dominant eigenvalue, which we denote by λ*.
sons who receive an M2 from their mothers will have reduced dominance of deleterious alleles at the primary locus. Daughters will have increased dominance of deleterious alleles, but this is partially offset by the reduction in dominance in their own sons; the result is that M2 invades for some values of h and k, where h + k < 1. Numerical analysis of the eigenvalues of (3) (data not shown) suggests condition (4) is both necessary and sufficient, provided that the magnitude of the dominant eigenvalue is not equal to one; the eigenvalue with the largest magnitude is called the dominant eigenvalue, which we denote by λ*.
Figure 1.—
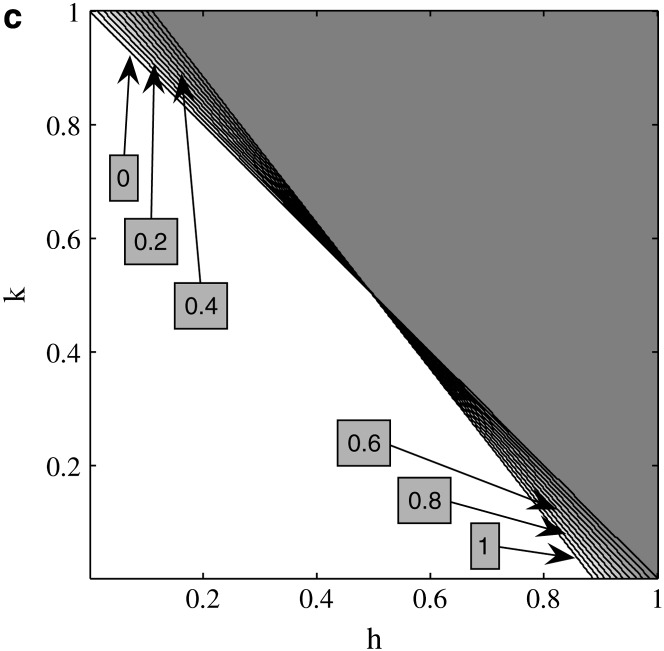
Invasion conditions for cis-acting autosomal modifiers under maternal imprinting when A1 is advantageous in females and males. (a) M2 invasion conditions with s = t. (b) M2 invasion conditions with h = k. (c) M1 invasion conditions with s = t. (d) M1 invasion conditions with h = k. (a and c) Contours represent different values of s = t; white regions indicate all values of s allow invasion; in the dark gray regions, no values of s allow invasion, and shaded areas indicate a subset of s values allow invasion. (b and d) White regions indicate invasion and gray regions indicate stability.
To explore the effect of sex-specific strength of selection where s ≠ t, we use the same coefficient of dominance in males and females by setting h = k. In this case,
 |
which yields the following sufficient condition for invasion by M2:
 |
(5) |
Condition (5) depends only on the difference s − t, and in Figure 1b, we show values of s − t and h that satisfy (5). When  M2 invades if selection against A2 is stronger in males, or t > s. As the strength of selection increases in males and decreases in females, smaller values of h permit invasion by M2;
M2 invades if selection against A2 is stronger in males, or t > s. As the strength of selection increases in males and decreases in females, smaller values of h permit invasion by M2;  is the required condition when t = 1 and s = 0. Stronger selection on males could act to increase the efficacy of dominance modification by M2 by removing sons who cannot pass imprinting alleles onto their offspring. The opposite pattern is seen when selection against A2 is stronger in females;
is the required condition when t = 1 and s = 0. Stronger selection on males could act to increase the efficacy of dominance modification by M2 by removing sons who cannot pass imprinting alleles onto their offspring. The opposite pattern is seen when selection against A2 is stronger in females;  is required for invasion by M2 when t = 0 and s = 1. Here, the efficacy of dominance modification may be reduced due to increased selection on females, which are the only ones capable of passing on imprinted alleles. Again, numerical analysis of the eigenvalues suggests that (5) is necessary and sufficient if λ* ≠ 1.
is required for invasion by M2 when t = 0 and s = 1. Here, the efficacy of dominance modification may be reduced due to increased selection on females, which are the only ones capable of passing on imprinted alleles. Again, numerical analysis of the eigenvalues suggests that (5) is necessary and sufficient if λ* ≠ 1.
To assess the persistence of imprinting, we look for conditions under which M1 can invade a population fixed for M2. This can be seen as the evolution of Mendelian expression from imprinted expression at the primary locus. Given maternal imprinting and the sex-specific viabilities listed above, we derive a mutation–selection balance using standard techniques (Spencer 1997) and arrive at
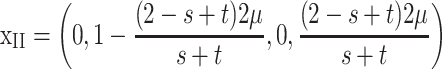 |
and
 |
The Jacobian matrix at this equilibrium is
 |
(6) |
where the entries of J2 can be found in the appendix. Setting s = t, the sufficient condition for invasion by M1 is
 |
or
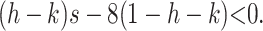 |
(7) |
Conditions under which (7) is satisfied are plotted in Figure 1c. Condition (7) is almost the complement of (4); M1 invades when  and when h + k < 1 if selection is weak. However, when the strength of selection increases (larger values of s = t) and
and when h + k < 1 if selection is weak. However, when the strength of selection increases (larger values of s = t) and  values of k > 1 − h allow M1 to invade. Female offspring who receive a rare M1 allele from their mothers will benefit from the dominance modification that results from biallelic expression, as will granddaughters of those daughters. This benefit could relax the condition on k. When
values of k > 1 − h allow M1 to invade. Female offspring who receive a rare M1 allele from their mothers will benefit from the dominance modification that results from biallelic expression, as will granddaughters of those daughters. This benefit could relax the condition on k. When  invasion by M1 is guaranteed over a smaller range of h than h < 1 − k as the strength of selection increases. In this case, sons benefit from dominance modification due to biallelic expression when they receive a maternal M1 but cannot pass that benefit onto their offspring. A consequence of the lack of full complementarity between conditions (4) and (7) is that Figures 1c and 1a contain a region in the top left quadrant where, under strong selection, both M2 and M1 can invade, producing a protected polymorphism at the modifier locus. Likewise, the bottom right quadrants of Figures 1a and 1c contain a region where both M1 and M2 fixations are stable. Numerical analysis suggests that if λ* ≠ 1, condition (7) is both necessary and sufficient for invasion of M2 by M1.
invasion by M1 is guaranteed over a smaller range of h than h < 1 − k as the strength of selection increases. In this case, sons benefit from dominance modification due to biallelic expression when they receive a maternal M1 but cannot pass that benefit onto their offspring. A consequence of the lack of full complementarity between conditions (4) and (7) is that Figures 1c and 1a contain a region in the top left quadrant where, under strong selection, both M2 and M1 can invade, producing a protected polymorphism at the modifier locus. Likewise, the bottom right quadrants of Figures 1a and 1c contain a region where both M1 and M2 fixations are stable. Numerical analysis suggests that if λ* ≠ 1, condition (7) is both necessary and sufficient for invasion of M2 by M1.
When dominance is the same in both sexes, h = k, and the strength of selection is allowed to vary,  which yields
which yields
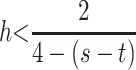 |
(8) |
as a sufficient condition for invasion by M1. Unlike the case in which s = t, condition (8) is the exact complement of condition (5) as can be seen in Figure 1d. As in previous cases, numerical analysis suggests that (8) is necessary and sufficient for instability if λ* ≠ 1. For 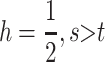 is required for M1 to invade. Stronger selection in males reduces the maximum value of h that allows invasion due to the increased efficacy of imprinting-induced dominance modification as detailed above. When selection is stronger in females, the maximum value of h that allows invasion increases due to the decreased efficacy of dominance modification due to imprinting.
is required for M1 to invade. Stronger selection in males reduces the maximum value of h that allows invasion due to the increased efficacy of imprinting-induced dominance modification as detailed above. When selection is stronger in females, the maximum value of h that allows invasion increases due to the decreased efficacy of dominance modification due to imprinting.
Opposing directional selection:
Although the fitness scheme above allows sex-specific selection and dominance, we have still assumed that selection favors A1 in both sexes. Consider now the case of opposing directional selection where A1 is favored in females and A2 is favored in males. In this case, selection can generate a stable polymorphism that maintains genetic variation at the primary locus. As equilibrium allele frequencies at this polymorphism will be large compared to μ, we neglect terms of order μ in the stability analysis of these equilibria. With certain viabilities, it is possible without imprinting and mutation for this stable polymorphism to coexist with a stable fixation state (Kidwell et al. 1977; Karlin and Lessard 1986). With those viabilities for which both fixation states are unstable, the polymorphism is globally stable. Global stability is assured due to the fact that the one-locus two-sex model has the nice property of being strongly monotone (Selgrade and Ziehe 1987). In strongly monotone systems, equilibria are ordered in a special way and the local stability of equilibria alternates with respect to this ordering. In our case, the fixation equilibria are at opposite ends of the ordering with polymorphisms in between. Since the assumption of directional selection excludes the possibility of three polymorphic equilibria, local instability at both fixation equilibria means there must be only one polymorphic equilibrium and it must be locally stable. As long as all equilibria have eigenvalues of nonunit magnitude, the polymorphic equilibrium is also globally stable (Selgrade and Ziehe 1987).
Assuming opposing directional selection in the females and males, define the viabilities from Table 1 such that 
 and
and  in females where h, s ∈ (0, 1) and h is the degree to which A2 is dominant over A1. In males, let
in females where h, s ∈ (0, 1) and h is the degree to which A2 is dominant over A1. In males, let 
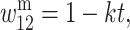 and
and 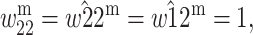 where k, t ∈ (0, 1) and k is the degree to which A1 is dominant over A2. Assuming that M1 is fixed and there is no imprinting at the primary locus, the conditions for instability at the A1 and A2 fixation states are, respectively (Kidwell
et al. 1977),
where k, t ∈ (0, 1) and k is the degree to which A1 is dominant over A2. Assuming that M1 is fixed and there is no imprinting at the primary locus, the conditions for instability at the A1 and A2 fixation states are, respectively (Kidwell
et al. 1977),
 |
(9) |
and
 |
(10) |
If (9) and (10) hold, a unique globally stable polymorphic equilibrium can be found from one root of an appropriate cubic equation (Owen 1953). The expression for that root is too complicated to inform biological intuition, and we refrain from including it here. When we plug this root into the Jacobian matrix evaluated assuming that M1 is fixed, the expression for P(1) also is too complex to convey any insight. Instead, we numerically evaluate the eigenvalues of the Jacobian matrix and determine conditions under which the magnitude of one of those eigenvalues exceeds one.
As before, we fix the strength of selection to be the same in both sexes, i.e., s = t, and look at the effect of sex-specific dominance at the primary locus. Under this assumption, conditions (9) and (10) become
 |
(11) |
The regions to the left and below each labeled contour line in Figure 2a indicate values of h and k, where (11) holds for values of s denoted by the contour labels. As s increases, the region in which the polymorphism at the primary locus is globally stable becomes larger, and for values of s close to one, only a small region of (h, k)-space does not satisfy (11). As s approaches zero, the polymorphism is guaranteed to be stable when h + k < 1. In regions where the polymorphism is stable, we determine whether a rare M2 allele can invade. Contour lines also indicate boundaries between regions where M2 can and cannot invade. Above the line h + k = 1, these contour lines overlap precisely with the contour lines that indicate when the polymorphism at the primary locus is stable. As was the case in Figure 1, in the white region of Figure 2a, M2 can invade for all values of s, dark gray indicates that no values of s allow invasion, and intermediate shades are regions in which some values of s allow invasion. Thus, when h + k > 1 and the polymorphism at the primary locus is stable, M2 can invade at the modifier locus. Although the polymorphism at the primary locus is stable for all values of s and h + k < 1, M2 can never invade at the modifier locus under these conditions. As in the previous case of weak selection favoring the same allele at the primary locus in both sexes, when selection favors different alleles in each sex, M2 invades for h + k > 1. In contrast to the previous case, stronger selection does not cause a qualitative departure from this condition; rather, increased selection only changes the region in (h, k)-space in which the polymorphism at the primary locus is stable. Also, the conditions for invasion by M2 are symmetric about the the line h = k, which means that they are the same regardless of which parent has which dominance coefficient. This implies that the invasion conditions are independent of which parent imprints its gametes; i.e., conditions for the invasion of the imprinting allele M2 in a population fixed for M1 are the same whether imprinting is maternal or paternal.
Figure 2.—
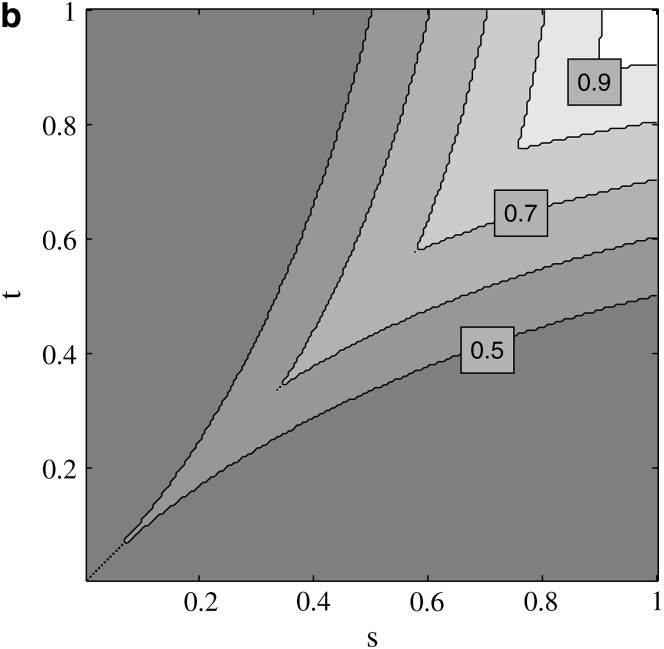
Invasion conditions for cis-acting autosomal modifiers under maternal imprinting when A1 is advantageous in females and A2 is advantageous in males. White regions indicate all values of s allow invasion; in the dark gray regions, no values of s allow invasion, and shaded areas indicate a subset of s values allow invasion. (a) M2 invasion conditions. Contours represent different values of s = t. (b) M2 invasion conditions. Contours represent different values of h = k. (c) M1 invasion conditions. Contours represent different values of s = t. (d) M1 invasion conditions. Contours represent different values of h = k. All labeled contours in c and d overlap exactly.
Allowing the strength of selection to vary independently in each sex, we fix the level of dominance at the primary locus to be the same in both sexes. When selection favors A1 at the primary locus in females and A2 in males, there are two natural ways to handle the dominance coefficients; one way is to set h = k, which means that the level of dominance of the allele preferred by selection is the same in both sexes, while the level of dominance of a specific allele in one sex is one minus the level of dominance of that allele in the other sex. The other natural parameterization is to set h = 1 − k, which means that the level of dominance for each specific allele is identical in both sexes. We choose the first parameterization because the second parameterization yields parameter values that lie on the boundary of stability in Figure 2a. Analysis of the eigenvalues of the Jacobian matrix when h = 1 − k (results not shown) shows that λ* = 1 in this case, which means that linearization cannot tell us whether or not the modifier allele invades. We avoid this difficult case and set h = k.
When h = k, conditions (9) and (10) become
 |
(12) |
As h increases, the region in (s, t)-space where the polymorphism at the primary locus is stable decreases in size and becomes arbitrarily small as h goes to one. For small h, the polymorphism is stable everywhere except in narrow regions where s is close to one and t is close to zero or vice versa. Where the polymorphism is stable at the primary locus, we can determine whether M2 can invade at the modifier locus. The contour lines in Figure 2b represent the boundaries between regions where condition (12) holds and regions where it does not hold, and the shading follows the same scheme as in Figure 2a. Contour lines are plotted only for values of h where M2 can invade somewhere in (s, t)-parameter space. In this case, no values of 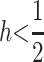 permit invasion of the population by M2. As was the case in Figure 2a, the contour lines that represent the boundaries between regions where M2 can and cannot invade overlap precisely with the contour lines for condition (12). This means that whenever the polymorphism at the primary locus is stable and
permit invasion of the population by M2. As was the case in Figure 2a, the contour lines that represent the boundaries between regions where M2 can and cannot invade overlap precisely with the contour lines for condition (12). This means that whenever the polymorphism at the primary locus is stable and  M2 can invade. The condition for invasion by M2 is independent of whether imprinting is maternal or paternal.
M2 can invade. The condition for invasion by M2 is independent of whether imprinting is maternal or paternal.
Now, assume that M2 is fixed at the modifier locus and all mothers imprint their gametes. We can determine the conditions for a polymorphism to be stable at the primary locus, and for those parameters, whether M1 can invade, introducing Mendelian expression. For a single imprinted locus, the condition for the existence and global stability of a polymorphism is (Anderson and Spencer 1999)
 |
(13) |
which is independent of h and k as imprinting makes every individual functionally hemizygous. We set s = t and allow sex-specific expression of dominance coefficients in those individuals that obtain a rare M1 allele; in this case, condition (13) is always satisfied. The conditions for an increase in the frequency of a rare M1 allele are shown in Figure 2c, which has the same format as Figures 2a and 2b. For all values of s, the boundary of stability is h + k = 1, where M1 invades for h + k < 1; except for the different region of stability for the polymorphic equilibrium at the primary locus, this condition is exactly complementary to the previous case, where M2 invades when h + k > 1. The same complementarity appears when we set h = k and vary s and t as shown in Figure 2d. The region where (13) is met and the polymorphic equilibrium at the primary locus is stable is shown in white. As before, the white region and the labeled contours indicate that the conditions for M1 to invade coincide with the existence and stability conditions for the polymorphism at the primary locus. With viabilities that meet condition (13), M1 can invade when  Due to the symmetry of the autosomal modifier model, this is true regardless of whether imprinting is maternal or paternal.
Due to the symmetry of the autosomal modifier model, this is true regardless of whether imprinting is maternal or paternal.
cis-acting X-linked modifiers:
Here we assume that the cis-acting modifier locus is X linked and focus on how X linkage changes conditions for invasion by the imprinting modifier M2 and the Mendelizing modifier M1. When the modifier locus is X linked, the gametic recursions in females that we derived earlier, Equations 1, remain unchanged. In males, we need to add two additional variables to keep track of gametes that contain a Y chromosome and lack a modifier allele; y5 is the frequency of such gametes with A1 at the primary locus, and y6 is the frequency of such gametes with A2. The altered gametic recursions that reflect these changes are
 |
(14) |
where 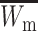 is the mean fitness,
is the mean fitness,  and
and  Viabilities for both sets of gametic recursions are contained in Table 1. Despite increasing the dimensionality of the dynamical system by adding two variables, we can still analyze the 4 × 4 Jacobian matrices (3) and (6) to determine whether or not M2 and M1, respectively, can invade a population fixed on the other allele at the modifier locus. Note that the only imprinted viabilities that appear in (14) are
Viabilities for both sets of gametic recursions are contained in Table 1. Despite increasing the dimensionality of the dynamical system by adding two variables, we can still analyze the 4 × 4 Jacobian matrices (3) and (6) to determine whether or not M2 and M1, respectively, can invade a population fixed on the other allele at the modifier locus. Note that the only imprinted viabilities that appear in (14) are  which indicates that viabilities in males can be altered by imprinting only when imprinting is maternal; paternal imprinting results in female-limited expression of imprinted viabilities. To focus on the effect of X linkage without the confounding effect of sex-limited expression of imprinting, we consider only maternal imprinting for X-linked modifiers.
which indicates that viabilities in males can be altered by imprinting only when imprinting is maternal; paternal imprinting results in female-limited expression of imprinted viabilities. To focus on the effect of X linkage without the confounding effect of sex-limited expression of imprinting, we consider only maternal imprinting for X-linked modifiers.
Directional selection favoring A1 in both sexes:
Assuming maternal imprinting and following our analysis for autosomal cis-acting modifiers, we initially assume selection favors A1 in both sexes and use the same parameterizations for 

 and
and  in terms of h, s, k, and t as were used in the autosomal case. When M1 is fixed at the modifier locus, gamete frequencies are given by xI and yI as defined above and the Jacobian matrix (3) evaluated at this point is given in the appendix. Setting s = t and focusing on sex-specific dominance at the primary locus, the sufficient condition for invasion by M2 is
in terms of h, s, k, and t as were used in the autosomal case. When M1 is fixed at the modifier locus, gamete frequencies are given by xI and yI as defined above and the Jacobian matrix (3) evaluated at this point is given in the appendix. Setting s = t and focusing on sex-specific dominance at the primary locus, the sufficient condition for invasion by M2 is
 |
(15) |
where P(λ) is the characteristic polynomial of matrix (3). Neglecting O(μ2) terms, condition (15) produces a picture qualitatively identical to the results in Figure 1a for autosomal modifiers. The slope of the boundary between the regions where X-linked M2 can invade and cannot invade becomes shallower as the strength of selection increases, just as it does for autosomal M2. The boundary does become slightly more convex for X-linked modifiers than autosomal modifiers, although this does not affect the qualitative results. When h = k and s and t are allowed to vary independently, the sufficient condition for invasion by M2 is exactly the same condition as found for autosomal modifiers, namely condition (8). If instead M2 is fixed at the modifier locus, the gamete frequencies at the mutation–selection balance are given by xII and yII; the Jacobian matrix (6) evaluated at this point can be found in the appendix. The sufficient condition for invasion by M1 when s = t is
 |
(16) |
When condition (16) is plotted for various values of s, the resulting figure (not shown) is almost indistinguishable from Figure 1c. If h = k, the invasion condition for an X-linked M1 is identical to (8), the condition for invasion by an autosomal M1. We conclude that under maternal imprinting, X linkage has only a very slight quantitative effect and no qualitative effect on the sufficient conditions for M2 to invade a population fixed for M1 and for M1 to invade a population fixed for M2.
Opposing directional selection:
For the case of opposing directional selection, 

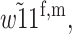 and
and  are parameterized in terms of h, s, k, and t in the same way they were for autosomal modifiers. Again, terms of order μ are ignored as mutation is negligible compared to the allele frequencies of the polymorphism generated by opposing directional selection. Conditions for the global stability of polymorphisms at the primary locus remain unchanged from the autosomal case; when M1 is fixed, the modifier locus does not alter viabilities at the primary locus, and when M2 is fixed, imprinting is unaffected by X-linkage as only maternal gametes are imprinted and mothers have two copies of each modifier allele.
are parameterized in terms of h, s, k, and t in the same way they were for autosomal modifiers. Again, terms of order μ are ignored as mutation is negligible compared to the allele frequencies of the polymorphism generated by opposing directional selection. Conditions for the global stability of polymorphisms at the primary locus remain unchanged from the autosomal case; when M1 is fixed, the modifier locus does not alter viabilities at the primary locus, and when M2 is fixed, imprinting is unaffected by X-linkage as only maternal gametes are imprinted and mothers have two copies of each modifier allele.
Figure 3a shows conditions for M2 to invade a population fixed for M1 at the modifier locus with the simplifying assumption that s = t. For parameter values such that h + k > 1, the results are identical to the autosomal case in Figure 2a; the region of stability for the polymorphism at the primary locus increases with increasing s, and whenever the polymorphism at the primary locus is stable, M2 can invade. In the autosomal case, M2 cannot invade for any s as long as h + k < 1. In Figure 3a, increasing the strength of selection opens up a region where low h and high k are sufficient to allow invasion of M2. One explanation for this effect might be that as selection increases, the positive effect due to dominance modification in sons grows faster than the negative effect due to such modification in daughters when both offspring receive a rare M2 from their mother; sons must pass this M2 on to their offspring whereas daughters will pass a rare M2 on to only half of their offspring. If instead h = k, Figure 3b gives the invasion conditions for M2. For h ≳ 0.52, the results are indistinguishable from the autosomal case in Figure 2b; M2 invades whenever s and t are such that the polymorphism at the primary locus is stable. The same is true for h ≲ 0.46 where M2 cannot invade. In contrast to the autosomal case, for 0.46 ≲ h ≲ 0.51 there are regions where M2 cannot invade even though the polymorphism at the primary locus is stable. When h = 0.46, M2 invades in a small region of high s and t along the top edge of the figure. As h increases to 0.51, the region of parameter values that permit invasion grows to encompass the whole region for which the primary locus polymorphism is stable. It appears that X linkage “smears” the sharp stability boundary at  that existed in the autosomal case.
that existed in the autosomal case.
Figure 3.—
Invasion conditions for cis-acting X-linked modifiers under maternal imprinting when A1 is advantageous in females and A2 is advantageous in males. White regions indicate all values of s allow invasion; in the dark gray regions, no values of s allow invasion, and shaded areas indicate a subset of s values allow invasion. (a) M2 invasion conditions. Contours represent different values of s = t. (b) M2 invasion conditions. Contours represent different values of h = k. (c) M1 invasion conditions. Contours represent different values of s = t. (d) M1 invasion conditions. Contours represent different values of h = k.
Invasion conditions for a rare M1 in a population fixed for M2 are given in Figures 3c and 3d assuming s = t and h = k, respectively. Not surprisingly, the pattern in Figure 3c when s = t is complementary to the pattern in Figure 3a; results are identical to the autosomal case for h + k > 1, namely M1 cannot invade, and when h + k < 1, increasing the strength of selection opens a region of low h and high k where M1 cannot invade. As before, differing effects of dominance modification in offspring of different sexes may account for this behavior. For h = k, Figure 3d shows that the invasion condition for autosomal M1,  is “smeared” in the X-linked case in a fashion similar to that in Figure 3b. In regions where s and t permit stability of the primary locus polymorphism, M1 can always invade when h ≲ 0.44 and cannot invade when h ≳ 0.59. Between those values of h, there are regions of (s, t)-space where the primary locus polymorphism is stable but M1 cannot invade. At h = 0.44, the region where M1 cannot invade lies in the top right-hand corner of Figure 3d, where selection is strong in both sexes; as h increases to 0.59, the only remaining region where M1 can invade lies close to s = 1 and t = 0.5. The general effect of X linkage on invasion conditions for modifier alleles M2 and M1 appears to be a slight relaxation of the
is “smeared” in the X-linked case in a fashion similar to that in Figure 3b. In regions where s and t permit stability of the primary locus polymorphism, M1 can always invade when h ≲ 0.44 and cannot invade when h ≳ 0.59. Between those values of h, there are regions of (s, t)-space where the primary locus polymorphism is stable but M1 cannot invade. At h = 0.44, the region where M1 cannot invade lies in the top right-hand corner of Figure 3d, where selection is strong in both sexes; as h increases to 0.59, the only remaining region where M1 can invade lies close to s = 1 and t = 0.5. The general effect of X linkage on invasion conditions for modifier alleles M2 and M1 appears to be a slight relaxation of the 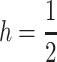 boundary; although the exact character of that relaxation depends on the position in parameter space, the relationship between the sum of the dominance coefficients and one remains crucial.
boundary; although the exact character of that relaxation depends on the position in parameter space, the relationship between the sum of the dominance coefficients and one remains crucial.
trans-acting autosomal modifiers:
In the case of trans-acting modifiers, the imprinting status at the primary locus is determined by the full parental genotype at the modifier locus. While each cis-acting modifier allele can determine the imprinting status of only one allele at a time at the primary locus, trans-acting modifier alleles can modify the expression of both alleles at the primary locus. Depending on the precise sequence of molecular events during gametogenesis, the trans-acting metaphor might be more biologically realistic, but such realism comes with the computational cost of tracking full genotype frequencies. Following our cis-acting model, we consider two alleles, A1 and A2, at the primary locus and two alleles, M1 and M2, at the modifier locus. Selection is directional in both females and males and either favors the same allele in both sexes or different alleles in each sex. While we allow for sex-specific selection, the fraction of gametes imprinted by each genotype at the modifier locus is the same in both sexes (i.e., no sex-specific imprinting, as proposed in Day and Bonduriansky (2004)). Individuals of genotype M1M1 generate gametes of which a proportion η are imprinted; genotype M1M2 imprints a proportion α of its gametes, and M2M2 imprints a proportion γ of its gametes. As was the case in the cis-acting model, we assume that the M2 modifier allele is unambiguously better at imprinting gametes than M1. This assumption is justifiable as we are interested in studying the evolution of genomic imprinting through the invasion of a new mutation and are less concerned with polymorphism at the imprinting locus. In addition, we assume that neither modifier allele is fully dominant over the other; these assumptions imply that γ > α > η.
As was the case in the cis-acting modifier model, our goal is to determine the conditions under which a rare M2 allele can invade a population fixed for M1 (and vice versa) as a function of the genotypic viabilities and proportions of gametes imprinted by each modifier locus genotype. To achieve this, we construct recursions for each two-locus genotype. At first, we assume that the modifier locus is autosomal and that females imprint their gametes; results for paternal imprinting are exactly analogous. The frequencies of the nine two-locus genotypes in females in males are defined by the variables in Table 3. Females produce eight different kinds of gametes: four unmodified gametes, A1M1, A2M1, A1M2, and A2M2, and four imprinted gametes, (A1)M1, (A2)M1, (A1)M2, and (A2)M2, where parentheses denote an imprinted allele. Let the frequencies of these gametes be given by x1 through x8, respectively. Since males do not imprint their gametes, they produce only four kinds of gametes, A1M1, A2M1, A1M2, and A2M2, whose frequencies we denote by y1 through y4, respectively. Recursions for the genotype frequencies in females in the next generation following viability selection are given by
 |
(17) |
where the viability coefficients  and
and  are defined in Table 1 exactly as in the cis-acting model and
are defined in Table 1 exactly as in the cis-acting model and 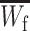 is a normalizing constant. Equations for male genotype frequencies in the following generation are obtained by replacing
is a normalizing constant. Equations for male genotype frequencies in the following generation are obtained by replacing 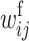 and
and 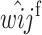 with
with  and
and  in (17). Gamete frequencies can be expressed as function of genotype frequencies in the current generation. To simplify the analysis, we assume that the primary locus and modifier are in linkage equilibrium; this means that we do not need to know the recombination rate or track the frequencies of reciprocal heterozygotes independently to calculate the gamete frequencies. Gamete frequencies in females are
in (17). Gamete frequencies can be expressed as function of genotype frequencies in the current generation. To simplify the analysis, we assume that the primary locus and modifier are in linkage equilibrium; this means that we do not need to know the recombination rate or track the frequencies of reciprocal heterozygotes independently to calculate the gamete frequencies. Gamete frequencies in females are
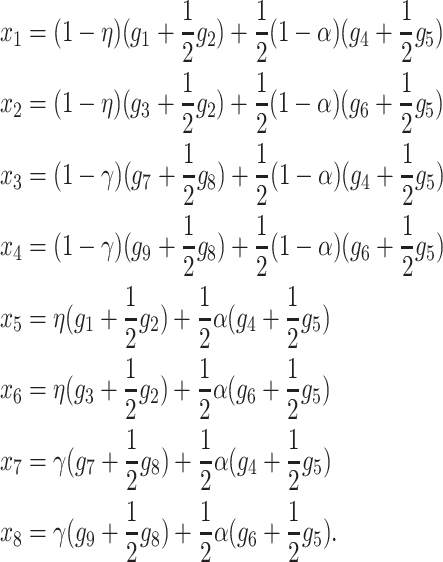 |
(18) |
TABLE 3.
Genotype frequency variables in the trans-acting modifier model
| Autosomal modifier |
X-linked modifier |
||||
|---|---|---|---|---|---|
| Female/male | Genotype | Female | Genotype | Male | Genotype |
| g1/h1 | A1A1M1M1 | g1 | A1A1M1M1 | h1 | A1A1M1 |
| g2/h2 | A1A2M1M1 | g2 | A1A2M1M1 | h2 | A1A2M1 |
| g3/h3 | A2A2M1M1 | g3 | A2A2M1M1 | h3 | A2A2M1 |
| g4/h4 | A1A1M1M2 | g4 | A1A1M1M2 | ||
| g5/h5 | A1A2M1M2 | g5 | A1A2M1M2 | ||
| g6/h6 | A2A2M1M2 | g6 | A2A2M1M2 | ||
| g7/h7 | A1A1M2M2 | g7 | A1A1M2M2 | h7 | A1A1M2 |
| g8/h8 | A1A2M2M2 | g8 | A1A2M2M2 | h8 | A1A2M2 |
| g9/h9 | A2A2M2M2 | g9 | A2A2M2M2 | h9 | A2A2M2 |
In males, the equations for y1 through y4 are the same as the first four equations in (18) except where η, α, and γ are set to zero as imprinting is maternal. Gamete frequencies following mutation of A1 to A2 at rate μ are derived exactly as in Equations 2 in the cis-acting modifier case.
Directional selection favoring A1 in both sexes:
Paralleling our analysis in the cis-acting modifier case, we parameterize the viability coefficients in two different ways. First, assume that selection favors A1 in both females and males and variation is maintained at the primary locus through a mutation–selection balance. The same parameterizations for 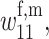

 and
and  in terms of h, s, k, and t are used as in the cis-acting modifier case. We start the population with M1 fixed at the modifier locus and set η = 0 so that imprinting is initially absent from the population. The mutation–selection balance at the primary locus is the same one as given by xI and yI in the cis-acting modifier case. We are concerned with how the remaining imprinting proportions, α and γ, affect the conditions under which M2 invades this population. Since the frequency of M2M2 individuals is negligible when M2 is rare, α is the only imprinting proportion we need to vary; γ is fixed at 1 without a loss of generality. We determine the invasion conditions for M2 using the methods described above for α = 0.25, 0.5, 0.75, and 1.0. Results from this analysis are presented in supplemental Figure 1 at http://www.genetics.org/supplemental/ and are qualitatively indistinguishable from the results for the cis-acting modifier results in Figure 1 for all values of α. When all maternal gametes are imprinted, i.e., M2 is fixed at the modifier locus and γ = 1, the equilibrium at the primary locus is given by xII and yII from the cis-acting case. The conditions for M1 to invade are given in supplemental Figure 1 and are exactly the same as in the cis-acting modifier model for all values of α. It appears that the conditions for modifier allele invasion are the same regardless of whether the modifier locus is cis- or trans-acting and are independent of the rate at which M1M2 heterozygotes imprint their gametes in the trans-acting case.
in terms of h, s, k, and t are used as in the cis-acting modifier case. We start the population with M1 fixed at the modifier locus and set η = 0 so that imprinting is initially absent from the population. The mutation–selection balance at the primary locus is the same one as given by xI and yI in the cis-acting modifier case. We are concerned with how the remaining imprinting proportions, α and γ, affect the conditions under which M2 invades this population. Since the frequency of M2M2 individuals is negligible when M2 is rare, α is the only imprinting proportion we need to vary; γ is fixed at 1 without a loss of generality. We determine the invasion conditions for M2 using the methods described above for α = 0.25, 0.5, 0.75, and 1.0. Results from this analysis are presented in supplemental Figure 1 at http://www.genetics.org/supplemental/ and are qualitatively indistinguishable from the results for the cis-acting modifier results in Figure 1 for all values of α. When all maternal gametes are imprinted, i.e., M2 is fixed at the modifier locus and γ = 1, the equilibrium at the primary locus is given by xII and yII from the cis-acting case. The conditions for M1 to invade are given in supplemental Figure 1 and are exactly the same as in the cis-acting modifier model for all values of α. It appears that the conditions for modifier allele invasion are the same regardless of whether the modifier locus is cis- or trans-acting and are independent of the rate at which M1M2 heterozygotes imprint their gametes in the trans-acting case.
Opposing directional selection:
In our second parameterization of the viability coefficients, selection maintains genetic variation at the primary locus by favoring A1 in females and A2 in males. Viability coefficients are parameterized in the same way as for the opposing directional selection case in the cis-acting modifier model. By setting η = 0 and γ = 1, we can assume that the population begins at the same globally stable polymorphism at the primary locus as in the cis-acting case and look at the fate of an invading modifier allele. Supplemental Figures 2 and 3 at http://www.genetics.org/supplemental/ show the invasion conditions for M2 and M1 and the results are identical to the results for the cis-acting modifier model in Figures 2 and 3.
Direct selection for imprinting:
Using the trans-acting modifier model, we can also determine how sex-specific direct selection for imprinted gene expression changes the conditions for an increase or decrease in the level of imprinting in the population. So far, we have assumed that there is no direct selection on imprinted gene expression because homozygotes without an imprinted allele are given the same viability as homozygotes with an imprinted allele. To focus solely on the effect of direct sex-specific selection on imprinted expression, we assume that the population is fixed for A1 at the primary locus and that females and males with an imprinted allele have viabilities of ω and ν, respectively, relative to individuals without an imprinted allele. As before, we consider maternal imprinting; paternal imprinting is exactly analogous. Under these assumptions, the only positive genotype frequencies are g1, g4, and g7 as they represent A1A1 homozygotes; their values following viability selection are
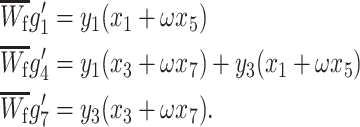 |
(19) |
Recursions for h1, h4, and h7 are identical except that ω is replaced by ν. Gamete frequencies are obtained by setting the frequencies of A1A2 and A2A2 genotypes to zero in (18) and simplifying. At the M1 and M2 fixations, the transformation defined by (19) and the analogous recursions for male genotype frequencies has two nonzero eigenvalues; for each modifier allele fixation, we explore the conditions under which the magnitude of the dominant eigenvalue exceeds one and the other modifier allele invades.
Under our assumption that γ > α > η, invasion of M2 into a population fixed for M1 constitutes an increase in the level of imprinted gene expression in the population. If imprinted gene expression is advantageous in both males and females, i.e., ω > 1 and ν > 1, then the magnitude of the dominant eigenvalue exceeds one and M2 always invades. Likewise, M2 does not invade when imprinted expression is disadvantageous in both sexes. This result is identical to the case where the strength of selection is the same in both sexes (Spencer and Williams 1997). If imprinted gene expression is advantageous in one sex and not the other, i.e., ω > 1 > ν or ν > 1 > ω, then M2 invades when
 |
where contours of f(ω, ν) are plotted in Figure 4. Given a fixed value of η, M2 can invade when the advantage of imprinted gene expression is large enough in one sex and the disadvantage small enough in the other sex. The white region in Figure 4, which indicates a net advantage to imprinted expression such that ω(ν − 1) + ν(ω − 1) > 0, is where M2 can invade for all values of η. M2 cannot invade for any value of η in the dark gray region where ω + ν < 2. Although we have assumed that imprinting is maternal, the condition for invasion by M2 does not depend on which sex has which viability but depends instead only on η and the relative values of the viabilities. Thus, even if imprinted expression is advantageous in one sex and not the other, the evolution of imprinting, or an increase in imprinted expression in the population, is equally likely for maternal and paternal imprinting as long as the net advantage is large enough.
Figure 4.—
Invasion conditions for trans-acting autosomal modifiers under maternal imprinting when there is direct selection for imprinting. Imprinting is assumed to be advantageous in one sex and disadvantageous in the other. Contour lines represent constant values of  assuming ω > 1 > ν or ν > 1 > ω.
assuming ω > 1 > ν or ν > 1 > ω.
The conditions for a reduction in the amount of imprinting in the population are obtained by determining when M1 invades a population fixed for M2. M1 invades when imprinted expression is disadvantageous in both sexes and does not invade when imprinted expression is advantageous in both sexes, which is identical to the result in Spencer and Williams (1997). When imprinted expression is advantageous in one sex and not another, M1 will invade and reduce the level of imprinted expression if the resident level of imprinting in the population, γ, is >f(ω, ν). In other words, M1 will invade when the net disadvantage of imprinted gene expression is large enough; as before, this condition is independent of which sex imprints its gametes.
trans-acting X-linked modifiers:
To determine whether the invasion conditions for an X-linked trans-acting modifier are any different from those of an autosomal trans-acting modifier, we alter the genotype frequency recursions to reflect the fact that males carry only one modifier allele. Following our analysis of the cis-acting model, we examine only maternal imprinting. As the necessary modifications of the relevant recursions are straightforward, we refrain from detailing them here and focus on the results. Invasion conditions for rare X-linked modifier alleles when selection is directional and favors A1 in both sexes are qualitatively identical to the invasion conditions in the cis-acting modifier case. Supplemental Figures 2 and 3 (http://www.genetics.org/supplemental/) show the modifier allele invasion conditions for opposing direction selection; again, these conditions are qualitatively identical to the invasion conditions for the cis-acting modifier in Figures 2 and 3. When there is direct selection on imprinted gene expression and a single allele at the primary locus, the modifier allele invasion conditions are almost identical to the autosomal case; M2 invades when imprinted expression is advantageous in both sexes and M1 when imprinted expression is disadvantageous in both sexes. If imprinted expression is advantageous in one sex but not the other, ω > 1 > ν or ν > 1 > ω, M2 invades when η < 2f(ω, ν) and M1 when γ > 2f(ω, ν). Thus, autosomal and X-linked trans-acting modifiers have qualitatively identical conditions for invasion by modifier alleles that change the degree of imprinting in the population.
DISCUSSION
We present two-locus evolutionary models for cis-acting and trans-acting modifiers of genomic imprinting. Both our cis-acting and trans-acting models show that a general condition for invasion by an imprinting modifier allele into a population without imprinting depends primarily on the coefficients of dominance at the primary locus in females and males. It is only when both coefficients of dominance are close to  that the relative strengths of selection in females and males come into play. Specifically, when selection is weak, the average dominance coefficient in females and males must be >
that the relative strengths of selection in females and males come into play. Specifically, when selection is weak, the average dominance coefficient in females and males must be > to guarantee invasion. The condition makes intuitive sense considering that when imprinting results in the silencing of alleles from a particular parent, the dominance coefficient at that locus is effectively
to guarantee invasion. The condition makes intuitive sense considering that when imprinting results in the silencing of alleles from a particular parent, the dominance coefficient at that locus is effectively 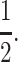 In the case of opposing directional selection in the sexes, the sufficient condition for the invasion of an imprinting allele is h + k > 1 regardless of the strength of selection. Only when selection favors the same allele at the primary locus in both females and males does the strength of selection change the invasion condition. In that case, increasing the strength of selection decreases the dependence of the invasion condition on the dominance coefficient in the nonimprinting sex only. When dominance is the same in both sexes, the invasion condition depends on the difference in female and male selection coefficients only if h is close to
In the case of opposing directional selection in the sexes, the sufficient condition for the invasion of an imprinting allele is h + k > 1 regardless of the strength of selection. Only when selection favors the same allele at the primary locus in both females and males does the strength of selection change the invasion condition. In that case, increasing the strength of selection decreases the dependence of the invasion condition on the dominance coefficient in the nonimprinting sex only. When dominance is the same in both sexes, the invasion condition depends on the difference in female and male selection coefficients only if h is close to  ; otherwise, the dominance coefficient primarily determines whether a rare modifier allele invades. In general, we find a great deal of symmetry with respect to sex-specific selection in the conditions for the invasion of an autosomal modifier allele that imprints maternal or paternal gametes. This belies the notion that stronger selection in one sex is a general or primary condition for the evolution of imprinting of gametes of the opposite sex.
; otherwise, the dominance coefficient primarily determines whether a rare modifier allele invades. In general, we find a great deal of symmetry with respect to sex-specific selection in the conditions for the invasion of an autosomal modifier allele that imprints maternal or paternal gametes. This belies the notion that stronger selection in one sex is a general or primary condition for the evolution of imprinting of gametes of the opposite sex.
Iwasa and Pomiankowski (2001) studied the evolution of genomic imprinting at X-linked (primary) loci under sex-specific selection using a quantitative genetic approach that assumed weak selection and explicitly considered only additive genetic variation. In the context of our model, this is equivalent to assuming that s is small and  Additionally, Iwasa and Pomiankowski (2001) assumed that female and male fitnesses were an increasing function of gene expression at the locus in question, which is equivalent to the case where selection favors the same allele in both females and males in our study. Their analysis shows that imprinting evolves in the sex whose fitness function responds more weakly to changes in gene expression. Figure 1b shows that our results agree with theirs in this case; when
Additionally, Iwasa and Pomiankowski (2001) assumed that female and male fitnesses were an increasing function of gene expression at the locus in question, which is equivalent to the case where selection favors the same allele in both females and males in our study. Their analysis shows that imprinting evolves in the sex whose fitness function responds more weakly to changes in gene expression. Figure 1b shows that our results agree with theirs in this case; when  t > s is the condition for invasion by a modifier allele that imprints maternal gametes, and s > t is the complementary condition for paternal imprinting. However, our results show that not only is
t > s is the condition for invasion by a modifier allele that imprints maternal gametes, and s > t is the complementary condition for paternal imprinting. However, our results show that not only is  a special case of a more general model, but it is often the boundary between regions of invasibility and noninvasibility. When the average of the dominance coefficients is close to
a special case of a more general model, but it is often the boundary between regions of invasibility and noninvasibility. When the average of the dominance coefficients is close to 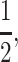 our results indicate that selection at the primary locus can determine whether or not an imprinting modifier invades; if that average is close to zero or one, dominance alone, not selection, determines invasion. In an autosomal two-locus model that assumed additive fitness, Day and Bonduriansky (2004) reported the same result as Iwasa and Pomiankowski (2001), namely invasion by an imprinting modifier that imprints alleles from the sex experiencing weaker selection, but for the case where selection favors different alleles in each sex. Our stability analysis is unable to resolve the invasion condition for
our results indicate that selection at the primary locus can determine whether or not an imprinting modifier invades; if that average is close to zero or one, dominance alone, not selection, determines invasion. In an autosomal two-locus model that assumed additive fitness, Day and Bonduriansky (2004) reported the same result as Iwasa and Pomiankowski (2001), namely invasion by an imprinting modifier that imprints alleles from the sex experiencing weaker selection, but for the case where selection favors different alleles in each sex. Our stability analysis is unable to resolve the invasion condition for 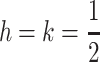 in this case (the dominant eigenvalue is one); excluding
in this case (the dominant eigenvalue is one); excluding  selection at the primary locus plays no role in determining whether an imprinting modifier can invade in our model. This would suggest that the evolution of imprinting in the sex that experiences weaker selection occurs only for a small window of dominance coefficients around
selection at the primary locus plays no role in determining whether an imprinting modifier can invade in our model. This would suggest that the evolution of imprinting in the sex that experiences weaker selection occurs only for a small window of dominance coefficients around  Outside this window, the invasion of an imprinting modifier depends primarily on the dominance coefficients, and when those dominance coefficients are large enough, maternal or paternal imprinting are equally likely to evolve.
Outside this window, the invasion of an imprinting modifier depends primarily on the dominance coefficients, and when those dominance coefficients are large enough, maternal or paternal imprinting are equally likely to evolve.
With directional selection on imprinted gene expression in the trans-acting model, we found that modifier alleles that imprint more gametes than the resident modifier invade when imprinting is advantageous in both females and males, and modifiers that imprint fewer gametes invade when imprinting is disadvantageous in the two sexes. As long as there are no stable modifier allele polymorphisms in these cases, recurrent invasion by new modifier alleles will lead either to imprinting of all gametes when imprinting is advantageous or to imprinting of no gametes when imprinting is disadvantageous. When imprinting is advantageous in one sex and not the other, invasion of a modifier allele that imprints more gametes than the resident allele occurs if the selective advantage in one sex is large enough relative to the disadvantage in the other sex. Invasion of a modifier allele that imprints fewer gametes than the resident occurs in a complementary scenario. If sex-specific viabilities are such that they fall into the region between the zero and one contours in Figure 4, recurrent invasion by new modifier alleles will likely result in individuals imprinting only a fraction of their gametes. Day and Bonduriansky (2004) observed a similar pattern where some simulation runs showed convergence to a stable polymorphism at the modifier locus, which in their model resulted in an intermediate amount of imprinting in the population as a whole.
The effect of X linkage of the modifier locus on the invasion conditions for rare alleles was seen to be modest in the case of both cis-acting modifiers and trans-acting modifiers. The invasion conditions that showed the greatest change with X linkage were for cis- and trans-acting modifiers under the assumption of opposing directional selection in the sexes. Whereas the invasion of autosomal modifiers at a stable polymorphism at the primary locus does not depend on s and t, the invasion of X-linked modifiers does depend on s and t for a narrow range of h close to  Previous models of the evolution of genomic imprinting have also reported only modest differences between results for autosomal and X-linked loci. For example, Spencer
et al. (1998) used an autosomal one-locus model to study the kinship theory in an explicit population genetic context; these authors found some support for the kinship theory but observed scenarios not predicted under the kinship theory, such as polymorphism in imprinting status. Using a similar framework, Spencer
et al. (2004) analyzed the kinship theory for X-linked loci and found a comparable level of support for the kinship theory, but fewer instances of polymorphism. Also, Iwasa and Pomiankowski (2001) assumed that their loci were X linked in analyzing sex-specific selection; their results mirrored those of Day and Bonduriansky (2004) who assumed autosomal loci. The similarity between the conditions for the evolution of imprinting for autosomal and X-linked loci in our results and the results of others suggests that there is no population-genetic barrier to the possible coevolution between imprinted XCI and genomic imprinting at autosomal loci (Reik and Lewis 2005). These results do not firmly assert which phenomenon evolved first; X-linked modifiers have a slightly larger range of dominance coefficients that permit invasion by alleles that increase imprinting, which suggests some support for the earlier evolution of imprinted XCI.
Previous models of the evolution of genomic imprinting have also reported only modest differences between results for autosomal and X-linked loci. For example, Spencer
et al. (1998) used an autosomal one-locus model to study the kinship theory in an explicit population genetic context; these authors found some support for the kinship theory but observed scenarios not predicted under the kinship theory, such as polymorphism in imprinting status. Using a similar framework, Spencer
et al. (2004) analyzed the kinship theory for X-linked loci and found a comparable level of support for the kinship theory, but fewer instances of polymorphism. Also, Iwasa and Pomiankowski (2001) assumed that their loci were X linked in analyzing sex-specific selection; their results mirrored those of Day and Bonduriansky (2004) who assumed autosomal loci. The similarity between the conditions for the evolution of imprinting for autosomal and X-linked loci in our results and the results of others suggests that there is no population-genetic barrier to the possible coevolution between imprinted XCI and genomic imprinting at autosomal loci (Reik and Lewis 2005). These results do not firmly assert which phenomenon evolved first; X-linked modifiers have a slightly larger range of dominance coefficients that permit invasion by alleles that increase imprinting, which suggests some support for the earlier evolution of imprinted XCI.
To assess the likelihood of the evolution of genomic imprinting through the invasion of a rare modifier allele, we need the prior probability distribution on the parameters in our model. While this distribution is unknown, experimental and comparative studies have estimated average values of these parameters. Average values for the primary parameter in our results, the dominance coefficient, have been calculated for deleterious mutations (Simmons and Crow 1977), and a recent analysis suggested that h varies from 0.04 to 0.4 in D. melanogaster as the value of s decreases (García-Dorado and Caballero 2000). As these estimates do not consider sex-specific values of h, they are most relevant if selection favors the same allele in females and males and mutation is the source of the disfavored allele; in this case, invasion by an imprinting modifier is unlikely since the condition for invasion is  When selection favors different alleles in females and males, whether an allele is classified as deleterious depends on the sex in which it is expressed, and it is no longer clear that these estimates apply. Estimates of the values of sex-specific dominance coefficients would shed light on the likelihood of modifier allele invasion, but these values remain largely unknown. Another key parameter is μ, the per-locus per-generation mutation rate. We can estimate μ from the average per-site per-generation mutation rate, which in mammals is 2 × 10−9 (Kumar and Subramanian 2002); if most nonneutral mutations are deleterious and occur at <10% of sites (Gaffney and Keightley 2006), the per-locus mutation rate is between 10−7 and 10−6 for genes 1–10 kbp long. In our model where selection favors the same allele in both sexes, mutation is the source of genetic variation. While we could not derive an explicit form for the eigenvalues of the Jacobian matrix and determine the initial rate of invasion of a rare modifier allele, it has been shown that without sex-specific selection this rate is of the order of the mutation rate (Spencer and Williams 1997); simulation work (results not shown) suggests that this is true of sex-specific selection as well. Most reasonable mammalian effective population sizes entail that an increase in the frequency of a rare allele by genetic drift would be more likely than invasion driven by selection for μ in this range. If selection favors different alleles in the two sexes, then selection, not mutation, is the source of genetic variation at the primary locus, and invasion can occur much more rapidly (Day and Bonduriansky 2004); our numerical analyses suggest that the rate of invasion, as assessed from the dominant eigenvalue, can be many orders of magnitude larger than the mutation rate for sufficiently larger dominance and selection coefficients. In this case, selection may be strong enough to determine the fate of a rare modifier rather than drift. Also, if imprinting has an explicit selective advantage, an increase in the degree of imprinting in the population is likely for reasonably large populations.
When selection favors different alleles in females and males, whether an allele is classified as deleterious depends on the sex in which it is expressed, and it is no longer clear that these estimates apply. Estimates of the values of sex-specific dominance coefficients would shed light on the likelihood of modifier allele invasion, but these values remain largely unknown. Another key parameter is μ, the per-locus per-generation mutation rate. We can estimate μ from the average per-site per-generation mutation rate, which in mammals is 2 × 10−9 (Kumar and Subramanian 2002); if most nonneutral mutations are deleterious and occur at <10% of sites (Gaffney and Keightley 2006), the per-locus mutation rate is between 10−7 and 10−6 for genes 1–10 kbp long. In our model where selection favors the same allele in both sexes, mutation is the source of genetic variation. While we could not derive an explicit form for the eigenvalues of the Jacobian matrix and determine the initial rate of invasion of a rare modifier allele, it has been shown that without sex-specific selection this rate is of the order of the mutation rate (Spencer and Williams 1997); simulation work (results not shown) suggests that this is true of sex-specific selection as well. Most reasonable mammalian effective population sizes entail that an increase in the frequency of a rare allele by genetic drift would be more likely than invasion driven by selection for μ in this range. If selection favors different alleles in the two sexes, then selection, not mutation, is the source of genetic variation at the primary locus, and invasion can occur much more rapidly (Day and Bonduriansky 2004); our numerical analyses suggest that the rate of invasion, as assessed from the dominant eigenvalue, can be many orders of magnitude larger than the mutation rate for sufficiently larger dominance and selection coefficients. In this case, selection may be strong enough to determine the fate of a rare modifier rather than drift. Also, if imprinting has an explicit selective advantage, an increase in the degree of imprinting in the population is likely for reasonably large populations.
Although a rough assessment of reasonable parameter values restricts the cases in which the evolution of imprinting under our model may occur, the range of taxa to which our model applies is wider than for other models. For example, the kinship theory (Haig 1997) posits that certain characteristics, such as a polygamous mating system and maternal care, are prerequisites for the evolution of genomic imprinting. In contrast, in our model genomic imprinting can evolve without assuming a particular mating system or a particular behavior, such as resource provisioning, in relation to kin. While the imprinting of genes such as Igf2 and Igf2r in mammals is consistent with the kinship theory (Wilkins and Haig 2003), imprinting occurs in taxa that do not fit as easily into the kinship theory, such as flies (Lloyd 2000; Bonduriansky and Rowe 2005). Additionally, a recent synthesis of known imprinted genes in mouse and human revealed a number of discordances in imprinting status between the two species even though many of these genes have similar functions in both species (Morison
et al. 2005). Different selective pressures in human and mouse unrelated to asymmetric kinship could account for some of these differences. This synthesis also revealed that many known imprinted genes are likely to be unrelated to maternal provisioning and offspring growth; some of these genes reside within introns or are derived from retrotransposition events (Morison
et al. 2005). Finally, our results indicate that maternal and paternal imprinting can be equally likely if dominance at the trait-coding locus is significantly different from  Sex-specific selection under additive fitness and the kinship theory both posit that maternal imprinting is more likely when there is a selective advantage to trait expression in males and vice versa. Although there are certainly genes whose phenotypic effect and imprinting status follow this pattern, it is unlikely that all imprinted genes conform to this framework (Wood and Oakey 2006). Our analysis suggests that sex-specific selection and dominance together may generate a more diverse pattern across species of imprinted genes than has previously been described.
Sex-specific selection under additive fitness and the kinship theory both posit that maternal imprinting is more likely when there is a selective advantage to trait expression in males and vice versa. Although there are certainly genes whose phenotypic effect and imprinting status follow this pattern, it is unlikely that all imprinted genes conform to this framework (Wood and Oakey 2006). Our analysis suggests that sex-specific selection and dominance together may generate a more diverse pattern across species of imprinted genes than has previously been described.
Acknowledgments
Research supported in part by National Institutes of Health grant GM 28016. J. V. is supported by an Anne T. and Robert M. Bass Stanford Graduate Fellowship.
APPENDIX
| Modifier linkage | Imprinting type | Resident modifier allele | Invading modifier allele | Jacobian matrix |
|---|---|---|---|---|
| Autosomal | Maternal | M1 | M2 | JAM1 |
| Autosomal | Maternal | M2 | M1 | JAM2 |
| X linked | Maternal | M1 | M2 | JSM1 |
| X linked | Maternal | M2 | M1 | JSM2 |
 |
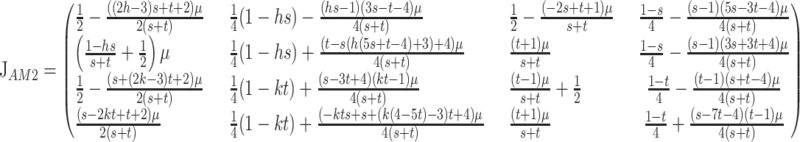 |
 |
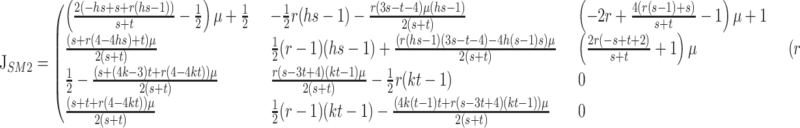 |
References
- Alleman, M., and J. Doctor, 2000. Genomic imprinting in plants: observations and evolutionary implications. Plant Mol. Biol. 43 147–161. [DOI] [PubMed] [Google Scholar]
- Anderson, R. J., and H. G. Spencer, 1999. Population models of genomic imprinting. I. Differential viability in the sexes and the analogy with genetic dominance. Genetics 153 1949–1958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson, M., 1994. Sexual Selection. Princeton University Press, Princeton, NJ.
- Bartolomei, M. S., and S. M. Tilghman, 1997. Genomic imprinting in mammals. Annu. Rev. Genet. 31 493–525. [DOI] [PubMed] [Google Scholar]
- Bodmer, W. F., and J. Felsenstein, 1967. Linkage and selection: theoretical analysis of the deterministic two locus random mating model. Genetics 57 237–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonduriansky, R., and L. Rowe, 2005. Intralocus sexual conflict and the genetic architecture of sexually dimorphic traits in prochyliza xanthostoma (diptera: Piophilidae). Evol. Int. J. Org. Evol. 59 1965–1975. [PubMed] [Google Scholar]
- Crouse, H. V., 1960. The controlling element in sex chromosome behavior in sciara. Genetics 45 1429–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day, T., and R. Bonduriansky, 2004. Intralocus sexual conflict can drive the evolution of genomic imprinting. Genetics 167 1537–1546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Koning, D. J., A. P. Rattink, B. Harlizius, J. A. van Arendonk, E. W. Brascamp et al., 2000. Genome-wide scan for body composition in pigs reveals important role of imprinting. Proc. Natl. Acad. Sci. USA 97 7947–7950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delaval, K., and R. Feil, 2004. Epigenetic regulation of mammalian genomic imprinting. Curr. Opin. Genet. Dev. 14 188–195. [DOI] [PubMed] [Google Scholar]
- Duesbery, N. S., and G. F. V. Woude, 2002. Developmental biology: an arresting activity. Nature 416 804–805. [DOI] [PubMed] [Google Scholar]
- Edelstein-Keshet, L., 2005. Mathematical Models in Biology. Society for Industrial and Applied Mathematics, Philadelphia.
- Feil, R., S. Khosla, P. Cappai and P. Loi, 1998. Genomic imprinting in ruminants: allele-specific gene expression in parthenogenetic sheep. Mamm. Genome 9 831–834. [DOI] [PubMed] [Google Scholar]
- Feldman, M. W., and S. Karlin, 1971. The evolution of dominance: a direct approach through the theory of linkage and selection. Theor. Popul. Biol. 2 482–492. [DOI] [PubMed] [Google Scholar]
- Gaffney, D. J., and P. D. Keightley, 2006. Genomic selective constraints in murid noncoding DNA. PLoS Genet. 2 e204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Dorado, A., and A. Caballero, 2000. On the average coefficient of dominance of deleterious spontaneous mutations. Genetics 155 1991–2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giannoukakis, N., C. Deal, J. Paquette, C. G. Goodyer and C. Polychronakos, 1993. Parental genomic imprinting of the human IGF2 gene. Nat. Genet. 4 98–101. [DOI] [PubMed] [Google Scholar]
- Haig, D., 1992. Genomic imprinting and the theory of parent-offspring conflict. Sem. Dev. Biol. 3 153–160. [Google Scholar]
- Haig, D., 1997. Parental antagonism, relatedness asymmetries, and genomic imprinting. Proc. Biol. Sci. 264 1657–1662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haldane, J. B. S., and S. D. Jayakar, 1972. Equilibrium between mutation and selection in bisexual diploids. J. Genet. 61 1–13. [Google Scholar]
- Iwasa, Y., and A. Pomiankowski, 2001. The evolution of X-linked genomic imprinting. Genetics 158 1801–1809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlin, S., and S. Lessard, 1986. Theoretical Studies on Sex Ratio Evolution. Princeton University Press, Princeton, NJ. [PubMed]
- Kidwell, J. F., M. T. Clegg, F. M. Stewart and T. Prout, 1977. Regions of stable equilibria for models of differential selection in the two sexes under random mating. Genetics 85 171–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar, S., and S. Subramanian, 2002. Mutation rates in mammalian genomes. Proc. Natl. Acad. Sci. USA 99 803–808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, J. T., 2003. Molecular links between X-inactivation and autosomal imprinting: X-inactivation as a driving force for the evolution of imprinting? Curr. Biol. 13 R242–R254. [DOI] [PubMed] [Google Scholar]
- Lloyd, V., 2000. Parental imprinting in Drosophila. Genetica 109 35–44. [DOI] [PubMed] [Google Scholar]
- Luedi, P. P., A. J. Hartemink and R. L. Jirtle, 2005. Genome-wide prediction of imprinted murine genes. Genome Res. 15 875–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGrath, J., and D. Solter, 1984. Completion of mouse embryogenesis requires both the maternal and paternal genomes. Cell 37 179–183. [DOI] [PubMed] [Google Scholar]
- Morison, I. M., J. P. Ramsay and H. G. Spencer, 2005. A census of mammalian imprinting. Trends Genet. 21 457–465. [DOI] [PubMed] [Google Scholar]
- Okamoto, I., A. P. Otte, C. D. Allis, D. Reinberg and E. Heard, 2004. Epigenetic dynamics of imprinted X inactivation during early mouse development. Science 303 644–649. [DOI] [PubMed] [Google Scholar]
- O'Neill, M. J., R. S. Ingram, P. B. Vrana and S. M. Tilghman, 2000. Allelic expression of IGF2 in marsupials and birds. Dev. Genes Evol. 210 18–20. [DOI] [PubMed] [Google Scholar]
- Owen, A. R. G., 1953. A genetical system admitting of 2 distinct stable equilibria under natural selection. Heredity 7 97–102. [Google Scholar]
- Pearce, G. P., and H. G. Spencer, 1992. Population genetic models of genomic imprinting. Genetics 130 899–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson, K., and C. Sapienza, 1993. Imprinting the genome: imprinted genes, imprinting genes, and a hypothesis for their interaction. Annu. Rev. Genet. 27 7–31. [DOI] [PubMed] [Google Scholar]
- Reik, W., and A. Lewis, 2005. Co-evolution of X-chromosome inactivation and imprinting in mammals. Nat. Rev. Genet. 6 403–410. [DOI] [PubMed] [Google Scholar]
- Reik, W., and J. Walter, 2001. Genomic imprinting: parental influence on the genome. Nat. Rev. Genet. 2 21–32. [DOI] [PubMed] [Google Scholar]
- Rice, W. R., and A. K. Chippindale, 2001. Intersexual ontogenetic conflict. J. Evol. Biol. 14 685–693. [Google Scholar]
- Sapienza, C., 1989. Genome imprinting and dominance modification. Ann. NY Acad. Sci. 564 24–38. [DOI] [PubMed] [Google Scholar]
- Selgrade, J. F., and M. Ziehe, 1987. Convergence to equilibrium in a genetic model with differential viability between the sexes. J. Math. Biol. 25 477–490. [DOI] [PubMed] [Google Scholar]
- Simmons, M. J., and J. F. Crow, 1977. Mutations affecting fitness in Drosophila populations. Annu. Rev. Genet. 11 49–78. [DOI] [PubMed] [Google Scholar]
- Spencer, H. G., 1997. Mutation-selection balance under genomic imprinting at an autosomal locus. Genetics 147 281–287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer, H. G., and M. W. Feldman, 2005. Adaptive dynamics, game theory and evolutionary population genetics. J. Evol. Biol. 18 1191–1193. [DOI] [PubMed] [Google Scholar]
- Spencer, H. G., and M. J. Williams, 1997. The evolution of genomic imprinting: two modifier-locus models. Theor. Popul. Biol. 51 23–35. [DOI] [PubMed] [Google Scholar]
- Spencer, H. G., M. W. Feldman and A. G. Clark, 1998. Genetic conflicts, multiple paternity and the evolution of genomic imprinting. Genetics 148 893–904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer, H. G., M. W. Feldman, A. G. Clark and A. E. Weisstein, 2004. The effect of genetic conflict on genomic imprinting and modification of expression at a sex-linked locus. Genetics 166 565–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surani, M. A., S. C. Barton and M. L. Norris, 1984. Development of reconstituted mouse eggs suggests imprinting of the genome during gametogenesis. Nature 308 548–550. [DOI] [PubMed] [Google Scholar]
- Walter, J., and M. Paulsen, 2003. Imprinting and disease. Semin. Cell Dev. Biol. 14 101–110. [DOI] [PubMed] [Google Scholar]
- Wilkins, J. F., 2005. Genomic imprinting and methylation: epigenetic canalization and conflict. Trends Genet. 21 356–365. [DOI] [PubMed] [Google Scholar]
- Wilkins, J. F., and D. Haig, 2003. What good is genomic imprinting: the function of parent-specific gene expression. Nat. Rev. Genet. 4 359–368. [DOI] [PubMed] [Google Scholar]
- Wood, A. J., and R. J. Oakey, 2006. Genomic imprinting in mammals: emerging themes and established theories. PLoS Genet. 2 e147. [DOI] [PMC free article] [PubMed] [Google Scholar]