Under Neutrality, Q_ST ≤ F_ST When There Is Dominance in an Island Model

TO test whether quantitative traits are under directional or homogenizing selection, it is common practice to compare population differentiation estimates at molecular markers (F_ST) (Wright 1951) and quantitative traits (Q_ST) (Spitze 1993). If the trait is neutral and its determinism additive, then theory predicts that Q_ST = F_ST, while Q_ST > F_ST is predicted under directional selection for different local optima, and Q_ST < F_ST is predicted under homogenizing selection (Merila and Crnokrak 2001). Goudet and Büchi (2006) recently evaluated the effects of dominance, inbreeding, and sampling design on Q_ST for neutral traits. Under dominance, Goudet and Büchi (2006) found that (1) dominance decreases on average the value of Q_ST relative to F_ST (i.e., Q_ST − F_ST ≤ 0), (2) the magnitude of the contrast Q_ST − F_ST increases with population differentiation (i.e., with increasing F_ST), and (3) dominance is unlikely to lead to Q_ST − F_ST > 0.

In a recent letter to Genetics, Lopez-Fanjul et al. (2007) questioned the evidence leading to these claims. In particular, they criticized Goudet and Büchi (2006) for using averages over allele frequencies and dominance deviations. Here, taking an analytical approach similar to that used in Lopez-Fanjul et al. (2007), we first show that under an island model, the result Q_ST ≤ F_ST with dominance obtained by Goudet and Büchi (2006) is strictly true over all allelic frequencies and dominance deviations. We then argue that independently of the underlying population structure, averaging over allele frequencies and dominance deviations is pertinent, since quantitative traits are polygenic, and this is what empiricists study when they estimate Q_ST. We conclude by emphasizing that the major problem faced by empiricists is not the slight negative bias in Q_ST due to nonadditive effects, but the very large variance in this quantity, particularly when the number of samples is small.

As Lopez-Fanjul et al. (2007) and Goudet and Büchi (2006) used different parameterizations, some clarification might be useful. Goudet and Büchi (2006) used −a, d, and a, while Lopez-Fanjul et al. (2007) used 1 − s, 1 − hs, and 1 for the genotypic values of AA, AB, and BB, respectively. These two notation schemes are equivalent when a = 1 (and therefore s = 2) and .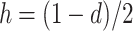

To obtain the expectation of 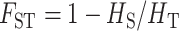and 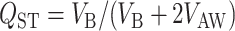, four quantities are needed: gene diversities within [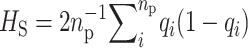] and over all [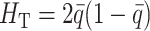] populations, where q represents the frequency of the recessive allele and n_p the number of populations, as well as the additive variance within (V_AW) and between (V_B) populations. Under strict additivity, these four quantities are functions of the first and second moments of the distribution of allele frequencies only. However, under dominance (when 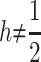), V_AW and V_B also depend on the third and fourth moments of this distribution. As we see below, the difference between Lopez-Fanjul et al. (2007) results and those of Goudet and Büchi (2006) stems partly from the assumed distribution of allele frequencies.

We consider exactly the same genetical setup as in Lopez-Fanjul et al. (2007): a biallelic locus with dominance h, additive effect s, and allele frequency q. Using their notation, the mean for the trait, in any given population, is given by M = 1 − 2qhs − q²s(1 − 2h). The variance of trait mean among populations is given by V_B = E(M²) − E(M)², where E denotes expectation with respect to the distribution of q among populations. This turns out to be a polynomial function of the first four moments of allelic frequencies. The additive variance in a given population is given by V_AW = 2αq(1 − q) [where α = s(h + (1 − 2h)q is the average effect; Lopez-Fanjul et al. 2003]. With 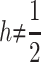the expectation of this additive variance among populations, E(V_AW), is also a polynomial function of the first four moments of allele frequencies.

The expectations of these quantities are obtained by replacing q, q², q³, and q⁴ in their expressions by the first, second, third, and fourth moments of allele frequency distribution (just as in Lopez-Fanjul et al. 2007). In their letter, Lopez-Fanjul et al. (2007) consider a specific model where isolated lines diverge by drift from an infinitely large panmictic population (pure drift model, PDM), while Goudet and Büchi (2006) considered the classical island model (IM) at equilibrium between migration and drift. For the infinite island model at equilibrium, and for a biallelic locus, the distribution of allelic frequencies follows a beta distribution with parameter 4Nm,

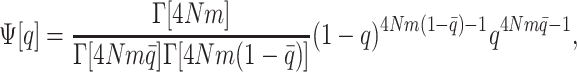(Wright 1937a,b), where 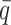is the average allele frequency among populations (for the multiallelic locus equivalent, the pertinent distribution is a Dirichlet, as used in Goudet and Büchi 2006; see Rannala and Hartigan 1996).

The first four moments of the beta distribution can be expressed in terms of 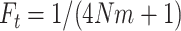as follows:

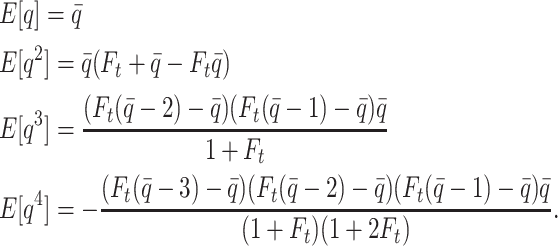(1)

Under the PDM, the moments of the allele frequency distribution are given by Equations 1–4 in Lopez-Fanjul et al. (2002). Note that the two models yield the same first and second moments, but differ in their third and fourth moments, which also influence V_B and V_AW when .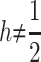

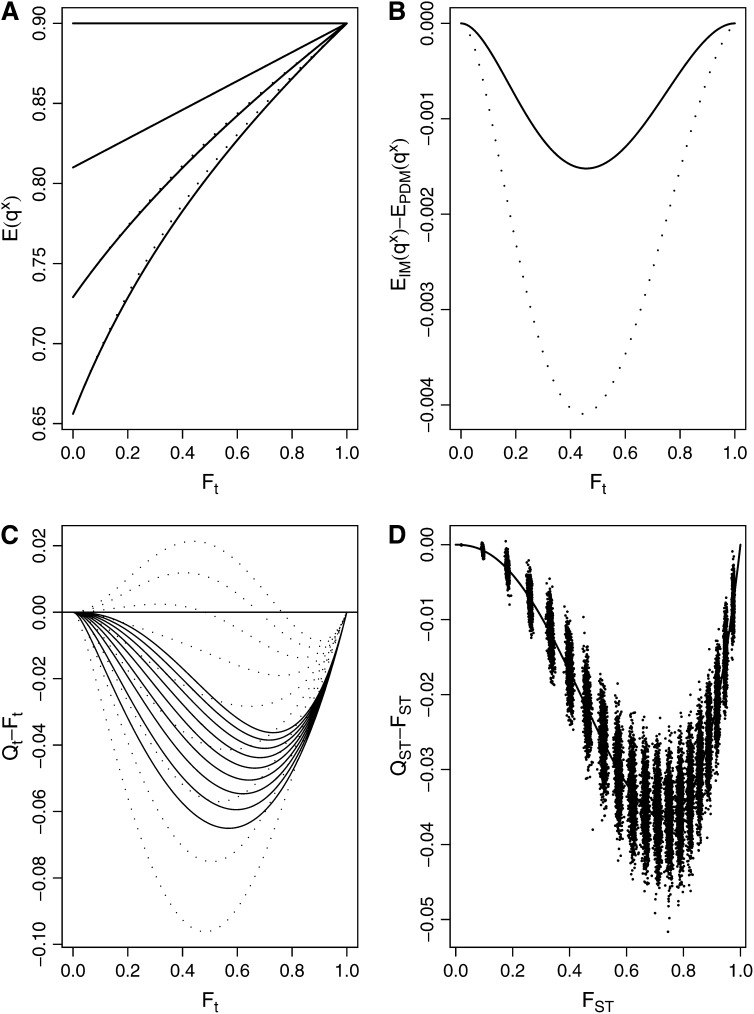
Figure 1A portrays the dynamics of the first four allele frequency moments of the two models, assuming an overall allele frequency of q = 0.9. This frequency was chosen because this is the frequency that gave rise to the largest positive difference between Q_ST and F_ST in Lopez-Fanjul et al. (2007) (see Figure 1 of their article). The discrepancies between the third and fourth moments are barely notable in Figure 1A, but when the differences between these moments are plotted against F_t (Figure 1B), we can clearly see that the expected third and fourth moments of allelic frequency are smaller in the IM than in the PDM. Figure 1C shows that these tenuous differences lead to a qualitative change in the difference Q_ST − F_ST. While in the PDM (dotted lines) this difference can be positive or negative, it is always negative in the IM (for any s and any h < 0.5). The formulas used by Lopez-Fanjul et al. (2007) therefore do not apply to an island model (at least at equilibrium), contrary to what they claim. And, since none of the overall allelic frequencies give rise to a positive difference between Q_ST and F_ST in the IM, it can be concluded that the results of Goudet and Büchi (2006) are true both for a single diallelic locus under the IM and for more realistic multilocus traits, at least under the IM and the PDM. Goudet and Büchi (2006) were therefore correct in identifying the population model as a likely reason for the discrepancies between their results and earlier work by Lopez-Fanjul et al. (2003). Finally, Figure 1D confirms that simulations of a single diallelic locus with overall recessive frequency of 0.9 and h = 0 give results entirely consistent with the theoretical expectations under an IM.

Figure 1.—

Moments of allele frequency for a one-locus, two-allele model, with a = 1, d = 0 (s = 2, h = 0). (A) First four moments for q = 0.9 as a function of F_t. Solid lines are for the island model (IM), and dotted lines are for independent lineages diverging from an ancestral large panmictic population (PDM). First to fourth moments from top to bottom. (B) Difference between IM and PDM for the third (solid line) and fourth (dotted line) moments of allele frequency for q = 0.9 as a function of F_t (the first and second moments for the IM and PDM are identical). (C) Expected value of the difference Q_t − F_t as a function of F_t for different frequencies of the recessive allele (0.1–0.9 in steps of 0.1 from bottom to top) for the IM (solid lines) and the PDM (dotted lines; same as Figure 1 in Lopez-Fanjul et al. 2007, with h = 0 instead of h = 0.25; Q_t and F_t are used for expectations of Q_ST and F_ST, respectively). (D) For q = 0.9, simulations of the difference Q_ST − F_ST in an island model made of 10,000 islands for different F_ST-values. The solid line is for the expectation of the difference Q_ST − F_ST in an IM.

Lopez-Fanjul et al. (2007) also assert that contrary to the results of Goudet and Büchi (2006), the difference between Q_ST and F_ST is largest around F_ST = 0.5 and decreases thereafter. It is clear that for extremely large population differentiation (e.g., F_ST ≈ 1) Q_ST and F_ST should be equal whatever the dominance deviation. This is because when populations are entirely differentiated, no heterozygotes remain, and hence dominance is not expressed. Figure 1, C and D, shows that in the IM the maximum difference between Q_ST and F_ST due to dominance is obtained for differentiation values of ∼0.7–0.8 rather than 0.5. A cursory survey of the literature shows that F_ST ≥ 0.7 is seldom reported. Accordingly, the simulation scheme in Goudet and Büchi (2006) did not investigate F_ST-values much larger than 0.8.

Although it was just shown that under an island model dominance always leads to Q_ST ≤ F_ST, one might be worried that this result depends on the underlying model of population structure. Indeed, the IM (which assumes an equilibrium between migration and drift) is by no means more realistic than the PDM (which assumes no migration), for which dominance does give rise to the pattern Q_ST > F_ST for certain allelic frequencies. It is essential to realize that all these results are the expectation of the difference between Q_ST and F_ST for a single diallelic locus (in the analytical section of Goudet and Büchi 2006, p. 1339 gives the expression of Q_ST for a single diallelic locus independently of the underlying model of population structure, from which it is possible to derive the conditions under which Q_ST > F_ST). As soon as several loci are considered, and because the parameter space leading to Q_ST > F_ST is so narrow, the general consequence of dominance deviations is Q_ST ≤ F_ST. Lopez-Fanjul et al. (2007) criticized Goudet and Büchi (2006) for using a far too wide parameter space in their simulations. First, as shown above for the IM, Q_ST ≤ F_ST independently of the distribution of s and h. For the PDM, restricting simulation scenarios within what is known about allelic frequencies and dominance deviations of recessive deleterious alleles (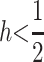, low q) also leads to Q_ST ≤ F_ST. The conditions leading to Q_ST > F_ST for a dominant trait are rather unlikely: over and above it occurring only for a specific population model (PDM), it also requires the frequencies of the recessive alleles at most loci coding for the trait to be large. While this might happen for an isolated locus, it is extremely unlikely that it will occur for any real traits (for which, for a neutral trait, we expect a symmetric distribution of q among loci). Thus, while for a single diallelic locus the relation between Q_ST and F_ST depends on the underlying model of population structure, for a polygenic trait the different models of population structures consistently lead to Q_ST ≤ F_ST.

It is perhaps unfortunate that Lopez-Fanjul et al. (2007) drew attention only to one of the conclusions of Goudet and Büchi (2006), namely the slight bias in Q_ST due to dominance, and did not take note of the rest of the article, where Goudet and Büchi (2006) quantified the variance in Q_ST under several experimental designs. From Figure 1 (and Figure 2 of Lopez-Fanjul et al. 2007), we see that the expected bias in Q_ST seldom exceeds 10% of the value of F_ST. This would matter if the variance of Q_ST was small. But Goudet and Büchi (2006) found that unless the number of populations analyzed to estimate Q_ST is very large (e.g., >20), only extremely large differences between Q_ST and F_ST (certainly >10% of the value of F_ST) are likely to be statistically significant.

The slight effect that dominance might have on Q_ST is therefore unlikely to lead to a spurious inference of selection, and the large variance of Q_ST is certainly more worrisome for the prospect of identifying traits under selection.