Abstract
Analysis of data on 1000 Holstein–Friesian bulls genotyped for 15,036 single-nucleotide polymorphisms (SNPs) has enabled genomewide identification of haplotype blocks and tag SNPs. A final subset of 9195 SNPs in Hardy–Weinberg equilibrium and mapped on autosomes on the bovine sequence assembly (release Btau 3.1) was used in this study. The average intermarker spacing was 251.8 kb. The average minor allele frequency (MAF) was 0.29 (0.05–0.5). Following recent precedents in human HapMap studies, a haplotype block was defined where 95% of combinations of SNPs within a region are in very high linkage disequilibrium. A total of 727 haplotype blocks consisting of ≥3 SNPs were identified. The average block length was 69.7 ± 7.7 kb, which is ∼5–10 times larger than in humans. These blocks comprised a total of 2964 SNPs and covered 50,638 kb of the sequence map, which constitutes 2.18% of the length of all autosomes. A set of tag SNPs, which will be useful for further fine-mapping studies, has been identified. Overall, the results suggest that as many as 75,000–100,000 tag SNPs would be needed to track all important haplotype blocks in the bovine genome. This would require ∼250,000 SNPs in the discovery phase.
THERE is great enthusiasm about the promise of genomewide association studies in cattle, with the recent availability of many thousands of single-nucleotide polymorphism (SNP) markers and rapid improvement in high-throughput SNP genotyping technologies (Craig and Stephan 2005; Gunderson et al. 2005; Hardenbol et al. 2005; Hirschhorn and Daly 2005).
For the whole-genome association approach to be applied successfully, there is a need to understand the structure of linkage disequilibrium (LD), particularly the distance to which LD extends and how much it varies from one chromosomal region to another in the population under study. LD maps have been found to be very useful for describing the pattern of LD in humans (De La Vega et al. 2005; Tapper et al. 2005; Service et al. 2006). The application of this approach in cattle has given preliminary pictures of the extent and pattern of LD (Khatkar et al. 2006a), which is being extended to the construction of dense genomewide bovine LD maps (M. S. Khatkar, unpublished data). While LD maps provide information on the extent and pattern of LD in populations, for high-resolution association mapping, it is also necessary to identify haplotype blocks and SNP(s) that most effectively “tag(s)” each block for high-resolution association mapping. Haplotype blocks are chromosome regions of high linkage disequilibrium and typically show low haplotype diversity. Haplotype blocks typically represent regions of low recombination flanked by recombination hotspots. Construction of haplotype blocks and identification of tag SNPs have been found to be quite informative in identification of specific markers for association mapping in humans (Barrett et al. 2005; Hinds et al. 2005; International HapMap Consortium 2005; Zhang et al. 2005; Pe'er et al. 2006).
Hinds et al. (2005) estimated that ∼300,000 and 500,000 tag SNPs would give the same power of association mapping as using 1.6 million randomly located SNPs, in non-African and African human populations, respectively. Similar observations were made in the recent HapMap report for three ethnic groups (International HapMap Consortium 2005).
The study of the haplotype blocks and tag SNPs is an active topic of research. Many algorithms have recently been developed for identifying blocks (reviewed in Cardon and Abecasis 2003; Wall and Pritchard 2003a,b). The criteria for block identification are mainly based on pairwise D′-values (as defined by Hedrick 1987), haplotype diversity, and the location of known recombination hotspots. Daly et al. (2001) searched for regions of low haplotype diversity by comparing the observed haplotypic heterozygosity in sliding windows. Dawson et al. (2002) used both D′ and a reduced haplotype diversity criterion. Zhang and Jin (2003) implemented several algorithms in a program named HaploBlockFinder.
Using the confidence interval of D′, Gabriel et al. (2002) defined a block as a region within which only a small proportion of SNP pairs (e.g., 5%) exhibit strong evidence of historical recombination (upper confidence bound of D′ is <0.9). Others (Phillips et al. 2003; Twells et al. 2003) have used a similar approach. We have adopted the approach of Gabriel et al. (2002) in this study.
Most studies in livestock have been mainly restricted to the estimation of the extent of LD based on pairwise measures of LD and have detected extensive long-range LD in cattle (Farnir et al. 2000; Tenesa et al. 2003; Vallejo et al. 2003; Khatkar et al. 2006b; Odani et al. 2006), sheep (McRae et al. 2002), pig (Nsengimana et al. 2004), and horse (Tozaki et al. 2005). Long-range LD in livestock populations appears to be much more extensive than in humans, where typically it extends for only a few kilobases (Hinds et al. 2005). So far there has been no attempt to construct a haplotype block map in cattle and other livestock species. However, this type of analysis is now possible with the availability of medium-density SNP panels covering the bovine genome.
As a result of a large-scale international resequencing collaboration (http://www.hgsc.bcm.tmc.edu/projects/bovine/), 10,410 bovine SNP markers became available in 2005. In addition, Hawken et al. (2004) identified 17,344 putative coding-region bovine SNPs from an analysis of a large number of expressed sequence tags (ESTs). Gene-centric variants are more likely to affect gene function than those that occur outside genes (Jorgenson and Witte 2006). We added the most promising 4626 of these gene-centric SNPs to the 10,410, to give a total pool of 15,036 SNPs that were genotyped in 1546 Holstein–Friesian bulls. In this article, we report the use of these data to construct haplotype blocks for the whole bovine genome and identify tag SNPs. The chromosomal coverage by the blocks was then determined. The usefulness of these methods based on present SNP density is discussed.
MATERIALS AND METHODS
DNA samples and selection of bulls:
A panel of 1546 Holstein–Friesian bulls born between 1955 and 2001 was selected for genotyping. Most of these bulls were born in Australia (1435) with smaller numbers being born in the United States (53), Canada (35), New Zealand (8), The Netherlands (8), Great Britain (3), France (3), and Germany (1). There were more bulls from the recent cohorts than from older cohorts. This panel of bulls represents near-to-normal distributions for Australian breeding values (ABVs) for the most common production traits recorded through the Australian Dairy Herd Improvement Scheme (ADHIS; http://www.adhis.com.au/). From ADHIS pedigree information and using FORTRAN programs in the PEDIG package of D. Boichard (http://dga.jouy.inra.fr/sgqa/diffusions/pedig/pedigE.htm), kinship (coefficient of coancestry) was calculated for each pairwise combinations of bulls. On this basis, the least-related 1000 bulls were chosen for this analysis, from the original 1546 bulls. The mean kinship (coefficient of coancestry) among these 1000 bulls is 0.012, with 0 and 0.017 for the first and third quartiles, respectively. These bulls were assumed unrelated for the purpose of the present analysis.
Extraction and amplification of DNA:
Semen samples for most of these bulls, obtained from Genetics Australia (Bacchus Marsh, Victoria, Australia), were the source of genomic DNA. The genomic DNA of 18 bulls was kindly provided by Jerry Taylor, University of Missouri, Columbia, Missouri. DNA was extracted from straws of frozen semen by a salting-out method adapted from Heyen et al. (1997). As the yields of some genomic DNA per straw were limited, all DNA samples were amplified using a whole-genome amplification (WGA) kit (Repli-G, Molecular Staging). A comparison of the genotypes of genomic DNA and the WGA DNA, for the SNP markers genotyped in this study, showed an average inconsistency of <1% (details are given in Hawken et al. 2006). All genotyping on which the present analysis is based was carried out using WGA DNA.
Identification and source of SNPs:
A genomewide high-density panel of 15,036 SNPs was assembled for genotyping across the panel of bulls. Of these SNPs, 10,410 (MegAllele Genotyping Bovine 10,000-SNP Panel, ParAllele) were generated as part of the community project of the International Bovine Genome Sequencing Consortium (IBGSC) (http://www.hgsc.bcm.tmc.edu/projects/bovine/). The remaining 4626 custom SNPs were selected from the Interactive Bovine In Silico SNP (IBISS) database (Hawken et al. 2004) (http://www.livestockgenomics.csiro.au/ibiss/), from in-house sequencing, and from publications (Grosse et al. 1999; Heaton et al. 1999; Prinzenberg et al. 1999; Olsen et al. 2000, 2005; Cohen et al. 2004). IBISS is a database application constructed by clustering all publicly available bovine ESTs. From each cluster, a consensus sequence was obtained. When a base in an EST differed from the corresponding base in the consensus sequence, the position was recorded as a SNP candidate. SNP candidates were organized according to their proximity to other SNP candidates and the number of ESTs exhibiting the alternate base at that same location. The custom SNPs described above were taken from a pool of what were considered to be the “best” SNP candidates in IBISS. The best SNP candidates are those where the alternate base occurs in at least 30% of the ESTs in that alignment and where no more than two SNP candidates occur in a sliding window of 10 bases. Bovine QTL regions of interest (Khatkar et al. 2004) were translated to the human genome. The 4626 custom SNPs were those with predicted human locations most closely corresponding to the QTL regions of interest and/or from key candidate genes.
SNP genotyping:
A high-throughput SNP assay service provided by Affimetrix was used for genotyping. A highly multiplexed molecular inversion probe (MIP) technology developed by ParAllele Bioscience (Hardenbol et al. 2005) was applied. MIPs are unimolecular oligonuclotide SNP-specific probes that are insensitive to cross-reactivity among multiple probe molecules. MIPs hybridize to genomic DNA, and an enzymatic “gap fill” process produces an allele-specific signature. The resulting circularized probe can be separated from cross-reacted or unreacted probes by a simple exonuclease reaction and then amplified with a universal set of primers for all probes. Each specific SNP assay is detected via hybridization to an Affymetrix gene chip that has a unique physical position (Hardenbol et al. 2003, 2005). To ensure strict data integrity, concealed duplicated DNA samples were included throughout the entire genotyping process. The mean concordance between 23 duplicated DNA samples was 99.4%.
Estimation of SNP locations:
The locations of the SNPs were determined on the bovine sequence assembly Btau 3.1 (ftp://ftp.hgsc.bcm.tmc.edu/pub/data/Btaurus/fasta/Btau20060815-freeze/). The SNPs were placed on chromosomal linearized scaffolds using sequence similarity. The FASTA sequence data for each candidate SNP were generated by taking 100 bases of flanking consensus (EST) sequence from either side of the SNP. These FASTA sequences were compared with sequences in the 3.1 assembly using BLAT (Kent 2002) similarity searching specifying a minimum of 95% identity. SNP positions within the flanking sequence were converted to “exact” positions within the assembly using the BLAT output. The positions for all the 15,036 genotyping assays on this sequence map could be estimated. However, only 13,705 SNPs were placed on sequence scaffolds that have been assigned to a real chromosome; the rest (1331 SNPs) were on chromosomally unanchored scaffolds. After screening out SNPs with low MAF (MAF < 0.05), deviations from Hardy–Weinberg equilibrium (as detected by Fisher's exact test, P < 0.0001), and other quality measures, 9195 SNPs mapped on autosomes were used in this analysis.
Identification of genes matching SNP locations:
Details of the bovine records in NCBI's Entrez Gene database were extracted from the files gene_info (downloaded from ftp://ftp.ncbi.nlm.nih.gov/gene/DATA/ on January 15, 2007) and seq_gene.md (downloaded from ftp://ftp.ncbi.nlm.nih.gov/genomes/Bos_taurus/mapview/ on January 6, 2007). Predicted genes that span SNP locations were noted.
Construction of the haplotype block map:
Haplotype blocks were identified as per the definition of Gabriel et al. (2002) for all autosomes, using Haploview software (Barrett et al. 2005), on the basis of estimates of D′ for all pairwise combinations of SNPs within each chromosome. As discussed in the preceding section, the animals included in the analysis were relatively unrelated. Hence estimates of LD are based on the estimates of population frequencies of haplotypes as determined from the unphased input, using the algorithm of Qin et al. (2002) implemented in Haploview. Ninety-five percent confidence bounds on D′ were generated as per the algorithm of Gabriel et al. (2002) implemented in Haploview. Following Gabriel et al. (2002), a pair of SNPs is defined to be in “strong LD” if the upper 95% confidence bound of D′ is >0.98 (consistent with no historical recombination) and the lower bound is >0.7. Using the Haploview default values for blocks (Gabriel et al. 2002), a haplotype block is defined as a region over which 95% of informative SNP pairs show strong LD.
Identification of tag SNPs:
Two approaches were used to identify tag SNPs. In the first approach, haplotype tag SNPs (htSNPs) were selected on a block-by-block basis. Specifically, the htSNPs in each block were identified that could define all the common haplotypes in that block. However, this set is not necessarily the most parsimonious one for the entire data set. Hence a second approach, which is based on a joint consideration of all SNPs, was also applied using the pairwise tagging method of the Tagger program (de Bakker et al. 2005) implemented in Haploview. This method selects a minimal set of markers such that all alleles to be captured are correlated at an r2 greater than a defined threshold (r2 ≥ 0.8) with a marker in that set. Pairwise tagging means that all tag SNPs will act as direct proxies to all other unselected SNPs because they are highly correlated with one another.
Haplotype diversity within blocks:
Haplotype frequency was calculated in Haploview using an accelerated EM algorithm method described by Qin et al. (2002). This estimated population frequency of haplotypes is based on maximum likelihood as determined from the unphased input. Haplotype diversity within a block was then computed as
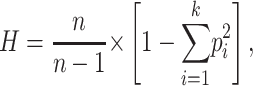 |
where k is the number of haplotypes observed with frequency pi, and n is the total number of chromosomes (Nei 1987).
RESULTS
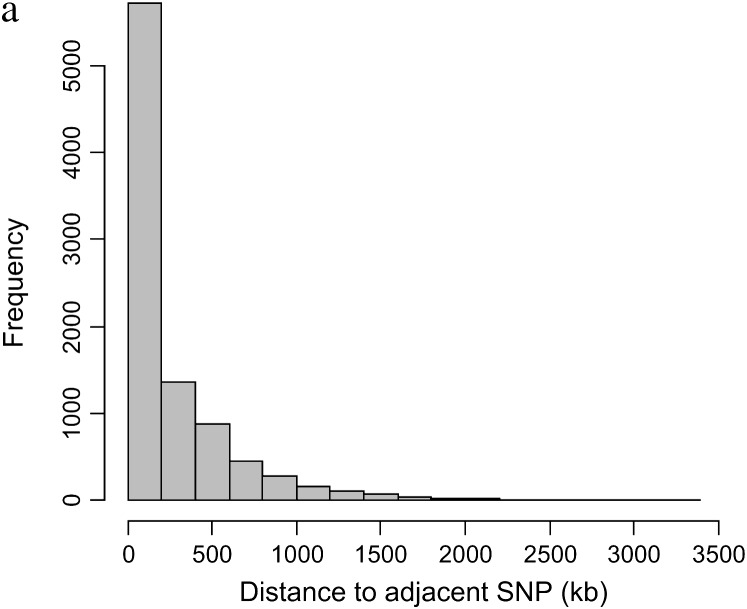
Of the 15,036 SNPs genotyped, 13,049 (87%) were polymorphic (minor allele frequency, MAF > 0) in the 1000 bulls finally included in this study. A further 1776 (14% of the biallelic) SNPs had <0.05 MAF. Of the polymorphic SNPs on the autosomes, 824 (7%) showed deviation from Hardy–Weinberg equilibrium (P < 0.0001) and were excluded from this analysis. The SNPs (232) typed in <50% of animals were also removed from the analysis. Of the remaining SNPs, 9195 were able to be located on autosomes in the bovine sequence assembly Btau 3.1 and were included in this analysis. Of these, 7057 (77%) of SNPs are from the MegAllele 10,000-SNP panel and 2138 (23%) are from the custom SNP panel. These SNPs were on an average typed on 992 bulls of 1000 included in this analysis with a minimum of 732 bulls for any SNP. The details of these SNPs, which compose the set used in these analyses, are provided in supplemental Table S1 at http://www.genetics.org/supplemental/. The number of SNPs on chromosomes varied from 158 on BTA27 to 528 on BTA1. The average intermarker spacing for the entire genome was 251.8 ± 4.0 kb with a median spacing of 93.9 kb. There were 59 intermarker intervals >2 Mb and only 5 intervals >3 Mb. The distribution of SNP spacing over the genome is shown in Figure 1a. The overall MAF of the SNPs used in these analyses was 0.286 ± 0.001.
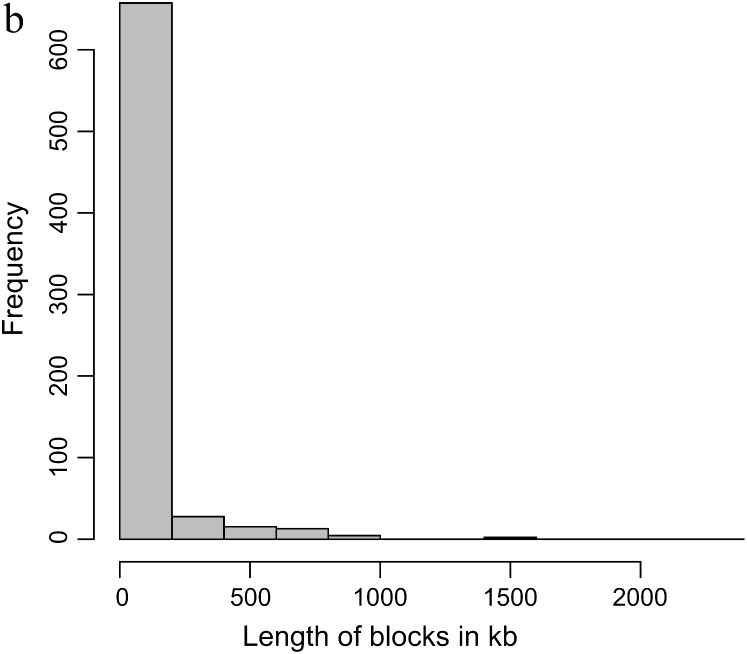
Figure 1.—
(a) The distribution of SNP spacing [the distance in base pairs (kilobases) from one SNP marker to the next SNP marker]. (b) Frequency distribution of size of haplotype blocks consisting of more than two SNPs.
In total, 727 haplotype blocks made up of ≥3 SNPs were identified, incorporating 2964 SNPs and covering 50,638 kb of the bovine sequence map, which corresponds to 2.18% of the combined length of all the autosomes (Table 1). The mean length of the blocks is 69.7 ± 7.7 kb, although the median length of 2.9 kb (geometric mean of 3.9 kb) indicates that most of the blocks are small (as can be seen from the distribution shown in Figure 1b). An additional 1068 haplotype blocks consisting of 2 SNPs were also identified (Table 2), for a grand total of 1795 blocks. The maximum number of SNPs in a block is 13. There are 82 blocks composed of >5 SNPs, 118 blocks with 5 SNPs, 217 blocks with 4 SNPs, and 310 blocks with 3 SNPs. Mean block length varies from 2.0 kb for the 2-SNP blocks to 153.8 kb for blocks with 5 SNPs. The biggest block covers 2296.3 kb on chromosome 5 and includes 4 SNPs. Detailed information on individual blocks in each chromosome is presented in supplemental Tables S1 and S2 at http://www.genetics.org/supplemental/.
TABLE 1.
Chromosomewide summary of haplotype blocks (consisting of three or more SNPs) in the bovine genome
| Chromosome | No. of SNPs | No. of blocks | Total block length (kb) | Block mean size ± SE (kb) | Block size (min) | Block size (max) | Chromosome length (Mb) | % coverage | No. of SNPs in blocks | htSNP | % htSNP | Tag SNPs (pairwise)a | % pairwise tag SNPsb |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 528 | 36 | 4,729 | 131.4 ± 51.5 | 0.100 | 1,502.3 | 145.9 | 3.24 | 156 | 75 | 48.1 | 381 | 72.2 |
| 2 | 462 | 35 | 2,236 | 63.9 ± 42.2 | 0.091 | 1,475.9 | 125.3 | 1.79 | 141 | 80 | 56.7 | 348 | 75.3 |
| 3 | 469 | 38 | 1,709 | 45.0 ± 17.5 | 0.201 | 537.0 | 116.3 | 1.47 | 145 | 79 | 54.5 | 357 | 76.1 |
| 4 | 384 | 29 | 1,180 | 40.7 ± 20.8 | 0.075 | 499.0 | 110.7 | 1.07 | 110 | 55 | 50.0 | 288 | 75.0 |
| 5 | 417 | 39 | 6,192 | 158.8 ± 75.8 | 0.176 | 2,296.3 | 118.5 | 5.23 | 146 | 73 | 50.0 | 309 | 74.1 |
| 6 | 443 | 37 | 3,569 | 96.4 ± 45.4 | 0.093 | 1,453.9 | 111.7 | 3.20 | 154 | 75 | 48.7 | 329 | 74.3 |
| 7 | 357 | 24 | 1,052 | 43.8 ± 26.1 | 0.135 | 611.5 | 100.7 | 1.04 | 93 | 48 | 51.6 | 283 | 79.3 |
| 8 | 389 | 28 | 1,699 | 60.7 ± 31.0 | 0.285 | 787.2 | 103.2 | 1.65 | 109 | 59 | 54.1 | 309 | 79.4 |
| 9 | 265 | 21 | 1,447 | 68.9 ± 44.9 | 0.184 | 725.5 | 94.6 | 1.53 | 78 | 34 | 43.6 | 198 | 74.7 |
| 10 | 403 | 27 | 470 | 17.4 ± 6.7 | 0.078 | 123.9 | 95.8 | 0.49 | 111 | 65 | 58.6 | 308 | 76.4 |
| 11 | 452 | 32 | 4,513 | 141.0 ± 48.6 | 0.115 | 955.6 | 101.1 | 4.46 | 139 | 86 | 61.9 | 343 | 75.9 |
| 12 | 276 | 22 | 563 | 25.6 ± 10.6 | 0.169 | 154.5 | 77.4 | 0.73 | 96 | 42 | 43.8 | 205 | 74.3 |
| 13 | 406 | 47 | 5,080 | 108.1 ± 35.0 | 0.125 | 1,345.6 | 82.7 | 6.14 | 204 | 112 | 54.9 | 280 | 69.0 |
| 14 | 303 | 27 | 1,969 | 72.9 ± 39.5 | 0.161 | 995.7 | 81.9 | 2.40 | 115 | 61 | 53.0 | 216 | 71.3 |
| 15 | 309 | 20 | 1,542 | 77.1 ± 41.5 | 0.058 | 771.1 | 75.1 | 2.05 | 85 | 40 | 47.1 | 224 | 72.5 |
| 16 | 317 | 31 | 1,345 | 43.4 ± 24.1 | 0.161 | 674.4 | 72.7 | 1.85 | 127 | 58 | 45.7 | 222 | 70.0 |
| 17 | 302 | 28 | 3,026 | 108.1 ± 36.0 | 0.193 | 661.3 | 69.5 | 4.35 | 117 | 67 | 57.3 | 225 | 74.5 |
| 18 | 294 | 27 | 493 | 18.3 ± 6.0 | 0.128 | 127.2 | 62.5 | 0.79 | 106 | 59 | 55.7 | 218 | 74.1 |
| 19 | 344 | 25 | 1,503 | 60.1 ± 21.0 | 0.249 | 423.9 | 63.0 | 2.38 | 110 | 58 | 52.7 | 269 | 78.2 |
| 20 | 254 | 17 | 888 | 52.2 ± 32.9 | 0.116 | 544.6 | 67.3 | 1.32 | 67 | 35 | 52.2 | 185 | 72.8 |
| 21 | 181 | 6 | 211 | 35.1 ± 21.5 | 0.199 | 138.4 | 62.9 | 0.33 | 31 | 12 | 38.7 | 154 | 85.1 |
| 22 | 252 | 17 | 656 | 38.6 ± 21.0 | 0.195 | 307.6 | 59.0 | 1.11 | 78 | 37 | 47.4 | 188 | 74.6 |
| 23 | 260 | 25 | 1,350 | 54.0 ± 25.4 | 0.127 | 454.3 | 48.6 | 2.78 | 98 | 57 | 58.2 | 191 | 73.5 |
| 24 | 222 | 18 | 565 | 31.4 ± 20.8 | 0.251 | 376.4 | 60.0 | 0.94 | 75 | 42 | 56.0 | 160 | 72.1 |
| 25 | 225 | 18 | 206 | 11.4 ± 4.3 | 0.089 | 71.6 | 41.9 | 0.49 | 67 | 35 | 52.2 | 172 | 76.4 |
| 26 | 184 | 16 | 462 | 28.9 ± 17.1 | 0.127 | 268.8 | 47.5 | 0.97 | 59 | 34 | 57.6 | 146 | 79.3 |
| 27 | 158 | 14 | 520 | 37.2 ± 20.0 | 0.190 | 281.9 | 43.2 | 1.20 | 53 | 28 | 52.8 | 120 | 75.9 |
| 28 | 159 | 12 | 741 | 61.7 ± 53.9 | 0.179 | 653.0 | 39.4 | 1.88 | 45 | 25 | 55.6 | 128 | 80.5 |
| 29 | 180 | 11 | 724 | 65.8 ± 45.6 | 0.373 | 497.6 | 44.9 | 1.61 | 49 | 21 | 42.9 | 134 | 74.4 |
| Total | 9,195 | 727 | 50,638 | 69.7 ± 7.7 | 0.058 | 2,296.3 | 2,323.4 | 2.18 | 2,964 | 1,552 | 52.4 | 6,890 | 74.9 |
The number of tag SNPs identified on the basis of the pairwise tagging method using all the SNPs on the chromosome.
The percentage of pairwise tag SNPs of all the SNPs on the chromosome.
TABLE 2.
Genomewide summary of haplotype blocks
| Summary | 2-SNP blocks | 3-SNP blocks | 4-SNP blocks | 5-SNP blocks | >5-SNP blocks | All blocks >2 SNPs |
|---|---|---|---|---|---|---|
| No. of blocks | 1068 | 310 | 217 | 118 | 82 | 727 |
| Mean block length (kb) | 2.0 (0.005–19.9) | 4.0 (0.058–29.4) | 114.3 (0.113–2296.3) | 153.8 (0.186–1502.3) | 78.6 (0.259–995.7) | 69.7 (0.058–2296.3) |
| Mean no. of haplotypes observed | 2.57 (2–3) | 2.87 (2–4) | 3.2 (2–5) | 3.54 (2–7) | 3.49 (2–7) | 3.15 (2–7) |
| Mean no. of haplotypes making 80% of total | 1.95 (1–3) | 2.08 (1–3) | 2.23 (1–4) | 2.4 (1–4) | 2.5 (1–5) | 2.22 (1–5) |
| Mean haplotype diversity | 0.47 (0.1–0.67) | 0.5 (0.1–0.74) | 0.54 (0.11–0.77) | 0.56 (0.17–0.77) | 0.59 (0.28–0.82) | 0.53 (0.1–0.82) |
| Mean no. of tag SNPs | 1.57 (1–2) | 1.87 (1–3) | 2.2 (1–4) | 2.51 (1–5) | 2.44 (1–5) | 2.13 (1–5) |
| % tag SNPs | 78.32 | 62.26 | 54.94 | 50.17 | 34.72 | 52.36 |
| Mean D′ within blocks | 0.997 ± 0.0002 (0.935–1) | 0.997 ± 0.0004 (0.963–1) | 0.996 ± 0.0005 (0.962–1) | 0.992 ± 0.0011 (0.946–1) | 0.994 ± 0.0011 (0.946–1) | 0.995 ± 0.0003 (0.946–1) |
| Mean r2 within blocks | 0.651 ± 0.0111 (0.022–1) | 0.69 ± 0.0158 (0.095–1) | 0.652 ± 0.0178 (0.148–1) | 0.656 ± 0.0218 (0.21–1) | 0.72 ± 0.0224 (0.24–1) | 0.676 ± 0.0096 (0.095–1) |
Ranges are shown in parentheses.
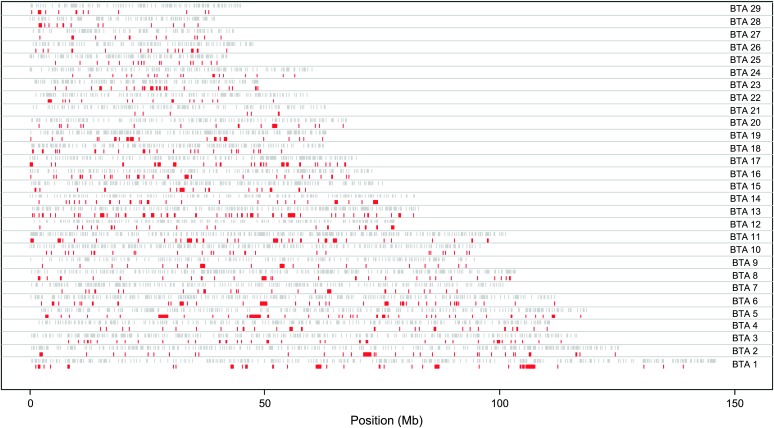
Haplotype-block maps of all the autosomes are presented in supplemental Figure S1 at http://www.genetics.org/supplemental/ in the form of an LD matrix heat map, in which all haplotype blocks identified in this analysis are shown in dark shading. Electronic copies of higher-resolution images of the haplotype-block maps can be obtained from the corresponding author. As an example, the haplotype-block map of a portion of chromosome 6 is presented in Figure 2. The locations of the 727 blocks made up of three or more adjacent SNPs are presented graphically on an actual megabase scale in Figure 3. Perusal of supplemental Figure S1 and Figure 3 indicates that most of these blocks exist at regions of high SNP density and that possibly the increased SNP density has allowed these blocks to be identified. There were 341 blocks in which gene names for at least two SNPs could be assigned. SNPs within blocks were compared for their gene names and it was found that in 72% of these 341 blocks, SNPs within a block occur in a single gene. Names of genes predicted to contain SNPs are given in supplemental Table S1 at http://www.genetics.org/supplemental/. It can also be noted in supplemental Table S1 that there are many regions where SNPs are in close proximity but do not form haplotype blocks.
Figure 2.—

Haplotype block map of a portion of BTA6 (89.5–111.76 Mb) in the form of a heat map of confidence bounds of D′. This map was prepared by Haploview software. Dark shading indicates strong LD, light shading is uninformative, and open areas suggest strong evidence of historical recombination. The haplotype block maps of all autosomes are presented in supplemental Figure S1 at http://www.genetics.org/supplemental/.
Figure 3.—
Haplotype blocks comprising three or more SNPs plotted to actual scale in red. Gray ticks indicate the positions of the SNPs analyzed.
The number of common haplotypes within a block as defined by haplotypes composing ≥80% of all haplotypes in a block, in the sample of 1000 bulls, ranges from 1 to 5 (mean 2.22). This represents limited haplotype diversity within a block, which is also indicated by an overall haplotype diversity of 0.53 for all haplotype blocks (Table 2). Haplotype diversity in the individual blocks is given in supplemental Table S2 at http://www.genetics.org/supplemental/.
The mean D′-values between SNPs within haplotype blocks are close to one for all the categories of blocks (Table 2). This is expected as per the stringent definition of haplotype blocks. Overall mean r2-values vary from 0.65 to 0.72 for the blocks comprising different numbers of SNPs. The mean D′- and r2-values within individual blocks are given in supplemental Table S2 at http://www.genetics.org/supplemental/. In contrast to average D′ within blocks, there is substantial variation in the mean r2-values of individual haplotype blocks and there are many blocks with a low mean r2 (supplemental Table S2). This may emphasize the importance of identifying tag SNPs with haplotype blocks.
The htSNPs identified for each block are presented in supplemental Table S1 at http://www.genetics.org/supplemental/ and are summarized in supplemental Table S2 at http://www.genetics.org/supplemental/ and in Table 1. A total of 1552 htSNPs were identified in the 727 blocks comprising ≥3 SNPs. This number represents 52.4% of all SNPs in these blocks. From the total length of the haplotype blocks and the number of htSNPs in the blocks composed of ≥3 SNPs, it can be estimated that on an average 1 SNP would be required each 33 kb in these blocks for association mapping. If only blocks comprising ≥4 SNPs are considered, on average 1 SNP would be required for each 50 kb in these blocks. However, there is considerable variation in LD and in the proportion of htSNPs in individual blocks, as shown in supplemental Table S2.
As mentioned in materials and methods, htSNPs, selected on a block-by-block basis, may not be the most parsimonious set of tag SNPs. Hence the second approach was used to identify tag SNPs on the basis of pairwise tagging (r2 ≥ 0.8) of all SNPs. The number of tag SNPs identified by this approach for each chromosome is also presented in Table 1. The genomewide percentage of tag SNPs identified was 74.9% and varies from 69.0% for BTA13 to 85.1% for BTA21 (Table 1). The rest of the SNPs in this data set are redundant for the purpose of association mapping.
Multiallelic D′ estimates were also computed between adjacent blocks, considering each block as one multiallelic locus. The mean of these interblock D′-values is 0.39. There was no relationship between interblock D′ and distance between blocks, for any of the chromosomes (data not shown).
DISCUSSION
This is the first extensive study defining haplotype blocks and haplotype diversity in the bovine genome. We have also identified a set of tag SNPs for these regions, which will be useful for further fine-mapping studies across the Holstein–Friesian population. The identified haplotype blocks cover only 2.18% of the total length of the autosomes. If the 2-SNP blocks are included, then coverage increases only to 2.27%. It appears that in a reasonable proportion of the 727 blocks comprising three or more SNPs, the SNPs are located within a particular gene and hence are relatively close to each other. This study also identified a number of genes/regions where SNPs are located very close to each other and are not present in haplotype blocks. These regions provide evidence of historical recombination. The SNPs in most of the regions (∼98%) are present as singletons showing no significant LD with adjacent SNPs.
The mean coverage of haplotype blocks defined as in this article has been reported to be 67–87% within the human ENCODE regions, with block sizes varying from 7.3 to 16.3 kb in different populations (International HapMap Consortium 2005). The far higher proportionate coverage in humans is due to the almost 1000-fold difference in SNP density: one SNP per 279 bp in the human ENCODE data compared with one SNP per 252 kb in the present data set. The substantially larger block size in cattle indicates substantially greater LD in cattle than in humans. However, many of the smaller blocks observed in the present study may be terminated by the reduced availability of SNP density in the adjacent region and may not represent the actual boundary of the block. Longer and overlapping blocks are expected to be identified in cattle with increased marker density.
The SNP density in humans was found to affect the number and size of the blocks (Ke et al. 2004). The effect of SNP density in the present study was tested on the number and size of blocks by randomly dropping 25 and 50% of the SNPs on one chromosome (BTA6) and this process was replicated 10 times. The results of different replicates were variable. On an average there was a decline in the number and size of haplotype blocks with reduced marker density. However, since the haplotype blocks constructed cover only 2.2% of the genome, the precise effect of marker density on block size could not be evaluated with the present marker density.
Smaller haplotype blocks ∼10 kb long were reported in dogs, on the basis of an across-breed analysis of 10 regions (Lindblad-Toh et al. 2005). To more fully understand the genome structure within a breed that has been under selection for the last 100 years, comparisons of haplotype structures with other breeds of bovidae are required.
A previous LD analysis of 220 SNPs on BTA6 (Khatkar et al. 2006a) indicated that long-range LD is extensive in cattle as compared to humans (Tapper et al. 2005). The apparent contradictory conclusion from the present study, namely that haplotype blocks cover only a small portion of the genome, is due to the relatively sparse coverage provided by even 9195 SNPs; i.e., there are substantial gaps in the map for across-population high-resolution association mapping with the present marker density. Therefore data on many more SNPs are required for identifying all haplotype blocks and hence for estimating the exact number of informative tag SNPs required to capture quantitative trait nucleotides using genomewide association mapping. Nevertheless, the present study is a first step toward a complete haplotype-block map of the bovine genome. More than 1 million SNPs were used to identify haplotype blocks in the human genome in the HapMap project (Hinds et al. 2005; International HapMap Consortium 2005), and it has been suggested that SNPs typed every 5–10 kb across the genome should be able to capture nearly all common variation in the human genome. However, Pe'er et al. (2006) and Taniguchi et al. (2006) argued that the extent of LD in the present HapMap data (phase I) may be inflated due to use of the public SNPs that have been discovered mostly on the basis of sequencing of a limited number of samples, causing an oversampling of specific haplotypes. Phase II of the HapMap project (http://www.hapmap.org) plans to genotype >3 million SNPs on 269 samples and is likely to give less-biased estimates of the extent of LD in the human genome (Pe'er et al. 2006). The gold standard would be to identify most variants in the genome or within a region of interest and select a subset of tag SNPs from that set.
From the present analysis, it is suggested that on average one tag SNP would be required to be typed for each 30–50 kb for association and fine mapping. Assuming at least a similar density would be required for the blocks still to be discovered in the remainder of the genome, then it can be estimated that ∼75,000–100,000 tag SNPs would be required for the entire bovine genome for genomewide association mapping studies. To identify such a set of SNPs, it may require genotyping ∼200,000–250,000 SNPs.
Such high-density SNP panels required for identification of genomewide haplotype blocks and tag SNPs are not practical at present in livestock species; however, they may be possible in the near future. In the meantime, it may be more practical to use the spread of SNPs on a linkage disequilibrium unit (LDU) scale on a metric LD map that takes account of variation in the extent of LD over the genome. An LD map has distances in LDUs and describes regions of high and low LD over the chromosome (Tapper et al. 2005). An LD map can be constructed with comparatively lower marker density (Khatkar et al. 2006a). However, it would still be possible to analyze haplotype block structure within candidate genes to understand the effect of different haplotype variants present in the candidate regions for fine mapping. Many haplotype blocks identified in this study exist within candidate genes. Given that the SNPs used in this study were deliberately biased toward coding regions, it is likely that a larger proportion of noncoding blocks will be discovered when higher-density scans can be conducted. However, in the short term, having knowledge of LD within important candidate genes is a distinct advantage.
The haplotype block map in this study was derived from 9195 SNPs positioned via the Btau 3.1 sequence assembly, which may have some imperfections. A detailed comparison of the Btau3.1 assembly map with individual public maps used as the basis for the Btau3.1 assembly (M. Hobbs, unpublished results) indicates that substantial areas of the Btau3.1 assembly will not be substantially altered in subsequent releases. For much of the genome, therefore, the Btau3.1 assembly provides a robust framework for positioning of SNP markers. To the extent that the SNP locations in the doubtful regions may be incorrect, the most likely effect is inaccurate estimation of the size of the haplotype blocks in those regions. When improved locations become available for doubtful regions, additional haplotype analyses can be readily performed.
We have described a first-generation haplotype-block map of the bovine genome. The haplotype blocks constructed from the present medium-density marker panel provide only a very limited coverage of the genome but nevertheless they are a random representative sample of the entire genome. This analysis identified a number of regions on the bovine genome where there is very limited or no evidence of historical recombination in this population. On average, these blocks are 5–10 times larger than similar haplotype blocks described in the human genome using equivalent procedures. These blocks provide useful information about the structure of LD in these regions. It seems that on average one tag SNP would be required to be typed for each 30–50 kb for association and fine mapping. Selection of tag SNPs is important for representation of variability within blocks. These results suggest that a higher density of SNPs would be required than undertaken in this study for construction of a complete haplotype-block map of the bovine genome and identification of tag SNPs for whole-genome populationwide LD studies in dairy cattle.
Acknowledgments
We thank Genetics Australia for semen samples and the Australian Dairy Herd Improvement Scheme for pedigree data. This research is supported by the Cooperative Research Centre for Innovative Dairy Products, Victoria, Australia.
References
- Barrett, J. C., B. Fry, J. Maller and M. J. Daly, 2005. Haploview: analysis and visualization of LD and haplotype maps. Bioinformatics 21 263–265. [DOI] [PubMed] [Google Scholar]
- Cardon, L. R., and G. R. Abecasis, 2003. Using haplotype blocks to map human complex trait loci. Trends Genet. 19 135–140. [DOI] [PubMed] [Google Scholar]
- Cohen, M., M. Reichenstein, A. Everts-van der Wind, J. Heon-Lee, M. Shani et al., 2004. Cloning and characterization of FAM13A1—a gene near a milk protein QTL on BTA6: evidence for population-wide linkage disequilibrium in Israeli Holsteins. Genomics 84 374–383. [DOI] [PubMed] [Google Scholar]
- Craig, D. W., and D. A. Stephan, 2005. Applications of whole-genome high-density SNP genotyping. Expert Rev. Mol. Diagn. 5 159–170. [DOI] [PubMed] [Google Scholar]
- Daly, M. J., J. D. Rioux, S. F. Schaffner, T. J. Hudson and E. S. Lander, 2001. High-resolution haplotype structure in the human genome. Nat. Genet. 29 229–232. [DOI] [PubMed] [Google Scholar]
- Dawson, E., G. R. Abecasis, S. Bumpstead, Y. Chen, S. Hunt et al., 2002. A first-generation linkage disequilibrium map of human chromosome 22. Nature 418 544–548. [DOI] [PubMed] [Google Scholar]
- de Bakker, P. I., R. Yelensky, I. Pe'er, S. B. Gabriel, M. J. Daly et al., 2005. Efficiency and power in genetic association studies. Nat. Genet. 37 1217–1223. [DOI] [PubMed] [Google Scholar]
- De La Vega, F. M., H. Isaac, A. Collins, C. R. Scafe, B. V. Halldorsson et al., 2005. The linkage disequilibrium maps of three human chromosomes across four populations reflect their demographic history and a common underlying recombination pattern. Genome Res. 15 454–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farnir, F., W. Coppieters, J. J. Arranz, P. Berzi, N. Cambisano et al., 2000. Extensive genome-wide linkage disequilibrium in cattle. Genome Res. 10 220–227. [DOI] [PubMed] [Google Scholar]
- Gabriel, S. B., S. F. Schaffner, H. Nguyen, J. M. Moore, J. Roy et al., 2002. The structure of haplotype blocks in the human genome. Science 296 2225–2229. [DOI] [PubMed] [Google Scholar]
- Grosse, W. M., S. M. Kappes, W. W. Laegreid, J. W. Keele, C. G. Chitko-McKown et al., 1999. Single nucleotide polymorphism (SNP) discovery and linkage mapping of bovine cytokine genes. Mamm. Genome 10 1062–1069. [DOI] [PubMed] [Google Scholar]
- Gunderson, K. L., F. J. Steemers, G. Lee, L. G. Mendoza and M. S. Chee, 2005. A genome-wide scalable SNP genotyping assay using microarray technology. Nat. Genet. 37 549–554. [DOI] [PubMed] [Google Scholar]
- Hardenbol, P., J. Baner, M. Jain, M. Nilsson, E. A. Namsaraev et al., 2003. Multiplexed genotyping with sequence-tagged molecular inversion probes. Nat. Biotechnol. 21 673–678. [DOI] [PubMed] [Google Scholar]
- Hardenbol, P., F. Yu, J. Belmont, J. Mackenzie, C. Bruckner et al., 2005. Highly multiplexed molecular inversion probe genotyping: over 10,000 targeted SNPs genotyped in a single tube assay. Genome Res. 15 269–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawken, R. J., W. C. Barris, S. M. McWilliam and B. P. Dalrymple, 2004. An interactive bovine in silico SNP database (IBISS). Mamm. Genome 15 819–827. [DOI] [PubMed] [Google Scholar]
- Hawken, R. J., J. A. Cavanagh, J. R. Meadows, M. S. Khatkar, Y. Husaini et al., 2006. Technical note: whole-genome amplification of DNA extracted from cattle semen samples. J. Dairy Sci. 89 2217–2221. [DOI] [PubMed] [Google Scholar]
- Heaton, M. P., W. W. Laegreid, C. W. Beattie, T. P. Smith and S. M. Kappes, 1999. Identification and genetic mapping of bovine chemokine genes expressed in epithelial cells. Mamm. Genome 10 128–133. [DOI] [PubMed] [Google Scholar]
- Hedrick, P. W., 1987. Gametic disequilibrium measures: proceed with caution. Genetics 117 331–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyen, D. W., J. E. Beever, Y. Da, R. E. Evert, C. Green et al., 1997. Exclusion probabilities of 22 bovine microsatellite markers in fluorescent multiplexes for semiautomated parentage testing. Anim. Genet. 28 21–27. [DOI] [PubMed] [Google Scholar]
- Hinds, D. A., L. L. Stuve, G. B. Nilsen, E. Halperin, E. Eskin et al., 2005. Whole-genome patterns of common DNA variation in three human populations. Science 307 1072–1079. [DOI] [PubMed] [Google Scholar]
- Hirschhorn, J. N., and M. J. Daly, 2005. Genome-wide association studies for common diseases and complex traits. Nat. Rev. Genet. 6 95–108. [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium, 2005. A haplotype map of the human genome. Nature 437 1299–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgenson, E., and J. S. Witte, 2006. A gene-centric approach to genome-wide association studies. Nat. Rev. Genet. 7 885–891. [DOI] [PubMed] [Google Scholar]
- Ke, X., S. Hunt, W. Tapper, R. Lawrence, G. Stavrides et al., 2004. The impact of SNP density on fine-scale patterns of linkage disequilibrium. Hum. Mol. Genet. 13 577–588. [DOI] [PubMed] [Google Scholar]
- Kent, W. J., 2002. BLAT—the BLAST-like alignment tool. Genome Res. 12 656–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khatkar, M. S., P. C. Thomson, I. Tammen and H. W. Raadsma, 2004. Quantitative trait loci mapping in dairy cattle: review and meta-analysis. Genet. Sel. Evol. 36 163–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khatkar, M. S., A. Collins, J. A. Cavanagh, R. J. Hawken, M. Hobbs et al., 2006. a A first-generation metric linkage disequilibrium map of bovine chromosome 6. Genetics 174 79–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khatkar, M. S., P. C. Thomson, I. Tammen, J. A. Cavanagh, F. W. Nicholas et al., 2006. b Linkage disequilibrium on chromosome 6 in Australian Holstein-Friesian cattle. Genet. Sel. Evol. 38 463–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindblad-Toh, K., C. M. Wade, T. S. Mikkelsen, E. K. Karlsson, D. B. Jaffe et al., 2005. Genome sequence, comparative analysis and haplotype structure of the domestic dog. Nature 438 803–819. [DOI] [PubMed] [Google Scholar]
- McRae, A. F., J. C. McEwan, K. G. Dodds, T. Wilson, A. M. Crawford et al., 2002. Linkage disequilibrium in domestic sheep. Genetics 160 1113–1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei, M., 1987. Molecular Evolutionary Genetics. Columbia University Press, New York.
- Nsengimana, J., P. Baret, C. S. Haley and P. M. Visscher, 2004. Linkage disequilibrium in the domesticated pig. Genetics 166 1395–1404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odani, M., A. Narita, T. Watanabe, K. Yokouchi, Y. Sugimoto et al., 2006. Genome-wide linkage disequilibrium in two Japanese beef cattle breeds. Anim. Genet. 37 139–144. [DOI] [PubMed] [Google Scholar]
- Olsen, H. G., D. I. Vage, S. Lien and H. Klungland, 2000. A DNA polymorphism in the bovine c-kit gene. Anim. Genet. 31 71. [DOI] [PubMed] [Google Scholar]
- Olsen, H. G., S. Lien, M. Gautier, H. Nilsen, A. Roseth et al., 2005. Mapping of a milk production quantitative trait locus to a 420-kb region on bovine chromosome 6. Genetics 169 275–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pe'er, I., Y. R. Chretien, P. I. de Bakker, J. C. Barrett, M. J. Daly et al., 2006. Biases and reconciliation in estimates of linkage disequilibrium in the human genome. Am. J. Hum. Genet. 78 588–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips, M. S., R. Lawrence, R. Sachidanandam, A. P. Morris, D. J. Balding et al., 2003. Chromosome-wide distribution of haplotype blocks and the role of recombination hot spots. Nat. Genet. 33 382–387. [DOI] [PubMed] [Google Scholar]
- Prinzenberg, E. M., I. Krause and G. Erhardt, 1999. SSCP analysis at the bovine CSN3 locus discriminates six alleles corresponding to known protein variants (A, B, C, E, F, G) and three new DNA polymorphisms (H, I, A1). Anim. Biotechnol. 10 49–62. [DOI] [PubMed] [Google Scholar]
- Qin, Z. S., T. Niu and J. S. Liu, 2002. Partition-ligation-expectation-maximization algorithm for haplotype inference with single-nucleotide polymorphisms. Am. J. Hum. Genet. 71 1242–1247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Service, S., J. Deyoung, M. Karayiorgou, J. L. Roos, H. Pretorious et al., 2006. Magnitude and distribution of linkage disequilibrium in population isolates and implications for genome-wide association studies. Nat. Genet. 38 556–560. [DOI] [PubMed] [Google Scholar]
- Taniguchi, H., C. E. Lowe, J. D. Cooper, D. J. Smyth, R. Bailey et al., 2006. Discovery, linkage disequilibrium and association analyses of polymorphisms of the immune complement inhibitor, decay-accelerating factor gene (DAF/CD55) in type 1 diabetes. BMC Genet. 7 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tapper, W., A. Collins, J. Gibson, N. Maniatis, S. Ennis et al., 2005. A map of the human genome in linkage disequilibrium units. Proc. Natl. Acad. Sci. USA 102 11835–11839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenesa, A., S. A. Knott, D. Ward, D. Smith, J. L. Williams et al., 2003. Estimation of linkage disequilibrium in a sample of the United Kingdom dairy cattle population using unphased genotypes. J. Anim. Sci. 81 617–623. [DOI] [PubMed] [Google Scholar]
- Tozaki, T., K. I. Hirota, T. Hasegawa, M. Tomita and M. Kurosawa, 2005. Prospects for whole genome linkage disequilibrium mapping in thoroughbreds. Gene 346 127–132. [DOI] [PubMed] [Google Scholar]
- Twells, R. C., C. A. Mein, M. S. Phillips, J. F. Hess, R. Veijola et al., 2003. Haplotype structure, LD blocks, and uneven recombination within the LRP5 gene. Genome Res. 13 845–855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallejo, R. L., Y. L. Li, G. W. Rogers and M. S. Ashwell, 2003. Genetic diversity and background linkage disequilibrium in the North American Holstein cattle population. J. Dairy Sci. 86 4137–4147. [DOI] [PubMed] [Google Scholar]
- Wall, J. D., and J. K. Pritchard, 2003. a Assessing the performance of the haplotype block model of linkage disequilibrium. Am. J. Hum. Genet. 73 502–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wall, J. D., and J. K. Pritchard, 2003. b Haplotype blocks and linkage disequilibrium in the human genome. Nat. Rev. Genet. 4 587–597. [DOI] [PubMed] [Google Scholar]
- Zhang, K., and L. Jin, 2003. HaploBlockFinder: haplotype block analyses. Bioinformatics 19 1300–1301. [DOI] [PubMed] [Google Scholar]
- Zhang, K., Z. Qin, T. Chen, J. S. Liu, M. S. Waterman et al., 2005. HapBlock: haplotype block partitioning and tag SNP selection software using a set of dynamic programming algorithms. Bioinformatics 21 131–134. [DOI] [PubMed] [Google Scholar]