Genetic influences on peripheral blood cell counts: a study in baboons

Abstract

Interperson differences in peripheral blood cell counts in healthy individuals result from genetic and environmental influences. We used multivariate genetic analyses to assess the relative impact of genes and environment on baseline blood cell counts and indices using a pedigreed colony of baboons, an animal with well-documented analogies to human blood physiology. After accounting for age, sex, and weight, we found that genetic influences explain a significant proportion of the remaining variability, ranging from a low of 13.7% for mean corpuscular hemoglobin concentration (MCHC) to a high of 72.4% for red blood cell (RBC) number. Genes influence 38.5% of the variation in baseline white blood cell (WBC) count, a characteristic that correlates with mortality in both the general human population and clinically defined subgroups such as individuals with sickle-cell disease. We examined the interaction between pairs of traits and identified those that share common genetic influences (pleiotropy). We unexpectedly observed that the same gene or group of genes influences both WBC count and mean platelet volume (MPV). We anticipate that this approach will ultimately lead to discovery of novel insights into the biology of related traits, and ultimately identify important genes that affect hematopoiesis.

Introduction

Peripheral blood cell counts represent a complex clinical phenotype—the end result of interactions between a multitude of genetic and environmental factors. Increasingly, baseline blood cell count phenotypes are emerging as important markers of risk for disease and disease severity. Examples include the correlation of steady-state white blood cell (WBC) count with mortality in the general population,^1-6 and with disease severity in patients with sickle-cell anemia (SS).^7-10 Efforts to dissect the genetic underpinnings of these complex traits have the potential to greatly enhance our understanding of hematopoiesis, pathophysiology, and disease modifier genes.

The primary genetic questions about quantitative traits such as peripheral blood cell counts (ie, traits measured on continuous rather than dichotomous scales) are formulated in terms of variation in the traits.¹¹ The amount of variation is expressed as the variance, or in statistical terms, the mean of the squared deviations from the population mean for the trait. The fundamental objective of statistical genetic analyses of any quantitative trait is to partition the total variance for that trait (the phenotype) into 2 components: those due to the effects of genes (the genetic component), and those influenced by environmental factors (the environmental component). In this study, we examine the patterns of normal quantitative variation in blood cell counts in a pedigreed colony of baboons, a nonhuman primate with well-documented analogies to human blood physiology,^12-15 in order to partition the blood cell phenotypes into their genetic and environmental components. Our specific aims are to quantify the genetic and environmental components, and determine which genetic effects on one cell count may also account for variation in other cell counts (pleiotropy).

Materials and methods

Subjects

We analyzed the blood counts and indices of 600 individual healthy pedigreed baboons (Papio hamadryas)^16,17 to quantify the range of values observed in this normal population. Housed at the Southwest National Primate Research Center, located at the Southwest Foundation for Biomedical Research (San Antonio, TX), this sample consisted mainly of olive baboons (Papio hamadryas anubis), yellow baboons (Papio hamadryas cynocephalus), and their hybrids, and initially included 415 females and 185 males, ranging in age from 5.5 to 30 years. While strict genetic management is used to control inbreeding, all nonfounder animals in this study were the results of matings that were random with respect to phenotypes analyzed here. The subjects were distributed among 11 pedigrees with 67 to 171 members each. Within these pedigrees there were 4714 relative pairs (Table 1).

Table 1.

Pedigreed baboons: relative pairs with data

Relative pair classes	N
Parent-offspring	177
Sibling	210
Grandparent-grandchild	20
Avuncular	46
Half-sibling	3441
Half-avuncular	648
First cousin	3
Half first cousin	96
Half first cousin, once removed	21
Half-sibling and first cousin	1
Half-sibling and half first cousin	40
Half-sibling and half avuncular	6
Double half avuncular	5

Since birth or arrival at the colony, all animals had been housed out of doors in social group cages and maintained on monkey chow diets to which they had ad libitum access. Animal care personnel and staff veterinarians provided daily maintenance and regular, urgent, and emergent health care to all animals in accordance with the Guide for the Care and Use of Laboratory Animals.¹⁸ All procedures related to their treatment during the conduct of this study were approved by the Institutional Animal Care and Use Committee in accordance with the established guidelines.¹⁸

Hematologic studies

After sedation with intramuscular ketamine and intravenous xylazine hydrochloride, atropine, acepromazine, and ketamine to assure relaxation, blood samples were obtained by femoral venipuncture. Blood was collected in EDTA (ethylenediaminetetraacetic acid), stored on ice, and analyzed within 4 hours using a Coulter JT (Beckman Coulter, Fullerton, CA), conditions that maintained the stability of the measured parameters. We measured hematocrit (HCT), hemoglobin (Hb), red blood cell (RBC) count, mean corpuscular volume (MCV), red cell distribution width (RDW), mean corpuscular hemoglobin (MCH), mean corpuscular hemoglobin concentration (MCHC), white blood cell (WBC) count, platelet (Plt) count, and mean platelet volume (MPV). Details regarding protocols for these assays, and measurements are reported elsewhere.¹⁹

Statistical analysis

Statistical genetic analyses were conducted by means of a maximum likelihood–based variance decomposition approach implemented in the computer package SOLAR (Sequential Oligogenic Linkage Analysis Routines; Southwest Foundation for Biomedical Research, San Antonio, TX).²⁰ This approach, which was developed following methodology originally proposed by Hopper and Mathews²¹ and Lange and Boehnke,²² has been described in detail elsewhere.²³

In short, we used this approach to partition the phenotypic variance (σ²_P) into components corresponding to the additive genetic (σ²_G) and nongenetic (ie, environmental) (σ²_E) effects. Because these components are additive, such that σ²_P =σ²_G +σ²_E, we estimated the heritability, or proportion of the phenotypic variance attributable to additive genetic effects, as h² =σ²_G /σ²_P. We estimated the proportion of the phenotypic variance attributable to nongenetic factors as e² = 1 – h². When covariate effects are included in the maximum likelihood model, the h² and e² estimates are obtained as proportions of the residual phenotypic variance in the trait (ie, that remaining after the accounting for the effects of the covariates) rather than as proportions the total phenotypic variance. Multiplication of h² by the proportion of the total variance not explained by covariates (ie, the quantity 1 – c², where “c²” refers to the proportion of the total variance attributable to covariate effects) yields a heritability value that is rescaled to the total phenotypic variance. We also simultaneously estimated the mean effects of sex, sex-specific age, and sex-specific age,² and body weight on each of the hematological phenotypes. We model the phenotype of an individual (y_i) as linear function of the population mean of the trait (μ), the covariates (x) and their regression coefficients (β), plus the additive genetic values (g) and random environmental deviations (e), such that y_i = μ + β₁ x₁+ β₂ x₂ + β_nx_n + g + e.

Using extensions to univariate genetic analysis that encompass the multivariate state,^21,22,24 we followed an approach presented in detail previously²⁵ to similarly model multivariate phenotypes in these baboons (ie, to simultaneously analyze measurements on pairs of traits in individuals within each pedigree). By maximizing these multivariate models, we obtained estimates of 2 additional parameters: the additive genetic correlation, ρ_G, and the environmental correlation, ρ_E, between trait pairs. Respectively, these correlations are estimates of the shared additive effects of genes (ie, pleiotropy) and shared environmental (ie, unmeasured, nongenetic) factors on the variance in a trait. Genetic correlations with values equal to (or not significantly different from) 1 or –1 are interpreted as evidence for complete pleiotropy (ie, where the additive genetic contributions to the variance in the 2 correlated traits are due entirely to the effects of the same gene or genes). Genetic correlations that are significantly different from both 0 and 1 or – 1 are evidence of incomplete pleiotropy (ie, where some but not all of the additive genetic effects on a pair of traits are due to the same gene or genes). The genetic and environmental components of the phenotypic correlation matrix are additive, like those of the corresponding variance-covariance matrix, so we could use the maximum likelihood estimates of the additive genetic and environmental correlations, to obtain the total phenotypic correlation between 2 traits, ρ_P, as .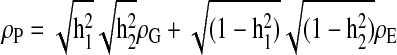

Using this approach as implemented in SOLAR,²⁰ we conducted a series of bivariate quantitative genetic analysis of all hematologic trait pairs.

Significance of the maximum likelihood estimates for heritability and other parameters was assessed by means of likelihood ratio tests.²⁶ The maximum likelihood for the general model in which all parameters were estimated was compared to that for restricted models in which the value of the parameter to be tested was held constant at some value (usually 0). For tests of parameters like h², for which a fixed value of 0 in a restricted model is at a boundary of the parameter space, twice the difference in the natural logarithm (ln) of the likelihoods of the 2 models compared is distributed asymptotically approximately as a 0.5:0.5 mixture of χ² with a point mass at 0. For tests of covariates, for which 0 is not a boundary value, this statistic is distributed asymptotically approximately as a χ² variate.²¹ Degrees of freedom can be obtained as the difference in the number of estimated parameters in the 2 models.²¹ However, in tests of parameters like h², whose values may be fixed at a boundary of their parameter space in the null model, the appropriate significance level is obtained by halving the P value.²⁴

Results

Inheritance of the individual peripheral blood cell counts

In these healthy pedigreed baboons, who live in a highly controlled environment designed to maximize the detection of genetic signals, a significant fraction of the phenotypic variance of all of the peripheral blood cell counts and indices is under genetic control (Table 2). After accounting for the individual and combined effects of age, sex, and weight, the additive effects of genes (h²) account for a low of 13.7% of the observed variability in MCHC, to a high of 72.4% of the variability of RBC counts.

Table 2.

Quantitative genetics of hematologic traits in pedigreed baboons: maximum likelihood parameter estimates

	Traits
Parameter	Hb	Hct	RBC	MCV	RDW	MCH	MCHC	Plt	MPV	WBC
μ	12.57	37.74	4.81	78.31	12.89	26.03	32.81	269.20	8.53	12.03
σ	1.10	3.29	0.40	2.89	1.04	1.18	0.82	82.15	1.00	4.56
h2 residual*	0.638	0.487	0.724	0.526	0.477	0.408	0.137	0.313	0.513	0.385
β age	-0.10	-0.37	0.40	—	—	-0.05	—	—	—	0.34
β sex	—	—	—	—	0.13	—	0.40	48.89	0.48	—
β age × sex	0.07	0.32	0.04	—	—	—	—	—	—	-0.44
β age2	—	—	—	—	—	—	—	—	—	—
β age2 × sex	—	—	—	—	—	—	—	—	—	—
β weight	0.04	—	—	—	—	—	0.03	—	—	—
c2‡	0.080	0.049	0.019	0	0.004	0.046	0.025	0.061	0.041	0.027

μ indicates mean; σ, standard deviation; h², residual heritability; β, estimated mean effect of significant (P < .10) covariates; —, covariate not included in final genetic model for trait because mean effect was not significant (P > .10); c², proportion of total trait variance due to significant covariates.

^*P (h² = 0) < .01 for all traits except MCHC, where P (h² = 0) < .05.

Phenotypic correlations between the individual cell traits

Many of the cell counts and indices are correlated with others. As shown in Table 3, the erythrocyte traits are highly correlated, some positively (eg, Hct and Hb), and some negatively (eg, RBC counts and MCV). Platelet count and MPV are negatively correlated. WBC count and MPV are positively correlated; WBC count and Plt are negatively correlated.

Table 3.

Genetic, environmental, and phenotypic correlations between pairs of hematologic traits

Trait pairs	ρp	ρg	ρe
Hb, Hct	0.616	1.000 ± 0.081*	0.673 ± 0.084†
Hb, RBC	0.731	0.920 ± 0.288*	0.742 ± 0.098*
Hb, MCV	-0.178	-0.266 ± 0.205	0.571 ± 0.158*
Hb, RDW	-0.129	-0.221 ± 0.163	-0.050 ± 0.189
Hb, MCH	0.170	0.220 ± 0.181	0.621 ± 0.181
Hb, MCHC	0.659	0.916 ± 0.113*	0.250 ± 0.126
Hb, Plt	0.039	0.057 ± 0.220	-0.102 ± 0.159
Hb, MPV	0.068	0.096 ± 0.162	-0.003 ± 0.178
Hb, WBC	0.088	0.207 ± 0.202	-0.162 ± 0.179
Hct, RBC	0.759	0.957 ± 0.029*	0.719 ± 0.081*
Hct, MCV	-0.150	-0.290 ± 0.221	0.377 ± 0.129†
Hct, RDW	-0.031	-0.042 ± 0.199	-0.123 ± 0.147
Hct, MCH	0.164	0.270 ± 0.188	0.148 ± 0.136
Hct, MCHC	0.241	0.870 ± 0.145†	-0.189 ± 0.137
Hct, Plt	0.035	0.070 ± 0.233	-0.114 ± 0.124
Hct, MPV	0.098	0.171 ± 0.179	-0.037 ± 0.142
WBC, Hct	0.148	0.341 ± 0.212	-0.235 ± 0.146
RBC, MCV	-0.541	-0.693 ± 0.141*	0.215 ± 0.214
RBC, RDW	-0.003	-0.002 ± 0.167	-0.084 ± 0.201
RBC, MCH	-0.143	-0.182 ± 0.178	-0.054 ± 0.191
RBC, MCHC	0.613	0.786 ± 0.187*	-0.333 ± 0.207
RBC, Plt	-0.002	-0.001 ± 0.206	-0.093 ± 0.175
RBC, MPV	0.153	0.197 ± 0.153	-0.157 ± 0.211
RBC, WBC	0.132	0.327 ± 0.186	-0.352 ± 0.210
MCV, RDW	-0.315	-0.553 ± 0.177*	0.051 ± 0.139
MCV, MCH	0.514	0.907 ± 0.050*	0.699 ± 0.057*
MCV, MCHC	0.035	-0.027 ± 0.287	0.167 ± 0.101
MCV, Plt	0.126	0.217 ± 0.222	-0.190 ± 0.126
MCV, MPV	-0.181	-0.309 ± 0.180	0.244 ± 0.139
MCV, WBC	-0.116	-0.240 ± 0.236	0.015 ± 0.125
RDW, MCH	-0.382	-0.673 ± 0.183*	0.083 ± 0.146
RDW, MCHC	-0.322	-0.567 ± 0.217	0.057 ± 0.121
RDW, Plt	0.159	0.276 ± 0.235	0.009 ± 0.126
RDW, MPV	-0.071	-0.129 ± 0.179	0.059 ± 0.144
RDW, WBC	0.149	0.340 ± 0.231	-0.203 ± 0.154
MCH, MCHC	0.275	0.430 ± 0.232†	0.760 ± 0.054*
MCH, Plt	0.041	0.085 ± 0.258	-0.032 ± 0.118
MCH, MPV	-0.122	-0.269 ± 0.197	0.214 ± 0.136
MCH, WBC	-0.182	-0.405 ± 0.270	0.203 ± 0.132
MCHC, Plt	0.092	-0.104 ± 0.315	0.084 ± 0.095
MCHC, MPV	-0.002	-0.132 ± 0.240	0.113 ± 0.107
MCHC, WBC	-0.228	-0.508 ± 0.310	0.256 ± 0.107†
Plt, MPV	-0.305	-0.478 ± 0.181†	-0.346 ± 0.101†
Plt, WBC	-0.187	-0.447 ± 0.353	0.392 ± 0.109
MPV, WBC	0.476	1.000 ± 0.160*	-0.161 ± 0.108

_ρp indicates random phenotypic correlation calculated as described in “Statistical analysis”; _ρg, maximum likelihood estimate of additive genetic correlation; and _ρe, maximum likelihood estimate of random environmental correlation.

^*Significant at P < .05.

^†Marginally significant at .10 > P > .05.

Evidence that shared genes influence more than one trait

Maximum likelihood estimates of correlations between traits due to the effects of shared genes are shown in Table 3. We found significant (P < .05) shared genetic influence between many of the erythrocyte measures (Hb and Hct, RBC, and MCHC; Hct and RBC and MCHC; RBC and MCHC and MCV; MCV and MCH; and RDW and MCH and MCV); and a strong (47.8%) genetic dependency between Plt and MPV (P = .10).

We had not anticipated finding significant genetic influences shared between WBC count and MPV (P < .05). In fact, similar to what we found in the case of Hct and Hb, the genetic effects shared between WBC count and MPV is virtually 100% (ie, complete pleiotropy (ρ_G = 1).

Useful measures of the relative importance of genetic dependency between trait pairs are shown in Table 4. The square of the genetic correlation is an estimate of the proportion of the additive genetic influence shared between pairs. For example, 84.6% of the estimated heritability for Hb and RBC count is due to the effects of the same genes or group of genes. These genes account for 49.7% of the total variance in Hb, and 60.1% of the total variance in RBC counts. In the case of WBC count and MPV, shared genes account for 100% of the genetic influence, and are responsible for 37.5% of the variance in WBC count and 49.2% of the variance in MPV.

Table 4.

Magnitudes of pleiotropic effects on hematological traits in pedigreed baboons: proportions of additive genetic variance and total phenotypic variance in pairs of traits due to effects of the same gene or genes

Trait pair Trait 1, Trait 2	Additive genetic variance, both traits	Total phenotypic variance
		Trait 1	Trait 2
WBC, RBC	0.107	0.040	0.076
WBC, RDW	0.116	0.043	0.055
WBC, Hct	0.116	0.043	0.054
WBC, Hb	0.043	0.016	0.025
WBC, MCH	0.164	0.061	0.064
WBC, MCHC	0.258	0.097	0.034
WBC, MCV	0.058	0.022	0.030
WBC, MPV	1.000	0.375	0.492
WBC, Plt	0.200	0.075	0.059
RBC, RDW	∼0	0.000	0.000
RBC, Hct	0.916	0.651	0.426
RBC, Hb	0.846	0.601	0.497
RBC, MCH	0.033	0.023	0.013
RBC, MCHC	0.618	0.439	0.083
RBC, MCV	0.480	0.341	0.252
RBC, MPV	0.039	0.028	0.019
RBC, Plt	∼0	0.000	0.000
RDW, Hct	0.002	0.001	0.001
RDW, Hb	0.049	0.023	0.029
RDW, MCH	0.453	0.215	0.176
RDW, MCHC	0.321	0.153	0.043
RDW, MCV	0.306	0.145	0.161
RDW, MPV	0.017	0.008	0.008
RDW, Plt	0.076	0.036	0.022
Hct, Hb	1	0.466	0.587
Hct, MCH	0.072	0.034	0.028
Hct, MCHC	0.185	0.086	0.025
Hct, MCV	0.084	0.039	0.044
Hct, MPV	0.029	0.014	0.014
Hct, Plt	0.005	0.002	0.001
Hb, MCH	0.048	0.028	0.019
Hb, MCHC	0.839	0.492	0.112
Hb, MCV	0.071	0.042	0.037
Hb, MPV	0.009	0.005	0.004
Hb, Plt	0.003	0.002	0.001
MCH, MCHC	0.185	0.072	0.025
MCH, MCV	0.823	0.320	0.432
MCH, MPV	0.072	0.028	0.035
MCH, Plt	0.007	0.003	0.002
MCHC, MCV	0.001	0.000	0.001
MCHC, MPV	0.017	0.002	0.008
MCHC, Plt	0.099	0.013	0.029
MCV, MPV	0.095	0.050	0.047
MCV, Plt	0.047	0.025	0.014
MPV, Plt	0.228	0.112	0.067

Discussion

Most of what we know about the genetics of the peripheral blood counts and indices comes from the study of patients and experimental animals whose counts lie outside the normal range. Humans and animals with too many or too few cells that are too big or too small have long been the focus of attention of hematologists, and have established the pathophysiologic importance of a variety of genes that control phenotype in a Mendelian fashion. Some of these genes include those that encode or control globins, membrane proteins, growth factors, receptors, ion channels, and adhesion molecules. In much the same way, clinical investigators have discovered critical environmental (ie, noninherited) modulators of blood counts such as normal aging, maturation and growth, pregnancy, diet (iron, folate, cobalamin), hypoxia, bleeding, smoking, infection, inflammation, and exogenous growth factors and cytotoxic agents.

In this study, we shift focus from the classical clinical study of hematologically abnormal individuals to a statistical genetic methodology that analyzes the normal variation of cell counts in a healthy pedigreed population (ie, a population of individuals that were not ascertained on the basis of a disease state). Conceptually, this method is very similar to studies of healthy human twins. In twin studies, the genetic influence is estimated by comparing degrees of similarity between 2 types of relative pairs: monozygotic and dizygotic twins. Studies of more complex, multigenerational pedigrees such as ours make use of information from a much larger range of relative pairs comprising parents and offspring, grandparents and grandchildren, siblings, cousins, aunts/uncles, and nieces/nephews (the “avuncular” relationship), etc. Although not unique to nonhuman primates, the baboon pedigrees from which data for this study were obtained also include large numbers of pairs exhibiting half relationships (eg, half-sibling and half-avuncular pairs). Because it uses information from more relative classes, this strategy offers demonstrably greater statistical power to both detect genetic effects and, when combined with genotype data, efficiently localize quantitative trait loci to specific chromosomal regions.^27,28 This approach considers the peripheral blood count a complex phenotype that is controlled by multiple underlying genetic and environmental factors, and is designed to quantify the impact and relatedness of those factors. We studied the baboon because of its close analogies to the human, and the ability to minimize the number and impact of environmental factors on interindividual variation.

We found that in the baboon, the steady-state set points for the number and size of peripheral blood cells are under significant genetic control (Table 1). These results are extremely similar to findings in humans by investigators working with major twin registries in the United Kingdom and Australia,^29-31 and underscore the advantages of using such populations to discover genetic influences.

Our analyses further allowed us to examine the patterns of interrelatedness among these traits and, more specifically, to dissect out the genetic and random environmental components underlying these patterns. The positive phenotypic correlations between the various Hb, RBC count, and Hct pairings, and negative correlation of Hb, Hct, and RBC count with MCV are generally similar to the patterns of correlations observed between these traits in healthy human^30-32 and other mammalian³² populations, although they have not been examined in detail. Many of these pairs demonstrated significant genetic contribution to the relationships—consistent with the findings that emerged from the Australian twin registry study.³⁰ A similar inverse phenotypic relationship between Plt and MPV reported by Whitfield and Martin³⁰ and others^33-40 was also found in this baboon study, but other studies did not decompose the phenotypic covariance between platelet count and MPV into genetic and environmental components.

The positive phenotypic correlation that we found between WBC count and MPV has not been previously reported; and the observation of complete pleiotropy (ie, that all or most of the genetic effects on WBC count [responsible for 37% of the total phenotypic variance] and all of the genetic effects on MPV [49% of the total phenotypic variance] are due to the effects of the same gene or group of genes) is remarkable. Conceptually, the MPV resembles the MCV. Like the reticulocyte, the newly formed platelet is large, contains mRNA,⁴¹ and as an analogy—the increased number of reticulocytes in immune hemolytic anemia causes an elevated MCV, just as the high number of young platelets in idiopathic thrombocytopenic purpura elevates the MPV.⁴²

Genetic abnormalities may make red cells small (thalassemia) or large (stomatocytosis), but we do not know what genes are responsible for that portion of variation in MCV (or MPV) that is due to the effects of genes in the healthy population. It may well be that these genes have little or no overlap with the globin genes that so dramatically influence cell size in abnormal populations.

It is interesting to note that high MPV^43-45 and high WBC count^1-6 both correlate with heart disease and stroke risk in the healthy population. While these may represent 2 genetically independent risk markers, it is tempting to speculate that genes exerting pleiotropic effects on both traits underlie the risk. Perhaps the genetic correlation between WBC count and platelet volume in relatively healthy individuals is attributable to the effects of genes that influence steps in hematopoiesis common to megakaryocytes and white cells, or genes that allow more mature platelets and white cells to respond to or enhance inflammation. It is important to point out that we do not know how much of the heart disease/stroke risk is influenced by the genetic component of the variation in WBC count and MPV, and how much by environmental factors. Similarly, we know that patients with sickle-cell anemia and high severity have high WBC counts, but do not know whether the high WBC count is an “environmental” (ie, nongenetic) reaction to disease severity, or whether the patients with a genetic predisposition to having a high WBC count are more likely to have severe disease as an expression of the role white blood cells play in disease pathophysiology.

Multivariate statistical genetic analyses of the type reported here offer a means to identify pairs and, in some cases, networks of traits that are bound together by the shared effects of the same gene or group of genes. In many instances, the detected pleiotropic relationships will be entirely consonant with our current expectations regarding the phenotypes under study (eg, RBC count and hemoglobin-related measures). In other cases however, previously unappreciated relationships, such as that between WBC count and MPV in this study, may be revealed or suggested by these sorts of analyses. The pleiotropic relationships detected in this study suggest a rationale for subsequent multivariate statistical analyses in both this pedigreed animal population, and in human families. Such analyses not only offer potentially novel insights into the biology of related traits but, in comparison to analyses of single traits, they also provide substantially greater amounts of information and improved statistical power to detect, localize, and identify quantitative trait loci contributing to the pleiotropic effects. Our plans to combine the data presented in this paper with genotypic data we are developing, will allow us to map the quantitative trait loci underlying patterns of covariation among these phenotypes and identify positional candidate genes in this nonhuman primate model for human hematological variation.