Mixed model analysis of quantitative trait loci

Abstract

We develop a mixed model approach of quantitative trait locus (QTL) mapping for a hybrid population derived from the crosses of two or more distinguished outbred populations. Under the mixed model, we treat the mean allelic value of each source population as the fixed effect and the allelic deviations from the mean as random effects so that we can partition the total genetic variance into between- and within-population variances. Statistical inference of the QTL parameters is obtained by using the Bayesian method implemented by Markov chain Monte Carlo (MCMC). This unified QTL mapping algorithm treats the fixed and random model approaches as special cases of the general mixed model methodology. Utility and flexibility of the method are demonstrated by using a set of simulated data.

Studies of the genetic basis for population differentiation are usually performed by methods of quantitative trait loci (QTL) analysis in line crossing experiments (1), each population being treated as an inbred line. Unfortunately, most natural populations are not inbred. Developing inbred lines and then conducting QTL analysis are unrealistic for some organisms. A common practice is to select a single parent from each population to form a cross. This approach may be practical for plants, but is not applicable for most animals because of their low fertility. In addition, a single parent may not be a good representative of the population from which the parent is sampled. Results obtained from this single cross may not represent the actual population difference, but largely reflect the genetic sampling error. These problems can be solved by sampling multiple parents from each population. Unfortunately, an optimal statistical method has not been available for such a design. Haley et al. (2) developed a least-squares method to map QTL in crosses between segregating populations, assuming that alleles of QTL have fixed alternatively between populations. The least-squares method will not detect QTL that have similar allele frequencies in the two populations. This is primarily because information comes from mean differences between populations. Another obvious flaw of the least-squares method is that the within-population variances will not disappear simply because they are not included in the model; rather, they will be absorbed by the residual variance. A large residual variance will decrease the power of QTL detection.

In this study, we develop a mixed model framework that allows the partitioning of the total genetic variance into within- and between-population variances. We show that the mixed model approach provides a unified QTL mapping algorithm in which we can analyze data collected from any complicated mating designs.

Mixed Model

Throughout the study, the genetic parameters are defined exclusively in terms of allelic rather than genotypic values. We consider only a single locus in the description of the mixed model methodology, although multiple loci will be used in the simulation study. For simplicity, we consider two source populations only. Let us define the expectation and variance of the allelic values for population one by b₁ and σ₁², respectively, and the corresponding parameters for population two by b₂ and σ₂². For diploid organisms, both the mean and variance of the additive genetic values take twice the values of their allelic counterparts. The total additive genetic variance of the combined population in the current generation (before the cross) is σ_A² = σ₁² + σ₂² + (b₁ − b₂)².

Let ½n₁ and ½n₂ be the numbers of founders from populations one and two, respectively. Assume that a parent from one population has an equal chance to mate with any parents from the other population. The mating of the F₁s are completely arbitrary so that the alleles of the two original populations are well integrated into the hybrid population. We can take F₂ as our mapping population, but including advanced generations can be more efficient because alleles from different populations are better integrated. Unfortunately, such a mating design produces complex pedigrees that prevent the use of a simple statistical method. In the next section, we will introduce a Bayesian method for mapping QTL in complex pedigrees. Assume that there are N individuals in the mapping population. We define the effects of the paternal and maternal alleles of individual j by v_j^p and v_j^m, respectively, for j = 1, … , N. The phenotypic value of individual j can be described by the following linear model:

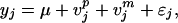1

where μ is the population mean (fixed effect) and ɛ_j is the residual error with a N(0, σ_ɛ²) distribution. Using the notation of Fernando and Grossman (3), we define v_p^p and v_p^m as the paternal and maternal alleles for the father of j so that v_j^p = z_j^pv_p^p + (1 − z_j^p)v_p^m, where z_j^p indicates the allelic inheritance of the paternal allele of the father. Similarly, define v_m^p and v_m^m as the paternal and maternal alleles of the mother and v_j^m = z_j^mv_m^p + (1 − z_j^m)v_m^m, where z_j^m indicates the allelic inheritance of the paternal allele of the mother. The above model can be rewritten as

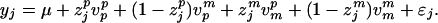2

We have now expressed the allelic values of the current generation as linear functions of the allelic values of their parents. The parental alleles can be further expressed as a linear function of the allelic values of their parents. With such a recursive process, each allele can be traced back to its origin in the two founder populations. Let us group the effects of the n = n₁ + n₂ founder alleles into an n × 1 vector named v. The elements of v are sorted by source population, the identification number (ID) of each founder within a source population and parental origin of each allele within a founder (paternal followed by maternal). Note that the IDs of founders are numbered from 1 to ½n. Consider a hybrid population originated from the crosses of 5 founders from population one and 3 founders from population two. In this case, n₁ = 10 and n₂ = 6, and vector v has n = 16 elements. The first 10 elements store the allelic values from population one and the last 6 elements store those from population two. If a founder has an ID of 4, we know that it comes from the first source population and the paternal and maternal alleles of this founder are stored as the 7th and 8th elements of v, respectively. In general, the two alleles of the ith founder are stored at elements 2i − 1 and 2i of v, respectively. Since each allele of individual j can be traced back to one of the founder alleles, we can express the phenotypic value of j by a linear model,

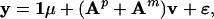3

where A^p or A^m is an N × n indicator matrix connecting the paternal or maternal alleles of all individuals to the founders. Each row of A^p or A^m contains one and only one nonzero (unity) element. The positions of the nonzero elements in the matrices correspond to the founder alleles that have been passed to the mapping individual through their parents.

Let us define v_i as the ith element of v. The distribution of v_i depends on which source population v_i comes from. If v_i comes from population one, then v_i ∼ N(b₁, σ₁²) is assumed. Otherwise, we assume v_i ∼ N(b₂, σ₂²). Define w_i = 1 if i comes from population one and w_i = 0 otherwise. These w_is are the source population indicators. We can express v_i by the following linear model, v_i = w_ib₁ + (1 − w_i)b₂ + u_i, where u_i is the deviation of the ith allelic value from its corresponding population mean and is distributed as u_i ∼ N(0, w_iσ₁² + (1 − w_i)σ₂²). Let W be a known n × 2 matrix storing the source population indicators, b = [b₁, b₂] and u be an n × 1 vector for all the u_is. Eq. 3 can be rewritten in matrix notation as v = Wb + u. Substituting this equation into 3, we have

4

Let X = (A^p + A^m)W and Z = A^p + A^m. The above model is then expressed as a typical mixed model:

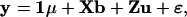5

where b is the vector of fixed effects and u is the vector of random effects, both being effects of QTL.

Paths of Gene Flow

Model 5 is different from the usual mixed model in that the design matrices are unknown because they are determined by the unobserved paths of gene flow. A complete description of the paths of gene flow is called a genetic descent graph (4). A probability statement of a genetic descent graph can be inferred by using marker information. From the inferred probability, we can draw a realization of the descent graph, which is then used to infer QTL parameters. In this section, we introduce a recursive algorithm to draw a descent graph.

Define i_j^p = 1, … , n as the founder allele identifier for the paternal allele of individual j and i_j^m = 1, … , n as that for the maternal allele of j. For example, if v_j^p is a copy of the first founder allele and v_j^m is a copy of the fourth founder allele, then i_j^p = 1 and i_j^m = 4. Using the founder allele identifiers, we can rewrite Eq. 1 by

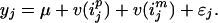6

Instead of using the awkward expression v_ij^p for element i_j^p of vector v, here we adopt a pseudo code expression v(i_j^p). We have now formulated the problem of QTL mapping as that of finding the appropriate subscripts of v that an individual can possibly take. A complete description of the subscripts for all individuals represents a genetic descent graph.

There may be many generations from j to the founders, and thus it may be difficult to directly sample i_j^p and i_j^m. We use a recursive algorithm to sample the founder allele identifiers. The algorithm requires individuals to be entered into the pedigree in a chronological order so that the allele identifiers of parents must be sampled before their children. The recursive algorithm is performed as follows:

If individual j is a founder and it is the ith founder, then i_j^p = 2i − 1 and i_j^m = 2i for i = 1, … , ½n. If j is not a founder, we use the following recursive equations:

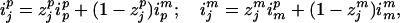7

where i_p^p and i_p^m are the allele identifiers for the father of j and i_m^p and i_m^m are those for j's mother. The allelic transmission indicator, z_j^p or z_j^m, reflects the event of only one meiosis, and thus is easy to sample. We have now turned the problem of identifying the founder alleles into that of finding the allelic transmission indicators from parents to children, a much simpler problem.

The formation of a zygote requires two meioses that must be inferred jointly. Define the ordered genotypes of the father and mother of j by Q_p^pQ_p^m and Q_m^pQ_m^m, respectively. Individual j can take one of the four possible genotypes, {Q_p^pQ_m^p, Q_p^pQ_m^m, Q_p^mQ_m^p, Q_p^mQ_m^m}. Define another variable, U_j = 1, … , 4, to indicate one of the four ordered genotypes. For example, U_j = 2 if j is of type Q_p^pQ_m^m. The values of z_j^p and z_j^m are determined solely by U_j using z_j^p = I_(Uj=1) + I_(Uj=2) and z_j^m = I_(Uj=1) + I_(Uj=3), where I_(Uj=k) = 1 if U_j = k and I_(Uj=k) = 0 otherwise.

We have now turned the problem of generating z_j^p and z_j^m into that of generating U_j. The joint distribution of U_j with marker genotypes is then used in the following Bayesian modeling.

Bayes and the Markov Chain Monte Carlo (MCMC) Algorithm

In Bayesian analysis, we first classify each item in the mixed model into one of two classes. The class of observables (also called data) includes the arrays of phenotypic values y and marker genotypes M. The class of unobservables includes the parameters of interest {μ, b, σ₁², σ₂², σ_ɛ², λ}, where λ is the position of the QTL, and the missing values, U = {U_j} and u. Define the collection of unobservables by θ = {μ, b, σ₁², σ₂², λ, σ_ɛ², U, u} and use p(x) as a generic notation for probability density whose actual form depends on the argument x rather than p. The joint posterior probability density of θ is

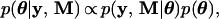8

where

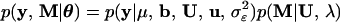9

is the likelihood and

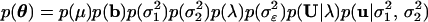10

is the joint prior. A uniform prior is chosen for each unobservable except u, which takes p(u|σ₁², σ₂²) ∝ 1/(σ₁^n₁σ₂^n₂) exp {−½u′G⁻¹u}, where G = diag{I_n1σ₁², I_n2σ₂²}. In practice, the priors should be customized according to the data structure and the experience of the researcher. The uniform priors selected in this study purely reflect our ignorance of the true parameters. With the uniform priors, the likelihood will play a major role in determining the posterior distribution of θ and the results will be more objective.

The actual Bayesian inference is to obtain the marginal posterior probability density for each parameter (θ_i) rather than the joint posterior density of all parameters. This requires multiple integration, p(θ_i|y, M) = ∫∫_θ−i p(θ_i, θ_−i|y, M)dθ_−i, where θ_−i stands for the array of remaining elements of θ that excludes θ_i. Unfortunately, there is no explicit form for the multiple integration. Here we adopt the MCMC algorithm to generate samples from the joint posterior distribution from which a marginal distribution can be easily inferred.

Given X and Z, model 5 is a standard mixed model. Bayesian inference of variance components under the standard mixed model has been extensively studied (e.g., refs. 5 and 6). Herein, we describe only methods of evaluating the likelihood, generating U, and simulating b and u.

Evaluating the Likelihood.

Conditional on their genotypic values, the phenotypic values of any two individuals are independent. Therefore, p(y|θ) = ∏_j=1^N p(y_j|μ, v(i_j^p), v(i_j^m), σ_ɛ²), where the sampled values of founder allele identifiers, i_j^p and i_j^m, are used to calculate the genotypic value of j. We evaluate the likelihood value for each individual immediately after its founder allele identifiers have been sampled (described in the next paragraph). Therefore, the algorithm requires individuals to be entered into the pedigree in the chronological order of their birth so that the likelihoods of parents are always evaluated before their children (7).

Sampling Founder Allele Identifiers.

Founder allele identifiers are the keys of the proposed method. Each allele is connected to one of the founder alleles through its founder allele identifier. Sampling allele identifiers is accomplished by sampling U, which is then converted into z_j^p and z_j^m, which are eventually used for computing the founder allele identifiers.

We use a Gibbs sampler (8, 9) algorithm to sample U_j from its conditional posterior distribution. For simplicity, we describe only the posterior probability conditional on the genotypes of two flanking markers. Similar to U_j, we denote the genotype indicator vectors for the left and right markers by M_j^L and M_j^R, respectively. Then the posterior distribution of U_j is

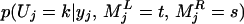11

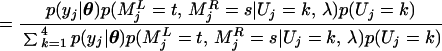for k, t, s = 1, … , 4. Calculation of p(y_j|θ) is straightforward. Conditional on U_j, M_j^L and M_j^R are independent so that p(M_j^L = t, M_j^R = s|U_j = k, λ) = p(M_j^L = t|U_j = k, λ)p(M_j^R = s|U_j = k, λ), where p(M_j^L = t|U_j = k, λ) or p(M_j^R = s|U_j = k, λ) is obtained from the following transition matrix:

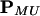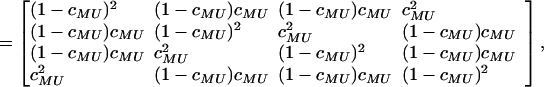where c_MU is the recombination fraction between the QTL and the left or right marker. It is calculated from λ by using the Haldane (10) map function. Finally, we take the Mendelian prior p(U_j = k) = 1/4 for k = 1, … , 4 and j = 1, … , N.

Since only two flanking markers are used to calculate the posterior probability of U_j, the approach is called interval mapping (1). In pedigree analysis, the markers are usually not fully informative. In this situation, we generate a realization of M_j^R and M_j^L based on loci flanking them. A flanking locus can be a marker or a QTL, depending on which one is closer to the marker of interest. In fact, our computer program has been equipped with this utility. Alternatively, we can take the multipoint method to infer the probability of U_j (11). The multipoint method can improve the mixing property of the Markov chain, but it is hard to implement in the program. However, both methods would ultimately generate the same result if the chains are sufficient long.

Updating Values of the Founder Alleles.

The effect of the ith founder allele (i = 1, … , n) has been expressed as a fixed effect, w_ib₁ + (1 − w_i)b₂, plus a random deviation, u_i (see Eq. 3). Because w_i is known, updating the effects of founder alleles is actually accomplished by updating b and u. Although b₁ and b₂ can be drawn independently if an informative joint prior is chosen, to increase the speed of convergence, we set b₁ = 0 and draw only b₂. The Metropolis–Hastings algorithm (12, 13) is used here for drawing b₂. Define θ_i^(t) = b₂^(t) as the current value of b₂ and θ_−i^(t) as the current values of the remaining unobservables. We want to generate a θ_i from the following conditional posterior distribution, p(θ_i|y, M, θ_−i) ∝ p(y, M|θ_i, θ_−i)p(θ_i, θ_−i). A random walk Metropolis algorithm is used to generate the new value of θ_i. First, a θ^*_i is proposed from θ^*_i ∼ N(θ_i^(t), Δ), where Δ is a predetermined proposal variance for b₂, a small positive value (tuning parameter). The transition probability from θ_i^(t) to θ^*_i is q(θ^*_i, θ_i^(t)) = N(θ_i^(t), Δ), which is identical to q(θ_i^(t), θ^*_i) = N(θ^*_i, Δ). Therefore, the acceptance probability for the candidate value of θ^*_i is min{1, α}, where α is

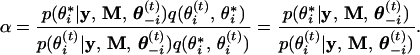12

If θ^*_i is accepted, θ_i^(t+1) = θ^*_i, otherwise, θ_i^(t+1) = θ_i^(t) and no action will be taken.

The random deviations, u, are drawn one pair at a time. In this case, θ_i = {u_2i−1, u_2i} is a 2 × 1 vector for i = 1, … , ½n. The proposal value is sampled from a joint bivariate normal distribution, θ^*_i ∼ N(θ_i^(t), I₂δ), where δ is the proposal variance common to both u_2i−1 and u_2i. The pair of us are accepted or rejected simultaneously according to the Metropolis–Hastings rule (see Eq. 12).

The population mean, the variance components, and the QTL position are updated by following the same Metropolis–Hastings rule. Detailed steps are described in ref. 14, in which the marker linkage phases and the number of QTL are also treated as unknown variables. Note that sampling the number of QTL involves change in the dimension of the model. We adopted the reversible jump MCMC algorithm developed by Green (15) to add or delete a QTL in each MCMC step.

A Simulation Study

For illustration, we simulated a hybrid population derived from the cross of two outbred populations. Ten parents were randomly selected and genotyped from each population and formed a complete cross experiment in which each parent from one population was mated to every parent from the other population, leading to a total of 100 full-sib families in the F₁ generation. One individual from each full-sib family was genotyped and phenotyped. From the 100 F₁ individuals, we formed 50 pairs of matings in a completely random fashion. Each mating pair produced 10 progenies, leading to a total of 500 F₂ individuals. The total sample size in the three-generation pedigree was 500 + 100 + 20 = 620. Note that all the families are interrelated, forming a large complicated pedigree with a total of 20 founders.

We then simulated two chromosomes 90 and 60 centimorgans (cM) long, respectively. The marker coverage is one marker in every 10 cM. Each marker allele in the founders was sampled from one of six equally frequent alleles. We put two QTL on chromosome I at positions 25 cM and 77 cM, respectively, and one QTL on chromosome II at position 32 cM. The effects of the three QTL are given in Table 1. The environmental error is distributed as N(0, 1). Given this setup, the first QTL explains 24% of the phenotypic variance, all due to the between-population variance. The second QTL explains 23% of the phenotypic variance, due to the between-population variance and the variance within population one, and the third QTL explains 15% of the phenotypic variance, due to only the within-population variances. The QTL allelic effects in the founders were sampled from normal distributions. One data set was simulated and analyzed by using two different models, the mixed model and the fixed model. To implement the fixed model analysis, we simply added one restriction to the same computer program: σ₁² = σ₂² = 0 for all QTL fitted to the model. The analysis was then identical to QTL mapping in an F₂ line cross.

Table 1.

Parametric values used in the simulation study

Parameter	QTL 1	QTL 2	QTL 3
Location, cM	25 (I)	77 (I)	32 (II)
b = b2 − b1	0.80	0.55	0.00
σ12	0.00	0.30	0.30
σ22	0.00	0.00	0.10
σA2 = b2 + (σ12 + σ22)	0.64	0.60	0.40
h2	0.24	0.23	0.15

The mean of the first population for each locus is set to zero so that the population difference is b = b₂ − b₁ = b₂. The proportion of the phenotypic variance explained by each QTL is expressed by h² = σ_A²/(σ_A² + σ_ɛ²), where σ_ɛ² = 1.0. 

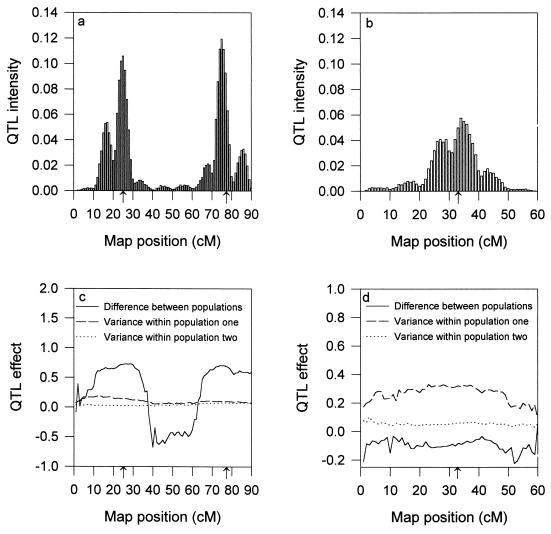
For the mixed model analysis, the MCMC was started with no QTL in the model. The distribution of the number of QTL appeared to reach its stationary distribution quickly. The total length of the chain was 10⁶ cycles. With the removal of 1,000 cycles for the burn-in period and the saving of one observation for every 50 cycles, the total number of saved data points was 20,000. These observations were subject to the post-Bayesian analysis. We recorded the number of hits by QTL within a short interval, say 1 cM, of the chromosome and defined the proportion of the hits among the posterior sample as the QTL intensity. We then plotted the QTL intensity against the chromosomal position and formed a QTL intensity profile for each chromosome (see Fig. 1 a and b). The intensity profiles indicated three possible QTL. The estimated positions of the QTL are close to the true locations. For each effect, we calculated the average QTL effect for each short interval (1 cM long). We then plotted the average effect against the chromosomal position, forming a profile for each QTL effect (see Fig. 1 c and d). As Sillanpää and Arjas (16) stated, the effect profile is meaningful only in the region where the QTL intensity is reasonably high. For example, the first QTL intensity is concentrated on (10, 30) cM on chromosome I. The population difference of the first QTL shows an average effect around 0.75 in that region. Similarly, the second QTL effect shows an average effect around 0.60 in the region corresponding to the peak of the second QTL. Interestingly, the population difference profile shows an average effect around −0.5 in the region between the two QTL. However, this region was rarely hit by QTL, and thus the negative effect does not mean anything.

Figure 1.

QTL intensity profiles (a and b) and profiles of the effects (c and d) for the mixed model analysis. Markers (codominant) are evenly distributed with 10 cM apart. (a and c) Chromosome I. (b and d) Chromosome II. The true positions of the three QTL are pointed to by the arrows on the horizontal axes. The solid, dashed, and dotted lines represent for the population difference b = b₂ − b₁, variance within population one σ₁², and variance within population two σ₂², respectively.

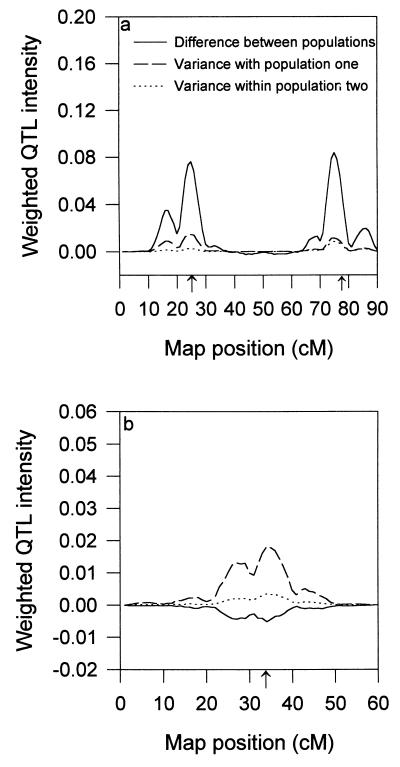
We proposed a method to partition the QTL intensity profile into various components, each corresponding to one specific effect. These effect-specific intensity profiles are also called the weighted intensity profiles because they are the QTL intensity weighted by the effects. The weighted profiles allow us to visualize the sources of genetic variation for the detected QTL. For instance, the weighted profiles for chromosome I (Fig. 2a) show that the two QTL are primarily caused by the population difference. In contrast, the weighted profiles for chromosome II (Fig. 2b) show that the QTL is caused primarily by the variance within population one, rather than by the population difference.

Figure 2.

Weighted QTL intensity profiles for the mixed model analysis. (a) Chromosome I. (b) Chromosome II.

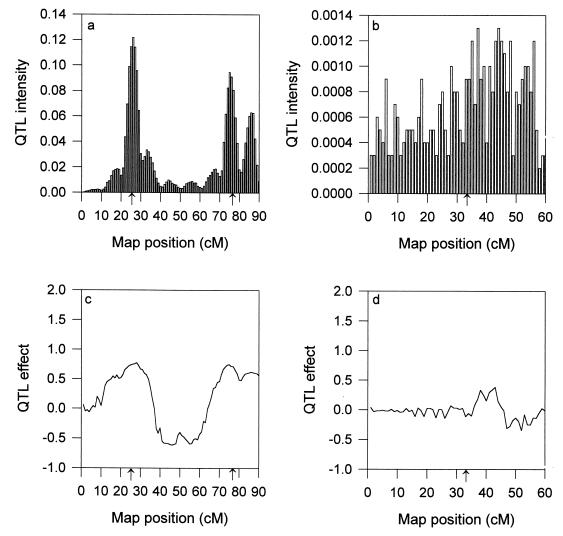
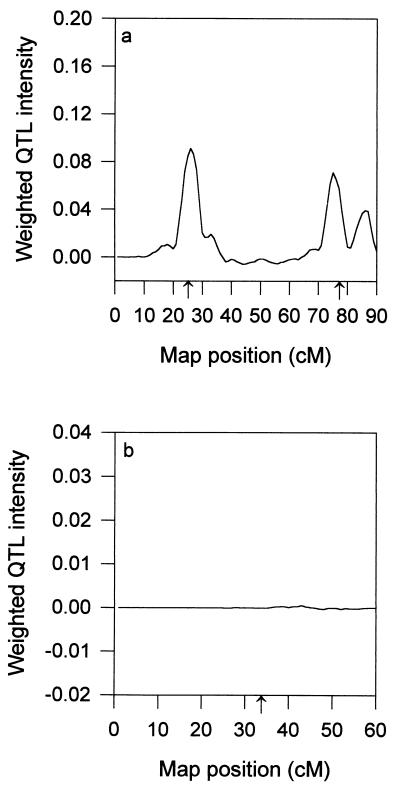
For the fixed model analysis in which σ₁² = σ₂² = 0 has been assumed, only two QTL were detected (Fig. 3a) and the third QTL on chromosome II was completely missing (Fig. 3b). By ignoring the within-population segregation, we not only missed the third QTL but also got a confused estimate of the position for the second QTL (Fig. 3a). The posterior mean of the QTL number is 2.4 rather than 2.0. This is because 28% of the posterior sample shows three QTL. The position of the third QTL detected is highly concentrated at the end (80–90 cM) of chromosome I rather than on chromosome II. This faulty QTL is essentially due to the split of the second QTL, another piece of evidence that the fixed model is inferior. The effect profiles for the fixed model analysis are given in Fig. 3 c and d. The weighted intensity profiles are given in Fig. 4, which shows no sign of QTL on chromosome II.

Figure 3.

QTL intensity profiles (a and b) and effect profiles (c and d) for the fixed model analysis. (a and c) Chromosome I. (b and d) Chromosome II.

Figure 4.

Weighted QTL intensity profiles for the fixed model analysis. (a) Chromosome I. (b) Chromosome II.

Bayesian mapping allows the number of QTL to change. This involves the change in the dimension of the model. We adopted the reversible jump algorithm of Green (15) to infer the posterior distribution for the number of QTL (see Table 2). The posterior mean of the QTL number in the mixed model analysis is ∼3.0, which coincides with the true value. The posterior mean in the fixed model analysis is ∼2.4, which is obviously inferior to the mixed model analysis.

Table 2.

The posterior distributions of the number of QTL under the mixed and fixed model analyses

Model	Relative frequency of QTL no.
	0	1	2	3	4	5	6
Mixed	0.000	0.000	0.132	0.743	0.115	0.010	0.000
Fixed	0.000	0.000	0.665	0.277	0.052	0.006	0.000

The posterior means for the mixed and fixed models are 3.0 and 2.4, respectively, while the true number of QTL is 3. 

Discussion

We recently proposed a Bayesian mapping method under the random model framework. This method can analyze data collected from arbitrary mating designs, including selfed and related founders, without any approximation (14). The method, however, is a pure random model approach and applicable only to situations where the founders are randomly sampled. The mixed model approach developed in this study is an extension of our random model to handle populations with a hybrid origin. Most of the sampling techniques used in this study—e.g., sampling the number and locations of QTL—have been described by Yi and Xu (14).

Bayesian analysis is preferable for its convenience and flexibility in regard to using pedigree data and mapping multiple QTL (17). It takes full account of the uncertainty associated with all unknowns, including the number and locations of QTL, and the genotypes of QTL. Earlier works of Bayesian mapping include Satagopan et al. (18) and Sillanpää and Arjas (16) for line crossing data, and Uimari and Hoeschele (19), Heath (20), and Bink and van Arendonk (21) for pedigree data. The works for line crossing data always use the fixed model approach. The works for pedigree data usually use the random model, but most often assume two alleles (20). When multiple alleles are assumed, the genotypes of QTL are not sampled, but the conditional expectations of allelic IBD (identical-by-descent) are calculated and used in place of the covariance matrix at the QTL of interest (21). This expected IBD method is an approximation to the Bayesian analysis because it uses an approximate likelihood. Nonetheless, the above Bayesian methods cannot handle data with arbitrarily complicated mating designs, especially when selfing is involved in pedigree data.

The mixed model approach provides a unified QTL mapping algorithm. It can analyze data collected from any complicated mating design. As demonstrated in the simulation study, when the within-population variances are set to zero, the algorithm becomes a fixed model approach and automatically analyzes a typical F₂ cross family. On the other hand, if we disregard the population difference and simply set b = 0, the algorithm will turn into a random model approach and automatically analyze an outbred population.

Under the mixed model framework, we treat the mean effects of the source populations as fixed effects and the allelic values within each population as random effects. If the number of founders within each population is small, a meaningful estimate of the within-population variance is impossible. In this case, the allelic values of the founders may be treated as fixed effects with the allelic variance, σ_k², treated as a prior variance. As a consequence, the model is considered as a fixed model. If the mapping population is derived from the hybrid of many source populations, it is not convenient to estimate the b_ks. Instead, we can treat b_k as a random variable sampled from a N(0, σ_b²) distribution. In this case, σ_b² is one of the parameters of interest. The within-population variances may not be estimated separately for individual populations; instead, they may be pooled as a consensus estimate of the within-population variance. This results in a hierarchical random model analysis of QTL. Therefore, the difference between a fixed model and a random model is vague in the context of Bayesian mapping. When the variances of effects are treated as hyperparameters (prior variances), the model is fixed. If the variances of effects are treated as the parameters of interest, the model is random. Both the fixed and random models can be implemented in the same mixed model computer program, with one additional statement to turn on/off the fixed/random option. The proposed mixed model approach provides a unified QTL mapping algorithm suitable for all kinds of populations.

Abbreviations

QTL

quantitative trait locus or loci

MCMC

Markov chain Monte Carlo

cM

centimorgans