Evolutionary responses of discontinuous gas exchange in insects

Abstract

The discontinuous gas-exchange cycles (DGCs) observed in many quiescent insects have been a cause of debate for decades, but no consensus on their evolutionary origin or adaptive significance has been achieved. Nevertheless, three main adaptive hypotheses have emerged: (i) the hygric hypothesis suggests that DGCs reduce respiratory water loss; (ii) the chthonic hypothesis suggests that DGCs facilitate gas exchange during environmental hypoxia, hypercapnia, or both; and (iii) the oxidative-damage hypothesis suggests that DGCs minimize oxidative tissue damage. However, most work conducted to date has been based on single-species investigations or nonphylogenetic comparative analyses of few species, despite calls for a strong-inference, phylogenetic approach. Here, we adopt such an approach by using 76 measurements of 40 wild-caught species to examine macrophysiological variation in DGC duration in insects. Potential patterns of trait variation are first identified on the basis of the explicit a priori predictions of each hypothesis, and the best phylogenetic generalized least-squares fit of the candidate models to the data is selected on the basis of Akaike's information criterion. We find a significant positive relationship between DGC duration and habitat temperature and an important interaction between habitat temperature and precipitation. This result supports the hygric hypothesis. We conclude that the DGCs of insects reduce respiratory water loss while ensuring adequate gas exchange.

At rest, many species of tracheated arthropod exchange respiratory gases with the atmosphere discontinuously. These discontinuous gas-exchange cycles (DGCs) are observed in a phylogenetically and ecologically diverse suite of species, having arisen independently within the Chelicerata and Myriapoda, and at least five times within Insecta (1, 2). DGCs are observed in species with subterranean and nonsubterranean lifestyles, winged and wingless species, and species from mesic and xeric environments (2). Generally, DGCs comprise three periods: closed (C), flutter (F), and open (O). During the C period, the spiracles are tightly closed and the partial pressure of oxygen (pO₂) within the tracheae declines as oxygen is consumed by respiration. Carbon dioxide, on the other hand, is buffered in the hemolymph and endotracheal pressure declines with pO₂ (3). At a pO₂ set point of ≈2–4 kPa, the spiracles begin to partially open and close in quick succession, and the F period is initiated. Inward convection during the early stages of the F period is thought to be an important means of restricting outward water movement in some, but not all, species showing DGCs (4–8). CO₂ continues to accumulate throughout the F period, which ends when endotracheal partial pressure of carbon dioxide reaches ≈3–6 kPa and the spiracles open widely (9). During the O period, O₂, CO₂, and H₂O are exchanged with the atmosphere by either diffusion or forced convection arising from active ventilatory movements.

Although early work stressed the importance of the C and F periods in restricting water loss, the debate over the evolutionary origin and adaptive significance of discontinuous gas exchange is far from resolved (10–12). Three main adaptive hypotheses have emerged and were reviewed recently by Chown et al. (8). The hygric hypothesis can be stated simply as, “DGCs are an adaptation to reduce respiratory water loss” (8; see also ref. 9). It is the most venerable of the hypotheses** and continues to attract empirical support (14). However, the hypothesis has been criticized on several grounds, and a variety of empirical studies have failed to find support for it (reviewed in ref. 15). Most recently, Lighton et al. (16) found that in the ant, Pogonomyrmex californicus, the presence or absence of a DGC does not alter respiratory water loss. In a related species, Pogonomyrmex barbatus, the ratio of respiratory water loss to CO₂ release does not differ between queens using DGC or cyclic or continuous gas exchange (17).

The second adaptive hypothesis, proposed by Lighton and Berrigan (10, 18), is that DGCs are an adaptation to effect gas exchange in hypoxic or hypercapnic environments in such a way that a water-loss penalty is not paid (see also ref. 17). This idea is now known as the chthonic-hygric hypothesis to distinguish it from Lighton's (10) later modification thereof, which simply emphasized the need for gas exchange in hypoxic or hypercapnic environments irrespective of water loss [the chthonic hypothesis (8)]. Both of these chthonic hypotheses remain controversial (10, 17, 19–21). The third, oxidative-damage, hypothesis proposes that DGCs “are an adaptation to provide adequate gas exchange while reducing oxidative damage to tissues at rest that would otherwise result from a tracheal system that has evolved to maximise oxygen availability during activity” (8). Bradley^†† postulated that the DGC may serve to reduce the supply of oxygen to the tissues during periods when the metabolic rate is low, and this idea was supported by Hetz and Bradley (12), who showed that pupae of the moth Attacus atlas maintained an endotracheal pO₂ of 4–5 kPa throughout the F period at ambient pO₂ values ranging from 6.4 to 50.2 kPa.

Each of these hypotheses makes firm predictions concerning the relationship between the duration of DGCs and ambient temperature, saturation deficit, pO₂, or some combination thereof (Table 1). In the case of the hygric hypothesis, if it is assumed that the respiratory surfaces are saturated with water vapor, then rates of water loss will be proportional to saturation deficit, which is influenced by the temperature and water-vapor pressure of ambient air. Because saturation deficit is highest at high temperatures and low ambient water-vapor pressures, a positive relationship is predicted between DGC duration and ambient temperature, and a negative correlation is predicted between DGC duration and precipitation (which is assumed to be related to ambient water-vapor pressure; see refs. 21 and 23–25). In addition, a significant interaction between precipitation and temperature is predicted because high temperatures will produce a low saturation deficit when precipitation is high but a high saturation deficit when precipitation is low. The chthonic hypothesis predicts that DGC duration in species that occupy hypoxic microhabitats will be longer than that of species that inhabit less hypoxic microhabitats (presuming that effects on C-period duration predominate; see refs. 3 and 6). An extended DGC will act to increase pO₂ gradients in hypoxia, and a negative association between microenvironment pO₂ and DGC duration is predicted. Predictions for the chthonic-hygric hypothesis essentially include a combination of those found for the chthonic and hygric hypotheses (Table 1). In the case of the oxidative-damage hypothesis, low endotracheal pO₂ values, resulting from low ambient pO₂ values, are predicted to relax the need for an extended DGC, which arises from a prolonged C period to reduce endotracheal pO₂ (12). A positive association, therefore, is predicted between pO₂ and DGC duration.

Table 1.

Predicted correlations between DGC duration and a range of environmental factors for each of the three hypotheses compared

Hypothesis	Factor
	Ta	P	Ta × P	O2
Hygric	+	−	y	o
Chthonic	o	o	o	−
Chthonic-hygric	+	−	y	−
Oxidative-damage	o	o	o	+/o

Factors are ambient (habitat) temperature (T_a, °C), precipitation (P, mm·yr⁻¹), and ambient oxygen (O₂); responses are positive correlation (+), negative correlation (−), no correlation/effect (o), and significant effect (y).

However, the signs of the relationships for the chthonic and oxidative-damage hypotheses might be different if species show phenotypic plasticity of a magnitude sufficient to obscure the adaptive signal. For example, if the oxidative-damage hypothesis is correct, a species from a low-oxygen environment might, in response to normoxic experimental conditions, increase duration of the C period to reduce endotracheal pO₂ (12). It could also increase the length of the O period to release CO₂ that accumulated during the prolonged C period (19) or that might have accumulated as a result of reduced rate of oxygen consumption per unit time during the F period (12). In such cases, the DGC duration would increase under normoxic experimental conditions. What the magnitude of this increase is likely to be relative to a species from a less hypoxic environment is difficult to determine given that no experiments of this kind have been undertaken, and those that have show substantial variation in species' responses (26). However, it seems plausible that the magnitude of such plasticity would decline as a species' typical environmental circumstances increasingly approach normoxia. Therefore, if complete plasticity is assumed and in the direction suggested, the sign of the relationship between DGC duration and environmental pO₂ is likely to be zero (i.e., no relationship). In consequence, the prediction for the oxidative-damage hypothesis is shown as +/0 (Table 1). The opposite argument could be made for the chthonic hypothesis, and so the sign is shown as −/0.

The present study provides a test of the adaptive explanations for DGCs by examining the predictions discussed above within a phylogenetic generalized least-squares (PGLS), strong-inference framework. The approach taken is to compile from the literature data for species that occupy a wide range of microhabitats and to evaluate the relationship between DGC duration and environmental data in light of the explicit predictions of the hygric, chthonic, chthonic-hygric, and oxidative-damage hypotheses. Other components of the DGC are not examined specifically, because Wobschall and Hetz (7) have demonstrated that, by using rate of carbon dioxide production (V̇CO₂) or oxygen-consumption-per-unit-time traces alone (i.e., in the absence of tracheal pressure measurements), the C and F periods cannot always be clearly distinguished. To date, no studies have undertaken a broad-scale comparative assessment of this nature within a phylogenetic framework. Indeed, most previous examinations of the adaptive hypotheses proposed to account for DGCs have usually examined a single hypothesis, typically adopted a binary approach to environmental conditions (e.g., mesic/xeric) (e.g., ref. 20), and/or have compared only a few species without explicit consideration of phylogenetic effects (e.g., refs. 27 and 28). Therefore, it has long been argued that the field is in substantial need of a strong-inference approach within an explicit phylogenetic context (15), the benefits of which have been realized in many other areas of physiology (29–31).

Results

Of the six models tested (Table 2), the best fit, given the data, was that which described DGC duration in terms of M + V̇CO₂ + T_m + T_a + P + T_a^∗P and incorporated information on the phylogenetic relationships among species, with branch lengths in the phylogeny set equal. This model was 1.5 times more likely to provide the best fit than the next best model, which was the model that also included the nonsignificant positive effect of ambient oxygen (a combination of the oxidative-damage and hygric models; Table 2). λ was close to 1 for all three models that incorporated explicit phylogenetic information and a punctuational model of evolution (equal branch lengths), indicating the need to account for phylogenetic correlation in these models (32). The probability that a conventional nonphylogenetic model provides the best fit to the data for DGC duration was negligible (Table 2; Σw_i ≪ 0.0001 for the three models without phylogenetic information).

Table 2.

Summary of the models examined to explain variation in discontinuous gas-exchange patterns of insects

Model	Analysis	Branch lengths	λ	AIC	wi
1. M + V̇CO2 + Tm + Ta + P + Ta∗P	Conventional			25.83	<0.0001
	Phylogenetic	Equal	0.83	−17.82	0.49
	Phylogenetic	Proportional	0.83	−7.40	0.003
2. M + V̇CO2 + Tm + O2	Conventional			31.15	<0.0001
	Phylogenetic	Equal	0.84	−15.87	0.19
	Phylogenetic	Proportional	0.83	−5.43	0.001
3. M + V̇CO2 + Tm + Ta + P + Ta∗P + O2	Conventional			27.40	<0.0001
	Phylogenetic	Equal	0.83	−16.95	0.32
	Phylogenetic	Proportional	0.82	−6.71	0.002

Model 1, pure hygric; model 2, oxidative damage and hygric; model 3, either oxidative and hygric or chthonic-hygric depending on the signs of the parameters (see Table 3). Each model was tested with an explicit model of phylogenetic relationships among species either incorporated or ignored (the latter actually assumes a star-shaped phylogeny with all species equally closely related and is equivalent to a conventional nonphylogenetic analysis), whereas the phylogenetic models either had equal or proportional branch lengths (see Methods). Models were constructed with the following factors: mass (M, mg), rate of CO₂ production (V̇CO₂, ml·h⁻¹), measurement temperature (T_m, °C), ambient (habitat) temperature (T_a, °C), precipitation (P, mm·yr⁻¹), and ambient oxygen (O₂). λ is a measure of phylogenetic correlation (32); w_i is the Akaike weight, the probability that the model is the correct one of those tested.

The best model included significant positive relationships between DGC duration and M and T_a and significant negative relationships between DGC duration and V̇CO₂ and T_m (Table 3 and Fig. 1). Although this model includes nonsignificant effects of P and its interaction with T_a, removing these variables, and notably the interaction term, increases model Akaike's information criterion (AIC); hence, the best-fit model includes these terms (Table 3). Removing M, V̇CO₂, T_m, and T_a^∗P also raises AIC, dramatically in the first two cases (>25), which justifies their inclusion in the analysis.

Table 3.

Parameter estimates for the hygric model

	Estimate	SE	P	ΔAIC
Intercept	−1.216	0.821	>0.05
M	0.795	0.117	<0.01	36.74
V̇CO2	−0.714	0.130	<0.01	25.42
Tm	−0.012	0.006	<0.05	1.60
Ta	0.066	0.029	<0.05	<0.001
P	0.712	0.368	>0.05	<0.001
Ta∗P	−0.035	0.018	>0.05	2.01

Factors are log mass (M, mg), log rate of CO₂ production (V̇CO₂, ml·h⁻¹), measurement temperature (T_m, °C), ambient (habitat) temperature (T_a, °C), log precipitation (P, mm·yr⁻¹), and ambient oxygen (O₂). T_a^∗P is the interaction between ambient temperature and log precipitation, and ΔAIC is the change in model AIC (64) when the parameter is removed from the model.

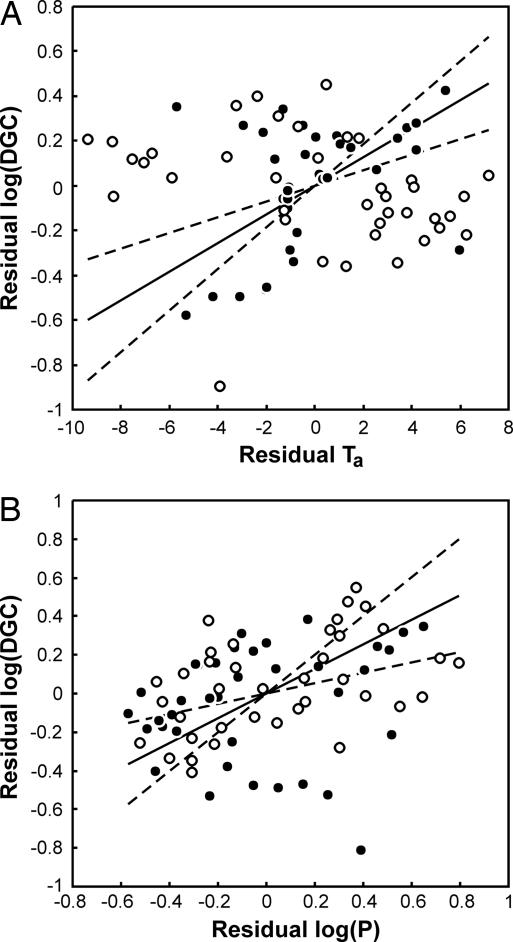
Fig. 1.

The effect of environmental variables on discontinuous gas exchange in insects. Relationship between DGC duration and (A) habitat ambient temperature (T_a) and (B) habitat precipitation (P). To remove the potential confounding effects of body mass, measurement temperature, rate of CO₂ production, and collinearity between environmental variables, residuals are presented. Residuals are calculated as the difference between measured values and those predicted by the best-fit model from Table 2 (the T_a^∗P interaction was excluded from residual calculations). In both A and B, the solid line is the phylogenetically correct correlation between log(DGC) and the environmental variable plotted through the bivariate mean and shown as ±1 SE of the appropriate coefficient from Table 3 (dashed lines). To indicate the effect of the interaction term (Table 3), filled symbols in A are log(DGC) values for species in which log(P) is lower than the median log(P) in the data set; unfilled symbols are log(DGC) values for species in which log(P) is higher than the median log(P) in the data set. The relationship between log(DGC) and T_a is apparently stronger when log(P) is low, which supports the hygric hypothesis. Similarly, in B, filled symbols are log(DGC) values for species in which T_a is lower than the median T_a in the data set; unfilled symbols are log(DGC) values for species in which T_a is higher than the median T_a in the data set.

Discussion

Our analysis supports the a priori predictions of the hygric hypothesis (Table 2). The best model incorporates phylogeny and included the significant effect of habitat ambient temperature, a nonsignificant effect of habitat precipitation, and an important interaction between temperature and precipitation (Table 3). Thus, species from warm habitats have long DGCs, especially when precipitation is low (Fig. 1). Similarly, cyclic and continuous gas exchange at rest are more likely in mesic than in xeric environments than are DGCs, but DGCs can evolve in both kinds of environments (2). However, the most likely model is only 1.5 times more likely than the second most likely, which adds a nonsignificant positive effect of oxygen availability, in keeping with the oxidative-damage hypothesis (Table 2). Overall, the probability that one of the pure hygric and chthonic/oxidative-hygric models is the best fit to the data is 0.81 (Table 2). Although the approach taken here represents a strong comparative test of the competing hypotheses, it does not provide information about the way in which selection might have led to the evolution of discontinuous gas exchange. However, it does suggest that, if not the evolutionary origin, then at least the continued maintenance of DGCs is associated with selection to reduce respiratory water loss while ensuring adequate gas exchange.

The nonsignificant relationship between DGC duration and environmental pO₂ raises the possibility that, if present, the signal of adaptive change in DGC duration in response to environmental pO₂ is obscured by plastic responses to experimental pO₂. Plastic responses to experimental pO₂ clearly do occur (19, 33); however, the magnitude of these kinds of plastic responses relative to adaptive differences among species has not been systematically explored. The strong phylogenetic signal in the data provides some support for adaptive variation in DGC duration, especially because experimental responses to altered oxygen concentrations and temperature vary considerably among species (3, 26). Nonetheless, the need for studies that determine the proportional contributions of plasticity and adaptive change to variation in DGC duration is clear.

In addition to the comparative approach adopted in the present study, several other avenues are available for investigating the adaptive significance of physiological variation, including single-species mechanistic laboratory studies and laboratory evolution, among others (34, 35). Perhaps unsurprisingly, the outcomes of studies that make use of these different approaches are not always in agreement. Indeed, in the case of the hypotheses proposed to account for DGCs, this tension has long been felt in the field, with comparative studies tending to support the hygric hypothesis and single-species, experimental investigations favoring a variety of explanations (9, 12, 14–16, 18, 19, 33, 36, 37). However, the present comparative study provides clear evidence for one of the competing hypotheses from both broad-scale (Tables 2 and 3) and individual assessments (e.g., ref. 14).

Although the present study provides evidence that the DGC of insects is maintained for adaptive reasons, the question of the evolutionary origin thereof remains open. In addition to the hygric, chthonic, and oxidative hypotheses considered here, two additional hypotheses have been advanced. The strolling-arthropod hypothesis suggests that “[d]iscontinuous gas exchange cycles are an adaptation to increase the frequency of spiracle closure to reduce the risk of parasitic infestation of the tracheae,” whereas the emergent-property hypothesis suggests that “[d]iscontinuous gas exchange cycles are a non-adaptive outcome of interactions between the O₂ and CO₂ setpoints that regulate spiracle opening and closure” (8). Because periodic ventilation is widespread in animals, Klok et al. (1) suggested that modification of the periodic component of the central pattern generator to produce the DGC pattern characteristic of tracheated arthropods is likely to have arisen independently several times and that there has been convergent evolution of DGCs in the Arthropoda. DGCs are typically not found among the basal insect orders (3) and seem to be polyphyletic in origin, having arisen independently multiple times (1, 2). The multiple independent origins of DGCs suggest that DGCs are not a basal characteristic of arthropods and are likely to be (or have been) adaptive. However, an implication of the emergent-property hypothesis is that cycle frequency increases with metabolic rate such that gas exchange becomes continuous at the highest metabolic rates. Consistent with this implication, Gibbs and Johnson (17) found that ants showing continuous gas exchange had the highest metabolic rates, those exhibiting rapid cycling had intermediate metabolic rates, and those performing classical discontinuous gas exchange had the lowest metabolic rates. In any event, the nonadaptive hypothesis does not preclude modification of discontinuous gas exchange for other reasons. Moreover, global differences in the patterns of covariation of environmental conditions such as water availability, temperature, and pO₂ might mean that under some circumstances DGCs can be harnessed for one need, whereas under others they may be used for a rather different purpose. Nonetheless, the present data suggest that reducing water loss while ensuring adequate gas exchange under desiccating circumstances is certainly a predominant feature selecting for or maintaining DGCs in the group of species that predominate in our database (92% beetles and ants).

Although our analysis does demonstrate that DGCs evolve to restrict respiratory water loss, a limitation of the study concerns the coarse resolution at which habitat variables were obtained, which potentially limits the reliability of our conclusions (see, e.g., ref. 38). For example, it seems unlikely that 30-year averages of annual temperature and precipitation at 0.5° latitude/longitude resolution are fully representative of insect microhabitat temperatures and water-vapor saturation deficits. However, in a broad-scale comparison such as the present study, it is not necessary for habitat variables to be numerically precise estimates of insect microhabitats. Instead, it is assumed that global trends are indicative of differences in microhabitat between the geographically distant sites from which insects were collected (39).

Similarly, the ability to identify and discriminate between the chthonic genesis and oxidative-damage hypotheses is potentially undermined by the extremely limited data on the extent of habitat hypoxia and hypercapnia. In the absence of more comprehensive information about microhabitat conditions, we accounted for as much nonhabitat variation as possible (e.g., mass, measurement temperature, phylogeny) and classified microhabitat O₂ on a multipoint ordinal scale, which we assumed would reduce the likelihood of confounding factors.

Overall, we are confident that our support for the hygric hypothesis is sound but suggest that the relationships be reexamined in light of any new information on microhabitat characteristics that become available. Given the technical difficulties involved in measuring the microenvironments of subterranean insects (40), measurements of species that have traditionally not been investigated might represent one way of dealing with this issue (2). For example, members of the Araceae are visited or pollinated by representatives of at least 15 families of beetle (41), and the accessibility of inflorescences would facilitate both the collection of beetles and the characterization of the microhabitats to which they are exposed. Given that the Araceae and other thermogenic flowers are widely distributed geographically and show a range of thermogenic strategies (e.g., refs. 42–44), it is also likely that the beetle pollinators of these species will be subjected to a suitably wide range of environmental conditions to allow for further investigation into environmental modulation of DGCs.

Methods

DGC characteristics of insects were compiled from the literature and are available online [76 measurements of 40 species; see supporting information (SI) Table 4]. DGCs were identified on the basis of the presence of C and F periods (see discussion in refs. 2 and 8), and only species exhibiting a discontinuous pattern of gas exchange were included. Species exhibiting cyclic gas exchange were excluded. Although many instances of cyclic gas exchange are undoubtedly real (45), others may be a consequence of slow flow rates in experimental work (46). DGC duration was calculated as either the sum of the durations of the C, F, and O periods or the inverse of DGC frequency and was log-transformed for analysis.

Environmental ambient temperature (T_a, °C) and precipitation (P, mm·yr⁻¹) were obtained for the capture locality of each species at 0.5° latitude/longitude resolution from the CLIMATE 2.1 database (W. Cramer, personal communication). Precipitation was log-transformed for analysis. Microhabitat ambient oxygen was classified on an ordinal 0-to-3 scale: 0 indicates severely hypoxic or close to anoxic (e.g., moist cow pats), 1 indicates moderately hypoxic (e.g., dry cow pats), 2 indicates mildly hypoxic (e.g., sand and sandy loams), and 3 indicates close to ambient. The analysis did not account for altitude (i.e., hypobaric hypoxia) because the binary diffusion coefficient of O₂ increases in hypobaric mixtures, which offsets the decreased pO₂ gradient such that diffusive O₂ flux is maintained (47, 48).

Three statistical models were evaluated (Table 2). In addition to the main factors, body mass (M, mg), measurement (experimental), temperature (T_m, °C), and rate of CO₂ production (V̇CO₂, ml·h⁻¹) were also included in the evaluated models because of their known effects on DGCs (reviewed in ref. 3). M and V̇CO₂ were log-transformed for analysis.

The method of PGLS was used to control for phylogenetic nonindependence (49–51). The PGLS approach was implemented in R (52) by using the APE (Analysis of Phylogenetics and Evolution) package (53), and code was written by R. P. Duncan. Full details of the PGLS approach are provided elsewhere (54). Each statistical model was run by using each of two different assumptions about phylogenetic relatedness (phylogeny incorporated or conventional nonphylogenetic). A metric of the degree of phylogenetic correlation [λ, derived by Pagel (55); see also ref. 32] was calculated for each of the three models of trait evolution considered (Table 2). λ is a multiplier of the off-diagonal elements of the covariance matrix (i.e., those quantifying the degree of relatedness between species) and normally varies between 0 and 1. If the covariance matrix is constructed assuming a Brownian-motion model of evolution, then λ = 1 retains that model, whereas λ = 0 specifies phylogenetic independence. Intermediate values of λ specify models in which trait evolution is phylogenetically correlated but to a lesser extent than expected under the Brownian-motion model.

The gross structure of the phylogeny used for PGLS analysis was the same as that used by Marais et al. (2). High-level relationships within Coleoptera (i.e., the relationships between Carabidae, Scarabaeoidea, and Tenebrionoidea) were resolved according to the Tree of Life Web Project (see www.tolweb.org/tree/phylogeny.html and references therein). Families within Scarabaeoidea were assumed to be related according to Browne and Scholtz (56). Relationships among Aphodiinae, Scarabaeinae, and Dynastinae were resolved according to Howden (57), Browne and Scholtz (58), and Philips et al. (59); relationships within Scarabaeus (Scarabaeidae) according to Forgie et al. (60) and Sole et al. (61); and within Onymacris (Tenebrionidae) according to Ward and Seely (62). Relationships within Pogonomyrmex were resolved according to Parker and Rissing (63). Other relationships were assumed to follow taxonomic hierarchy. Because the branch lengths in the phylogeny are unknown, the analysis was conducted with two different assumptions. First, we assumed that all branches in the phylogeny were of equal length, which is equivalent to a punctuational model of evolution in which all change occurs at speciation events. Second, we assumed that all branches in the phylogeny were proportional in length to the number of taxa descended from the node to which the branch leads, which is one model by which gradualistic evolutionary change may occur and produces an ultrametric phylogeny with short recent branches and longer ancient branches. Because measurements at multiple temperatures were available for many species, multiple measurements for a single species were included by placing them in very short branches (0.001). Branch lengths were calculated by using TreeEdit 1.0a10. A copy of the phylogeny is available on request.

Burnham and Anderson's (13) framework for model comparison was used to identify the most plausible model(s) among the nine fitted (three statistical by three phylogenetic) on the basis of AIC as a measure of model fit (see also ref. 22). The best of all of the statistical models tested was that with the lowest AIC. The probability that any given model is actually the best fit of those tested was measured by its Akaike weight, w_i (13).

Abbreviations

DGC

discontinuous gas-exchange cycle

C

closed

F

flutter

O

open

pO₂

partial pressure of oxygen

V̇CO₂

rate of carbon dioxide production

AIC

Akaike's information criterion

PGLS

phylogenetic generalized least squares.