Neural interactions between flicker-induced self-organized visual hallucinations and physical stimuli

Abstract

Spontaneous pattern formation in cortical activity may have consequences for perception, but little is known about interactions between sensory-driven and self-organized cortical activity. To address this deficit, we explored the relationship between ordinary stimulus-controlled pattern perception and the autonomous hallucinatory geometrical pattern formation that occurs for unstructured visual stimulation (e.g., empty-field flicker). We found that flicker-induced hallucinations are biased by the presentation of adjacent geometrical stimuli; geometrical forms that map to cortical area V1 as orthogonal gratings are perceptually opponent in biasing hallucinations. Rotating fan blades and pulsating circular patterns are the most salient biased hallucinations. Apparent motion and fractal (1/f) noise are also effective in driving hallucinatory pattern formation (the latter is consistent with predictions of spatiotemporal pattern formation driven by stochastic resonance). The behavior of these percepts suggests that self-organized hallucinatory pattern formation in human vision is governed by the same cortical properties of localized processing, lateral inhibition, simultaneous contrast, and nonlinear retinotopic mapping that govern ordinary vision.

The visual cortex is active even in the absence of retinal stimulation; this spatiotemporally structured neural activity may have perceptual implications (1–9). For example, Kenet et al. (3) (in visual cortex of anesthetized cats) find a succession of spontaneous patterned neural states that correspond to those induced by simple oriented geometric patterns. These specific neural patterns, if present in awake humans, must be subliminal. This result raises two intriguing questions (6). (i) Do analogous perceptible patterns arise in humans? (ii) If so, can they interact with neural activity evoked by physical stimuli to affect perception? To tackle these questions we consider stereotyped geometric hallucinations, often triggered by migraine, drug intoxications, and empty-field flicker (10–20); these phenomena are thought to arise from autonomous activity in visual cortex. Although little is known about how spontaneous activity affects the perception of physical stimuli, it is possible to approach the second question from another direction: How do physical stimuli affect perception of spontaneous activity? Here we explore three circumstances in which physical stimuli dictate perceivable cortical pattern formation.

The most common geometric hallucinatory forms are lattices, spirals, concentric circles, and fan shapes (Fig. 1). We regard these hallucinations as spontaneous states because they are apparently self-organized by visual cortex (14–20) and can arise without visual stimulation; these perceptible states may be analogous to Kenet et al.'s (3) subliminal states (9). Their geometric forms are predicted by neural network models that generate stripe patterns of neural activity whose spatial orientation on cortex combines with the nonlinear retinocortical mapping to determine the perceptual effect (14–20) (Fig. 1). To study self-organized perceptual pattern formation and its interactions with physical stimuli, we used flicker-induced hallucinations. Unfortunately, perception of flicker-induced form is multistable, the fleeting shapes obscured by a riot of dynamic form and color that thwarts serious study. Related patterns are found throughout nature; a well studied case is convective current in fluids heated from below and cooled from above. Parallel rolls (rotating cylinders of rising and falling liquid) may form in any random orientation, but if an upwelling is imposed at a specific orientation (Fig. 2) the rest of the system falls in line (21). The upwelling is an initial internal boundary condition that constrains the global behavior of the entire system, like a seed pattern guiding crystal growth [see supporting information (SI) Text]. We tried to create an analogous perceptual system by “seeding” flicker-induced pattern formation. We flickered a monitor to induce geometric hallucinations and introduced small geometric patterns to try to induce specific geometric forms (e.g., a physical set of central concentric circles was expected to bias the surrounding hallucination to circles as well). Instead, to our surprise, we found that centrally presented flickering circles biased the surrounding hallucination to fan-shaped patterns and vice versa (Fig. 3 a and b). This led to a series of three experiments, the first to document the effect and the others to place it in context with related pattern formation phenomena.

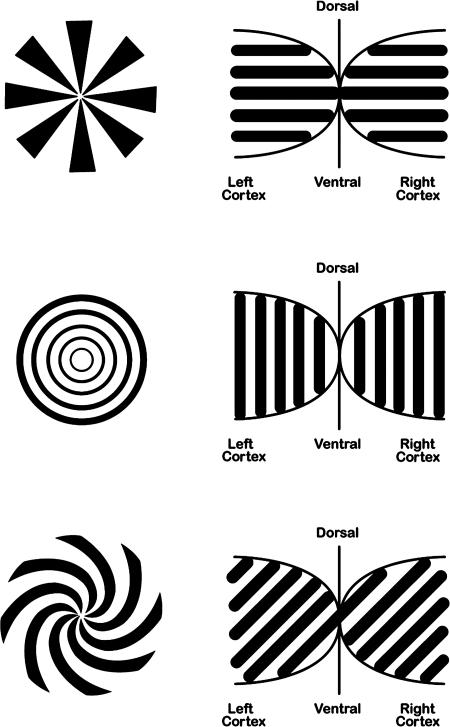
Fig. 1.

Some visual stimulus geometries on retina (Left) that map to cortex (Right) as parallel stripes of various orientations (14, 15). Conversely, if a parallel stripe neural activity pattern is produced on cortex (e.g., by flickering an empty field), its orientation determines the form of the induced hallucination. The patterns shown in Left can also be used to bias flicker-induced hallucinations by inducing simultaneous contrast effects (between orthogonal patterns) in adjacent flickering fields (e.g., Fig. 3).

Fig. 2.

Biasing pattern formation in fluid dynamics. Simulations of Rayleigh–Bernard convection in a pan of fluid heated from below and cooled from above. Convection organizes into spinning cylinders of rising hot and falling cool fluid, which look like stripes when viewed from above. The orientation of the stripe patterns is usually random but is biased by injection of fluid along a particular orientation, shown by the straight bars in the first (T = 0) row. (a and b) Two biasing experiments during 200 time steps. (c) A conflict set up by two orientated injections, one 90% as strong as the other. The induced patterns compete, but the one induced by the stronger injection wins out. [Reproduced with permission from ref. 21 (Copyright 2004, Springer Science and Business Media).]

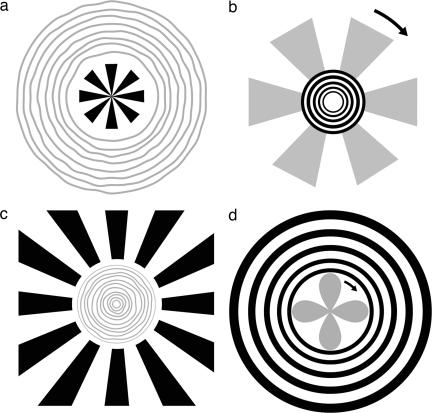
Fig. 3.

Lateral interactions between some biasing stimuli and hallucinatory percepts. Shown are an artist's depictions of some subject reports. Physical biasing patterns are shown in black, and hallucinations are shown in gray (depicting the shadowy nature of the percepts). (a) If the area around a small fan shape is flickered, subjects report seeing illusory circular patterns. (b) If the area around a circular pattern is flickered, all subjects report seeing an illusory rotating fan shape. If the circles are flickering too, the rotating fan shape extends through the physical circles. The direction of rotation is arbitrary and subject to reversal; the number of illusory features is often but not always proportional to the physical stimulus. (c) Similar geometrical effects occur if the biasing area is presented in the periphery and the empty central area is flickered. In this case the percept is often of tightly packed rings. (d) A rotating petal-like pattern often appears in the flickering central area.

Experiment 1

Simultaneous Contrast in Biased Hallucinations.

To better understand this counterintuitive spatially opponent hallucinatory pattern formation, we considered MacKay's effect (22, 23); if flickered, radial patterns seem to be overlaid with circles and vice versa. MacKay's effect is consistent with a sequential contrast mechanism: the physical image seen in the on-flash of the illuminant and its opponent form seen in the off-phase (like a negative afterimage, but in geometry instead of contrast). Could the phenomena we observed be the analogous result of simultaneous contrast: spatial opponency between a pattern and its opponent form? If so, we expect both central and surrounding (annular) forms (Fig. 3) would bias flicker-induced hallucinations.

Results.

(i) Observers reported induced hallucinations over the full range of viewing conditions and flicker rates used; all observers reported strong hallucinations for 15-Hz flicker and 2-m viewing distance (the distance we adopted for Exp. 2 and Exp. 3). For both center and surround stimuli (e.g., bold portions of Fig. 3), the induced hallucinations (gray portions of Fig. 3) were orthogonal to the physical inducing stimuli, consistent with a simultaneous contrast mechanism: radial patterns induce illusory circles in adjacent flickering fields; circular patterns induce illusory radial (typically fan blades) shapes; and clockwise spirals induce counterclockwise illusory spirals. In general, induced fan shapes are easier to see than induced circles, and both are clearer than induced spirals: seven of seven subjects saw both the induced circles and fan shapes, only four of seven subjects saw spirals, and the other subjects saw some kind of fleeting radial pattern. Compared with empty-field flicker-induced geometric patterns, which may take as long as 30 s of viewing before appearing, and then change unpredictably, the biased hallucinations are far more stable and appear much faster, generally within a few seconds. A pilot study of two observers found that, for the center-based physical stimuli, physical extents of 1/10th to one-third of screen size were all effective in inducing hallucinations, and for the one-third of screen size condition the number of induced hallucinatory features was roughly proportional to the number of physical features in the stimulus. (ii) The effects are tightly localized to the flickering field; the hallucination can extend through the biasing stimulus, but only if the biasing region is flickered in-phase with the adjacent flickering regions where the pure hallucination is seen. Thus, the classic MacKay effect occurs when the biasing stimulus is enlarged to include the entire flickering field. (iii) The biasing effect is seen whenever the contrast of the biasing stimulus is just above detection threshold, and no hysteresis is observed when the contrast is reduced below detection threshold or increased above it. (iv) The induced fan shapes and spirals usually rotate; direction of rotation was multistable. Based on comparison to a rotating disk, rotation rate was between 0.75 and 1.3 revolutions per second. All of these effects are easily demonstrated^§ (see SI Text).

Experiment 2

Hallucinations Induced by Apparent Motion.

Exp. 1 provides a line of evidence that spontaneous cortical activity can perceptually interact with activity induced by physical stimuli, but this inference would be more compelling if additional lines of evidence were available. Of course, empty-field flicker is not the only photopic way to induce geometric hallucinations; two other methods are found in the literature, and these motivated further study on how universal the results of Exp. 1 might be. The first method was reported by Mayzner (24) but was never confirmed or followed up. Mayzner (24) remarks in passing that, under low-light conditions, illusory motion produced by turning icons on and off around a circular or square area (e.g., Fig. 4) induces a rotating illusory fan-like pattern. Because of the similarity of this description to the flicker-induced hallucinatory rotating fan shapes of Exp. 1, we explored hallucinatory patterns induced by apparent motion of N icons around a square or circle of 16–40 lightable icons.

Fig. 4.

An apparent motion stimulus configuration for inducing pattern formation. A square is defined by the illusory movement of 20 icons. If, for example, every fourth icon is lit and then extinguished followed by the icons clockwise to them, and so on, the percept is of five icons moving clockwise around an imaginary square. If the room lights are extinguished, the interior of the square fills with illusory colored textures (generally smoky or taffy-like) and a five-bladed fan appears and rotates in time with the icons. Additional blades can appear fleetingly if visual persistence leaves some extinguished icons visible (depicted here as filled gray squares). Active icons are shown here as filled white squares; inactive icons are depicted as black squares with a broken white outline.

Results.

We found the following: (i) The initial perception (in the area enclosed by illusory motion) is a streaked texture resembling multicolored smoke or taffy. It is initially gray but acquires color after a few seconds (e.g., green, purple, and black). The overall organization of this texture is circular or spiral, like a bird's nest or storm pattern. The icons can also take on color, usually pinks, blues, and yellowish greens, but these are less saturated than the colors in the haze. These color effects were not as striking as those reported by Mayzner (24). (ii) Long gray spiral arms emerge from this central storm pattern and reach toward the moving icons, rotating in time with them. Upon continued inspection, the rotating spiral arms straighten to form a rotating fan shape or propeller shape (Fig. 4). If no ghost icons are visible, the blades of the fan can be broad and can appear to reach between the icons. The percept's transition from grayish texture to rotating fan evolves over ≈10–30 s. (iii) Number of arms is always an integer multiple of the number of lit icons, with extra arms appearing when visual persistence leaves ghost icons on the screen; the extra arms are not as stable as those associated with active icons and are reminiscent of illusory spokes and streaks seen in some motion-induced effects (25, 26). (iv) At high presentation rates (so that all icons are visible), the arms often appear stationary. When they do rotate, direction and speed are multistable and can be reversed or nulled by mental effort. As in Exp. 1, the perceptual pattern formation is localized; hallucinatory arms and colors are confined to the region enclosed by the icons. (v) At the highest speeds, color is lost and the icons appear identical. There is no apparent motion of the icons for this case. The central figure resembles a gear with as many teeth as icons, and the flickering or shimmering of the icons appears as if it were due to the nubbly teeth of the gear rotating over the icons, or as if seen through a shimmering rotating haze.

Experiment 3

MacKay Effects in Filtered Noise.

The evoked percepts of Exp. 1 are simultaneous contrast versions of the sequential contrast hallucinatory orthogonal forms described by MacKay (22). There are other versions of these “MacKay effects” that are seen when viewing spatiotemporal “white” noise through a black-and-transparent geometric mask (23). For example, TV “snow” viewed through a transparency of concentric circles appears to stream in a radial fashion, but the same white noise pattern viewed through a fan-shaped mask appears to stream in a circular fashion. Moreover, the noise through the mask can appear to organize into coherent orthogonal patterns. Our preliminary observations indicated that MacKay's method produced weak and fleeting results, an improved method would needed to study interactions between spontaneous activity and physical stimuli. Intriguingly, these MacKay effects depended on which unused TV channel generated the noise, suggesting that the statistics of the noise might be important. In follow-up experiments using filtered noises, we found that some noise statistics were far more effective in generating hallucinatory patterns. The resulting hallucinatory rotating fans and pulsating concentric rings were strikingly similar to those seen in Exp. 1 and Exp. 2. There is a growing literature on noise-mediated stimulus amplification and pattern formation (27, 28). In this “stochastic resonance” the statistics of the noise is often important (see SI Text for review); therefore, we systematically explored the effects of spatiotemporal filtered noise in the MacKay effect in hope of optimizing the pattern formation.

Results.

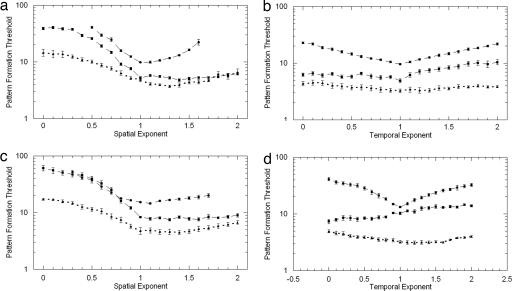
(i) All observers report that for, low spatial exponents (whiter Fourier spectra), the classic MacKay effect often occurs: subjects report noise streaming orthogonally to the black-and-transparent geometric mask. As the spatial exponent increases (becoming “pink noise”; see SI Fig. 6, for example), actual pattern formation occurs; subjects report shadowy illusory fan shapes overlying both the physical circles and the noise and illusory circles overlying the physical fan shapes and noise (two-thirds of our observers also saw these forms for white noise, but only at much higher noise contrasts). (ii) Illusory fan shapes (very similar to those seen in Exp. 1 and Exp. 2) rotate; rotation direction is stable and can be reversed by mental effort. Illusory circular shapes (very similar to those seen in Exp. 1) pulsate or wobble. Interestingly, rotating fan and pulsating circular hallucinations in the presence of noise are predicted by Tass (17). (iii) For all subjects, the noise contrast required for pattern formation dropped dramatically as the spatial exponent was increased from 0 to ≈1.0–1.4 (Fig. 5 a and c); these exponents are typical of the statistics of natural images (29). This effect is similar to that predicted by Busch et al. (28) from simulations of spatiotemporal stochastic resonance in pattern-forming neural networks. Similar tuning for temporal frequency exponents is not evident (Fig. 5 b and d), but illusory fans/circles appear to rotate/pulsate faster for lower temporal exponents. (iv) Noise contrast affected the time required for pattern formation; at superthreshold contrast levels, the hallucinatory patterns appeared within a few seconds or were immediately visible, whereas at threshold the pattern could take ≈10–45 s to appear. (v) The hallucination disappears if the biasing mask is reduced in contrast (e.g., by raising the luminance of the opaque sections); no perceptual inertia (hysteresis) was observed as mask contrast was varied above/below threshold.

Fig. 5.

Effects of 1/f filtered noise on hallucinatory pattern formation. We plot the rms contrast of the spatiotemporal noise needed to induce illusory pattern formation when spatiotemporal noise is viewed through a geometric mask pattern. The independent variable is the exponent (α or β) of the spatial or temporal frequency spectra of the kf_t^−αf_s^−β noise being varied in each experiment. Three observers' data are shown; each line of data is the average of nine runs (≈9 h of data); error bars are ± 1 SE. (a) Circular mask: detection of illusory fan shapes as a function of spatial spectra (α fixed at 1.0). (b) Circular mask: detection of illusory fan shapes as a function of temporal frequency spectra (β fixed at 1.0). (c) Fan-shaped mask: detection of illusory pulsating rings as a function of spatial frequency (α fixed at 1.0). (d) Fan-shaped mask: detection of illusory rings as a function of temporal spectra (β fixed at 1.0).

Discussion

Kenet et al. (3) find a succession of spontaneous patterned neural states in visual cortex of anesthetized animals that correspond to activity elicited by oriented optical stimuli. Arieli et al. (1) and Ringach (6) suggest that spontaneous ongoing cortical activity might interact with activity evoked by sensory signals, with implications for perception. Our experiments provide three relatively independent existence proofs for such interactions: it is easy to use physical stimuli to select specific hallucinations from the class of those patterns previously predicted to arise from spontaneous cortical activity. Moreover, in our experiments the interactions between induced pattern formation and physical stimuli follow simple rules and display striking similarities to the findings of Kenet et al. (3) and related pattern formation studies, which we summarize below.

Multistability.

Empty-field flicker elicits a bewildering succession of perceptual states. A subject may fleetingly perceive a fan shape before a hexagonal lattice appears, which in turn gives way to a spiral. Theoretically, no spontaneous state is predominant, and, experimentally, none are stable, perhaps because each flicker can disturb the previously elicited state. This is analogous to the random succession of spontaneous orientation states in cat cortex found by Kenet et al. (3).

Salience.

Some interaction patterns are more salient and stable than others. Induced fan-shape hallucinations are more salient and stable than hallucinatory circles, which are more salient and stable than hallucinatory spirals. This is analogous to Kenet et al.'s finding that some spontaneous orientation states occur more often than others (3). Goldberg et al. (9) treat the orientation states that Kenet et al. (3) find, as well as the orientation patterns of Ermentrout and Cowan (14), as subsets of the larger domain of possible spontaneous cortical states; if so, the most salient/stable states we found may be biased by the underlying spontaneous activity.

Pattern Formation Rules.

The induced shapes are orthogonal in inferred neural activity to the cortical mapping of the physical stimulus, suggesting an interesting perceptual and neural opponency consonant with similar opponencies seen in other circumstances (22, 23, 30–33). The opponency is not predictable from the Ermentrout and Cowan simplest model (14) but would likely be accommodated by modified versions of models that have anisotropic cortical connection properties (e.g., refs. 19, 20, and 34) (see SI Text). The interaction between the physical stimulus and the induced hallucinatory state displays spatial opponency (lateral inhibition) as well as pattern opponency. If the physical stimulus is presented centrally, the hallucination appears in the flickering surround; if the physical stimulus is an annulus, the hallucination appears in the flickering center. This spatial interaction is localized; the hallucination does not extend through the physical stimulus unless the physical stimulus flickers in-phase with the adjacent flickering field. Nor do hallucinations extend into empty nonflickering regions. This implies that the connectivity of the underlying neural network is not global. We saw no evidence of perceptual inertia (e.g., hysteresis) under any condition; the biased hallucination appears to be stimulus-locked to the interacting physical pattern.

Spatial and Temporal Scales.

Spontaneous percepts have preferred spatial and temporal scales, which can be manipulated by stimulus and cognitive conditions. Fan-shaped mescaline hallucinations have a spatial frequency of up to ≈15 features per hemifield, suggesting a spatial scale of ≈2 mm on primary visual cortex, comparable to the size of an orientation hypercolumn (15, 19, 20). This spatial scale can be altered by physical interactions; e.g., the illusions driven by fractal noises or apparent motion are highly dependent on the spatial and temporal statistics of the noise or the speed of the apparent movement. The ability to manipulate the spatial and temporal scales of these phenomena has implications for functional imaging tests of the underlying Ermentrout and Cowan (14) theory of perceptual pattern formation (see SI Fig. 6 and SI Text). Finally, we note that the phenomena we found result from exploration of a small corner of the larger parameter space of potential experimental manipulations; other phenomena may remain unrevealed.

Materials and Methods

Experiment 1.

Stimuli were generated on a photometrically calibrated VisionWorks system (Vision Research Graphics, Durham, NH). For center stimuli (e.g., Fig. 3 a and b, bold, or Fig. 1 Left), black/white targets were 8 cm in diameter on a 25 × 30-cm cathode ray tube display. For surround stimuli (e.g., Fig. 3 c and d) targets were 24 cm wide with an 8-cm aperture. Both the stimulus and flickering field had a space-time averaged luminance of 40 cd/m². The seven subjects (the authors and five psychophysicist colleagues) all had 6/6 or better corrected acuity; two available subjects made detailed observations, while the other five subjects were used to confirm the generality of the percepts.^§ Informed consent was given; all experiments were in accord with our institutions' human use rules. Subjects free-viewed each stimulus for a few minutes and described any illusory percepts that formed. Because little was known about biased hallucinations, we allowed subjects to maximize percept strength by varying viewing distance from 1 to 3 m and flicker rate from 10 to 20 Hz. Both binocular and monocular viewing was used, with natural pupils in a dark room.

Experiment 2.

Apparatus and subjects were as for Exp. 1; two available subjects made detailed observations, while the other five subjects were used to confirm the generality of the percepts. Dynamic arrays of small (5 × 5 mm) square white (80 cd/m²) icons on a black cathode ray tube screen were binocularly viewed at a distance of 2 m in a dark room. The icons were arranged into circular or square geometries of 16–40 lightable icons, with 4–10 active at any instant. Apparent motion was induced by turning on and off adjacent icons in a sequence. For example, Fig. 4 shows a square defined by 20 icons. If we light every fourth icon, then turn them off and light the icons clockwise to the first set, and so on, we see five lights moving around an imaginary square, “taking the corners like ducks in a shooting gallery” (24). If time between switching icons is short, visual persistence leaves “ghost” icons on the screen as well. Subjects viewed each stimulus for several minutes and made continuous reports on illusory forms appearing on the display.

Experiment 3.

Three observers were corrected to 6/6 or better acuity.^§ Subject 1 (an author) and subject 2 are psychophysicists with prior work in the psychophysics of white and filtered spatial noise and who participated in the above experiments. Subject 3 was also an experienced observer. Subjects 2 and 3 were naïve about the experiment's rationale. Observers were seated and viewed stimuli binocularly with natural pupils in a dark room. The stimuli were spatiotemporal, gray-scale, random-phase fractals viewed through digital black-and-transparent geometric masking patterns on a linearized cathode ray tube 2 m away. Each stimulus sequence was created by producing 64 frames of random white noise images (each 256 × 256 pixels with 256 grayscale). This formed a data matrix (256 × 256 × 64) that was Fourier-transformed. The resulting spectra were digitally filtered so that the amplitude spectrum varied over time following the power law relationship 1/f_t^α, and over space (isotropically over both coordinates) following the power law relationship 1/f_s^β, f_s = (f_x² + f_y²)^1/2; e.g., the spatiotemporal amplitude spectra were of the form A(f_t,f_s) = kf_t^−αf_s^−β. The spectra were inverse-Fourier-transformed to produce the stimulus image sequence; average luminance was constant at 18.8 cd/m². The geometric patterns used as masks of the noise were fan shapes and concentric circles; in pilot experiments we found that fan-shaped patterns with alternating 16 black and 16 transparent sectors worked well, as did a concentric circular pattern consisting of alternating nine black and nine transparent circles; these masks were used in all subsequent measurements. The masks were shown at 512 × 512 resolution to avoid aliasing (which manifest as “jaggies” on fan-shaped patterns and “terraces” on circular patterns). To combine the 256 × 256 noise stimuli and the 512 × 512 mask, noise pixels were “fattened” by making each computed pixel occupy a 2 × 2 pixel area on the monitor. For spatial tuning experiments, the temporal exponent was fixed at 1.0 and 21 spatial exponents (β = 0.0–2.0) were shown. In temporal tuning experiments, the spatial exponent was fixed at 1.0 and 21 temporal exponents (α = 0.0–2.0) were shown. Each stimulus subtended 5.55° and lasted 2 s (at a frame rate of 32 Hz) and was shown in a continuous loop. Subjects used the method of adjustment to find the rms noise contrast (the standard deviation of the noise pixels' gray level distribution) needed to see illusory fan shapes or concentric circles in the noise (each trial took ≈4–5 min). Subjects were familiarized with unmasked noise stimuli to avoid reporting filtered noise patterns; even so, one subject could not do the experiment for very high spatial exponents. For each stimulus condition, each subject made this determination three times for three different values of the random number generator, and the results of these nine runs were averaged. These experiments took ≈50 h per subject, broken into 1- to 2-h blocks over several months.