Measuring the Force Production of the Hormogonia of Mastigocladus laminosus

Abstract

The cyanobacterium Mastigocladus laminosus forms hormogonia, which glide slowly away from the parent colony by extruding slime out of nozzles. Using video microscopy, we observed hormogonia embedded in and moving through 1–4% agar solutions with an average velocity of 0.5 μm/s. Agar is non-Newtonian and is subject to shear-thinning so that its viscosity greatly increases at low shear rates. We measured the viscosity of these agar solutions at the very low shear rates appropriate for gliding hormogonia and found it to vary from 1 to 52 million centipoise. Then, by applying a Newtonian drag coefficient for a 100-μm-long, cigar-shaped hormogonium, we found that it produced a force of several million pN. A typical hormogonium has 10–100 thousand 9-nm-wide slime extrusion nozzles. Wolgemuth et al. have proposed hydration-driven swelling of the polyelectrolyte slime ejected from these nozzles as the force production mechanism, and our experiment found a large nozzle force that was consistent with this hypothesis. Average single nozzle force depended on viscosity, being large when the viscosity was high: 71 pN in 3% and 126 pN in 4% agar.

INTRODUCTION

Mastigocladus laminosus (ML) is a thermotolerant, filamentous, true-branching cyanobacterium that lives in a viscous biofilm on surfaces in hot springs up to 64°C (1). In laboratory culture, the optimum temperature for reproduction was 48°C (1). Mature cultures consist of relatively old, wide filaments that branch frequently to form younger, thinner filaments, shaping a dense mat of intertwined filaments. The cells of the older filaments are round, whereas the cells of the younger ones are cylindrical. These younger filaments can differentiate into motile hormogonia when growing on a wettable surface.

When hormogonia are produced, they consist of a chain of three to several hundred cylindrical cells. The cells at the two ends of a hormogonium are slightly tapered. These hormogonia move through the surrounding medium away from their branching filaments, or parental trichome, for ∼24 h before they begin to differentiate into sedentary thick filaments (2). ML hormogonia employ “gliding” motility, apparently propelling themselves by extruding slime. This slime has the advantage of creating a viscous niche that excludes other bacteria. By contrast, other bacteria move by rotary flagellar motors (3), polymerization force (3), or by attaching pili to other bacteria and then retracting them (4).

Different kinds of motility involve distinct molecular motors: in mammals kinesin-tubulin generates force in the 4-6 pN range, myosin-actin 1-10 pN, RNA polymerase up to 25 pN, and DNA polymerase as high as 34 pN (3). In the realm of bacteria, a 2-μm-long Escherichia coli swimming with its six flagella in water at 20 μm/s produces ∼1 pN of force (5). The 1-μm-long pathogenic bacterium Listeria monocytogenes uses actin polymerization to produce a force in the piconewton range that allows it to puncture the cell wall and move through the cytoplasm of a host cell at ∼1 μm/s (3). We chose to investigate ML because its hormogonia are able to move in an extraordinarily viscous environment (2), indicating that they likely possess a formidable molecular motor.

A typical 120-μm-long hormogonium has ∼50,000 9-nm-wide nozzles (see Fig. 1 E) that extrude polyelectrolyte slime. Here we will show that in high background viscosity a single nozzle is able to generate more than 100 pN of force, considerably more than these other molecular motors.

FIGURE 1.

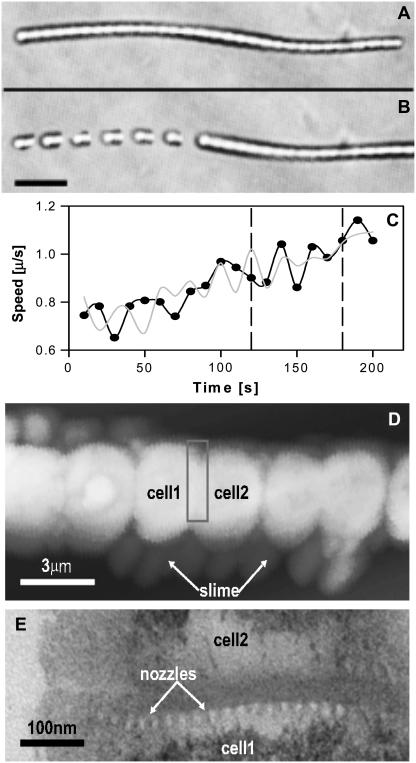
A 120-μm-long hormogonium (A) embedded in a 1% agar solution and (B) gliding rightward at 0.9 μm/s (composite image with snapshots at 10-s intervals; 20-μm scale bar). (C) Velocity versus time for its left (back) end (dark trace) and right (front) end (light trace). Images in B were taken from between the dashed lines. (D) AFM of slime being ejected from a hormogonium (3-μm scale bar). (E) The bright dots in the horizontal band are slime-ejection nozzles on a septum between two cells (TEM; 100-nm scale bar, part E taken as if box in part D were enlarged and rotated 90°).

METHODS

We used Difco granulated agar (Becton Dickinson, Sparks, MD) and mixed it into medium B buffered with HEPES to a pH of 8.0 (B-HEPES or BH) as previously described (2). We then employed a DV-II spindle viscometer (Brookfield Engineering, Middleborough, MA) to measure the viscosity of these agar-BH solutions at ∼48°C (6) because this is where ML hormogonia exhibit their greatest motility (2). We first tested our spindle viscometer with 1-cP and 500-cP standards. Also, because close proximity to a wall is known to increase viscosity, our 3- to 10-mm spindles were placed in the center of a 10-cm-wide beaker. As a control, we placed a spindle 1 cm away from the beaker wall and observed that the measured viscosity increased by ∼50%. We kept the ratio of our spindle diameter to beaker diameter <0.1. Additionally, we measured viscosity in a larger beaker 14 cm in diameter and saw no significant difference in the measured viscosity, indicating that we were measuring the bulk viscosity of the agar.

We grew ML UTEX 1931 cultures by first incubating them in 250-ml culture tubes filled with BH (no agar). The tubes were heated by a circulating 48°C bath and lit by fluorescent light provided by two Phillips Coolwhite bulbs. We bubbled a sterile 2% CO₂/air (vol/vol) mixture through the cultures.

We removed millimeter-sized ML colonies from the culture tubes and implanted them in a thin layer of agar-BH in petri dishes, pouring agar-BH on top and allowing it to gel, thereby insuring that the ML was completely embedded in the agar-BH. Then we incubated the dishes for a period of 31 h at ∼48°C on a copper table lit by an array of 100-watt incandescent bulbs. We then took samples from the petri dishes, placed them on slides, and viewed them on a temperature-regulated microscope stage held at 47°C.

We imaged the gliding hormogonia at 200× magnification using a Nikon Optiphot microscope (Nikon, Garden City, NY). To record images we used a CCD camera connected to a Metamorph image processing system (Molecular Devices, Downingtown, PA) running on a PC. Image processing was done both on Metamorph and on GIMP (GNU Image Manipulation Program, version 2.2.10) running on a laptop. Polystyrene microspheres 1.8 μm in diameter (Sigma Aldrich, Saint Louis, MO) were sometimes also embedded into the agar-BH to increase contrast to track the drag effects a gliding hormogonium had on its agar surround. Here we employ the GIMP function called grain extraction between an earlier and a later image. Grain extraction starts with a gray background and overlays a subtraction of the second image from the first, so that identical features are turned gray and differences become white or black. Thus, grain extraction is ideal for showing wakes that trail moving objects.

Atomic force microscopy (AFM) images were taken with a Digital Instruments NanoScope IIIa scanning probe microscope equipped with a digital camera. For transmission electron microscopy (TEM) hormogonia were centrifuged at 2000 × g for 10 min, rinsed in 0.1 M sodium cacodylate buffer (adjusted to pH 7.2–7.4), and fixed overnight in 2.5% glutaraldehyde in the same cacodylate buffer. After primary fixation the hormogonial pellet was postfixed in osmium tetroxide for 52 h. Pellets were then dehydrated in a graded ethanol series and infiltrated with Epon for 2 h at 50°C, embedded in fresh Epon, and polymerized overnight at 60°C. Ultrathin sections were taken with a Reichert-Jung Ultracutt E ultramicrotome and placed on uncoated copper mesh grids. Sections were routinely stained in Reynold's lead citrate, uranyl acetate, then again in Reynold's lead citrate for 30 s, 4 min, and 30 s, respectively. TEM images were taken with a JEOL JEM1200EXII equipped with a digital camera.

RESULTS

A sequence with a motile hormogonium embedded in an agar solution gliding rightward is shown in Fig. 1, A and B. The background is clear, and the bulk viscosity was measured to be 900,000 cP. Fig. 1 C is a velocity plot at 10-s intervals, which shows large fluctuations indicating that either the hormogonium's force production mechanism is intrinsically noisy or that the drag it experiences is nonuniform, or possibly both. The hormogonium's front and back ends move simultaneously at velocities that can differ by as much as 20%. Later (see Fig. 3) we show evidence that individual sections of the hormogonium move close to stall in a sort of stick-slip motion through the viscoelastic agar. Fig. 1 D is an AFM that shows slime that is being ejected by a hormogonium's nozzles. Fig. 1 E is a TEM that shows how the nozzles are grouped into rings at both ends of a cell.

FIGURE 3.

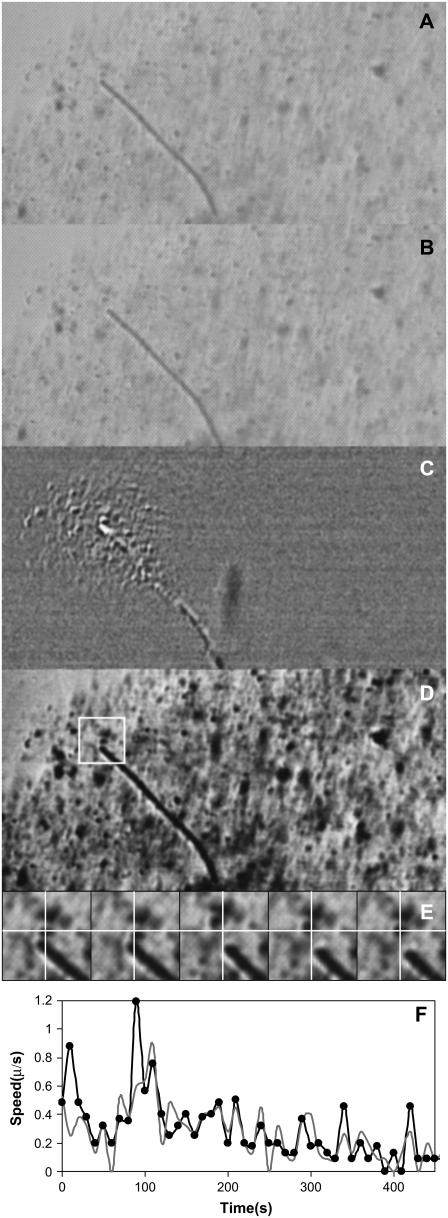
A gliding hormogonium couples to and disturbs a large volume of the agar that surrounds it. (A) Video image of a hormogonium gliding southeast at 0.1 μm/s through 1% agar. To enhance contrast a 0.05% volume fraction of 1.8-μm-diameter polystyrene microspheres was embedded in the agar. (B) Video image of the same hormogonium 60 s later. (C) Contrast-enhanced grain extraction between images A and B (see Methods). Undisturbed regions of agar turn gray, whereas a pattern of light and dark reveals a difference in the surround that is caused by the hormogonium's motion. The right part of the image contains no moving hormogonia and is uniformly gray. (D) Contrast-enhanced version of A. Punctate black dots are polystyrene microspheres. (E) Evidently the surrounding agar moves in a sort of stick-slip motion as the hormogonium passes. Shown is the motion of a single microsphere near the tail of the hormogonium (white box in D). The white cross-hairs remain fixed on the pixel marking the sphere's center in the first image. This sphere oscillates back and forth ∼10 times as the hormogonium passes (a single oscillation is shown; images spaced at 5-s intervals; image 24 μm wide). (F) Velocity versus time for the hormogonium's front end (light trace) and back end (dark trace). Note that here the hormogonium is gliding very close to stall.

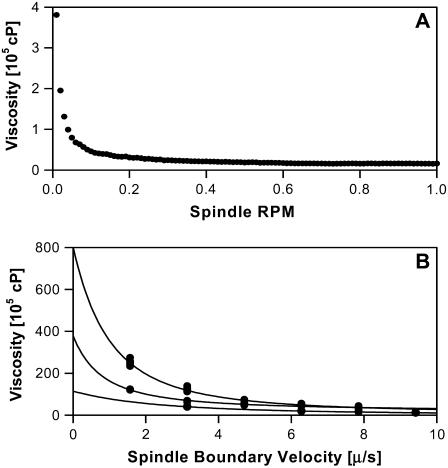
Viscosity is defined as the ratio of shear stress to shear rate (6). Hormogonia glide slowly through agar, a non-Newtonian pseudoplastic, which is shear-thinning so that its viscosity greatly increases at low shear rates (6,7). Here low-velocity motion is thought to provide insufficient energy to disrupt the binding structure of a shear-thinning fluid's surround so that the result is a significantly higher measured viscosity (7). Hormogonia glide at ∼0.5 μm/s, are ∼100 μm in length, and we later show that they leave behind them a wake of disturbed agar similar to this length scale. Thus, the velocity gradient in their vicinity is such that their 0.5 μm/s velocity declines to near zero across ∼100 μm, which implies that a shear rate of 0.01 s⁻¹ should reasonably approximate the gliding motility of a hormogonium. Therefore, we measure the agar's viscosity with our spindle rotating at 0.01 rpm, the minimum rate at which our Brookfield viscometer is able to measure viscosity, noting that this corresponds approximately to a shear rate of 0.01 s⁻¹ (7) and that the spindle boundary is rotating in the micrometer-per-second range. Fig. 2 A is a plot of viscosity versus spindle rotation rate that demonstrates shear-thinning behavior for 1% agar and fits well to the power law fluid model with a power law exponent n = 0.1, which is indicative of strong shear-thinning (6). Fig. 2 B shows viscosities at higher agar concentrations for spindle boundary velocities approaching the micrometer-per-second range. We note that 2%, 3%, and 4% agar did not fit well to the power law fluid model and that we were unable to see any plateau in the viscosity at very low shear rates.

FIGURE 2.

(A) Plot of viscosity versus spindle rotation speed for a 1% agar solution that demonstrates shear-thinning behavior. Note that 0.01 rpm corresponds to a spindle boundary velocity of 5.5 μm/s (LV2C spindle). (B) Viscosity versus the velocity at the spindle boundary for dense agar solutions (2% bottom, 31 dp at each speed; 3% middle, 30 dp at each speed; 4% top, 21 dp at each speed). Note that gliding hormogonia move in the micrometer-per-second velocity range and that the fits are simply guides for the eye.

Another consideration is whether a motile hormogonium experiences the same viscosity as does our viscometer. Viscometer spindles are 3–10 mm in diameter and measure macroscopic viscosity. However, an entangled polymer solution such as agar is full of pores with a characteristic size scale so that when a rigid object is larger than the pore size the effective viscosity it sees approaches that of the entangled solution, whereas if it is smaller than the pore size its movement is controlled by the viscosity of the pure solvent (8). The pore size for our 1–4% agar solutions is <200 nm (9) and is ∼30 nm in 4% agar (10,11), which are far below the size of a 3-μm-diameter hormogonium. Thus, it is reasonable to conclude that a hormogonium's movement should be controlled by the macroscopic viscosity of the entangled agar solution.

Also, a second possibility exists in which the hormogonium employs its polyelectrolyte slime to “grease” its way through the agar without greatly disturbing its surroundings. If this were true, then it should be required to produce much less force than expected. Fig. 3 A is a video image of a hormogonium, whereas Fig. 3 B shows the same hormogonium 60 s later. Fig. 3 C is a grain extraction between A and B, a technique that is used to reveal motion within a region (see Methods). The hormogonium is moving through a 1% agar solution whose contrast has been enhanced by the addition of polystyrene microspheres. These microspheres remain trapped in the agar and give no evidence of diffusion, consistent with their 1.8-μm diameter being well above the agar's pore size (8,9). However, when the hormogonium passes, it disturbs the agar and displaces the microspheres. The hormogonium leaves a large white and black triangular region in its wake, evidence that its motion is disturbing a large volume of agar several hundred micrometers in diameter. Fig. 3 D is a contrast-enhanced image of the same hormogonium that emphasizes the locations of the microspheres. Fig. 3 E focuses on a single microsphere (in the box in D) that is trapped in the agar and oscillating back and forth in the hormogonium's wake. The microsphere is dragged along by the hormogonium, then slips back because of the viscoelastic agar, is dragged again, slips back, etc. This sphere oscillated ∼10 times as the hormogonium passed. Evidently the hormogonium is strongly coupled to its high-viscosity agar surround. Fig. 3 F (like Fig. 1 C) shows the velocity fluctuations of the hormogonium's head and tail. Here quite clearly the hormogonium is moving very close to stall, which is caused by its dragging a large mass of agar along with it. We show this in a short movie, an animated gif with 60 frames and 600 s of video compressed down to 6 s, located at http://www.geocities.com/zorukonotsu/horm3.gif.

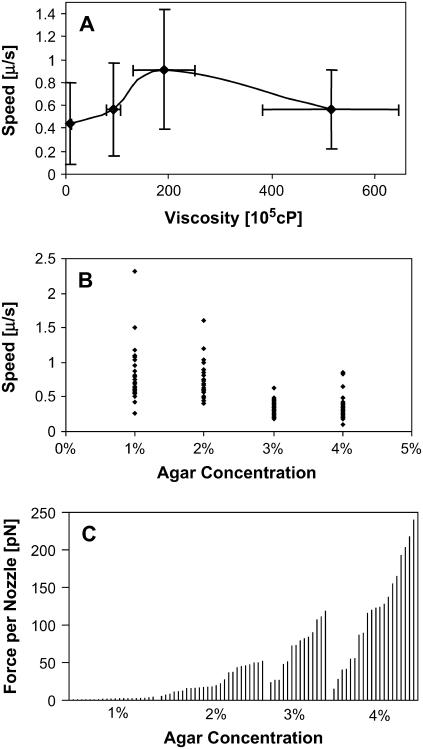
Fig. 4 A shows that hormogonia are able to move at ∼0.5 μm/s in solutions with viscosities ranging from 1 to 52 million centipoise. Fig. 4 B emphasizes that the movement of a single hormogonium has intrinsic large-velocity fluctuations. Fig. 4 C is a force/nozzle histogram for 80 hormogonia. To obtain the force, we multiplied the Newtonian drag coefficient for a cigar-shaped hormogonium by its velocity,

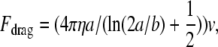where a = semimajor axis (half of the cigar's long axis), b = semiminor axis (half of the cigar's width), η is viscosity, and v is velocity (5).

FIGURE 4.

(A) Hormogonial velocity versus agar viscosity for 1%, 2%, 3%, and 4% agar concentrations (20 hormogonia per concentration; 1 standard deviation error bar). (B) Velocity fluctuations for four hormogonia. The movement of a single hormogonium is intrinsically noisy. (C) Force per nozzle for 80 individual hormogonia. Average nozzle force depends on the background viscosity.

There are many competing theories as to the appropriate drag coefficient to use for a shear-thinning fluid such as agar. The power law fluid model predicts an increase in the Newtonian drag coefficient by a factor between 1 and 2; however, the Carreau and Ellis models predict virtually no change from the Newtonian drag coefficient if the Reynolds number and shear rate are both small (6), both of which are true for our gliding hormogonia. Hence, we use a Newtonian drag coefficient.

We next estimate the number of nozzles as follows. Each cell can have up to three concentric rings of nozzles in an annulus near the septa separating one cell from another, with a spacing of 21 nm between nozzles (12). For a conservative estimate of the force per nozzle, we assume that all nozzles are operational, that all the cells have three rings of nozzles, and that each of these rings has a radius equal to the outer radius of the cell. This obtains ∼1300 nozzles for a typical 3.0-μm-wide cell. To obtain the number of cells, we measure the length of a hormogonium and divide by 3.5 μm, the average length of our cells. For example, we would estimate the 120-μm-long hormogonium in Fig. 1 A to have ∼45,000 left-pointing nozzles. Also note that our nozzle estimate is conservatively high, as not all septa actively produce slime (Fig. 1 D).

DISCUSSION

Wolgemuth, Hoiczyk, Kaiser, and Oster (WHKO) have proposed that polyelectrolyte slime experiences a hydration-driven swelling into a gel as it exits a nozzle, thus producing an entropic force (4). Further, they hypothesize that the negatively charged polyelectrolyte is kept in a deswelled state by a high nozzle concentration of Ca²⁺ counterions, which are then exchanged for K⁺ at the exit. Two terms act to swell the slime and produce force: Π_entropic, a pressure caused by the polyelectrolyte's entropy-driven expansion into the surround, and Π_ion, in which the Ca²⁺ counterions also make an entropy-driven pressure at the nozzle exit.

They fit their theory to Myxococcus xanthus (MX), a bacterium ∼10 μm long with several hundred nozzles at each end and moving through an environment with a viscosity in the range of 1–300 cP. The MX nozzle cavity is shaped like a barrel embedded in the bacterial cell wall: 32 nm in length, 6.5 nm in diameter at its entrance and exit ends, and bulging to 14 nm in the middle of the hydrophobic region (4). The nozzle is larger in size but similar in structure to the chamber of water that stabilizes ion transport through the hydrophobic region in the midbilayer of the K⁺ channel (13). Here it likely serves a similar function, as the lipid bilayer is a low-dielectric material, which necessarily makes repelling image charges that inhibit ion transport (14).

ML has more and larger nozzles than does MX. An ML hormogonium appears to have ∼10,000–100,000 9-nm exit-diameter nozzles (12). A variation of the WHKO theory that is easy to calculate and also able to produce considerable force would simply have the nozzles ejecting a stream of negatively charged monomers along with their Ca²⁺ counterions. This would require avoiding polymerization until outside the nozzle. There is precedence for such a trick: sea cucumber sperm block polymerization by avoiding nucleation centers so that the polymer chain is unable to begin growing (3). There is also some visual evidence for polymerization occurring outside the nozzle (not shown;12) in that ML's extruded slime appears to become more filamentous with increasing distance from the nozzle. If this mechanism were employed, then a nozzle could obtain a very large entropic force as both the monomers and counterions exit from their highly concentrated “nozzle” state. As an example, assume 1 M = 0.6/nm³ concentrations of Ca²⁺ and monomer in the nozzle. The osmotic pressure difference across the nozzle exit would be 2 Π = 2 ΔC K_BT = 2 (0.6/nm³) (4.1 pN nm), which leads to a force of ∼5 pN/nm². Thus, a nozzle with an exit surface area of 60 nm² could theoretically produce a force of ∼300 pN.

We observe hormogonia of the cyanobacterium ML moving at an average velocity of 0.5 μm/s through dense agar solutions with a viscosity in the many tens of millions of centipoise. A typical hormogonium has many tens of thousands of nozzles, which extrude slime and are thought to be responsible for its motility. We show that in a high background viscosity a single nozzle is able to produce a force in the 100-pN range.