Intermonolayer Friction and Surface Shear Viscosity of Lipid Bilayer Membranes

Abstract

The flow behavior of lipid bilayer membranes is characterized by a surface viscosity for in-plane shear deformations, and an intermonolayer friction coefficient for slip between the two leaflets of the bilayer. Both properties have been studied for a variety of coarse-grained double-tailed model lipids, using equilibrium and nonequilibrium molecular dynamics simulations. For lipids with two identical tails, the surface shear viscosity rises rapidly with tail length, while the intermonolayer friction coefficient is less sensitive to the tail length. Interdigitation of lipid tails across the bilayer midsurface, as observed for lipids with two distinct tails, strongly enhances the intermonolayer friction coefficient, but hardly affects the surface shear viscosity. The simulation results are compared against the available experimental data.

INTRODUCTION

Membranes play a vital role in living cells, where they act as semipermeable barriers, host numerous proteins, and provide mechanical strength while retaining a high degree of flexibility (1–3). Membranes consist of lipids, i.e., biological amphiphiles, which in an aqueous environment cluster into locally planar bilayered structures under a combination of hydrophobic and hydrophilic interactions. In the absence of covalent bonds between the lipids, a bilayer behaves as a two-dimensional liquid whose resistance against shear deformations is characterized by the surface shear viscosity η_s. Any relative motion between the two leaflets of a bilayer is opposed by a friction force; the ratio between the force per unit area and the slip velocity is known as the intermonolayer friction coefficient b. Living cells actively control these two flow properties by varying the mixture of lipids and sterols present in their membranes. Here we are interested in the flow properties of homogeneous bilayers, and how these are related to the constituent lipids.

Current experiments to measure surface shear viscosities of membranes are all based on a theory by Saffman (4) relating η_s to the translational diffusion coefficient D of a tracer particle confined to a membrane, i.e., a geometry-specific analog of the familiar Stokes-Einstein relation. Most viscosity measurements employ labeled membrane-bound proteins as the diffusing tracer particle (5,6), while recently latex spheres (7–9) and phase-separated lipid domains (10) have been used. Typical surface shear viscosities reported in the literature lie in the range of 10⁻⁷–10⁻⁶ surface poise (where 1 SP = 10⁻³ Pa m s). The best-studied tracer particles, however, are the lipids constituting the bilayer (6,11–15), but their lateral diffusion coefficients are rarely converted into surface viscosities because these tracers are considered too small for Saffman's continuum hydrodynamics model to hold true, and because lipids are strongly affected by microdomain formation within the membrane (6,9). Fluorescence-after-photobleaching experiments (11) indicate that the symmetric phosphatidylcholine lipids 1,2-dilauroyl-phosphatidylcholine (DLPC, diC12:0), 1,2-dimyristoyl-phosphatidylcholine (DMPC, diC14:0), and 1,2-dipalmitoyl-phosphatidylcholine (DPPC, diC16:0) have surprisingly similar diffusion coefficients at 50°C, despite the variation of their saturated tails from 12 to 16 carbon atoms, while the diffusion coefficient of the asymmetric 1-palmitoyl-2-oleoyl-phosphatidylcholine (POPC, C16:0/C18:1_c9) is lower by approximately one-third. In nuclear magnetic resonance measurements (13), however, the lipids DMPC, POPC, and 1,2-dioleoyl-phosphatidylcholine (DOPC, diC18:1_c9) are found to possess nearly identical diffusion coefficients, suggesting a remarkable insensitivity to tail length, symmetry, and saturation. A recent nuclear magnetic resonance study (15) reports a decrease in the lateral diffusion with increasing tail length for monounsaturated lipids with tails of up to 22 carbons. Addition of cholesterol, which is known to increase the ordering of the lipids and to induce domain formation, slows the lateral diffusion down, as does a reduction of the temperature (11,13). The surface shear viscosity, for which much fewer data are available, is expected to follow trends counter to those of the diffusion coefficient, i.e., η_s declines with increasing D and vice versa.

The intermonolayer friction coefficient, whose existence first came to prominence a decade ago (16–20), has been measured by a number of techniques. In the experiments described by Evans and Yeung (19), Raphael and Waugh (21), and by Chizmadzhev et al. (22), a mechanical force was used to pull a bilayer through a region of extremely high local curvature, causing the leaflets to slip past one another. Merkel et al. (23) fixed the bottom monolayer of a membrane to a glass substrate and deduced a friction coefficient from the diffusion of tracer lipids in the top monolayer. Pfeiffer et al. (24) and Pott and Méléard (25) derived friction coefficients from the decay rates of the time-correlations of thermal undulations in a bilayer stack and in vesicles, respectively, but the interpretation of these measurements proved to be complicated. From these various experiments, a typical range of 10⁸–10⁹ Pa m⁻¹ s is obtained for the intermonolayer friction coefficient. The relation between lipid architecture and intermonolayer friction has hardly been explored. The friction coefficient of an OMPC bilayer lies ∼35% below that of an SOPC bilayer, with the latter showing a remarkable insensitivity of b to temperature over the range from 15 to 35°C (private communication with A. Yeung, University of Alberta, Canada). Cholesterol was found to increase the friction coefficient by roughly 50%, while the value for a mixed bovine brain sphingomyelin-cholesterol (CHOL) membrane is nearly five times that of 1-stearoyl-2-oleoyl-phosphatidylcholine (SOPC, C18:0/1_c9)-CHOL and 1-oleoyl-2-myristoyl-phosphatidylcholine (OMPC, C18:1_c9/C14:0)-CHOL membranes (all in a 1:1 mixture). It is our expectation that b is affected by interdigitation, i.e., long lipid tails whose ends cross the bilayer midsurface and protrude among the tails of the opposing bilayer leaflet (26–28), as this enhances the grip between the two monolayers.

Computer simulations of membranes have provided a wealth of detailed information, as reviewed in the literature (29–32), but there are few studies focusing on the flow properties of bilayers. A number of authors have reported lateral diffusion coefficients of lipids (33–38), also in relationship to tail length (39,40), but these have not been related to the surface shear viscosity. In a recent simulation study of solvated membranes, Guigas and Weiss (41) found the diffusion coefficient of a membrane-bound tracer to decrease logarithmically with the radius of the tracer, in agreement with Saffman's theory. We believe that a similar decay observed by these authors in simulations without solvent cannot be explained by Saffman's theory, since its derivation crucially relies on the presence of a solvent surrounding the membrane (see (4) and Eq. 6), but instead reflects the logarithmic radius dependence predicted by hydrodynamics for diffusion in a periodically continued two-dimensional fluid (42). The exponential relaxations of thermal undulations (43) and the relative Brownian motions of the monolayers (37,40) are, in principle, connected to the intermonolayer friction. The first direct calculations of η_s and b have been reported only recently, using bilayers under shear (44) and at equilibrium (44–46). Here we extend our previous studies by using a series of coarse-grained model lipids to explore the relationship between lipid architecture and bilayer flow behavior—a relationship that has thus far not been studied systematically in the experimental literature. Furthermore, the employed nonequilibrium simulation techniques have the advantage that they provide unequivocal access to the flow characteristics, whereas the current interpretations of experiments are rather involved and nontrivial. A final motivation for this study is to investigate the origin of the discrepancy, by several orders of magnitude, between the η_s and b as obtained in previous course-grained simulations versus the values deduced from experiments.

The outline of this article is as follows: The techniques used to calculate surface shear viscosity and intermonolayer friction, from both equilibrium and nonequilibrium molecular dynamics simulations, are briefly described in Theory. The Simulation Model is then introduced, and several basic properties of the membrane and solvent are calculated. We then present the Simulation Results, followed by Discussion and Conclusions.

THEORY

The aim of this section is to provide a concise introduction of the theory on the thermodynamics and hydrodynamics of membranes, and to describe the simulation techniques employed to calculate the key parameters.

Static properties

In the analytical continuum description of a membrane, the configuration of a near-planar bilayer is conveniently described, in the Monge representation, by the elevation u(x) of the midsurface of the bilayer relative to a flat reference plane for any point x on this plane. The free energy of a bilayer with conformation u is then given by the Helfrich theory (3,47,48),

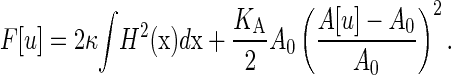(1)

The first term on the right-hand side yields the bending free energy, with bending rigidity κ and mean curvature An additional bending contribution from the Gaussian curvature has been ignored here, as this term is constant in the current setup. The second term on the right-hand side describes the global elastic energy, where the area A[u] of the midsurface is a functional of the bilayer conformation, A₀ is the equilibrium area, and K_A the bilayer elastic modulus. Note that at this level of description, which is the starting point for most experimental and simulation studies on the mechanical properties of membranes, the twinned nature of the bilayer is irrelevant.

In our simulation setup (see Fig. 1), the nearly flat bilayer is oriented parallel to the square xy ground plane of a periodic simulation box with dimensions L_‖ × L_‖ × L_⊥. Differentiating the average free energy with respect to the ground-plane area at constant volume, one arrives at

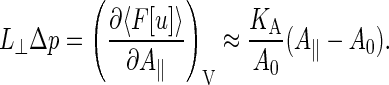(2)

FIGURE 1.

Cartoons of the simulation setup of a membrane under shear, with the arrows indicating the flow fields. A perpendicular shear flow (left) is used to determine the surface shear viscosity of the bilayer; a parallel shear flow (right) yields the intermonolayer friction coefficient.

The left-hand side is exact, with 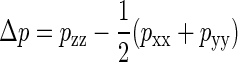and p the stress tensor. On the right-hand side, we have made the common assumptions that the projected-area dependence of the free energy is dominated by the elastic term, and that A[u] ≈ A_‖ for a nearly flat bilayer, although these approximations are to be regarded with care (49). In the absence of externally imposed restraints, a freely floating bilayer of N molecules will adapt a tensionless state with an average area equal to the equilibrium area of A₀ = Na₀/2. In our simulations we have reproduced this state as closely as possible, by varying the ground-plane area of the box until Δp = 0.

Exploiting the periodicity of the simulation box, it proves convenient to express the undulations of the midsurface of the bilayer as a Fourier series,

(3)

where q = 2πn/L_‖ is a wave vector with integer vector n = (n_x, n_y). By noting that u_q = u_–q* for a real function u(x), with the asterisk denoting a complex conjugate, the summation can be reduced to two quadrants. Inserting this series into the Helfrich expression and using the equipartition theorem, one readily recovers the structure factors (3,48)

(4)

for a bilayer in the tensionless state, with T the temperature, k_B the Boltzmann's constant, and the angle brackets denoting a canonical average.

Surface shear viscosity

The surface shear viscosity of a membrane is easiest established in molecular dynamics simulations by shearing the bilayer (44), analogous to standard shear viscosity calculations for liquids (50). A so-called perpendicular shear flow is imposed on the bilayer by applying Lees-Edwards sliding boundary conditions (50) along the y direction (see Fig. 1), culminating in a linear flow field in both the membrane and the surrounding solvent. The surface shear viscosity is defined as the proportionality constant between the applied shear rate 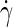and the corresponding shear force acting on the bilayer per unit length (44),

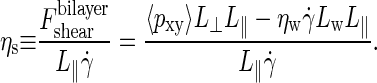(5)

Simulation algorithms readily provide the total force applied to shear the bilayer plus the solvent, which is calculated as the product of the off-diagonal stress tensor element p_xy and the area L_‖L_⊥, but they do not yield the separate force contribution to shear the bilayer. In the last numerator of Eq. 5, therefore, we have explicitly calculated the shear force on the solvent by using the solvent viscosity η_w and the height of the layer of solvent, L_w = L_⊥ − h with h the thickness of the membrane, and subtracted this force from the total shear force to arrive at the desired bilayer shear force.

In simulations and experiments with quiescent membranes, the surface viscosity can also be deduced from the lateral diffusion coefficient of an embedded tracer particle by means of the Saffman-Stokes-Einstein expression (4),

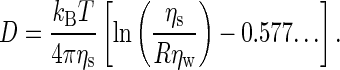(6)

Here, the tracer particle is a mesoscopic cylinder of radius R, oriented parallel to the membrane normal, with a length exceeding the membrane thickness. The membrane is regarded as a single planar two-dimensional fluid, surrounded by solvent on both sides.

Intermonolayer friction

Shear simulations are also an attractive tool for inducing slip between the two leaflets of a bilayer (44), by using Lees-Edwards sliding boundary conditions along the z direction to create a so-called parallel shear flow (see Fig. 1). The imposed periodic flow field, results in a nonlinear velocity profile (depicted in Fig. 2), because the sheared system is nonhomogeneous along the bilayer normal. In this graph, one readily recognizes the monolayers as two slabs of thickness h/2 moving with equal but opposing velocities 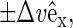resulting in friction forces 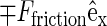acting at the midsurface of the bilayer. The solvent on either side of the membrane displays a linear velocity profile with a shear rate 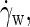which clearly exceeds the imposed rate 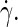By assuming stick boundaries at the interfaces, the tangential solvent forces acting on the top and bottom leaflets of the membrane are readily deduced from 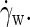The intermonolayer friction coefficient is then calculated as

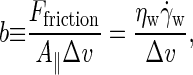(7)

where, in the last step, the steady-state force balance of a monolayer has been used to equate the intermonolayer friction force to the solvent shear force (44).

FIGURE 2.

The average particle velocity along the flow (x) direction, as a function of the height (z) in the simulation box, for a bilayer exposed to a parallel shear with a very high shear rate, 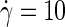ns⁻¹. The two monolayers, each ∼20 Å thick, are seen to slide along one another at the midsurface, while the solvent shows a linear flow field with shear rate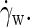

The velocity profile of Fig. 2 was obtained at a high shear rate of 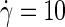ns⁻¹, to emphasize the slip at the midsurface of the bilayer against the background of thermal noise. At the one-to-two-orders lower shear rates employed in all production simulations, it becomes increasingly difficult to extract Δv directly from the velocity profile. The slip velocity is then calculated either from the average distance traveled by an amphiphile i along the flow direction over a time interval t, Δv = ± 〈x_i(t) − x_i(0)〉/t, or from combining the overall velocity difference across the box with the velocity drop over the solvent, 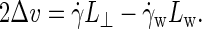Note that the observed agreement between both methods confirms the existence of stick boundary conditions at the membrane-solvent interface, which is a prerequisite for the validity of the latter method and Eq. 7 (44).

Intermonolayer friction not only rises to prominence during a forcedly induced slip, but also in any thermal motion of the bilayer, which causes the two monolayers to move relatively to one another. Seifert and Langer (17,18) and Evans and Yeung (19,20) independently derived the coupled equations of motion for the undulations and the monolayer densities of bilayers in near-planar and axial-symmetric configurations, respectively. In these equations, which are valid in the creeping-flow limit, the driving forces originating from the bending and elastic free energies in a generalized Helfrich equation are opposed by dissipative forces due to intermonolayer friction, surface shear viscosity, and solvent viscosity. We refer the interested reader to previous work (17,18,46) for the detailed analytical solution of this model, and directly proceed to the final result: the time correlations of the Fourier coefficients u_q of a thermally undulating near-planar membrane reads as

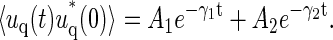(8)

The positive amplitudes A_i are functions of the wave number, and obviously obey A₁ + A₂ = S(q). The relaxation rates γ_i converge to power-law behavior on either side of a crossover wavenumber 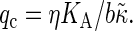Here the effective bending rigidity is defined by 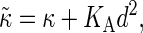with the distance d between the bilayer midsurface and the monolayer neutral surfaces approximately equal to half the monolayer thickness (hence, d = h/4) (17,46,48). By inserting typical experimental values, one finds that q_c ≈ (0.5–5.0) μm⁻¹ lies well below the smallest wavenumbers currently accessible in membrane simulations with molecular details, q_min = 2π/L_‖ ≈ 0.5 nm⁻¹. We therefore expect in our simulations a slow relaxation process dominated by intermonolayer friction, 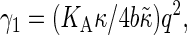and a fast relaxation process through viscous dissipation in the solvent, 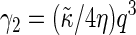(17,45). The double exponential decay has been observed in experiments on vesicles (25) and in simulations of planar membranes (45,46), where it proved sensitive to the surface tension. Note that similar rate laws (with 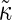replaced by κ) are recovered in the opposing limit of low wavenumbers, 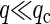(17). The fast relaxation process then dissipates by intermonolayer friction, while the slow solvent-viscosity dominated relaxation recovers the conventional dispersion relation for membrane undulations (51,52).

SIMULATION MODEL

Fully atomic simulation models of membranes place a heavy burden on available computer resources and are therefore limited to small time- and length-scales. These drawbacks can be overcome by using a coarse-grained (CG) simulation model, in which a number of atoms are grouped together into one interaction site, known as a CG particle (31,32). Here we employ a CG model recently developed by Marrink et al. (35) to simulate DPPC and related amphiphiles. These authors chose a parameterization in which groups of approximately four heavy atoms, and their attached hydrogens, are reduced to a single CG particle. In this section we first present a summary of the model, referring the reader to the original work (35) for more details and an extensive motivation. Next, several characteristics of the model are calculated to provide a basis for the analysis of membrane dynamics.

Force field

The model discerns four major types of particles, representing groups of atoms with different properties: charged groups (Q), polar hydrophilic groups (P), weakly polar groups (N), and apolar hydrophobic groups (C). Particle types Q and N are subdivided into four categories according to their hydrogen-bonding capabilities, of which only the a (acceptor) and 0 (no capabilities) subtypes will be used here. The head of a DPPC lipid (molecule A₄₄ in Fig. 3) is then represented by one Q₀ particle with charge q = e for the choline group and one Q_a particle with charge q = −e for the phosphate group. The glycerol ester linkage is modeled by two particles of type N_a, while each C₁₆H₃₃ tail is reduced to a chain of four C particles. Four water molecules are lumped into one bead of type P.

FIGURE 3.

Cartoons of the double-tailed lipids simulated with the coarse-grained model by Marrink et al. (35). The shorthand notation is included below the lipids, the particle type on the left and right.

The nonbonded interactions between particles i and j at a distance r_ij are described by a Lennard-Jones potential, Φ_LJ(r_ij) = 4ε_ij[(σ/r_ij)¹² − (σ/r_ij)⁶]. The strength ε_ij of the interaction can be read from Table 1. An effective radius σ = 0.47 nm applies to all interactions, and only bonded nearest neighbors are excluded from LJ interactions. The potential is cut off at r_c = 1.2 nm, using a switch function to create a smooth shift to zero between r_s = 0.9 nm and r_c. Charged particles also interact by a Coulombic potential, Φ_el(r_ij) = q_iq_j/(4πε₀ε_rr_ij), which is screened by both a relative dielectric constant ε_r = 20 and a switch function running from r_s = 0 to r_c; here ε₀ denotes the dielectric constant of vacuum. A harmonic potential is used to describe covalent bonds between connected particles, 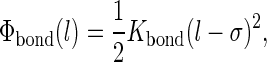with K_bond = 1250 kJ/mol nm². The bending stiffness of the tails is introduced by an angle potential, 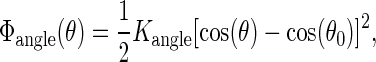with K_angle = 25 kJ/mol and θ₀ = 180°, while there is no dihedral potential. All particles have the same mass of m = 72 a.u. In the DlPoly 2.0 package (53) a Nosé-Hoover thermostat is used to maintain a temperature of 323 K and in some runs a Hoover barostat was invoked to establish an isotropic pressure of 1 bar. The Verlet leap-frog algorithm allows a maximum time step of 20 fs.

TABLE 1.

Lennard-Jones interaction parameters ε_ij (in kJ/mol) between the five particle types of the coarse-grained lipid model by Marrink et al. (35)

	P	Na	C	Q0	Qa
P	5.0	3.4	1.8	5.0	5.0
Na	3.4	4.2	2.6	3.4	3.4
C	1.8	2.6	3.4	1.8	1.8
Q0	5.0	3.4	1.8	3.4	3.4
Qa	5.0	3.4	1.8	3.4	3.4

Basic properties of the model

Before simulating a lipid bilayer in a solvent matrix, we first assess the quality of the model by separate studies of the solvent and the lipid tails, i.e., linear alkanes. To determine the dynamical properties of the aqueous solvent, a cubic box containing 6072 P-type particles was prepared. Using a barostat at 1 bar and a thermostat at 323 K, the specific gravity of the solvent converged to nearly 1 g/cm³. The diffusion coefficient of the CG particles was established at which lies very close to the experimentally measured value for a water molecule at these conditions, 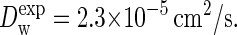Simulations under shear yield a viscosity 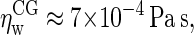independent of the applied shear rate and in close proximity to the experimental value 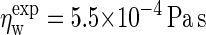under the prevailing conditions (54). The dynamics of bulk C₄ tails, i.e., the CG equivalent of liquid n-hexadecane, was analyzed using a cubic box containing 1518 molecules, again at 1 bar and 323 K. The simulations yield a diffusion coefficient 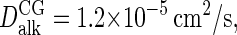or nearly twice as high as the 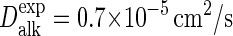obtained by extrapolating the available experimental data (55) to the current temperature. In conformity with the Stokes-Einstein expression, the simulated viscosity of 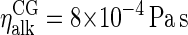is approximately half the experimental value (56).

Groot and Rabone (57) argued that the diffusion coefficient of a CG particle or CG molecule representing k_x real molecules is related to the experimental molecular diffusion coefficient by 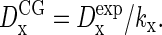By inserting the above diffusivities of water in this expression, with k_w = 4, Marrink et al. (35) concluded that the dynamics of the solvent is four-times too fast. Acceleration factors of ∼2 were obtained by comparing simulated bulk CG alkanes (C_n with n ≤ 5) with the corresponding experimental linear alkanes (C_4nH_8n+2), with k_alk = 1. These authors subsequently accounted for the anticipated speedup of the bilayer dynamics by simply scaling every nanosecond of simulation time into 4 ns of real time. Although the diffusivity mapping should obviously hold true for a CG particle or molecule representing one real molecule (k_x = 1), its validity for a compound (k_x > 1) CG particle is less evident: correlations between the molecules constituting the CG particle seriously complicate the picture. Since the major purposes of the solvent particles are to provide a hydrophilic and viscous environment to the bilayer, it appears more natural to match the viscosity rather than the diffusion coefficient of the solvent. Based on the aforementioned viscosities, we are thus led to the conclusion that the model yields an adequate description of the dynamics of bulk water and bulk alkanes, which are expected to carry over to the membrane simulations, without the introduction of a scaling factor for the time.

A bilayer-solvent system was prepared by expanding a smaller box, made available by Marrink (35,58), to 256 DPPC (A₄₄) lipids and 3000 solvent particles. The system was equilibrated by a 100 ns simulation at constant temperature, T = 323 K, followed by a 100 ns simulation at constant temperature and pressure, p = 1 bar. As a final step in locating the equilibrium tensionless state, the tension versus strain curve of the bilayer was calculated by varying the ground-plane area around the final area of the NPT simulation. The zero tension intercept of this curve, see Eq. 2, is reached for an average area per amphiphile of a₀ = 0.66 nm², which is slightly higher than the experimental value of 0.64 nm² at this temperature (59). The deviation from the 0.64 nm² reported by Marrink et al. (35), as well as other small differences with their simulation results, are attributed to slight deviations in the simulation setup, including a smaller time step, the rescaling of the ground-plane area at constant volume rather than at constant normal pressure p_zz, and the use of different simulation packages.

The equilibration simulations yield two additional mechanical properties of the membrane, which will be needed later. From the slope of the tension versus strain curve follows an area compressibility K_A = 370 mN/m for the 256 lipid bilayer, while a larger 6400 lipid bilayer yields 220 mN/m. This decrease results from the approximate area calculation A[u] ≈ A_‖, which renders the effective area compressibility defined by Eq. 2 system-size-dependent, 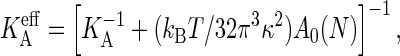with K_A the intrinsic compressibility defined by Eq. 1 (49). The K_A obtained by this system-size correction is ∼2% larger than the 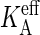of the smaller bilayer, but some 40% larger than the 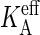of the large bilayer, while reported experimental values for DPPC (59) and a range of other PC-s (60) are typically ∼230 mN/m. The structure factors of the thermal undulations at A_‖ = A₀ closely adhere to the predicted scaling law (see Eq. 4), confirming that we have indeed reached a state with vanishing tension. At κ = 8 × 10⁻²⁰ J or 18 k_BT, the bending rigidity is higher than the ∼6 × 10⁻²⁰ J anticipated from experiments (60). In summary, the A₄₄ membrane is a bit less flexible than a real DPPC membrane, and we expect similar small deviations in the dynamical properties.

SIMULATION RESULTS

In this section, the dynamical properties of membranes are calculated using the equilibrium and nonequilibrium techniques outlined in Theory. The results obtained for bilayers composed of DPPC (A₄₄) lipids are first discussed in some detail, followed by simulations of A_i,j lipid membranes to investigate the influence of tail lengths on the dynamical properties of the bilayer. We discuss asymmetric lipids, i ≠ j, with a combined total tail length of i + j = 8 particles, symmetric lipids with two elongated tails, i = j > 4, and finally a lipid with one straight and one bend tail, i = j = 5. Each simulated membrane contains 256 identical lipids surrounded by 3000 solvent particles, and is thoroughly equilibrated to a tension-less state at 1 bar. All lipids have identical headgroups, and the tail particles are, as before, of the C type.

DPPC membrane

The flow properties of a DPPC membrane, and their shear-rate dependencies, were studied by exposing the small A₄₄ bilayer patch of the previous section to shear rates 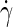ranging from 0.1 to 1 ns⁻¹. In the perpendicular shear orientation, the off-diagonal element p_xy of the pressure tensor is used to calculate the surface shear viscosity (see Eq. 5 and Table 2), to arrive at η_s = 1.2 × 10⁻¹¹ Pa m s, independent of the applied shear rate. Under parallel shear, the aforementioned range of shear rates induces slip velocities of 0.03–0.27 nm/ns between the two bilayer leaflets. Equation 7 then yields an intermonolayer friction coefficient b = 2.4 × 10⁶ Pa m⁻¹ s, independent of the slip velocity. It appears, therefore, that this coarse-grained membrane model underestimates the experimental values of η_s and b by one-to-two orders of magnitude, although it does an excellent job on many thermodynamic properties. A discussion of the possible sources of these discrepancies, which were also observed for a single-tail CG lipid membrane model (44), will be postponed until Discussion and Conclusions. In the remainder of this subsection, the equilibrium approaches for determining η_s and b will be applied, to validate the numerical results from the nonequilibrium simulations and to ascertain the possible impact of nonzero shear on these parameters.

TABLE 2.

Surface shear viscosities η_s and intermonolayer friction coefficients b obtained for the various coarse-grained lipid models of this study

Lipid	ηs (× 10−11 Pa m−1 s) Driven*	Equilibrium	b (×106 Pa m−1 s) Driven	Equilibrium
A44 (DPPC)	1.2	1.0	2.4	3.0
A53	1.0	1.0	3.9	4.1
A62	1.0	1.0	7.1	7.3
A55	1.8	1.8	2.8	2.7
A66	2.9	4.2	3.3	2.5
A77	4.8	7.5	3.2	2.4
A5′5		2.1	2.8
DPPC				∼1†
DMPC				0.7‡
DMPC	500§	17,¶ 500§		30–3000¶
DOPC		17¶		45–450¶
SOPC	300‖	300‖	100,** 450††	500–104‡‡

The values in the two columns marked “Driven” are obtained from membranes flowing under external forces, while those in the columns marked “Equilibrium” are extracted from thermal motions. Simulation results from atomic models are presented in rows 8 and 9, and experimental data in the bottom three rows.

^*The simulation data under perpendicular shear flow have been extrapolated to zero shear rate.

^†Derived from the relaxation of thermal undulations; see Lindahl and Edholm (43) and this work.

^‡Based on the relative diffusion of monolayers; see Wohlert and Edholm (37).

^§Obtained from Brownian and driven motion of latex spheres bound to a vesicle; see Dimova et al. (9).

^¶From the diffusion of lipids in supported bilayers; see Merkel et al. (23).

^‖Obtained from Brownian and driven motion of latex spheres bound to a vesicle; see Velikov et al. (7) and Dimova et al. (8).

^**Derived by pulling a tether from a vesicle; see Evans and Yeung (19).

^††Tether pulling experiments; see Raphael and Waugh (21).

^‡‡Analyzing the thermal undulations of a vesicle by two theories; see Pott and Méléard (25).

An independent conformation of the surface shear viscosity is provided by the satisfactory agreement between the lateral diffusion coefficient of a lipid in a quiescent bilayer as calculated by Saffman's theory, D_Saffman = 1.4 × 10⁻⁶ cm²/s, and the actual value of D_msd = 1.5 × 10⁻⁶ cm²/s determined from the mean-square displacement. The former should be regarded with some care, however, as the simulation conditions do not adequately match the assumptions underlying the Saffman theory (see Surface Shear Velocity). In applying Eq. 6, we have approximated the floppy lipid by a rigid cylinder of radius 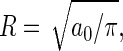and regarded the bilayer as a continuum fluid on this length scale. Furthermore, since the lipids span only one leaflet rather than the entire membrane, we followed previous experiments (5) and simulations (44) in substituting the bilayer surface shear viscosity in Eq. 6 by the monolayer surface shear viscosity η_m = η_s/2. Considering the assumptions made, the agreement between the two diffusion coefficients is satisfactory.

As described in Intermonolayer Friction, intermonolayer friction also manifests itself during the Brownian thermal undulations of a membrane. Fig. 4 shows the time correlations of the six undulation modes u_q corresponding to the three smallest wavenumbers commensurate with the box dimensions. Single-exponential decays are clearly observed to set in after some 250 ps, especially for the modes with smaller wavenumbers. The decay rates agree with the slow relaxation rates γ₁(q) of the theory of Seifert and Langer—the exact curves calculated by Eq. 8 are included in the graph as dashed lines—thus confirming the value of the intermonolayer friction coefficient. Only one parameter in this theory could not be determined a priori from an independent simulation, to wit, the distance d between the midsurface of the bilayer and the neutral surfaces of the monolayers (17). We judiciously chose this distance to be equal to half the monolayer thickness, i.e., a quarter of the bilayer thickness, d = h/4 ≈ 1.1 nm, as this choice has worked out well in previous studies (45,46). In summary, the dynamical properties calculated from nonequilibrium simulations are confirmed by the equilibrium simulations for the DPPC (A₄₄) membrane. Since the latter calculations consume more computer time and are less straightforward in their interpretation, we recommend the nonequilibrium simulations as the more practical and more reliable techniques.

FIGURE 4.

The autocorrelations (solid lines) of the thermal undulations of a bilayer of A₄₄ lipids, for the six smallest wave vectors commensurate with the box dimension, i.e., q = 0.069 Å⁻¹ (top), q = 0.097 Å⁻¹ (middle), and q = 0.137 Å⁻¹ (bottom). Dashed lines indicate the theoretical predictions by Eq. 8, where the amplitudes A_i and relaxation rates γ_i have been calculated using the intermonolayer friction coefficient determined in the parallel shear simulations.

Lipids with asymmetric tails

The effect of asymmetric tail lengths on the membrane properties was studied by comparing the reference A₄₄ lipid to its cousins A₅₃ and A₆₂ (see Fig. 3). Two new membranes, each containing only one type of lipid, were made and thoroughly equilibrated to their tensionless states. By exposing these bilayers to perpendicular shear, using the aforementioned range of shear rates, both lipids were found to yield nearly identical surface viscosities to the A₄₄ lipid, which in Fig. 5 are seen to be independent of the shear rate. These viscosities are in good agreement with the values derived, by means of the Saffman expression, from the lateral diffusion coefficients of lipids in nonsheared bilayers; the latter are represented in the graph by the markers at Because the equilibrium area a₀ and membrane thickness h are only slightly different for the three lipids, one may expect comparable lateral interactions in all three membranes and, hence, nearly identical surface shear viscosities.

FIGURE 5.

The surface shear viscosity as a function of the shear rate for the A₄₄ lipid (circles and solid line), two lipids with asymmetric tails (squares and diamonds), three lipids with extended tails (triangles and dotted lines), and the A_5′5 lipid (pluses). Viscosities derived from the lipid lateral diffusion coefficients by the Saffman-Stokes-Einstein theory are plotted at

The intermonolayer frictions obtained under parallel shear, however, rise with increasing tail length difference (as shown in Fig. 6). Since the equilibrium dimensions of the three membranes are comparable, this rise results from differences in the packing of the tails inside the hydrophobic core of the bilayer. The probability distributions of the amphiphilic particles along the normal to the membrane, as presented in Fig. 7 for the three lipids, indicate that the tails of the opposing leaflets are not interdigitated for the A₄₄ lipid. The long tails of the A₅₃ lipids interdigitate by approximately one particle with their counterparts from the opposing leaflet, while the long tails of A₆₂ lipids interdigitate by approximately three particles. Note that the peaks of the particle distributions have shifted with increasing asymmetry, thereby reducing the actual number of interdigitating particles to less than the values of 2 and 4 expected on simple geometric grounds for A₅₃ and A₆₂, respectively. The interleaflet contacts created by interdigitation strengthen the interaction between the two monolayers and are responsible for the growth of the intermonolayer friction with increasing asymmetry. Intermonolayer friction coefficients were also deduced from the slow relaxation rates γ₁ (see Eq. 8) of the two thermal bilayer undulations with the smallest possible wavenumber, q = 2π/L_‖. Sampling deficiencies of the time-correlation functions were minimized by prolonging all simulations until 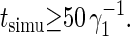With increasing tail asymmetry, the idea of a smooth midsurface where monolayers gently slide past one another becomes obscured and the assumption d = h/4 might be less well founded. Nevertheless, the simulations strongly suggest that the intermonolayer friction coefficients are independent of the slip velocity.

FIGURE 6.

The intermonolayer friction coefficient as a function of the slip velocity for the A₄₄ lipid (circles and solid line), two lipids with asymmetric tails (squares, diamonds, and dotted lines), three lipids with extended tails (triangles), and the A_5′5 lipid (pluses). Friction coefficients obtained by the Seifert-Langer theory from the slow relaxation rates γ₁ of the thermal undulations are plotted at Δv = 0.

FIGURE 7.

Probability distributions along the bilayer normal of all 12 particles in the lipid, for A₄₄ (bottom), A₅₃ (middle), and A₆₂ (top), with the particles of the first (long) tail as solid lines, the particles of the second (short) tail as dashed lines, and the head particles as dash-dotted lines. The terminal and interdigitating particles are marked by dark lines, while light lines are used for the remaining tail particles. The asymmetric lipids form a so-called partially interdigitated bilayer, in which a long tail packs end-to-end with a short tail from the opposing leaflet.

Lipids with symmetric tails

In the simulations of symmetric lipids, the reference lipid A₄₄ is compared against three lipids with longer tails: A₅₅, A₆₆, and A₇₇. Along this series of lipids, the equilibrium dimensions of the tensionless bilayers gradually grow according to a_o,i = (0.655 + 0.009i) nm² and h_i = (19 + 6i) Å, with i the number of particles per tail. The ratios of bending rigidity to elastic modulus are well fitted by (κ_i/K_A,i)^1/2 = α(h_i − h₀), with α = 0.16 and h₀ = 1.2 nm, in good agreement with 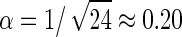and h₀ = 1 nm obtained by the experiments and theory of Rawicz et al. (60). Simulations under parallel shear reveal that the intermonolayer friction coefficients vary by <50% between the four lipids, and show no significant dependence on the slip velocity (see Fig. 6). Because both tails are of equal length, the monomer distributions along the bilayer normal are similar to those of the A₄₄ membrane, and show no appreciable interdigitation of tails from opposing leaflets. The distributions of the extremal tail particles become wider with increasing tail length, while the average distance between the opposing end particles reduces, suggesting a slightly rougher interface and hence a higher intermonolayer friction for lipids with longer tails. This trend is indeed observed at the highest slip velocity, while the friction coefficients obtained from the thermal undulations, plotted at Δv = 0, are curiously sorted in the reverse order.

The surface shear viscosities rise rapidly with increasing tail length (see Fig. 5), as expected from the increased lateral interactions in a thicker membrane. For the A₄₄ and A₅₅ lipids, the surface shear viscosity is virtually independent of shear rate, and there is a good agreement between the η_s obtained by equilibrium and nonequilibrium simulations. A pronounced shear-thinning is observed for bilayers with the longer A₆₆ and A₇₇ lipids. The shear-thinning is probably caused by the ordering of the straightened lipids into monolayers and perhaps enhanced by additional flow-induced ordering, because the bulk alkane liquids, C_i with 4 ≤ i ≤ 7, behave as Newtonian liquids over the same range of shear rates. Note that the shear viscosities of these liquids are linear in the tail length, η_alk = (4i − 8) × 10⁻⁴ Pa s. Interestingly, the lipids with long tails also reveal a discrepancy between the viscosities under low shear rates and those derived at zero shear from the lipid diffusivity, indicating that the limits of the Saffman have been reached here.

In the final A_5′5 lipid model (depicted in Fig. 3), a monounsaturated tail is mimicked by reducing the equilibrium bending angle at the central particle of the tail to θ₀ = 130° and by stiffening the bending potential of this particular angle to K_angle = 250 kJ/mol. Figs. 5 and 6 show that the impact of the boomerang-shaped tail on the membrane properties is rather modest. The surface shear viscosity has increased slightly relative to its closest saturated counterpart, the A₅₅ lipid, while the intermonolayer friction coefficient shows a small decrease.

DISCUSSION AND CONCLUSIONS

The flow properties of bilayer membranes have been studied for a variety of coarse-grained (CG) lipids using equilibrium and nonequilibrium molecular dynamics simulations. Intermonolayer friction coefficients b are obtained from simulations of membranes exposed to parallel shear, which forces the two membrane leaflets to slide past one another, and from analyzing the relaxation rates of thermal membrane undulations using the Seifert-Langer theory (17); the results of both approaches are in good agreement. Surface shear viscosities η_s have been calculated from simulations of membranes under perpendicular shear and from the lateral self-diffusion of lipids by the Saffman-Stokes-Einstein expression (4). A majority of the simulated membranes display Newtonian behavior under shear and quantitative agreement between η_s from sheared and nonsheared simulations. The two lipids with the longest tails, however, revealed shear-thinning behavior and a gradual departure from the Saffman theory. The generally satisfying agreement between the results of equilibrium and nonequilibrium simulations may also be interpreted as support for both aforementioned theories.

The intermonolayer friction coefficient and surface shear viscosity obtained with the current double-tailed CG lipid model, introduced by Marrink et al. (35), are ∼15 times and twice as high, respectively, as those reported previously (44) for the single-tailed CG lipid model of Goetz and Lipowsky (33). Since the latter model underestimates the viscosities of water and liquid alkanes, we have since compensated for these deficiencies by introducing pairwise-additive friction and random forces between all particles, following the methodology of dissipative particle dynamics (61,62). These additional forces arise naturally in any coarse-graining procedure as representatives of the omitted internal degrees of freedom of the CG particles; for computational speed, and because they do not affect thermodynamic properties, these forces are often ignored in CG models. After tuning the extra force parameters for solvent-solvent and tail-tail interactions to reproduce the viscosities of bulk water and hexadecane, respectively, the resulting membrane flow properties η_s and b approach those of the Marrink model to within a factor 2 (63). This suggests that the reported values are generic for coarse-grained lipid models. Note, however, that these values underestimate the experimental b and η_s, as collected in Table 2, by approximately two orders of magnitude. We will return to this discrepancy shortly.

A thin layer of bulk liquid with viscosity η_l and thickness h_l is readily shown to posses a surface shear viscosity η_s = η_lh_l resisting perpendicular shear flow and a friction coefficient b = η_l/h_l opposing a velocity difference across the layer (19,22). By comparing the bilayers with symmetric lipids against these rules of thumb, we find that the low shear-rate results are adequately described by η_s ≈ 3η_alkh and b ≈ 12η_alk/h, with η_alk the viscosity of a bulk liquid of corresponding CG alkanes. The prefactors appearing in these expressions reflect that the bilayer is not a simple bulk liquid of tails, but that the lipids are straightened, oriented, and ordered in a bilayer. Experimental data yield prefactors of the order of 100–1000, with the intermonolayer friction requiring a higher prefactor than the surface viscosity (19), suggesting that the impact of ordering on η_s and b is considerably higher for real lipids than for the coarse-grained model lipids studied here. We hypothesize that these differences reflect the weakness of coarse-grained models to accurately mimic the detailed interactions between alkanes, and hence their packing in dense phases. This is also illustrated by the viscosities of the bulk C_i liquids, which we found to be linear in the length i for chains of 4–7 particles. Experimental viscosities (56), however, rise rapidly with increasing chain length, while n-tetracosane (i = 6) and longer linear alkanes adopt a waxlike state at the simulation temperature of 323 K. In the more ordered bilayer structure, a similar transition is observed at an even lower tail length, with 1,2-dipalmitoyl-phosphatidylcholine (DPPC, diC16:0, i = 4) in the liquid-crystalline phase and 1,2-distearoyl-phosphatidylcholine (DSPC, diC18:0, i = 4.5) in the gel phase at 323 K. The coarse-grained lipids, for which no chain-length induced transitions were observed, are apparently less sensitive to ordering and dense packing effects, which could also explain their relatively low surface shear viscosity and intermonolayer friction coefficient. Since the more realistic atomically detailed simulation models are capable of reproducing phase transitions, one might expect that they yield a quantitative agreement with experimental flow properties of membranes.

The efficient nonequilibrium simulation techniques for establishing η_s and b have not yet been applied to an atomic membrane model, but the equilibrium methods provide a first glimpse at what may be expected from these models. Various studies (37,40) show that the lateral diffusion coefficients obtained in atomic molecular dynamics simulations are in good agreement with experimental data, suggesting that they will also yield quantitatively satisfying surface shear viscosities. As we have seen, however, a direct translation of D into η_s should be regarded with caution, and simulations under perpendicular shear are recommended. In a recent study, Wohlert and Edholm (37) estimated an intermonolayer friction coefficient of 0.7 × 10⁶ Pa m⁻¹ s from the relative diffusion between the two leaflets of an atomic DMPC membrane. By reanalyzing the autocorrelations of the thermal undulations in an atomic DPPC membrane, published by Lindahl and Edholm (43), within the framework of the Seifert-Langer theory (Eq. 8), we find that b ∼ 10⁶ Pa m⁻¹ s fits the simulation data reasonably well. These first indications suggest, therefore, that intermonolayer friction coefficients by atomic membrane models are in close proximity to those obtained with coarse-grained models, while both are two-to-three orders of magnitude smaller than the few reported experimental values. With the stacking deficiency of the coarse-grained model ruled out, the interpretation of the experimental data appears as the most likely source of the discrepancy. Small gel-like domains surviving in a predominantly fluidlike phase could result in a drastic increase of the resilience against flow, but these domains are expected to exist only within ∼10°C above the melting transition (9). Thermal undulations of the membrane, which are relatively small in the simulations and conveniently ignored when analyzing the experiments, might also affect the flow properties.

By varying the tail lengths of a double-tailed lipid, we observed two clear trends for the flow properties of bilayers. First, the intermonolayer friction coefficient is sensitive to the asymmetry of the tails, as interdigitation of the longer tails roughens the interface between the two membrane leaflets. Second, the surface shear viscosity is modulated by the combined lengths of the two tails, and hardly varies with the asymmetry of the tails. The experimental data at our disposal are inconclusive to confirm these trends. Finally, we express the expectation that this study inspires future experimental and simulation studies on the flow properties of membranes and their relation to the membrane composition.