Protein Free Energy Landscapes Remodeled by Ligand Binding

Abstract

Glucose/galactose binding protein (GGBP) functions in two different larger systems of proteins used by enteric bacteria for molecular recognition and signaling. Here we report on the thermodynamics of conformational equilibrium distributions of GGBP. Three fluorescence components appear at zero glucose concentration and systematically transition to three components at high glucose concentration. Fluorescence anisotropy correlations, fluorescent lifetimes, thermodynamics, computational structure minimization, and literature work were used to assign the three components as open, closed, and twisted conformations of the protein. The existence of three states at all glucose concentrations indicates that the protein continuously fluctuates about its conformational state space via thermally driven state transitions; glucose biases the populations by reorganizing the free energy profile. These results and their implications are discussed in terms of the two types of specific and nonspecific interactions GGBP has with cytoplasmic membrane proteins.

INTRODUCTION

Enteric bacteria (1) use glucose/galactose binding protein (GGBP) in separate pathways to actively transport methylgalactosides across the cell membrane (2,3) and to chemically sense them as part of the swimming regulatory scheme (1,4,5). In addition to the fundamental importance of GGBP in the molecular and cellular biology of enteric bacteria, the potential to exploit GGBP for glucose detection has motivated extensive study (6–15). Crystallographic (16) and bulk steady-state (6,7,17–19) studies of GGBP have investigated its binding of glucose, which is usually described by a single (5–7,19) binding constant, though some studies have suggested otherwise (17,18). GGBP undergoes large structural fluctuations that are decreased, but not eliminated upon binding of glucose (19). Thermodynamic characterization of the structural changes associated with ligand recognition and docking to the membrane-protein complex can be difficult. The role of conformation in ligand binding and delivery to the cytosol, or in activation of the methyl-accepting chemotaxis protein, Trg, is not well characterized. Here we show that GGBP fluctuates on a shallow free energy landscape between at least three conformations, the relative weights of which are modulated by the binding of glucose. Each structure has a different binding affinity and thermodynamic properties. The single binding site of GGBP was considered to have a single association constant; our results suggest that the binding constant is conformationally dependent. Moreover, ligand binding does not induce the conformational change, rather, it remodels the free energy landscape, biasing the distribution of conformation by stabilizing the high-affinity receptor-competent structures. Computational predictions for the closely related ribose binding protein (RBP) have shown qualitatively similar results (20).

The presence of two high-affinity binding structures is suggestive of the different membrane receptors to which GGBP must bind to provide either active transport or chemotaxis. Conformational plasticity is increasingly becoming recognized as an important issue in drug resistance (3,21). ABC transporter systems, like the one to which GGBP belongs, are common targets for therapeutics (3). An inhibitor for flexible targets like GGBP would need to interact with all parts of the binding-competent conformational ensemble.

METHODS

Materials

Acrylodan-labeled GGBP was provided by Ge et al. (6). The protein was suspended in 20 mM phosphate buffer at pH 7.5 with 0.2 mM calcium chloride. Samples were centrifuge filtered with Amicon 5000 MWCO centrifuge filters (Houston, TX) for 30 min, four times to remove any free dye or glucose in solution.

Experimental

Time-correlated single photon counting (TCSPC) measurements of polarized fluorescence were performed as previously described (22). The pulsed-laser excitation used was 390 nm, and the fluorescence emission was observed at 510 nm. Temperature was maintained using a Quantum Northwest TLC150 Peltier controller (Spokane, WA). Photons were counted for 3–6 min to obtain transients with ∼10,000 peak counts.

TCSPC measurements of the fluorescence lifetime and anisotropy were performed across 11 concentrations of glucose (0.0, 0.0, 0.2, 0.5, 1.0, 1.3, 2.5, 4.5, 6.0, 10.0, and 45.0 μM) at seven temperatures ranging from (T = 5, 10, 15, 20, 25, 30, 35°C) and three polarizations (0°, 54.7°, and 90°) for a total of 231 TCSPC decays. Global fitting of all data from each temperature using a regularized nonnegative linear least squares procedure showed six spectroscopically distinguishable states, all of which were sensitive to the glucose concentration.

Global regularized distribution fits

TCSPC fluorescence lifetime data are typically fit to a linear combination of one or more exponentials convoluted by the instrument response function. If a basis set of exponentials with regularly spaced decay constants is used, then the fitting procedure is reduced to solving a set of linear algebraic equations (23). The number of free parameters in this case is very large and the solution to the fitting problem is not statistically unique and therefore not mathematically stable. Regularization is a technique used to stabilize results by mathematically imposing prior knowledge to constrain the immense set of available solutions. The regularizer acts as a constraint that reduces the number of effective free parameters. The prior knowledge that is tacitly assumed in most regularization procedures is piecewise continuity of the solution in the fluorescence lifetime dimension as represented by a line. In the case of several possible conformations of GGBP this is not necessarily a valid assumption. However the population of a particular species should be piecewise continuous with respect to a changing ligand concentration.

We have formulated a general global regularization scheme that will incorporate prior knowledge of the evolution of a data set over a changing variable. This minimal model that assumes only continuity with respect to glucose concentration allows evaluation of possible models without choosing them a priori. We fit 11 isotropic fluorescent decays (3456 points per decay) at seven temperatures using a continuity-in-glucose-concentration regularizer to estimate the fluorescence lifetimes and amplitudes in our data set. The strength of regularization was estimated using the L-curve method (24). The regularization parameter value was then optimized using the F-test at P = 0.5 to compare the residuals from the final regularized fits with the unregularized fit (25). In the final fits, the estimated number of effective free parameters was ∼60. A typical result of the totally nonnegative linear least squares procedure is shown in Fig. 1.

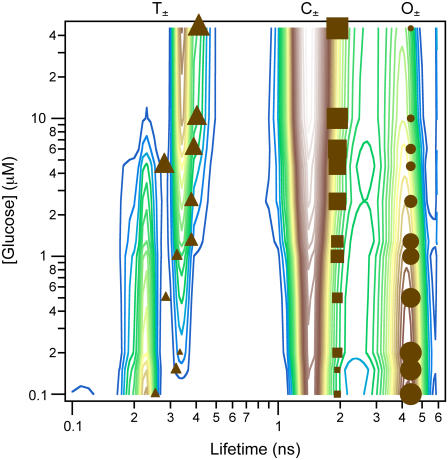
FIGURE 1.

Glucose modulated fluorescence in GGBP. Contour plots representing the isotropic fluorescence lifetime distributions from globally regularized fitting of a glucose titration at 35°C. The solid symbols represent the parameters from a discrete three-exponential global fit to the same data set, but also including the parallel and perpendicular fluorescence components. The size of the symbols represents the relative amplitude changes of the components. Quantitative populations for all data appear in Fig. 2. Two lifetime distributions (∼1.5 and 4.5 ns) are nearly constant with glucose concentration, whereas a third lifetime shifts from ∼250 to 400 ps with increasing glucose.

Discrete fitting

Fluorescence lifetimes were also analyzed using a convolute-and-compare, nonlinear, least-squares technique (26). The data sets at each temperature were fit with one, two, three, and four exponential terms. Three exponents was the highest statistically justifiable number of exponential terms and correlated well with the results of the minimal model regularized totally nonnegative linear least-squares fits.

Analysis of fluorescence anisotropy decay was performed based on the results of the isotropic analysis (27). A typical fit to the transients measured for the three polarization angles for a single temperature and glucose concentration is shown in Fig. 2.

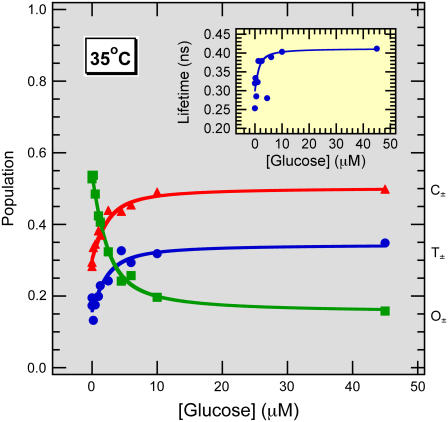
FIGURE 2.

Discrete least-squares data fit. Fluorescence lifetime populations as a function of glucose concentration at 35°C resulting from global least-squares fitting. The inset shows the third lifetime, which is fit locally to each glucose concentration. This lifetime showed isotherm-type behavior with a binding constant of ∼0.2 μM.

Based on the above results, magic-angle (isotropic), parallel, and perpendicular polarized fluorescence decay transients were simultaneously analyzed for the 11 different glucose concentrations. Fluorescence decay rates were globally linked across all glucose concentrations and a third decay rate was allowed to vary with glucose concentration, g, according to A_M(t) in the following equation:

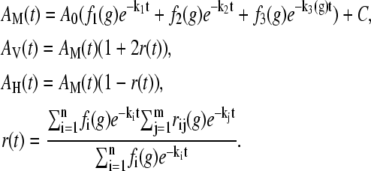(1)

The global results of a typical discrete fit are shown in Fig. 2 and represented by the solid symbols in Fig. 1.

With this technique, we were able to observe changes in the relative populations of the three decay rates (i.e., the three spectroscopically distinct structures) as a function of glucose concentration. To verify this model, we also analyzed the data with global populations (f_i) and local fluorescent rates (k_i), as well as all of the permutations of local versus global rates and populations. All other models resulted in a significant increase in the reduced χ².

The residuals from the global fits were nearly Gaussian across the entire global data set, indicating a good fit to the data. Each of the seven temperatures from 5 to 35°C was globally analyzed with this methodology giving a reduced χ² ranging between 1.03 and 1.05. Error estimates for the parameters were determined from the diagonal elements of the covariance matrix.

RESULTS AND DISCUSSION

Conformationally dependent fluorescence

The L255C mutant of GGBP, labeled in the interdomain hinge at residue 255 with acrylodan (6-acryloyl-2-dimethylaminonaphthalene) gives fluorescence that is conformationally sensitive without interfering with glucose binding (6,7,28). Acrylodan fluorescence is highly sensitive to local environment polarity changes; increased exposure to water decreases its lifetime and anisotropy (28). Ruthemium bis(2,2′-bipyridyl)-1,10 phenanthroline-9-isothiocyanate attached at the N-terminus acts as a fluorescent reference. The right panel of Fig. 3 shows different structures of GGBP and the location of the mutation and fluorophores.

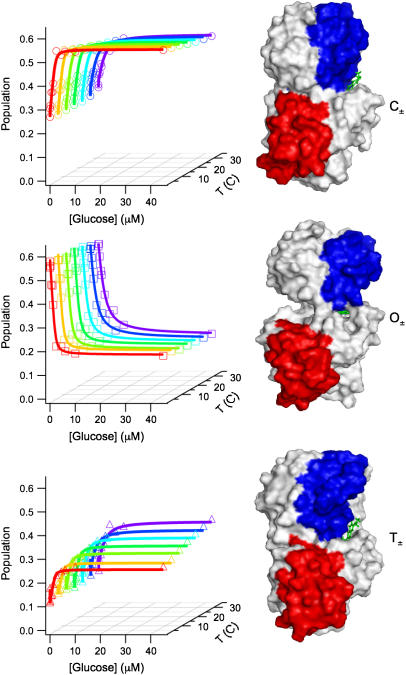
FIGURE 3.

Fluorescence of three GGBP conformations. The three structures on the right side of the figure illustrate the placement of the acrylodan fluorescent probe on GGBP. The blue and red surface regions emphasize the type of conformational change by their relative alignment. The structures were created from molecular dynamics simulations of 2GBP from the Protein Data Bank and exhibit the closed (top), open (center), and twisted (bottom) structures of GGBP. The graphs directly to the left of the structures show the dependence of the population of each contribution on glucose concentration ([g] = 0.0, 0.0, 0.2, 0.5, 1.0, 1.3, 2.5, 4.5, 6.0, 10.0, 45.0 μM) and temperature (T = 5, 10, 15, 20, 25, 30, 35°C). The population of the open form can be seen to decrease with increasing [g] whereas the population of the closed and twisted forms increases.

Initial model evaluation was performed using a global regularization technique to extract lifetime distributions in the isotropic fluorescence decays. The resulting distributions for data at 35°C are shown in the contour plot of Fig. 1. Three states have significant contributions at high glucose concentration but not at zero glucose; the other three states dominate in the absence of glucose but disappear at high glucose concentrations. Therefore, we assign three of the states to glucose-bound structures (O_⊕, C_⊕, T_⊕) and the other three to apo-GGBP structures (O_⊖, C_⊖, T_⊖). Two pairs of states (O_⊕, O_⊖ and C_⊕, C_⊖) undergo modest (∼10%) shifts in lifetime upon binding glucose whereas the other pair of states (T_⊕, T_⊖) undergo a twofold change in lifetime. This change in lifetime between the bound and unbound versions of a pair of states suggests that additional small structural differences may exist between them. However, the resolution of fluorescence in this case is adequate to distinguish the coarse structures, but not adequate to reliably distinguish all six states.

The global regularized analysis provided the rationale to reduce the number of free parameters in the fitting procedure using a specific model consisting of three bound/unbound pairs of states (C_±, O_±, T_±) each contributing a discrete exponential decay corresponding to a particular protein structure. We then used global analysis across the glucose concentrations to fit the three exponential lifetimes, each with its own anisotropy decay, for each temperature (solid symbols in Fig. 1). The relative contribution of each component showed Langmuir isotherm behavior with glucose binding (see left panels of Fig. 3). All conformations exhibited binding affinities on the order of 0.05–5 μM consistent with previous experiments (1,5–7,17,18). The lifetime of the third component changed by a factor of ∼2 and shows Langmuir isotherm behavior with an affinity constant of 0.1–0.2 μM. The observed binding and temperature dependence were different for each state.

These results show that three structures of the protein contribute to the conformational ensemble with populations of >10%, suggesting that interchange between the structures is dynamic and thermally driven. The presence of the ligand modifies the populations of the three structures biasing the equilibrium in favor of the binding-competent portion of the ensemble.

Based on the global discrete fitting we further characterize the three pairs of observed states based on their binding and thermodynamic behavior, the known properties of acrylodan, molecular modeling, and comparison to literature disulphide trapping (19) and umbrella sampling molecular dynamics simulation studies (20). Motion between the two domains changes the geometry of the binding cleft as well as the area on the other side of the hinge from the binding cleft where the acrylodan dye is attached. “Hinge” motion opens the binding cleft between the domains; “twist” changes the alignment of the domains. Because only one crystal structure is available, we performed adiabatic steered structural energy minimizations over a large hinge and twist phase space. The energy minimized structures were used for umbrella sampling molecular dynamics simulations. Three low energy structures resulted from the simulations that correspond well with our predictions. Full details of the computational work is the subject of a future manuscript. Structures obtained from the molecular dynamics are shown on the right of Fig. 3. Relative alignment of red and blue colored surface regions are shown to make the structural changes apparent. Based on molecular modeling of the GGBP-acrylodan conjugate, hinge-opening motion crowds the acrylodan, suggesting an increase in both its fluorescence lifetime and anisotropy. Positive (negative) twist angles move the N-terminal domain away from (toward) the acrylodan providing more (less) exposure to solvent and a decreased (increased) lifetime and anisotropy.

Binding behavior

The thermodynamically averaged affinity constant ranged from 0.097 to 1.18 μM across the temperature range (5–35°C). In the absence of glucose the dominant structure (O_± in Fig. 3) has the most sequestered acrylodan with a lifetime that is longer than the average lifetime reported for acrylodan in methanol (28), ranging from 4.7 to 4.3 ns over T = 5–35°C, with an anisotropy decay of ∼20 ns, consistent with GGBP rotational diffusion. The total fraction of O_± decreases with glucose concentration showing an affinity constant of 0.301–4.15 μM over the temperature range. The low glucose affinity, the decrease in population with glucose concentration, and long lifetime suggest that this is an open structure. That the acrylodan is sequestered from solvent at the back side of the hinge suggests that the labeling may prevent the clamshell from opening completely. This would suggest that the open structure might have a slightly higher binding affinity in these studies than might otherwise be observed. Because this is only one element of the conformational ensemble, the effect on the overall binding affinity is expected and observed to be small.

The dominant structure at high glucose concentrations (C_± in Fig. 3) shows intermediate sequestration of acrylodan with a lifetime between that of methanol and water ranging from 2.4 to 1.9 ns over T = 5–35°C, and with an anisotropy decay of ∼20 ns, consistent with GGBP rotational diffusion. The total fraction of C_± increases with glucose concentration showing an affinity constant of 0.052–0.703 μM over the temperature range, suggesting a closed, binding-competent structure.

The population of the third acrylodan fluorescence component (T_± in Fig. 3) also increases population with glucose showing an apparent affinity constant of 0.047–0.562 μM. The fluorescence lifetime of this state is shorter than the average lifetime of acrylodan in water and shows a substantial shift in the fluorescence lifetime from ∼0.28 to ∼0.48 ns (average of all temperatures) upon binding of glucose and has a faster anisotropy decay of ∼1 ns, consistent with more orientationally free acrylodan. This may indicate that there is a substantial conformational difference between the apo- and holo-forms of this state and may be better considered to be distinguishable states. The short lifetime may be indicative of transient contact of the acrylodan with an amino acid that can act as a quencher such as tryptophan or tyrosine. Crystal structures of GGBP and RBP suggest that the alternate high-affinity binding state may consist of a closed hinge with a twisted domain alignment (29).

The observation of multiple apo-GGBP structures is consistent with reports of large conformational fluctuations being present under glucose-free conditions (19). The observation of two dominant high-affinity holo-GGBP structures is also consistent with reduced conformational fluctuations under saturating glucose conditions (19). These results are qualitatively similar to predictions made for the closely related RBP (20). Computational results on RBP have shown qualitatively similar behavior where the secondary states for the bound and unbound limits show somewhat different free energy minima in the hinge and twist angles between the domains.

Thermodynamic properties

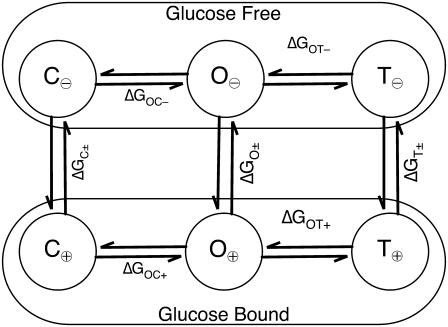
The population of each structural state showed binding isotherm behavior and systematic temperature dependence. Furthermore, even in the absence of glucose, the closed and twisted conformations (Fig. 3 (C_± and T_±)) were ∼25% and 15% of the total population, respectively. Similarly, the open form contributes ∼12% to the high glucose limit. This is clear evidence that the protein is always in a dynamic equilibrium between all three states. The thermodynamics of this equilibrium are addressed via binding constants of the three states and by comparing the three populations in the limits of no ligand and infinite ligand. We have done this by fitting the isotherms based on the six-state model shown in Fig. 4.

FIGURE 4.

Six-state model for GGBP. A model based on the time-correlated fluorescence analysis described in this article. The open (O_±), closed (C_±), and twisted (T_±) structures each exhibit spectroscopically distinguishable apo-GGBP (O_⊖, C_⊖, T_⊖) and holo-GGBP (O_⊕, C_⊕, T_⊕) states.

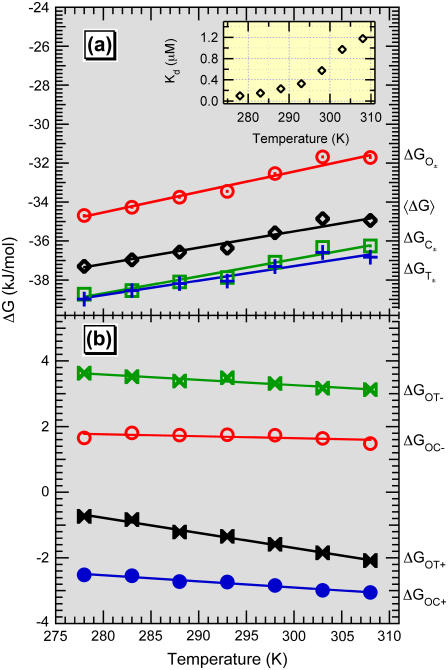
Fig. 5 displays the temperature dependence of the relative free energies. Temperature changes populate the states as one would expect for these assignments. The open conformation is favored in the absence of glucose and exhibits the smallest gain in free energy with the addition of ligand. The other two conformations are closer to one another in their relative free energies and exhibit very similar entropies. The T_± state has a slightly higher entropy than the ligand-bound, closed state. The free energy differences between conformations are comparable to k_BT at physiological temperatures and relevant glucose concentrations, allowing thermal fluctuations to drive transitions between different protein conformations. The enthalpy and entropy changes between states are summarized in Table 1.

FIGURE 5.

Free energies of GGBP. (a) Free energy difference between glucose-free and glucose-bound conformations. The apparent free energy is calculated as 〈ΔG〉 = −RT ln(K_d). (Inset) The apparent binding constant, K_d, as a function of temperature. (b) The free energy difference between conformational states of apo-GGBP (upper two traces) shows a lower temperature dependence than that of holo-GGBP (lower two traces).

TABLE 1.

Enthalpy and entropy changes, by state, for binding of glucose and for transitions between conformations in the holo- and apo-GGBP as determined from linear, least-squares fits to the free-energy changes determined from the global fits

Initial: final	ΔH (kJ mol−1)	ΔS (J mol−1K−1)
C⊖: C⊕	−64.5 ± 2.5	−91.9 ± 8.5
T⊖: T⊕	−61.4 ± 2.7	−80.4 ± 9.3
O⊖: O⊕	−65.2 ± 2.7	−109 ± 9
Apparent	−61.8 ± 2.5	−87.8 ± 8.4
O⊖: C⊖	3.0 ± 1.1	4.4 ± 3.8
O⊖: T⊖	7.3 ± 0.5	14.1 ± 1.7
O⊕: C⊕	3.6 ± 0.4	21.8 ± 1.4
O⊕: T⊕	11.1 ± 0.5	42.9 ± 1.8

Reported errors are derived from diagonal elements of the covariance matrix.

Implications for GGBP Function

These results have implications for the mechanisms of glucose active transport and chemotaxis. GGBP is one of several periplasmic chemoreceptor proteins that are responsible for signaling the cell to swim toward attractants and away from repellants (4). GGBP is expressed as part of the methylgalactoside ABC transport system, mgl (2). Both GGBP and ribose binding protein (RBP) interact with the methyl-accepting chemotaxis membrane protein, Trg, to influence chemotaxis. GGBP and RBP have separate transport complexes, however. To accommodate the generality of chemotaxis and the specificity of transport, there should be both a common and an orthogonal binding mode for these proteins. The presence of two high-affinity structures implied by our data suggests an allosteric resolution to the two functional roles that GGBP plays in enteric bacteria. The conformational lability in holo-GGBP could provide a mechanism for it to share the Trg chemotaxis receptor with RBP, but have selective interaction with the ABC transporter membrane receptor, mglA.

Allostery is one mechanism for accommodating multiple regulatory functions and is often discussed in terms of two models, KNF (30) and MWC (31), that were introduced roughly 40 years ago. These models make implicit assumptions about the energy required to convert the protein between active and inactive forms as well as the how the ligand binding energy compares to and influences the conversion energy. From a thermodynamic perspective, the difference between the models is the implied magnitude of these energy changes. KNF suggests that the apo-protein is normally inactive with binding of ligand inducing a conformational change that activates the holo-protein, implying conformational energy differences in substantial excess of thermal energy (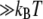). MWC suggests that the apo-protein hops between active and inactive forms, with binding of a ligand trapping the holo-protein in the active form. This implies conformational energy changes and barriers comparable to thermal energy (∼k_BT) with ligand binding stabilizing the active structure's energy by at least several k_BT. Though our data suggest that the MWC model is more reasonable in this case as the difference between conformations is (∼k_BT), there is measurable ligand affinity for each of the structures. Also the amount of conformational bias implied by MWC is substantially greater than we observe.

The measurable affinity for glucose in the open state GGBP has implications for active transport. If the binding cleft of GGBP is exposed to the cytosol during active glucose transport, then GGBP must have another conformation that is too rare to contribute to our bulk fluorescence measurements and has a binding constant on the order of 10⁻³ M. Alternatively, the membrane receptor complex could trap the GGBP when it fluctuates to the lower-affinity open form. The membrane receptor complex would need to be open to the periplasm and closed on the cytoplasm side of the membrane. Release of the glucose into the receptor complex could trigger the hydrolysis of ATP switching the membrane complex to a form with the interior cavity facing the cytoplasm.