Abstract
The αβ T cell receptor (TCR) is responsible for recognizing peptides bound and “presented” by major histocompatibility complex (MHC) molecules. We recently reported that at 25°C the A6 TCR, which recognizes the Tax peptide presented by the class I MHC human leukocyte antigen-A*0201 (HLA-A2), binds with a weak ΔH°, a favorable ΔS°, and a moderately negative ΔCp. These observations were of interest given the unfavorable binding entropies and large heat capacity changes measured for many other TCR-ligand interactions, suggested to result from TCR conformational changes occurring upon binding. Here, we further investigated the A6-Tax/HLA-A2 interaction using titration calorimetry. We found that binding results in a pKa shift, complicating interpretation of measured binding thermodynamics. To better characterize the interaction, we measured binding as a function of pH, temperature, and buffer ionization enthalpy. A global analysis of the resulting data allowed determination of both the intrinsic binding thermodynamics separated from the influence of protonation as well as the thermodynamics associated with the pKa shift. Our results indicate that intrinsically, A6 binds Tax/HLA-A2 with a very weak ΔH°, an even more favorable ΔS° than previously thought, and a relatively large negative ΔCp. Comparison of these energetics with the makeup of the protein-protein interface suggests that conformational adjustments are required for binding, but these are more likely to be structural shifts, rather than disorder-to-order transitions. The thermodynamics of the pKa shift suggest protonation may be linked to an additional process such as ion binding.
INTRODUCTION
Recognition of an antigenic peptide bound and presented by a major histocompatibility complex (MHC) protein is required for the initiation and propagation of a cellular immune response, as well as generation and maintenance of the T cell repertoire. Peptide/MHC complexes are recognized by hypervariable αβ T cell receptors (TCR), which are expressed on the surface of CD4+ or CD8+ T lymphocytes. Structurally, TCRs bind their ligand with a diagonal-to-orthogonal binding mode (1), making contacts to both the antigenic peptide as well as the presenting MHC molecule. TCR binding affinities tend to be in the low micromolar range, with relatively slow on-rates and fast off-rates (2).
There is significant interest in the biophysics of TCR recognition of ligand. The relative contributions of the peptide, the MHC, and the various TCR complementarity determining region (CDR) loops to TCR specificity and cross-reactivity are topics of frequent discussion, as are the roles of conformational changes and flexibility in receptor recognition and signaling. TCR binding thermodynamics have been measured in a number of instances, contributing to proposals that link thermodynamic parameters to various immunological phenomena. For example, based on a deconvolution of entropy and heat capacity changes, Boniface et al. proposed that local folding of TCR CDR loops upon binding allows for TCR “scanning” of diverse peptides (3). A number of investigators have measured unfavorable entropy changes for different TCR-peptide/MHC interactions (4–9), which together with comparisons of structures of bound and free TCRs (10–12) have lent support to the notion that receptor binding coincides with a reduction in CDR loop flexibility. Recently, Krogsgaard et al. measured very large negative heat capacity changes for a number of TCR-peptide/MHC interactions, which were interpreted as evidence of even larger TCR structural changes occurring upon binding (8), potentially influencing the quality of the signal transmitted across the T cell membrane.
The αβ TCR A6, isolated from a human leukocyte antigen-A*0201 (HLA-A2)-restricted CD8+ T cell clone from an HTLV-1+ individual (13), recognizes the epitope spanning residues 11–19 of the HTLV-1 Tax protein (sequence LLFGYPVYV) presented by the class I MHC molecule HLA-A*0201 (HLA-A2) (13). The interaction between A6 and Tax/HLA-A2 has been studied in detail, and, as one of the first TCR-peptide/MHC interactions to be crystallized (14), has served as a model for probing the structural, biochemical, and biophysical aspects of TCR recognition of ligand. We recently reported that A6 bound Tax/HLA-A2 with a favorable entropy change (at 25°C) and a moderately negative ΔCp (6). These findings were of interest given the observations of unfavorable binding entropies and large heat capacity changes for other TCR-ligand interactions (4–9), particularly because structures of the A6 TCR bound to modified Tax peptides presented by HLA-A2 showed that the A6 TCR can adopt alternate conformations both inside and outside of the antigen binding site (15,16).
To further investigate the molecular recognition properties of the A6 TCR, here we performed a detailed calorimetric investigation of the A6-Tax/HLA-A2 interaction. Our previous thermodynamic studies of this interaction were based predominantly on surface plasmon resonance (SPR) (6), an approach that is limited in that determination of accurate thermodynamic parameters is dependent on having a large number of accurate free energy measurements across a wide temperature range. Isothermal titration calorimetry (ITC) bypasses this limitation, providing a direct measure of not just ΔG° but also the underlying thermodynamic parameters (ΔH°, ΔS°) and their temperature dependence (ΔCp). Furthermore, calorimetry provides a direct method for assaying the influence of equilibria linked to binding, which can dramatically influence observed binding thermodynamics (17–21) but are otherwise difficult to characterize.
In examining the thermodynamics of A6 binding Tax/HLA-A2, we observed that binding proceeds with a shift in the pKa of at least one ionizable group. The resulting linkage of receptor binding to protonation imparts significant solution dependencies on all of the observed binding thermodynamics, such that the thermodynamics determined previously using SPR only approximate the intrinsic values most useful for comparison with structural properties such as buried surface areas. Determination of these intrinsic binding thermodynamics required a global analysis of calorimetric data collected as a function of pH, buffer ionization enthalpy, and temperature (17,22). The results of this analysis indicate that intrinsically, separated from the influence of protonation, the A6 TCR binds Tax/HLA-A2 at 25°C with a very weak binding enthalpy change, a large positive entropy change, and a large negative heat capacity change. The intrinsic binding enthalpy change is overpredicted and the heat capacity change is underpredicted using empirical calculations that take into account the polar and apolar character of the protein-protein interface (23), possibly reflecting conformational rearrangements that are necessary for binding. Interestingly, the protonation that is linked to binding occurs with a very large heat capacity change, suggesting that protonation is coupled to an additional process, possibly ion binding. These results are discussed in the context of molecular recognition by the A6 TCR, as well as general mechanisms of TCR binding and cross-reactivity.
MATERIALS AND METHODS
Proteins and peptide
Soluble versions of HLA-A2 and A6 were expressed and refolded as described (16,24,25). Briefly, inclusion bodies of the HLA-A2 heavy chain and β2-microglobulin (β2m) or the TCR α- and β-chains were generated separately in Escherichia coli. Inclusion bodies were isolated and denatured in 8 M urea. For the TCRs, the α- and β-chain inclusion bodies were diluted into refolding buffer, with the α-chain at 50% excess. For Tax/HLA-A2, the HLA-A2 heavy chain and β2m inclusion bodies were diluted into refolding buffer at a 1:2 ratio along with excess Tax peptide, which was synthesized and purified locally using an ABI 433A instrument (Applied Biosystems, Foster City, CA). After a 24-h incubation at 4°C, the refolding solution was desalted via dialysis. Refolded protein was purified using anion exchange followed by size-exclusion chromatography. The A6 TCR construct terminated just after the membrane-proximal interchain disulfide bond and included a heterodimeric coiled-coil at the C-terminal end that drives formation of the interchain disulfide, preventing dissociation of the α- and β-chains (16,26). Concentrations of refolded proteins were determined spectroscopically. For each protein, the average of three readings of the absorbance at 280 nm was taken. Extinction coefficients were 95,839 M−1 cm−1 for Tax/HLA-A2 and 84,503 M−1 cm−1 for the A6 TCR (16). Concentrations of Tax/HLA-A2 were at or above 12 μM. As the affinity of the Tax peptide for HLA-A2 is 18 nM at 25°C, with a dissociation rate of 3 × 10−5 s−1 (2 × 10−4 s−1 at 37°C) (27), peptide dissociation from HLA-A2 was judged to be inconsequential.
Isothermal titration calorimetry
Titration calorimetry was performed with a Microcal VP-ITC (Microcal, Studio City, CA). Most titrations were performed with A6 in the syringe and Tax/HLA-A2 in the calorimeter cell, although the reverse titration was occasionally performed as a control. Starting protein concentrations in the calorimeter cell ranged from 12 to 20 μM, whereas concentrations in the syringe were 119–150 μM. Solution conditions were 20 mM of the specified buffer and 150 mM NaCl. Temperature ranged from 4°C to 37°C. pH was varied from 5.4 to 7.4 and is specified at the experimental temperature (i.e., pH was adjusted at room temperature to maintain constant pH across the experimental temperature range). ITC injection volumes were 10 μl, and injections were performed over 20 s spaced 120–180 s apart to allow for a complete return to baseline. Data were processed and integrated with the Origin software distributed with the instrument. Single data sets were fit to a single site ITC binding model (28) with the nonlinear fitting package NLREG, using a baseline offset parameter to account for heats of dilution. The first data point was excluded from analysis due to dilution across the injection needle tip. The c value, or the product of the binding equilibrium constant and the concentration of the molecule in the calorimeter cell (28), was between 10 and 50 for all experiments.
Global analysis of proton-linked binding
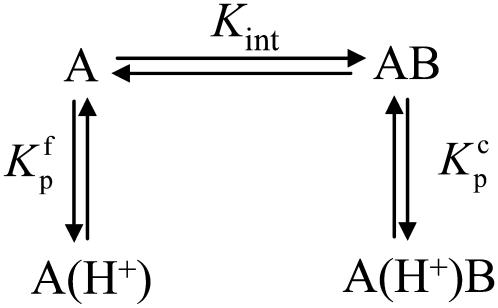
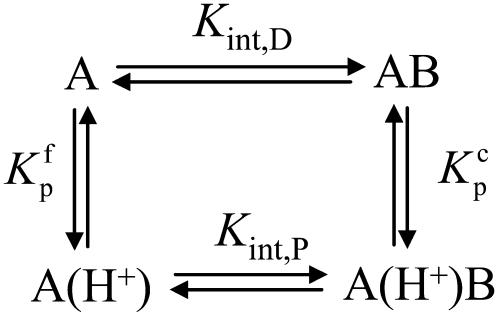
Data as a function of pH, buffer, and temperature were fit globally (29) to a model describing a protein-ligand interaction linked to a single pKa shift as described by Baker and Murphy (17) and summarized by the following cycle: where Kint is the “intrinsic” ligand binding constant describing the affinity of B for deprotonated A, 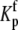 is the equilibrium constant for protonation of free A, and
is the equilibrium constant for protonation of free A, and 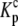 is the equilibrium constant for protonation of the AB complex (equal to 10pKa,free and 10pKa,complex, respectively). The definition of the intrinsic binding affinity as the affinity of B for deprotonated A is consistent with previous work describing the influence of linked protonation on protein binding energetics (17,22,30,31). It is also appropriate considering the measured pKa shift, which as discussed below is likely to be attributable to a basic amino acid and thus neutral in the deprotonated state (the consequences of instead defining the intrinsic binding thermodynamics as B binding to protonated A are discussed in the Appendix).
is the equilibrium constant for protonation of the AB complex (equal to 10pKa,free and 10pKa,complex, respectively). The definition of the intrinsic binding affinity as the affinity of B for deprotonated A is consistent with previous work describing the influence of linked protonation on protein binding energetics (17,22,30,31). It is also appropriate considering the measured pKa shift, which as discussed below is likely to be attributable to a basic amino acid and thus neutral in the deprotonated state (the consequences of instead defining the intrinsic binding thermodynamics as B binding to protonated A are discussed in the Appendix).
According to Scheme 1, the observed AB binding affinity is a function of pH, as described by
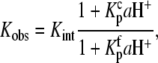 |
(1) |
where aH+ is the proton activity, given by 10−pH.
SCHEME 1.
The pKa shift in Scheme 1 necessitates a release of protons into (or from) the buffer upon AB binding. This directly influences the observed binding enthalpy, as described by
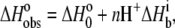 |
(2) |
where 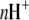 is the number of protons released (+nH+) or absorbed (−nH+) by the buffer,
is the number of protons released (+nH+) or absorbed (−nH+) by the buffer, 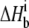 is the buffer ionization enthalpy, and
is the buffer ionization enthalpy, and 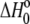 is the enthalpy observed in a buffer with an ionization enthalpy of zero. Equation 2 is a linear equation, indicating that the presence of proton-linked binding can be detected by measuring the binding enthalpy under identical conditions but in buffers with different ionization enthalpies (e.g., phosphate, imidazole, HEPES, etc.). The value of nH+ results from the difference between the fractional proton saturation of the AB complex and free A, as described by
is the enthalpy observed in a buffer with an ionization enthalpy of zero. Equation 2 is a linear equation, indicating that the presence of proton-linked binding can be detected by measuring the binding enthalpy under identical conditions but in buffers with different ionization enthalpies (e.g., phosphate, imidazole, HEPES, etc.). The value of nH+ results from the difference between the fractional proton saturation of the AB complex and free A, as described by
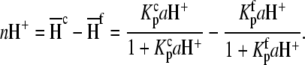 |
(3) |
The value of 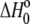 in plots of observed binding enthalpies versus buffer ionization enthalpies is not necessarily the intrinsic binding enthalpy as defined in Scheme 1 (i.e., the enthalpy of B binding deprotonated A). For Scheme 1,
in plots of observed binding enthalpies versus buffer ionization enthalpies is not necessarily the intrinsic binding enthalpy as defined in Scheme 1 (i.e., the enthalpy of B binding deprotonated A). For Scheme 1, 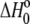 can be deconstructed by following the thermodynamic cycle:
can be deconstructed by following the thermodynamic cycle:
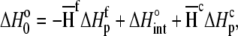 |
(4) |
where 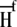 and
and 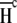 are the fractional proton saturations of free A and the AB complex as defined in Eq. 3, and
are the fractional proton saturations of free A and the AB complex as defined in Eq. 3, and 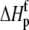 and
and 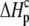 are the proton binding enthalpies of free A and the AB complex. Equation 4 indicates that
are the proton binding enthalpies of free A and the AB complex. Equation 4 indicates that 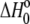 can include contributions from pH and the magnitude of the pKa shift and its enthalpic component (17,19), highlighting the need to perform a global analysis to fully account for the influence of linked protonation. As has been discussed (17), such accounting is necessary when binding thermodynamics are to be compared with empirical calculations that do not explicitly account for the effects of protonation.
can include contributions from pH and the magnitude of the pKa shift and its enthalpic component (17,19), highlighting the need to perform a global analysis to fully account for the influence of linked protonation. As has been discussed (17), such accounting is necessary when binding thermodynamics are to be compared with empirical calculations that do not explicitly account for the effects of protonation.
The temperature dependencies of Eqs. 1–4 can be accounted for by including the temperature dependence of each enthalpy change and equilibrium constant assuming a temperature-independent heat capacity change:
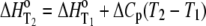 |
(5) |
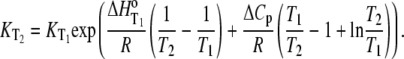 |
(6) |
Recasting Eq. 6 in terms of free energy, enthalpy, and entropy yields the modified Gibbs-Helmholtz equation:
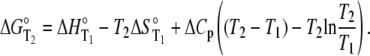 |
(7) |
For the global fitting of ITC data as a function of pH, buffer ionization enthalpy, and temperature, Eqs. 1–7 were used in a nonlinear least-squares function for a single site ITC binding model (28), with the binding equilibrium constant represented by Eq. 1 and the binding enthalpy by Eqs. 2–4. During fitting, the temperature dependencies of all enthalpies and equilibrium constants were accounted for by Eqs. 5–7. In the fitting function, Kint was fit as the intrinsic binding free energy change (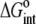 ) and the pKa shift as the protonation free energy change in the free protein and its change upon binding (
) and the pKa shift as the protonation free energy change in the free protein and its change upon binding (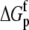 and
and 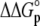 ) using the standard relationship ΔG° = −RTlnK. The protonation enthalpy of the complex (
) using the standard relationship ΔG° = −RTlnK. The protonation enthalpy of the complex (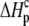 ) was fit as the change in
) was fit as the change in 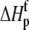 upon binding (
upon binding (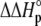 ). Recasting these parameters in this way added stability to the fit and reduced parameter correlation. Seventeen data sets were fit simultaneously. Each data set had as local variables a stoichiometry (n) and a baseline offset. Global variables common to all data sets were the intrinsic binding free energy at 25°C, the intrinsic binding enthalpy change at 25°C, the intrinsic binding heat capacity change, the free protein protonation free energy and its change upon binding at 25°C, the free protein protonation enthalpy and its change upon binding at 25°C, and the protonation heat capacity change. We attempted to include the change in protonation heat capacity change upon binding (ΔΔCp,p) as a fitted parameter, but as discussed below this resulted in large fitting errors and unacceptable levels of parameter correlation. There were 420 degrees of freedom in the fit. Fitting was performed using the Levenberg-Marquardt algorithm in a custom routine written in OriginPro 7.5 (OriginLab, Northampton, MA). Initial guesses for parameters were systematically varied to ensure convergence to a global minimum. Error analysis and propagation of error for the derived values in Table 2 and Fig. 5 were performed via Monte Carlo analysis (32). Briefly, the fitted parameters were used to generate 2000 additional data sets with Gaussian-distributed pseudorandom noise added, with the standard deviation of the initial fit to the experimental data providing the width of the Gaussian distribution. These simulated data sets were then fit as described above. Errors for the fitted and derived parameters were taken as the standard deviations of the parameters from the 2000 Monte Carlo runs. For the fitted parameters, the Monte Carlo-derived errors differed from the standard errors of the fit by no more than 6%. All errors are reported at one standard deviation. Values for buffer ionization enthalpies and heat capacities were from Fukada and Takahashi (33) and Christensen et al. (34).
). Recasting these parameters in this way added stability to the fit and reduced parameter correlation. Seventeen data sets were fit simultaneously. Each data set had as local variables a stoichiometry (n) and a baseline offset. Global variables common to all data sets were the intrinsic binding free energy at 25°C, the intrinsic binding enthalpy change at 25°C, the intrinsic binding heat capacity change, the free protein protonation free energy and its change upon binding at 25°C, the free protein protonation enthalpy and its change upon binding at 25°C, and the protonation heat capacity change. We attempted to include the change in protonation heat capacity change upon binding (ΔΔCp,p) as a fitted parameter, but as discussed below this resulted in large fitting errors and unacceptable levels of parameter correlation. There were 420 degrees of freedom in the fit. Fitting was performed using the Levenberg-Marquardt algorithm in a custom routine written in OriginPro 7.5 (OriginLab, Northampton, MA). Initial guesses for parameters were systematically varied to ensure convergence to a global minimum. Error analysis and propagation of error for the derived values in Table 2 and Fig. 5 were performed via Monte Carlo analysis (32). Briefly, the fitted parameters were used to generate 2000 additional data sets with Gaussian-distributed pseudorandom noise added, with the standard deviation of the initial fit to the experimental data providing the width of the Gaussian distribution. These simulated data sets were then fit as described above. Errors for the fitted and derived parameters were taken as the standard deviations of the parameters from the 2000 Monte Carlo runs. For the fitted parameters, the Monte Carlo-derived errors differed from the standard errors of the fit by no more than 6%. All errors are reported at one standard deviation. Values for buffer ionization enthalpies and heat capacities were from Fukada and Takahashi (33) and Christensen et al. (34).
TABLE 2.
Energetics for the binding of A6 to Tax/HLA-A2 at 25°C
| Intrinsic binding energetics | |
|---|---|
Free energy change (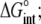 kcal/mol) kcal/mol) |
−9.2 ± 0.1 |
| Binding affinity (KD,int; μM) | 0.19 ± 0.02 |
Enthalpy change (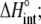 kcal/mol) kcal/mol) |
−1.8 ± 0.3 |
Entropy change (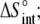 cal/mol/K) cal/mol/K) |
25 ± 1 |
Heat capacity change (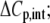 kcal/mol/K) kcal/mol/K) |
−0.52 ± 0.05 |
| Protonation energetics
| |
Free protein protonation free energy (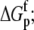 kcal/mol) kcal/mol) |
−10.3 ± 0.1 |
Change in 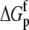 upon binding (ΔΔGp; kcal/mol) upon binding (ΔΔGp; kcal/mol) |
0.87 ± 0.04 |
pKa in free protein (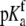 ) ) |
7.53 ± 0.05 |
pKa in complex (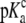 ) ) |
6.90 ± 0.03 |
Free protein protonation enthalpy (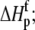 kcal/mol) kcal/mol) |
−4.9 ± 0.7 |
Change in 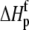 upon binding (ΔΔHp; kcal/mol) upon binding (ΔΔHp; kcal/mol) |
−1.4 ± 0.3 |
Free protein protonation entropy (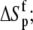 cal/mol/K) cal/mol/K) |
18 ± 2 |
Change in 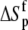 upon binding (ΔΔSp; cal/mol/K) upon binding (ΔΔSp; cal/mol/K) |
−8 ± 1 |
Protonation heat capacity change (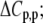 kcal/mol/K) kcal/mol/K) |
−0.8 ± 0.2 |
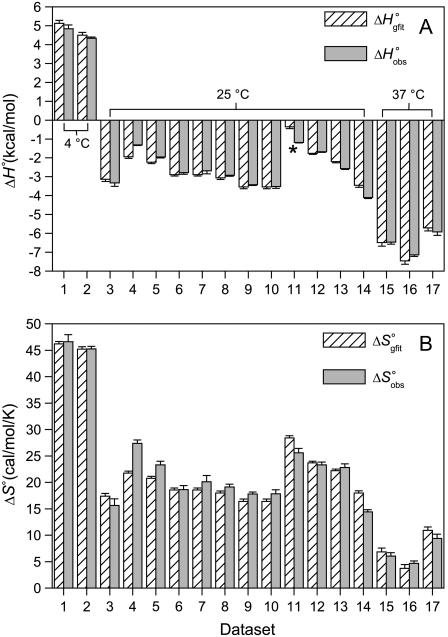
FIGURE 5.
Comparison of the A6-Tax/HLA-A2 binding enthalpies (A) and entropies (B) observed for each titration in Fig. 4 fit individually (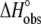 and
and 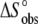 ) with the enthalpies and entropies calculated from the global fitted parameters in Table 2 (
) with the enthalpies and entropies calculated from the global fitted parameters in Table 2 (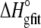 and
and 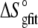 ). Errors for the individual values are confidence intervals from each individual fit shown in Fig. 4; errors for the calculated values were determined by Monte Carlo analysis as described in Materials and Methods. Data set 11 is highlighted, as the results indicate that the binding enthalpy is extremely weak under the conditions used, accounting for the discrepancy in Fig. 4.
). Errors for the individual values are confidence intervals from each individual fit shown in Fig. 4; errors for the calculated values were determined by Monte Carlo analysis as described in Materials and Methods. Data set 11 is highlighted, as the results indicate that the binding enthalpy is extremely weak under the conditions used, accounting for the discrepancy in Fig. 4.
RESULTS
Binding of A6 to Tax/HLA-A2 is linked to changes in protonation
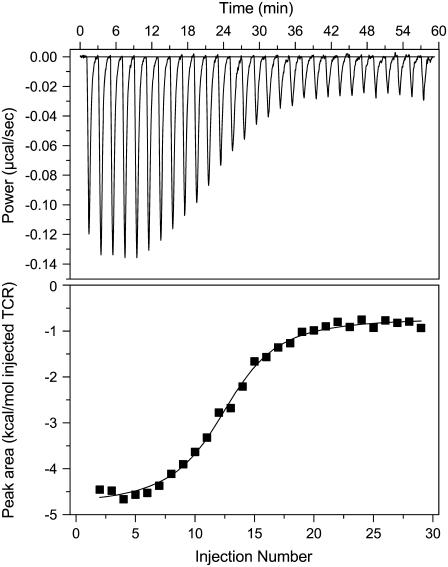
Fig. 1 shows a calorimetric titration of A6 with Tax/HLA-A2 in 20 mM imidazole buffer, pH 6.4, 25°C. Fitting these data to a bimolecular binding model yielded a binding enthalpy change of −3.4 kcal/mol, an entropy change of +18 cal/mol per K, and an affinity (KD) of 0.4 μM. Although qualitatively similar, these values differed quantitatively from the thermodynamics at 25°C reported earlier (ΔH° of −4.2 kcal/mol, ΔS° of +12 cal/mol per K, affinity of 2.2 μM), even when considering parameter error at two standard deviations (6). However, there are important differences between the experiments. The earlier thermodynamic data were not determined calorimetrically but by fitting binding free energies measured by SPR as a function of temperature. Although a number of reports show good agreement between SPR and calorimetrically measured thermodynamic data (e.g., 35–37), achieving close agreement places considerable demands on the accuracy and precision of the individual free energy measurements, which can be difficult to achieve when weak-to-moderate affinity interactions are studied with SPR.
FIGURE 1.
Isothermal calorimetric titration of 120 μM A6 TCR into 20 μM Tax/HLA-A2 in 20 mM imidazole, pH 6.4, 150 mM NaCl, 25°C. Under these conditions, the fit to a single-site binding model (solid line in lower panel) yielded an enthalpy change of −3.4 kcal/mol, an entropy change of +18 cal/mol per K, and a KD of 0.4 μM.
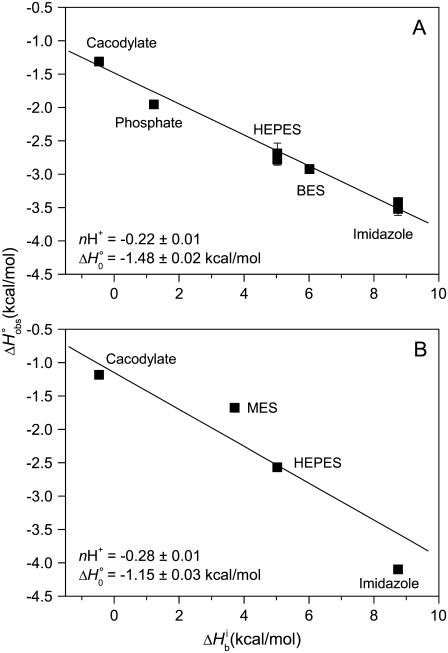
Another difference between the two experiments is the buffer and pH used: HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid), pH 7.4 was used in the SPR experiment, whereas imidazole, pH 6.4 was used in the ITC experiment. Aside from the influence of direct buffer-protein interactions (31), buffer and pH choice can have a dramatic influence on ligand binding thermodynamics when binding is linked to changes in protonation states (i.e., a pKa shift occurs upon binding) (17,22). To investigate the possible role of proton linkage in accounting for the discrepancy between the calorimetric and SPR-derived data, we repeated the ITC experiment in Fig. 1, except we used cacodylate, phosphate, HEPES, and BES (2-[bis(2-hydroxyethyl)amino]ethanesulfonic acid) as buffers. Proton linkage is indicated when binding enthalpies vary systematically with the ionization enthalpy of the buffer, as protons that are bound or released by the protein are in turn released or bound by the buffer, with an enthalpic consequence given by the buffer ionization enthalpy as described by Eq. 1. The buffers used cover a wide range of ionization enthalpy, from −0.5 kcal/mol (cacodylate) to +8.7 kcal/mol (imidazole) at 25°C (33,34).
The results of these experiments are shown in Fig. 2 A. Observed binding enthalpy varied linearly with buffer ionization enthalpy, a clear indication that receptor binding is linked to changes in protonation. The negative slope indicates a pKa decrease upon binding, with 0.22 protons released to the buffer at pH 6.4. The intercept of the line in Fig. 2 A (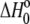 ) is small at −1.5 kcal/mol, indicative of a weak intrinsic binding enthalpy, but as described by Eq. 4, this term will still include contributions from pH and the magnitude of the pKa shift and its accompanying energetics (17,19).
) is small at −1.5 kcal/mol, indicative of a weak intrinsic binding enthalpy, but as described by Eq. 4, this term will still include contributions from pH and the magnitude of the pKa shift and its accompanying energetics (17,19).
FIGURE 2.
A6-Tax/HLA-A2 observed binding enthalpies (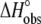 ) versus buffer ionization enthalpies (
) versus buffer ionization enthalpies (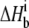 ) at 25°C in pH 6.4 buffer (A) and pH 7.4 buffer (B). Buffers used are indicated in each panel. The nonzero slopes of the weighted linear fits to the data (solid lines) indicate the presence of proton linkage. The slopes of the lines give the number of protons released by the buffer (nH+) at each pH and are indicated on each plot. The values at
) at 25°C in pH 6.4 buffer (A) and pH 7.4 buffer (B). Buffers used are indicated in each panel. The nonzero slopes of the weighted linear fits to the data (solid lines) indicate the presence of proton linkage. The slopes of the lines give the number of protons released by the buffer (nH+) at each pH and are indicated on each plot. The values at 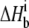 = 0 (observed binding enthalpy in a buffer with a zero ionization enthalpy) are also given on each plot.
= 0 (observed binding enthalpy in a buffer with a zero ionization enthalpy) are also given on each plot.
To further characterize the influence of proton linkage in the A6-Tax/HLA-A2 interaction, we repeated the binding measurements as a function of buffer ionization enthalpy at pH 7.4, using cacodylate, MES (2-(N-morpholino)-ethanesulphonic acid), HEPES, and imidazole as buffers. Binding enthalpy again varied with buffer ionization enthalpy, with 0.28 protons released to the buffer (Fig. 2 B). Using Eq. 3, the number of protons released at the two pH values permitted an initial estimate of 7.3 and 6.8 for the pKa of the titrating group in the free protein and the complex, respectively. Considering the typical pKas for ionizable groups in proteins (38), these results suggest a basic functionality for the titrating group. The difference in the intercepts of the lines in Fig. 2, A and B, highlights the pH dependency of 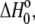 as shown by Eqs. 3 and 4.
as shown by Eqs. 3 and 4.
Finally, the thermodynamics as determined by ITC in HEPES, pH 7.4 are qualitatively but not quantitatively similar to the SPR-derived experiments performed in HEPES, pH 7.4 (ΔH° and ΔS° of −2.6 kcal/mol and +23 cal/mol per K by ITC vs. −4.2 kcal/mol and +12 cal/mol per K by SPR). As discussed below, the differences are attributable not only to the influence of protonation but also differences in accuracy and precision between the ITC and SPR measurements.
Proton linkage has a small influence on the binding heat capacity change
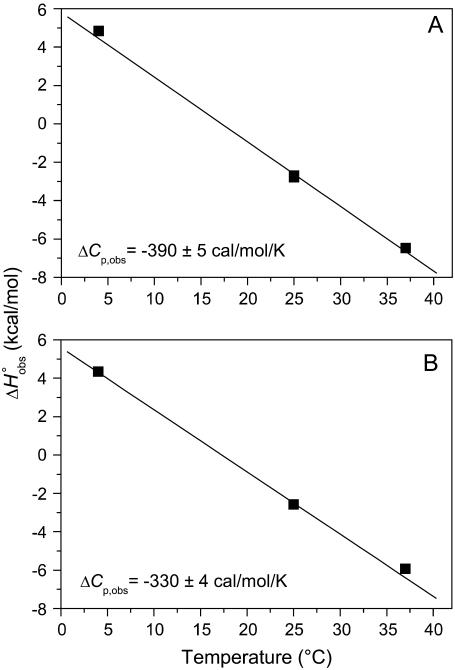
We next examined the heat capacity change for A6 recognition of Tax/HLA-A2. As proton linkage can influence the observed ΔCp (17,19,20), we performed the measurements at pH values of 7.4 and 6.4, collecting additional calorimetric data in HEPES buffer at 4°C and 37°C (pH is given at the experimental temperature). As shown in Fig. 3, there was a small but noticeable influence of pH on the observed ΔCp. At pH 6.4, ΔCp was measured as −0.39 cal/mol per K; this decreased to −0.33 cal/mol per K at pH 7.4. The reduction in the observed ΔCp with increasing pH is consistent with the presence of a negative pKa shift occurring upon binding (17).
FIGURE 3.
A6-Tax/HLA-A2 observed binding enthalpies (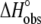 ) versus temperature in HEPES buffer at pH 6.4 (A) and pH 7.4 (B). The slopes of linear fits to the data (solid lines) yield the observed heat capacity change at each pH, indicated on each plot. pH was constant across the temperature range.
) versus temperature in HEPES buffer at pH 6.4 (A) and pH 7.4 (B). The slopes of linear fits to the data (solid lines) yield the observed heat capacity change at each pH, indicated on each plot. pH was constant across the temperature range.
Global analysis of binding as a function of pH, temperature, and buffer ionization enthalpy
To more fully examine the thermodynamics of A6 binding Tax/HLA-A2, we performed a global analysis of calorimetric data collected as a function of pH, temperature, and buffer ionization enthalpy. To facilitate a complete analysis, we collected additional data at pH 5.4, 25°C in MES buffer and pH 6.4, 37°C in imidazole buffer. A list of all ITC experiments included in the analysis is given in Table 1.
TABLE 1.
ITC data for the binding of A6 to Tax/HLA-A2 as a function of pH, temperature, and buffer ionization enthalpy
| Experiment no. | pH* | Buffer | Buffer ionization enthalpy † | Temperature (°C) |
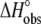 (kcal/mol) (kcal/mol) |
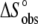 (cal/K/mol) (cal/K/mol) |
Kobs (× 105) | KD,obs (μM) ‡ |
|---|---|---|---|---|---|---|---|---|
| 1 | 6.4 | HEPES | 5.02 | 4 | 4.84 ± 0.20 | 46.6 ± 1.4 | 2.3 ± 0.7 | 0.4 ± 0.1 |
| 2 | 7.4 | HEPES | 5.02 | 4 | 4.34 ± 0.06 | 45.3 ± 0.5 | 2.9 ± 0.4 | 0.3 ± 0.1 |
| 3 | 5.4 | MES | 3.71 | 25 | −3.33 ± 0.18 | 15.6 ± 1.3 | 0.7 ± 0.2 | 1.4 ± 0.5 |
| 4 | 6.4 | Cacodylate | −0.47 | 25 | −1.31 ± 0.03 | 27.5 ± 0.7 | 8.8 ± 2.5 | 0.11 ± 0.03 |
| 5 | 6.4 | Phosphate | 1.22 | 25 | −1.95 ± 0.05 | 23.3 ± 0.7 | 3.3 ± 0.9 | 0.3 ± 0.1 |
| 6 | 6.4 | HEPES | 5.02 | 25 | −2.78 ± 0.08 | 18.7 ± 0.7 | 1.3 ± 0.3 | 0.8 ± 0.2 |
| 7 | 6.4 | HEPES | 5.02 | 25 | −2.69 ± 0.16 | 20.1 ± 1.2 | 2.3 ± 0.8 | 0.4 ± 0.2 |
| 8 | 6.4 | BES | 6.02 | 25 | −2.92 ± 0.05 | 19.1 ± 0.5 | 2.1 ± 0.4 | 0.5 ± 0.1 |
| 9 | 6.4 | Imidazole | 8.75 | 25 | −3.42 ± 0.05 | 17.8 ± 0.4 | 2.5 ± 0.3 | 0.4 ± 0.1 |
| 10 | 6.4 | Imidazole | 8.75 | 25 | −3.52 ± 0.10 | 17.8 ± 0.8 | 3.0 ± 0.7 | 0.3 ± 0.1 |
| 11 | 7.4 | Cacodylate | −0.47 | 25 | −1.18 ± 0.03 | 25.6 ± 0.8 | 2.9 ± 1.1 | 0.3 ± 0.1 |
| 12 | 7.4 | MES | 3.71 | 25 | −1.67 ± 0.04 | 23.3 ± 0.5 | 2.1 ± 0.4 | 0.5 ± 0.1 |
| 13 | 7.4 | HEPES | 5.02 | 25 | −2.57 ± 0.05 | 22.8 ± 0.9 | 7.3 ± 1.9 | 0.14 ± 0.04 |
| 14 | 7.4 | Imidazole | 8.75 | 25 | −4.10 ± 0.06 | 14.4 ± 0.4 | 1.4 ± 0.2 | 0.7 ± 0.1 |
| 15 | 6.4 | HEPES | 5.02 | 37 | −6.47 ± 0.11 | 6.0 ± 0.7 | 0.7 ± 0.1 | 1.3 ± 0.2 |
| 16 | 6.4 | Imidazole | 8.75 | 37 | −7.14 ± 0.09 | 4.7 ± 0.4 | 1.1 ± 0.1 | 0.9 ± 0.1 |
| 17 | 7.4 | HEPES | 5.02 | 37 | −5.92 ± 0.17 | 9.4 ± 0.8 | 1.7 ± 0.2 | 0.6 ± 0.1 |
pH is given at the experimental temperature.
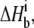 kcal/mol at 25°C.
kcal/mol at 25°C.
KD,obs = 1/Kobs.
The data sets summarized in Table 1 were fit globally to a bimolecular binding model including a single linked pKa shift as described in Materials and Methods. This allowed for the determination of the “intrinsic” A6-Tax/HLA-A2 binding energetics (i.e., those describing A6 binding Tax/HLA-A2 with the titrating group fully deprotonated) as well as the thermodynamics associated with the pKa shift (pKa free and in complex, protonation ΔH° free and in complex, and protonation ΔCp). The global analysis implicitly accounted for the error in each experiment, and the subsequent Monte Carlo analysis allowed us to propagate the error in the fitted parameters without assumptions regarding correlation between errors (32,39).
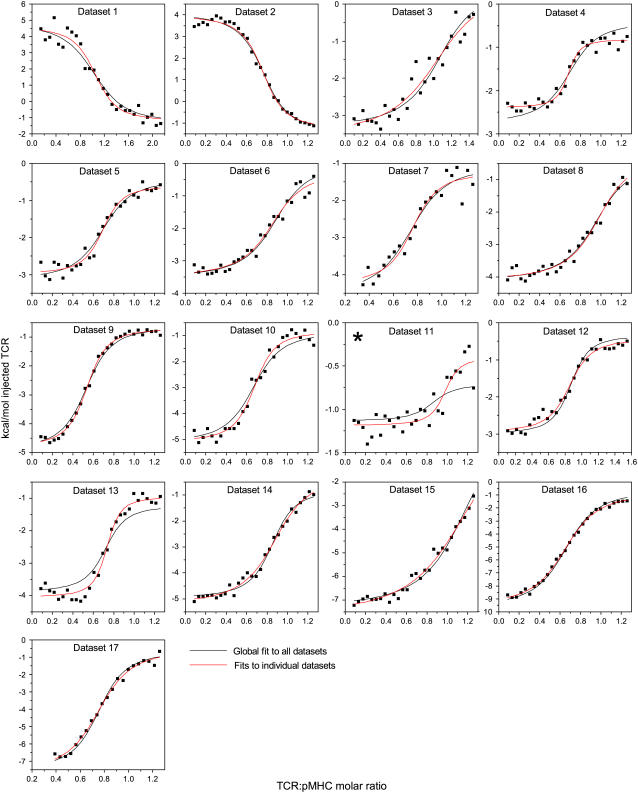
The global analysis did very well at capturing the variation in binding thermodynamics with solution conditions. This is apparent in Fig. 4, which shows each data set along with curves calculated from the global fit and curves generated from individual fits to each data set. Generally speaking, the two curves are in excellent agreement. The major exception is data set number 11 (cacodylate, pH 7.4, 25°C), where, although the global analysis reproduces the observed binding enthalpy (points to the left of the curve), it does not capture the values near the end of the titration. However, the signal under these conditions was extremely weak, below the reported detection limit of the VP-ITC. As noted below, the global fit indicates that the binding enthalpy in cacodylate, pH 7.4, 25°C is expected to be near zero, suggesting that the individual fit to the data taken under these conditions is a fit to mostly noise.
FIGURE 4.
A6-Tax/HLA-A2 titrations collected as a function of pH, temperature, and buffer ionization enthalpy used in the global analysis. Red lines indicate individual fits to each data set; black lines indicate the results from the simultaneous, global analysis of all 17 data sets. The key to each data set and the results from the individual fits are shown in Table 1. Data set 11 is starred, as the results indicate that the binding enthalpy is extremely weak under the conditions used and that the individual fit is a fit to mostly noise.
Fig. 5 shows a comparison of the observed binding enthalpies and entropies measured under each experimental condition with those calculated from the parameters generated from the global fit. The close agreement between the two sets of enthalpies and entropies further demonstrates that the global analysis well describes the variation in binding thermodynamics with solution conditions. Note that the binding enthalpy expected in cacodylate, pH 7.4, 25°C (conditions for data set 11, discussed in the preceding paragraph) is expected to be near zero (starred in Fig. 5 A).
The values for the fitted global parameters and associated errors are shown in Table 2 (values for the stoichiometries and baselines are provided in the Supplementary Material; the average stoichiometry was 0.9 ± 0.2). A matrix showing correlation coefficients for the global parameters is shown in Table 3, indicating that no two parameters were correlated outside of the limiting value of ±0.98 (39) (a complete correlation matrix is provided in the Supplementary Material).
TABLE 3.
Correlation coefficients for global parameters in the global analysis
 |
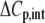 |
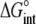 |
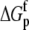 |
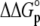 |
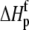 |
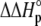 |
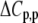 |
|
|---|---|---|---|---|---|---|---|---|
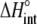 |
1 | |||||||
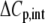 |
0.80 | 1 | ||||||
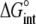 |
0.25 | 0.49 | 1 | |||||
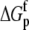 |
0.51 | 0.87 | 0.57 | 1 | ||||
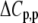 |
−0.17 | −0.47 | −0.42 | −0.59 | 1 | |||
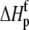 |
0.96 | 0.75 | 0.26 | 0.46 | −0.13 | 1 | ||
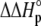 |
−0.89 | −0.78 | −0.43 | −0.55 | 0.06 | −0.81 | 1 | |
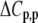 |
0.80 | 0.97 | 0.54 | 0.83 | −0.30 | 0.76 | −0.82 | 1 |
The binding energetics in Table 2 indicate that intrinsically, the A6 TCR binds Tax/HLA-A2 with a weakly favorable enthalpy change and a large positive entropy change at 25°C. The intrinsic heat capacity change is negative and, due to the influence of the proton linkage, larger than the apparent ΔCp values determined from the slopes of 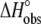 versus temperature in Fig. 3. The intrinsic binding affinity at 25°C is 0.2 μM, nearly an order of magnitude stronger than that determined by SPR (6).
versus temperature in Fig. 3. The intrinsic binding affinity at 25°C is 0.2 μM, nearly an order of magnitude stronger than that determined by SPR (6).
The global analysis indicates a pKa shift from 7.5 to 6.9 at 25°C, in good agreement with the values determined separately from the number of protons released as a function of pH. The pKa is entropic in origin, arising from a more unfavorable entropy of protonation in the complex (ΔΔSp = −8 cal/mol per K), but this is offset slightly by a more favorable enthalpy of protonation in the complex (ΔΔHp = −1.4 kcal/mol). Interestingly, the heat capacity change for protonation is very large at −0.8 kcal/mol per K, considerably larger than the protonation heat capacity changes for any of the standard ionizable amino acid side chains (34), possibly indicating that protonation is coupled to another process. As noted in Materials and Methods, the model used for the global analysis does not include a change in the ΔCp of protonation occurring upon binding. We did attempt to fit to a model that included a ΔΔCp,p; although this fit converged on values similar to those in Table 2 and a very small value for the protonation ΔΔCp, it resulted in unacceptably high fitting errors and parameter correlations (an F-test indicated that including ΔΔCp,p as a fitting parameter did not result in an improved fit).
DISCUSSION
αβ TCRs recognize a composite surface consisting of a peptide and a class I or class II MHC molecule. Although the immune response initiated by TCR recognition of an antigenic peptide can be exquisitely sensitive, TCRs themselves are inherently cross-reactive, with the number of recognizable ligands for any given T cell estimated to be on the order of 106 (40). Related to this dichotomy of specificity and cross-reactivity is the need for a given TCR to identify a cognate ligand on the surface of an antigen presenting cell, likely to be present at an extremely low density. Multiple mechanisms have been proposed to account for these remarkable molecular recognition properties, including flexibility or adaptability of the TCR CDR loops (3,8,10–12,16,41,42), the TCR variable domains (15,43), and the presented peptide (15,44,45).
To further understand the potential role of these and other processes involved in TCR recognition of ligand, we have been studying the αβ TCR A6, which recognizes the Tax peptide presented by HLA-A2. In this work, we sought to obtain a detailed description of the thermodynamics of the A6-Tax/HLA-A2 interaction. In our previous SPR-based studies of the A6-Tax/HLA-A2 interaction, we reported that at 25°C, A6 binds with a weakly favorable enthalpy change, a favorable entropy change, and a moderately negative heat capacity change (6). These measurements were of interest as many other TCR-ligand interactions that have been studied are characterized by unfavorable binding entropy changes (4–9) and, in some cases, very large heat capacity changes (8), observations supporting the notion that TCR recognition of ligand occurs with a loss of CDR loop flexibility and/or other types of conformational changes. Yet, despite differing binding thermodynamics, ligand recognition by the A6 TCR can occur with large conformational changes both inside and outside of the antigen binding site (15,16). We thus sought to investigate the binding thermodynamics of the A6 TCR in greater detail using ITC.
Our observations indicated that the binding of the A6 TCR is linked to changes in protonation states, i.e., TCR binding results in a change in the pKa of at least one ionizable group upon binding. The linkage of binding to protonation imparts significant solution dependencies on all of the observed thermodynamic parameters. For example, changing the buffer from cacodylate to imidazole resulted in approximate fourfold changes in the observed TCR binding enthalpy and entropy. Changing the pH but keeping the buffer constant resulted in smaller yet still significant changes in 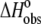 and
and 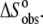 Even the observed heat capacity change was influenced by buffer and pH. Although under most conditions the binding thermodynamics were qualitatively similar to those reported earlier (weak ΔH°, favorable ΔS°, moderately negative ΔCp), the variability with solution conditions complicates quantitative comparisons of binding thermodynamics with structural and functional features. Obtaining the “intrinsic” thermodynamics most useful for comparison with structural properties such as buried surface areas required a global analysis of binding data collected as a function of pH, buffer ionization enthalpy, and temperature (17). In addition to providing the intrinsic binding energetics, this analysis allowed us to determine the thermodynamic parameters associated with the pKa shift.
Even the observed heat capacity change was influenced by buffer and pH. Although under most conditions the binding thermodynamics were qualitatively similar to those reported earlier (weak ΔH°, favorable ΔS°, moderately negative ΔCp), the variability with solution conditions complicates quantitative comparisons of binding thermodynamics with structural and functional features. Obtaining the “intrinsic” thermodynamics most useful for comparison with structural properties such as buried surface areas required a global analysis of binding data collected as a function of pH, buffer ionization enthalpy, and temperature (17). In addition to providing the intrinsic binding energetics, this analysis allowed us to determine the thermodynamic parameters associated with the pKa shift.
Origin of the linkage between receptor binding and changes in protonation
The identity of the ionizable group responsible for the proton linkage and whether it resides on A6 or HLA-A2 is unknown. There are 16 ionizable groups in or around the A6-Tax/HLA-A2 interface (14). Those expected to titrate over the pH range studied include His-151 on the HLA-A2 α2 helix and the A6 α-chain N-terminal amine. Considering His-151, although the pKa of 7.5 in the unbound protein is high compared to the 6.0–7.0 range expected for a histidine side chain (38), perturbed pKas are common in protein structures, and the pKa of 6.9 seen in the bound state is within the expected range. Although the protonation enthalpy and entropy changes in either free or bound protein differ from the protonation thermodynamics expected for a free histidine side chain (−7 through −8 kcal/mol for ΔH°, −3 through +6 cal/mol per K for ΔS°, compared to the values of −5 kcal/mol and +18 cal/mol per K we measure for the free protein) (46,47), they are close to the values for histidines measured in other proteins. For example, His-12 in ribonuclease has protonation enthalpy and entropy changes of −4 kcal/mol and +16 cal/mol per K (46); the values for His-119 in metamyoglobin are −5 kcal/mol and +14 cal/mol per K (47).
Considering the A6 α-chain N-terminus, the pKas of 7.5 free and 6.9 bound are both within the expected range for a protein N-terminus (38). Again, the protonation enthalpy and entropy changes differ from those expected for an isolated α-amino group (34). There are few data available for protonation thermodynamics of α-amino groups in proteins, but, as in the case of histidine, it is reasonable to expect deviations from those expected for a free primary amine.
Interestingly, the fitted value for the heat capacity change for protonation, −800 cal/mol per K, is unusually large compared to the heat capacity changes for protonation of a histidine side chain or an α-amino group. Measurements of the protonation ΔCp for a free histidine side chain range from −7 to −150 cal/mol per K (22,34); the ΔCp for protonation of free imidazole is near −4 cal/mol per K (33,34). Heat capacity changes for protonation of the α-amino groups of the standard amino acids are in the range of −15 to −40 cal/mol per K (34). Thus, the protonation ΔCp we measure is severalfold larger than expected. This could arise from the linkage of protonation to another process. One possibility is ion binding. Guinto and Di Cera have reported a very large ΔCp of −1100 cal/mol per K associated with the binding of a sodium ion to thrombin, thought to result from the release of restricted water molecules (48). Perhaps protonation of Tax/HLA-A2 or the A6 TCR results in the creation of an ion binding site, with ion binding occurring with a similarly large ΔCp. Under this mechanism, deprotonation of the protein would result in ion release. We note that the A6-Tax/HLA-A2 interaction results in the release of 0.39 ions at pH 7.4 (6), close to the value of 0.28 protons released upon TCR binding at pH 7.4. Ion coordination by a positively charged group would be expected to result in an elevated pKa, potentially accounting for the discrepancy between the measured and expected pKa in the unbound state if His-151 is responsible for the proton linkage. The thermodynamic consequences of any linkage between ion and proton binding in A6 recognition of Tax/HLA-A2 represents an avenue for further investigation.
Influence of proton linkage on the observed A6-Tax/HLA-A2 binding energetics
Although the identity of the group (or groups) responsible for the linkage of A6 binding to changes in protonation is unknown, the proton linkage significantly influences the observed TCR binding thermodynamics. This is most apparent in Fig. 5, which shows the variation in the observed binding enthalpy and entropy changes with pH and buffer. In the absence of direct protein-buffer interactions, the influence of proton linkage will show enthalpy/entropy compensation (17), as indicated by the compensatory shifts in enthalpy and entropy seen in Fig. 5, A and B. As the various contributions to the observed binding enthalpy can have different temperature dependencies, proton linkage is also expected to influence the observed heat capacity change (17). Some influence may be visible in the small variation of the observed A6 binding ΔCp with pH (Fig. 3). However, a more dramatic influence of protonation on the observed heat capacity change is seen when comparing the observed values, which range from −0.33 to −0.39 kcal/mol per K, and the intrinsic value, −0.52 kcal/mol per K. The difference between the observed and intrinsic values arises from the large heat capacity change associated with protonation (−0.8 kcal/mol per K). As the pKa shift upon A6 binding results in proton release, the net result is a positive shift in the observed binding ΔCp. At pH 7.4, where ∼0.3 protons are released upon binding, this amounts to a heat capacity increment due to protonation near 0.25 kcal/mol per K. Similarly large contributions of linked protonation to observed binding heat capacity changes have been observed previously (19,49).
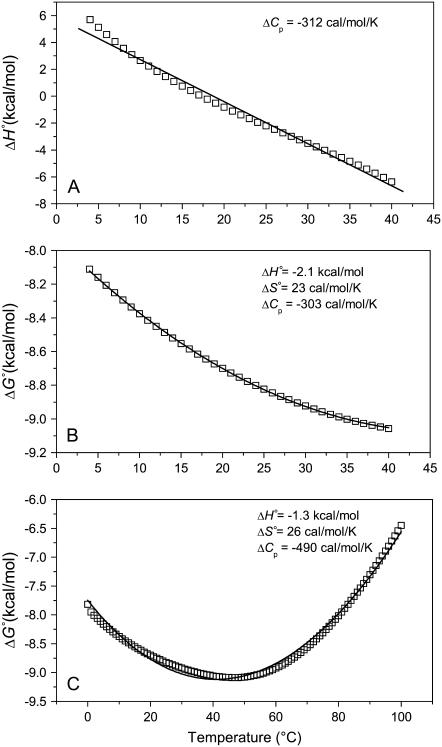
It is instructive to examine the influence of proton linkage on thermodynamic parameters derived from experiments where its contributions might otherwise be undetected. Fig. 6 A shows plots of the A6-Tax/HLA-A2 observed binding enthalpy as a function of temperature, simulated over the experimentally accessible temperature range of 4–40°C in HEPES buffer at pH 7.4, using Eqs. 1–7 with the parameters in Table 2. The simulated data are markedly curved, indicating that proton linkage imparts a temperature dependence to the observed heat capacity change. Given experimental error and limited sample, however, it is doubtful that this curvature would be seen with actual measurements. Indeed, our experiments at a restricted number of temperatures do not reveal this temperature dependence and in fact yield an observed ΔCp almost identical to that obtained from a linear fit to the simulated data (−0.33 vs. −0.31 kcal/mol per K). Considering free energy, the observed binding ΔG° calculated over the same temperature range and under the same conditions yields data that fit extremely well to the modified Gibbs-Helmholtz equation (Eq. 7) (Fig. 6 B). Yet, the fitted parameters deviate significantly from the intrinsic values. Expanding the temperature range to 0–100°C more effectively illustrates how proton linkage results in deviations from the expected variation in observed ΔG° with temperature, and again the fitted parameters do not agree with the intrinsic values. Not only does this analysis emphasize the need to investigate and account for the influence of linked protonation, it also emphasizes the difficulties in doing so via noncalorimetric methods, as recently discussed by Horn et al. (18).
FIGURE 6.
Proton linkage in the A6-Tax/HLA-A2 interaction results in deviations from ideal behavior. (A) Calculated binding enthalpy changes as a function of temperature in HEPES buffer at pH 7.4 show how proton linkage results in a temperature-dependent observed heat capacity change. The solid line is a fit to the data and the slope (i.e., the apparent heat capacity change) is indicated. (B) Calculated binding free energy changes over the experimentally accessible temperature range of 4–40°C in HEPES at pH 7.4. The solid line represents a nonlinear fit to the modified Gibbs-Helmholtz equation; results are indicated in the inset. Despite an excellent fit, the resulting parameters differ considerably from the intrinsic binding energetics used to generate the data. (C) The simulations in panel B extended to 0–100°C, revealing a much poorer fit to the temperature dependence of ΔG° when an expanded temperature range is used. For all panels, calculated data points were generated using the parameters in Table 2 and Eqs. 1–7. pH was set as 7.4 at the reference temperature of 25°C and allowed to vary with temperature.
Clearly, at least some of the differences between the intrinsic A6-Tax/HLA-A2 binding thermodynamics and those measured earlier via SPR (which were not corrected for protonation) (6) can be attributed to the influence of proton linkage: Fig. 6 B shows that, even with perfect data, an SPR analysis in one buffer and at one pH would not have reproduced the intrinsic binding thermodynamics. Yet, proton linkage cannot account for all of the differences: our earlier SPR analysis in HEPES, pH 7.4 generated results that, at least for ΔH° and ΔS°, were qualitatively but not quantitatively similar to the values in Fig. 6 B (ΔΔH° = 2.1 ± 1.1 kcal/mol; ΔΔS° = 11.6 ± 3.5 cal/mol per K). More problematic are the ΔCp measurements, which differ by ∼260 cal/mol per K. These discrepancies, which cannot be attributed to the influence of proton linkage as both sets of data were collected in the same buffer and at the same pH, are most likely attributable to issues of accuracy and precision, particularly in the SPR measurements (although the variation in solution pH with temperature will have a small influence on the SPR results). Both accurate and precise free energy measurements are required for extracting highly reliable thermodynamics from a ΔG° versus temperature analysis (18,50). This is particularly true for heat capacity, which as the second derivative of free energy with respect to temperature can vary wildly with the value (or error) in a single free energy measurement. Although a number of reports show good agreement between SPR and calorimetrically measured thermodynamic data (35–37), achieving such agreement places considerable demands on the quality of the individual free energy measurements.
Intrinsic A6 TCR binding thermodynamics and the recognition of Tax/HLA-A2
The global analysis indicates that, separated from the influence of linked protonation, at 25°C the A6 TCR binds Tax/HLA-A2 with a very weak binding enthalpy change, a large positive entropy change, and a large negative heat capacity change. These “intrinsic” thermodynamics are most useful for comparison with structural features, particularly buried solvent accessible surface areas and binding thermodynamics calculated from empirical, surface area based prediction algorithms that do not account for linked protonation (23,51).
What do the intrinsic binding thermodynamics indicate about ligand recognition by the A6 TCR and, in particular, the presence or absence of TCR loop dynamics or conformational changes? Perhaps most interesting is the intrinsic binding heat capacity change, measured at −0.52 kcal/mol per K. This value is larger than that calculated from the polar/apolar character of the TCR-peptide/MHC interface. Assuming a rigid body interaction, with 1256 Å2 of apolar solvent accessible surface area and 817 Å2 of polar solvent accessible surface area buried (6), commonly used empirical relationships between surface area and ΔCp contributions predict a value between −0.33 and −0.29 kcal/mol per K (23,51).
Discrepancies between empirically predicted and measured heat capacity changes are often taken as evidence of a nonrigid body interaction (e.g., 51). Following these examples, the predicted ΔCp for A6 binding Tax/HLA-A2 suggests that one or both proteins are more solvent exposed in their unbound states than is apparent from the A6-Tax/HLA-A2 crystal structure. As the structure of the unligated Tax/HLA-A2 complex indicates little difference in solvent accessible surface area between the bound and free forms (14,52), any greater accessibility must be attributed to the A6 TCR. Thus, the heat capacity data are compatible with the need for A6 to shift to a less solvent-accessible conformation for binding to proceed. As burial of apolar and polar surface contributes oppositely to ΔCp (53,54), the amount of additional surface that would need to be buried to account for the excess heat capacity change (i.e., the magnitude of the conformational shift) cannot be reliably estimated. However, a conclusion that relatively small conformational shifts are required for TCR binding is consistent with our recent kinetic studies, which showed that in the absence of electrostatic influences, A6 binds Tax/HLA-A2 at a rate slightly below that expected for a diffusion-limited but geometrically constrained protein-protein interaction (6).
Is there evidence that structural rearrangements necessary for A6 to bind Tax/HLA-A2 might result from the ordering or “folding” of otherwise mobile loops, as has been suggested to occur for other TCR-peptide/MHC interactions (4,42)? On one hand, the observation that A6 binding is entropically driven at room temperature would seem to argue against this, particularly because the model of CDR loop ordering upon binding was derived in part from TCR binding reactions that proceed with unfavorable binding entropy changes (4). Yet, application of empirical methods for calculating binding entropy changes suggests some configurational entropy must be overcome for binding to proceed. The approach of Murphy and co-workers (23) indicates that, after accounting for solvation and translational/rotational contributions, a configurational entropy change of 100 cal/mol per K must be overcome for binding. The approach of Spolar and Record (51) yields a remarkably similar 99 cal/mol per K. Using the value of 5.6 cal/mol per K derived by Spolar and Record for the “folding” of one amino acid indicates that 18 amino acids must be ordered upon TCR binding. However, the method of Murphy and co-workers, which differs from the Spolar and Record approach in that it attempts to account for the loss of side-chain conformational entropy, indicates that 164 cal/mol per K of side-chain entropy must be overcome upon binding, suggesting that no changes in backbone configurational entropy occur upon binding. These opposing results from two widely used empirical methods for deconstructing binding entropy changes force us to conclude that the value of the intrinsic binding entropy change cannot be used directly to infer the extent of any CDR loop dynamics.
With regard to the very weak intrinsic binding enthalpy change, to a first approximation, the value is consistent with the makeup of the A6-Tax/HLA-A2 interface, which is 61% hydrophobic and includes only three intermolecular hydrogen bonds and one salt bridge (14). A more detailed analysis using empirical parameters that relate changes in solvent accessible area to enthalpy changes predicts a value for the binding ΔH° of −3.5 kcal/mol at 25°C (23). Although twice the experimental intrinsic value, the predicted enthalpy change is still relatively small. As with the heat capacity change, the difference between the predicted and measured binding ΔH° may result from conformational shifts necessary for binding of the A6 TCR. If this is the case, the more favorable predicted binding enthalpy would indicate that the conformational shifts necessary to bind are enthalpically unfavorable and thus entropically driven. As structural transitions which result in the ordering of peptide backbones are characterized by opposite thermodynamic signatures (i.e., favorable enthalpy changes and unfavorable entropy changes) (55,56), this suggests that conformational shifts necessary for A6 binding do not include an ordering of highly mobile loops as discussed above but more defined structural shifts such as block motions of CDR loops or shifts in domain orientation, as seen in A6 recognition of variant Tax peptides presented by HLA-A2 (15,16). This conclusion is compatible with recent suggestions by Garcia and Adams (57), who indicated that rather than possessing the kind of flexibility typically associated with unstructured regions, TCR binding loops may populate an ensemble of more defined structural states, as recently seen in cross-reactive antibodies (58) and further developed by Holler and Kranz in their “conformer model” of TCR binding and cross-reactivity (59).
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Alison Wojnarowicz and Rene Rodriguez for outstanding technical assistance, Rebecca Davis-Harrison for helpful comments on the manuscript, and Aaron Lucius for inspiring discussion. Origin and NLREG scripts for single and global ITC data analysis and Monte Carlo error analysis are available upon request.
This work was supported by grant No. GM067079 from National Institute of General Medical Sciences, National Institutes of Health.
APPENDIX: DEFINITION OF THE INTRINSIC BINDING ENERGETICS
As noted above in Scheme 1, we have defined the intrinsic binding energetics as those describing the binding of B to deprotonated A. This definition is in keeping with previous work studying the influence of linked protonation on protein binding energetics (17,22,30,31) and is appropriate here given the observation of a pKa shift of 7.5 to 6.9, which is likely to originate from a basic rather than acidic group. Yet as the identity of the titrating group (or groups) remains unknown, it is still informative to consider the consequences of redefining the intrinsic binding thermodynamics as those describing B binding to protonated rather than deprotonated A.
Although analogs of Eqs. 1–4 that refer to deprotonation instead of protonation could easily be derived, the most straightforward way to illustrate the consequences of changing the definition of the intrinsic binding energetics is to define the thermodynamics of B binding protonated A with reference to the thermodynamics of B binding unprotonated A, i.e., in terms of the values we have already measured.
To do this, we modify Scheme 1 to explicitly show the equilibrium for B binding protonated A, referring to this equilibrium constant as Kint,P. The binding of B to deprotonated A is now described by Kint,D:
SCHEME 2.
The definitions of 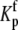 and
and 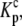 the proton binding constants for free A and the AB complex, respectively, remain the same. By the properties of a thermodynamic cycle, then
the proton binding constants for free A and the AB complex, respectively, remain the same. By the properties of a thermodynamic cycle, then
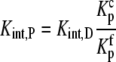 |
(8) |
and
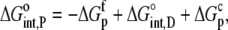 |
(9) |
where 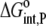 and
and 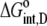 are the free energy changes for B binding to protonated and deprotonated A, respectively, and
are the free energy changes for B binding to protonated and deprotonated A, respectively, and 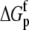 and
and 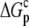 are the proton binding free energies for free A and the AB complex, respectively.
are the proton binding free energies for free A and the AB complex, respectively.
The enthalpy, entropy, and heat capacity changes for B finding protonated A are then
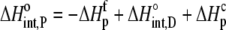 |
(10) |
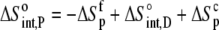 |
(11) |
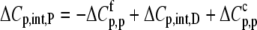 |
(12) |
with definitions analogous to those used for Eq. 9.
Using Eqs. 8–12 and the values in Table 2, we determined the values of Kint,P, 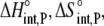 and ΔCp,int,P for the A6-Tax/HLA-A2 interaction (Table 4). Do these parameters alter our conclusions regarding conformational changes or loop dynamics in A6 recognition of Tax/HLA-A2? Much of our discussion centered on the intrinsic heat capacity change, which, as we could not measure a change in the ΔCp of protonation upon binding, is unaltered with the revised definition of the intrinsic binding energetics. Likewise, the A6-Tax/HLA-A2 binding reaction remains entropically favorable. The only substantial difference arises in comparison of the intrinsic binding enthalpy change with that predicted from buried solvent accessible surface areas (−3.2 kcal/mol for
and ΔCp,int,P for the A6-Tax/HLA-A2 interaction (Table 4). Do these parameters alter our conclusions regarding conformational changes or loop dynamics in A6 recognition of Tax/HLA-A2? Much of our discussion centered on the intrinsic heat capacity change, which, as we could not measure a change in the ΔCp of protonation upon binding, is unaltered with the revised definition of the intrinsic binding energetics. Likewise, the A6-Tax/HLA-A2 binding reaction remains entropically favorable. The only substantial difference arises in comparison of the intrinsic binding enthalpy change with that predicted from buried solvent accessible surface areas (−3.2 kcal/mol for 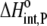 vs. −3.5 kcal/mol predicted). To the extent that the discrepancy between calculated and observed heat capacity changes reflects conformational shifts required for binding, the redefined value of the intrinsic binding enthalpy change still requires that any A6 TCR conformational shifts are entropically driven. Thus, regardless of whether the intrinsic energetics reflect binding to deprotonated or protonated protein, they are inconsistent with the need to organize disordered regions of the A6 TCR.
vs. −3.5 kcal/mol predicted). To the extent that the discrepancy between calculated and observed heat capacity changes reflects conformational shifts required for binding, the redefined value of the intrinsic binding enthalpy change still requires that any A6 TCR conformational shifts are entropically driven. Thus, regardless of whether the intrinsic energetics reflect binding to deprotonated or protonated protein, they are inconsistent with the need to organize disordered regions of the A6 TCR.
TABLE 4.
Comparison of A6-Tax/HLA-A2 binding energetics for either protonated or deprotonated protein
| Protonated case | Deprotonated case* | ||
|---|---|---|---|
| KD,int,P | 0.81 ± 0.02 | KD,int,P | 0.19 ± 0.02 |
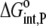 |
−8.3 ± 0.2 | 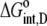 |
−9.2 ± 0.1 |
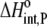 |
−3.2 ± 1.1 | 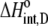 |
−1.8 ± 0.3 |
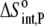 |
17 ± 3 | 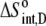 |
25 ± 1 |
| ΔCp,int,P | −0.52 ± 0.05 | ΔCp,int,D | −0.52 ± 0.05 |
KD values in micromolar at 25°C, free energies and enthalpies in kcal/mol at 25°C, entropies in cal/mol/K at 25°C, and heat capacities in kcal/mol/K.
Values from Table 2.
Editor: Jonathan B. Chaires.
References
- 1.Rudolph, M. G., R. L. Stanfield, and I. A. Wilson. 2006. How TCRs bind MHCs, peptides, and coreceptors. Annu. Rev. Immunol. 24:419–466. [DOI] [PubMed] [Google Scholar]
- 2.Davis, M. M., J. J. Boniface, Z. Reich, D. Lyons, J. Hampl, B. Arden, and Y. Chien. 1998. Ligand recognition by αβ T cell receptors. Annu. Rev. Immunol. 16:523–544. [DOI] [PubMed] [Google Scholar]
- 3.Boniface, J. J., Z. Reich, D. S. Lyons, and M. M. Davis. 1999. Thermodynamics of T cell receptor binding to peptide-MHC: evidence for a general mechanism of molecular scanning. Proc. Natl. Acad. Sci. USA. 96:11446–11451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Willcox, B. E., G. F. Gao, J. R. Wyer, J. E. Ladbury, J. I. Bell, B. K. Jakobsen, and P. A. van der Merwe. 1999. TCR binding to peptide-MHC stabilizes a flexible recognition interface. Immunity. 10:357–365. [DOI] [PubMed] [Google Scholar]
- 5.Anikeeva, N., T. Lebedeva, M. Krogsgaard, S. Y. Tetin, E. Martinez-Hackert, S. A. Kalams, M. M. Davis, and Y. Sykulev. 2003. Distinct molecular mechanisms account for the specificity of two different T-cell receptors. Biochemistry. 42:4709–4716. [DOI] [PubMed] [Google Scholar]
- 6.Davis-Harrison, R. L., K. M. Armstrong, and B. M. Baker. 2005. Two different T cell receptors use different thermodynamic strategies to recognize the same peptide/MHC ligand. J. Mol. Biol. 346:533–550. [DOI] [PubMed] [Google Scholar]
- 7.Garcia, K. C., C. G. Radu, J. Ho, R. J. Ober, and E. S. Ward. 2001. Kinetics and thermodynamics of T cell receptor-autoantigen interactions in murine experimental autoimmune encephalomyelitis. Proc. Natl. Acad. Sci. USA. 98:6818–6823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Krogsgaard, M., N. Prado, E. J. Adams, X. He, D. C. Chow, D. B. Wilson, K. C. Garcia, and M. M. Davis. 2003. Evidence that structural rearrangements and/or flexibility during TCR binding can contribute to T cell activation. Mol. Cell. 12:1367–1378. [DOI] [PubMed] [Google Scholar]
- 9.Boulter, J. M., N. Schmitz, A. K. Sewell, A. J. Godkin, M. F. Bachmann, and A. M. Gallimore. 2007. Potent T cell agonism mediated by a very rapid TCR/pMHC interaction. Eur. J. Immunol. 37:798–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Reiser, J. B., C. Gregoire, C. Darnault, T. Mosser, A. Guimezanes, A. M. Schmitt-Verhulst, J. C. Fontecilla-Camps, G. Mazza, B. Malissen, and D. Housset. 2002. A T cell receptor CDR3beta loop undergoes conformational changes of unprecedented magnitude upon binding to a peptide/MHC class I complex. Immunity. 16:345–354. [DOI] [PubMed] [Google Scholar]
- 11.Kjer-Nielsen, L., C. S. Clements, A. W. Purcell, A. G. Brooks, J. C. Whisstock, S. R. Burrows, J. McCluskey, and J. Rossjohn. 2003. A structural basis for the selection of dominant αβ T cell receptors in antiviral immunity. Immunity. 18:53–64. [DOI] [PubMed] [Google Scholar]
- 12.Garcia, K. C., M. Degano, L. R. Pease, M. Huang, P. A. Peterson, L. Teyton, and I. A. Wilson. 1998. Structural basis of plasticity in T cell receptor recognition of a self peptide-MHC antigen. Science. 279:1166–1172. [DOI] [PubMed] [Google Scholar]
- 13.Utz, U., D. Banks, S. Jacobson, and W. E. Biddison. 1996. Analysis of the T-cell receptor repertoire of human T-cell leukemia virus type 1 (HTLV-1) Tax-specific CD8+ cytotoxic T lymphocytes from patients with HTLV-1-associated disease: evidence for oligoclonal expansion. J. Virol. 70:843–851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Garboczi, D. N., P. Ghosh, U. Utz, Q. R. Fan, W. E. Biddison, and D. C. Wiley. 1996. Structure of the complex between human T-cell receptor, viral peptide and HLA-A2. Nature. 384:134–141. [DOI] [PubMed] [Google Scholar]
- 15.Gagnon, S. J., O. Y. Borbulevych, R. L. Davis-Harrison, R. V. Turner, M. Damirjian, A. Wojnarowicz, W. E. Biddison, and B. M. Baker. 2006. T cell receptor recognition via cooperative conformational plasticity. J. Mol. Biol. 363:228–243. [DOI] [PubMed] [Google Scholar]
- 16.Ding, Y. H., B. M. Baker, D. N. Garboczi, W. E. Biddison, and D. C. Wiley. 1999. Four A6-TCR/peptide/HLA-A2 structures that generate very different T cell signals are nearly identical. Immunity. 11:45–56. [DOI] [PubMed] [Google Scholar]
- 17.Baker, B. M., and K. P. Murphy. 1996. Evaluation of linked protonation effects in protein binding reactions using isothermal titration calorimetry. Biophys. J. 71:2049–2055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Horn, J. R., J. F. Brandts, and K. P. Murphy. 2002. van 't Hoff and calorimetric enthalpies II: effects of linked equilibria. Biochemistry. 41:7501–7507. [DOI] [PubMed] [Google Scholar]
- 19.Kozlov, A. G., and T. M. Lohman. 2000. Large contributions of coupled protonation equilibria to the observed enthalpy and heat capacity changes for ssDNA binding to Escherichia coli SSB protein. Proteins Suppl. 4:8–22. [DOI] [PubMed] [Google Scholar]
- 20.Fisher, H. F., and N. Singh. 1995. Calorimetric methods for interpreting protein-ligand interactions. Methods Enzymol. 259:194–221. [DOI] [PubMed] [Google Scholar]
- 21.Eftink, M. R., A. C. Anusiem, and R. L. Biltonen. 1983. Enthalpy-entropy compensation and heat capacity changes for protein-ligand interactions: general thermodynamic models and data for the binding of nucleotides to ribonuclease A. Biochemistry. 22:3884–3896. [DOI] [PubMed] [Google Scholar]
- 22.Baker, B. M., and K. P. Murphy. 1997. Dissecting the energetics of a protein-protein interaction: the binding of ovomucoid third domain to elastase. J. Mol. Biol. 268:557–569. [DOI] [PubMed] [Google Scholar]
- 23.Baker, B. M., and K. P. Murphy. 1998. Prediction of binding energetics from structure using empirical parameterization. Methods Enzymol. 295:294–315. [DOI] [PubMed] [Google Scholar]
- 24.Garboczi, D. N., D. T. Hung, and D. C. Wiley. 1992. HLA-A2-peptide complexes: refolding and crystallization of molecules expressed in Escherichia coli and complexed with single antigenic peptides. Proc. Natl. Acad. Sci. USA. 89:3429–3433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Garboczi, D. N., U. Utz, P. Ghosh, A. Seth, J. Kim, E. A. VanTienhoven, W. E. Biddison, and D. C. Wiley. 1996. Assembly, specific binding, and crystallization of a human TCR-αβ with an antigenic Tax peptide from human T lymphotropic virus type 1 and the class I MHC molecule HLA-A2. J. Immunol. 157:5403–5410. [PubMed] [Google Scholar]
- 26.O'Shea, E. K., K. J. Lumb, and P. S. Kim. 1993. Peptide ‘Velcro’: design of a heterodimeric coiled coil. Curr. Biol. 3:658–667. [DOI] [PubMed] [Google Scholar]
- 27.Binz, A. K., R. C. Rodriguez, W. E. Biddison, and B. M. Baker. 2003. Thermodynamic and kinetic analysis of a peptide-class I MHC interaction highlights the noncovalent nature and conformational dynamics of the class I heterotrimer. Biochemistry. 42:4954–4961. [DOI] [PubMed] [Google Scholar]
- 28.Wiseman, T., S. Williston, J. F. Brandts, and L.-N. Lin. 1989. Rapid measurement of binding constants and heats of binding using a new titration calorimeter. Anal. Biochem. 179:131–137. [DOI] [PubMed] [Google Scholar]
- 29.Beechem, J. M. 1992. Global analysis of biochemical and biophysical data. Methods Enzymol. 210:37–54. [DOI] [PubMed] [Google Scholar]
- 30.Horn, J. R., S. Ramaswamy, and K. P. Murphy. 2003. Structure and energetics of protein-protein interactions: the role of conformational heterogeneity in OMTKY3 binding to serine proteases. J. Mol. Biol. 331:497–508. [DOI] [PubMed] [Google Scholar]
- 31.Edgcomb, S. P., B. M. Baker, and K. P. Murphy. 2000. The energetics of phosphate binding to a protein complex. Protein Sci. 9:927–933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Straume, M., and M. L. Johnson. 1992. Monte Carlo method for determining complete confidence probability distributions of estimated model parameters. Methods Enzymol. 210:117–129. [DOI] [PubMed] [Google Scholar]
- 33.Fukada, H., and K. Takahashi. 1998. Enthalpy and heat capacity changes for the proton dissociation of various buffer components in 0.1 M potassium chloride. Proteins. 33:159–166. [PubMed] [Google Scholar]
- 34.Christensen, J. J., L. D. Hansen, and R. M. Izatt. 1976. Handbook of Proton Ionization Heats. John Wiley & Sons, New York.
- 35.Day, Y. S., C. L. Baird, R. L. Rich, and D. G. Myszka. 2002. Direct comparison of binding equilibrium, thermodynamic, and rate constants determined by surface- and solution-based biophysical methods. Protein Sci. 11:1017–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ely, L. K., T. Beddoe, C. S. Clements, J. M. Matthews, A. W. Purcell, L. Kjer-Nielsen, J. McCluskey, and J. Rossjohn. 2006. Disparate thermodynamics governing T cell receptor-MHC-I interactions implicate extrinsic factors in guiding MHC restriction. Proc. Natl. Acad. Sci. USA. 103:6641–6646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Myszka, D. G., Y. N. Abdiche, F. Arisaka, O. Byron, E. Eisenstein, P. Hensley, J. A. Thomson, C. R. Lombardo, F. Schwarz, W. Stafford, and M. L. Doyle. 2003. The ABRF-MIRG'02 study: assembly state, thermodynamic, and kinetic analysis of an enzyme/inhibitor interaction. J. Biomol. Tech. 14:247–269. [PMC free article] [PubMed] [Google Scholar]
- 38.Thurlkill, R. L., G. R. Grimsley, J. M. Scholtz, and C. N. Pace. 2006. pK values of the ionizable groups of proteins. Protein Sci. 15:1214–1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Johnson, M. L. 2000. Parameter correlations while curve fitting. Methods Enzymol. 321:424–446. [DOI] [PubMed] [Google Scholar]
- 40.Mason, D. 1998. A very high level of crossreactivity is an essential feature of the T-cell receptor. Immunol. Today. 19:395–404. [DOI] [PubMed] [Google Scholar]
- 41.Reiser, J. B., C. Darnault, C. Gregoire, T. Mosser, G. Mazza, A. Kearney, P. A. van der Merwe, J. C. Fontecilla-Camps, D. Housset, and B. Malissen. 2003. CDR3 loop flexibility contributes to the degeneracy of TCR recognition. Nat. Immunol. 4:241–247. [DOI] [PubMed] [Google Scholar]
- 42.Wu, L. C., D. S. Tuot, D. S. Lyons, K. C. Garcia, and M. M. Davis. 2002. Two-step binding mechanism for T-cell receptor recognition of peptide MHC. Nature. 418:552–556. [DOI] [PubMed] [Google Scholar]
- 43.Li, H., M. I. Lebedeva, E. S. Ward, and R. A. Mariuzza. 1997. Dual conformations of a T cell receptor Vα homodimer: implications for variability in VαVβ domain association. J. Mol. Biol. 269:385–394. [DOI] [PubMed] [Google Scholar]
- 44.Probst-Kepper, M., H.-J. Hecht, H. Herrmann, V. Janke, F. Ocklenburg, J. Klempnauer, B. J. van den Eynde, and S. Weiss. 2004. Conformational restraints and flexibility of 14-meric peptides in complex with HLA-B*3501. J. Immunol. 173:5610–5616. [DOI] [PubMed] [Google Scholar]
- 45.Lee, J. K., G. Stewart-Jones, T. Dong, K. Harlos, K. Di Gleria, L. Dorrell, D. C. Douek, P. A. van der Merwe, E. Y. Jones, and A. J. McMichael. 2004. T cell cross-reactivity and conformational changes during TCR engagement. J. Exp. Med. 200:1455–1466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Roberts, G. C., D. H. Meadows, and O. Jardetzky. 1969. Nuclear magnetic resonance studies of the structure and binding sites of enzymes. VII. Solvent and temperature effects on the ionization of histidine residues of ribonuclease. Biochemistry. 8:2053–2056. [DOI] [PubMed] [Google Scholar]
- 47.Bhattacharya, S. 1997. Temperature dependence of histidine ionization constants in myoglobin. Biophys. J. 73:3241–3256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Guinto, E. R., and E. Di Cera. 1996. Large heat capacity change in a protein-monovalent cation interaction. Biochemistry. 35:8800–8804. [DOI] [PubMed] [Google Scholar]
- 49.Barbieri, C. M., and D. S. Pilch. 2006. Complete thermodynamic characterization of the multiple protonation equilibria of the aminoglycoside antibiotic paromomycin: a calorimetric and natural abundance 15N NMR study. Biophys. J. 90:1338–1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Horn, J. R., D. Russell, E. A. Lewis, and K. P. Murphy. 2001. van't Hoff and calorimetric enthalpies from isothermal titration calorimetry: are there significant discrepancies? Biochemistry. 40:1774–1778. [DOI] [PubMed] [Google Scholar]
- 51.Spolar, R. S., and M. T. Record Jr. 1994. Coupling of local folding to site-specific binding of proteins to DNA. Science. 263:777–784. [DOI] [PubMed] [Google Scholar]
- 52.Khan, A. R., B. M. Baker, P. Ghosh, W. E. Biddison, and D. C. Wiley. 2000. The structure and stability of an HLA-A*0201/octameric Tax peptide complex with an empty conserved peptide-N-terminal binding site. J. Immunol. 164:6398–6405. [DOI] [PubMed] [Google Scholar]
- 53.Murphy, K. P., and S. J. Gill. 1991. Solid model compounds and the thermodynamics of protein unfolding. J. Mol. Biol. 222:699–709. [DOI] [PubMed] [Google Scholar]
- 54.Spolar, R. S., J. R. Livingstone, and M. T. Record. 1992. Use of liquid hydrocarbon and amide transfer data to estimate contributions to thermodynamic functions of protein folding from the removal of nonpolar and polar surface from water. Biochemistry. 31:3947–3955. [DOI] [PubMed] [Google Scholar]
- 55.Hilser, V. J., J. Gomez, and E. Freire. 1996. The enthalpy change in protein folding and binding: refinement of parameters for structure-based calculations. Proteins. 26:123–133. [DOI] [PubMed] [Google Scholar]
- 56.Murphy, K. P., and E. Freire. 1992. Thermodynamics of structural stability and cooperative folding behavior in proteins. Adv. Protein Chem. 43:313–361. [DOI] [PubMed] [Google Scholar]
- 57.Garcia, K. C., and E. J. Adams. 2005. How the T cell receptor sees antigen—a structural view. Cell. 122:333–336. [DOI] [PubMed] [Google Scholar]
- 58.James, L. C., P. Roversi, and D. S. Tawfik. 2003. Antibody multispecificity mediated by conformational diversity. Science. 299:1362–1367. [DOI] [PubMed] [Google Scholar]
- 59.Holler, P. D., and D. M. Kranz. 2004. T cell receptors: affinities, cross-reactivities, and a conformer model. Mol. Immunol. 40:1027–1031. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.