Explicit-Solvent Molecular Dynamics Simulations of the Polysaccharide Schizophyllan in Water

Abstract

Schizophyllan is a β(1→3)-D-glucan polysaccharide with β(1→6)-branched lateral glucose residues that presents a very stiff triple-helical structure under most experimental conditions. Despite the remarkable stability of this structure (which persists up to 120°C in aqueous solution), schizophyllan undergoes a major change of state around 7°C in water that has been hypothesized to result from an order-disorder transition in the lateral residues. This hypothesis is only supported by indirect experimental evidence and detailed knowledge (at the atomic level) concerning hydrogen-bonding networks, interactions with the solvent molecules, orientational freedom of the lateral residues, and orientational correlations among them is still lacking. In this study explicit-solvent molecular dynamics simulations of a schizophyllan fragment (complemented by simulations of its tetrasaccharide monomer) are performed at three different temperatures (273 K, 350 K, and 450 K) and with two different types of boundary conditions (finite nonperiodic or infinite periodic fragment) as an attempt to provide detailed structural and dynamical information about the triple-helical conformation in solution and the mechanism of the low-temperature transition. These simulations suggest that three important driving forces for the high stability of the triple helix are i), the limited conformational work involved in its formation; ii), the formation of a dense hydrogen-bonding network at its center; and iii), the formation of interchain hydrogen bonds between main-chain and lateral glucose residues. However, these simulations evidence a moderate and continuous variation of the simulated observables upon increasing the temperature, rather than a sharp transition between the two lowest temperatures (that could be associated with the state transition). Although water-mediated hydrogen-bonded association of neighboring lateral residues is observed, this interaction is not strong enough to promote the formation of an ordered state (correlated motions of the lateral residues), even at the lowest temperature considered.

INTRODUCTION

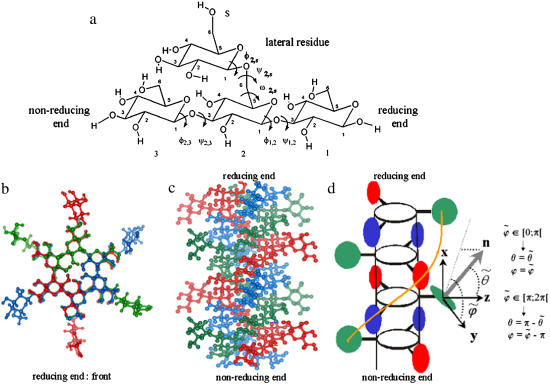
Schizophyllan is a cell-wall polysaccharide of the fungus Schizophyllum commune (1) possessing a number of interesting properties, including i), its ability to stimulate the human immune system (2–6); ii), its role as a colloidal carrier for trace metals and pollutants in natural water (7,8); iii), its widespread use in industry as a viscosity-control agent (9,10); iv), its ability to form hybrid complexes with nucleic acids (11–14); v), its use in the formulation of matrices for drug delivery (15–19); and vi), its use in the fabrication of nanofiber structures (20,21). The repeating tetrasaccharide unit of schizophyllan is shown in Fig. 1 a and consists of three β(1→3)-linked glucose molecules together with a β(1→6)-linked (lateral) glucose residue. Under most experimental conditions, the structure of schizophyllan is that of a very stiff triple helix with a persistence length between 150 and 200 nm (22,23), as illustrated in Fig. 1, b and c. For this reason, schizophyllan is a popular model for rod-like or stiff-worm-like polymers (24–26). The core of the helix is formed by three β(1→3)-D-glucan chains, held together by hydrogen bonds. The β(1→6)-D-glucose lateral residues, branched from every third glucose unit along each chain, are directed toward the exterior of the helix, as shown schematically in Fig. 1 d.

FIGURE 1.

(a) Repeating tetrasaccharide monomer of schizophyllan, with the labeling of glucose residues, carbon atoms, and glycosidic dihedral angles used in this study. (b and c) Atomistic representations of two pitches of the schizophyllan triple helix with the three individual chains represented in different colors (each chain involves two tetrasaccharide monomers per pitch of 1.8 nm); the two representations correspond to projections in a plane perpendicular to the helix axis with the reducing end at the front (b) or in a plane parallel to this axis with the reducing end at the top (c). (d) Schematic representation of two pitches of the schizophyllan triple helix (same orientation as in c; adapted from Itou et al. (40)); the central cylinder represents the helix core; the colored disks represent lateral residues; the definitions of the angles 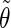and 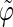characterizing the orientation of a given lateral residue relative to the helix axis are indicated; an example of the postulated water-mediated hydrogen-bonding network between closest neighbor lateral residues (hypothesized for the low-temperature state of schizophyllan (40)) is indicated by an orange line.

In contrast to most polysaccharides, usually poorly soluble in water, schizophyllan exhibits a fairly high solubility due to the presence of its lateral residues (27). The triple-helical conformation found in the crystallographic structure (28) has been shown to persist in aqueous solution up to a temperature of 120°C (29–31). Despite this remarkable stability schizophyllan undergoes a major state transition around 7°C in water (32–37). This reversible and highly cooperative transition has been monitored using measurements of optical rotation and heat capacity (38–41), dielectric dispersion (42,43), viscosity, and ¹³C-NMR spectra (40,44). Based on the combined analysis of these experimental results, it has been hypothesized that the observed changes result from an order-disorder transition in the lateral residues (40). In particular, the ¹³C-NMR experiments indicate that rotational motion of lateral residues is possible at 40°C (postulated disordered state) but strongly restricted at 5°C (postulated ordered state). The motional restriction observed at low temperatures has been suggested to follow from the hydrogen-bonded association of the lateral residues with tightly bound water molecules in the ordered state (40). These strong glucose-water interactions would involve the first one or two hydration layers at the helix surface (42,43). In contrast, the disordered state would involve much fewer tightly bound water molecules and an increased (though not complete) rotational freedom of the lateral residues.

The mechanism suggested above is also supported by indirect experimental evidence. For example, the existence of a water-mediated hydrogen-bonding network bridging neighboring lateral residues in the ordered state provides an easy way to interpret the solvent isotope effects on the transition, the smaller hydrodynamic radius of the polysaccharide above the transition temperature, as well as the cooperativity of the transition over large length scales along the helix axis (40). However, detailed knowledge (at the atomic level) concerning hydrogen-bonding networks, interactions with the solvent molecules, and rotational freedom of the lateral residues is still lacking.

Explicit-solvent molecular dynamics (MD) simulations investigating the state transition of schizophyllan (simulations performed at 273 and 300 K) have been reported recently (45). Restricted motion of the lateral residues was observed in the simulation performed at 273 K. The residence times of water molecules close to the lateral residues were also found to be substantially influenced by the change in the temperature, whereas those for water molecules close to the core chains were only weakly affected. However, it is not obvious whether the differences found between the simulations at 273 and 300 K really stem from a transition between an ordered and a disordered state or simply reflect an (expected) increase in flexibility upon increasing the temperature.

In this study, explicit-solvent MD simulations were performed as an attempt to provide detailed structural information about the triple-helical conformation in solution and insight into the mechanism of the postulated order-disorder transition. Due to computational limitations, the MD simulations were carried out for a limited (but hopefully representative) segment of a schizophyllan triple helix (four tetrasaccharide monomers in each of the three chains). Simulations of a single tetrasaccharide unit also investigated the conformational behavior of the isolated monomer. All simulations were performed at either 0°C (273 K) or 77°C (350 K), two temperatures that should be representative of the ordered and disordered states, respectively. In addition, to accelerate the conformational sampling in the disordered state, additional simulations were carried out at 177°C (450 K).

COMPUTATIONAL METHODS

All simulations were performed using the GROMOS96 simulation program (46,47), together with the OPLS-AA-SEI force field (48) and the TIP3P water model (49). The OPLS-AA-SEI force field, an improved version of the OPLS-AA (all atoms) force field for carbohydrates (50) involving the scaling of specific electrostatic nearest-neighbor interactions), has been parameterized against ab initio calculations and experimental data in solution in the context of hexopyranoses. A considerable effort has been paid in particular to the derivation of torsional parameters for the hydroxyl and hydroxymethyl groups. The force field has been subsequently further refined in the specific context of β(1→3)- and β(1→6)-linked disaccharides (51), with the ultimate goal of simulating schizophyllan (this work).

For the monomer simulations (isolated tetrasaccharide unit), one solute molecule (85 atoms) was surrounded by 959 water molecules within a truncated octahedron box derived from a cube of edge length 3.8 nm, subjected to periodic boundary conditions. For the triple-helix segment, two alternative types of boundary conditions were used in the simulations. In system A, a two-pitches (nonperiodic) helix fragment of schizophyllan (three chains of four tetrasaccharide units each; total 1017 atoms) was placed in the center of a truncated octahedron box derived from a cube of edge length 6.5 nm containing 4410 water molecules. In system B, a two-pitches (periodic) helix fragment of schizophyllan (1008 atoms) was placed within a rectangular box containing 2679 water molecules, with the helix oriented along the x axis of the box. The box edges along the y and z axes were set to 4.9 nm. The box dimension along the x axis was chosen so that the three glucose residues forming one extremity of the fragment could be linked by glycosidic bonds (involving the removal of three oxygen and six hydrogen atoms) to the three glucose residues forming the other extremity of the fragment. Therefore, the triple helix in this system is formally of infinite length. The two approaches clearly represent approximations of the real polysaccharide. On the one hand, the molecular mass of the schizophyllan fragment modeled in system A (7839 Da) is extremely small compared to the typical weights of naturally occurring schizophyllan polysaccharides (∼100–6000 kDa (52)). On the other hand, system B formally models an infinite chain, involving an artificial periodicity constraint (the coordinates of the residues are translationally equivalent after two helix pitches), which is expected to substantially rigidify the helix.

In the absence of a high-resolution experimental structure for schizophyllan, the initial coordinates for all systems (monomer and triple-helix fragments under boundary conditions A or B) were taken from a model of the schizophyllan triple helix based on the crystallographic structure of curdlan (53). The latter polysaccharide presents the same basic structure as schizophyllan but lacks the lateral residues. These residues were incorporated into the model (Y. Takahashi, T. Kobatake, and H. Suzuki, Osaka University, Japan, personal communication, 2003) to be directed toward the exterior of the helix (glycosidic dihedral angle ψ set to 180°), together with the glycosidic dihedral angle φ set to 60° (exoanomeric effect) and the glycosidic dihedral angle ω set to 60° (dominant gt conformation found in the β(1→6)-linked disaccharide gentiobiose (51)).

For all systems (monomer and triple-helix fragments under boundary conditions A or B), three MD simulations were performed at temperatures of 273 K, 350 K, and 450 K. The simulations at 273 K and 350 K were performed at a constant pressure of 1 bar, whereas the simulation at 450 K was performed at constant volume. After energy minimization of the initial system (solute plus solvent) configurations (see above), a 50-ps equilibration MD simulation was performed at 273 K with all solute atoms positionally restrained (force constant 2.5 × 10⁴ kJ.mol⁻¹.nm⁻²), followed by a 50-ps MD simulation at the same temperature in which the restraining force was applied only to nonhydrogen atoms. The production simulation at 273 K was initiated from this point and carried out for a duration of 5 ns. For the simulation at 350 K, the equilibration at 273 K was followed by four successive MD simulations of 25 ps at 350 K, with position restraints of decreasing magnitude on all the solute atoms (from 2.5 × 10⁴ kJ.mol⁻¹.nm² to 0.3 × 10⁴ kJ.mol⁻¹.nm⁻²). The production simulations at 350 K and 450 K were both initiated from this point and carried out for durations of 5 ns. All production runs (after the initial equilibration time, which is excluded during the analysis of the simulations) are fully unrestrained.

For all simulations, the equations of motion were integrated based on the leapfrog scheme using a 2-fs time step. Bonds between hydrogen and heavy atoms as well as the geometry of the solvent molecules were constrained using the SHAKE algorithm (54) with a relative geometric tolerance of 10⁻⁴. The temperatures of solute and solvent degrees of freedom were controlled by coupling them separately to a Berendsen thermostat (55) with a relaxation time of 0.1 ps. For the monomer and system A (system B), the pressure was maintained by coupling to a Berendsen barostat (55) via isotropic (anisotropic) coordinate scaling with a relaxation time of 0.5 ps and a compressibility of 4.575 × 10⁻⁶ (kJ.mol⁻¹.nm⁻³)⁻¹. Consistently with the OPLS/TIP3P parameterization scheme, nonbonded interactions were truncated on a charge-group basis at a (relatively short) cutoff distance of 0.9 nm based on a pair list updated every 10 fs. This force field combination has proved extremely successful at reproducing experimental results for pure liquids (56) as well as solvation properties (57), provided that a short (0.9–1.1 nm) cutoff is used without long-range correction. Changing (improving) the electrostatic scheme (e.g., by increasing the cutoff distance or turning to reaction-field (58) or lattice-sum (59,60) methods) without rederiving the atomic charges (and van der Waals parameters) is likely to impair the force field consistency and accuracy. For this reason, the choice was made here to stick to the original OPLS/TIP3P-consistent electrostatic scheme. Note, however, that all charge groups in this system are neutral (no ions or ionizable groups). This should largely reduce the magnitude of cutoff artifacts because the truncation applies to dipole-dipole interactions (∼r⁻³) rather than charge-charge (∼r⁻¹) or charge-dipole (∼r⁻²) interactions. Configurations were recorded every 0.5 ps for analysis.

The simulations were analyzed in terms of heavy-atom (carbon and oxygen) root mean-square atomic positional deviation (rmsd) from the (modeled) initial structure, heavy-atom root mean-square atomic positional fluctuations (rmsf), rotameric populations of the glycosidic dihedral angles (distinguishing between the β(1→3)- and β(1→6)-linkages), orientation of the lateral residues relative to the helix axis, intra- and interchain hydrogen bonds (distinguishing the bonds within the helix core from those between the helix core and the lateral residues), solute-solvent hydrogen bonds (distinguishing the bonds between the helix core and the solvent from those between the lateral residues and the solvent), and solvent-mediated hydrogen-bonded bridges between lateral residues (involving one or two bridging water molecules).

The definition used for assessing the presence of a hydrogen bond is based on a geometric criterion. If the distance between the hydrogen of the donor and the oxygen of the acceptor is below 0.25 nm and the donor-hydrogen-acceptor angle is larger than 135°, the atoms are assumed to participate in a hydrogen bond. The conformations around the glycosidic dihedral angles φ and ψ are labeled g⁺, t, and g⁻, corresponding to torsional-angle ranges of widths 120° centered at 60°, 180°, and 300°, respectively. The conformation of the hydroxymethyl group in a glucose unit or of the ω glycosidic dihedral angle in a (1→6)-linkage are labeled gt, tg, and gg (wells centered at 60°, 180°, and 300°, respectively), where the conformation around O6-C6-C5-O5 is indicated by the first letter (gauche or trans) and the conformation around O6-C6-C5-C4 by the second letter (see Fig. 1 a).

The analysis of the lateral residue orientation relative to the helix axis relies on the definition of two angles θ and ϕ for each lateral residue as depicted in Fig. 1 d. First, a unit vector x directed along the helix axis (toward the reducing end) is evaluated by averaging the unit vectors normal to the 12 planes defined by the C2 atoms of the three chains located at the same level along the entire helix. Second, for a given lateral residue, the projection P of the center of the helix at the level of this residue (defined as the center of geometry of the three C2 atoms of the core at this level) into the plane perpendicular to x containing the center of geometry of the lateral residue is determined. Third, a unit vector z is defined along the line connecting the point P to the center of geometry of the lateral residue (i.e., directed toward the exterior of the helix). Fourth, a unit vector y perpendicular to x and z is defined so that the triplet (x, y, z) is positively oriented. Finally, a unit vector n normal to the sugar ring (and directed toward its β side) is evaluated by averaging the unit vectors normal to the planes defined by atoms C1, C3, and C5 and by atoms C2, C4, and O5 of the glucose ring, respectively. The calculation of the four vectors (n, x, y, z) is performed for each lateral residue at every time step. Expressing the vector n in spherical coordinates within the system defined by the vectors x, y, and z leads to the angles 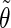(between n and z) and 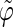(between y and the projection of n in the x, y-plane). The angles 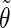and 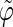belong to the ranges [0;π] and [0;2π], respectively. However, for simplicity, part of the analysis is performed in terms of derived angles θ and ϕ defined as follows. If 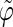is in the range [0;π] then and If 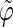is in the range [π;2π] then 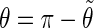and 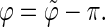In practice, this change amounts to disregarding the direction of the vector n and only considering the overall orientation of the ring with its two faces considered indistinguishable. The angles θ and ϕ both belong to the range [0;π].

The correlation coefficients between the angles 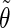and 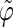characterizing the orientations of each pair of lateral residues was calculated following the standard formula for the correlation between two statistical series αⁱ and α^j of N elements each,

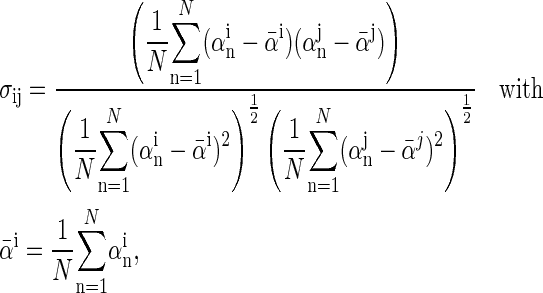(1)

where α stands for the angles 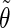or 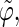i and j label two different lateral residues, and N is the number of configurations in the trajectory. For this analysis, three classes of lateral residue pairs were defined depending on their degrees of proximity, and the absolute values of the correlation coefficients were averaged for each class. Class 1 corresponds to closest neighbors (distance ∼1.30 nm; e.g., successive residues along the orange line in Fig. 1 d). Class 2 corresponds to the residue pairs located at the same level along the helix axis (distance ∼1.85 nm) and those located at the same position in the successive levels along the helix axis (distance ∼1.81 nm). Class 3 corresponds to all other residue pairs (distance ≥ 2.4 nm).

To simplify the discussion of the results, a systematic nomenclature is used, as illustrated in Fig. 1 a. The glucose residues involved in the schizophyllan monomer are designated using the labels 1, 2, or 3 for the β(1→3)-linked glucose units (from the reducing to the nonreducing end) and s for the β(1→6)-linked glucose unit. Each carbon Cn in a unit i (Cn_i) gives its label to the associated aliphatic hydrogen (HCn_i) and hydroxyl group (On_i, Hn_i). The ring oxygens are labeled O5_i and the glycosidic oxygens O1_i. The glycosidic dihedral angles are indicated using the labels of the two linked glucose units as subscripts (φ_1,2 = HC1₂ - C1₂ - O1₂ - C3₁; ψ_1,2 = C1₂ - O1₂ - C3₁ - HC3₁; φ_2,3 = HC1₃ - C1₃ - O1₃ - C3₂; ψ_2,3 = C1₃ - O1₃ - C3₂ - HC3₂; φ_2,s = HC1_s - C1_s - O1_s - C6₂; ψ_2,s = C1_s - O1_s - C6₂ - C5₂; ω_2,s = O1_s - C6₂ - C5₂ - O5₂).

RESULTS AND DISCUSSION

The heavy-atom rmsd values from the (modeled) initial structure, either including or excluding the lateral residues, are reported in Table 1 for the simulations of the monomer, of the nonperiodic schizophyllan fragment (system A), and of the periodic schizophyllan fragment (system B) at 273, 350, or 450 K. Irrespective of the temperature and for both the monomer and the individual chains of the schizophyllan fragments, the rmsd values excluding the lateral residues are rather low (0.05–0.12 nm). This indicates that the core residues remain structurally very close to the triple helix crystal structure in all simulations. As expected from the constraint imposed by artificial chain periodicity in the periodic schizophyllan fragment of system B, the corresponding rmsd values (0.05–0.06 nm) are systematically lower than the values for the nonperiodic fragment of system A (0.08–0.12 nm). For both systems A and B, the rmsd values for the entire schizophyllan fragment excluding the lateral residues is higher (0.17–0.19 nm), which dominantly results from a slightly reduced distance between the three chains compared to the crystallographic structure (data not shown). For all systems considered, the rmsd values calculated with inclusion of the lateral glucose residues are systematically higher by ∼0.1 nm compared to the values calculated excluding these residues, reflecting the flexibility of the β(1→6)-linkage. However, in all cases, no significant changes are observed when the temperature is increased from 273 K to 350 K, and further to 450 K.

TABLE 1.

Heavy-atom rmsd values from the (modeled) initial structure

		Monomer			System A			System B
		273 K	350 K	450 K	273 K	350 K	450 K	273 K	350 K	450 K
		[nm]	[nm]	[nm]	[nm]	[nm]	[nm]	[nm]	[nm]	[nm]
Fragment	Overall	0.22	0.21	0.22	0.30	0.30	0.31	0.25	0.27	0.28
	Core	0.11	0.10	0.12	0.19	0.18	0.19	0.17	0.17	0.17
Chain I	Overall	–	–	–	0.20	0.20	0.23	0.13	0.18	0.17
	Core	–	–	–	0.09	0.08	0.12	0.06	0.05	0.05
Chain II	Overall	–	–	–	0.21	0.21	0.22	0.16	0.16	0.17
	Core	–	–	–	0.09	0.09	0.10	0.05	0.05	0.06
Chain III	Overall	–	–	–	0.22	0.23	0.24	0.20	0.21	0.21
	Core	–	–	–	0.08	0.08	0.09	0.05	0.05	0.05

Values are reported for the simulations of the schizophyllan monomer, of the nonperiodic schizophyllan fragment (system A), and of the periodic schizophyllan fragment (system B) at 273, 350, or 450 K. Averaging is performed over the last 2.5 ns of the trajectories. The results are reported either for the entire fragment (or monomer) or for each of the three chains individually (i.e., both least-squares fit superposition and rmsd calculation are performed for the specific chain only) and either including (overall) or excluding (core) lateral residues.

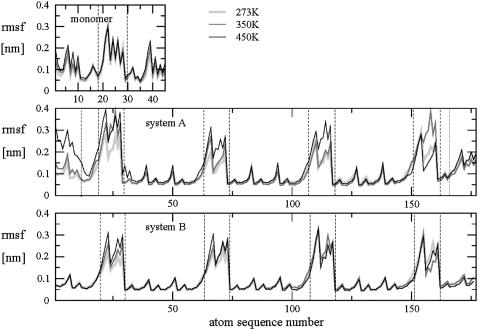
The heavy-atom rmsf values are displayed in Fig. 2 as a function of the atom sequence number for all simulations. The rmsf values are typically low for main-chain atoms (0.05–0.15 nm except for the terminal glucose residues) and significantly higher (up to 0.40 nm) for the atoms of the lateral residues. The main-chain rmsf values are also highest in the free monomer (compared to the schizophyllan fragments), indicating a substantial rigidification of the β(1→3)-linkage within the triple-helical structure. The rmsf values for the nonperiodic schizophyllan fragment of system A are significantly larger for the atoms belonging to the six main-chain residues forming the two extremities of the triple helix. Visual inspection of the conformations sampled during these simulations shows that the triple helix partially unwinds at its ends (data not shown). Such a ‘polymer-chain-end’ effect has already been reported to be significant for schizophyllan (61). Obviously, this effect is absent for the periodic fragment of system B. This difference is the main cause for the larger rmsd values observed previously for the helix core in system A compared to system B (Table 1). In all cases, the effect of increasing the temperature on the rmsf values of main-chain atoms is negligible, suggesting that the helix core is very stable at all temperatures considered. The corresponding values for the lateral residues increase with increasing temperature, indicating an increased rotational sampling around the β(1→6)-linkages.

FIGURE 2.

Heavy-atom rmsf values calculated for the simulations of the schizophyllan monomer, of the nonperiodic schizophyllan fragment (system A), and of the periodic schizophyllan fragment (system B) at 273 K (light shaded, thick line), 350 K (dark shaded, normal line), or 450 K (solid, thin line) and displayed as a function of the atom sequence number (as defined in the OPLS-AA-SEI force field (48,51)). Vertical dashed lines indicate the boundaries of the lateral residues and vertical dotted lines the boundaries of the terminal glucose residues (system A only). The calculations are based on the entire 5-ns trajectories. For the schizophyllan fragments, the rmsf values are averaged over the equivalent atoms in the three chains.

The stability of the triple-helical structure at 450 K contrasts with the experimental schizophyllan melting temperature of about 400 K. For the periodic fragment of system B, this may be explained by the constraints due to artificial chain periodicity. For the nonperiodic schizophyllan fragment of system A, this may simply be due to a simulation time (5 ns) insufficient for permitting such a large conformational change as the full separation of the individual chains. However, it should also be kept in mind that the force field used in this study has not been optimized for such an elevated temperature and that the simulations at 450 K, performed at constant volume (to preserve a reasonable density for the solvent), involve an elevated pressure.

The experimental and simulated average values of the glycosidic dihedral angles are summarized in Table 2 for laminarabiose (β(1→3)-linked glucose disaccharide), gentiobiose (β(1→6)-linked glucose disaccharide), the schizophyllan monomer, and the schizophyllan fragments of systems A and B. These average angles are typically close (within at most 30°) to ideal values of 60°, 180°, or 300° associated with staggered configurations, the main exception being the ψ dihedral angle in its g⁺ and g⁻ conformation for both types of linkages.

TABLE 2.

Experimental and simulated average values of the glycosidic dihedral angles in laminarabiose, in gentiobiose, in the schizophyllan monomer, in the nonperiodic schizophyllan fragment (system A), and in the periodic schizophyllan fragment (system B)

			Laminarabiose			Gentiobiose			Schizophyllan monomer			Schizophyllan fragment
			Exp		MD	Exp		MD	MD	MD	MD	Exp	MD System A			MD System B
			X-ray	NMR	300 K	X-ray	NMR	300 K	273 K	350 K	450 K	X-ray	273 K	350 K	450 K	273 K	350 K	450 K
			[deg]	[deg]	[deg]	[deg]	[deg]	[deg]	[deg]	[deg]	[deg]	[deg]	[deg]	[deg]	[deg]	[deg]	[deg]	[deg]
β(1→3)-linkage	φ	g+	46	32	61	–	–	–	59	59	58(97)	29	42	43	43	41	40	41
		t	–	–	–	–	–	–	–	–	157(3)	–	–	–	–	–	–	–
		g−	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–
	ψ	g+	13	27	25	–	–	–	20	18	11(97)	10	9	6	6	6	6	6
		t	–	–	–	–	–	–	–	–	191(3)	–	–	–	–	–	–	–
		g−	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–
β(1→6)-linkage	φ	g+	–	–	–	50	–	59(95)	59(100)	58(95)	59(90)	–	55(94)	55(98)	56(97)	56(94)	55(98)	55(96)
		t	–	–	–	–	–	161(5)	–	163(5)	159(9)	–	167(6)	165(2)	158(3)	167(6)	160(1)	158(2)
		g−	–	–	–	–	–	–	–	–	334(1)	–	–	–	–	–	339(1)	330(2)
	ψ	g+	–	–	–	–	–	88(6)	101(5)	84(14)	76(9)	–	–	–	71(2)	–	–	–
		t	–	–	–	197	–	183(90)	185(73)	185(78)	183(77)	–	191(65)	187(39)	195(63)	184(80)	188(72)	198(75)
		g−	–	–	–	–	–	265(4)	267(22)	261(8)	278(13)	–	254(35)	250(60)	257(35)	245(20)	243(28)	255(25)
	ω	gt	–	–	–	69(57)	79(66)	57(62)	56(77)	54(64)	54(70)	–	57(78)	56(89)	56(90)	80(86)	75(95)	73(96)
		tg	–	–	–	–	–	154(2)	–	–	159(3)	–	157(18)	159(4)	156(3)	144(14)	141(5)	140(4)
		gg	–	–	–	295(43)	292(34)	308(36)	318(23)	309(36)	309(27)	–	310(4)	306(7)	309(7)	–	–	–

The average experimental values reported for laminarabiose and gentiobiose are obtained from a selected set of x-ray crystallographic structures of six β(1→3)- and seven β(1→6)-linked disaccharides, respectively, involving a limited degree of functionalization (51) (for laminarabiose, this set corresponds to compounds with functionalization precluding the formation of interresidue hydrogen bonds), and from NMR measurements (51) (hetero- and homonuclear coupling constants and nuclear Overhauser effects). The experimental values reported for the β(1→3)-linkage in schizophyllan are those found in the x-ray crystallographic structure of curdlan (53). Simulated values are averaged over the entire 5-ns trajectories and over all dihedral angles of a specific type present in the molecule considered and are reported for simulations at 273, 350, or 450 K. The corresponding values for laminarabiose and gentiobiose (300 K only) are based on previous work (51). When more than one conformer is populated for a given dihedral angle, the populations (in percentage) are indicated between parentheses.

The average values of the glycosidic dihedral angles φ and ψ involved in the β(1→3)-linkage (Table 2) are both smaller by ∼15–20° for the simulations of the triple helix fragments compared to those of the schizophyllan monomer and of laminarabiose. However, these values are in good agreement (∼5–10°) with those found in the crystallographic structures of curdlan (53) and a set of six β(1→3)-linked disaccharides (51). This suggests that the triple helix respects the intrinsic conformational preferences of the β(1→3)-linkage, i.e., that the formation of favorable interchain interactions in this structure is not offset by a significant conformational work. Based on the analysis of crystallographic structures, NMR experiments, molecular mechanics calculations, and MD simulations, it has been suggested that the dominant conformation of laminarabiose in water (with φ ≈ 46° and ψ ≈ 13°) is not the one resulting from the formation of interresidue hydrogen bonds (in particular the H4 - O5 hydrogen bond associated to the conformation with φ ≈ 28° and ψ ≈ −38° found in some crystallographic structures), due to the competition between intra- and intermolecular hydrogen bonds in this solvent (49). In all systems considered and at the three temperatures, the probability distributions of the glycosidic dihedral angles φ and ψ involved in the β(1→3)-linkage (data not shown) are rather narrow and only weakly sensitive to the temperature (apart from a slight broadening).

The orientation of a lateral residue relative to the helix core is mainly determined by the three glycosidic dihedral angles φ, ψ, and ω associated with the β(1→6)-linkages (Table 2). Although similar conformational preferences are observed for gentiobiose and for the schizophyllan monomer, these differ significantly from those found in the schizophyllan fragments. The dihedral angle φ almost exclusively adopts a g⁺ configuration in all cases (exoanomeric effect). However, the dihedral angle ψ sees its g⁻ population increase at the expense of the g⁺ one upon going from the dimer and tetramer to the schizophyllan fragments, although the t conformation remains dominant for all systems considered (except system A at 350 K). Simultaneously, for the dihedral angle ω, the gg population decreases from 30% to 40% to nearly zero at the benefit of the gt one, which is the conformation almost exclusively found in the fragments. This change in the conformational preferences of the β(1→6)-linkage is probably due to the formation of (more or less stable) hydrogen bonds between the lateral and main-chain residues in the schizophyllan fragments.

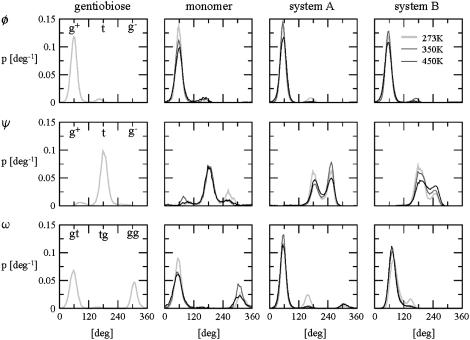
The probability distributions associated with the dihedral angles φ, ψ, and ω of the β(1→6)-linkages are displayed in Fig. 3 for all simulations. The main difference observed when going from system A to system B is a shift of the (dominant) gt population peak for ω to a slightly larger angle and the disappearance of a (minor) peak associated with the gg conformation. The trends observed upon increasing the temperature are similar for systems A and B. The (dominant) g⁺ population around φ slightly decreases at the benefit of the t one, the t and g⁻ populations around ψ tend to become more homogeneous (especially visible for system B), and the tg population around ω decreases at the benefit of the (dominant) gt one.

FIGURE 3.

Normalized probability distributions associated with the dihedral angles φ, ψ, and ω of the β(1→6)-linkages in gentiobiose (300 K, from previous work (51)), in the schizophyllan monomer, in the nonperiodic schizophyllan fragment (system A), and in the periodic schizophyllan fragment (system B) at 273 K (light shaded, thick line), 350 K (dark shaded, normal line), or 450 K (solid, thin line). The calculations are based on the entire 5-ns trajectories. For the schizophyllan fragments, the distributions are averaged over the 12 lateral residues.

The number of transitions observed over 5 ns for the three glycosidic dihedral angles φ, ψ, and ω associated with the β(1→6)-linkages is reported in Table 3 for all simulations. In all cases the dihedral angle ψ presents the highest number of transitions and the most important sensitivity to a temperature increase. This observation may be related to the closeness (partial overlap) of the population peaks associated with the three (or two) accessible conformations around this dihedral angle (Fig. 3). The number of transitions about φ and ω in the schizophyllan monomer presents a high sensitivity to temperature that is dramatically reduced in the case of the schizophyllan fragments. The results obtained for the schizophyllan fragments of systems A and B are very comparable.

TABLE 3.

Number of transitions observed for the three glycosidic dihedral angles φ, ψ, and ω associated with the β(1→6)-linkages during the 5-ns simulations of gentiobiose, of the schizophyllan monomer, of the nonperiodic schizophyllan fragment (system A), and of the periodic schizophyllan fragment (system B) at 273, 350, or 450 K

	Gentiobiose	Monomer			System A			System B
	273 K	273 K	350 K	450 K	273 K	350 K	450 K	273 K	350 K	450 K
φ	3	2	10	46	3	2	10	3	3	10
ψ	16	17	35	94	9	31	73	6	27	66
ω	13	7	15	84	3	4	14	7	9	12

A transition is considered to have occurred if the dihedral angle has changed well during more than 5 ps. For φ, ψ (gentiobiose and monomer only), and ω the three wells are defined by torsional angle ranges of widths 120° centered at 60°, 180°, and 300° and for ψ (schizophyllan fragments), they are defined by torsional-angle ranges of widths 90° centered at 85°, 175°, and 265° (based on the distributions of Fig. 3). For the schizophyllan fragments, the number of transitions are averaged over the 12 lateral residues and rounded to the nearest integer number.

For the schizophyllan fragments, monitoring the direction of vectors normal to the glucose rings of the lateral residues over the course of the MD simulations permits one to assess the effect of the temperature on the orientational fluctuations. This direction (relative to the helix axis and to a vector normal to the helix axis going though the residue center permits one to, and omitting the distinction between the two faces of the glucose rings) can be represented by two angles, θ and ϕ (Fig. 1 d). The results of this analysis are presented in Fig. 4 for the periodic schizophyllan fragment of system B. The distributions of the lateral-residue orientations (on the 5-ns timescale) are very sensitive to temperature. At 273 K, the trajectories only cover a limited part of the available (θ,ϕ)-space and the orientational preferences vary significantly between the different lateral residues. The sampling is improved and the differences reduced upon increasing the temperature. At 450 K, most of the lateral residues present similar broad ring-shaped distributions centered at (θ,ϕ) ≈ (90°, 90°), i.e., the corresponding configuration with the plane of the glucose ring perpendicular to the helix axis (i.e., horizontal in Fig. 1 d) is strongly disfavored.

FIGURE 4.

Distributions of the angles θ and ϕ (Fig. 1 d) characterizing the orientation of the different lateral residues in the periodic schizophyllan fragment (system B) at 273 K, 350 K, and 450 K. The different panels are positioned following the representation of Fig. 1 d. For example, the panels at lines and columns (1, 3), (2, 2), (3, 2), and (4, 1) correspond to those along the orange line in Fig. 1 d. The individual points in each panel represent (θ, ϕ)-values characterizing the orientation of the corresponding lateral residue (at a sampling interval of 0.5 ps).

The extent of correlation between the orientations of neighboring lateral residues can be assessed by the determining the correlation coefficients between the two unit vectors n (Fig. 1 d) characterizing the orientation of pairs of lateral residues (including the distinction between the two faces of the glucose rings). The results of this analysis are reported in Table 4 for the periodic schizophyllan fragment of system B. Separate averaging of the absolute values of the correlation coefficients is made for the closest neighbors (class 1), medium-range neighbors (class 2), and longer-distance neighbors (class 3). Even for the closest neighbors and at the lowest temperature, the average correlation coefficients remain very low (0.07–0.15). Furthermore, no clear trend (expected decrease in average correlation) can be evidenced when the distance between residues becomes larger (classes 2 or 3) or when the temperature is increased to 350 K. The average coefficients are slightly smaller at 450 K (0.04–0.09), but the effect remains very small. Thus, it appears that although increasing the temperature leads to an increase in the extent of the orientational motion of the lateral residues (Fig. 4), it does not induce any significant change in the motional correlations among neighboring residues, which remains very low at all temperatures considered.

TABLE 4.

Correlation coefficients (Eq. 1) between the angles 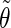and 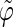characterizing the orientation of pairs of lateral residues (Fig. 1 d) for the periodic schizophyllan fragment (system B) at 273 K, 350 K, and 450 K

		273 K			350 K			450 K
		Mean	σ	Max	Mean	σ	Max	Mean	σ	Max
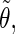Class 1	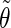′	0.07	0.08	0.34	0.12	0.07	0.30	0.07	0.05	0.21
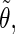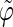	′	0.12	0.13	0.57	0.10	0.08	0.25	0.09	0.07	0.30
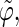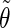	′	0.08	0.06	0.21	0.15	0.10	0.34	0.05	0.04	0.16
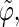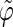	′	0.07	0.06	0.24	0.10	0.10	0.36	0.04	0.05	0.25
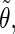Class 2	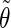′	0.10	0.10	0.35	0.13	0.12	0.39	0.07	0.05	0.26
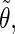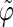	′	0.10	0.13	0.58	0.11	0.11	0.49	0.06	0.06	0.26
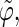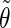	′	0.09	0.08	0.30	0.12	0.12	0.51	0.06	0.05	0.13
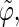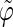	′	0.15	0.11	0.39	0.15	0.12	0.43	0.08	0.04	0.16
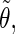Class 3	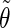′	0.07	0.06	0.29	0.11	0.09	0.40	0.06	0.05	0.19
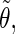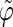	′	0.08	0.09	0.27	0.11	0.14	0.52	0.07	0.07	0.36
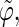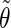	′	0.10	0.11	0.56	0.13	0.09	0.29	0.06	0.03	0.14
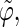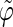	′	0.11	0.12	0.55	0.10	0.08	0.28	0.06	0.05	0.21

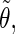
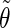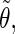
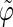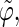
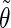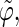
The coefficients are reported for the four possible combinations of angle pairs (′; ′; ′; ′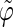). Averaging is done separately over closest neighbors (class 1; distance ∼1.30 nm), medium-range neighbors (class 2; distance ∼1.8–1.85 nm), and longer-distance pairs (class 3; distance ≥ 2.4 nm). The results are based on the entire 5-ns trajectories. The absolute values of the correlation coefficients are averaged over all residue pairs belonging to a given class (mean) and reported together with the corresponding standard deviations (σ) and maximum values (max).

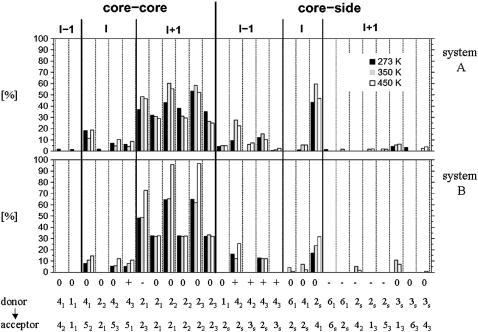
The occurrences of intrasolute hydrogen bonds are reported in Fig. 5 for the schizophyllan fragments of systems A and B. Hydrogen bonds between the core residues within a given main chain are almost exclusively found between the OH4 of a glucose unit and the O5 ring oxygen of the following unit in the direction of the nonreducing end (the same hydrogen bond also transiently occurs in laminarabiose and in the schizophyllan monomer; data not shown). The occurrences of these hydrogen bonds are limited (5–20%), similar in both systems A and B, and only weakly sensitive to the temperature. These hydrogen bonds tend to present higher occurrences at the extremities of the triple helix in system A (especially at 450 K; data not shown), as a result of the partial unwinding of the triple-helical structure at the chains ends (which precludes the formation of interchain hydrogen bonds).

FIGURE 5.

Occurrences of intrasolute hydrogen bonds in the nonperiodic schizophyllan fragment (system A) and the periodic schizophyllan fragment (system B) at 273 K (solid), 350 K (shaded), or 450 K (open). The occurrences represent the percentage of the MD simulation time where the hydrogen bond is formed and are averaged over the 12 monomers in the fragment. Distinction is made between hydrogen bonds within the helix core (core-core) or between the helix core and the lateral residues (core-side); between hydrogen bonds with donor and acceptor in the same chain (I), with an acceptor belonging to the next (clockwise in the representation of Fig. 1 b) chain relative to the donor (I + 1), or with an acceptor belonging to the previous chain (I − 1); between hydrogen bonds involving monomers at the same level along the helix axis (0), with an acceptor belonging to the next (in the direction reducing to nonreducing end, i.e., from top to bottom in the representation of Fig. 1 c) monomer relative to the donor (+), or with an acceptor belonging to the previous monomer (−). The atom labels of the donor and acceptor involved in the different hydrogen bonds are also indicated (full size: atom number of the hydrogen or oxygen atom; subscript: label of the glucose unit in the monomer; see Fig. 1 a). The calculations are based on the entire 5-ns trajectories.

Interchain hydrogen bonds between core residues, which contribute to holding the three main chains together, are mostly found between the OH2 groups of the glucose residues located at the center of the triple-helical structure (Fig. 1 b). These hydrogen bonds involve two OH2 groups with the acceptor belonging to the next chain (clockwise in the representation of Fig. 1 b) at either the same level along the helix axis (occurrence ∼30%) or shifted by one unit in the direction of the reducing end (occurrence ∼40–95%). Note that the two latter hydrogen-bonding patterns can occur simultaneously (data not shown) because each OH2 group can act both as donor and as acceptor. This network of solvent-inaccessible hydrogen bonds at the center of the triple helix (involving hydroxyl groups functioning simultaneously as donor and as acceptor, as well as the existence of multiple alternative hydrogen-bonding patterns) is probably one of the main driving forces responsible for the remarkable stability of this structure. It is interesting to note that this hydrogen-bond network is regular (i.e., the relative locations of the donor and acceptor hydroxyl groups are preserved along the entire triple helix) and oriented (i.e., the hydrogen bonds only occur in a clockwise fashion according to the representation of Fig. 1 b and are either perpendicular to the helix axis or tilted toward the reducing end). Based on these simulations, it is not possible to assess whether this specific orientation of the network is due to a higher thermodynamic stability (e.g., favorable interaction between the network dipole and overall helix dipole) or to a kinetic effect (cooperativity between successive hydrogen bonds leading to large interconversion barriers between networks with opposite orientations). The occurrences of interchain hydrogen bonds are only moderately sensitive to the temperature, except for the periodic schizophyllan fragment of system B at 450 K. In this case, the occurrences of hydrogen bonds with the acceptor shifted by one unit in the direction of the reducing end become very large (∼70–90%). This may be in part a consequence of the simulations at 450 K being performed at constant volume rather than at constant pressure (as is the case for the simulations at 273 K and 350 K). In system A, the resulting increased water pressure acts isotropically on the fragment. However, in system B, it only acts in the directions perpendicular to the helix axis, presumably resulting in a denser packing of the three chains. A more detailed analysis of the hydrogen-bond time series (data not shown) also reveals that the formation of an intrachain OH4 - O5 hydrogen bond between a specific pair of residues is often correlated with a loss of the interchain OH2 - O2 hydrogen bonds involving these same residues. This suggests that water may indirectly stabilize the triple-helical structures by attenuating the former (solvent-exposed) intrachain hydrogen bonds.

Hydrogen bonds between lateral residues and core residues of the same chain exclusively occur with the residue adjacent to the one bearing the lateral residue in the direction of the reducing end. The same feature is observed for the isolated schizophyllan monomer (data not shown). The dominant hydrogen bond of this type is OH2_s - O4₁ (occurrence ∼50–60% for system A, ∼20–30% for system B). A more detailed analysis of the hydrogen bond time series (data not shown) reveals a clear correlation between the appearance of this hydrogen bond with g⁻ and gt conformations of the dihedral angles ψ and ω around the β(1→6)-linkage of a given residue. Hydrogen bonds between the lateral residues and core residues of a different chain do also occur. The dominant hydrogen bonds of this type are OH4₂ - O2_s and OH4₃ - O2_s with the acceptor belonging to the previous (counterclockwise in the representation of Fig. 1 b) chain and shifted by one monomeric unit in the direction of the nonreducing end relative to the donor (occurrence ∼20–30%). Thus, the lateral residues may also contribute significantly to the stability of the schizophyllan triple helix in water through these hydrogen bonds. The formation of these hydrogen bonds is also correlated with g⁻ and gt conformations of the ψ and ω glycosidic dihedral angles. As for the network of interchain core-core hydrogen bonds, the network of interchain hydrogen bonds involving core and lateral residues is regular and oriented. The temperature has only a limited effect on the occurrences of hydrogen bonds between core and lateral residues (of all types). The global trend is toward an increase in their occurrences and the appearance of additional hydrogen bonds (with relatively low occurrences). However, these trends are not systematic and remain moderate.

The average numbers of solute-solvent hydrogen bonds are reported in Table 5 for the schizophyllan fragments of systems A and B. Distinction is made between the solute donor and acceptor groups belonging to the core and to the lateral residues. The moderate drifts in the corresponding time series (estimated by the slope of a regression line) suggest that the corresponding average numbers essentially represent equilibrium values. Despite the limited exposition of main-chain hydroxyl groups to the solvent (in particular, the OH2 groups are directed toward the interior of the triple helix and completely inaccessible to water molecules), they are still able to form a significant number of hydrogen bonds with the solvent (∼2–4 per glucose unit). However, the number of hydrogen bonds per glucose unit is much larger for the lateral groups, with values between 5 and 8 that get close to the maximal hydrogen-bonding capacity of these residues (six acceptor and four donor sites). The triple helix formed by β(1→3)-D-glucan chains without lateral residues (curdlan) is essentially insoluble in water, and the tight interaction between the lateral residues and water molecules in schizophyllan is probably the main reason for the solubility of this polysaccharide in water (29–31). The number of solute-solvent hydrogen bonds involving core residues is significantly lower in system B compared to system A, probably because the (partially unwound) chain ends in the former system enjoy a larger exposure to solvent. As expected from the increased thermal motion, the total number of solute-solvent hydrogen bonds decreases when the temperature is increased. However, the differences between the number of hydrogen bonds involving core and lateral residues is essentially independent of the temperature.

TABLE 5.

Number of solute-solvent hydrogen bonds calculated for the nonperiodic schizophyllan fragment (system A) and the periodic schizophyllan fragment (system B) at 273 K, 350 K, and 450 K

	System A
	H-bonds		s [ns−1]		σ
	Core	Side	Core	Side	Core	Side
273 K	150 (4.2)	100 (8.3)	−7.50	−4.26	13.6	7.8
350 K	123 (3.4)	80 (6.7)	−1.73	−0.96	9.1	5.8
450 K	115 (3.2)	64 (5.3)	−1.40	−0.77	10.0	6.2
	system B
	H-bonds		s [ns−1]		σ
	Core	Side	Core	Side	Core	Side
273 K	111 (3.1)	101 (8.4)	−1.96	−0.27	9.3	5.3
350 K	91 (2.5)	86 (7.2)	−1.13	−1.04	8.6	5.5
450 K	79 (2.2)	72 (6.0)	0.58	0.23	9.7	6.0

Distinction is made between the solute donor and acceptor groups that belong to the main chains (core) and to the lateral residues (side). The results are reported as averages over the 5-ns trajectories (H-bonds; between parentheses: corresponding number of hydrogen bonds per glucose unit), together with the corresponding slope of a least squares fit regression line (s; number of hydrogen bonds as a function of time) and standard deviation (σ).

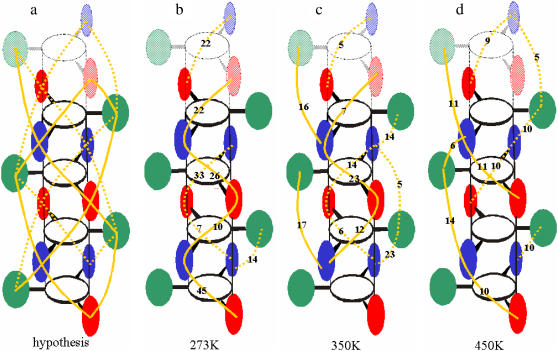
The structural model hypothesized for the ordered (low temperature) state of schizophyllan suggests the existence of water-mediated hydrogen-bonded bridges restricting the motional freedom of the lateral residues (40) (Fig. 6 a). The occurrences of such bridges (involving two intervening water molecules) during the simulations of the periodic schizophyllan fragment of system B are reported schematically in Fig. 6, b–d, for the three temperatures considered. Bridges with a single intervening water molecule were never observed in the simulations. At 273 K, water-mediated bridges are found almost exclusively between two of the three chains and present relatively high occurrence (7–45%). When the temperature is increased, the network tends to spread over the entire triple helix whereas the corresponding occurrences tend to decrease (5–23% at 350 K, 5–11% at 450 K). However, despite this moderate temperature dependence, the results of this analysis do not suggest the presence of an abrupt transition occurring between 273 K and 350 K.

FIGURE 6.

Locations and occurrences of water-mediated hydrogen-bonded bridges (with two intervening water molecules) between lateral residues, as hypothesized for the low-temperature state of schizophyllan (40) (a) and as observed from the simulations of the periodic schizophyllan fragment (system B) performed at 273 K (b), 350 K (c), and 450 K (d). The schematic representation of the schizophyllan triple helix is the same as in Fig. 1 d, except that the periodic images of the three bottom monomers are displayed (shaded) at the top of the cylinder. Bridges are indicated by a solid (dotted) orange line when they are located in front of (behind) the plane defined by the green lateral residues. The numbers indicate the occurrence of each bridge as percentage of the MD simulation time. A bridge between two lateral residues is assumed to be present when there exist at least two water molecules, each hydrogen bonded to one of the residues, that are also hydrogen bonded to each other. The calculations are based on the entire 5 ns of the simulation. Water-mediated hydrogen-bonded bridges involving a single intervening water molecule were never observed in the simulations.

CONCLUSION

In this work, explicit-solvent MD simulations of a schizophyllan fragment (complemented by simulations of the constituting tetrasaccharide monomer) were performed at three temperatures (273 K, 350 K, or 450 K) and with two different types of boundary conditions (finite nonperiodic or infinite periodic fragment) to provide a detailed picture (at the atomic level) of the conformational behavior of this polysaccharide in water. The simulation results evidence a remarkable stability of the schizophyllan triple-helical conformation (even at the artificially elevated temperature of 450 K), in agreement with experimental observations. Three main factors are identified that are likely to contribute significantly to this high stability: i), the intrinsic conformational preferences of the β(1→3)-linkage are respected in the triple-helical structure (limited conformational work for chain association); ii), this structure is stabilized at its center by a dense network of solvent-inaccessible hydrogen bonds involving the main-chain OH2 hydroxyl groups (acting as donors as well as acceptors) and the existence of multiple alternative hydrogen-bonding patterns; and iii), the structure is further stabilized by interchain hydrogen-bonding interactions involving main-chain and lateral residues. The extensive hydrogen bonding interactions between the lateral residues and the solvent are probably largely responsible for the solubility of schizophyllan in water (contrasting with the insolubility of curdlan, the analogous polysaccharide lacking lateral residues). The analysis of the effect of a temperature increase on the simulated properties leads to the following main observations: i), the triple-helical core structure remains essentially unaltered; ii), the distributions of lateral residue orientations relative to the helix axis become more homogeneous (among residues) and isotropic (apart from a clearly disfavored orientation with the plane of the glucose ring perpendicular to the helix axis); iii), the number of transitions around the glycosidic dihedral angles associated with the β(1→6)-linkages increases only marginally for the φ and ω angles but more significantly for the ψ angle; iv), the correlations between the orientations of neighboring lateral residues are essentially unaffected, remaining very low at all temperature considered; v), the hydrogen-bonding network of the polysaccharide is only weakly affected; and vi), the occurrences of water-mediated hydrogen-bonding bridges (with two intervening water molecules) decrease (but without abrupt transition between 273 K and 350 K). Taken together, these results do not provide any evidence for the order-disorder transition that has been postulated as a mechanism for the state change experimentally observed in schizophyllan at 7°C (280 K) in water (40). Although water-mediated hydrogen-bonded bridges are observed in the simulations, they are present at the three temperatures considered and insufficient to promote significant motional correlations between the lateral residues (even at the lowest temperature considered and for the closest-neighbor lateral groups).

The results here may be compared with those of previously reported MD simulations investigating schizophyllan (two 8-ns explicit-solvent simulations at 273 and 300 K using the GROMOS87/FFGMX force field and the SPC/E water model (45)). Two main observations of the latter study were i), the timescale associated with the orientational motion of the lateral residues (ω dihedral angle) is longer at 273 K (4.5 ns) compared to 300 K (2.4 ns); and ii), the fraction of the water molecules close (<0.35 nm) to specific glucose oxygen atoms and that have long (>20 ps) residence times is more sensitive to the temperature increase in the neighborhood of the lateral residues (decrease from ∼4.4% to 2.1%) compared to the core residues (∼7.7–5.2%). These two observations were interpreted as being consistent with the experimental low-temperature cooperative transition in schizophyllan and with the key role assumed to be played by the mobility and solvation of lateral residues during this transition. However, we believe that these observations alone are insufficient to claim that a transition has occurred between the two simulations, because i), an increase in the lateral-residue mobility and a decrease in the average water residence times may also simply reflect an (expected) increase in flexibility and water mobility upon increasing the temperature (without any transition being involved); and ii), the differences in populations of “long” residence-time water molecules are very small and actually nearly equal for core and lateral residues (∼2.4% in both cases). A (first-order) order-disorder transition involving the lateral residues and bound water molecules should be accompanied by a sudden change in entropy, i.e., in correlations between the motions of distinct lateral residues and within a possible water-mediated hydrogen-bonding network connecting them. These properties have been monitored in this study. The weak correlation between lateral residues observed in all simulations and the absence of abrupt transition in the number of water-mediated hydrogen-bonded bridges suggest that the system is essentially in the disordered state at the three temperatures considered (within the force field and simulation methodology employed).

The absence of an ordered state in the simulations, even at the lowest temperature considered (273 K), appears to be at odds with this experiment. Possible causes for this discrepancy are the following. First, the cooperative transition is experimentally strongly dependent on the molecular weight (as the molecular weight is decreased, the transition is shifted to lower temperature and becomes more gradual). However, the simulations here have been carried out using both a finite and an infinite (periodic) fragment, and the results found to be very similar. Second, there is (to our knowledge) no experimental information about the timescale on which the transition occurs, and the simulation time (5 ns) may be insufficient to permit relaxation to an ordered state at the lowest temperature considered (starting from a somewhat arbitrary initial conformation). Although the timescale associated with the orientational relaxation of the individual lateral residues is probably in the nanosecond range at 273 K (Table 3), the timescale associated with a global cooperative transition may be much longer and exceed the simulation lengths in this work, in which case the system could have been trapped in a long-lived (but not thermodynamically most stable) disordered state. Third, due to the approximate nature of the force field description, it may be that the transition would occur within the force field employed but in a slightly shifted temperature range. If this range was lower than the experimental range, the transition may have already occurred at the lowest temperature of 273 K. On the other hand, the simulation of a system at even lower temperatures may be problematic, due to a further reduction of the sampling efficiency. Fourth, the use of a relatively short cutoff distance (0.9 nm) in the MD simulations presented here and the absence of approximate long-range (e.g., reaction-field (58) or lattice-sum (59,60)) corrections for electrostatic interactions beyond this range, although consistent with the OPLS/TIP3P parameterization scheme (49,56), could represent a source of inaccuracy in the evaluation of direct (or water-mediated) interactions between lateral residues (in particular concerning the rotational diffusion of the lateral residues and their orientational correlations). For this reason, new simulations are currently being undertaken (using lattice-sum electrostatics and a GROMOS parameter set recently developed for the simulation of carbohydrates (62) with inclusion of long-range interactions) to assess the effect of a more accurate treatment of electrostatic interactions on the correlation between the motions of lateral residues and its temperature dependence.