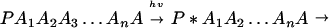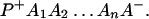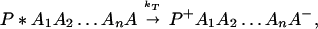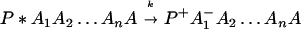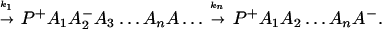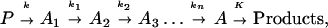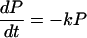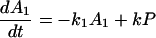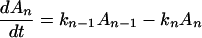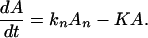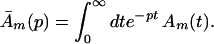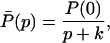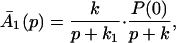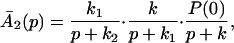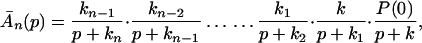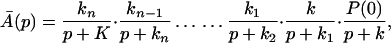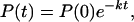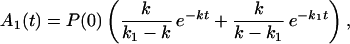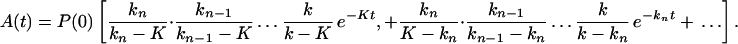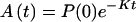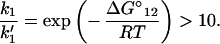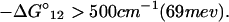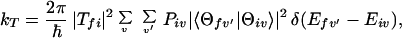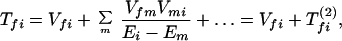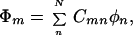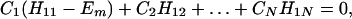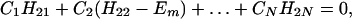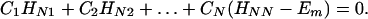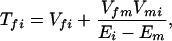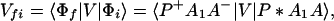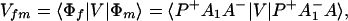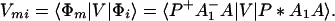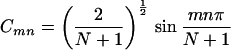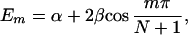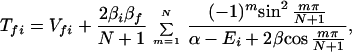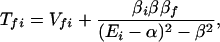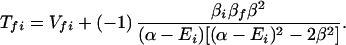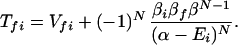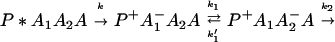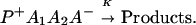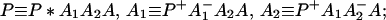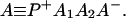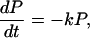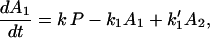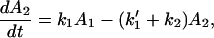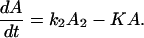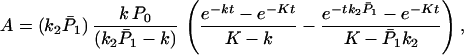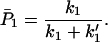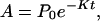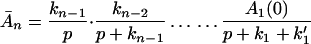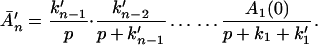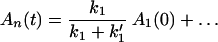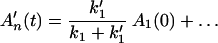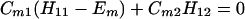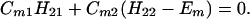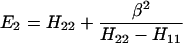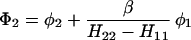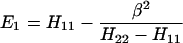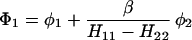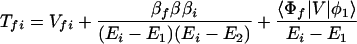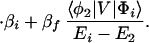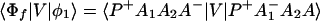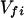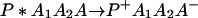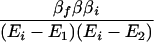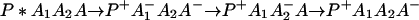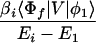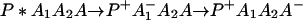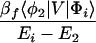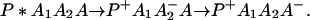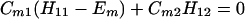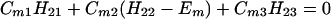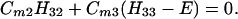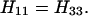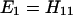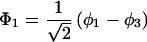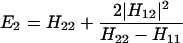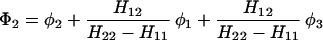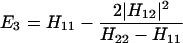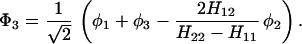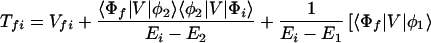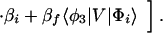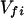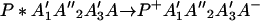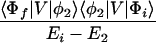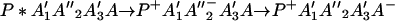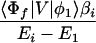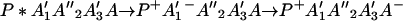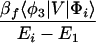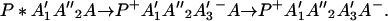Dynamical principles in biological processes

Abstract

The purpose of this paper is to propose certain dynamical principles in biological systems, which can be used to explain the effectiveness of charge transfer or excitation transfer in biological systems. Some of these systems are accessible experimentally.

1. INTRODUCTION

In this paper we shall discuss some dynamical principles that govern biological processes. For convenience of discussion, we use the biological electron transfer as an example. Of course, the same principles can be applied to other biological processes. The states involved in the process under consideration may be detected and characterized by experimental means such as ultrafast spectroscopy.

Electron transfer reactions play key roles in a great many biological processes, including collagen synthesis, steroid metabolism, immune response, drug activation, neurotransmitter metabolism, nitrogen fixation, respiration, and photosynthesis (1–4). The latter two processes are of fundamental significance because they provide most of the energy that is required for the maintenance of life. From the viewpoint of global bioenergetics, aerobic respiration and photosynthesis are complementary processes. The oxygen that is evolved by photosynthetic organisms is consumed by aerobic microbes and animals. Similarly, the end products of aerobic respiratory metabolism, (CO₂ and H₂O), are the major nutritional requirements of photosynthetic organisms. The global C, H, and O cycles thus are largely caused by aerobic respiration and photosynthesis. In other words, most biological processes consist of a series of dynamical events with different time scales. In this paper we attempt to find some general principles that strongly influence the biological processes.

2. THEORY

A typical model for biological electron transfer (ET) can be expressed as (1–4)

2-1

where the first step denotes photoexcitation, and the second step represents ET. This charge separation is of paramount importance. However, charge separation must be maintained, and therefore the energy-wasting back reaction must be minimized. Although in Eq. 2-1 we use the photoinduced ET as illustration, the theoretical treatment that follows can be easily generalized to other cases.

From Eq. 2-1 we can see that the ET can be accomplished either in one step

2-2

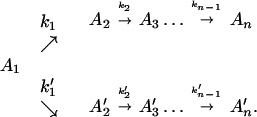
or in several steps (i.e., sequential ET),

2-3

The ET described by Eq. 2-2 usually is called the ET by super-exchange interaction (or ET through bonds). We first shall treat the model described by Eq. 2-3. For convenience we shall rewrite Eq. 2-3 as

2-4

where K represents the rate constant for any reaction associated with P⁺A₁A₂ … A_nA_nA⁻ after ET. For example, P ≡ P^*A₁ … A_nA, A₁ ≡ P⁺A₁⁻A₂ … A_nA, A ≡ P⁺A₁A₂ … A_nA⁻, etc.

Notice that

2-5

2-6

2-7

2-8

Here we have ignored the back transfers; the condition for its validity will be discussed later. To solve Eqs. 2-5 through 2-8 we shall use Laplace transformation;

2-9

It follows that

2-10

2-11

2-12

2-13

and

2-14

where P(0) denotes the initial concentration of P(t).

Carrying out the inverse Laplace transformation of Eqs. 2-10 through 2-14 it yields:

2-15

2-16

2-17

If K ≪ k_n, k_n−1 … k₁, k then in the time region of K t ∼ 1, Eq. 2-17 reduces to

2-18

Eq. 2-18 shows that for the case in which the ET is very effective, the intermediate steps involving ET do not have any effect on the chemical reaction (or other processes) described by K.

Next, we discuss the condition under which the reverse processes in Eq. 2-4 can be ignored. For example, if we let the rate constant for the reverse process A₂ → A₁ be k′₁, then

2-19

At room temperature, we find

2-20

It is well known that in photosynthesis charge separation is of paramount importance. The key problem is to maintain the charge separation, which involves minimizing the energy-wasting back reaction. Reaction centers contain an ordered array of secondary electron acceptors, (A₁, A₂, A₃ … ), that optimize the ΔG⁰ that occurs at each step described by Eq. 2-3. Thus the back reaction is circumvented by optimizing forward electron transfer that rapidly removes electrons from A₁⁻ (see Eq. 2-19). As the acceptors are separated by greater and greater distances from P⁺, the probability of the back electron transfer to P⁺ decreases.

Now we consider the one-step model described by Eq. 2-2. In this case, the quantum mechanical rate constant for k_T can be expressed as (5-9)

2-21

where the electronic matrix element T_fi is given by

2-22

and V_fi, etc. denote the ET matrix elements i.e., V_fi = 〈Φ_f|V|Φ_i〉. The first term in Eq. 2-22 V_fi describes the so-called direct ET or ET through space, whereas the second term T_fi⁽²⁾ in Eq. 2-22 describes the super-exchange ET or ET through bonds (or bridge groups). The summation over m in Eq. 2-22 covers all the possible intermediate states. In other words, all the possible paths are to be included in the calculation of T_fi⁽²⁾ (see Appendix).

We consider the calculation of T_fi⁽²⁾. In this case, we have

2-23

where, φ₁ ☰ P⁺A₁⁻A₂ … A_NA, φ₂ ☰ P⁺A₁A₂⁻A₃ … A_NA, etc. If we consider only the most effective path, it follows that

2-24

In particular if Φ_m = φ₁, i.e., φ₁ ☰ P⁺A₁⁻A, then

2-25

where

2-26

2-27

and

2-28

Other examples are discussed in the Appendix.

In most cases, no general expressions can be obtained except for the case where all the intermediate groups are equivalent. In this case, the theory of molecular exciton can be applied and we find

2-29

and

2-30

where m = 1, 2, … N, α = H₁₁H₂₂ … =H_NN, and β = V_nn+1 = V_nn−1.

It follows that

2-31

where β_i = 〈φ₁|V|Φ_i〉 and β_f = 〈Φ_f|V|φ_N〉. Here we have φ_i = P*A₁A₂ … A_NA. For N = 2,

2-32

and for N = 3,

2-33

For the case of (α−E_i)² ≫ β², Eq. 2-31 reduces to

2-34

It is important to note that the ET rate constant (see Eq. 2-21) can be separated into the electronic part |T_fi|² and the nuclear part, Σ_v Σ_v′ P_av|〈Θ_fv′|Θ_iv〉|²δ(E_fv′−E_iv). Although |T_fi|² will depend on the intermediate groups, the nuclear part that determines the temperature and free energy dependence of ET is relatively insensitive to the intermediate groups and is determined mainly by the donor and acceptor groups.

Proteins that function as electron transfer entities typically place their prosthetic groups in a hydrocarbon environment and may provide hydrogen bonds (in addition to ligands) to assist in stabilizing both the oxidized and the reduced forms of the cofactor. Metal-ligand bonds remain intact upon electron transfer to minimize inner-sphere reorganization (10, 11). Many of the complex multisite metalloenzymes (e.g., cytochrome c oxidase, xanthine oxidase, and nitrogenase FeMo protein) contain redox centers that function as intramolecular electron transferases, moving electrons to/from other metal centers that bind exogenous ligands during enzymatic turnover.

3. DISCUSSION

We show, in the following example, that the existence of one or more fast reverse processes in the same reaction does not favor ET,

3-1

For convenience, we let

3-2

Therefore

3-3

3-4

3-5

3-6

For the case in which k₁ and k′₁ are fast enough that the equilibrium is established in the ET processes, we obtain

3-7

where

3-8

Under the conditions P̄₁k₂ ≫ K, and kt ≫ 1, P̄₁k₂ ≫ t, Eq. 3-7

reduces to

3-9

which suggests that only in this case will the ET still be very effective.

Next we consider the branching effect.

3-10

Using Laplace transformation, we find

3-11

and

3-12

It follows that

3-13

and

3-14

That is, the branching effect is determined by the relative magnitudes of k₁ and k′₁.

4. CONCLUSION

In this paper we have used the ET process as means for discussing some dynamical principles associated with biological processes. We have compared the sequential ET process with the through bond (i.e., super-exchange) ET process, and discussed the conditions under which the sequential process is most effective. We also have shown that various paths associated with the super-exchange ET process can be represented diagrammatically. The effect of branching and reversible processes also has been presented.

ABBREVIATION

ET

electron transfer

Appendix

In this appendix we shall consider the N = 2 case and N = 3 case. For the N = 2 case, we have

A-1

A-2

The results for the case of equivalent intermediate groups are given by Eq. 2-32. Here we shall consider an interesting case in which the A₂ group has a much higher energy than that the A₁ group, i.e., H₂₂ ≫ H₁₁. In this case, we find

A-3

A-4

A-5

and

A-6

where β = H₁₂.

It follows that

A-7

Notice that

A-8

and

A-9

Eq. A-7 can graphically be expressed as follows:

In other words, each term in Eq. A-7 can be represented by a reaction path. To determine which path is most important, one has to examine the magnitudes of E_i − E_m and the ET matrix element β, 〈Φ_f|V|φ₁〉 and 〈φ|V|Φ_i〉.

Next we consider the N = 3 case. In this case we have

A-10

A-11

A-12

Suppose that

A-13

That is, we have PA′₁A”₂A′₃A.

We shall consider only the case in which A”₂ has the highest energy, i.e., H₂₂ ≫ H₁₁ = H₃₃. The approximate solution of Eqs. A-10–A-12 is given by

A-14

A-15

A-16

A-17

A-18

and

A-19

It follows that

A-20

Again Eq. A-20 can be graphically represented as follows