Using RNA secondary structures to guide sequence motif finding towards single-stranded regions

Abstract

RNA binding proteins recognize RNA targets in a sequence specific manner. Apart from the sequence, the secondary structure context of the binding site also affects the binding affinity. Binding sites are often located in single-stranded RNA regions and it was shown that the sequestration of a binding motif in a double-strand abolishes protein binding. Thus, it is desirable to include knowledge about RNA secondary structures when searching for the binding motif of a protein. We present the approach MEMERIS for searching sequence motifs in a set of RNA sequences and simultaneously integrating information about secondary structures. To abstract from specific structural elements, we precompute position-specific values measuring the single-strandedness of all substrings of an RNA sequence. These values are used as prior knowledge about the motif starts to guide the motif search. Extensive tests with artificial and biological data demonstrate that MEMERIS is able to identify motifs in single-stranded regions even if a stronger motif located in double-strand parts exists. The discovered motif occurrences in biological datasets mostly coincide with known protein-binding sites. This algorithm can be used for finding the binding motif of single-stranded RNA-binding proteins in SELEX or other biological sequence data.

INTRODUCTION

Genes that encode for RNA-binding proteins are abundant in eukaryotic genomes. RNA-binding proteins influence various pre-mRNA processing steps like splicing and editing, and regulate mRNA transport, localization, stability, translation by binding to cis-acting mRNA elements. These cis-acting elements are often located in the 5′ or 3′-untranslated regions (5′ or 3′-UTR) of mRNAs (1).

Many RNA-binding proteins are equipped with domains that bind single-stranded RNA like the RNA recognition motif (RRM) or the K homology (KH) domain (2,3). Although these proteins bind RNA in a sequence-specific manner, it was shown that the RNA secondary structure plays an important role in defining the binding site. For example, the mouse Prrp protein binds two motifs located in single-stranded conformation (4). The αCP-2KL and hnRNP K proteins, both containing three KH domains, bind single-stranded C-rich sequences (5) and the neuron-specific splicing factor Nova-1 recognizes TCAT sequence repeats located in the loop of a hairpin (6) (throughout the paper we write T instead of U also when referring to an RNA sequence).

A crucial step towards the understanding of the function of an RNA-binding protein is to elucidate the binding motif and to identify target RNAs. One common experimental approach to identify the binding motif is the ‘selection of ligands by exponential enrichment’ (SELEX) (7–9). The result of a SELEX experiment is a set of sequences that are bound by a specific protein and that contain one (or more) yet unknown binding motifs. To identify these motif(s), motif finder programs are usually applied to this set of sequences. Motif finder programs like MEME (10,11) or Gibbs sampler (12) only work at the sequence and not at the structure level. However, sequestering a sequence motif in a double-stranded RNA part has been shown experimentally to have a strong negative correlation with binding affinity (9) or even to abolish protein-binding (4,5). For example, the HuR protein influences mRNA stability by binding to the motif NNTTNNTTT (13). It has been demonstrated that HuR affinity correlates with the single-strandedness of its binding motif. Interestingly, small antisense oligonucleotides that are designed to bind outside the HuR motif can influence mRNA stability by modulating the secondary structure of the binding site (13,14). In light of these findings, it is desirable to include information about the secondary structure when searching for sequence motifs in SELEX data or other RNA sequences.

One can argue to use programs that search for sequence-structure motifs in RNA sequences (15–18) or programs that perform RNA sequence-structure alignments (19–21) for detecting the binding motif. However, these methods expect that the motif consists of specific sequence-structure elements, such as a stem–loop structure possibly with additional sequence constraints. Hence, they would not be able to find a sequence motif with a general structural property, such as being located in single-stranded parts of arbitrary structure elements. For example, these programs would fail to identify a sequence motif that is found in the loop of a hairpin or in the single-stranded part between two stems (5).

Here, we introduce an approach that searches for sequence motifs that are preferably located in any single-stranded conformation. This approach is implemented as an extension of the widely used MEME motif finder and is called MEMERIS—MEME in RNAs Including secondary Structures. MEMERIS precomputes values that characterize the single-strandedness of all putative motif occurrences. These values are then used to guide the motif search towards single-stranded regions. We provide an easy way for the user to adjust the importance of the single-strandedness. The performance of the approach is evaluated for artificial and real biological datasets and the results demonstrate that MEMERIS is able to accurately detect known protein-binding sites. The general principle can be utilized in the other motif finding applications, such as finding the binding motif of transcription factors.

MATERIALS AND METHODS

Measurement of single-strandedness

To characterize the single-strandedness of a substring in a given RNA sequence between positions a and b, MEMERIS allows the choice between two different measurements: (i) the probability that all bases in the substring are unpaired (denoted PU_a,b) (14,22) and (ii) the expected fraction of bases in the substring that do not form base pairs (denoted EF_a,b). PU_a,b is defined as

$$P{U}_{a,b}=e^{\frac{E^{\text{all}}-E_{a,b}^{\text{unpaired}}}{RT},}$$

where E^all is the free energy of the ensemble of all structures, $E_{a,b}^{\text{unpaired}}$ is the free energy of the ensemble of all structures that have the complete substring unpaired, R is the gas constant and T is the temperature. E^all and $E_{a,b}^{\text{unpaired}}$ are computed with the partition function version of RNAfold (23). For $E_{a,b}^{\text{unpaired}}$, we assure that the region a − b is unpaired by applying additional constraints (RNAfold parameter -C). Note that PU values can also be computed with RNAup (22). EF_a,b is defined as

$$E{F}_{a,b}=1-\frac{{\displaystyle \sum _{i=a}^b}{\displaystyle \sum _{j=1}^L}{p}_{i,j}}{b-a+1},$$

where L is the length of the RNA sequence, and p_i,j is the probability that base i and j are paired. The base pair probabilities p_i,j are also computed with the RNAfold program. These measurements have the advantage that they account for all possible secondary structures and that they abstract from specific structural elements. For all input sequences, the EF or PU values are precomputed for each possible motif start position.

Integrating secondary structure information (MEMERIS)

To integrate motif finding and the secondary structure information given as EF or PU values, we decided to extend the MEME motif finder. MEME is a program for finding motifs in a set of n unaligned nucleotide or protein sequences (denoted X = X₁,X₂, … , X_n) (10,11,24). A motif is described as a position-specific probability matrix (PSPM) Θ₁ = (P₁,P₂, … , P_W), where W is the length of the motif and the vector P_i the probability distribution of the letters at position i. A given input sequence X_i is modeled as consisting of different parts: (i) zero, one or more non-overlapping motif occurrences sampled from the matrix Θ₁ and (ii) random samples from a background probability distribution Θ₀ = P₀ for the remaining sequence positions. We denote Θ = (Θ₀,Θ₁). The number of motif occurrences depends on a user specified model. MEME considers three different models: (i) exactly one motif occurrence per sequence (OOPS model), (ii) zero or one motif occurrence per sequence (ZOOPS model) and (iii) zero or more motif occurrences per sequence (TCM model). To find a motif, MEME uses an expectation maximization (EM) algorithm to perform a maximum likelihood (ML) estimation of the model given the data. EM algorithms are commonly used for ML estimations where a part of the complete data are not given or ‘hidden’. In MEME, the complete data are the set of sequences (given data) and the start positions of the motif occurrences (hidden data). The hidden data are described by indicator variables Z_i,j with Z_i,j = 1 if a motif occurrence starts at position j in sequence X_i, and Z_i,j = 0 otherwise.

The EM algorithm iteratively (i) computes the expectation of the hidden variables using the current model (E-step) and (ii) performs a ML estimation of the model parameters on the joint probability of the complete data (M-step).

OOPS model

MEME makes no assumption about the start position of a motif occurrence in a sequence. Thus, MEME uses a uniform probability distribution $\forall jP(Z_{i,j}=1)=\frac{1}{m}$, where m = L − W + 1 is the number of possible starting points for a given motif length W in a sequence of length L (just for convenience we assume that all sequences have the same length). Since, there is exactly one motif occurrence per sequence in the OOPS model ${\sum }_{j=1}^{m}P(Z_{i,j}=1)=1$.

The additional information about the single-strandedness of each substring of length W can be considered as an informative prior about putative motif starts since single-stranded sequence parts are more likely to be real motif occurrences than parts that are sequestered in a double-stranded region. Therefore, we integrate the single-strandedness by replacing the uniform probability distribution by a distribution that depends on the EF or PU values. For convenience, we focus on PU values in the following, although everything below holds for EF values too. Instead of 1/m as in MEME, the prior probabilities for the OOPS model in MEMERIS are

$$P(Z_{i,j}=1\mid P{U}_i)=\frac{P{U}_{i,j}+\pi }{{\displaystyle \sum _{k=1}^m}(P{U}_{i,k}+\pi )},$$

where PU_i is the vector of PU values for sequence X_i and π is a user-given parameter that is used to smooth the distribution (Figure 1). The higher the PU value for position j, the higher is the prior probability of being a motif start position P(Z_i,j = 1∣PU_i). Despite X_i is used to compute the PU values, we assume that they are given as prior knowledge. By definition ${\sum }_{j=1}^{m}P(Z_{i,j}=1\mid P{U}_i)=1$, thus the underlying model assumption (one motif occurrence per sequence) remains unchanged. The prior probability distributions for two random sequences are shown in Supplementary Figure 1.

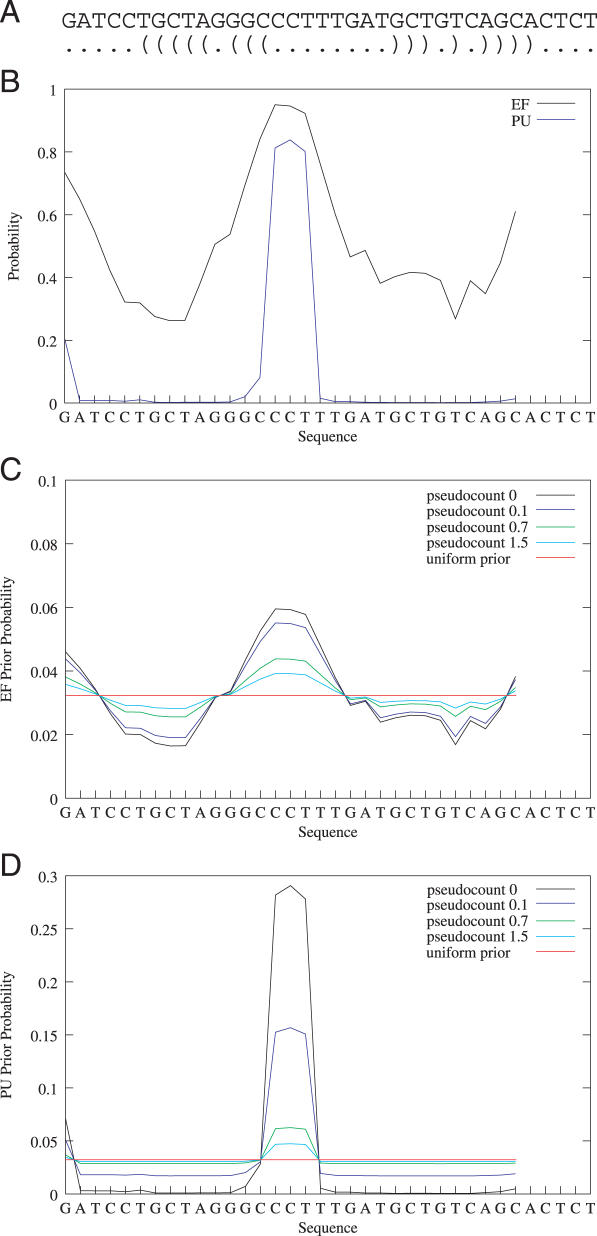
Figure 1.

Effect of the pseudocount on the prior probability distribution. The figure shows a randomly chosen sequence and its optimal secondary structure (A), the EF and PU values for a motif length of 6 nt (B), and the prior probability distribution for a OOPS/ZOOPS model using EF (C) and PU values (D) with different pseudocounts. Each data point represents the value for the motif starting at the respective position. The uniform prior refers to a prior probability distribution p = 1/31 (sequence length is 36 nt).

In iteration t of the EM algorithm, the expected values $Z_{i,j}^t$ of the hidden variables Z_i,j are computed given the parameters Θ^t. The E-step in MEMERIS is

$$Z_{i,j}^t=\frac{P(X_i\mid Z_{i,j}=1,{\Theta }^t)P(Z_{i,j}=1\mid P{U}_i)}{{\displaystyle \sum _{k=1}^m}P(X_i\mid Z_{i,k}=1,{\Theta }^t)P(Z_{i,k}=1\mid P{U}_i)}.$$

Assuming that a sequence X_i contains at positions j₁ and j₂ the same motif occurrence, only the prior probabilities constitute the difference for the expected values $Z_{i,j_1}^t$ and $Z_{i,j_2}^t$ in the E-step equation. Hence it is an advantageous property of the prior probabilities that the ratio of the PU values for j₁ and j₂ is preserved in $P(Z_{i,j_1}=1\mid P{U}_i)$ and $P(Z_{i,j_2}=1\mid P{U}_i)$ if π = 0, since

$$\frac{P(Z_{i,j_1}=1\mid P{U}_i)}{P(Z_{i,j_2}=1\mid P{U}_i)}=\frac{\frac{P{U}_{i,j_1}}{{\displaystyle \sum _{k=1}^m}P{U}_{i,k}}}{\frac{P{U}_{i,j_2}}{{\displaystyle \sum _{k=1}^m}P{U}_{i,k}}}=\frac{P{U}_{i,j_1}}{P{U}_{i,j_2}}$$

The pseudocount π is used to reduce this ratio. The higher π, the more this distribution equals the uniform distribution of MEME.

The M-step is not affected by the modified prior distribution (Supplementary Data). Except for the offset due to the computation of the secondary structure values, MEMERIS has the same runtime as MEME.

ZOOPS and TCM model

We use the same prior probability distribution as for the OOPS model to integrate the single-strandedness into the ZOOPS and TCM model. This is described in detail in the Supplementary Data.

Datasets

We tested MEMERIS on artifical and biological datasets. Each artificial test sequence consists of a random sequence part at the 5′ and 3′ end and a stem–loop structure that contains the single-stranded motif in the hairpin loop and the double-stranded motif in either side of the stem (Figure 2A). A random RNA sequence was generated by sampling from the uniform distribution (probability of 0.25 for A,C,G or T). We allowed base pairs between A and T, C and G, G and T. With probability of 0.5 we changed one position from the complementary part of the double-stranded motif so that it cannot base pair anymore. This mutation and the possibility of base pairs between G and T assure that the complementary part of the double-stranded motif is not a fixed string. The stem consists of 12 bp, the total length of the random sequence up- and downstream was set to 20 nt. The motif length is set to 6 nt which is a typical motif length for an RNA-binding protein. For test set 6, the motif length is 12 nt. For test set 2, the second PSPM was derived from the first one by randomly permutating the letter probabilities. This results in two PSPMs with an equal information content. The information content of a PSPM measures the strength of the motif and is computed as ${\sum }_{i=1}^W{\sum }_j{f}_{i,j}lo{g}_2\left(\frac{f_{i,j}}{q_j}\right)$ where f_i,j is the probability of the jth letter in the alphabet at position i of the motif and q_j is the background probability of the jth letter. All test sets are described in the Supplementary Data.

Figure 2.

Overview of the artificial test sets. (A) The figure shows an artificial sequence with a single-stranded motif (ssMotif, highlighted yellow) and a double-stranded motif (dsMotif, highlighted blue) together with its optimal secondary structure. The general scheme for constructing sequences is (i) to randomly sample an up- and downstream flank with a total length of 20 nt, (ii) to generate a stem of 12 bp that contains the dsMotif and (iii) to insert the ssMotif as the hairpin loop. The dsMotif can occur on either side of the stem. (B) The sequences in test sets 1–4 contain a ssMotif as well as a dsMotif. For test sets 1 and 3, we used a fixed string as the ssMotif (ACCGTA in this example, highlighted yellow) and a permutation of it as the dsMotif (TGACAC, blue). These motifs are sampled from two PSPMs for test sets 2 and 4. In test set 3, a single mutation is introduced in 25% of the ssMotifs. (C) Test set 5 contains only one motif in double-stranded conformation (sampled from a PSPM). (D) Sequences in test set 6 contain a 12 nt motif as a fixed string where only the 6 nt in the middle of the motif (yellow) are single-stranded. (E) Sequences in test set 7 contain either a ssMotif, a dsMotif or no motif (sampled from a PSPM). (F) Test set 8 contains sequences with a ssMotif and a dsMotif, with two ssMotifs, with one ssMotif, with one dsMotif, and without a motif (sampled from a PSPM). The percentages indicate to which fraction sequences with the respective features are contained in the dataset.

For the biological datasets, we used SELEX sequences and sequences of cis-acting RNA elements taken from the Rfam database (25). SELEX sequences were taken from the respective publications. For the Rfam entries, we used the sequences from seed alignment for the IRE and TAR Rfam and from full alignment for the PIE and SLDE Rfam. Redundant sequences with complete identity were taken only once.

MEMERIS was run with a pseudocount π of 0.1 (test sets 1–6 and 9) or 0.01 (test sets 7 and 8). We found MEMERIS to perform better if the EM starting point is relaxed (MEME parameter -spfuzz 2 was used for all tests). For MEME and MEMERIS, we used a uniform background frequency distribution since the sequences are too small for an accurate frequency estimation and the artificial sequences were sampled from a uniform distribution.

RESULTS

Measurement of single-strandedness

MEMERIS first computes EF or PU values for all substrings (i.e. all putative motif occurrences) of a fixed length W of the input sequences. Then, these values are used to guide the search for one or more motifs of length W towards single-stranded regions. The pseudocount π can be used to adjust the importance of the single-strandedness (Figure 1). Naturally, PU values (the probability that a complete substring is unpaired) are stricter than EF values (the fraction of the substring that is not involved in base pairing). Thus, MEMERIS using PU values will favor single-stranded regions stronger than MEMERIS using EF values (Figure 1 and Supplementary Figure 2).

While EF values are virtually independent of the length of the substrings, PU values drop if the length W increases since it is unlikely for a longer substring to have no base pairs (Supplementary Figure 2). Thus, the values for two substrings can only be compared if both substrings have the same length. However, the motif length for RNA-binding proteins is generally shorter than 10 nt which causes no problems with too low PU values.

Artificial test sets

In order to check whether the secondary structure information integrated into MEMERIS is able to guide the motif search towards single-stranded regions, we first performed extensive tests with artificial datasets.

OOPS model

First, we tested the OOPS model by comparing MEME with MEMERIS. Each of the following test sets consists of 20 sequences that are designed to contain motifs either as a fixed string or as a sample from a PSPM in single- and/or double-stranded conformation. All test sets and results are described in detail in the Supplementary Data.

We asked whether the EF or PU values influence which motif is found in the first pass, given that one motif is rather single-stranded (denoted ssMotif) while the other one is rather double-stranded (denoted dsMotif). This will be important if a user wants to discover only a single motif. The sequences in test set 1 contain both a ssMotif and a dsMotif as a fixed string (Figure 2B). In contrast to MEME, MEMERIS using EF or PU values detects the ssMotif first. These results are not affected by increasing the sequence length or sampling the motifs from two PSPMs (test set 2, Supplementary Data).

Next, we asked whether MEMERIS also detects the ssMotif in the first pass, even if the ssMotif is weakened by introducing a single mutation in 25% of its occurrences (test set 3) or by sampling from a PSPM with a lower information content (test set 4, Figure 2B). While MEME detects the stronger dsMotif in the first pass, MEMERIS identifies the weaker ssMotif first. To exclude that these findings are affected by some unknown bias in the motif or the sequences, we repeated all tests two times with new random sequences and different motifs and found consistent results (Supplementary Data). In general, PU values perform equally well or better than EF values in these tests.

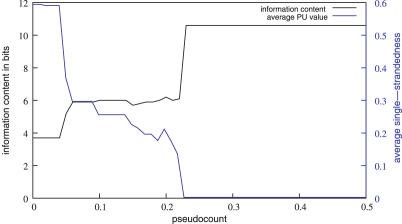
To illustrate the effect of varying the pseudocount π, we designed a test set containing only a dsMotif (test set 5, Figure 2C). MEMERIS using PU values detects the dsMotif, if the pseudocount π is higher than 0.22 (Figure 3). Lower values for π lead to the detection of other motifs with a higher average single-strandedness. Here, the average single-strandedness is the average of the PU values for all detected motif occurrences. These motifs differ from the dsMotif and are therefore weaker (indicated by a lower information content of the resulting motif matrix in Figure 3) and less significant. Thus, the pseudocount π provides an easy means for the user to adjust the importance of the secondary structures. In agreement with the finding that PU values are stricter than EF values, usage of the EF values results in the discovery of the dsMotif in this example independent of the pseudocount.

Figure 3.

Effect of varying the pseudocount. The figure shows the information content of the motif matrix found by MEMERIS in bits (black curve) and its average single-strandedness (average PU values of all motif occurrences, blue curve) for pseudocounts from 0 to 0.5 in steps of 0.01. Test set 5 that contain sequences with only one dsMotif (10.6 bits, average single-strandedness 0.003) was used. This motif is found by MEMERIS for a pseudocount greater than 0.22. In general, the lower the pseudocount, the higher is the average single-strandedness.

Next, we tested the ability of MEMERIS to identify the single-stranded part of a longer sequence motif as the potential protein-binding site. We designed a test set containing a 12 nt motif whose three positions at the beginning and at the end form base pairs (test set 6, Figure 2D). Setting the motif width to 6 nt, MEME identifies the first 6 nt of this 12 nt motif, while MEMERIS exactly finds the 6 nt that are not involved in base pairing.

We conclude that MEMERIS preferably selects single-stranded motif occurrences and that it is able to identify a weaker over a stronger motif if the average single-strandedness is sufficiently higher.

ZOOPS and TCM model

In addition to identifying the motif locations, the ZOOPS and TCM model have to solve a further question: how many motif occurrences are in the dataset? We intended to integrate the secondary structure information in a way that guides but not restricts the motif search to single-stranded regions. Therefore, this additional question is only marginally affected in MEMERIS. Up to which single-strandedness a motif occurrence is believed to be a real protein-binding site is hard to determine in an automatic manner since this would necessitate statistical measures that take the motif sequence and its structural properties into account. Furthermore, the requirement for single-strandedness certainly depends on the dataset and on the (putative) binding-protein. However, we propose a simple procedure that requires the user to decide according to the motif sequence and the EF or PU values how many occurrences are there in the given dataset.

1. Run MEMERIS using a rather high pseudocount π, which mimics a MEME run and leads to the detection of motif hits nearly independent of the single-strandedness.

2. Inspect the sequence and the single-strandedness of all detected motif hits and determine the number of motif occurrences.

3. Run MEMERIS again with a low pseudocount π and a fixed number of motif occurrences.

The second MEMERIS run with a fixed number of motif occurrences should result in the identification of single-stranded occurrences and thus a refinement of the motif matrix. We tested this for the ZOOPS model on a dataset that contains sequences with either (i) one ssMotif, (ii) one dsMotif or (iii) without a motif (test set 7, Figure 2E). For the TCM model, we applied this procedure to a dataset consisting of sequences having either (i) one ssMotif and one dsMotif, (ii) two ssMotifs, (iii) one ssMotif, (iv) one dsMotif or (v) no motif (test set 8, Figure 2F). Since point 2 involves manual inspection, we have to avoid any bias arising from our knowledge about the PSPM and the dataset. Thus, we assessed the number of motif occurrences in an automatic manner by simply counting the number of motif hits having an EF or PU value greater than 0.5. Comparing MEME and MEMERIS with a given number of motif hits, MEMERIS identifies the single-stranded motif occurrences, even if this leads to a lower information content of the motif (Supplementary Data). One example for the TCM model is shown in Figure 4. Again PU values often lead to better results than EF values.

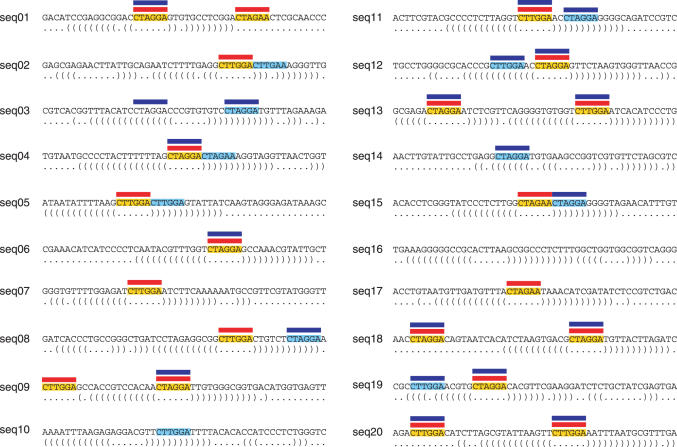
Figure 4.

Comparison of MEME and MEMERIS for test set 8 (testing the TCM model). The figure shows 20 sequences that contain ssMotifs (highlighted yellow) and/or dsMotifs (highlighted light blue). The optimal structure is shown below each sequence. Red and blue bars indicate the position of the motif occurrences found by MEMERIS and MEME, respectively. While MEMERIS detects all ssMotifs and no dsMotif leading to an information content of the motif matrix of 10.4 bits, MEME identifies a stronger motif (11.1 bits) but detects eight dsMotif occurrences. MEMERIS results are shown for PU values and a pseudocount of 0.01. The number of motif hits was set to 21 for MEME and MEMERIS.

Motifs in single-strands of arbitrary structures

The above test sets often contain the ssMotif in the loop of a hairpin and the dsMotif in the stem. In contrast to programs that search for RNA sequence-structure elements, MEMERIS should be able to identify a single-stranded motif regardless of the structural element in which it is contained. We designed a test set where the motif is located either (i) in a hairpin loop, (ii) in an internal loop, (iii) in a single-stranded part of a multiple loop or (iv) between two stems (test set 9, Supplementary Data). While MEMERIS and MEME clearly detect the motif, two RNA motif finders, RSMatch (17) and CMfinder (18), (that are not designed for this task) are not able to discover any motif in this test set.

Biological test sets

SELEX data

We tested MEMERIS on SELEX data that are found to contain sequence motifs in single-stranded conformations. Buckanovich and Darnell (6) identified 33 TCAT or ACAT repeats in the hairpin loops of the SELEX winner sequences of the neuron-specific splicing factor Nova-1. Searching for 33 motif occurrences with a TCM model and a motif length of 4 nt, MEMERIS exactly identifies those 33 TCAT and ACAT hits that are described in (6). MEME also detects the correct motif but at least two of its motif hits are located outside the hairpin loop and are presumably no Nova-1 binding sites (Figure 5). We also compared MEME and MEMERIS for the SELEX datasets of the nucleolin protein (26), the Drosophila ortholog of human SRp55 (27), and the αCP-2KL protein (5) and found very similar results for both programs which is due to the fact that the known motif is the strongest one in these datasets (data not shown).

Figure 5.

Comparison of MEME and MEMERIS for the SELEX sequences of the Nova-1 protein. The figure shows the sequences and labels of the individual clones described in (6). The random oligonucleotides are in blue letters. The optimal secondary structure is shown below each sequence. The primer binding sites (black letters) were included in the RNA secondary structure prediction but not in the motif search. Yellow bars represent the TCAT and ACAT motifs identified in (6). Blue and green bars indicate the position of the motif hits found by MEME and MEMERIS, respectively. The motif matrix found by MEME has an information content of 7.6 bits, the MEMERIS motif matrix has 7.4 bits. MEME and MEMERIS were run with the TCM model and the number of motif hits was set to 33. MEMERIS results are shown for PU values and a pseudocount of 0.01.

Protein-binding sites in cis-acting RNA elements

Cis-acting elements in the UTR regions of mRNAs determine mRNA stability and translation efficiency by providing binding sites for regulatory proteins. These elements are often conserved at the sequence and secondary structure level, thus they are fundamentally different compared to the randomly generated SELEX sequences. To test the ability of MEMERIS to identify protein-binding sites in the larger context of conserved sequence-structure elements, we selected cis-acting RNA elements having a defined secondary structure and a known protein-binding site from the Rfam database (25).

The iron responsive element (IRE, RF00037) located in the 5′-UTR of mRNAs is essential for the expression of proteins that are involved in the iron metabolism (28). The IRE consists of a stem–loop structure and the nucleotides in the hairpin loop were found to be essential for binding of iron-regulatory proteins. MEMERIS detects the hairpin loop as the motif hit in all sequences (10 bits), while MEME discovers a stronger motif (10.8 bits) that is moved to one position upstream. In addition, MEME identifies a different motif occurrence in the upstream stem in two sequences (Supplementary Data).

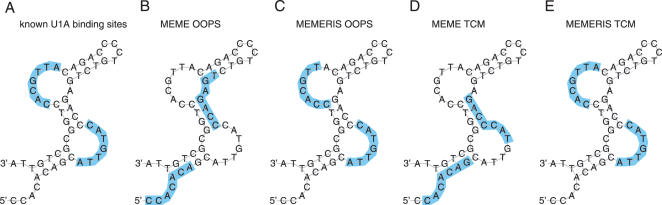
The polyadenylation inhibition element (PIE) contains two binding sites for U1A proteins (29). U1A binding leads to an inhibition of the poly(A) polymerase and a reduced mRNA stability and translation efficiency due to a shortened poly(A) tail. U1A autoregulates itself by binding to a PIE element in its own 3′-UTR. PIE consists of a stem structure with two asymmetric internal loops that represent U1A binding sites. Both internal loops are identified by MEMERIS using the TCM model or searching for two motifs with the OOPS model (Figure 6). MEME detects stronger motifs in both models that are different from the known binding sites.

Figure 6.

Results of MEME and MEMERIS for the PIE Rfam (RF00460) dataset. The figure shows the consensus sequence and structure of the PIE RNA. The U1A protein binds the single-stranded sequences in the two asymmetrical internal loops in a cooperative manner (A). Using the OOPS model, MEME finds two motifs (14 and 13.3 bits, respectively) that do not overlap the real binding site (B) while MEMERIS finds the real upstream binding site exactly (11.8 bits) and the downstream site (10.5 bits) with a shift of one position. (C) Since both individual binding sites are very similar, we used the TCM model to search for a motif with two occurrences in each sequence. Again MEME finds a different motif (11.6 bits) (D) while MEMERIS detects the correct protein-binding sites (10.7 bits) (E). The known binding sites and the predicted motifs are highlighted in blue. The motif length was set to 7 nt. For MEMERIS, the PU values were used with a pseudocount of 0.01.

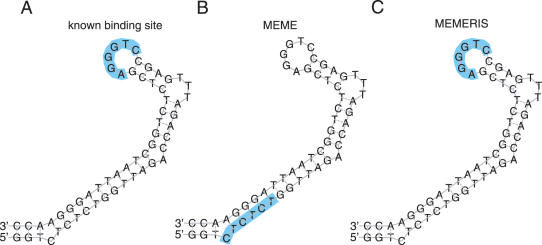
The trans-activation response (TAR) element of the HIV-1 virus is required for efficient transcription (30,31). The hairpin loop is bound by a heterodimer consisting of Tat and CycT1. MEMERIS clearly identifies the motif in the hairpin loop, while MEME detects a stronger motif located in the stem (Figure 7). The Tat protein also binds the pyrimidine-rich 3 nt bulge loop of the TAR element. However, neither MEMERIS nor MEME is able to identify this binding site because this motif is too degenerate and in several TAR elements this bulge consists of only 2 nt.

Figure 7.

Results of MEME and MEMERIS for the TAR Rfam (RF00250) dataset. The figure shows the consensus sequence and structure of the TAR element. The hairpin loop is bound by the Tat protein (A). We searched for one binding site in each sequence (OOPS model) with MEME (B) and MEMERIS using PU values (C). MEME detects a motif (12 bits) that does not overlap the known binding site, while MEMERIS identifies the binding site, although the respective motif is noticeable weaker (10 bits). The known binding sites and the predicted motifs are highlighted in blue. The motif length was set to 6 nt. For MEMERIS, the PU values were used with a pseudocount of 0.01.

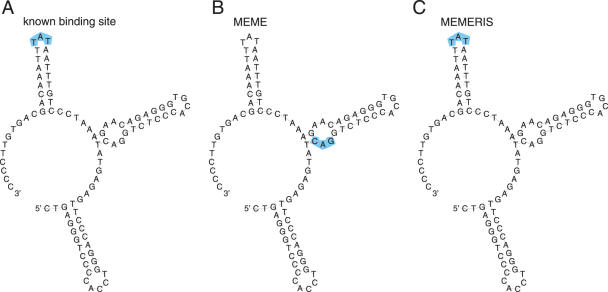
The stem–loop destabilizing element (SLDE) consists of three stems located in the 3′-UTR of G-CSF mRNAs and is used to regulate the stability of the mRNA (32). The hairpin loop sequence of the third stem is essential for the function of this element and assumed to be bound by an unknown protein. Again, MEMERIS detects this loop as the motif, while MEME finds a different motif (Figure 8).

Figure 8.

Results of MEME and MEMERIS for the SLDE Rfam (RF00183) dataset. The figure shows the consensus sequence and structure of the SLDE element. The hairpin loop of the essential third stem is bound by an unknown protein factor (A). MEME detects a CAG motif which does not overlap the binding site (B). In contrast, MEMERIS identifies the TAT sequence of the hairpin loop as the motif (C). Both motif matrices have an information content of 6 bits. The known binding sites and the predicted motifs are highlighted in blue. The motif length was set to 3 nt. For MEMERIS, the PU values were used with a pseudocount of 0.01.

DISCUSSION

RNA-binding proteins often bind in a sequence-specific manner to RNAs but prefer a characteristical structural conformation of the binding site. In several examples, this structural conformation was shown to be either the sequence of a hairpin loop (5,6,26,30), the sequence of an internal loop (29,30), or the single-stranded sequences between two stems (5). Furthermore, the sequestration of the binding motif in a double-strand was found to abolish protein binding (13). Thus, RNA secondary structure properties are important for distinguishing real from spurious protein-binding sites and should be considered when searching for the binding motif of a protein.

Currently available motif finders either work only at the sequence level or search for larger structural elements like a stem with a bulge loop as in case of the IRE element (16–18). Here, we present a method for simultaneously searching a sequence motif and integrating information about the secondary structures. To abstract from specific structural elements, we compute a single value for each substring that measures its single-strandedness. This measurement is based on the base pair probabilities, thus avoiding the more inexact consideration of only the optimal or an arbitrary number of suboptimal secondary structures.

Performing tests with artificial and biological data, we demonstrate that MEMERIS is able to identify single-stranded sequence motifs which often represent the known protein-binding motif. To maintain a secondary structure, a mutation in a base pair often requires a compensatory mutation. This may result in a stronger selection pressure to double-stranded compared to single-stranded sequence regions. Consistently, RNA-binding proteins may bind a rather degenerate consensus sequence (7). Therefore, it is a valuable property that MEMERIS is also able to select a weaker over a stronger motif if this motif has a higher average single-strandedness (exemplified in Figures 6 and 7). We conclude that MEMERIS is useful for motif detection in SELEX or other RNA sequences or for predicting protein-binding sites in cis-acting RNA elements. The MEMERIS source code is available at http://www.bioinf.uni-freiburg.de/~hiller/MEMERIS/.

The general principle to include prior knowledge about the motif start sites can be extended to other applications. It is straightforward to search for sequence motifs in double-stranded structure parts, e.g. by computing the expected fraction of bases that are paired (1-EF) or the probability that the complete motif occurrence is paired. Moreover, it might be advantageous to guide the motif search to loosely defined structural elements, such as arbitrary hairpins or tRNA-like structures. The respective probabilities can be computed by means of RNA shapes (33). A further application can be the search for transcription factor binding sites in DNA promotor sequences. If information is available that a DNA motif is preferably located promotor-proximal, the prior start site distribution can be adjusted to have higher probabilities for the 3′ sequence ends of promotor sequences. Since highly condensed DNA regions are inaccessible to transcription factors (34), prior knowledge about chromatin condensation and higher-order chromosomal structures can be used to prevent the detection of motifs in inaccessible regions.

In future, it would be desirable to automatically determine the number of single-stranded motifs in a ZOOPS or TCM model. This is challenging because the degree to which a real binding site has to be single-stranded certainly depends on the respective protein. Furthermore, this requirement for single-strandedness may be affected by the presence of RNA helicases that are involved in several important processes like splicing and translation. Finally, the statistical models need to be extended to account for the sequence and the secondary structure context of a motif.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online.