Carbon nanotube-based synthetic gecko tapes

Abstract

We have developed a synthetic gecko tape by transferring micropatterned carbon nanotube arrays onto flexible polymer tape based on the hierarchical structure found on the foot of a gecko lizard. The gecko tape can support a shear stress (36 N/cm²) nearly four times higher than the gecko foot and sticks to a variety of surfaces, including Teflon. Both the micrometer-size setae (replicated by nanotube bundles) and nanometer-size spatulas (individual nanotubes) are necessary to achieve macroscopic shear adhesion and to translate the weak van der Waals interactions into high shear forces. We have demonstrated for the first time a macroscopic flexible patch that can be used repeatedly with peeling and adhesive properties better than the natural gecko foot. The carbon nanotube-based tape offers an excellent synthetic option as a dry conductive reversible adhesive in microelectronics, robotics, and space applications.

Flexible adhesive tapes are indispensable in our daily lives, whether it is to leave a note to a friend or to seal packages. However, we rarely hang heavy objects on a wall using these tapes because the stickiness is time- and rate-dependent. The viscoelastic tapes do not work under vacuum, such as space applications, and where repeated attachment and detachment is required, such as wall-climbing robots. Nature has found an alternate solution to stick to surfaces without using sticky viscoelastic liquids. Natural selection has developed the wall-climbing lizard's foot (Fig. 1A) in a hierarchical structure, consisting of microscopic hairs called setae, which further split into hundreds of smaller structures called spatulas (Fig. 1B) (1–4). On coming in contact with any surface, the spatulas deform, enabling molecular contact over large areas, thus translating weak van der Waals interactions into enormous attractive forces (4). There have been several theoretical models to elucidate the mechanism of gecko adhesion (5). However, it is not clear why nature has developed this intricate hierarchical structure of micrometer-size setae and nanometer-size spatulas on the gecko foot, instead of covering the whole feet with only setae or spatulas. Many synthetic structures using uniform polymer pillars and in some cases hierarchical structures (6, 7) have been constructed before, although the performance of these structures has not been as good as natural gecko (8, 9). One limitation of these polymer pillars with a high aspect ratio is that they are mechanically weak in comparison to keratin used in the natural foot-hairs.

Fig. 1.

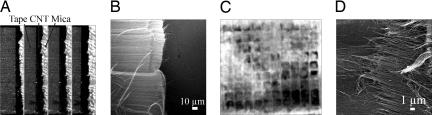
Microfabricated aligned multiwalled carbon nanotube setae and spatulas. (A) Optical picture of gecko foot showing that the setae are arranged in many lobes along the foot. (B) SEM image of natural gecko setae terminating into thousands of smaller spatulas (4). (E–H) SEM images of synthetic setae of width 50 (E), 100 (F), 250 (G), and 500 (H) μm. (C and D) Side views (C) and higher-magnification SEM image (D) of the 100-μm setae.

Here we have replicated the multiscale structure of setae and spatulas using microfabricated multiwalled carbon nanotubes and found that not only nanometer-length scales of spatulas (individual carbon nanotubes) but also micrometer-length scales of setae (patterns of carbon nanotubes) are important to support large shear forces. Our results show that a 1-cm² area of the carbon nanotube patterns transferred on a flexible tape (referred as a “gecko tape” hereafter) supports 36 N. These shear forces are a factor of four times higher than the natural gecko foot-hairs, a factor of 10 higher than polymer pillars (8, 9), and a factor of four times higher than unpatterned carbon nanotube patches on silicon (10). Similar shear forces are obtained on both hydrophilic (mica and glass) and hydrophobic (Teflon) surfaces. These synthetic gecko tapes show shear and peeling properties that are similar to those found on gecko feet and offer an excellent synthetic option as a dry conductive reversible adhesive in microelectronics, robotics (11), and space applications.

Results and Discussion

The natural gecko foot (Fig. 1A) has 25-μm-diameter setae arranged in many lobes along the foot, and the SEM image in Fig. 1B shows 100- to 200-nm-diameter spatulas (4). The synthetic setae and spatulas fabricated using aligned carbon nanotubes are shown in the SEM images in Fig. 1 C–H. Fig. 1 C and D shows the picture of carbon nanotubes on a flexible gecko tape to illustrate the similarity in the natural and synthetic hairs. We have also fabricated different sizes of the carbon nanotube patches ranging from 50 to 500 μm in width (Fig. 1 E–H). The synthetic setae consist of thousands of synthetic spatulas, which are individual bundles of aligned carbon nanotubes (average diameter of 8 nm) shown at higher magnification in Fig. 1D. We have chosen carbon nanotubes to construct the synthetic setae because our recent atomic force microscopy results show that the vertically aligned carbon nanotubes have strong nanometer-level adhesion with a silicon tip (12) and have excellent mechanical properties. The synthetic setae were fabricated by using a conventional photolithography patterning process. The catalyst (Fe and Al) was deposited on a silicon substrate as patches with dimensions shown in Fig. 1 D–H. The carbon nanotubes were grown at 750°C using a mixture of ethylene and hydrogen gas, and the carbon nanotubes grew only in the areas covered with the catalyst. The length of carbon nanotubes was controlled by the reaction time and was ≈200–500 μm for the structures fabricated for this study.

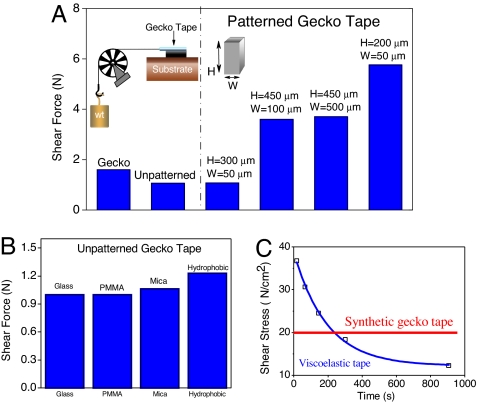
To measure the macroscopic adhesion forces, small areas of flexible gecko tapes were pressed against a smooth mica sheet using a cylindrical roller. This is equivalent to a pressure of 25–50 N/cm² to deform the gecko tape and the carbon nanotube structures to achieve good contact between the tape and the substrate. The actual shear measurements were done under no external normal load as shown in Fig. 2A Inset. We have chosen this geometry to compare these synthetic materials with the force measurements on live geckos that were done by using an almost vertical geometry by Irschick et al. (13). This is equivalent to dragging the gecko almost parallel to the surface. The shear force for the unpatterned gecko tape for a 0.16-cm² patch is shown in Fig. 2A. We have compared these shear forces with the force supported by the live geckos calculated in the units of force supported by a 0.16-cm² area (10 N/cm² × 0.16 cm²). The forces supported by the synthetic structures are comparable to the live gecko measurements. The force supported by 0.12-cm² and 0.25-cm² patch was 1.2 N and 1 N, respectively, and the shear force does not increase with the area of the tape. This is a disadvantage because we cannot scale up the weight supported by the gecko tape by increasing the contact area.

Fig. 2.

Weight supported by synthetic gecko tapes is compared with the force supported by a live gecko for a 0.16-cm² area. (A) The shear force supported by unpatterned and patterned gecko tapes on mica substrate. Inset shows the geometry we used in the shear measurements. (B) The shear stress for 0.16-cm² unpatterned gecko tape on mica, glass, poly(methyl methacrylate), and poly(octadecyl acrylate) (comb polymer) surfaces. The surface energies of mica and glass are >100 mJ/m². The surface energy of poly(methyl methacrylate) is ≈40 mJ/m², and that of comb polymer is 20–25 mJ/m². (C) Different weights (y axis) were suspended on a viscoelastic tape using shear geometry, and the maximum time it can support that particular weight is plotted on the x axis. As a comparison, the gecko tapes (0.16-cm² area and 500-μm setae) support 20 N/cm² shear force, recorded over a period of 8–12 h, without any cohesive break.

To support larger shear forces, micrometer-size setae are required in addition to nanometer-size features of carbon nanotubes. Fig. 2A shows the measured shear force for patterned carbon nanotube (sizes shown in Fig. 1 D–H) tapes of 0.16 cm² total area. Using patterned surfaces with features of 50 and 500 μm wide, we obtained a factor of four to seven times higher shear force as compared with the unpatterned surfaces of similar area. The shear force supported by the 100- to 500-μm patches is 3.7 N, which is two to three times higher than the natural gecko. The advantages of patterns became less prominent on reducing the patch size to 50 μm (and 300 μm in height) because a decrease in the ratio of the width to its height makes setae mechanically weak. When we use a smaller height of the 50-μm setae (200 μm), we measure the shear force of 5.8 N, a factor of four times higher than the natural gecko.

Similar to the natural gecko, these synthetic gecko tapes stick to both hydrophobic and hydrophilic surfaces. Fig. 2B shows the shear forces supported by the unpatterned gecko tape (0.16 cm² area) on hydrophilic surfaces such as mica and glass (water wets both surfaces). We have also shown in Fig. 2B the shear stress of a partially hydrophobic surface (coated with polymethylmethacrylate that shows a water contact angle of 70–80°) and a very hydrophobic surface [coated with poly(octadecyl acrylate) comb polymer that shows a water contact angle of 110°]. Surprisingly, the measurements on rough Teflon surfaces also show large shear stress that is comparable to that obtained for hydrophilic surfaces. The shear stress is similar for both hydrophobic and hydrophilic surfaces, and this finding supports the idea that van der Waals forces may play an important role in the shear mechanism (4, 14).

Interestingly, the shear forces supported by the gecko tape are very stable and time-independent as shown in Fig. 2C. The weight supported by the patterned gecko tape is stable for many hours (we have measured this for a period of 8–12 h). In contrast, a Scotch adhesive tape shows strong time dependence as expected for viscoelastic materials (Fig. 2C). The viscoelastic tape is stronger than the synthetic gecko tape when it is measured for a short time and much weaker than the gecko tape when compared at long times. If the gecko foot-hairs were made of viscoelastic adhesives, then the gecko would require much stronger muscles to move rapidly up the wall, and it would not be able to support its own weight if it remained stationary.

To understand why these carbon nanotubes support such large forces, we show a series of optical and SEM images during loading and after the cracks have propagated through the sample. In Fig. 3A we show four cropped optical images of the edge of the tape under increasing load. The black regions are the carbon nanotubes sticking out of the edges and making contact with the substrate. On application of the shear load one can observe the increase in the width of the carbon nanotube edge showing that the tape and the carbon nanotubes are deformed and that the crack propagation is pinned at the interface. The SEM picture of the edge after pressing the tape in contact with the substrate is shown in Fig. 3B. The stretching of the tape increases with an increase in load, and after reaching a certain critical load a catastrophic rupture is initiated; the failure is cohesive, and carbon nanotube residues are left behind on the mica surface (Fig. 3C). No carbon nanotube residue is left behind on the mica substrate when the tapes are peeled at different angles (in a peeling geometry rather than shear geometry), similar to how a gecko walks, and the results are discussed later. This cohesive failure indicates that the interfacial adhesion strength is sufficient to support large shear forces. The 50- to 500-μm patterned surfaces are important in supporting larger shear stress and increasing the total shear force supported by the tape by increasing the contact area (similar force/area values were obtained for gecko tapes of 0.16 cm² and 0.25 cm² area).

Fig. 3.

Optical and SEM images of the carbon nanotubes during loading and after the crack has propagated through the sample. (A) Four optical pictures of the tape (5 mm × 5 mm area) cropped to show only the edges of the tape under different shear loads (20, 70, 140, and 190 g). The black region is the compressed carbon nanotubes sticking out of the edges of the tape and making intimate contact with the substrate. (B) A SEM picture of the edge of tape where we observe the deformation of the carbon nanotubes after it has been pressed in contact with the mica surface. The edge observed in the middle of the SEM picture is the boundary between the carbon nanotubes and the substrate. (C) The optical picture of the mica surface showing the carbon nanotubes left on the mica surface after the crack has propagated. (D) SEM image of the carbon nanotubes left behind on the mica surface.

The SEM image of the carbon nanotube residues remaining on the mica surface is shown in Fig. 3D. The aligned and broken strands of the carbon nanotube bundles indicate that there is large energy dissipation in the cohesive failure. In the case of unpatterned gecko tapes, the failure was interfacial with very little carbon nanotube remaining on the mica surface after peeling. The optical and SEM images show that the 50- to 500-μm patches deform and hinder the crack growth. In fracture mechanics it has been demonstrated that the resistance to the propagation of cracks is very important in increasing the toughness of the materials (15). In the case of adhesive tapes, Kendall has shown that the peeling strength of tapes with patches of different stiffness or thickness can be much higher than the tapes with uniform thickness and stiffness (16). Chaudhury and coworkers have shown that 100- to 200-μm patches on poly(dimethylsiloxane) sheets increases the peeling force by a factor of 10–20 in comparison to a unpatterned poly(dimethylsiloxane) sheet (17). We postulate that the mechanism in all of these cases, including the patterned gecko tape, is to stop, deviate, and reinitiate the crack propagation in comparison to materials with uniform properties (also referred to as the Cook–Gordon mechanism) (15). It is interesting to note that the enhancement in shear stress in the case of natural gecko, poly(dimethylsiloxane) patterns, and synthetic gecko tapes are observed for sizes of patterns that are comparable to the thickness or height of the setae.

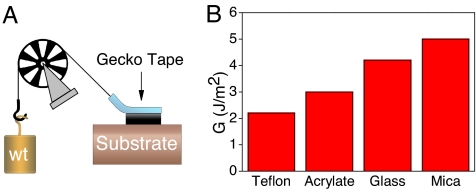
We have also measured the force required to peel the gecko tapes at different angles as shown in the Fig. 4A. This peeling measurement is important for two reasons. First, the peeling resistance has to be much smaller in comparison to shear forces in mimicking the gecko feet. The gecko moves or gets unstuck from a surface by uncurling its toes. This is necessary because, at those peeling angles, the peeling forces are weak and the gecko can effortlessly move on a vertical surface by using its foot-hairs repeatedly without any damage. Second, the peeling force divided by the width of the tape (F/w) provides us an approach to determine the energy of detachment (G). The 500-μm patterned synthetic tape peels off the mica substrate with an adhesive force/width of only 16 N/m at a 45° angle, 20 N/m at a 30° angle, and 96 N/m at a 10° angle. This peeling process at angles >10° does not involve any breaking or transfer of the carbon nanotube on the substrate, and the synthetic gecko tape can be reused many times without damage. The low peeling forces at a non-zero angle are due to the preexisting crack at the peeling front. A similar effect is also observed if you peel off the viscoelastic tapes from substrates, where the shear forces are much higher than the peeling forces at non-zero angles (18).

Fig. 4.

Peeling measurements of the gecko tapes on various substrates. We performed the peeling measurements at different angles using the setup shown in A. (B) The energy of detachment, G (J/m²), plotted at a peeling angle of 45° on various substrates.

We can calculate the energy of detachment (G) using G = F(1 − Cosθ)/width (18), where F is the peeling force and θ is the peeling angle. This equation is for peeling angles ≥45°, and the elastic stiffness of the gecko tape is important at lower peeling angles (18). We find that G is 5 J/m² on mica at a 45° peeling angle, which is much larger than the thermodynamic work of adhesion. On Teflon substrates, G = 2.2 J/m² at a 45° peeling angle, consistent with the lower surface energy of Teflon in comparison to mica (summarized in Fig. 4B). These values of G for the carbon nanotube tapes are much larger than the poly(dimethylsiloxane)-based patterned surfaces reported in the literature (17).

Finally, we would like to discuss whether the shear forces supported by the carbon nanotube gecko tapes are due to adhesion or high friction as suggested recently for micrometer-size polypropylene fibers (19). Currently, there are several arguments that support the idea of adhesion playing an important role. First, the shear experiments were done under negligible normal load (just the weight of the tape, ≈20 mg). Second, when the tape breaks under load we observe the crack front (by video camera) moving at speeds >10 m/s, which are expected for adhesive stick to sliding (or breaking) transition. Third, the high nanometer-level pull-off forces were observed by using atomic force microscopy silicon tip in contact with carbon nanotube bundles (12). Fourth, we were also able to support normal loads of 3–5 N/cm² for patterned and unpatterned gecko tapes on mica substrate, which has to result from adhesion rather than friction.^§

In summary, we have fabricated hierarchical structures of setae and spatulas found on the gecko foot using aligned multiwalled carbon nanotubes. The multiscale structures with length scales of micrometers (setae) and nanometers (spatulas) are necessary to achieve high shear and peeling forces. Using these concepts, we have shown that a 1-cm² area can support nearly 4 kg of weight and that much larger forces can be supported by increasing the area of the tape.

Methods

Procedure to Grow Carbon Nanotubes.

The experimental process for the growth of aligned carbon nanotubes involves three steps: photolithography, catalyst deposition, and a chemical vapor deposition process. After the photolithographic pattern process, an electron beam was used to deposit a 10-nm-thick aluminum (Al) buffer layer on a Si or Si/SiO₂ wafer. On top of the Al layer, a 1.5-nm-thick iron catalyst layer (which forms nanosized particles for catalytic growth of carbon nanotubes) was deposited. Chemical vapor deposition set up to grow carbon nanotubes consists of a tubular furnace with an alumina processing tube (inner diameter 45 mm). Aligned carbon nanotube films were prepared by thermal decomposition of ethylene (with a flow rate of 50–150 standard cubic centimeters per minute) on the catalyst film at 750°C. An Ar/H₂ gas mixture (15% H₂) with a flow rate of 1,300 standard cubic centimeters per minute was used as the buffer gas during the whole chemical vapor deposition run. A very low concentration of water vapor with a dew point of −20°C was carried to the reaction furnace by a fraction of Ar/H₂ flow during carbon nanotube growth (20). The growth time is 10–30 min, and the length of carbon nanotubes is ≈200–500 μm. The average diameter of the carbon nanotubes is 8 nm (two to five walls).

Adhesion Measurements.

A freshly cleaved mica surface was prepared by lifting off a thin layer of mica sheet with an adhesive tape. The glass substrate was cleaned in a base bath, followed by rinsing with deionized water. The final washing was done in water containing a small amount of surfactant, which coats the glass with a monolayer of surfactant and prevents any further condensation of impurities from the atmosphere. The glass substrate was plasma-treated for 5 min in oxygen plasma before the adhesion measurements. The poly(methyl methacrylate) and poly(octadecyl acrylate) films were prepared by spin coating a 100- to 200-nm-thick layer on a silicon substrate. The samples were annealed above the glass transition temperature for poly(methyl methacrylate) and above the melting temperature for poly(octadecyl acrylate) polymer under vacuum. The Teflon sample was cleaned for 6 h in a mixture of Nochromix and sulfuric acid. The Teflon sample was rinsed with deionized water and dried under nitrogen. The carbon nanotubes on the silicon substrate were transferred on flexible adhesive tapes (for the force measurements we have used 3M Scotch tapes), and the carbon nanotubes were peeled off the silicon substrate with exposing the ends that were in contact with the silicon substrate (synthetic gecko tape). The synthetic gecko tape was pressed lightly with the substrate by using a cylindrical roller. All measurements were performed at ambient conditions.