Tentacle probes: eliminating false positives without sacrificing sensitivity

Abstract

The majority of efforts to increase specificity or sensitivity in biosensors result in trade-offs with little to no gain in overall accuracy. This is because a biosensor cannot be more accurate than the affinity interaction it is based on. Accordingly, we have developed a new class of reagents based on mathematical principles of cooperativity to enhance the accuracy of the affinity interaction. Tentacle probes (TPs) have a hairpin structure similar to molecular beacons (MBs) for enhanced specificity, but are modified by the addition of a capture probe for increased kinetics and affinity. They produce kinetic rate constants up to 200-fold faster than MB with corresponding stem strengths. Concentration-independent specificity was observed with no false positives at up to 1 mM concentrations of variant analyte. In contrast, MBs were concentration dependent and experienced false positives above 3.88 μM of variant analyte. The fast kinetics of this label-free reagent may prove important for extraction efficiency, hence sensitivity and detection time, in microfluidic assays. The concentration-independent specificity of TPs may prove extremely useful in assays where starting concentrations and purities are unknown as would be the case in bioterror or clinical point of care diagnostics.

INTRODUCTION

Field-deployable biosensors require more rapid and sensitive, single-step identification methods. However, efforts to enhance assay rapidity, sensitivity and simplicity can result in an increase in false positives or in false negatives (1). Such false positives and negatives can have immense impact in biosensing for medical and biowarfare applications as even rare occurrences can have disastrous consequences. A paradigm shift in understanding and designing for the specificity–sensitivity trade-off is absolutely essential to developing field-deployable biosensors experiencing few to no false positives and negatives.

Molecular beacons (MBs) are one probe methodology used to move towards more rapid, single-step genomic sensors (2,3). A fluorescent label is attached to one end of a polynucleotide and a quencher is attached to the other. Complementary base-pairs near the label and quencher cause a hairpin-like structure, placing the fluorophore and quencher in proximity. This hairpin opens in the presence of the target producing an increase in fluorescence. The proximity of the quencher to the fluorophore can result in reductions of fluorescent intensity of up to 98% (4). The perceived efficiency can further be adjusted by altering the stem strength (length of the stem) which affects the number of beacons in the open state in the absence of the target. Accordingly, one trade-off a MB experiences is with regard to its stem strength, low strength limits fluorescent increase upon hybridization whereas high strength limits kinetics of hybridization (5).

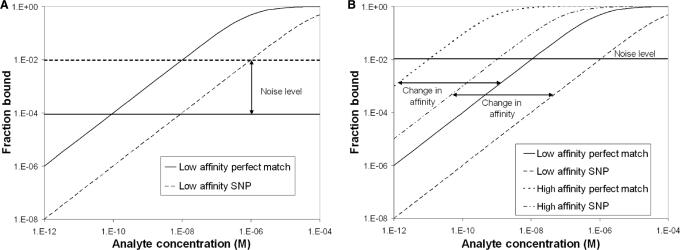
Regardless of the detection platform or strategy, the majority of biosensors incorporate molecular recognition through a biological affinity interaction. A biosensor cannot be more accurate than this interaction (6). This interaction is used for one or more functions that include identifying the presence of a given analyte, determining changes in expression level and quantifying the agent (7). Specificity and sensitivity in biosensor research often refer to the ability of the sensor to eliminate false positives and negatives respectively for one or more of the foregoing objectives. Unfortunately, there is usually a trade-off between specificity and sensitivity (7,8) as shown in Figure 1.

Figure 1.

These isotherms show the results of typical methods of altering sensitivity/specificity. The y-axis shows the fraction of probes bound and the x-axis shows the analyte concentration. The intersection of the noise level (horizontal lines in both graphs) and the fraction bound is the approximate location of the detection limit. Multiple curves are present representing fraction of specific and nonspecific analyte bound. (A) shows that increasing the signal-to-noise ratio may increase sensitivity as it is the focus of many instrument designers, but at the expense of specificity. Decreasing the signal-to-noise ratio has the opposite effect. (B) shows an increase in specificity by lowering affinity as it is often done by increasing temperatures or lowering salt concentrations causes losses in sensitivity. Increasing the affinity causes an increase in sensitivity at the loss of specificity. The absolute accuracy of the assay is not changed in either case, as indicated by the ratio of detection limits.

In support of the limitations in improving biosensor accuracy, the numbers tell a compelling story. By way of identification of the presence of specific species, Peplies et al. tested six strains of bacteria with a 1% rate of false positives and 41% rate of false negatives (9). Diagnostic PCR, although rarely having false-negatives owing to its extreme sensitivity, experiences a reported rate of false-positives between 9 and 57% (10). Detectors monitoring expression level are worse having a 10–30% false negative rate for samples above the sensitivity threshold and a false positive rate of 10% (11). While this rate of false positives and negatives may be damaging for phenotypic or other biological exploration, even one error can prove lethal in clinical diagnostics and could result in loss of life (false negative) or economic harm (false positive) in homeland security applications.

In order to overcome the deficiency with these reagents and assays, we have developed a new class of reagent that performs with heightened affinity and with greater selectivity compared to single oligomer reagents. We adapted the principles of cooperativity abundantly described in cell targeting (12–16) to combat the specificity–sensitivity trade-off. Cooperativity has already been shown to enhance SNP detection and assay sensitivity (17,18). Here, we combine principles of cooperativity with a label-free hairpin in what we term tentacle probes (TPs). We discuss the effects of cooperativity on sensitivity, specificity and kinetics, demonstrating an increase in each without sacrificing the others. These faster, more sensitive and more specific probes may offer a number of advantages in many of the diagnostic applications where MBs have already been applied.

In this study, we derive a mathematical model predicting the cooperative behavior of TPs. We test theoretical descriptions of increased kinetics and specificity over MBs and demonstrate these results without a loss in sensitivity. By so doing, we introduce the first class of reagents to our knowledge to be originated as a mathematical solution to problems associated with molecular recognition in biosensors.

MATERIALS AND METHODS

Oligonucleotide synthesis

MBs, TPs and target sequences were synthesized and purified through dual HPLC by Biosearch Technologies (Novato, CA). MBs were made with stem lengths from five to nine bases. Analogous TPs were created by attaching a capture region to the hairpin via a polyethylene glycol (PEG) sequence (9 mer). This required modifying the 5′ dye in the MB to be an internal dye attached to an inert base. In order to demonstrate that the PEG linker and internally modified dye were not the source of difference between TPs and MBs, the MBs were modified at their 5′ end to include a PEG linker attached to an internally modified dye identical to that used in the cooperative probes.

Four target sequences were synthesized representing the wild-type target (WT), a single nucleotide polymorphism (SNP) in the capture region of the TP (SNP_cap), a SNP in the detection region (SNP_det) and a SNP in both regions (SNP_both). All probes and target sequences were suspended in TE buffer (10 mM Tris-HCl, 1 mM EDTA, pH 7.0) with 0.18 M NaCl and 0.1% SDS and are summarized in Table 1.

Table 1.

The abbreviated terms for each probe and target sequence

Name	Sequence
Tentacle Probes
Tp 5	GAT TAA AAT GTC CAG TGT ACC AG - PEG 9mer - CF560 - c TGG CGG AAA AGC TAA TAT AGT AA gccaga - BHQ1
Tp 6	GAT TAA AAT GTC CAG TGT ACC AG - PEG 9mer - CF560 - c TGG CGG AAA AGC TAA TAT AGT AA cgccaga - BHQ1
Tp 7	GAT TAA AAT GTC CAG TGT ACC AG - PEG 9mer - CF560 - c TGG CGG AAA AGC TAA TAT AGT AA ccgccaga - BHQ1
Tp 8	GAT TAA AAT GTC CAG TGT ACC AG - PEG 9mer - CF560 - cc TGG CGG AAA AGC TAA TAT AGT AA ccgccagga - BHQ1
Tp 9	GAT TAA AAT GTC CAG TGT ACC AG - PEG 9mer - CF560 - ccc TGG CGG AAA AGC TAA TAT AGT AA ccgccaggga - BHQ1
Molecular Beacons
MB 5	PEG 9 mer - CF560 - c TGG CGG AAA AGC TAA TAT AGT AA gccaga - BHQ1
MB 6	PEG 9 mer - CF560 - c TGG CGG AAA AGC TAA TAT AGT AA cgccaga - BHQ1
MB 7	PEG 9mer - CF560 - c TGG CGG AAA AGC TAA TAT AGT AA ccgccaga - BHQ1
MB 8	PEG 9mer - CF650 - cc TGG CGG AAA AGC TAA TAT AGT AA ccgccagga - BHQ1
MB 9	PEG 9mer - CF560 - ccc TGG CGG AAA AGC TAA TAT AGT AA ccgccaggga - BHQ1
Targets
WT	ATT ATT ACT TTA CTA TAT TAG CTT TTC CGC CAT CTA AAA TTC TAT TTT CTG GTA CAC TGG ACA TTT TAA TCA ATG TAT TC
SNPcap	ATT ATT ACT TTA CTA TAT TAG CTT TTC CGC CAT CTA AAA TTC TAT TTT CTG GAT CAC TGG ATA TTT TAA TCA ATG TAT TC
SNPdet	ATT ATT ACT TTA CTA TAT TAT CTT TTC CGC CAT CTA AAA TTC TAT TTT CTG GTA CAC TGG ACA TTT TAA TCA ATG TAT TC
SNPboth	ATT ATT ACT TTA CTA TAT TAT CTT TTC CGC CAT CTA AAA TTC TAT TTT CTG GTA CAC TGG ATA TTT TAA TCA ATG TAT TC

The numbers in the names represent the number of bases in the stem. TP, MB, CF560, BHQ1, WT, SNPcap, SNPdet, SNPboth stand for tentacle probes, molecular beacons, Cal-fluor 560 fluorescent dye, Black Hole Quencher-1, wild type, SNP in the capture region SNP in the detection region and SNP in both regions respectively. Lower case bases in the probes represent bases added to help form the stem. Italics in the target represent complementary regions to the probes and bold letters are SNPs.

Kinetics

Kinetics were measured on a Victor2 plate reader (Perkin Elmer) at room temperature. Due to the rapidity of the TP reactions, low concentrations were used and samples had to be run individually. For the TPs, 20 μl of each probe (100 nM) was inserted into the plate. Here, 20 μl of an excess of target (1 μM) was quickly (<5 s) added to each well and the measurements were started. Ninety-nine measurements were taken over 10 min. The experiment was repeated three times. MB kinetics were measured identically except 10 μM target was used and fluorescence was monitored over 1 h.

Fluorescent data was plotted against time and the rate constants were fit using the kinetic equation for polynucleotide reactions in an excess of target by minimizing the sum of square errors. The rate constants from each of three trials were averaged and plotted against stem strength with 95% confidence intervals.

(1)

where F is fluorescence, F_max is the maximum fluorescence achieved at equilibrium, k_f is the effective forward rate constant, T is the target concentration and t is time.

Selecting optimal probes

Melting curves of each TP and MB were generated for each target type on a Stratagene Mx4000 plate reader. Here, 20 μl of solutions with final probe concentration of 50 nM and target concentrations of 50 nM, 500 nM, 5 μM and 50 μM were prepared. Fluorescence was monitored from 90 to 15°C at the end of a 15-min incubation period following each 1°C increment. The experiment was also repeated from 15 to 90°C. All melting curve results presented came from this set of experiments.

The fluorescence ratio of specific (WT) to nonspecific (SNP_det) targets was calculated for the 50-nM target concentration and plotted versus temperature. The TP and MB with the largest peaks were selected as the optimum probes after verifying first that their kinetic rate constants were each above 1000 M⁻¹ s⁻¹.

Fitting melting curves

Melting curves were fit to an adaptation of models used by others in describing MB thermodynamics (19,20). These models were enhanced by the addition of a cooperative stem and the possibility of more configurations (Figure 2). Cooperative models are derived from collision theory, where the rate of the first binding event is proportional to the product of the reagent concentrations:

(2)

where p_r is the probability of reaction, v is the average velocity, R is the sum of the radii of the two molecules, P is the probe concentration, T is the target concentration and k_f is the association rate constant. The second binding event follows the same model, but with an enhanced local probe concentration, P_L = 1 molecule/(volume swept out by linker length × Avogadro's number), reacting with the newly formed complex, C, and with an adjusted cooperative reaction probability, p_{r, coop}, reflecting enthalpic and entropic penalties:

(3)

Figure 2.

Tentacle probes function similarly to molecular beacons except the presence of a capture region allows additional pathways. In the lower left, the probe (P) and target (T) can interact forming a hybrid with either the detection probe (C_det) or the capture probe (C_cap). Once the first binding event occurs, a second binding event can occur at a much accelerated rate over the free solution rate due to the enhanced local concentration, forming a hybrid with both detection probes (C_both). The equilibrium constants together with effective equilibrium constants for each state are shown between the states and are as defined in Equations (4)–(7).

Assuming no cross-reactions, the following equilibrium constants for TPs can be derived:

(4)

(5)

(6)

(7)

where K is the equilibrium constant, with added subscripts, cap, det, both and eff, referring to capture probe, detection probe, both capture and detection probes, and effective, respectively, P = P₀ − C_cap − C_det − C_both, T = T₀ − C_cap − C_det − C_both, where P₀ and T₀ are initial probe and target concentrations respectively, F_pen refers to the collective enthalpic and entropic penalties (F_pen = e^{(−ΔHpen/T+ΔSpen)/R}), and all other variables are as previously defined.

Fluorescence as a function of temperature can be adapted from models for MBs (19,20) by:

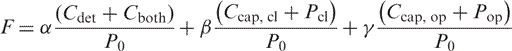(8)

where F is fluorescence as a function of temperature. Alpha, beta and gamma refer to characteristic fluorescence of bound probes, closed probes (subscript cl) and random coil probes (subscript op) respectively.

For T₀ ≫ P₀, which eliminates calculation of quadratics:

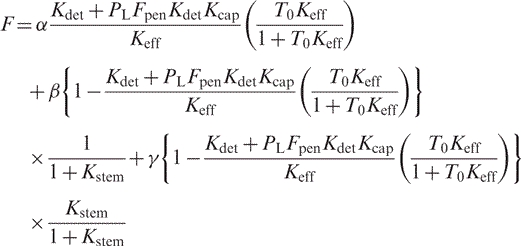(9)

K_stem is fit first by measuring fluorescence as a function of temperature for beacons with no target and minimizing sum of square errors as performed by Bonnet et al. and Tsourkas et al. (19,20):

(10)

Next K_det is fit on probes with no capture probe (e.g. on an MB):

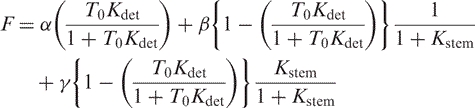(11)

The thermodynamic parameters necessary for calculating K_cap were estimated with Mfold (21) for 0.18 M NaCl (about the same sodium concentration as 1 × SSC). Using the Mfold estimates provided, theoretical curves that diverged at ∼61°C for differing concentrations of target with TP 5, while adjusting the predicted entropy from −0.4989 to −0.494 kcal mol⁻¹ K⁻¹ moved the divergence to ∼65°C forming a more accurate visual fit to the data. Therefore the latter value was used for all remaining tests. Finally, F_pen was fit to the fluorescent curves of three different dilutions of target mixed with TPs using the original equation. All parameters necessary for calculations are summarized in Table 2.

Table 2.

Parameters used in theoretical calculations and source of values

Table of parameters
Fitted parameteres		Known parameters
α	Equal to greatest fluorescence in presence of target	P0	Initial probe concentration
β	Equal to lowest fluorescence in absence of target	T0	Initial target concentration
γ	Equal to greatest fluorescence when hairpin melts
ΔHstem	Fit to probes with no target
ΔSstem	Fit to probes with no target
ΔHdet	Fit to molecular beacons with target	Estimated parameters
ΔSdet	Fit to molecular beacons with target	PL	Calculated from linker length
ΔHpen	Fit to tentacle probes with target	ΔHcap	Estimated by Mfold
ΔSpen	Fit to tentacle probes with target	ΔScap	Estimated by Mfold

The best fit enthalpies and entropies were used to calculate the equilibrium constants which in turn were used to calculate the amount of analyte bound to the detection probe and producing fluorescence as a function of temperature in an excess of target for MBs for specific (subscript s) and nonspecific (subscript ns) analyte:

(12)

(13)

And for TP:

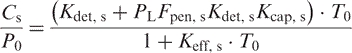(14)

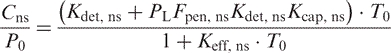(15)

These equations were then matched with normalized fluorescent data in order to verify accuracy of thermodynamic parameters in predictions at the lowest detectable binding levels and to identify trends in binding below the level of detection. Thermodynamic values provided from best fits often fit high-level binding tightly at the expense of fitting low-level binding data due to inequalities arising from the sum of square errors. A manual adjustment to the best fit (e.g. ±0.6 kcal mol⁻¹ for enthalpy and ±0.0016 kcal mol⁻¹ K⁻¹ for entropy) provided a fit that more thoroughly represented both high and low binding data. Once the parameters provided a perfect visual fit to low-level binding as well as high-level binding, they were kept constant in order to make predictions.

Specificity and sensitivity

The Stratagene Mx4000 plate reader was used to read the fluorescence of 1-μM nine-base stem TP and 1-μM five-base stem MB (both probes chosen as described in Selecting Optimal Probes) in WT and SNP_det targets at concentrations of 0, 2, 10, 20, 100 nM, 1 and 10 μM. Higher concentrations of 100 μM and 1 mM SNP_det were also used where detection limits had not yet been established. Fluorescence was read at equilibrium for both probe types. The reading was performed at 60°C for the TP and 55°C for the MB. Three replicates of each type were performed.

The predicted binding curves as a function of target concentration were generated using best fit thermodynamic parameters for MBs:

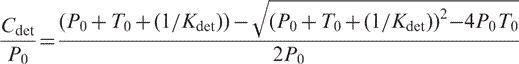(16)

And for TP:

(17)

These predictions were compared to experimental data plotted with 95% confidence intervals. Before plotting, data was normalized by subtracting the background fluorescence measured at 0 nM target concentration and dividing by the maximum intensity experienced at 100 μM WT target at room temperature. The background fluorescence level plotted was the average plus one standard deviation of the signals of experiments run below and including the highest concentration that could not be statistically confirmed as having fluorescence greater than the preceding concentrations (t-test, P > 0.05).

The detection limits were determined as the analyte concentration at which the theoretical binding curve intersected with the background fluorescence level and were validated by experimental data. The ratio of detection limits was also calculated. Accordingly, the ratio of detection limits can be viewed as a measure of diagnostic accuracy, giving the total range of concentrations over which an assay is expected to achieve 100% true positives and negatives. Throughout this article, this ratio is referred to as the molecular or absolute accuracy of an assay.

RESULTS

Kinetics

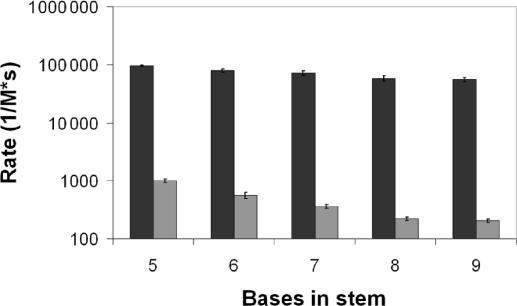
TPs have measured rate constants ranging from 100 to 200 times larger than their MB counterparts (Figure 3). In comparison with literature, the TP rates are several times faster than those reported for standard linear DNA-probe-binding kinetics and stand in contrast to the MB rates which are slightly slower than literature values (20). The faster rates of TP over linear probes can be explained by the presence of two probes, a capture and a detection probe, providing for increased probability of reaction. In addition, these probes are longer than the linear probes used by Tsourkas et al. (20). The MB's slower reaction than what was reported in literature can be explained by their longer stems and the fact that the reactions were monitored at room temperature instead of 37°C. Although molecular beacons are not expected to perform well at room temperature, this setting was selected to better contrast TPs with MBs. The rate constants indicate that TPs react in ∼1% of the time that MBs with the same stem strength require. The room temperature rates of TPs are still >10-fold faster than those reported by Tsourkas et al. using MBs with short stems and higher reaction temperatures (20).

Figure 3.

Rate constants are shown for TP (dark bars) and MB (light bars) for each stem strength with 95% confidence intervals.

Fitting melting curves

Melting curves were used to extract thermodynamic constants (Figure 4, Table 3). As was expected, the enthalpy of the stem increased with stem length, whereas the enthalpy of the hybridization reaction decreased. The enthalpic and entropic penalties also decreased with increasing stem strength, as did the kinetic rate constants. The only unexpected finding was that for the shorter stems (five and six bases), the stem melting temperature varied greatly between TP and MB. Since these two probe types were constructed identically including choice of dyes and even the attachment of a PEG linker, the only other explanation for this difference in melting temperatures appeared to be that the proximity of the capture probe allowed for some interaction with the stem-loop structure.

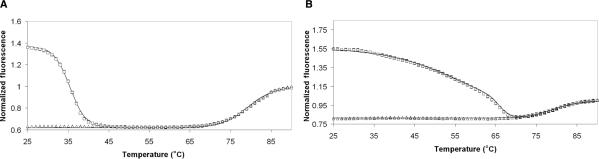
Figure 4.

Example of fitted melting curves. (A) shows MB (50 nM probe with seven-base stem in 500 nM SNP target) and (B) shows TP (50 nM probe with eight-base stem in 5 μM wild type target) fitted curves with data (squares with target, triangles probe only).

Table 3.

Enthalpies and entropies for beacon stems, capture probes and detection probes in addition to kinetic data for the wild-type target

Name	ΔHstem	ΔSstem	ΔHdet	ΔSdet	ΔHcap	ΔScap	ΔHpen	ΔSpen	Rate
MB 5	−70.03	−0.2030	−93.43	−0.2596	NA	NA	NA	NA	1000.1
MB 6	−72.20	−0.2070	−85.44	−0.2373	NA	NA	NA	NA	562.4
MB 7	−76.13	−0.2161	−83.27	−0.2323	NA	NA	NA	NA	362.4
MB 8	−84.60	−0.2392	−76.56	−0.2118	NA	NA	NA	NA	219.3
MB 9	−93.91	−0.2639	−70.26	−0.1947	NA	NA	NA	NA	205.0
TP 5	−56.59	−0.1654	−93.43	−0.2596	−175.80	−0.4940	69.32	0.1993	96 233.9
TP 6	−62.42	−0.1804	−85.44	−0.2373	−175.80	−0.4940	67.49	0.1948	79 300.5
TP 7	−76.69	−0.2188	−83.27	−0.2323	−175.80	−0.4940	57.28	0.1657	72 428.2
TP 8	−78.78	−0.2237	−76.56	−0.2118	−175.80	−0.4940	52.33	0.1500	58 422.9
TP 9	−91.02	−0.2568	−70.26	−0.1947	−175.80	−0.4940	39.79	0.1129	55 861.1

Units are in kcal mol⁻¹ for enthalpic parameters, kcal mol⁻¹ K⁻¹ for entropic values and in M⁻¹ s⁻¹ for rate constants. TP detection probes were assumed to have the same thermodynamic parameters as the molecular beacons. Sign convention is for hairpin closing then binding with target.

Tsourkas et al. have performed the most extensive work on thermodynamics in MBs (20). Their data for MB enthalpies of reaction ranged from −80 to −221 kcal mol⁻¹ and entropies of reaction ranged from −0.21 to −0.61 kcal mol⁻¹ K⁻¹. While these numbers appear similar to what was recorded in our experiments, it should be noted that our beacons were larger, which should produce larger enthalpies, and had stronger stems, which should result in lower net enthalpies for probe–target interactions. Therefore a direct comparison cannot be made. However, we feel confident in the accuracy of the thermodynamic parameters recorded inasmuch as adding the energetic losses due to the stem to the probe enthalpy (−ΔH_stem + ΔH_det) produces consistent values near the predicted enthalpies for binding to linear probes of −175.3 kcal mol⁻¹ and similarly for the predicted entropies of −0.4936 kcal mol⁻¹ K⁻¹ (21).

The capture probe parameters were calculated on Mfold. The predicted enthalpy and entropy of reaction were −175.8 kcal mol⁻¹ and −0.4989 kcal mol⁻¹ K⁻¹, respectively (21). It should be noted that the design criterion for both the detection probe and capture probe affinities was a melting temperature 10°C above the desired reaction temperature. The optimal TP stem strength was designed to have a melting temperature 30°C above the reaction temperature. In practice, in order to achieve specificity, we had to increase the reaction temperature such that the predicted melting temperatures for the detection and capture probes were 5°C below the reaction temperature, whereas the predicted stem melting temperature was only 15°C above the reaction temperature.

Once the parameters were fitted, they could be used to calculate binding curves and be double checked for accuracy by comparing theoretical curves against normalized data in a semi-log plot (Figure 5). These predictions reveal a slightly different binding pattern for TP than for MB. TP exhibit a slight bend in the binding curves ∼70°C. This is mathematically due to the melting of the capture probe, causing an instant loss in the cooperative interaction and consequent signal.

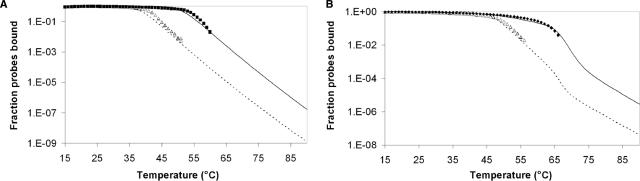
Figure 5.

Log plot of the fraction of probes bound by wild type (filled squares) and SNP targets (open triangles) in 1 μM concentrations as a function of temperature. Fitted curves are also displayed for wild type (solid line) and SNP containing analyte (dashed line). (A) shows molecular beacon binding and (B) shows tentacle probe binding.

Selecting optimal probes

Optimal candidates were selected by looking at the specific to nonspecific signal ratio for each stem at 50 nM probe and target concentrations (data not shown). The optimal candidates were then verified with the kinetic results in order to assure that the kinetics were ideal as well. Since TP 9 had the greatest signal differentiation and its kinetics were still much faster than the fastest MB, it was selected as the optimal TP. MB 5 was the fastest and most selective of the MBs, so it was chosen as the best MB.

Application in SNP detection

Negligible differences exist between the melting curves of WT and SNP_cap and between SNP_det and SNP_both for both the TP and MB (Figure 6, data not shown for MB). This is most likely due to the relatively high affinity of the capture probes. By utilizing a capture probe which does not respond to SNPs, the location of a SNP can be pinpointed to the region of the detection probe. However, if greater selectivity is required, it may be possible to design the capture probe to respond to SNPs by reducing the probe length. This also indicates that the design of the capture region is probably not as significant as the choice of the detection probe.

Figure 6.

Melting curves for 50 nM TP 9 with 500 nM of each target type.

Because of the cooperative interaction of TP, their melting curves do not change significantly over a wide range of concentrations (Figure 7). A reaction temperature can be chosen for TPs (vertical line in Figure 7A) such that there is 100% accuracy in SNP determination based merely on whether or not a signal is detected. This would be ideal for real-time PCR in SNP discrimination. Additional mismatches, such as are common in organism detection, should allow for greater resolution. In contrast, the melting temperatures of MB change with concentration making it difficult to find a reaction temperature which allows for discrimination over a wide range of concentrations.

Figure 7.

Melting curves for 50 nM TP 9 (A) and 50 nM MB 5 (B) for WT and SNP_det analyte concentrations from 50 nM to 50 μM.

Specificity and sensitivity

We performed an experiment at the optimum SNP resolution temperatures for both TP (60°C) and MB (55°C). Theoretical predictions were graphed alongside the experimental results for binding as a function of target concentration (Figure 8). The theoretical predictions appeared to describe experimental data well. TP isotherms reveal wild-type detection limit of 15.4 nM and no SNP detection at concentrations tested up to 1 mM. The model predictions indicate that binding to mutant targets possessing a SNP will never be sufficient to cause a signal above the background resulting in false positives regardless of how high the concentration is. In contrast, mutant targets resulted in false-positive signals for MB at concentrations above 3.88 μM, 154 times greater than the detection limit for the wild-type target of 22.7 nM. The ratio of specific to nonspecific detection limits for the TP was tested in excess of 53 200 and is predicted to increase indefinitely. In contrast with Figure 1, TP specificity was improved without sacrificing sensitivity.

Figure 8.

Isotherms of wild-type binding (solid diamonds) and SNP binding (open triangles) as a function of target concentration performed at 60°C (TP, Figure 8A) and 55°C (MB, Figure 8B). Theoretical predictions (solid line—WT, dashed line—SNP) are produced from thermodynamic constants extracted from melting curves and are plotted against experimental data. The 95% confidence intervals are shown for each data point but are not visible on higher binding values because of the log axis. Lower confidence intervals do not appear on some data points because they include zero. The horizontal line is the detection threshold set at one standard deviation over background and shows that even with this sensitive threshold, SNPs do not cause false positives for tentacle probes even at millimolar concentrations.

DISCUSSION

Due to the thermodynamic principles that govern molecular interactions, it is extremely difficult to develop an assay that increases specificity without sacrificing sensitivity. Likewise, sensitivity is not easily increased without a loss in specificity. We have developed a new class of reagents that does not improve specificity or sensitivity via a trade-off, but that improves overall assay accuracy as indicated by the ratio of detection limits by utilizing cooperativity.

The difficulty in increasing sensitivity or specificity without sacrificing the other lies in the fact that efforts to address assay performance are often directed at instrumentation and buffers. For example, the temperature is raised to increase specificity or lowered to increase sensitivity. Salt concentrations are raised and lowered to optimize binding. Detection volumes are decreased and filter sets are optimized to increase sensitivity (22,23). However none of these methods addresses the fundamental issue of how affinity reagents recognize and bind an analyte. Altering instrumentation does not affect thermodynamic parameters governing binding and thus only affects the threshold of detection. Altering the threshold merely results in a sensitivity–specificity trade-off as demonstrated by receiver operating curve analysis (1). Raising the temperature or decreasing salt concentrations lowers the equilibrium constant for both specific and nonspecific binding, leading to greater specificity at the expense of sensitivity. Likewise decreasing the temperature or increasing salt concentrations increases the equilibrium constant for specific and nonspecific binding, resulting in increased sensitivity at the expense of specificity. None of these methods decreases the nonspecific equilibrium constant while maintaining or increasing the specific equilibrium constant. Accordingly, trade-offs in specificity and sensitivity can be achieved but the ability of the affinity reagent to discriminate between specific and nonspecific targets remains largely unchanged.

TPs represent a novel innovation inasmuch as they are mathematically engineered to manipulate thermodynamic principles that govern affinity reagent recognition of a biomolecule. Collision theory dictates that a second binding event from a molecule already bound to a substrate and held at an enhanced local concentration will typically occur at a faster rate than it would in free solution. This principle was used to develop mathematical models that predicted both enhanced kinetics and specificity of cooperative probes. For a homovalent probe pair with no penalty term, the effective equilibrium constant reduces to K_eff = K_eq(2 + P_L · K_eq), which is identical to antibody theory as originally derived by Crothers and Metzger (24) and as embodied by Kaufman and Jain (25). Others have also used this approximation for modeling bivalent interactions and have experimentally confirmed its accuracy (26–29). However, we are the first to our knowledge to use this model to examine the specificity–sensitivity trade-off in biosensors. These derivations of the equilibrium constant apply a different approach from that which has already been done for multivalent systems (16,25,30,31). However, the result confirms thermodynamic estimates where the avidity is equal to the sum of the free energies of each individual reaction plus an interaction effect, which is typically an entropic penalty (32,33).

It might be expected in cooperative interactions that an SNP would not be as easily recognized due to an overall higher binding affinity. However, in our experiments, the bivalent accuracy was >345-fold greater than the monovalent accuracy (the ratio of concentrations at which the signal is greater than the detection limit, from Figure 8). This added enhancement to selectivity in our experiments is due to the unique structure of the TPs. By utilizing only one probe in the pair as the detection probe, cooperativity can be designed to allow theoretically asymptotic separation of specific and nonspecific detection limits. For analyte concentrations greater than probe concentrations, the capture probe has a sufficiently high affinity to present the detection probe with a constant local concentration of bound target. This allows for detection that is independent of increasing concentrations, effectively reducing the mechanism in Figure 2 to the top two reaction states. With no shift in the melting curve for increasing concentrations, SNPs can be identified with greater confidence using TPs than with conventional probes.

For analyte concentrations below the probe concentration, melting curves were observed to shift with increasing analyte concentrations (data not shown). We believe the reason that concentration independence occurs only for target concentrations above the probe concentration is due to target saturation of the detection-probe-binding site. For relatively low target concentrations, the detection-probe-binding sites are not saturated and can continue to bind more analyte as it is added to solution, presenting a variable concentration to the detection probe. However, once the capture probes have been saturated with analyte, a constant local concentration is presented to the detection probes, causing concentration independence of reaction. Having biphasic concentration dependence is an advantage of TPs. Quantification of analyte can be performed for anlayte concentrations below the probe concentration. However, once analyte concentrations exceed probe concentrations entering into the nonlinear region of binding where quantification is no longer possible, melting curves cease to be affected by concentration and specificity is rendered concentration independent.

As the analyte concentrations continue to increase, it might be thought that the unreacted hairpins in the detection probe would be forced to bind, such that each TP would be bound to two target molecules (one on the capture probe and one on the detection probe). However, as observed in the TPs with even the weakest stem, the melting curves still remained immobile with increasing concentrations (data not shown). The analogous MB, on the other hand, continued to show increases in fluorescence with increasing analyte concentrations (Figure 6), demonstrating that the hairpin strength was not the cause of failure to fluoresce in TPs. Rather, the lack of an increase in fluorescence with increasing analyte concentrations in TPs demonstrates that a second molecule is not bound to the free detection probe. We believe that the mechanism preventing a second binding event to the detection probe at high analyte concentrations may involve the affinity between the detection probe and the captured analyte. While the affinity is not enough to keep the captured analyte firmly bound to the detection probe, we believe it is sufficient to keep the captured analyte close, continually binding and releasing it, thereby precluding a binding event from the bulk solution. Taken together, the constant local concentration and the ability to preclude binding of more than one molecule, these mathematically designed assets give TPs an accuracy in SNP discrimination that is matched by no other probe set to our knowledge.

MBs, on the other hand, are known to possess greater specificity than linear probes due to the competition from stem formation (19). Discrimination between wild type and mismatched targets is expected to increase with stem strength (20). However, utility of stronger stems in MBs is compromised by reduced sensitivity from lower affinity and by slower kinetics. By combining the unique secondary structure of MBs with the idea of cooperative probes, we have created a label-free, highly specific reagent that has greater specificity than a MB, but that reacts up to 200 times faster. Again TPs show no sign of a trade-off. This may make the use of TPs in room temperature assays where MB reaction rates are extremely slow or in continuous flow detection where reagents passing by only have a short time to react an ideal candidate over MB.

The sensitivity loss from stronger stems in MBs has been studied by Tsourkas et al. (20). The loss in fluorescence experienced by MBs is replaced by gains in TPs with identical stem strengths because of the lower free energy available from cooperative binding. We collected thermodynamic parameters in order to compare with the results of Tsourkas et al. In order to get their thermodynamic parameters, they fit a line through the fluorescence at the melting temperature of six different concentrations of target. We deviated from this method because we felt it was statistically more relevant to use the entire set of fluorescent data for each concentration rather than a single point. Also, their method did not directly apply to fitting thermodynamic parameters for TPs.

In addition to a melting curve which does not shift significantly with target concentration, Figure 5 reveals a difference between TP and regular probes in the amount of specific and nonspecific binding resulting in fluorescence as a function of temperature. Data points are plotted to where fluorescent levels are no longer distinguishable from the background. Since the actual data could not be observed at low amounts of binding, the fitted thermodynamic parameters were used to calculate binding as a function of temperature beyond where data could be collected. Since the models and fitted parameters account for the majority of the TP behavior, and because these models have been derived for other applications as previously discussed, we feel justified in their use to examine the thermodynamic patterns of cooperative binding.

As a further justification of the use of the models in describing TP behavior, the models were used to predict binding as a function of concentration (Figure 8). Theoretical predictions estimated that a target molecule possessing a SNP in the detection region would never be detected by TPs regardless of target concentration, virtually eliminating false positives. We were able to test this hypothesis to 1 mM SNP concentrations with no false detections. We note that the models were sufficiently accurate to predict this trend. We also note that the models predict the ability to concentrate nonspecific analyte to levels that are not physically possible without false positives. This is supported by the fluorescent signals of TP 9 at 60°C, which seem to be completely independent of target concentration (Figure 7). The fact that we were unable to create SNP analyte concentrations sufficiently high for TP detection without sacrificing the sensitivity of wild-type detection illustrates the point of this article. This stands in stark contrast to any other probe set of which we are aware. By creating cooperative probes, we have been able to effectively reduce false positives without sacrificing sensitivity.

This high level of specificity may find utility in a number of research and diagnostic applications. Real-time PCR, for example, is often required to perform SNP discrimination. While comparative analysis of a multiplexed assay often yields good results in a laboratory, field tests do not always have the same options of sample purity or multiplexing and those running the tests do not always have the capacity to interpret the results. Rather many field test units resolve the complexity of analysis by resorting to a signal/no signal report. Few probes possess the capacity to distinguish SNPs by the presence or absence of a signal. This problem is compounded in homeland security where a number of select agents like Bacillus anthracis and Yersinia pestis have near neighbors with large portions of similar genetic content (34,35). TPs may again provide an answer to this real-world need.

Although TPs have shown benefits in several areas, there is still room for improvement. This set of experiments only examined the effect of stem length on binding. Other options for adaptation include linker length and composition, capture and detection probe affinities, the distance between capture and detection regions on the target polynucleotide, and the interactions of each of these features. Given the large enthalpic and entropic penalties, there may be a great deal of room for improvement, potentially producing a much sharper slope in the melting curves. This in turn could lead to higher signal-to-noise ratios and greater detection limit ratios, while maintaining the incredible specificity.

Six years ago, Iqbal et al. called for the creation of new affinity reagents as the most important means of improving biosensor accuracy (6). We have created a new class of label-free affinity reagents, TPs. These special beacons manipulate thermodynamic principles in order to increase kinetics up to 200-fold and molecular accuracy in SNP detection by at least 345-fold, with predicted enhancements of near infinite improvement. Because of their cooperative interaction, they truly allow significant enhancements in sensitivity, specificity and kinetics without a trade-off.