Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1998 Feb 17;95(4):1490–1494. doi: 10.1073/pnas.95.4.1490

Is the molten globule a third phase of proteins?

Vijay S Pande *, Daniel S Rokhsar *,†,‡
PMCID: PMC19058  PMID: 9465042

Abstract

The equilibrium properties of proteins are studied by Monte Carlo simulation of two simplified models of protein-like heteropolymers. These models emphasize the polymeric entropy of the fluctuating polypeptide chain. Our calculations suggest a generic phase diagram that contains a thermodynamically distinct “molten globule” state in addition to a rigid native state and a nontrivial unfolded state. The roles of side-chain packing and loop entropy are discussed.

A typical small protein can fold and unfold reversibly in vitro, undergoing a first-order (i.e., two-state) transition (1)§ between its unfolded state U and its “native” (i.e., folded) state N, depending on temperature, pH, denaturant concentration, etc. (2). Under certain conditions, proteins can also exhibit a collapsed state with partial order known as the “molten globule” (MG) that has some native secondary and tertiary structure but lacks well-packed side chains (3–5). A scaling analysis of the thermodynamic properties of proteins of various lengths suggests that the MG is indeed a distinct phase, separated by first-order transitions from both the folded and unfolded states (6), although this remains controversial; for example, the U ⇌ MG transition in α-lactalbumin appears to be continuous [i.e., noncooperative (7, 8)]. The thermodynamic forces that stabilize the MG relative to N and U remain unclear.

Herein we address the polymeric properties that govern the stability of the MG of proteins and, more generally, the global phase diagram of protein-like heteropolymers. From the perspective of polymer physics, proteins may be viewed as a subset of a more general class of heteropolymers whose sequences are “designed” to fold reproducibly to a preselected conformation (the native state) at low enough temperature and denaturant concentration (9, 10). Random-sequence heteropolymers do not generically have this property (11, 12). It has been shown both analytically (V.S.P., A. Y. Grosberg, and T.T., unpublished work) and computationally (14) that designed heteropolymers exhibit a discontinuous (i.e., first order) U ⇌ N transition, which corresponds to the cooperative two-state behavior of proteins. As in many polymer problems (15), such general conclusions are likely to be independent of specific details of the underlying chemistry (10) and can, therefore, be addressed by studying simplified models.

We present Monte Carlo simulations of two models of protein-like heteropolymers: a lattice model (9, 16–19) and a new off-lattice model for proteins that includes a caricature of helical secondary structure but omits side-chain packing effects. Although neither of these models faithfully represents all biologically important details of protein structure, both retain general heteropolymeric features that are critical for a complete physical understanding of protein states. The generality of our results is emphasized by physical arguments that appeal to polymeric entropy rather than model-specific details. Our approach complements molecular dynamics studies of more realistic models of specific proteins (20) and phenomenological three-state models for U–MG–N stability (21).

Our main results are derived from the free energy landscapes shown in Figs. 1A and 2, which exhibit the free energy minima of both the U and MG phases. The unfolded states of both of our models contain a significant fraction of native contacts as seen from the location of the U minima in Figs. 1A and 2. These contact are fluctuating, in the sense that conformations with similar Boltzmann weight in the U phase will generally possess different combinations of native contacts (22). The MG phase we find is consistent with the recent picture of the MG (3–5). In comparison to the U state, the MG phase has more native contacts, but more importantly, many of these contacts are preserved from conformation to conformation in the MG ensemble.

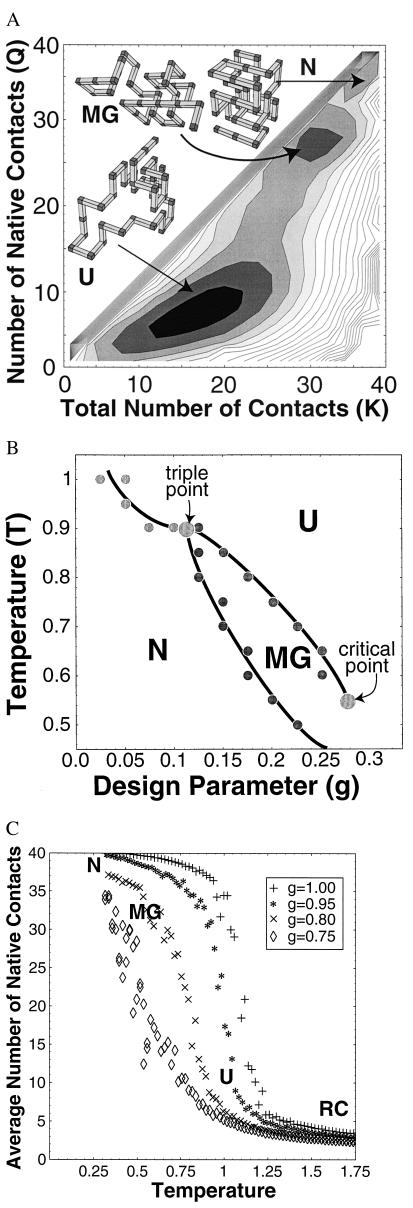
Figure 1.

Figure 1

Open in a new tab

Lattice model results. See , for simulation details. (A) Free energy. Free energy G(Q, K) vs. the number of native contacts Q and the total number of contacts K for a lattice 36-mer near the triple point (temperature T = 0.95 and design parameter g = 0.1), computed by Monte Carlo sampling. In this experiment, temperature is measured in units of the average free energy of a native contact (which itself depends on temperature and denaturant concentration). The free energy surface exhibits three distinct local minima separated by barriers, corresponding to the U, MG, and N states. Typical conformations are shown for each. (B) Phase diagram. Phase diagram of the lattice model vs. temperature T and design parameter g. The parameter g models perturbations that nonspecifically destabilize the N state, crudely modeling changes in pH and denaturant concentration. All transitions are first order. There is a triple point at T* = 0.9 and g* = 0.1. For T > T* or g < g*, the MG is never globally stable. Finally, our simulations suggest that the line of first-order (cooperative) transitions between MG and U ends at a critical point at Tc = 0.55 and gc = 0.28. (C) Cooperativity of the U ⇌ MG transition. To study the cooperativity of U from the MG, we calculated the average number of native contacts Q vs. temperature T for several different values of design parameter g. As g increases (modeling the addition of denaturant), the transition becomes less cooperative, while simultaneously stabilizing the MG. These competing effects of denaturant may reconcile the disagreement between experimental studies of the U ⇌ MG transition, which report both cooperative (5) and noncooperative (7) transitions in different proteins under different conditions.

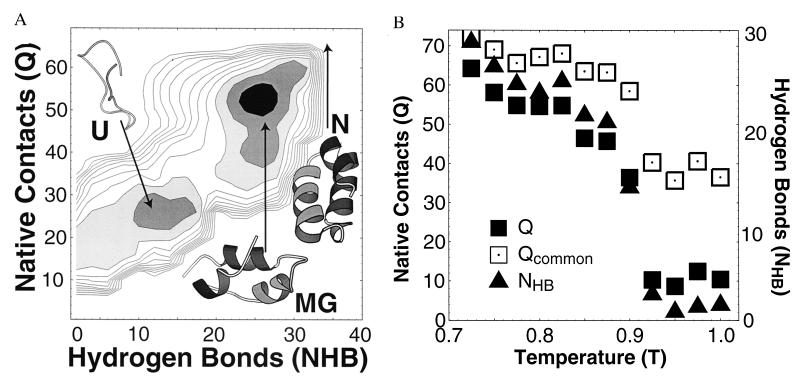
Figure 2.

Figure 2

Open in a new tab

Off-lattice model results. (A) Free energy. The free energy G(NHB, Q) at T = 0.6 for an off-lattice model of fragment B of protein A has two minima (MG/N and U). (Temperature is measured in units of the free energy of a native contact.) As temperature decreases, the MG minima smoothly shifts toward the N state, N (Q = 72, NHB = 21). Typical conformations from each minima are shown, as well as the N state. In contrast with the lattice simulation, the absence of side-chain packing in the off-lattice model eliminates the barrier between the N and MG phases that is found in the lattice model. (B) Temperature dependence. Plot of 〈Q〉, 〈NHB〉, and 〈Qcommon〉 vs. temperature T. 〈Qcommon〉 is the typical number of native contacts in common between four conformations chosen from an equilibrium ensemble and thus describes the degree to which the contacts are fluctuating. The small value of 〈Qcommon〉/〈Q〉 in the U state implies large fluctuations—in contrast with the folded state, in equilibrium the “native” contacts present in U conformations vary greatly from conformation to conformation. In our model, 〈NHB〉 measures α-helical content, and Qmax − 〈Q〉 corresponds crudely to solvent exposure.

For well-designed heteropolymers, we find that the U and MG phases are separated by a free energy barrier, which results in a first-order U ⇌ MG transition. We show that this barrier is created by the entropy of polymer loops fluctuating around a rigid core. This transition—and the MG itself—is, therefore, a generic feature of heteropolymers. The presence of a barrier between the MG and N states in the lattice model (Fig. 1A) but not in the off-lattice model (Fig. 2) suggests that side-chain packing is critical for the distinction between these two states.

Lattice Model

In the lattice model (9, 16–19), a polymer chain of length N is restricted to pass through adjacent sites of a cubic lattice, which represent residues. The “internal free energy” of a given conformation is given by Fint ≡ ∑i>j B(si, sj) Cij, where i and j are positions along the chain and si is the species of the ith residue. Note that this internal free energy includes not only the intrapolymeric enthalpy but also the free energy of the solvent in the presence of the given conformation. Thus hydrophobic interactions appear in our calculations via Fint. B(s, s′) is the internal free energy of interaction between residues of species s and s′, and Cij is the “contact map”; i.e., Cij = 1 if residues i and j are in contact (but not neighbors along the chain) and zero otherwise. [By adopting this simple pairwise interaction, we are neglecting the variation in the strength of a contact in different contexts (23). However, this should not change the qualitative features of our results.]

Monte Carlo sampling of conformations is used to compute the total free energy G(Q, K) as a function of K ≡ ∑i>j Cij, the total number of “contacts” (i.e., residues that lie on adjacent lattice sites but are not consecutive along the chain) and Q ≡ ∑i>j CijCijN, the total number of native contacts (i.e., contacts that occur in the native state).

For a given interaction matrix B, a sequence is designed to fold to a preselected native conformation by simulated annealing in sequence space (9, 10). We use the independent interaction model for interactions, in which B is a symmetric Gaussian random matrix of unit variance (24). We have also used the Go model (25) and Miyazawa-Jernigan interactions (26); as expected, our qualitative results are insensitive to the particular model used.

The free energy G(Q, K) for a lattice 36-mer (Fig. 1A) displays three distinct local minima corresponding to the U, MG, and N states, separated by free energy barriers. Each local minimum represents a distinct thermodynamic phase (1).§ The locations and depths of these minima shift with temperature T and “design parameter” g. The parameter g models perturbations that nonspecifically destabilize the N state, crudely modeling changes in pH and denaturant concentration. The phase diagram shown in Fig. 1B is constructed by identifying the global minimum of G(Q, K) for each region of the (T, g) plane. The three two-phase coexistence lines meet at a triple point. There also appears to be a critical endpoint to the MG–U coexistence line, at which these two minima coalesce as the barrier between them disappears.

Off-Lattice Model

For our off-lattice calculations, we use a coarse model for proteins (ref. 28, to which our model is similar in spirit) that represents the polypeptide as a chain of tethered hard spheres centered on the α-carbon of each residue. The spheres represent the entire residue, including side chains; they are elastically coupled to represent the local bending energies of polypeptides and also interact via amino acid-dependent con-tact terms.‖ We have incorporated a new method of simulating backbone hydrogen bonds to model α-helical secondary structure.** We stress that our goal herein is not to predict structure but, rather, to capture the interplay between secondary and tertiary structure formation and polymeric (backbone) entropy. Our model is simple enough that we can easily simulate the folding and unfolding of a small protein by using Monte Carlo kinetics. (For a movie of the unfolding of the three-helix bundle with increasing temperature, see http://hubbell.berkeley.edu/UFbprotA.mpg).

Fig. 2 shows a free energy surface corresponding to a small (43 residues) three-helix bundle‡‡ derived from Staphylococcus aureus protein A (Protein Data Base code 1fc2), computed with our off-lattice model. [Similar results were obtained for another three-helix bundle ER-10 (ref. 33†† and data not shown).] The free energy surface is shown as a function of Q, the number of native contacts, and NHB, a measure of the α-helical content of the conformation. For the off-lattice model, there are only two free energy minima, corresponding to unfolded and structured states, respectively. The relative stability of the two minima varies with temperature, and we find a first-order transition between U and a partially folded MG-like state with fluctuating contacts. As temperature is reduced, the MG-like minimum shifts smoothly toward the more rigid N state. The smooth MG–N crossover of the off-lattice model differs from the cooperative MG ⇌ N transition of the lattice polymer, as we discuss further below.

Although the U state has less secondary structure than the MG (or the N state) in our model, it still possesses many native contacts. Unlike the N state, however, these contacts are fluctuating (Fig. 2B), in the sense that conformations with similar Boltzmann weight in the U phase will generally possess different combinations of native contacts (24).

Because our off-lattice model treats each amino acid residue as a sphere, it neglects both the stereochemical specificity of side-chain interactions and the entropy lost as side-chain degrees of freedom freeze in the process of side-chain packing.§§ The lattice simulation, however, models packing in the sense that residues in contact can rigidly lock into place on the lattice. The two models we consider are, therefore, complementary with respect to their treatment of packing effects. Below, we compare and contrast the results of the lattice and off-lattice calculations to distinguish polymeric effects (common to both models) from those that depend on rigid packing (found only in the lattice model).

The U–MG Barrier

One of our principal results is the existence of a first-order U ⇌ MG transition in both models. This result implies that side-chain packing is not required to establish the free energy barrier between the U and MG minima (as found experimentally in, e.g., ref. 35); this barrier is a generic property of designed heteropolymers.

The physical basis of the free energy barrier between MG and U is demonstrated more directly in Fig. 3, which shows the entropy for the lattice polymer computed by Monte Carlo sampling. The total entropy can be divided into three distinct contributions (V.S.P., A. Y. Grosberg, and T.T., unpublished work). First, there is a linear term −soQ that corresponds to the average entropy lost per contact, where the average entropy lost per contact is so ≡ [Stot(0) − Stot(Qmax)]/Qmax.

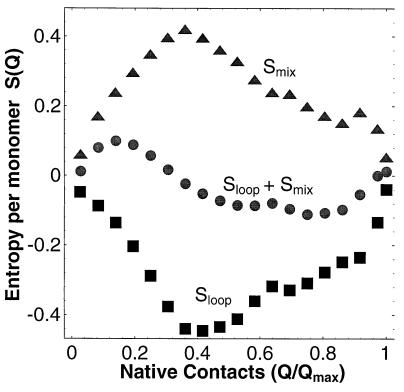
Figure 3.

Figure 3

Open in a new tab

Entropy of lattice model. Mixing (triangles) and loop (squares) entropies as a function of the number of N contacts Q of the lattice 36-mer at T = 1 and g = 0. The free energy barrier at intermediate Q and the U free energy minima at nonzero Q are the result of the interplay of these two entropies, as shown by the respective entropic minima and maxima in Sloop + Smix.

Conformations with Q native contacts can be divided into groups or “mesostates,” according to the specific native contacts they possess. The “loop entropy” Sloop(Q) represents the number of conformations in a typical mesostate with Q native contacts, and the “mixing entropy” Smix(Q) represents the number of these mesostates. Total (Stot) and mixing (Smix) entropies are computed directly by Monte Carlo sampling. Loop entropy Sloop is obtained from the relation Stot = Smix + Sloop − soQ.

Fig. 3 shows that the loop entropy exhibits a deep minimum for partially folded structures: at small Q, there are few long loops, and at large Q, there are many small loops; in both of these limits Sloop is large (compared with intermediate Q) (13). Conversely, the mixing entropy is peaked at intermediate Q, where there is the greatest combinatorial choice for residues in the core. The sum of the loop and mixing entropies generates an entropic minimum at intermediate Q (Fig. 3). This effect is independent of the nature of the N state and the details of the interactions and is, therefore, expected to be a general property of designed heteropolymers.

It has been shown (9–12) that the internal free energy Fint of designed heteropolymers is linear in Q, as is the average entropy loss −soQ. Neither of these linear terms can generate barriers in free energy G(Q). Because we find such a free energy barrier, it must be caused by the entropy minimum found in Fig. 3. (Of course, the specific location of the barrier depends on the linear terms.) We conclude that the free energy barrier separating the U and MG states is a consequence of general heteropolymeric entropy considerations rather than protein-specific details. Recent analytic treatments of heteropolymer folding support this conclusion (V.S.P., A. Y. Grosberg, and T.T., unpublished work). Although the presence of hydrogen bonds in the off-lattice model does sharpen the U ⇌ MG transition (which we have tested by changing the hydrogen bonding energy in the off-lattice simulation), tertiary rather than secondary structure formation is the dominant physical mechanism of this transition.

Barriers to the N State

We find that the MG and N states are not thermodynamically distinct when side-chain packing effects are omitted, as in our off-lattice model. This result implies that the first-order MG ⇌ N transition found in the lattice model is a result of cooperative packing rigidity, in keeping with the analytic theory of Shakhnovich and Finkelstein (13). In our lattice calculation, the barrier between the MG and N states is caused by the scarcity of low internal free energy conformations in which only a few residues have fluctuated from their native positions. Because our off-lattice model has no side-chain packing, the polymer can continuously swell from its native conformation to a molten state with increasing temperature and thus there is no MG–N barrier in this off-lattice model.

Discussion

One might think that the U and MG states could be viewed as two limiting cases of the same non-native phase. Our simulations show, however, that for designed heteropolymers this is generally not the case, because both simulations display a discontinuous, i.e., first-order, U ⇌ MG transition. This is in contrast to the continuous coil-globule transition in homopolymers (15) and random heteropolymers (14). We can understand this striking difference between the behavior of homo- and heteropolymers by considering the loops that are found in partially collapsed states (V.S.P., A. Y. Grosberg, and T.T., unpublished work).

Consider a polymer that is only slightly collapsed. It will have a “liquid” core of contacts surrounded by a “gas” of unfolded flexible loops. As folding conditions are approached, the core grows as more contacts are made, and the remaining loops become shorter. For a homopolymer, these contacts form preferentially where loops enter and exit the nucleus, because this process maximizes the entropy of the remainder of the fluctuating loop while gaining the same internal free energy as any other contact. Loops are therefore smoothly reeled in. This physical picture describes why the homopolymer coil-globule transition is continuous.

For proteins and other designed heteropolymers, however, only specific contacts have favorable internal free energy, and as folding conditions are approached, these contacts will form preferentially. As a result, a given loop is much more likely to be split into two parts by a newly formed contact than to be smoothly absorbed into the nucleus. This fundamental discontinuity in the formation of the core of the globule is responsible for the discontinuous U ⇌ MG transition for well-designed heteropolymers.

By contrast, for random heteropolymers the coil-globule transition is continuous (14) rather than cooperative. We therefore expect that in the limit of large g, the line of first-order U ⇌ MG transitions should either terminate in a critical endpoint or be preempted by a glass transition (10–12, 16, 17). From our simulations we find that the U and MG minima coalesce near Tc = 0.55 and gc = 0.28, which would represent a critical endpoint. (The possibility of a nearby glass transition is, however, difficult to rule out based on our simulations.)

The existence of a critical endpoint to the U–MG coexistence line suggests a unified picture of the U ⇌ MG transition that can explain why some experiments find a first-order transition (6), whereas others (with different proteins and under different conditions) observe a continuous crossover (8): beyond the critical point, the barrier between the U and MG states disappears, and they are no longer distinct phases, in the same way that a vapor and liquid are no longer distinct past their critical point.

Although the loop entropy is central to the nature of the U ⇌ MG transition, mixing entropy accounts for the very existence of the MG by stabilizing a partially folded state whose free energy increases by forming more native contacts. Although more native contacts would reduce the internal free energy of the polymer, the increased structure of the nucleus leads to a more than compensatory reduction in mixing entropy. In this sense, the MG should be a universal phase of proteins, because its stability arises from general physical principles. It follows that the MG phase should appear generically in protein phase diagrams (Fig. 1B), although the triple point may in some cases be difficult to access experimentally.

Conclusions

Is the MG a third phase of proteins? On the basis of the computer simulations and physical arguments detailed above, we find that the MG is analogous to the liquid state of a bulk system. The N/U/MG phase diagram of proteins parallels the solid/vapor/liquid phase diagram of fluids. Each state corresponds to a thermodynamic phase, i.e., a local free energy minimum. The transition between two distinct phases corresponds to the exchange of stability of the respective minima, a first-order (i.e., cooperative) transition. Like the vapor–liquid coexistence line, the U–MG phase boundary appears to end at a critical point. Beyond this point (which corresponds to conditions that destabilize native interactions), there is only a smooth crossover (i.e., noncooperative transformation) from MG to U state with increasing temperature or denaturant. This scenario is consistent with experimental evidence (6, 8).

It remains to be seen whether similarly simplified models can provide useful information regarding the kinetics of protein folding. In particular, the free energy landscapes of Figs. 1 and 2 exhibit well-defined minima separated by saddle-point barriers. If the coordinates Q, NHB, etc., are appropriate reaction coordinates for folding—which is by no means obvious–then each saddle point would define the transition state ensemble of a folding reaction. A more detailed study of these transition states and the role of the MG in the kinetics of folding is in progress.

Acknowledgments

We thank S. Marqusee, A. Chamberlain, and D. Chandler for a critical reading of the manuscript. We acknowledge support from the Miller Institute for Basic Research. D.S.R. acknowledges support from Lawrence Berkeley National Laboratory (LDRD-3669-57) and the National Science Foundation (DMR 91-57414). This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Energy Research of the US Department of Energy.

ABBREVIATIONS

U

unfolded state

N

native state

MG

molten globule

Footnotes

§

Because proteins are finite they cannot exhibit phase transitions in the rigorous sense, but they do show sharp crossovers that resemble first-order transitions whose thermodynamic behavior is well described by a two-state model.

The interaction matrix used for folding Bfold is a weighted sum of the matrix used for design Bdes and a symmetric Gaussian distributed random matrix Bnoise, i.e., Bfold = (1 − g2)½Bdes + gBnoise. As g increases, the degree of design diminishes monotonically (see ref. 27).

‖

We model residues by a sphere of diameter 3.7 Å at the α-carbon position. To model polymeric bonds, these spheres are tethered and their centers must lie between 3.7 Å and 4.0 Å apart. The rigidity of the polypeptide backbone is modeled by harmonic potentials for bending and dihedral angles, with spring constants of 1 kcal per mol per Å and 0.3 kcal per mol per radian, respectively. Two residues are in “contact” if their centers are within 7 Å of each other. For the calculations reported herein, contact free energies of 1 kcal/mol and 0.3 kcal/mol are used for native and non-native contacts, respectively. Our general results do not depend strongly on particular choices for these parameters.

**

In an α-helix, the formation of hydrogen bonds between residues i and i + 4 is determined by the relative orientation and position of the respective carbonyl and amide groups, which are completely specified by positions of the α-carbons i to i + 4. When the simulated α-carbons are properly located, i.e., within 1 Å of the typical distances obtained from the Brookhaven protein database, we say that a hydrogen bond has formed, with a free energy of 4 kcal/mol. The number of such bonds NHB is content of the conformation. This method of modeling secondary structure cannot describe β-sheet formation.

‡‡

The folding of this fragment has been studied previously both experimentally (29, 30) and theoretically (31, 32).

††

In our calculations, we have not considered the disulfide bonds.

§§

Our off-lattice model should also apply to protein-like systems such as de novo designed proteins, which are unlikely to have well-packed side chains (for example, see ref. 34).

References

  • 1.Privalov P L. Adv Prot Chem. 1979;33:167–241. doi: 10.1016/s0065-3233(08)60460-x. [DOI] [PubMed] [Google Scholar]
  • 2.Creighton T E. Protein Folding. New York: Freeman; 1992. [Google Scholar]
  • 3.Ptitsyn O B. Advances in Protein Chemistry. 1995;47:83–229. doi: 10.1016/s0065-3233(08)60546-x. [DOI] [PubMed] [Google Scholar]
  • 4.Ptitsyn O B, Uversky V N. FEBS Lett. 1994;341:15–18. doi: 10.1016/0014-5793(94)80231-9. [DOI] [PubMed] [Google Scholar]
  • 5.Kuwajima K. Prot Struct Funct Genet. 1989;6:87–103. [Google Scholar]
  • 6.Uversky V N, Ptitsyn O B. Fold Des. 1996;1:117–122. doi: 10.1016/S1359-0278(96)00020-X. [DOI] [PubMed] [Google Scholar]
  • 7.Schulman B A, Kim P S, Dobson C M, Redfield C. Nat Struct Biol. 1997;4:630–634. doi: 10.1038/nsb0897-630. [DOI] [PubMed] [Google Scholar]
  • 8.Schulman B A, Kim P S. Nat Struct Biol. 1996;3:682–687. doi: 10.1038/nsb0896-682. [DOI] [PubMed] [Google Scholar]
  • 9.Shakhnovich E I. Fold Des. 1996;1:R50–R54. doi: 10.1016/s1359-0278(96)00027-2. [DOI] [PubMed] [Google Scholar]
  • 10.Pande V S, Grosberg A Yu, Tanaka T. Macromolecules. 1995;28:2218–2227. [Google Scholar]
  • 11.Sfatos C, Gutin A, Shakhnovich E. Phys Rev E. 1993;48:465–475. doi: 10.1103/physreve.48.465. [DOI] [PubMed] [Google Scholar]
  • 12.Pande V S, Grosberg A Yu, Tanaka T. Phys Rev. 1995;E51:3381–3392. doi: 10.1103/physreve.51.3381. [DOI] [PubMed] [Google Scholar]
  • 13.Shakhnovich E I, Finkelstein A V. Biopolymers. 1989;28:1667–1680. doi: 10.1002/bip.360281003. [DOI] [PubMed] [Google Scholar]
  • 14.Pande V S, Grosberg A Yu, Tanaka T. J Chem Phys. 1997;107:5118–5124. [Google Scholar]
  • 15.Grosberg A Y, Khokhlov A R. Statistical Physics of Macromolecules. New York: Am. Institute of Physics; 1994. [Google Scholar]
  • 16.Bryngelson J D, Onuchic J N, Socci N D, Wolynes P G. Proteins. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
  • 17.Dill K A, Bromberg S, Yuc S, Fiebig K, Yee D P, Thomas P D, Chan H S. Protein Sci. 1995;4:561–602. doi: 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Kolinski A, Skolnick J. Proteins. 1994;18:338–352. doi: 10.1002/prot.340180405. [DOI] [PubMed] [Google Scholar]
  • 19.Park B H, Levitt M. J Mol Bio. 1995;249:493–507. doi: 10.1006/jmbi.1995.0311. [DOI] [PubMed] [Google Scholar]
  • 20.Daggett V, Levitt M. Proc Natl Acad Sci USA. 1992;89:5142–5146. doi: 10.1073/pnas.89.11.5142. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Haynie D T, Freire E. Proteins. 1993;16:115–140. doi: 10.1002/prot.340160202. [DOI] [PubMed] [Google Scholar]
  • 22.Shortle D. Curr Opin Struct Biol. 1996;6:24–30. doi: 10.1016/s0959-440x(96)80091-1. [DOI] [PubMed] [Google Scholar]
  • 23.Kay M S, Baldwin R L. Nat Struct Biol. 1996;3:439–445. doi: 10.1038/nsb0596-439. [DOI] [PubMed] [Google Scholar]
  • 24.Shakhnovich E, Gutin A. Biophys Chem. 1989;34:187–199. doi: 10.1016/0301-4622(89)80058-4. [DOI] [PubMed] [Google Scholar]
  • 25.Ueda Y, Taketomi H, Go N. Int J Peptide Res. 1975;7:445–459. [PubMed] [Google Scholar]
  • 26.Miyazawa S, Jernigan R. Macromolecules. 1985;18:534–552. [Google Scholar]
  • 27.Pande V S, Grosberg A Yu, Tanaka T. Fold Des. 1997;2:109–114. doi: 10.1016/s1359-0278(97)00015-1. [DOI] [PubMed] [Google Scholar]
  • 28.Levitt M, Warshel A. Nature (London) 1975;253:694–698. doi: 10.1038/253694a0. [DOI] [PubMed] [Google Scholar]
  • 29.Deisenhofer J. Biochemistry. 1981;20:2361–2370. [PubMed] [Google Scholar]
  • 30.Gouda H, Torigoe H, Saito H, Sato M, Arata Y, Shimada I. Biochemistry. 1992;31:9665–9672. doi: 10.1021/bi00155a020. [DOI] [PubMed] [Google Scholar]
  • 31.Boczko E M, Brooks C L., III Science. 1995;269:393–396. doi: 10.1126/science.7618103. [DOI] [PubMed] [Google Scholar]
  • 32.Olszewski K A, Kolinski A, Skolnick J. Proteins. 1996;25:286–299. doi: 10.1002/(SICI)1097-0134(199607)25:3<286::AID-PROT2>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
  • 33.Brown L R, Mronga S, Bradshaw R A, Ostenzi C, Lupurini P, Wuthrich K. J Mol Bio. 1993;231:800–816. doi: 10.1006/jmbi.1993.1327. [DOI] [PubMed] [Google Scholar]
  • 34.Hecht M, Richardson J S, Richardson D C, Ogden R C. Science. 1990;249:884–891. doi: 10.1126/science.2392678. [DOI] [PubMed] [Google Scholar]
  • 35.Quinn T P, Tweedy N B, Williams R W, Richardson J S, Richardson D C. Proc Natl Acad Sci USA. 1994;91:8747–8751. doi: 10.1073/pnas.91.19.8747. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES