The aerodynamics of Argentavis, the world's largest flying bird from the Miocene of Argentina

Abstract

We calculate the flight performance of the gigantic volant bird Argentavis magnificens from the upper Miocene (≈6 million years ago) of Argentina using a computer simulation model. Argentavis was probably too large (mass ≈70 kg) to be capable of continuous flapping flight or standing takeoff under its own muscle power. Like extant condors and vultures, Argentavis would have extracted energy from the atmosphere for flight, relying on thermals present on the Argentinean pampas to provide power for soaring, and it probably used slope soaring over the windward slopes of the Andes. It was an excellent glider, with a gliding angle close to 3° and a cruising speed of 67 kph. Argentavis could take off by running downhill, or by launching from a perch to pick up flight speed. Other means of takeoff remain problematic.

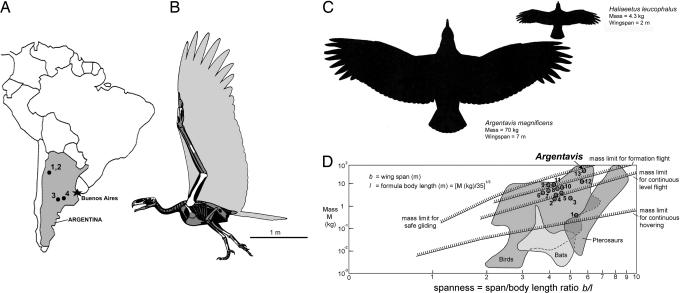
Few prehistoric animals have captured the imaginations of paleontologists so profoundly as has Argentavis magnificens from the upper Miocene (≈6 million years ago) of Argentina with its enormous size and predatory lifestyle. With an estimated mass of 70–72 kg and a wingspan of ≈7 m, it was the world's largest known flying bird (1–10), about the size of a Cessna 152 light aircraft. As a result, the aerodynamics of Argentavis has been fertile ground for speculation for the last 25 years by qualitative analogy with other large flying birds (4, 6–8). Argentavis fossils are known from four localities of upper Miocene continental deposits of central and northwestern of Argentina (Fig. 1A and B), of which localities 1 and 2 lie near the western side of the Andean foothills, whereas localities 3 and 4 are located in the pampas (7, 8). Argentavis is a member of the extinct avian family Teratornithidae, a predatory group of birds known from Miocene to Pleistocene deposits that was related to storks (Ciconiidae) and New World vultures (Vulturidae) within the order Ciconiiformes (10). The most prolific fossil remains of teratorns include hundreds of specimens from >105 individuals of Teratornis merriami entrapped in the upper Pleistocene Rancho La Brea tar pits in Los Angeles, California (2). With an estimated wingspan of 3.5 m and body mass of 13.7 kg, Teratornis merriami shows a body plan and skeletal proportion similar to those of Argentavis and provides important clues to scaling of the missing elements of Argentavis (Table 1). In this report, we present aerodynamic analyses to calculate the flight performance of Argentavis using a flight simulation model originally developed by helicopter designers (11) that reveals details not only of its takeoff and landing strategies, but also its postulated skillful thermal soaring techniques and possible inability to sustain powered or flapping flight.

Fig. 1.

Location and size of Argentavis. (A) Map of Argentina showing four fossil localities of Argentavis from upper Miocene deposits (≈6 Ma); 1 and 2, Andalhualá Formation, near Catamarca in Valle de Santa Maria in the foothills of the Andes; and the Epecuén Formation at 3, Carhué; and 4, near Salinas Grandes de Hidalgo in the Argentinean pampas (simplified from ref. 8). (B) Skeletal restoration of Argentavis showing the known elements by white, based upon corresponding bones of Teratornis merriami in the Natural History Museum of Los Angeles County. (C) Dorsal wing profile in silhouette of Argentavis is compared for scaling with those of a Bald Eagle (after ref. 9). (D) Relation between mass and spanness of three groups of flyers (birds, bats, and pterosaurs) occupying their distinct areas in the chart, each showing the range of their flying styles as size increases. The chart shows four sloping hatched bands, the lower edges of which correspond to the theoretical estimates in the upper mass limits, respectively; note that Argentavis occupies the upper size limit of gliding flight (after ref. 11). Numbers next to circles in the bird island correspond to 13 species of soaring landbirds listed in Table 1 (modified from ref. 15).

Table 1.

Aerodynamic data of 13 species of thermal soaring birds and a motor glider Schleicher ASK-14

Species	Body length (l), m	Mass (M), kg	Weight (W), N	Wing area (S), m2	Wing span (b), m	Aspect ratio (A=b2/S)	Wingspan/body length (ratio b/l)	Wing loading (WL = Mg/S), N/m2	Root-chord/ body length ratio co/l (4S/π)1	Power available (Pavail), W	Cruising speed
											m/s	km/h
1. Black kite (Milvus migrans)	0.26	0.63	6	0.24	1.37	7.8	5.26	25.8	0.86	7	9	33
2. Egyptian vulture (Neophron percnopterus)	0.38	1.9	19	0.32	1.68	8.8	4.42	58.2	0.64	15	14	50
3. Tawny eagle (Aquila rapax)	0.39	2		0.45	2	8.89	5.13	44	0.73	16	12	44
4. White stork (Ciconia ciconia)	0.46	3.4	33	0.54	2.18	7.42	4.74	61.8	0.69	23	15	53
5. White-headed vulture (Trigonoceps occipitalis)	0.47	3.7	36	0.67	2.23	6.7	4.74	54.2	0.8	24	14	50
6. Golden eagle (Aquila chrysaetos)	0.51	4.6	45	0.65	2	6.15	3.92	69.4	0.81	28	16	59
7. White-backed vulture (Gyps africanus)	0.54	5.38	53	0.69	2.18	6.9	4.03	76.5	0.75	31	17	60
8. Marabou stork Leptoptilos crumeniferus)	0.59	7.09	70	0.94	2.62	7.3	4.44	74	0.77	37	16	58
9. Rüppell's griffon (Gyps rueppellii)	0.6	7.57	74	0.83	2.41	7	4.02	89.5	0.73	39	18	64
10. White pelican (Pelecanus onocrotalus)	0.62	8.5	83	0.99	2.91	8.6	4.69	84.2	0.7	42	17	59
11. California condor (Gymnogyps californianus)	0.65	9.5	93	1.32	2.74	5.7	4.22	70.6	0.94	45	17	61
12. Teratornis merriami	0.73	13.7	134	1.74	3.93	8.9	5.38	77.2	0.77	57	16	57
13. Argentavis magnificens	1.26	70	687	8.11	7	6.04	5.56	84.6	1.17	170	19	67
14. Scheicher ASK-14	2.13	340	3,335	12.6	14.3	16.2	6.71	265	0.53	916	25	90

Cruising speed was calculated from ANFLTSIM (table modified from ref. 15).

Flight Performance

Although Argentavis was close to the theoretical upper size limit for safe gliding (12), and ≈16 times heavier than the Bald Eagle (Haliaeetus leucophalus) (Fig. 1 C and D), the fact that it flew is evident from a suite of anatomical evidence, including light and pneumatic bones, robust and elongated wing elements, and large and widely spaced quill nodes on the ulna for the attachment of secondary feathers. Its primary feathers (scaled up from those of California Condor) would have been ≈140–150 cm long and 12–14 cm wide (3). Despite its flight adaptation, there is a great deal of controversy over how this giant extinct bird could take off, fly, and safely land (1–4, 6–9).

Flapping flight, although more versatile than gliding, requires a constant supply of power derived from the flight muscles. The larger the bird, the greater the amount of power required to sustain flapping flight. Flight muscles average 17% of the body mass irrespective of the size of birds, of which the pectoralis muscle represented the major bulk, or ≈91% of the total flight muscle (13), as it provides the crucial downstroke for powered flight. For Argentavis, using a conservative mass estimate of 70 kg, the pectoralis muscle would approximate 11 kg, which is not large enough to produce enough power for continuous flapping for such a heavy animal. However, the sternum of Teratornis merriami is twice as wide as that of a California Condor, while being of the same length, and the carina, or keel, is half again as deep. The body mass of Teratornis was ≈33% greater than that of a California Condor, but the mass of the pectoral musculature is estimated to have been ≈200% greater. Size and mass of the flight muscles could be scaled, if the sternum of Argentavis were known. We have used empirical methods to calculate the metabolic energy and mechanical power from the body weight of Argentavis [see supporting information (SI) Text]. The key to understanding the biomechanics of powered flight lies with the margin between the power required for flight and the power available for that purpose (14).

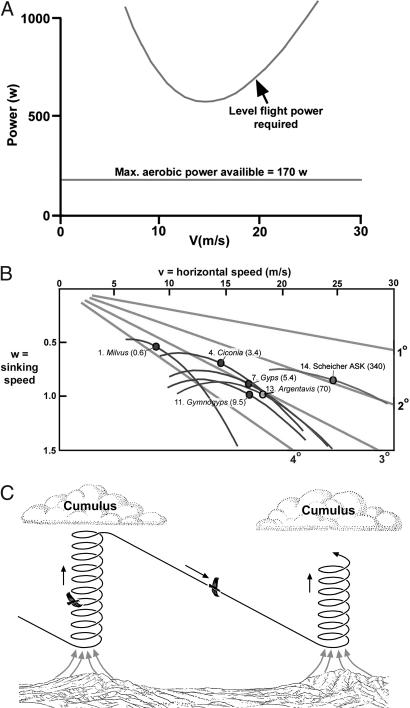
To analyze the flight performance of Argentavis and to determine whether it was a flapper or a glider, as well as its takeoff and landing capabilities, we used two computer algorithms, ANFLTPWR (animal flight power) and ANFLTSIM (animal flight simulation), which are based on the streamtube model (11, 12) using several flight parameters (Table 1). Using ANFLTPWR program, we generated the power curve of Argentavis (Fig. 2A), where the U-shaped curve is the power required for steady level flight, and the horizontal line is the estimated maximum steady power available. Because the two curves, that is, power required and power available, do not coincide, Argentavis, like most of the large soaring landbirds, seems to have been too large to sustain powered flight. For Argentavis, the estimated mechanical power available was 170 W [see SI Text], whereas a minimum power required for sustained fight was 600 W, or ≈3.5 times the estimated power available (Fig. 2A).

Fig. 2.

Flight performance of Argentavis. (A) Power curve (steady level flight) for Argentavis. The horizontal line represents the estimated maximum continuous power available (170 W), assuming pectoral muscle mass comparable with average percent of all birds, and the U-shaped curve represents the power required for steady powered level flight (>600 W). Because these two curves do not intersect, continuous flapping flight was almost certainly not possible for Argentavis. (B) Glide polar for Argentavis, compared with four species of extant soaring raptors: Black Kite (Milvus migrans), White Stork (Ciconia ciconia), White-backed Vulture (Gyps africanus), and California Condor (Gymnogyps californianus), as well as a motor glider ASK-34 (15); body mass of each bird is shown in parentheses (see Table 1). Lines of glide slope angles are also shown. For most birds including Argentavis, the minimum glide slope is close to 3°, indicating excellent gliding capability. (C) Many landbirds soar by circling in thermals that require climbing successive thermals and gliding in the desired direction. It is likely that Argentavis also exploited thermals for cross-country flight in the Argentinean pampas.

We used ANFLTSIM program (11) to calculate gliding performance for four species of extant predatory birds (Black Kite, White Stork, White-backed Vulture, and California Condor), as well as Argentavis and a motor glider, the Scheicher ASK-34 (15) as shown in individual polar curves relating sinking speed versus horizontal speed (Fig. 2B). For most birds including Argentavis, the minimum glide slope is close to 3°, which indicates that these birds are high-performance gliders. Interestingly, the gliding performance of birds does not depend on size as such, but on the maximum lift/drag ratio, which remains nearly constant for birds of similar wing/body geometry. The best gliding speed is roughly proportional to the square root of the wing loading, which is 70.6 N/m² for the California condor and 84.6 N/m² for Argentavis. The glide polar curves show that there is a progression of cruising speed in birds as size increases: the larger the size, the faster the potential glide speed (Table 1). Like modern gliding birds, Argentavis would continually morph its wings to control its glide performance, especially during landing.

Soaring

Landbirds take advantage of updrafts from wind currents to use two types of static soaring while holding their wings still: slope soaring and thermal soaring (14–16). Because the fossils of Argentavis are found from the foothills of the Andes to the pampas (Fig. 1A), it is likely that it used primarily slope soaring over the windward slopes of the Andes and thermal soaring over the open pampas. In slope soaring, a bird flies in a region of rising air caused by upward deflection of wind over a ridge or a cliff. If the sinking speed of the animal is less than the velocity of the rising air, the bird is able to remain airborne indefinitely without flapping its wings. Using ANFLTSIM, we have calculated the sinking speed of Argentavis, which is ≈1 m/s (Fig. 3B). As long as the upward velocity of the rising air over the Andean slope is >1 m/s, which should be fairly common, Argentavis could exploit slope soaring for a long time. For example, a moderate wind blowing at 20 km/h directly along a 10° slope will have a vertical component of ≈1 m/s. The constant blowing of the east wind that originates in the South Atlantic and blows west across the pampas against the eastern Andean foothills would create a steady source of rising air along the line of the slope enabling Argentavis to cover long distances with little effort (17). Under optimal wind conditions, Argentavis could attain speeds estimated to reach ≈67 kph by soaring along the long ridges of the Andes (Table 1).

Fig. 3.

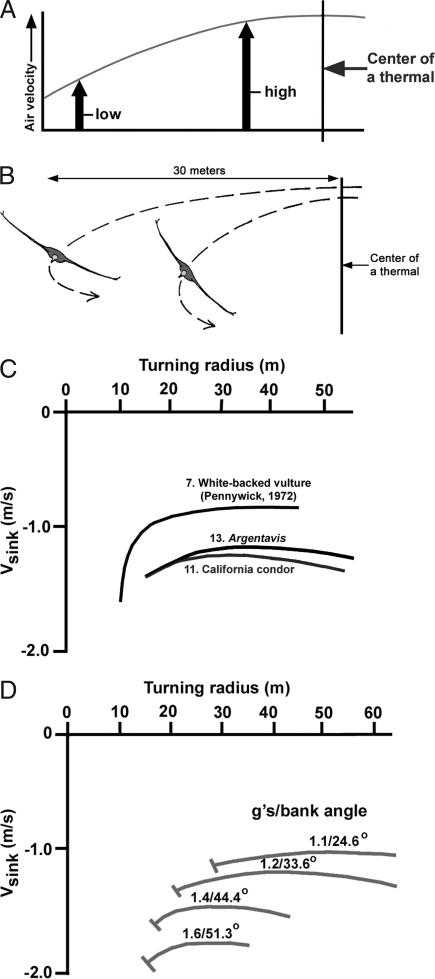
Thermal soaring technique. (A) The upward air velocity in a symmetrical thermal decreases with distance from the center (14). (B) A bird turning in a small circle is able to climb faster than a bird flying in a wider circle because there is less lift round the outside of the thermal. To fly in circles, the wings must be banked, and increasing the angle of bank can tighten the turn. The most efficient circling radius is proportional to the wing loading. (C) Turning radius plotted against the sinking speed for three soaring birds: White-backed Vulture (14), California Condor, and Argentavis (see Table 1 for aerodynamic data). (D) The turn can be tightened by banking further at higher g levels. For Argentavis, it is seen that the sinking speed increases rapidly as the turn is tightened, but there seems little difficulty in holding turns of 30 m radius at sinking speeds close to 1 m/s.

Argentavis probably used thermal soaring over the vast open expanses of the pampas to remain airborne while searching for prey. This mode of nonflapping flight would have been energetically very economical and efficient for Argentavis, a strategy used by many modern carnivorous birds for foraging. Large broad-winged landbirds, such as eagles, buzzards, storks, and vultures with slotted wings are masters of thermals and travel cross-country by gliding in circles where the altitude is maintained or gained by rising air. They soar effortlessly for hours and often climb 2–3 km into the air within a thermal in subtropical and tropical regions (15, 16). Thermal soaring does not depend on wind, but on convection currents created by solar radiation that heats the ground to well above air temperature. Air close to the surface is heated by the ground and rises in columns. Thermals can be continuous chimneys of rising air, or a series of discrete, doughnut-shaped bubbles (18). A thermal generally contains a zone of rising air of limited extent, with the vertical air velocity strongest in the middle, and decreasing outwards (15) (Fig. 3A). Pennycuick (15) mentions areas of lift 1–2 km in diameter over the Serengeti Plain in East Africa, but points out that the strongest uplift occurs at the center and that during cross-country soaring the birds tend to flock in narrow circles as they move from thermal to thermal. Moreover, many thermals over unevenly heated ground are of relatively small diameter. A canopy of cumulus clouds, which may form often in humid condition by condensation of cooler air at high altitude, is the landmark for locating a thermal (18). Once within a thermal, a bird can circle and climb vertically within the rising column as long as the upward speed of the thermal is greater than the sinking speed of the bird. As it reaches the top of the thermal, the bird can glide straight to an adjoining thermal and gain height again by riding the rising air (Fig. 2C). Vultures over the Serengeti can make a round trip of 200 km by skillfully riding updrafts while searching for carrion (15, 16).

To stay within a thermal, a bird must be capable of turning fairly tight circles as close as possible around the center. When circling, the bird banks such that its wing lift has a force component directed toward the center of the turn to balance the centrifugal force (Fig. 3B). The circling capability of a bird within a thermal can be deduced by plotting the turning radius against the sinking speed (14–16). Argentavis could circle by holding a turn of 30 m radius as long as the upward velocity is 1 m/s or more (usually 5 m/s). The minimum turning radius is achieved by flying as close as possible to stalling speed, but at some cost to sinking speed (Fig. 3C). The thermal size needed by Argentavis to climb near the ground is of the order of 100 m diameter. Argentavis could tighten its turn by banking more steeply, which entails an increase in the rate of sink (Fig. 3D); the smaller the radius of circling, the greater the sinking speed (15). Likely, Argentavis could travel by gliding from thermal to thermal, sometimes over long distances between its roost sites and feeding areas.

Takeoff and Landing

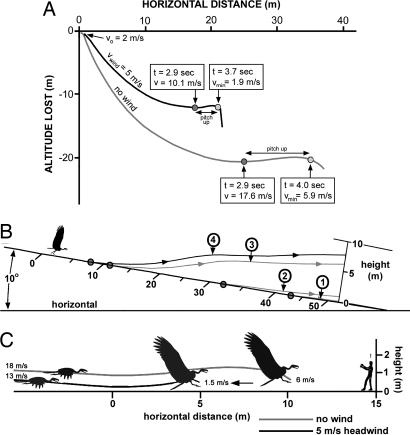
Takeoff and landing are the two most arduous tasks for large flying birds. The Great Kori Bustard (Ardeotis tardi) is the largest modern flying bird, with body masses up to 18 kg (19), but it takes off only with great difficulty by running like taxiing aircraft (20). Could Argentavis, ≈3.5 times heavier than the Great Kori Bustard, take off from the ground? The large size of Argentavis and its postulated inability to maintain sustained flight raise questions about how it was able to launch itself into the air. We have used ALFLTSIM to calculate the metabolic power (P) needed to take off, distance required for lift-off, and speed of Argentavis (11). One possibility for Argentavis is to take off from an elevated perch (8). A light headwind (≈5 m/s) is helpful in reducing the necessary ground speed and distance during takeoffs. Fig. 4A shows two such glide trajectories after horizontal launches at 2 m/s, one without wind and one with a 5 m/s headwind blowing toward the bird. As airspeed increases, lift becomes greater than the bird's weight and the path flattens rapidly to near level after dropping ≈20 m with no wind and ≈12 m with a 5 m/s headwind.

Fig. 4.

Takeoff and landing capabilities of Argentavis. (A) Glide paths of Argentavis from a perch at 2 m/s, and then pulling up at a maximum continuous power. Note the sensitivity of headwind of 5 m/s blowing toward bird that greatly reduces height loss and the minimum speed in the pitchup. (B) Figure shows four simulated takeoff runs on a 10° sloping surface along which the gravity component of force is equivalent to an additional 600 W of propulsive power at a running speed of 5 m/s. Argentavis could take off by running downhill with a light headwind of 5 m/s. (C) Safe landing strategy of Argentavis. Because a maximum landing speed of ≈5 m/s is considered marginally safe (11), the presence of some wind seems essential.

Although the pampas were probably a part of the home range for Argentavis (2, 3, 8, 21), specially during the summer months with plentiful thermals, the presumed lack of sufficient power and a high stalling speed suggests that Argentavis was incapable of making a successful running takeoff from level ground. However, even a gentle down-slope and a light headwind (≈5 m/s) add a significant increase in forward thrust and power, which would have enabled Argentavis to take off from the ground, a technique often used by the extant albatrosses (22) and hang glider pilots. For example, 10° of downward slope adds a forward thrust of 120 N, and at a running speed of 5 m/s, the added thrust power is 600 W. This power is more than the difference between the level flight power and the aerobic power available to Argentavis (Fig. 4B). If Argentavis could run at speeds up to 5 m/s, takeoff down a short 10° sloping surface should be possible, even with little wind, provided of course that thermal drafts of at least 1 m/s are occurring in the vicinity. The problem of ground takeoff might well have set the upper limit to the size of flying vertebrates such as pterosaurs and birds (20).

Could Argentavis take off by merely spreading its large wings in a strong headwind of more than ≈10 m/s? Probably not, because its enormous size and postulated lack of sufficient muscle power might have worked against it. Simulation with a 3D version of ANTFLTSIM has shown that, regardless of whether flight continues into the headwind, or follows a rapid 180° climbing turn downwind, a gliding descent to level ground is postulated within a few seconds if no thermal uplift is available, and maintenance of steady level flight was also improbable for this underpowered bird. However, getting airborne must have been the most difficult part of flight for Argentavis, and if the muscle power available to it was significantly greater than the average percentage for flying birds, then maneuvering in strong winds might not have been problem.

Landing is hazardous for large birds because of high body mass and wing loading. If a bird lands too hard or fast, it could crush and hurt itself. Birds use their feet as air brakes, lowering them to lose speed. In our simulations, a rapid pitchup was initiated for Argentavis with the wing acting as a horizontal high-drag sloping parachute that retains some lift. This pitchup is similar to the landing technique of some large birds as they approach landing on the ground. In the two cases (with and without headwind) the minimum speed reaches 5.9 and 5.0 m/s, respectively. Because a maximum landing speed of ≈5 m/s is considered marginally safe (11), the presence of some wind seems essential. Landings can also be made at the end of a long flat glide (Fig. 4C). The flattest sustainable glide angle of Argentavis is estimated to be ≈3° at airspeed of 18 m/s. This landing speed is well above a safe speed for touchdown, but the two flight simulations show how the high-drag pitchup, often seen in the final approach of many birds, can rapidly brake a landing, especially if made into a moderate headwind.

Discussion and Conclusion

We employ aerodynamic techniques to model the flight performance of the giant bird Argentavis in the Miocene environment of Argentina. The Neogene uplift of the Andes Mountains has caused extensive changes in South American climate and atmospheric circulation. By the late Miocene, the major structural uplift of the Andes Mountain in the Argentinean sector by the continued subduction of the Nazca plate beneath the South American plate led to nearly modern elevations (23), which formed a barrier to southeast trade winds in the subtropics and for westerly trade winds in the mid-latitudes. Also, the South American plate has occupied the present geographic position since the late Miocene (24). If the orographic barrier of the Andes during the Miocene approached that of today, the wind circulation patterns would have differed little from those of today. However Argentina was more arid and warmer during the age of Argentavis than it is today, as documented by extensive evaporite sequence along the western part, which when combined with intense solar radiation, would have been ideal for creating large thermals in the open, nonforested areas of cliffs and pampas (23). Argentavis would be generally confined to areas where appropriate winds were available to support its soaring flight. These habitats include dry pampas that produce strong thermals and high Andean mountains with deflected winds off the steep slopes. Because of longitudinal and elevation amplitudes, the wind regime of Argentina is variable showing a diurnal seasonal circulation alternating between easterly upslope mountain winds, influenced by warm, moist air of the South Atlantic Anticyclone, and downslope valley winds of westerlies, controlled by the atmospheric circulation of the East Pacific Ocean (17). From known fossil localities it seems that Argentavis occupied a large subtropical territory (Fig. 1A), possibly characterized by hot, humid summers with periodic droughts and mild winters. The topography of the habitat of Argentavis was essentially that of a large plain, which rises gradually from east to west, with interspersed high ground. Argentavis probably exploited both slope and thermal soaring to travel long distances.

The extant Andean Condor (Vultur gryphus), the largest soaring land bird of South America, with a wingspread up to 3.2 m, might provide some clue to the habitat of Argentavis. Like the condors, Argentavis could have frequented mountain areas, where the more irregular terrain would offer suitable launching sites for taking off. Argentavis also visited, or lived in, the pampas, as their fossil records demonstrate, where they could count on brisk winds and strong thermals. Like condors, Argentavis was undoubtedly suited for long-distance travel and would have adapted similar strategies to maximize its chances of finding food. Argentavis must have preferred open areas, because its large wings would have made maneuvering around trees and tall shrubs hazardous. Cranial morphology indicates that Argentavis, like other teratorns, was an active predator (2) rather than a scavenger (21) (Fig. 1B). It was probably a diurnal predator, dependent on thermals for flight activity for much of the time much as large, broad-winged carnivorous birds we see today. Strong thermals occur by mid-day and disappear in the evening, so thermal soaring for Argentavis would have been possible only between those times. With a skull >55 cm long and 15 cm wide, Argentavis was capable of catching sizeable prey with its formidable beak (2).

Methodology

Various skeletal measurements were calculated from several specimens of Argentavis at the collection of the Natural History Museum of Los Angeles County; the missing parts were calibrated from skeletons of Teratornis (1–4, 6, 7). There is no direct evidence for the overall shape of the wing of teratorns, so we have reconstructed it by extrapolation from that of Teratornis merriami, which is very comparable in wing bone structure with condors (2, 3). The wingspan (b) and wing area (S) were estimated from dorsal reconstruction of Argentavis (4, 6). We digitized the wing margin in dorsal aspect with a computer program by F. J. Rohlf (http://life.bio.sunysb.edu/morph) and estimated the wing area. We used the conservative mass estimate of 70 kg for Argentavis employing a multivariate analysis proposed by Atanassov and Strauss^¶; the previous bivariate estimate of mass was 71.9 kg (5). Wingspan value of Argentavis used in the analyses was 7 m and the wing area is 8 m². The flight parameters of Argentavis and other soaring birds are shown in Table 1. To analyze the flight performance of Argentavis, we used two computer algorithms, which are based on the streamtube model (11) and also described in Flight Performance. In all cases, the body and drag coefficients are computed as functions of the Reynolds number (see refs. 11 and 12 and SI Text for detailed methodology).