Probing genetic overlap among complex human phenotypes

Abstract

Geneticists and epidemiologists often observe that certain hereditary disorders cooccur in individual patients significantly more (or significantly less) frequently than expected, suggesting there is a genetic variation that predisposes its bearer to multiple disorders, or that protects against some disorders while predisposing to others. We suggest that, by using a large number of phenotypic observations about multiple disorders and an appropriate statistical model, we can infer genetic overlaps between phenotypes. Our proof-of-concept analysis of 1.5 million patient records and 161 disorders indicates that disease phenotypes form a highly connected network of strong pairwise correlations. Our modeling approach, under appropriate assumptions, allows us to estimate from these correlations the size of putative genetic overlaps. For example, we suggest that autism, bipolar disorder, and schizophrenia share significant genetic overlaps. Our disease network hypothesis can be immediately exploited in the design of genetic mapping approaches that involve joint linkage or association analyses of multiple seemingly disparate phenotypes.

In “simple” disorders with proven Mendelian inheritance, a single-nucleotide aberration in the genome can cause one disease while protecting against another; one nucleotide substitution can also manifest in multiple physiological systems. For example, a single-nucleotide substitution in a human β-globin gene (HBB) triggers in its bearer a drastic change of erythrocyte shape (sickle-cell anemia) but protects against invasion of the protozoan parasite (Plasmodium falciparum) that causes malaria. When designing a mathematical model that describes pairs of disease phenotypes, we can think of sickle-cell anemia and malaria as competing for the same nucleotide site in the human genome. In another example, a single-nucleotide polymorphism in the CFTR gene profoundly affects the bearer's digestive, reproductive, and respiratory systems and causes excessive loss of salt through sweating (a group of symptoms collectively known as cystic fibrosis). By analogy with our metaphor of phenotype competition for genes, we will say that these disparate phenotypic manifestations in cystic fibrosis cooperatively share the same nucleotide substitution (i.e., the substitution has a pleiotropic effect).

Does this logic of competitive or pleiotropic genetic polymorphisms extend to human disorders that have more complex (and largely unknown) genetics? We think it does. Here, we suggest a method for assessing such overlaps between complex phenotypes (a reframed comorbidity analysis), then demonstrate its application to a set of 161 disorders described in 1.5 million patient records from a clinical database at the Columbia University Medical Center.

We selected disorders that represent a broad spectrum of maladies, from common to rare, affecting diverse physiological systems, yet we also placed special emphasis on neurological phenotypes [Fig. 1 gives a complete account of phenotypes that we analyzed; we provide information on symptoms and patient statistics for each phenotype in supporting information (SI)]. Our choice of phenotypes reflect a view that the etiology of every human malady, even one as recently encountered and as clearly linked to an environmental cause as AIDS, includes a significant component of hereditary predisposition and/or resistance. For example, a series of recent studies showed that a significant proportion of people are partially or completely resistant to HIV infection, whereas other people have a predisposition to rapid AIDS progression once HIV infection has occurred (1).

Fig. 1.

Probability that a person manifests symptoms of a disorder before or at age t (given that she/he will be eventually diagnosed with the disease D_i [P(T_i ≤ t-T_i < ∞, e, g; Θ) = 1 − F_i(t-e, g; Θ)]) for the 161 disorders we consider in this study. Each graph has the same format: the x axis represents the individual's age (bounded by 0 and 100 years); the y axis represents the probability that the individual is diagnosed with the specific disorder before or at age t (bounded by 0 and 1). The red and blue curves represent data for female and male patients, respectively. The numbers shown in red and blue indicate the number of records describing female and male patients, respectively, that we used to estimate each disorder-specific curve.

Results and Discussion

Outline of Our Approach.

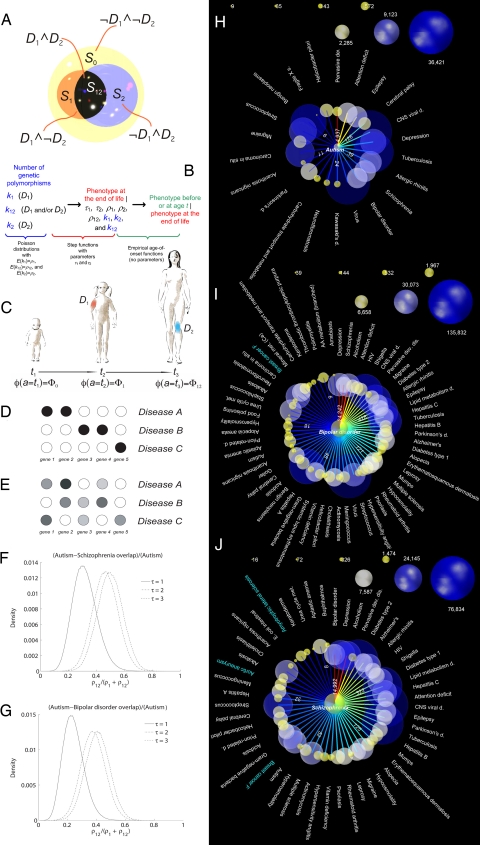
We developed a probabilistic model linking the unobserved genetic variation in human genomes to the observed succession of healthy and disease phenotypes in individual humans. Before formulating the model's assumptions and explaining details of its implementation, let us briefly outline its main components (Fig. 2B). In our description, when we consider a pair of disorders (D₁ and D₂), we model an individual's phenotype at or before a certain age (Fig. 2C). A person is born with (or without) a set of disease-predisposing variations (represented by random variables k₁, k₂, and k₁₂ in Fig. 2B); these variations determine the probability that the person eventually will be diagnosed with the disease (age-integrated phenotype; see Fig. 2 B and C). Given that the age-integrated phenotype involves disease D_i and the individual's life span, the individual can manifest symptoms of D_i at any time during his/her lifetime with probability specified by the time-of-onset function specific to this disease and possibly by the individual's ethnicity and gender (see Fig. 2 B and C). We need to take into account the time course of each disorder to “subtract” all correlations between disorder pairs that are merely due to a commonality or a difference in their onset times. Without this age adjustment, an early-onset disease, such as autism, and a late-onset disease, such as Parkinson's disease, would misleadingly appear as negatively correlated.

Fig. 2.

Model assumptions, definitions, and results of the following analysis. (A–C) The structure and main concepts associated with our model, which describes a pair of disorders, D₁ and D₂. (A) We partition all nucleotide sites in the human genome into four disjoint sets, S₀, S₁, S₂, and S₁₂. (B) Structure of our probabilistic model. Arrows indicate the sequence of probabilistic conditioning in computation of the likelihood under our model (see Methods). (C) Time course of phenotype change as the person ages, as described by our model. In this example, the person starts as a healthy individual at t₁ (phenotype Φ₀); at time points t₂ and t₃, the person displays D₁ and D₂, respectively, so φ(t₂) = Φ₁, and φ(t₃) = Φ₁₂. (D–G) Two hypothetical models of gene-disease mappings (D and E) and estimates of the proportion of autism-specific nucleotide sites that autism “shares” with schizophrenia (F) and bipolar disorder (G). (D) A simple hypothetical model, probably most appropriate for Mendelian disorders, where different disorders are mapped to disjoint sets of genes, with a deterministic relationship between genetic polymorphism and phenotype. (E) A more complicated hypothetical model, probably applicable to common (highly prevalent) disorders, where multiple genes determine predisposition to a disease in a probabilistic and combinatorial fashion. (F) Posterior distribution for estimate of relative size of genetic overlap of autism with schizophrenia under three different models of genetic penetrance (we used an uninformative prior distribution). Parameter τ represents the smallest number of deleterious polymorphisms in disease-specific nucleotide sites required for the disease phenotype to manifest itself. (G) Similar estimate of genetic overlap between autism and bipolar disorder, relative to the genetic basis of autism. (H–J) Significant correlations between pairs of disorders. In each of the four plots, we compare one disorder (in the center of the plot) against the other 160 disorders that we selected for this study. The color of the arc, with corresponding number, represents the value of the Λ statistic. The warm-colored edges have the highest Λ values, and those in the colder part of the color spectrum represent smaller Λ values. All values of Λ >8 are highly significant. The white and turquoise labels indicate disorders that are positively and negatively correlated, respectively, with the disorder in the center of the subplot. The size of a node indicates the number of the disorder-specific patient records in our data set (note that the node scale is different for different plots). (H) Autism, data for male patients only (see SI for analogous analyses of female patients and joint analysis of both male and female patients). (I and J) Bipolar disorder and schizophrenia, joint analyses of both genders.

To implement the model, we need a set of assumptions making our computation tractable.

Assumptions.

Environmental factors (such as physiological stress, diet, lifestyle, and exposure to pathogens) affect human phenotypes through the action of numerous molecules that are produced, distributed within cells and tissues, and used according to gene-encoded scripts. Therefore, our first assumption here is that, if the same environmental effect triggers two (or more) different maladies, it typically does so through molecular mechanisms that are common between these two maladies. Although this assumption is likely to be violated for some pairs of disorders, it is a reasonable starting point for the model. This assumption allows us to develop a probabilistic model linking the unobserved genetic variation to the observed phenotypes. We take into account environmental influence via a data-derived function that approximates the classical age-of-onset distribution, the cumulative probability that a disease manifests itself before or at any given age and given that the person will eventually get the disease (see Fig. 1). Note that these disease-specific functions are highly informative on their own and would merit careful examination. For example, allergic rhinitis, breast cancer, and especially viral infections have markedly different patterns of incidence in males and females; the function shapes are notably variable across disorders.

Our second assumption is that, for each phenotype pair (D₁ and D₂), the whole human genome can be divided into four disjoint sets of nucleotide sites (Fig. 2A). One set (S₀) comprises nucleotide sites that can affect neither of the two phenotypes, regardless of each site's state. Sites within another set (S₁₂) can affect both phenotypes simultaneously, either via a competitive or a cooperative mechanism. The remaining two site sets have the potential of predisposing the bearer exclusively to either phenotype D₁ (set S₁) or D₂ (set S₂) (see Fig. 2A). Depending on our choice of phenotypes, some of these four site sets may be empty.

Our third assumption involves a spectrum of hypothetical mechanisms that connect genetic variation within the four sets of nucleotide sites to the disease phenotype (genetic penetrance). All mechanisms we consider here have in common an intuitive property that, the larger the number of genetic aberrations within the disease-predisposing set of sites, the more likely the disease phenotype will manifest itself. We consider here two families of genetic-penetrance functions: sharp and soft threshold. With a sharp-threshold function, the bearer must have at least τ disease-related polymorphisms (where τ is a positive integer) if she/he is eventually to manifest symptoms of the disease. With τ = 1, we obtain the classic multilocus heterogeneity model, whereas larger values of the parameter represent more complex epistatic gene interaction models (2). With a soft-threshold function (see SI), the relationship between the number of deleterious polymorphisms and the time-integrated phenotype is more complicated: the likelihood that an individual's age-integrated phenotype will include a specific disorder at the end of the individual's life is nonzero for any number of the disease-related variations in her/his genome but grows quickly with an increase in the number of deleterious variations related to the disorder (see SI for details).

Competing Models.

In our data analysis, for every pair of disorders, we choose one of three competing models (hypotheses): (i) the disorders are uncorrelated (which we interpret as a lack of a genetic overlap), (ii) the disorders are significantly negatively correlated (which we interpret as a genetic overlap via competition), or (iii) the disorders are significantly positively correlated (genetic overlap via cooperation; see Methods). The cooperative model is slightly more general than the standard genetic pleiotropy model. The two models are identical when two phenotypes are caused by exactly the same set of genetic polymorphisms; however, unlike the pleiotropy model, the cooperation model allows each phenotype (in addition to the shared polymorphisms) to be associated with a pool of genetic polymorphisms that does not affect the other phenotype. The independence model is a special case of both overlap models, so we can represent results of our analysis with the two log-likelihood-ratio statistics (Λ), comparing both overlap models to the model of independence (Figs. 2 H–J and 3). Furthermore, our parametric model provides an estimate of the size of the hypothetical genetic overlap (Fig. 2E and SI).

Fig. 3.

Significant correlations (that we interpret as genetic overlap) among three neurodevelopmental disorders (autism, bipolar disorder, and schizophrenia; corresponding nodes are shown in yellow) and all other disorders in our data set (blue nodes). The volume of each sphere (disease) is proportional to the number of patient records annotated with the corresponding phenotype, as explained in the key. The arcs represent significant correlations among phenotypes, with negative correlations shown in blue and positive correlations shown in red. Thicker arcs represent stronger correlations; see key.

Correlations and Overlaps.

Our analysis of genetic overlap reveals numerous correlations among disorders, many of which are well established (e.g., see refs. 3–8), whereas other correlations appear previously undescribed.

It is not surprising that autism is strongly correlated with pervasive developmental disorders and fragile X syndrome (Fig. 2H), because autism is included (along with several other disorders) in the formal definition of pervasive developmental disorders, and fragile X syndrome has autism as one of its manifestations. However, it is less obvious why autism, which typically manifests before the affected child is 3 years old, has a strong positive correlation with a number of neurological disorders, some of which have a late-age onset (ordered by decreasing statistical significance; see also Fig. 2H): attention deficit, epilepsy, cerebral palsy, depression, schizophrenia, bipolar disorder, neurofibromatosis, Parkinson's disease, and migraine. Our estimated significant overlap between autism and tuberculosis may indicate that both diseases are associated with genetic changes weakening the immune system.

Another group of phenotypes that overlaps with the most highly prevalent neurological disorders comprises various bacterial, viral, and protozoan infections. In the case of autism, the most strongly positively correlated phenotypes of this group include viral infections of the central nervous system (such as viral encephalitis), tuberculosis, viral infections of other systems, and staphylococcal and Helicobacter pylori infections (phenotypes are sorted here by decreasing significance of correlation). The third group of phenotypes, comorbid with autism and with many highly prevalent neurological disorders, includes allergies and autoimmune disorders, such as allergic rhinitis. Schizophrenia and bipolar disorder are positively correlated with many additional disorders of this group, including diabetes, rheumatoid arthritis, and psoriasis (see Figs. 2 I and J and 3). The fourth group of autism-correlated disorders includes both benign and malignant neoplasms. Autism is also comorbid with Kawasaki's disease [a relatively rare phenotype whose etiology is ill-understood and that probably relies on an unknown pathogen; similar to autism, it affects male individuals significantly more frequently than females (see SI)], acanthosis nigricans, and aberrations of carbohydrate metabolism. Similar groups of highly correlated phenotypes are visible in our analyses of schizophrenia and bipolar disorder (see Fig. 2 I and J), with the important addition that female breast cancer shows strong negative correlations with both schizophrenia and bipolar disorder (unlike other malignancies, including male breast cancer; see SI). This negative correlation is highly significant even when only female patients are analyzed (see SI). The negative correlation may indicate in the framework of our model a competition for genes in the cell cycle/cell death regulation: both schizophrenia and bipolar disorder under this explanation are associated with genetic polymorphisms that increase the probability of abnormal cell death in some tissues, whereas breast cancer is linked to (only partially known) genetic variation leading to an increased probability of abnormal cell proliferation. Although the competitive genetic overlap between bipolar disorder and female breast cancer has not been reported, there is recent indirect evidence that supports it: a well established breast cancer-treatment drug, tamoxifen, was recently discovered to be effective in treating symptoms of bipolar disorder (9).

We show a composite representation of correlations (interpreted as genetic overlaps) for autism, bipolar disorder, and schizophrenia (yellow spheres) and the rest of 158 disorders (blue spheres) in Fig. 3. All blue spheres have one, two, or three incoming arcs, indicating they correlate significantly with one, two, or all three of the yellow-sphere disorders. For example, acanthosis nigricans and cerebral palsy are positively correlated with every member of the yellow-sphere disease triplet. Female breast cancer is significantly negatively correlated with bipolar disorder and schizophrenia (blue arcs) but shows no significant correlation with autism. Neurofibromatosis is significantly positively correlated with autism and bipolar disorder (red arcs) but not with schizophrenia. Aortic aneurysm is negatively correlated with schizophrenia but is independent of autism and bipolar disorder.

Proportion of Autism-Predisposing Polymorphisms That Also Contribute to Schizophrenia or Bipolar Disorder.

So long as our model is designed for estimating the mean number of disease-related polymorphisms (per a randomly sampled human genome) in disease-specific site sets and in genetic overlap among disease pairs, we can use such estimates to assess the proportion of autism-predisposing variation that is shared with bipolar disorder and with schizophrenia (see Fig. 2 F and G).

Despite the fact that the absolute estimates of the expected number of disease-related polymorphisms are different under different models of genetic penetrance (see the model description and tables in SI), the proportion of the polymorphisms that autism shares with bipolar disorder and schizophrenia is consistent across different models (Fig. 2 F and G): we estimate that ≈20–60% of autism-predisposing variations also predispose the bearer to bipolar disorder, and 20–75% of autism-predisposing variations also predispose the bearer to schizophrenia. It is therefore extremely likely that there is a three-way positive correlation among autism, bipolar disorder, and schizophrenia, a correlation that probably arises from a genetic variation that predisposes to all three disorders.

Corollaries.

Our analysis suggests that, instead of following the familiar model of “unique malady–unique (disjoint with others) set of broken genes” applicable to most Mendelian disorders (Fig. 2D), most complex phenotypes are probably rooted in genetic variation that is significantly shared (in either a competitive or cooperative manner) by multiple disease phenotypes (Fig. 2E).

Phenotypes of non-Mendelian disorders are often defined with a considerable degree of fuzziness, especially those that are neurological: it is not uncommon to define a neuropsychiatric disease phenotype as comprising, for example, at least five of a list of 10 symptoms (4). This fuzziness arises because, in many cases, the observed disease is a heterogeneous collection of multiple maladies that have partially similar symptoms and potentially different genetic causes. However, these genetically heterogeneous maladies are combined because of the history of disease identification and the incompleteness of our knowledge about the disease causes.

Our interpretation of genetic overlap among pairs of disorders does not exclude the possibility that one disorder can cause the other. For example, it is possible that comorbidity of autism (or schizophrenia, or bipolar disorder) with infectious and autoimmune maladies indicates that the neurodevelopmental disorder can be triggered by different developmental insults, including viral or bacterial infection, or an autoimmune disease launched by a benign allergen. Another possibility is that the same molecular features that make a child more susceptible to infection or to autoimmune attack have a pleiotropic effect on brain development and function.

Our analysis has immediate practical implications for the design of gene-mapping studies that examine complex phenotypes. Imagine that we can study a set of families (pedigrees) whose members are affected by multiple disorders (for example, autism, bipolar disorder, schizophrenia, diabetes, and psoriasis). If we have reasons to believe that these disorders overlap in terms of disease-predisposing genetic variation, to extract maximum information from available data, we might be able to design genetic linkage or association strategies that analyze multiple complex disorders jointly. Furthermore, by selecting different sets of seemingly disparate disorders, we might be able to examine systematically the genetic background of a wide spectrum of complex phenotypes. In addition, we hope that the estimated disease overlaps will be useful in defining sharper (more specific) phenotypes that are also more genetically homogeneous.

Methods

Data.

Our input data comprise anonymized statistics about patients in the Columbia University Medical Center clinical database (1.5 million records). This database was designed for pragmatic purposes (such as billing) rather than for basic research; thus, in this study, we used a predefined data representation not specifically optimized for our purposes (see SI). With respect to the two diseases, D₁ and D₂, the ith patient (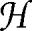 in the notation 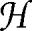_i stands for human) is described with the following pentaplet of variables.

where N is the total number of patients in the database, 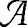_i is the patient's age, 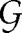_i is the patient's gender, 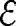_i is his/her ethnicity, and _1,i and _2,i are the patient's ages at the time she/he was first diagnosed with diseases D₁ and D₂, respectively. For the sake of encoding simplicity, we set _k,i to infinity (∞) for patients who were never diagnosed with disease D_k.

The ethnicity, 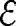_i, attributed to the ith patient in our data can have one of the following codes: A, B, D, E, H, I, M, N, L, O, P, U, W, or X. A table in SI provides the key to these codes.

Variable 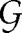_i takes values F (female), M (male), O (other, usually indicating an ambiguity/difficulty in gender assignment), and U (unknown, usually indicating missing data).

Models.

Let us focus on two human diseases, D₁ and D₂, each of which has a distinct hereditary component. We can divide the whole genome into four disjoint sets of nucleotide sites, S₀, S₁, S₂, and S₁₂ (see Fig. 2A). The first set, S₀, comprises genomic sites that have no potential to contribute to either of the two diseases. The second and the third sets of sites, S₁ and S₂, include genomic loci that, when they harbor deleterious polymorphisms, predispose the polymorphisms' bearers to D₁ and D₂, respectively (see Fig. 2A). Finally, the fourth set of sites, S₁₂, involves portions of the genome that predispose an individual who bears mutations in them to both D₁ and D₂ simultaneously. Although here we focus on point mutations, our approach can be extended to other types of genetic polymorphism, such as insertions, deletions, inversions, and translocations.

Phenotypes.

We define the following four phenotypes with respect to diseases D₁ and D₂: Φ₁, Φ₂, Φ₁₂, and Φ₀ correspond to “affected by disease D₁ but not by disease D₂,” “affected by disease D₂ but not by disease D₁,” “affected by both diseases D₁ and D₂,” and “affected by neither disease D₁ nor D₂,” respectively.

Genotypes: Probability of G_i = {k_i,1, k_i,2, k_i,12}.

We denote the total number of deleterious polymorphisms that fall into S₁, S₂, and S₁₂ for individual i with a triplet of random variables {k_i,1, k_i,2, k_i,12}. In our model, these three variables completely describe the individual's genotype, G_i, with respect to diseases D₁ and D₂. We assume that the random variables k_i,1, k_i,2, and k_i,12 independently follow Poisson distributions (10) with rates ρ₁, ρ₂, and ρ₁₂, respectively. If a disease-related nucleotide site set S_k is small, as in the case of sickle-cell anemia (just two sites), we can assume that the observed number of disease-relevant polymorphisms per genome follows a binomial distribution instead of a Poisson distribution (see SI).

Probability of φ(∞) given G_i = {k_i,1, k_i,2, k_i,12} (penetrance function).

We use the notation φ(∞) to denote an individual's phenotype with respect to diseases D₁ and D₂ at the end of his/her life (eventual or age-integrated phenotype; see Fig. 2B). We consider here two definitions of the penetrance function. The first definition postulates that disease D₁ manifests itself only if the number of deleterious variations in S₁ and S₁₂, k_i,1 + k_i,12 is equal or greater than a threshold, τ₁ (similarly, D₂ develops eventually if k_i,2 + k_i,12 ≥ τ₂). The second definition postulates that the threshold value itself is a random variable, so that the probability of developing a disease gradually increases with the number of deleterious polymorphisms (see SI for details).

Probability of φ(t) given φ(∞).

We use the notation φ(t) to indicate an individual's phenotype at or before age t. Let T₁ and T₂ be the ages at onset (or first diagnosis) of diseases D₁ and D₂, respectively. φ(t) = Φ₁ is then equivalent to {T₁ ≤ t, T₂ > t}. Thus, the likelihood of the two-disease phenotype status can be studied using the joint failure time model (11) for T₁ and T₂, based on the genetic factors and covariates such as age and gender. We then define the following conditional distributions for T₁ and T₂,

where k = 1, 2. Note that we can estimate F_k(t_k-e, g; Θ) directly from our data (estimates of 1 − F_k(t_k-e, g; Θ) are shown in Fig. 1). Finally, we define the probability of φ(t) given φ(∞) in terms of probabilities F_k(t_k-e, g; Θ), as shown in Table 1.

Table 1.

Conditional probability of the age-t phenotype [φ(t)] given the ultimate phenotype [φ(∞)]

P(φ(t)|φ(∞), e, g; Θ)	φ(∞)
	Φ0	Φ1	Φ2	Φ12
Φ0	1	F1(t|e, g; Θ)	F2(t|e, g; Θ)	F1(t|e, g; Θ) F2(t|e, g; Θ)
φ(t) Φ1	0	1 − F1(t|e, g; Θ)	0	(1 − F1(t|e, g; Θ))F2(t|e, g; Θ)
Φ2	0	0	1 − F2(t|e, g; Θ)	F1(t|e, g; Θ)(1 − F2(t|e, g; Θ))
Φ12	0	0	0	(1 − F1(t|e, g; Θ))(1 − F2(t|e, g; Θ))
Total	1	1	1	1

Two genetic overlap models: Cooperation and competition.

In the cooperation (generalized pleiotropy) model, the overlap genes can simultaneously contribute to both diseases, whereas in the competition model, the overlapped genes can contribute to only one of the diseases (the choice is made stochastically with probability specific to each pair of diseases; see SI).

Likelihood and Likelihood Ratio Test.

To compute a likelihood value for data representing the ith patient, we need to sum the probability of the observed phenotype [given k_i,1, k_i,2, k_i,12, and φ(∞)] over all admissible values of k_i,1, k_i,2, k_i,12 (k_i,j = 0, 1, …, ∞), and φ(∞) (see SI for description of an efficient computation of this value). If we assume that the vector of parameters, Θ, is the same for all values of e (ethnicity) and g (gender), then the likelihood function is just a product (over all patients) of probabilities of the observed phenotypes given common parameter values (see SI). (Alternatively, we subdivide the data by ethnicity and gender and estimate a separate set of parameters for each data subset.)

At its heart, our analysis is a model selection problem. First, we have two versions of the same model where two disorders have an arbitrarily large genetic overlap (via either a cooperation or competition scenario). Second, we have a simpler model that is nested in both former models, where the two disorders are genetically independent. Put differently, the model where two disorders, D₁ and D₂, are genetically independent (the genetic overlap, nucleotide set S₁₂, is empty [ρ₁₂ = 0]) is a special case of the two models where the same two disorders are either genetically overlapping or independent (S₁₂ = ∅ [ρ₁₂ = 0] or S₁₂ ≠ ∅ [ρ₁₂ ≠ 0]). Therefore, we can use a standard log-likelihood ratio statistic, Λ, for nested models. This Λ statistic asymptotically (as the sample size grows) follows a χ² distribution with the number of degrees of freedom equal to the difference in the number of parameters between the two models (1, in our case) (12).

In the presence of a statistical signal, we can distinguish among the three models (independence, cooperation, and competition) by computing two statistics: Λ_cooperation and Λ_competition.

Availability.

Detailed information on estimated disease overlaps for all pairs of disorders mentioned in this study is available as SI.