The pressure dependence of hydrophobic interactions is consistent with the observed pressure denaturation of proteins

Abstract

Proteins can be denatured by pressures of a few hundred MPa. This finding apparently contradicts the most widely used model of protein stability, where the formation of a hydrophobic core drives protein folding. The pressure denaturation puzzle is resolved by focusing on the pressure-dependent transfer of water into the protein interior, in contrast to the transfer of nonpolar residues into water, the approach commonly taken in models of protein unfolding. Pressure denaturation of proteins can then be explained by the pressure destabilization of hydrophobic aggregates by using an information theory model of hydrophobic interactions. Pressure-denatured proteins, unlike heat-denatured proteins, retain a compact structure with water molecules penetrating their core. Activation volumes for hydrophobic contributions to protein folding and unfolding kinetics are positive. Clathrate hydrates are predicted to form by virtually the same mechanism that drives pressure denaturation of proteins.

A decade ago, Walter Kauzmann (1) challenged the commonly held view that a hydrophobic core stabilizes globular proteins, by poignantly remarking that the “liquid-hydrocarbon model (2) fails almost completely when one attempts to extend it to the effects of pressure on protein folding.” Although a variety of forces stabilize folded proteins (3–6), the formation of a hydrophobic core is thought to play a dominant role. This view is supported by the temperature dependence of hydrophobic contributions to protein unfolding showing remarkable similarities to the transfer of hydrocarbons from a nonpolar phase into water, notably a convergence of the entropy of transfer (2, 7, 8). However, Kauzmann (1) pointed out that the pressure dependence of protein unfolding is at odds with the hydrophobic-core model: The volume change ΔV upon unfolding is positive at low pressures but negative at pressures of about 100–200 MPa. The transfer of hydrocarbons into water shows exactly the opposite behavior, with ΔV being negative at low pressures and positive at high pressures.

Evidently, pressure unfolding of a protein (9–16) does not correspond to the transfer of a nonpolar molecule from a nonpolar environment into aqueous solution. Unlike heat-denatured proteins, the ensemble of pressure-denatured proteins retains elements of structural organization (13, 17). Consequently, an understanding of the thermodynamics of pressure denaturation might focus on the free energy of water transfer into the hydrophobic core of the protein (18) rather than transfer of nonpolar solutes into water. Our conceptual framework for pressure denaturation is as follows: the protein interior is largely composed of efficiently packed residues, more likely hydrophobic than those at the surface (19). Increasing hydrostatic pressure then forces water molecules into the protein interior, gradually filling cavities, and eventually breaking the protein structure apart.

We therefore study the effects of pressure on the association of nonpolar residues in water. We use the information theory model of hydrophobic interactions, a unification (20–22) of the Pratt–Chandler (23) and scaled particle theories (24, 25) of hydrophobic effects. The information theory model accounts for the primitive hydrophobic effects of solvation, association, and conformational equilibria of small nonpolar solutes in water (20). We have previously studied the temperature dependence of hydrophobic hydration by using the information theory model (8). This study reproduced the characteristic entropy increase with temperature and entropy convergence at about 400 K, in accord with calorimetry experiments (2). Here, we use the information theory model to predict the association of hydrophobic particles as a function of pressure. Specifically, we focus on the potential of mean force (pmf) between two and three nonpolar solutes (23, 26–32). The effect of water insertion into a nonpolar aggregate is then quantified by calculating the free energy difference between the contact minimum and the solvent-separated minimum in the pmf.

MATERIALS AND METHODS

The information theory model (8, 20, 21) describes the occupancy fluctuations for molecular volumes within liquid water by using the water number density ρ and water-oxygen pair correlation function g(r). The probability p₀ of zero occupancy yields chemical potentials of cavity formation (33–35) for nonpolar solutes,

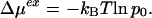1

In its simplest form, the information theory model utilizes the experimentally accessible first and second moments of the number of solvent centers inside the cavity volume v,

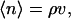2

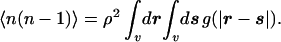3

The moments are used as constraints in the maximum-entropy calculation that estimates the probabilities p_n to observe n solvent centers inside the solute cavity v. In its simplest form the p_n are of discrete Gaussian form, p_n = exp(λ₀ + λ₁n + λ₂n²) with n = 0, 1, 2, … , where λ₀, λ₁, λ₂ are Lagrange multipliers to be determined from the constraints of available information and the normalization condition, Σ_n=0^∞p_n = 1.

The water–oxygen pair correlation functions used in the information theory calculations were determined from Monte Carlo simulations of 256 SPC water molecules (36) at 298 K for densities between 0.975 and 1.2 times the standard density ρ₀ = 997.07 kg⋅m⁻³ at density intervals of 0.025 ρ₀. Ewald summation was used for electrostatic interactions (37). The pressure p was calculated from p = ρk_BT − 〈∂U/∂V〉, where the last term is the ensemble average of the volume derivative of the potential energy that contains contributions from the volume dependence of the effective Ewald potential. The pressure behavior of SPC water was found to be in good agreement with experimental data. The isothermal compressibility χ_T at standard density was ρ₀k_BTχ_T = 0.061, in excellent agreement with the experimental value of 0.062. The pressure at a density 1.2ρ₀ was 725 MPa compared with an experimental pressure of 775 MPa.

RESULTS AND DISCUSSION

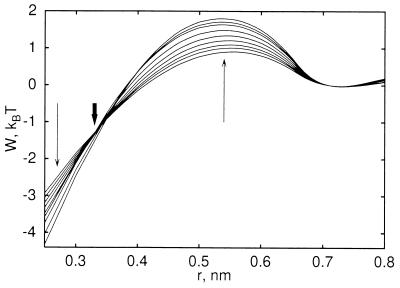
Fig. 1 shows the calculated pmfs between two methane-sized cavities (water-oxygen exclusion radius d = 0.33 nm) (8, 20) for pressures between −16 to 725 MPa (−0.16 to 7.25 kbar), relative to the solvent-separated minimum. We observe two effects: increasing pressure heightens the desolvation barrier between the solvent-separated and contact minimum, and lowers the pmf at complete cavity overlap (r → 0). The desolvation-barrier increase follows from the increased energetic cost at high pressure of forming a small void between the two solutes; the free energy decrease at short distances reflects the increased gain in solvation free energy of bringing two cavities to perfect overlap (r = 0) with increasing pressure. These opposite trends with pressure lead to a region near r = d, where the pmfs cross.

Figure 1.

Pmf between two methane-sized cavities for different pressures, normalized at the solvent-separated minimum. Results are shown for pressures between −16 and 725 MPa. Thin arrows indicate changes with increasing pressure. The thick arrow indicates the crossover region at r = d.

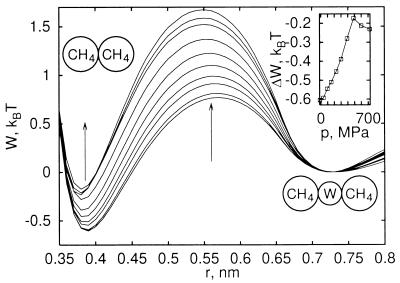
The pmfs shown in Fig. 1 do not contain the contributions of direct methane–methane Lennard–Jones interactions (38). The total pmfs, the sum of direct and solvent contributions (20), are shown in Fig. 2. We observe that increasing pressure destabilizes the contact minimum of the methane–methane pmf at r ≈ 0.39 nm relative to the solvent-separated minimum at 0.73 nm. Fig. 2 Inset shows the free energy difference between the two pmf minima as a function of pressure. Increasing the pressure to about 700 MPa reduces the relative stability of the contact minimum by about 0.35 k_BT (0.9 kJ⋅mol⁻¹). The results of Monte Carlo simulations (39) show a similar shift of about 0.25 k_BT. Simulations of concentrated methane solutions in water showed the destabilizing effect of pressure on methane aggregates (40): At low pressures, methane aggregates form, suggestive of liquid phase separation; at pressures of a few hundred MPa, those aggregates dissolve.

Figure 2.

Pmf for methane association for varying pressure, including Lennard–Jones and solvent contributions. Results are shown for pressures between −16 and 725 MPa, where arrows indicate changes with increasing pressure. (Inset) Difference in free energy between the contact (r ≈ 0.39 nm) and solvent-separated minimum (r ≈ 0.73 nm) as a function of pressure. Equilibrium of those two states would also involve an ideal contribution −ln(r₂/r₁)² deriving from relative volume changes of spherical shells. Note that the stable contact minimum moves inward slightly with increasing pressure.

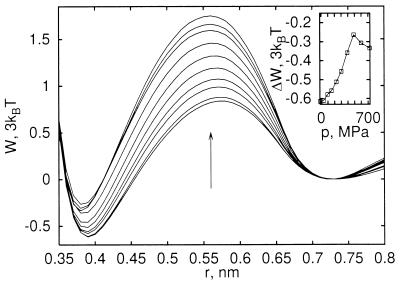
Methane–methane pmfs are a valuable model for studying interactions of hydrophobic groups. However, many-body contributions beyond pairwise might arise from the packing of hydrophobic side chains in the protein interior. To investigate those many-body contributions, we calculated the pmf of three methane molecules in an equilateral configuration as a function of distance. We find that the three-body pmfs, shown in Fig. 3, are well approximated by the sum of the two-body pmfs. Increasing pressure to 700 MPa again destabilizes the contact minimum relative to the solvent-separated minimum by about 0.83 k_BT, with the three-body interactions reducing the pressure destabilization by about 20%.

Figure 3.

Pmf for association of three methane molecules in an equilateral configuration for varying pressure, including Lennard–Jones and solvent contributions. Note that the energy unit is 3k_BT for comparison with the pair pmfs shown in Fig. 2. The three-body pmfs are shown as a function of the pair distance r for pressures between −16 and 725 MPa, where the arrow indicates changes with increasing pressure. (Inset) Difference in free energy between the contact and solvent-separated minimum as a function of pressure.

Consideration of solute-size effects is also important because the effective size of a hydrophobic amino acid side chain is larger than a methane molecule. Inspecting the pressure-dependent pmfs for cavities of sizes d from 0.31 to 0.35 nm, we find that the crossover between the increasing desolvation barrier and decreasing overlap minimum is at a distance r ≈ d, where d ≈ R_W + R_S is approximately the sum of the van der Waals radii of water, R_W, and the solute, R_S. The minimum of the van der Waals interaction between the solutes, on the other side, is at a distance 2R_S and thus in the desolvation-barrier region for all solutes larger than water, R_S > R_W. For nonpolar particles with contact distances in the desolvation barrier, increasing pressure destabilizes the contact configuration relative to the solvent-separated configuration. As a consequence, the effect of pressure destabilization is expected to be even stronger for interacting nonpolar amino acid side chains compared with methane pairs.

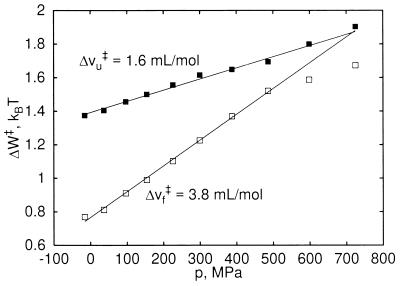
Fig. 4 illustrates kinetic effects expected from the present model. The free-energy differences ΔW_f^‡ between the solvent-separated minimum and the desolvation barrier, as well as ΔW_u^‡ between the contact minimum and the barrier depend linearly on pressures between 0 and 500 MPa. ΔW_f^‡ and ΔW_u^‡ correspond to the activation barriers for pressure-induced “folding” and “unfolding” of one hydrophobic contact pair (i.e., the transition from the solvent-separated to the contact minimum and vice versa). We define activation volumes as the derivative of the activation barriers with respect to pressure, Δv_f/u^‡ = ∂W_f/u^‡/∂p. Both activation volumes are positive and approximately independent of pressure in the range 0 to 500 MPa, Δv_f^‡ = 3.8 ml/mol and Δv_u^‡ = 1.6 ml/mol. Accordingly, pressure slows down the interconversion between the two states.

Figure 4.

Activation free energy as a function of pressure. ΔW_u^‡ and ΔW_f^‡ are the free energy differences of the contact (□) and solvent-separated minima (▪), respectively, to the desolvation barrier of the pmf for methane association (Fig. 2). Activation volumes Δv_u^‡ and Δv_f^‡ are derived from a linear fit for pressures between 0 and 500 MPa.

These results are consistent with an experimental study of the pressure dependence of folding and unfolding rates for staphylococcal nuclease (41). Both the protein folding and unfolding rates decrease with increasing pressure, corresponding to positive activation volumes in a two-state model, ΔV_f^‡ = 92 ± 4 ml/mol and ΔV_u^‡ = 20 ± 3 ml/mol. In a simplified picture neglecting polar and many-body contributions, the activation volumes for folding and unfolding of staphylococcal nuclease correspond to breaking ΔV_f/u^‡/Δv_f/u^‡ ≈ 10–25 hydrophobic contacts upon formation of the transition state. In the crystal structure (42), 155 pairs of carbon atoms (excluding carbonyl carbons) are found within 0.4 nm for all carbon atoms on polar and nonpolar amino acids that are not neighbors along the peptide chain. With the same criterion, 34 nonneighboring amino acids are found to be paired. The energy landscape theory and folding-funnel model predict that approximately 40% of the native contacts between amino acids are broken at the transition state (43, 44). Accordingly, the crude estimate of 10–25 disrupted interactions gives the right order of magnitude. Vidugiris et al. (41) also conclude that the transition state corresponds to a collapsed, loosely-packed solvent-excluded structure. This finding agrees with the present model, where the desolvation barrier corresponds to an extended structure (relative to the contact configuration) that does not allow solvent penetration.

The present model, together with the results of Fig. 2, answers the question why “expanded” protein structures that eliminate close hydrophobic contacts are more stable at higher pressures: The protein–water system may be packed more efficiently and have a lower total volume when water molecules are mixed into the structure, swelling the protein globule. Pressure stabilization of clathrate hydrates (45) provides a simple analogous behavior. High pressure stabilizes the crystalline phase that eliminates close solute contacts. But this does not violate the thermodynamic principle that increasing pressure stabilizes the phase of lower volume.

CONCLUSIONS

The results for the pressure dependence of nonpolar interactions have implications on our understanding of protein unfolding thermodynamics, kinetics, and structure. They establish that the model of folded proteins stabilized by a hydrophobic core does not contradict the experimental observations that proteins can be denatured by pressure, thus resolving the pressure denaturation puzzle pointed out by Kauzmann (1). We find that pressure destabilizes the contact configuration of nonpolar molecular groups relative to a solvent-separated configuration. This observation leads to our most significant conclusion regarding the mechanism of pressure denaturation: Pressure denaturation corresponds to the incorporation of water into the protein, whereas heat denaturation corresponds to the transfer of nonpolar groups into water. With increasing pressure, packing forces compete more favorably with the tendency to form a tetrahedral hydrogen bond network (46). The resulting increase in the coordination number causes energetic frustration (47). This in turn reduces the relative cost of inserting water molecules into a nonpolar aggregate, an otherwise unfavorable environment. That insertion of water molecules is manifest in the increasing importance of the solvent-separated minimum in the free energy of association.

Our results lead to a picture of the ensemble of pressure-denatured protein structures, where water molecules penetrate the protein interior. This finding is in agreement with experimental observations (13), most notably the observed increase in the hydrodynamic radius upon denaturation (48, 49) and an increase in the hydrogen-exchange rates of lysozyme and RNase A with pressure (50). This swelling process results in structures with reduced compactness that, however, retain considerably more order than heat-denatured proteins, as probed by NMR experiments of hydrogen exchange (17). Adding glycerol as a cosolvent to water increases the pressure required for denaturation of the Arc repressor (51). An extrapolation to a pure glycerol solvent suggests that the Arc repressor protein could not be pressure denatured in glycerol. Oliveira et al. (51) therefore conclude that water is crucial for pressure denaturation, and that the denatured state is solvated. Tryptophan-phosphorescence lifetime studies of dimeric alcohol dehydrogenase under pressures exceeding 250 MPa were interpreted as pressure-induced water penetration into the dimer interface (52).

X-ray crystallography of lysozyme at 100 MPa did not show an increased hydration of the protein interior (53, 54), but that study was carried out at pressures significantly below the denaturation pressure (48, 55, 56). A sharp increase of the hydrodynamic radius of lysozyme has been observed for pressures above about 500–600 MPa (48). The slow rates of unfolding observed in pressure-jump experiments (41, 57, 58) suggest that sub-nanosecond molecular-dynamics simulations of pressure denaturation (59–62) do not fully cover the relevant time scales, although an increase in the solvent exposure of residues in the hydrophobic core has indeed been observed in an 800-ps simulation calculation (62).

We compared observed activation volumes for folding and unfolding (41) and calculated activation volumes for forming and breaking hydrophobic contacts. From the ratio of those activation volumes, one can estimate that the equivalent of about 10–25 hydrophobic contacts are broken in the transition state of pressure unfolding of staphylococcal nuclease (41). Exploring the characteristics of pressure-denaturated proteins in relation to proteins unfolded by temperature or chemical denaturants provides valuable input to theories of protein folding. Bryngelson et al. (43) pointed out that pressure can be used to explore the roughness of the folding energy landscape. In agreement with the present model, the experimental data (41) show that pressure slows down folding and unfolding kinetics, corresponding to an increasingly rough landscape.

The swelling of the protein core with increasing pressure will affect protein structure, dynamics, and stability, to be characterized in intensified studies of that largely unexplored thermodynamic dimension, pressure (63). A better understanding of proteins under pressure will also help to elucidate adaptation processes of barophilic organisms, such as those living in the deep sea under pressures of up to about 120 MPa (64–66).