Molecular picture of folding of a small α/β protein

Abstract

We characterize, at the atomic level, the mechanism and thermodynamics of folding of a small α/β protein. The thermodynamically significant states of segment B1 of streptococcal protein G (GB1) are probed by using the statistical mechanical methods of importance sampling and molecular dynamics. From a thermodynamic standpoint, folding commences with overall collapse, accompanied by formation of ∼35% of the native structure. Specific contacts form at the loci experimentally inferred to be structured early in folding kinetics studies. Our study reveals that these initially structured regions are not spatially adjacent. As folding progresses, fluid-like nonlocal native contacts form, with many contacts forming and breaking as the structure searches for the native conformation. Although the α-helix forms early, the β-sheet forms concomitantly with the overall topology. Water is present in the protein core up to a late stage of folding, lubricating conformational transitions during the search process. Once 80% of the native contacts have formed, water is squeezed from the protein interior and the structure descends into the native manifold. Examination of the onset of side-chain mobility within our model indicates side-chain motion is most closely linked to the overall volume of the protein and no sharp order–disorder transition appears to occur. Exploration of models for hydrogen deuterium exchange show qualitative agreement with equilibrium measurement of hydrogen/deuterium protection factors.

The protein folding problem—understanding how a polypeptide chain reaches its native conformation—is a long-standing challenge in molecular biophysics. There has been a significant effort to develop a theoretical basis for this phenomenon in recent years (1–3). Theoretical models of protein folding are based on analogy with better-studied physical phenomena, e.g., spin glasses and polymer physics, and on simulations involving highly simplified representations of protein energetics and structure. These studies have suggested a general framework for understanding the folding process. However, direct testing of this framework and a compelling demonstration of its relevance to real proteins has not been realized. Furthermore, despite significant advances in experimental methodologies (4–6), a complete and unambiguous description of folding at the atomic level has yet to emerge. These points motivate the current theoretical studies to explore the folding thermodynamics of a small protein with molecular simulations.

We attempt, in this study, to address some of the issues underlying a more accurate energetic description of folding, on the one hand, and a more complete atomic description, on the other, by using a full-atomic model of the solvated protein with empirically derived interaction forces. The empirical force field we use, charmm (7), has been developed to represent equilibrium properties of both native proteins and peptides (or unstructured fragments of polypeptide chains), thus the use of this force field to study protein conformational transitions under native conditions seems appropriate. Furthermore, we make no a priori assumption about the nature of the folding process but build a database of conformations for starting points in our free energy sampling by considering high-temperature unfolding trajectories of the protein in solution. We demonstrate that our procedure is resilient to the choice of a different subset of initial conditions, and we verify the convergence of our sampling within the set of initial conditions that we have used. Our calculations produce models that conform with experimental findings, providing a demonstration of the insight into folding phenomenon that may be gained through consideration of detailed theoretical models.

Often protein folding studies, experimental and theoretical, focus on a single protein as a paradigm. Helical proteins have been particularly well studied in this vein, and our earlier work on an all-helical protein has demonstrated the successful application of simulations to explore the folding landscape for this class of molecules (8, 9). In the present work, we explore the folding mechanism of an α/β protein, providing an important, and hitherto less well understood, paradigm. Our theoretical study complements the elegant experiments of Fersht and coworkers (10, 11) on the folding of chymotrypsin inhibitor 2, another α/β protein. Insight into the thermodynamics of folding and the molecular picture provided by our study extend beyond the scope of previous theoretical studies on α/β proteins (12).

Models and Methods

Segment B1 of streptococcal protein G (GB1), the protein on which we focus our present efforts, is a 56-residue single-domain protein that is stable in isolation. NMR (13) and x-ray (14) structure determinations reveal a four-stranded β-sheet packed against an α-helix. GB1 contains no proline residues, disulfide bridges, or prosthetic groups. It is therefore expected to exhibit general features of folding for small α/β proteins.

To generate the free energy surfaces used to study the folding of GB1, we first characterized the native state of the protein. Two native simulations (2 ns and 1 ns) were performed as a reference point for the folding study (15). From an analysis of these native simulations, the properties characteristic of the naive basin were defined. Fifty-four side-chain contacts, formed between residues not adjacent in sequence and present for more than two-thirds of each simulation, were identified as “native contacts” and used to define a reaction coordinate:

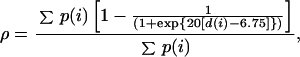for characterization of the progress of folding. In this expression, d(i) is the distance between centers of geometry of side chains forming contact i, and p(i) is the weight of the ith contact. The probability of a given side-chain contact being formed in the native state is defined on the basis of the fraction of time the contact is present in the native trajectories and ranges between 66% and 100% [∀ i, 0.66 < p(i) < 1.0]. We note that this choice of reaction coordinate clearly distinguishes between native and nonnative protein conformations, a necessary condition for any reaction coordinate. Furthermore, it provides us with the ability to make direct connections with simpler lattice-based and analytical models of protein folding and with experimental data on interresidue distance contacts.

Three high-temperature unfolding simulations at a temperature of 400 K were used to generate a database of initial conditions. Although such a database is certainly not encompassing of all conformational states accessible to the protein as it folds, particularly in the most nonnative conformational regions, we believe it provides a representative ensemble of configurations. Alternative methods of generating nonnative conformations might be imagined, and we address one such method briefly below. However, if the alternative approaches produce conformations that, when solvated, are of very high energy, these nonrepresentative conformations will never achieve proper equilibration in the time period of sampling accessible for calculations of this sort. The database generated from the unfolding simulations was partitioned into “bins” along the reaction coordinate ρ. The conformations in each of these bins were clustered, resulting in a total of 76 clusters, and the cluster centers served as initial conditions for our free energy sampling. The database was clustered on the basis of the content of native contacts, native hydrogen bonds, and the solvation energy, by using a hierarchical scheme as described (9). The cluster centers were resolvated in a preequilibrated volume of water (at 298 K and 1 g/ml) and then further equilibrated for 20 ps. These final structures were used as initial conditions for importance sampling (16).

Importance sampling was performed with a harmonic biasing potential defined along the reaction coordinate ρ. The biasing potential force constant was chosen to yield an energy change of 0.6 kcal/mol (k_BT at 298 K; 1 cal = 4.184 J) when the coordinate ρ was displaced half the bin width from the center. This gave a force constant of 2,000 kcal/mol for the biasing potential. Sampling of 100–200 ps was produced from each initial condition. These data were combined with the weighted histogram analysis method (17, 18) to generate potential of mean force surfaces. The precision of the one-dimensional surface was tested with 5-fold cross-validation, whereby 20% of the data was randomly excluded from each bin and the surface was regenerated by using the remaining 80%. The deviation from the surface based on all data was less than 0.1 kcal/mol at any point, suggesting that our sampling, within the manifold of initial conditions we used, has converged.

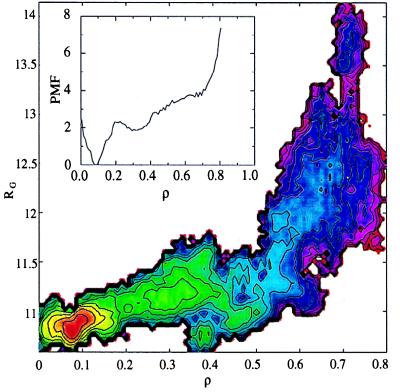
To test whether the shape of the two-dimensional potential of mean force (free energy surface versus radius of gyration R_g and ρ) was biased by the choice of initial conditions, alternative initial conditions were generated by unfolding of the protein with a harmonic potential defined on the radius of gyration (9, 19). More expanded structures with the same number of native contacts were produced with this procedure. Two simulations were initiated from structures with R_g = 12.05 Å and ρ = 0.32 and with R_g = 13.31 Å and ρ = 0.46 to see what the nature of sampling from these initial conditions would be. After 200 ps of dynamics, the first structure equilibrated to a local free energy minimum of the basin at R_g = 11.2 Å and ρ = 0.3 (Fig. 1) and the second structure approached the free energy basin at R_g = 12.1 Å and ρ = 0.45. Thus, we concluded that the regions of conformational space corresponding to more expanded structures are indeed of higher free energy, and our representative sampling of initial conditions from high temperature unfolding, although certainly not complete, is adequate to produce a characteristic representation of the free energy landscape in regions of conformational space that are of intermediate compactness and “nativeness.”

Figure 1.

Free energy surfaces along the reaction coordinate ρ (defined by the number of native contacts) (Inset) and as a function of ρ and R_g (the radius of gyration). Contours are drawn every 0.5 kcal/mol.

All molecular dynamics simulations were carried out with the charmm package (7), using a polar hydrogen parameter set (TOPH19/PARAM19) and the TIP3P water model (20). The protein was solvated in a truncated octahedron constructed from a box that was 62 Å on a side. Corresponding periodic boundary conditions were applied. Dynamics were propagated with a time step of 0.002 ps. X–H bonds were fixed with the shake algorithm (21). Nonbonded interactions were processed by using a list updated every 25 steps (22). Truncation of nonbonded interactions was done at 11 Å with a list extending to 12.5 Å. Temperature was maintained at 298 K by reassigning individual atomic velocity components from a Gaussian distribution if the average temperature drifted outside a window of ±10 K. Coordinates were saved every 100 steps for subsequent analysis and data processing. Calculations were done on CRAY C90, T3D, and T3E supercomputers at the Pittsburgh Supercomputing Center.

The Folding Landscape and Mechanism for GB1

The potential of mean force constructed along the reaction coordinate ρ and as a two-dimensional function of the fraction of native contacts (ρ) and overall compactness (R_g) is shown in Fig. 1. These functions describe the free energy landscape encountered during folding. Our calculated free energy landscape indicates that the folding of GB1 under native conditions occurs without large barriers and thus is anticipated to be diffusion controlled. In a thermodynamic sense, overall collapse to a radius of gyration only 10% greater than that of the native state occurs early in folding and is accompanied by the formation of 30–40% of the native contacts. This finding contrasts that observed for an all-helical protein (8, 9) and suggests that the degree of correlation in conformations near the native manifold (i.e., the extent of nonlocal secondary structure in the native protein) has a significant influence on the gross details of the mechanism of folding. Thus, the introduction of correlation into the theoretical description of folding in the landscape model is likely to be important in more accurately describing the folding of nonhelical proteins (23). These geometric factors clearly play a role in determining the mechanism of collapse followed by a search through compact states for the native state in this protein.

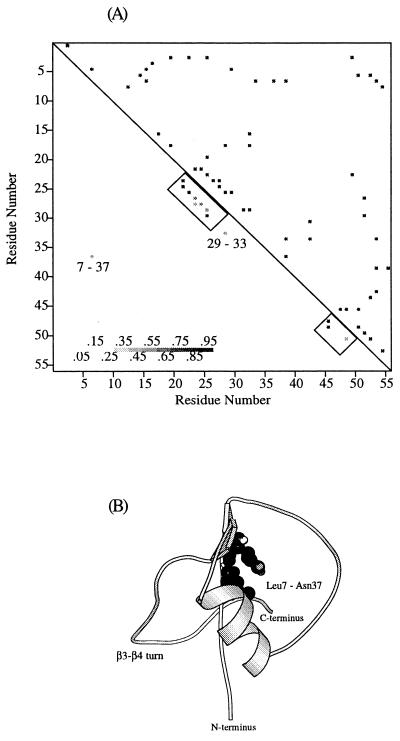
A more detailed picture of the folding mechanism can be gained by examining the nature of side-chain contacts formed early in the folding process. The native contacts possessing a high probability of forming, P > 0.5, in the early stage of folding (defined by 0.7 < ρ < 0.8) are shown in Fig. 2A. Structure forms at the N terminus of the α-helix and at the turn connecting the third and fourth β-strands. Two additional native contacts formed at this stage of folding are Val²⁹–Tyr³³, in the middle of the α-helix, and Asn³⁷–Leu⁷, between the C terminus of the α-helix and the first β-strand. An additional nonnative contact between Phe³⁰ and Leu⁷ also forms. This result is in accord with the characterization of the initial collapsed state (formed during the dead time of the experiment) of GB1 by quenched-flow deuterium–hydrogen exchange (24). In this study, larger than average protection factors were identified in the N terminus of the α-helix, in the β3–β4 turn, and to a lesser degree in the middle of the α-helix (residues Lys³¹, Gln³², and Tyr³³). From this experimental work and the structure of the native state, it was proposed (24) that these two regions are stabilized simultaneously and serve as a single center for subsequent growth of structure. However, our calculations reveal an absence of contacts between these regions, demonstrating that these two loci are not spatially close in the early stages of folding. This observation seems to contradict the idea that a single nucleus first forms and from that subsequent folding occurs (25). It is most likely that the β3–β4 turn region forms as a stable structural element early in folding and that the helix is stabilized via interactions with the compact chain. Further support for this picture comes from studies of peptides excised from GB1. NMR characterization of peptides from GB1 has shown that the peptide containing the third and fourth β-strands forms a β-hairpin in isolation and the peptide from the helical region does not form detectable helix under native conditions (26). The probabilities of forming contacts between the N terminus of the α-helix and the β3–β4 turn fluctuate (0 < P < 0.75) as the protein folds and approach unity only in the late stages of folding (ρ < 0.2). A structure, representative of the early stage of GB1 folding is shown in Fig. 2B. Particular features of interest involve the contacts around the β3–β4 turn, the degree of helix formation, and the nonlocal native contact involving residues 7 and 37 (27).

Figure 2.

(A) Contact maps for the native state and the initial stage of GB1 folding. Fifty-four native contacts are shown above the diagonal of the contact map, and the subset of native contacts present in the early stage of folding are shown below the diagonal. Only contacts occurring with a high probability (P > 50%) are shown, the gray scale indicates the probability for a particular contact to be formed. (B) Representative structure of GB1 during early stages of folding.

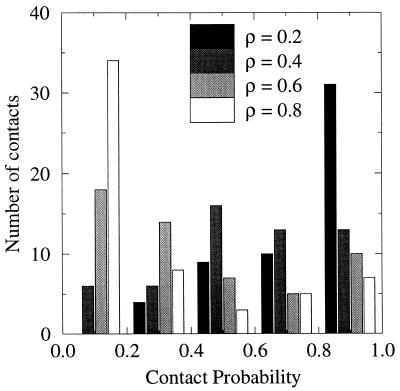
As folding progresses, a large number of nonlocal fluid-like contacts form. Fig. 3 shows the number of contacts with given probabilities of formation at different points along the reaction coordinate. Contacts with high probability (P > 0.8) at ρ = 0.8 correspond primarily to the local contacts formed in two loci of the protein chain (N terminus of the α-helix and the β3–β4 turn, see Fig. 2). Intermediate points along the folding coordinate ρ = 0.4 and ρ = 0.6 show a broad distribution of native contacts with intermediate probabilities. Near the native state, ρ = 0.2, contacts become relatively localized. At ρ = 0.4, ∼60% of contacts have intermediate probability (0.2 < P < 0.8). Thus, the energy of the protein at a given stage of folding is determined by a large number of labile contacts rather than by a subset of rigid ones surrounded by as yet unstructured polypeptide chain. This picture indicates that, rather than a single pathway, an ensemble of different paths defines the folding process (28). Such a picture also emerges in describing the nature of the folding transition state in lattice-based simulations and in analysis of mutational studies on proteins (10, 29).

Figure 3.

Number of contacts with a given probability to be formed along the folding coordinate. Probabilities are binned every 0.2 unit.

After overall collapse has occurred, but before 80% of the contacts have formed, 2–2.5 times more water than present in the native state occurs with high probability in the protein core† (data not shown). The role of these water molecules may be to facilitate conformational transitions by lubricating structural rearrangements. Consistent with this suggestion is the observation of formation of backbone hydrogen bonds through water-mediated intermediates.

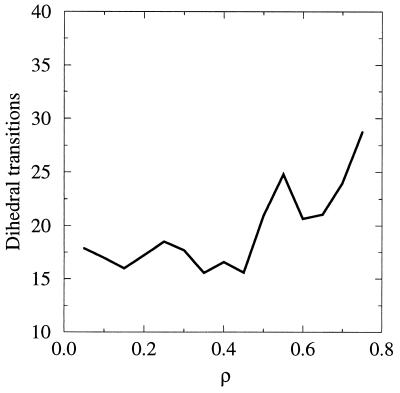
The mobile nature of the water in the core may also facilitate the repacking of side chains and, thus, a disorder–order transition. When the protein descends into the native state, water is forced out of the protein core (see Fig. 1). However, this desolvation, or conversely the initial solvation of the protein core, near ρ ≃ 0.2 is not coupled to a sharp change in the mobility of core side chains (30). This point is illustrated in Fig. 4. In the present work, we defined “core” side chains as those with less than 5% surface accessibility in the native state, when compared with a fully exposed conformation. The side chains identified in this manner are Tyr³, Leu⁵, Leu⁷, Ala²⁰, Ala²⁶, Phe³⁰, Ala³⁴, Val³⁹, Phe⁵², and Val⁵⁴. To evaluate the mobility of the core side chains at different stages of folding, we counted the number of dihedral transitions for the 10 core side chains during 100 ps of dynamics in different regions of the reaction coordinate ρ. On the basis of the measurements of fluorescence anisotropy, the rotational correlation time of the tryptophan residue is estimated to be about 30 ps (31). Furthermore, Sneddon and Brooks (32) studied motions in isolated tyrosine residue by using molecular dynamics simulations. They reported the time scales of 25 ps for χ¹ rotation and 15 ps for χ² rotation. Thus we conclude that a measure of the average number of transitions over this 100-ps period is sufficient to indicate altered mobility of the side chains. It is observed from the results in the figure that the mobility of side chains seems to correlate with the overall expansion rather than with the loss of the native architecture (and correspondingly the solvation of the core).

Figure 4.

Number of dihedral transitions of core side chains per 100 ps of dynamics in different regions of the reaction coordinate.

We observe that the α-helix and β-sheet of GB1 form during different stages of folding. Formation of the α-helix begins early and is virtually complete (except for two hydrogen bonds at the C terminus) when ∼40% of the native contacts have formed. In contrast, β-sheet formation occurs in parallel with overall topological assembly. The majority of interstrand β-sheet hydrogen bonds form when 70–80% of the native contacts are already in place. Such a picture indicates that folding scenarios involving early formation of secondary structure (33–35) may not be applicable for proteins containing β-sheets. However, the idea of early formation of localized structure may be important in understanding the overall structure organization process of folding.

Our methodology of studying the folding process is most similar in spirit to the native-state hydrogen–deuterium exchange experiment, in that both methods probe nonnative protein conformations coexisting with the native state under native conditions. Experimental data on native state hydrogen exchange in GB1 is available (36), and thus some comparison with the experiment can be made.

Interpretation of the hydrogen exchange kinetics relates the observed rate of exchange to different modes of fluctuations, transiently exposing the proton to solvent under the conditions of experiment. A sampling of states populated by a protein under native conditions allows one to investigate in which states a given proton will be exposed to exchange and to evaluate the relative population of these states, which in turn relates to the observed rate of the proton’s exchange. In the commonly observed EX2 limit (4), the rate of exchange can be written as

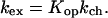1

Where K_op is the equilibrium constant for the opening reaction, k_ex is the rate of exchange at given conditions, and k_ch is the rate of exchange in the open state (unstructured peptide). From this relationship, K_op can then be converted into a free energy for the opening reaction:

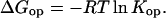2

To explore hydrogen exchange from our simulation results, we must first relate exchange to some physical property of our atomic model. Two models relating the rate of a proton’s exchange to its accessible surface area can be considered. In the first, one assumes that the rate of exchange is linearly proportional to the accessible surface area (ASA) of the amide group. Given the two boundary conditions (k_ex = 0, if ASA = 0; and k = k_ch, if ASA = ASA_max), one arrives at the expression

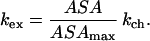3

Then, the average rate of the exchange of a proton under a given set of thermodynamic conditions is

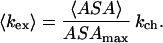4

In this expression 〈ASA〉 is the Boltzmann-weighted average of the accessible surface area of the given amide group under the conditions of the experiment. This average can be calculated over all structures sampled under the given conditions. The weight of a particular conformation is defined by the value of the potential of mean force for this conformation. Thus, from the calculation of the ASA for each exchangeable amide group and our computed potential of mean force, we can construct a model for K_op.

In the second model, one assumes that the proton starts to exchange with solvent only if its exposure reaches some threshold value. In this model,

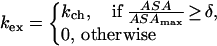5

and

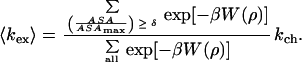6

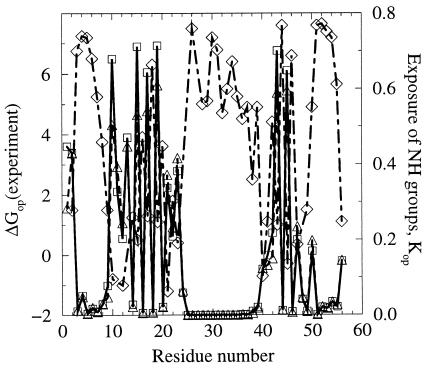
In Fig. 5, we show values of the equilibrium constants K_op, defined from Eq. 1 and calculated on the basis of our sampling and Eqs. 4 (model 1) or 5 (model 2). The value of ASA_max for each proton is assessed by calculating the ASA of the amide group in the residue with the side chain in the trans conformation and flanked by glycines on both sides. The values of K_op calculated by Eq. 6 are shown for δ = 0.3. The two methods give very similar estimates of K_op (or protection factor p = 1/K_op). Fig. 5 also shows the free energies for the opening reaction determined experimentally for GB1 (36). A qualitative anticorrelation between the average exposure of the amide estimated from our sampling and the experimentally determined ΔG_op is clear in the figure. Such correspondence is not observed when a single protein conformation (e.g., the x-ray structure) is used to estimate the exposure of amides (data not shown).

Figure 5.

Fractional exposure of backbone amides under native conditions calculated by two methods as described in the text (□, model 1; ▵, model 2). Experimental values for the free energy required for transient opening in hydrogen–deuterium exchange experiments on GB1 (34) (⋄). Exchange rates could not be obtained for several protons (e.g., Ala⁴⁸) because of either fast exchange or peak overlap.

Fractional exposure of the amide protons is certainly not the only factor that determines their rate of exchange. This point is particularly evident, for example, for Leu¹², for which the rate of exchange in the native protein is faster than in the unstructured peptide (ΔG_op < 0). Orban et al. (36) note that one possible explanation for this effect might be the presence of positively charged Lys¹³ that withdraws electron density from the amide and makes it more acidic than in the unstructured peptide. Such effects are not seen in our model. Nevertheless, we see that qualitative aspects of hydrogen–deuterium exchange during folding can be understood from simulations such as those we present herein.

Discussion

Our findings for the case of GB1 provides a link between the extent of conformational correlation involved in the formation of the native folded topology and the overall mechanism of folding. For structures involving significant nonlocal secondary structure, as in the α/β topology of GB1, the protein first collapses to a relatively compact manifold of states from which the search for the native state proceeds (37). This is in contrast with our findings for a simple helical bundle, where native tertiary and secondary structure are formed more or less concomitantly (8, 9). Despite differences in the detailed manner in which these two proteins of differing topology fold, both studies indicate that folding does not progress via a single pathway. Instead, many different native side-chain contacts are sampled in a relatively compact state that represents a minimum of the folding free energy surface. For GB1 it also appears that water may play a key role in “lubricating” conformational transitions in this search. Significant core solvent molecules exist late into the folding process and appear to mediate, through shared hydrogen bonds, interchain interactions. However, we do no find a significant correlation between the incorporation of water into the core and the onset of side-chain motion. Finally, we note that free energy calculations of folding, such as those presented here, provide a means to probe hydrogen–deuterium exchange during folding. We proposed and examined two models for this process and showed that qualitative agreement with experimental findings were obtained for both models.

One may ask whether it is feasible to study protein folding, a process that occurs on time scales approaching minutes in some cases, by using methods of molecular dynamics, which are limited to time scales between hundreds of picoseconds and tens of nanoseconds. Clearly it is infeasible to study the folding process directly by using all-atom explicit-solvent non-equilibrium simulation methods, given current or foreseeable increases in computational technologies. Even though the observation of a single “folding event” may be possible, the statistical analysis and associated calculation of thermodynamic “weights” is not. Thus the direct exploration of folding, as done by using simple “minimalist” models of protein folding (38, 39), is not possible. However, by employing the statistical mechanical methods of umbrella sampling, as we have done in the present work, one can study the thermodynamic aspects of the folding processes and hence gain insights into the folding mechanism from this point of reference. We note that it is well established that a short simulation of a small homogeneous system (e.g., 10 ps of 200 water molecules) suffices to obtain structural and energetic properties (i.e., thermodynamic properties) that correspond very well with experiment, despite sampling only a small fraction of accessible states (40). Although similar rigorous experimental verification of the properties of the protein folding reaction as revealed by importance sampling is beyond reach, the relative insensitivity of our procedure to alternative initial conditions and differing amounts of data (convergence) and the correlation of our findings with experimental data strengthen our confidence in the molecular picture presented herein. Thus we conclude that the development of insights into thermodynamic aspects of the folding mechanism of proteins can be approached by using modern methods of computer simulation with an explicit solvent. Furthermore, it is through these investigations that we can begin to develop detailed insights between the global features of folding as captured in folding theories or minimalist model simulations and sequences of real proteins in realistic environments.