Two-Step Mechanism of Homogeneous Nucleation of Sickle Cell Hemoglobin Polymers

Abstract

Sickle cell anemia is a debilitating genetic disease that affects hundreds of thousands of babies born each year worldwide. Its primary pathogenic event is the polymerization of a mutant, sickle cell, hemoglobin (HbS); and this is one of a line of diseases (Alzheimer's, Huntington's, prion, etc.) in which nucleation initiates pathophysiology. We show that the homogeneous nucleation of HbS polymers follows a two-step mechanism with metastable dense liquid clusters serving as precursor to the ordered nuclei of the HbS polymer. The evidence comes from data on the rates of fiber nucleation and growth and nucleation delay times, the interaction of fibers with polarized light, and mesoscopic metastable HbS clusters in solution. The presence of a precursor in the HbS nucleation mechanism potentially allows low-concentration solution components to strongly affect the nucleation kinetics. The variations of these concentrations in patients might account for the high variability of the disease in genetically identical patients. In addition, these components can potentially be utilized for control of HbS polymerization and treatment of the disease.

INTRODUCTION

Sickle cell anemia (1–3) was the first disease whose molecular basis was identified: electrophoresis showed that hemoglobin from sickle cell patients had an excess of positive charge in comparison with hemoglobin from healthy adults (4). The charge difference was attributed to a mutation from glutamate to valine (5) at the sixth site of the two β-chains of hemoglobin. The mutated protein (sickle cell hemoglobin or HbS) forms 14-member fibers (6–8) when the protein is in its T-conformation (9) in deoxy-state (10). In the fibers, hydrophobic contacts are formed between valine of one HbS molecule and alanine, phenylalanine, and leucine from an adjacent HbS molecule (7,8,11,12). The formation of HbS fibers, which is also called polymerization, is a first-order phase transition, similar to gas-solid transformations (13,14), and this allows the application of the thermodynamic and kinetic rules of phase transitions to the analyses of HbS polymerization. Deoxy-HbS solutions with high degrees of polymerization exhibit gel-like rheological behavior (15), which was attributed to intertwined polymers and polymer domains (16).

Like any first-order phase transition (17,18), HbS polymerization is initiated by a nucleation event (19–21) in which a certain number of molecules assemble into an embryo of the new phase (21–23). Nucleation is followed by growth of the initial fibers and their branching due to secondary nucleation of new fibers on top of the existing ones. This “double-nucleation” mechanism has been studied in detail (21–24); for recent developments, see (25–37). These efforts brought a wealth of information of the physicochemical and biochemical fundamentals of HbS polymerization (36,38), yet no drug which would inhibit HbS polymerization in sickle cell patients was proposed (39). A major obstacle for antisickling drugs has been the high concentration of hemoglobin inside the erythrocytes, which requires unacceptable concentrations of a ligand targeting most HbS molecules (40). The current clinical treatment strategies do not include attempts to directly inhibit hemoglobin polymerization (41), suggesting that the studies of HbS polymerization have reached a dead end.

In this work we propose a new mechanism for the first step of HbS polymerization, the homogeneous nucleation of HbS fibers. In studies to date, including a previous article from our group (42), it has been implicitly or explicitly assumed that this nucleation is a one-step process: the disordered HbS molecules from the solution assemble into an ordered nucleus which has the same structure as long HbS fibers. A different outlook on nucleation of ordered structures has been suggested by recent results on another first-order phase transition with proteins: formation of crystals. Both experiment and theory revealed that, for protein crystallization, the formation of dense liquid droplets may precede the formation of ordered nuclei (43–46) (Fig. 1 a). Further studies pointed out that whereas in some cases the dense liquid may be stable with respect to the dilute solution (47,48), in other cases it may be metastable (46,49,50) (Fig. 1 b). Mesoscopic metastable liquid clusters were identified as likely precursors for ordered-phase nucleation (51).

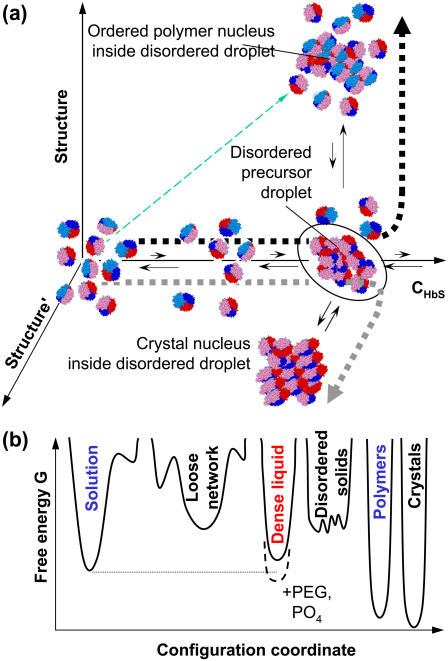
FIGURE 1.

Schematic representation of the two-step nucleation mechanism of HbS polymers. (a) The nucleation pathway in the space of order parameters. Horizontal axis is HbS concentration, along which dilute solution and dense liquid can be distinguished. Axes of evolution of ordered structures are orthogonal to concentration axis, only two leading to polymers and crystals, respectively, are shown. Other possible structure axes include other crystal polymorphs, disordered aggregates, and gels. Thin dashed arrow along the diagonal indicates pathway of the one-step nucleation mechanism. Thick short-dashed lines indicate pathways of the two-step mechanism leading to polymers or crystals, respectively. (b) Free energy G landscape for different phases possible in HbS solutions. The abscissa is a one-dimensional projection of the full set of order parameters characterizing the phases in the hemoglobin plus solvent system. This coordinate can be approximately thought of as HbS density plus degree of ordering of the HbS molecules. Lower G corresponds to higher stability; thus, the dense liquid is metastable with respect to the solution in HbS solutions and becomes stable upon the addition of PEG (60) or concentrated phosphate (84).

After the first data obtained with protein solutions, the applicability of the two-step mechanism has been demonstrated for crystallization in a variety of systems—colloid materials (52), molecular (53,54) and ionic (55) small-molecule compounds—and even for the formation of another ordered solid phase of proteins, the amyloid fibrils (56). Still, the applicability of this mechanism to any system of interest should be independently tested. Below, we provide evidence that the two-step mechanism applies to the nucleation of HbS fibers.

EXPERIMENTAL PROCEDURES

Sample preparation and the microscope experiment setup are described in Galkin and Vekilov (42); here we summarize only the main details. Hemoglobin S was prepared by lysis of red blood cells and purified by fast protein liquid chromatography. Nucleation experiments were performed with HbS solution in 0.15 M potassium phosphate buffer, pH = 7.35. The final concentration of HbS was determined using Drabkin reagent; ∼3 μl of solution was loaded on a standard microscope slide. The experiment setup was built around a Leica DM R fluorescence microscope (Leica Microsystems, Wetzlar, Germany). HbS polymer formation was initiated by photolysis of carbonmonoxi-hemoglobin with an Nd³⁺:YAG (yttrium aluminum garnet) laser. The process of fiber nucleation and growth was monitored in real time using differential interference contrast (DIC) optics (42).

Controlling the state of polarization of the photolysing beam turned out to be a challenge. We use DIC optics to monitor the formation of HbS polymers and this technique uses two crossed polarizers and two Nomarski prisms that modify the polarization of the illuminating light. To achieve linear polarization of the laser illumination, the polarization plane of the laser beam should be aligned with one of the axes of the Nomarski prism in the illuminating optical pathway.

To get linearly polarized light and the ability to arbitrarily rotate its angle of polarization, in a set of experiments we placed a linear polarizer (Melles Griot, Carlsbad, CA) in a rotating turret in the place of the Nomarski prism. The sample was illuminated through this polarizer for a period of time, during which the spherulite evolution was not monitored. After that, the DIC elements were restored into place and the fibers were imaged for determination of their orientations.

Light scattering experiments were performed on an ALV goniometer equipped with a He-Ne laser (632.8 nm) and an ALV-5000/EPP Multiple Tau Digital Correlator (ALV, Langen, Germany). Samples were filtered through a 0.22-μm Millipore (Bedford, MA) filter, and ∼30 μl of solution was sealed in a glass capillary tube with a 1.5-mm inner diameter. Intensity correlation functions were acquired at 90° for 60 s and were processed with the ALV software package based on the CONTIN algorithm (57). For further details, see Pan et al. (58).

RESULTS

The kinetics of nucleation and growth of HbS polymers

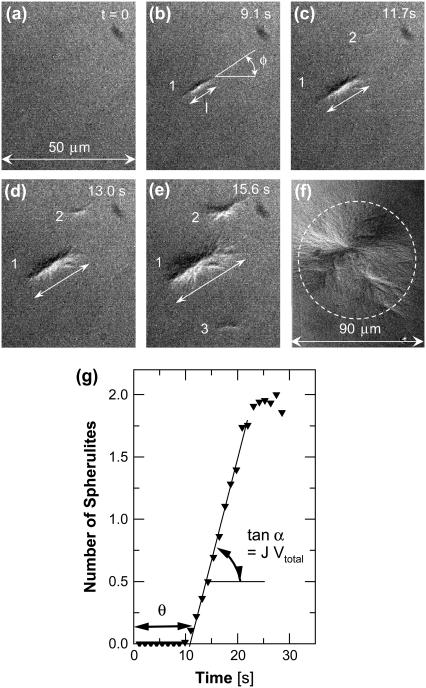
We initiate polymerization by laser photolysis of CO-HbS to deoxy-HbS and monitor the nucleation and growth of HbS polymers (42) (Fig. 2). The HbS polymer phase consists of twisted fibers of ∼22-nm diameter (8,59,60). Heterogeneous nucleation of secondary fibers on top of existing ones changes polymer morphology: from single long fibers to elongated spherulites (Fig. 2 b), isometric spherulites (Fig. 2 f), and eventually thick gel (38). Each spherulite corresponds to one event of homogeneous fiber nucleation (61). The relative error introduced by this assumption is equal to the probability of having two nuclei within the slide area occupied by one spherulite. Nucleation kinetics data are extracted from images of an area of ∼2500 μm², containing fewer than 10 spherulites, each occupying an area of <10 × 1 μm². The probability of having a second spherulite hidden under or within 1 of the 10 is ∼(10/2500)² × 10 = 1.6 × 10⁻⁴. By monitoring the number of spherulites appearing at different times and averaging over 80–200 series of images, we obtain the time dependence of the mean number of nuclei (Fig. 2 g). These time dependencies allow evaluation of two fundamental nucleation variables (62,63): the slope of the intermediate part of steady-state nucleation (42) yields a nucleation rate, J, whereas its intercept with the time axis is equal to the nucleation delay time θ.

FIGURE 2.

Evolution of HbS polymerization. (a–f) DIC images of a 25-μm-thick slide of polymerizing HbS solution. Times for (a–e) indicated on panels, image in f corresponds to equilibrium between polymers and solution reached after ∼1 min of polymerization. Elongated spherulites in b–e evolve into isometric spherulites in f. Width of panels (a–e) is shown in a. Determinations of fiber length, l, and orientation angle, φ, are illustrated in b. Individual fiber spherulites traced through (b–e) are labeled with numbers. (g) Evolution of the mean number of polymer spherulites determined from 85 series of images similar to those in (a–f). Determination of delay time, θ, and slope of dependence tanα = J V_total (V_total, volume in which polymerization occurs; J, nucleation rate) is illustrated. At long times the spherulites compete for supply and the nucleation of new fibers is hampered in the regions between them; for details, see Galkin and Vekilov (42).

The assumption of one nucleated fiber per one observable spherulite also means that orientation of the elongated spherulite corresponds to the orientation of the initial fiber. Images as in Fig. 2 yield these orientations in terms of angles with the horizontal axis, φ (Fig. 2 b). We also determine the time-dependent lengths, l (Fig. 2, c–e), and from the l the growth rates, R, of the polymers.

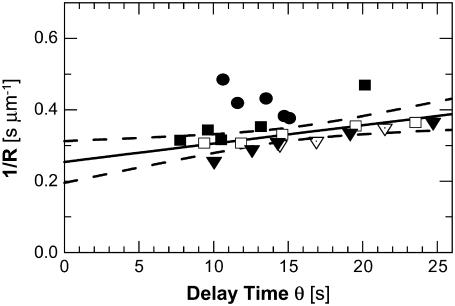
Fig. 3 shows that at all tested concentrations θ has a strong temperature dependence: θ decreases by factors of up to 3× for ΔT = 5°C. The growth rate, R, in Fig. 3 changes by ∼30% with the same ΔT. Plotting the R(T) data in Arrhenius coordinates ln R versus 1/T yields a reasonable value ∼50 kJ mol⁻¹ for the activation energy of the incorporation of HbS molecules into a polymer fiber (64).

FIGURE 3.

Correlation between reciprocal fiber growth rate 1/R and delay time for nucleation θ at four HbS concentrations and different temperatures. (Circles) C_HbS = 201 mg ml⁻¹, (triangles) C_HbS = 210 mg ml⁻¹, (diamonds) C_HbS = 220 mg ml⁻¹, and (squares) C_HbS = 230 mg ml⁻¹, different fills correspond to different runs in the same solution; within a run, different data points are taken at different temperatures, which vary within ΔT = 5°C for each run. Solid line represents a linear fit through all points with an intercept A = 0.254 ± 0.027. Dashed lines show 95% confidence interval for this fit (i.e., in 95% of experiments the fit line is expected to lie inside the confidence interval). A t-test for the hypothesis that A = 0, i.e., 1/R is proportional to θ, gives a probability p < 0.0001.

Preferred orientation of nucleating HbS polymers

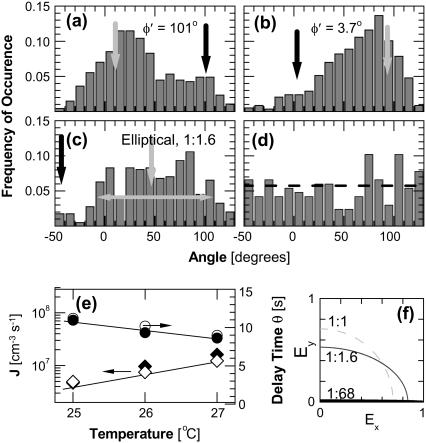
In the absence of interactions of the polymers with external fields one expects that the orientations of the spherulites should be random due to Brownian rotation in the solution (65). In contrast, we found that in all experiments the spherulites had a preferred direction: perpendicular to the plane of polarization of the laser beam used to photolyse CO-HbS (Fig. 4 a) (the illuminating light in our experiments is always polarized by the optical elements necessary for the DIC imaging of the HbS polymers). To test for trivial explanation of this preferred orientation, we rotated the slide with the HbS solution and the microscope objective lens and varied the laser intensity: we saw no changes in the angular distribution. These observations rule out undetectable directional patterns on the slide surfaces or temperature inhomogeneity due to nonuniform illumination stemming from imperfections of the optical system.

FIGURE 4.

Distributions of the angles of orientation of the HbS polymer spherulites defined in Fig. 2 b. (a and b) Illumination with linearly polarized light, the orientation of plane of polarization φ′ is indicated and marked with a solid arrow; the direction at 90° from that of the plane of polarization is marked with a shaded arrow. (c) Illumination with elliptically polarized light, ratio between axes of ellipse is shown; halfwidth of distribution is indicated with double-sided arrow. (d) Fiber nucleation in solution deoxy-HbS by temperature jump without illumination. C_deoxy-HbS = 261 mg ml⁻¹, horizontal dashed line indicates mean value of distribution. Total number of analyzed spherulites: (a) 470, (b) 586, (c) 398, and (d) 162. (e) The nucleation rate, J (diamonds), and delay times, θ (circles), at three temperatures during illumination by linearly (solid symbols) and elliptically (open symbols) polarized light. (f) Schematic of light polarization states used in experiments: linearly polarized light has ratio of intensities of the two perpendicular directions of 1:68; elliptically polarize light: 1:1.6. Circularly polarized or nonpolarized light, not used in experiments discussed here, would have a ratio of 1:1.

In further tests, we rotated the plane of polarization of the illumination (see Materials and Methods for details), and this resulted in rotation of the preferred orientation to the new orthogonal direction (Fig. 4 b). Determinations with crossed polarizer and analyzer revealed that the ratio of the amplitudes in the plane perpendicular to the optical axis during the experiments represented in Fig. 4, a and b, was 1:68 (Fig. 4 f), i.e., the light is nearly linearly polarized.

We also generated elliptically polarized light with a ratio between amplitudes of 1:1.6 (Fig. 4 f) and determined the orientational distribution of HbS polymer spherulites generated with this illumination (Fig. 4 c). The center of the distribution of the orientations of the spherulites is perpendicular to the longer of the two ellipse axes. The distribution is broader, as expected for a broader angular distribution of the intensity of the illuminating light.

As a control, nucleation of the HbS polymers in a deoxy-HbS solution was induced in the dark by raising the temperature from 5°C to 25°C. The microscope illumination was turned on to image the spherulites and determine their orientations. The results in Fig. 4 d show that the orientations are randomly distributed. This result highlights the crucial role of polarized light for the observed fiber orientation.

As another control, polymerization was carried out by a temperature jump in a solution of deoxy-HbS in an illuminated slide. The polymers were preferentially perpendicular to the main plane of polarization introduced by the microscope components needed for DIC imaging. This observation shows that the preferred fiber orientation is not introduced by preferred photolysis of CO-HbS of certain orientations.

Metastable mesoscopic clusters in deoxy-HbS solutions

To test for metastable dense liquid clusters within which the HbS polymer nucleation may occur, we monitor deoxy-HbS solutions by dynamic light scattering. Fig. 5 a shows a typical intensity correlation function of a such solution (correlation functions with similar features were also seen in oxy-HbS and oxy-HbA solutions). The correlation function reveals two processes. The one with characteristic time of ∼0.04 ms is the Brownian motion of single HbS molecules and it is present at all solution concentrations. A second process has a longer characteristic time and its amplitude increases with higher hemoglobin concentrations. This slower time could come from HbS clusters suspended in the HbS solution or from single HbS molecules embedded in a loose network structure constraining their free diffusion. A loose network would increase the low-shear viscosity of the solution from its high-shear value (a loose network would be destroyed by shear flow) measured by a flow-through viscometer (66). We determined the viscosity of deoxy-HbS solutions over millisecond timescales and 10–1000-nm length scales by monitoring the Brownian motion of 400-nm probe particles (the shear rate associated with this motion is ∼1 s⁻¹) (67). The values were in the range 2–4 cP, equal to those determined using high shear rates in a flow-through viscometer (66), i.e., no loose networks in HbS molecules exist in these solutions. Thus, the long times in Fig. 5 a correspond to HbS clusters.

FIGURE 5.

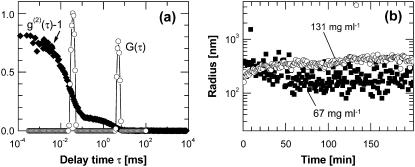
Light scattering characterization of dense liquid clusters. (a) Examples of correlation function (diamonds) and its delay time density function (open circles) of a deoxy-HbS solution with C_HbS = 67 mg ml⁻¹. (b) Time dependence of the radii of dense liquid droplets in deoxy-HbS with C_HbS = 67 mg ml⁻¹ (squares) and C_HbS = 131 mg ml⁻¹ (circles). From Pan et al. (68).

The mean hydrodynamic radius of the cluster population can be determined from the long characteristic time in the correlation functions such as those in Fig. 5 a by using the Stokes-Einstein relation and the viscosity of the HbS solution as a scaling factor (see Pan et al. (68) for details), and its time dependence is shown in Fig. 5 b. At both HbS concentrations probed, the clusters are present immediately after solution preparation, and overall their radius is relatively steady after an initial transient. (The apparent fluctuations in the cluster radii at C_HbS = 67 mg ml⁻¹ are likely due to noise in the dynamic light scattering signal (68)). The clusters could consist of any of the condensed phases in Fig. 1 b. However, both tested HbS concentrations are below the polymer solubility; hence, these are not short HbS fibers. Their fast appearance after solution preparation precludes crystalline or disordered, compact or loose, solid aggregate nature—the nucleation of such phases is much slower. In contrast, clusters of dense liquid could exhibit any of the observed behaviors. Extremely fast formation of 1–2 μm in size dense liquid droplets has been observed with the protein lysozyme (69). Fast formation and decay of mesoscopic clusters have been recorded with the protein lumazine synthase (51). Thus, we conclude that these are clusters of dense liquid of HbS.

Further results on the behavior of clusters of dense liquid in solutions of deoxy- and oxy-HbS and oxy-HbA are presented in Pan et al. (68). We found that with all three Hb variants, the clusters exist in broad temperature and Hb concentration ranges. Although the cluster lifetime could not be directly determined, it was estimated from the angular dependence of the characteristic rate of cluster diffusion, as discussed in Pan et al. (68). This procedure only yields the lower bond of the cluster lifetime, and it was found to be 15 ms (68). The HbS clusters occupy φ = 10⁻⁴–10⁻² of the solution volume. Higher φs within this range are observed at higher temperatures and HbS concentrations (68).

DISCUSSION

The delay time-growth rate correlation

The first piece of evidence supporting the two-step nucleation mechanism stems from the temperature dependencies of delay time, θ, for the nucleation of the HbS polymers and their growth rate, R. The delay time, θ, defined from the dependencies of the number of nuclei on elapsed time after supersaturation is imposed, is a characteristic of the homogeneous nucleation only and is unaffected by the kinetics of growth and branching (62). In this respect, it is fundamentally different from the characteristic times, defined in Ferrone et al. (21) and Cao and Ferrone (30), which account for a certain degree of HbS polymerization, e.g., 10%, and depend on the rates of growth and branching. If θ is determined from plots of the observable domains of new phase on time, as in Fig. 2 g, it consists of two parts: the time Δt_g for growth of the polymer nuclei from the critical to a detectable size (62) and an intrinsic θ, which has a different meaning depending on the nucleation mechanism. With the fiber growth rate R > 2 μm s⁻¹ (Fig. 3) and a detection size of <1 μm, Δt_g < 1 s and the contribution of Δt_g to θ is relatively insignificant. Since the detection size is identical for single fibers of 22-nm thickness and for fiber bundles and spherulites (42,60), the determination of θ does not depend on the rate of heterogeneous nucleation and fiber branching. Thus, we use the values of θ determined as illustrated in Fig. 2 g as a measure of the intrinsic nucleation delay time.

If a two-step nucleation mechanism operates, a recently developed theory (63) shows that θ = 1/J_cυ₀, where J_c is the rate of nucleation of the ordered polymers within the precursor droplets and υ₀ is the volume occupied by these droplets during steady-state nucleation. Temperature increases below 35°C increase supersaturation, reducing the size of the ordered nuclei and the barriers for both steps in Fig. 1. Since the nucleation rate, J_c, depends exponentially on the nucleation barrier, J_cυ₀ and θ depend exponentially on temperature (J_c increases and θ decreases with increasing T) if the two-step mechanism operates.

If a one-step nucleation mechanism operates, i.e., no precursor is present and ordered nuclei form directly from HbS molecules in the solution, the delay time, θ, represents the time for establishment of steady-state nucleation (70,71). The definition of θ is based on an integral description of the nucleation process, which explicitly accounts for the slower growth of the new phase at subcritical and near-critical sizes (62,70). θ is calculated as θ = 2(3πZ²f*)⁻¹, where Z is the Zeldovich factor and f* is the frequency of attachment of HbS molecules to the polymer nucleus (62). Both Z and f* are functions of temperature. The Zeldovich factor Z = i*⁻¹(ΔG*/3πk_BT)^1/2, where i* is the number of molecules in the nucleus and ΔG* the nucleation barrier, proportional to Δμ⁻² (72). When temperature is increased, the supersaturation also increases: the solubility of HbS has a retrograde temperature dependence at T < 35°C (38). Accounting for nonideality (42), the supersaturation for all experiments depicted in Fig. 3 varies between 1.2 < Δμ/k_BT < 1.8. The nucleus size is approximately unchanged in the probed temperature range (42), whereas increasing supersaturation lowers the nucleation barrier. Thus, Z weakly decreases with increasing temperature proportionally to Δμ⁻¹.

To evaluate the response of f* to temperature, we correlate it to the fiber growth rate, R. Since the roughness of the growing end of a polymer fiber is similar to the roughness of a polymer nucleus, f* ≈ f⁺, where f⁺ is the frequency of attachment of molecules to a long fiber. The linear rate of growth of a 14-molecule fiber R = a (f⁺ − f⁻)/14, where f⁻ is the detachment frequency, a = 5.5 nm is the size of a HbS molecule, and 14 is the number of HbS molecules in a cross section of a fiber. The ratio f⁺/f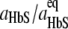⁻ = = exp(Δμ/k_BT), where a_HbS and 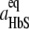are the HbS activities in the solution and at equilibrium with the polymer at temperature T. In our experiments, C_HbS = 200–250 mg ml⁻¹ and 1.2 <Δμ/k_BT < 1.8, and so f⁺/f⁻ ≈ 3–5. Thus, assuming f⁻/f⁺, which leads to R ≈ af⁺/14 ≈ af*/14, introduces <30% error in the R(f*) relation. Since R increases with increasing supersaturation and increasing temperature (Fig. 3 b), θ should decrease proportionally to 1/R; the estimated error of the assumption that f* is proportional to R is insufficient to mask this proportionality. Accounting for the Z(T) dependence, θ(T) should be weaker than 1/R(T) if a one-step nucleation mechanism operates.

Fig. 3 shows that θ has an exponential dependence on temperature, which is significantly stronger than the R(T) dependence. Furthermore, the correlation between 1/R and θ in Fig. 3 is far from proportionality; in fact, 1/R is almost independent of θ. These two observations suggest that a two-step mechanism of nucleation of HbS polymers operates.

Interaction of HbS molecules and fibers with the optical field and Brownian rotation

The results in Fig. 4, a–d, show that HbS polymer fibers are preferentially oriented perpendicularly to the plane of polarization of the illuminating light. This orientation could be due to one of the following mechanisms:

1. The illuminating light orients the individual HbS molecules in the solution, which then preferentially incorporate in fibers with certain orientation.

2. The molecules have random orientation and the nuclei are generated with random orientations, but the fibers orient in a direction which minimizes their energy of interaction with the optical field.

3. The fibers are nucleated with an orientation determined by interaction with the optical field and their orientation is not randomized by Brownian rotation.

Testing mechanism 1, we estimate the energy of interaction of a light wave with the HbS molecule. The electric field of the light wave illuminating the HbS solution can be evaluated using the link between the power density of an electromagnetic wave, F, and its electric field, E:

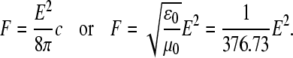On the other hand, the power density, F, at the center of Gaussian beam is 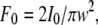where I₀ is intensity of laser beam and w is its halfwidth. With values typical for our experiments, I₀ = 10 mW and w = 40 μm, we get E = 614 V/cm. Accounting for local field with the Lorenz-Lorentz formula gives 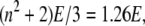where n = 1.33 is the refractive index of water and the electric field E = 773 V/cm. This value is too low for any nonlinear effects. The direction of the electric vector is in the plane of polarization of the illuminating beam.

The permanent dipole moment of HbS molecules in normal solutions only plays a role in interactions with permanent or slowly varying fields. To estimate the induced dipole moment of HbS, we determine from its absorption spectrum the polarizability, α₉₀, at the wavelength of the illumination λ = 532 nm from 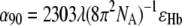(73), where ɛ_Hb = 3.32 × 10⁷ cm²/mol is the HbS extinction coefficient at this wavelength. We get α₉₀ = 85.5 nm³ (which is reasonably close to a volume occupied by an Hb molecule, V = πa³/6 = 87.1 nm³). Then the induced dipole moment for one molecule is 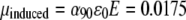Debye, where ɛ₀ is the dielectric permeability of vacuum.

We compare the energy of dipole-field interaction μ_inducedE with the thermal energy k_BT at temperature T = 300 K and get 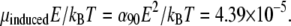This low value of 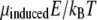shows that the interaction of single HbS molecules with the optical field is insufficient to overcome randomization due to Brownian rotation with energy k_BT, refuting mechanism 1.

Mechanism 1 is also contradicted by the observations of spherulites of ∼20 μm, as in Fig. 2 f: they are isometric, indicating isotropic incorporation of molecules to constituent fibers pointing in all directions. The isometric spherulites in Fig. 2 f also refute another, somewhat unlikely hypothesis: the preferred orientation is due to higher temperature of the ends of fibers with a certain orientation with respect to the plane of polarization of the illuminating light.

For tests of mechanism 2, we numerically solved the rotational diffusion equation for growing HbS fibers, which have increasing dipole moments and decreasing rotational diffusivity, in the presence of an external electric field. Rotational diffusion in external electric field is described by an equation analogous to the generalized Fick's law (65),

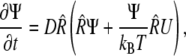where Ψ(φ,t) is the angle distribution function, D is the rotational diffusion coefficient, 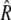is the rotational operator, and U is the potential of the external field. Assuming cylindrical symmetry with an axis coinciding with the axis of the illuminating beam, 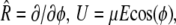where φ is the angle between the direction of electric field and the rotating object, HbS molecule, fiber, or other, and

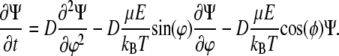The physical picture of rotational diffusion described by the above equation is simple. In the absence of electric field the first, diffusive term widens any initial distribution until it becomes uniform. If an electric field is applied, an initially uniform distribution is directed along the field. The width of the distribution depends on the strength of interaction with the field.

As the fibers grow, their dipole moments and the strength of their interaction with the field continuously increase. The model of rotational diffusion has two time-dependent parameters: the rotational diffusion coefficient, D, and the ratio of the energy of the interaction with electric field to thermal energy, 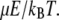The rotational diffusion coefficient of the fibers can be modeled like that of long cylinders (65). In this case

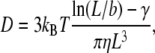where b = 22 nm is the fiber diameter, γ = 0.8 is a hydrodynamic correction factor, and η is the viscosity of the solution. L is the length of the fiber and we take into account continuous growth with rate, R, by using L = a + Rt, where R = 1 μm s⁻¹ and a = 5.5 nm is the HbS diameter, used to avoid singularity at t = 0. The rotational diffusivity decreases as L⁻³ (increasing D(L) dependence, suggested by the above equation, is unphysical; it occurs at L comparable to b and, since b ≪ L_final, does not affect the outcome of the simulations).

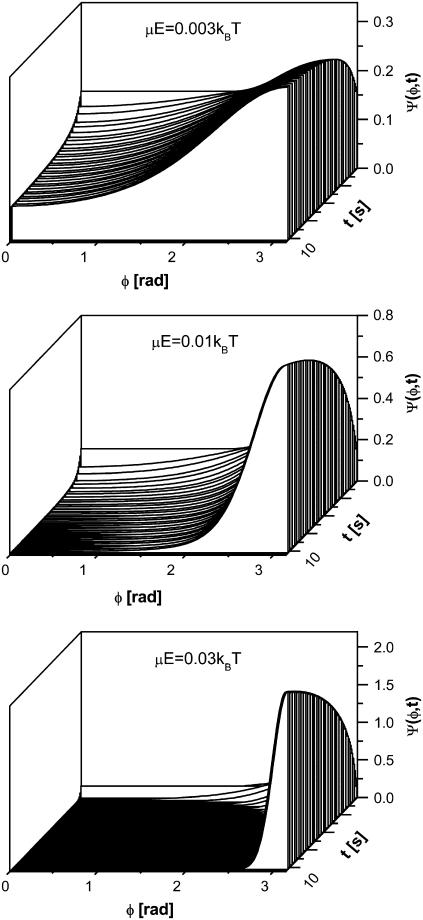
We solve the rotational diffusion equation numerically with a fully implicit, finite difference scheme. Fig. 6 shows that the lowest energy of interaction for which a nonuniform distribution of fiber orientation can be induced is μE/k_BT = 0.003. This is ∼2 orders of magnitude stronger than the energy of interaction of the fibers with the electric field via the HbS polarizability. This observation supports the conclusion that the observed orientational distribution of the HbS fibers are not due to interactions of the electric field with the induced dipole moment of the HbS molecules in the growing fibers (refuting mechanism 2).

FIGURE 6.

Evolution of the distribution of fiber orientations Ψ at three energies of interaction with external electric field, indicated in the plots. φ, angle between fiber dipole moment and direction of electric vector of optical field. Since fiber dipole moment is perpendicular to fiber axis, the fiber orientation is shifted by π/2 with respect to those shown here. Fiber growth with rate R = 1 μm s⁻¹ increases dipole moment, μ, and length, L, and changes rotational diffusion coefficient according to the expression in the text.

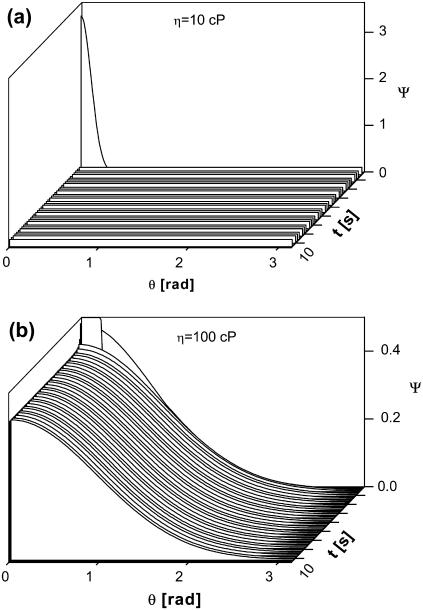
This leaves mechanism 3. This mechanism could explain the results in Fig. 4, a–d, only if two conditions are met: i), the viscosity of the domains, within which the HbS polymers nucleate, is sufficiently high to prevent them from randomizing their orientation after nucleation; and ii), the domains are sufficiently large that their own rotational diffusion would not lead to randomization of the orientation of the polymers contained within them. Probing the feasibility of i, we searched for the minimum viscosity at which a fiber generated with a particular orientation would retain it, rather than attain a random orientation driven by the thermal motion of the solvent molecules. We assumed a narrow initial angular distribution. Since, as shown above, the interaction of growing fiber with an external electric field is insignificant, E = 0 was assumed. Since the rotational mobility of the fibers is determined by the solution viscosity, several values of the viscosity were probed. With these assumptions, we solved the equation of rotational diffusion above. Because of the strong dependence of diffusion coefficient on fiber length, the fibers tend to randomize their orientations when they are small in length and tend to preserve the angular distributions when they are long. Fig. 7 a shows that an initial nonuniform distribution is randomized over very short times if the viscosity of the environment is ∼10 cP. This is the approximate viscosity of the red cell cytosol and is higher than the viscosity of the HbS solutions used in the nucleation experiments of ∼5 cP (66,74). This result shows that even if the fibers were nucleated with a preferred orientation, if they grow in typical HbS solutions, their orientation would be randomized before they reached observable sizes.

FIGURE 7.

Randomization of fiber orientation due to thermal motion. φ is an angle between a fiber and an arbitrarily chosen direction. A highly nonuniform initial distribution is assumed. Solutions of viscosity, η, are shown in the plots; rate of growth of fibers is the same as in Fig. 6.

Fig. 7 b shows that the viscosity of the environment around the growing spherulites, which, during the duration of our experiments, could preserve an initially nonuniform distribution of orientations, is >100 cP. This threshold viscosity value is significantly higher than the viscosity of the HbS solutions in the experiments or in the erythrocyte cytosol (74). To reconcile the latter controversy, the high viscosity values must belong to domains occupying a minor fraction of the total solution volume. On the other hand, the viscous domains should be sufficiently large to resist Brownian rotation as a whole, which would also randomize the fiber orientations, condition ii above.

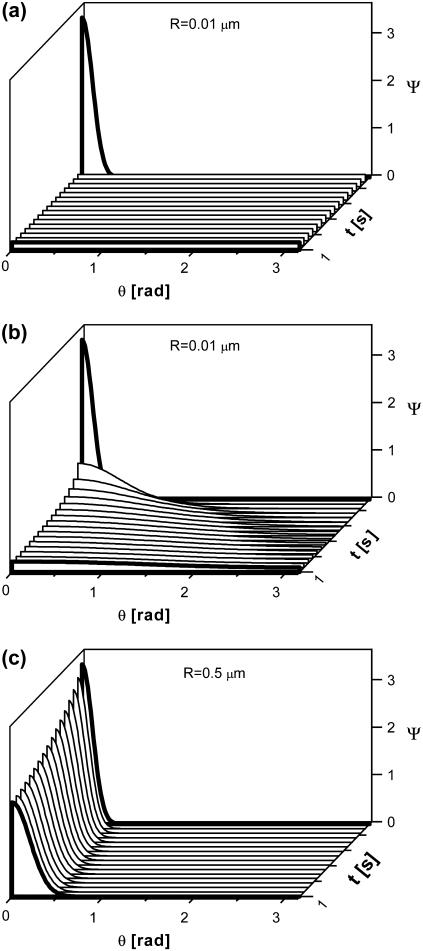
For tests of condition ii, we solved the rotational diffusion equation for spherical objects whose rotational diffusivity complies with the Stokes law, 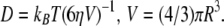We assumed solution viscosity of 5 cP, corresponding to HbS concentration of 250 mg ml⁻¹ (66). Fig. 8 shows that if the droplets are larger than 500 nm, thermal motions will not lead to a loss of their preferred orientation within the time of 10 s of typical HbS experiments.

FIGURE 8.

Evolution of the distribution of orientations of spherical objects with radii, R, indicated in the plots.

The above numerical results show that the nonuniform distribution of the HbS spherulites could be observed only if they nucleate within droplets of size ∼0.5 μm with viscosity >100 cP inside the droplets. Similar viscosity values have been observed in HbS solutions with concentration >450 mg ml⁻¹ (66). Thus, the preferred orientation of the spherules is another piece of evidence in favor of a mechanism of HbS polymer nucleation, in which the nucleation of the HbS polymer is preceded and occurs within a droplet of dense HbS liquid.

The dense liquid clusters as a medium for the HbS polymer nucleation

The two sets of kinetic evidence in favor of a nucleation mechanism of HbS polymers involving dense liquid droplets appear to contradict a previous observation of a lack of dense liquid phases in HbS solutions. Dense liquid was only observed upon the addition of 2 mM polyethylene glycol (PEG) (60). Thus, these previous observations show that the free energy of the dense liquid phase is higher than the one for the dilute HbS solution and that the addition of PEG lowers it, as illustrated in Fig. 1 b. If the free energy of the dense liquid is higher than that of the dilute solution, the metastable dense liquid could exist as clusters of limited lifetime and limited size, similar to clusters observed with other proteins and colloids (51). The clusters seen in Fig. 5 present such metastable phases with limited lifetimes and mesoscopic sizes below the resolution limit of optical microscopes.

The cluster sizes in Fig. 5 b are compatible with those required to ensure the orientational distributions in Fig. 4. We conclude that these are the dense liquid clusters, which serve as precursor to the ordered nuclei of HbS polymers in the two-step nucleation mechanism.

The value φ, the fraction of the total solution volume occupied by the dense liquid clusters, 10⁻⁴–10⁻² (58), allows determination of υ₀ = φV_total, the volume occupied by the clusters, used in the definition of the delay time, θ, above (63). This volume fraction, φ, increases with increasing temperature and this increase correlates with increasing HbS nucleation rates, J, and shorter nucleation delay times, θ (58).

Electric fields, the orientation of HbS fiber nuclei, and the rate-determining step in the two-step mechanism

The preferred orientation of the HbS fibers to light's electric field indicates that this field is involved either in the HbS polymer nucleation or in the orientation of the emerging nuclei within the dense liquid clusters. The environment within these clusters is crowded, viscous, and likely structured and inhomogeneous (75). Models of the nucleation of the fibers and their interaction with the electric field in this environment require accounting for nonequilibrium time-dependent, single-molecule, and collective dynamics. Such models do not currently exist. If such a model is developed, it will likely rely on the interaction of the permanent dipole moment of the HbS polymer, μ_polymer, with the electric field. This μ_polymer is mostly perpendicular to the polymer fiber axis (the perpendicular and longitudinal components are 454 and 3.7 Debye (59)), and minimization of its energy of interaction with the electric field would ensure the observed perpendicular orientation of the fibers with respect to the electric vector.

Although there is a lack of theoretical understating of the effects of electric fields on nucleation of ordered solids in viscous crowded media, there is convincing evidence that these effects are not limited to HbS polymer nucleation. Experiments with urea and lysine have demonstrated strong effects on nucleation by optical and permanent electric fields with intensity similar to the one employed here (53,54). These effects were interpreted via a nucleation mechanism with a dense liquid precursor, a mechanism identical to the one proposed here for HbS polymers.

Fig. 4 e shows that the degree of polarization does not affect the nucleation rates and delay times at three temperatures. Furthermore, experiments with increasing illumination power (data not shown) showed no effects on the overall nucleation rate or delay time. This observation is in contrast to results by Garetz et al. (53), who found that the nucleation of crystals of two glycine polymorphs and urea is significantly enhanced by polarized laser light. The explanation of the effects of illumination on the nucleation of crystals of the two materials is via a two-step mechanism, nearly identical to the one invoked above for the nucleation of HbS polymers. This raises the question of the origin of the discrepancy. We offer that during nucleation of crystals the second step, i.e., the nucleation of a crystal within the dense liquid precursor, is rate limiting. Its rate is enhanced by the polarized laser light and this increases the observable nucleation rate. Since the data in Fig. 4, a–c, show that HbS polymer nucleation is affected by the laser illumination, it is likely that polarized light also enhances the formation of HbS polymers. The apparent contradiction between the data in Fig. 4, a–c and e, indicates that, in contrast to glycine and urea, the rate-limiting step for HbS polymer nucleation is the formation of the dense liquid precursor. This conclusion seems reasonable: the nucleation rates of HbS polymers, of order 10⁸ cm⁻³ s⁻¹, are comparable to measured rates of nucleation of stable dense liquid droplets in solutions supersaturated with respect to them (69). It is unlikely that the rate of formation of metastable droplets, within which the HbS polymers nucleate, can be sufficiently higher than those to make polymer nucleation rate limiting.

A phenomenological model of the two-step nucleation mechanism of ordered solids was recently proposed (63). This model relates the rate of formation of the dense liquid clusters, their volume, and the rates of nucleation of ordered structures within them to the nucleation progress curves, illustrated in Fig. 2 g. This model was used for the estimate of the temperature dependence of the nucleation delay time, θ, above. A basic assumption of this model is that the first step, the formation of the dense liquid clusters, is rate limiting (63). The experiments with linearly polarized light in Fig. 4 e justify this assumption for the nucleation of HbS polymers.

CONCLUDING COMMENTS AND CLINICAL IMPLICATIONS

We have demonstrated that the homogeneous nucleation of the HbS polymers follows a two-step mechanism, consisting of the formation of a metastable dense liquid cluster and the nucleation of an ordered polymer nucleus within this cluster. The evidence for the two-step mechanism comes from two sets of kinetics data: on the response of the nucleation delay times to temperature and of the fiber orientation in optical electric field. This evidence is supported by direct detection of the metastable dense liquid clusters by dynamic light scattering. Because the cluster size is smaller than the microscope resolution limit, the evidence for nucleation of the HbS polymers within the dense liquid clusters is indirect. However, in a previous work in which the dense liquid was stabilized by the addition of PEG, we directly showed that polymer nuclei appear within macroscopic dense liquid droplets (60).

The two-step mechanism of homogeneous nucleation of HbS polymers treats the first step of the overall mechanism of HbS polymerization, consisting of homogeneous nucleation, fiber growth, and secondary nucleation causing fiber branching, often called double nucleation mechanism (21,22,38). Thus, no contradictions between the two models exist, and most of the polymerization kinetics data used to justify the double-nucleation mechanism are compatible with the newly proposed two-step mechanism. On the other hand, some of the data interpretation may need to be revisited. Thus, in Galkin and Vekilov (42) HbS nucleation rate data were interpreted via one-step mechanisms and the nucleus sizes were determined using the nucleation theorem for such one-step nucleation (62,76). The nucleation theorem, which correlates the nucleation barrier with the nucleus size, has to reformulated for two-step nucleation and then the nucleus sizes for each of the two steps can be determined anew (63).

The validity of the two-step nucleation mechanism for the nucleation of HbS polymers has fundamental and clinical consequences. Its value to the fundamental understanding of phase transitions is that it provides an example of the applicability of this mechanism for a new class of systems and suggests that the presence of a disordered precursor may be a general feature of the self-assembly of ordered structures. Several potential clinical implications can be discussed. The huge clinical variability of sickle cell anemia has been attributed to processes occurring independently of the HbS polymerization: erythrocyte and endothelial wall adhesion, erythrocyte deformability, erythrocyte membrane damage, and others (77–79). On the other hand, experiments with transgenic sickle cell mouse reconfirm that the primary pathogenic event of the disease is HbS polymerization: when polymerization was delayed, the mice were cured (80). If polymerization follows the accepted scenario of one-step homogeneous nucleation, followed by growth, branching, and gelation, the rate of HbS polymerization is entirely determined by the HbS activity. The HbS activity is mostly determined by the HbS concentration since the HbS molecules only interact through their excluded volume (38,81). Since most nonhemoglobin components of the red cell cytosol occupy low volume fractions, HbS activity is unaffected by variations in their concentrations. Thus, the primary role of HbS polymerization has been hard to reconcile with the clinical variability among patients with identical expression of HbS in the erythrocytes (82,83).

To understand the different response of the rates of HbS polymerization and cluster formation to the HbS activity, we rely on the following considerations. The thermodynamic driving force for HbS polymer nucleation is the chemical potential difference between the HbS solution and the polymer. The HbS chemical potential in a supersaturated solution is uniquely determined by its activity, whereas the solubility reflects the balance between the HbS chemical potential in the polymer and in an equilibrium solution. On the other hand, the driving force for the formation of the dense liquid clusters, the difference in chemical potential between the HbS solution and the metastable dense liquid, is negative, as illustrated in Fig. 1 b. This is why the lifetime of the clusters is limited. The clusters are metastable and their numbers, sizes, and total volume fraction depend not only on the HbS solution activity but also on the thermodynamic barrier for their decay, illustrated in Fig. 1 b. Furthermore, numerous kinetic factors of cluster stability should be considered.

A consistent theory of the metastable dense liquid clusters is still to be developed (V. Lubchenko, University of Houston, personal communication, 2006). Even without such a theory, it is likely that the thermodynamic and kinetic factors for the clusters' behavior include details of intermolecular interactions, modification of the interactions in the crowded environment inside the clusters, viscosity of the HbS solution, viscosity within the clusters, solution flows, and others. In turn, these factors are a very sensitive function of the solution composition, temperature, and the hydrodynamics of the HbS solution in vitro or in the red cell cytosol. This multitude of governing parameters rationalized by the two-step mechanism allows reconciliation between the primary role of HbS polymerization and the clinical variability of sickle cell anemia: the sizes, properties, and volume fractions of the dense liquid precursors likely are strongly modified by components of the red cell cytosol at submillimolar concentrations (43,60). Other effectors on the precursors include solution flows inside and outside of the red cells and features of the blood circulation that may vary between patients, vary between different locations along the capillaries, venules, and veins of a patient, and evolve and vary for the same patient within timescales as short as minutes or as long as years.