Two-State Model of Acto-Myosin Attachment-Detachment Predicts C-Process of Sinusoidal Analysis

Abstract

The force response of activated striated muscle to length perturbations includes the so-called C-process, which has been considered the frequency domain representation of the fast single-exponential force decay after a length step (phases 1 and 2). The underlying molecular mechanisms of this phenomenon, however, are still the subject of various hypotheses. In this study, we derived analytical expressions and created a corresponding computer model to describe the consequences of independent acto-myosin cross-bridges characterized solely by 1), intermittent periods of attachment (t_att) and detachment (t_det), whose values are stochastically governed by independent probability density functions; and 2), a finite Hookian stiffness (k_stiff) effective only during periods of attachment. The computer-simulated force response of 20,000 (N) cross-bridges making up a half-sarcomere (F_hs(t)) to sinusoidal length perturbations (L_hs(t)) was predicted by the analytical expression in the frequency domain, 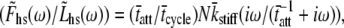where 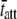= mean value of t_att, 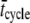= mean value of t_att + t_det, 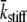= mean stiffness, and ω = 2π × frequency of perturbation. The simulated force response due to a length step (L_hs) was furthermore predicted by the analytical expression in the time domain, 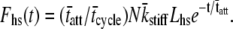The forms of these analytically derived expressions are consistent with expressions historically used to describe these specific characteristics of a force response and suggest that the cycling of acto-myosin cross-bridges and their associated stiffnesses are responsible for the C-process and for phases 1 and 2. The rate constant 2πc, i.e., the frequency parameter of the historically defined C-process, is shown here to be equal to 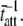Experimental results from activated cardiac muscle examined at different temperatures and containing predominately α- or β-myosin heavy chain isoforms were found to be consistent with the above interpretation.

INTRODUCTION

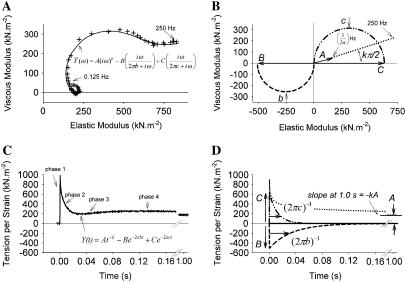
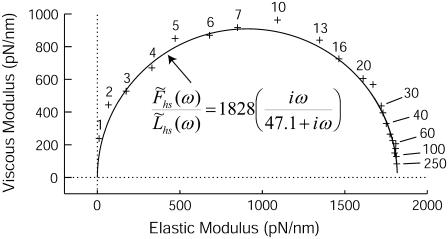
The application of small length perturbations to activated striated muscle at steady state permits the measurement of its mechanical properties, i.e., the elastic and viscous moduli, whose frequency dependencies (Fig. 1 A) are often ascribed the so-called A-, B-, and C-processes (Fig. 1 B) (1–11). The application of an instantaneous length change of small amplitude results in a time domain force response, which has been historically characterized with readily identifiable phases 1–4 (Fig. 1 C) (12–16). Interestingly, the observed force responses depicted in Fig. 1, A and C, and the hypothetical underlying processes depicted in Fig. 1, B and D, appear to be, respectively, the frequency and time domain representations of the same physiological phenomena (1,4,7,17,18). The molecular mechanisms responsible for these phenomena, however, are still the subject of various hypotheses.

FIGURE 1.

Frequency and time domain representations of the force response to length perturbation analysis. (A) The complex modulus recorded at frequencies ranging 0.125–250 Hz (+) for human epicardial myofilaments at pCa 4.5 and 37°C is presented here as a Nyquist plot (viscous versus elastic moduli) and is characterized well by Eq. 1A (inset) represented by the solid line. (B) The complex modulus like that shown in panel A has been attributed to three underlying processes. The graphical representation of the A-process (······) is displayed as a linear relationship between the viscous and elastic moduli. The B-process (–––) and C-process (··-··-··) are represented as semicircles, which are indicative of exponential responses in the frequency domain. (C) A recorded tension change after a step length change of 0.1% muscle length can be fit closely by Eq. 1B (inset), which represents the step response of the tension per unit length change. (D) The time courses of the individual A-, B-, and C-processes in Eq. 1B are illustrated here in the time domain.

A simple two-state model of acto-myosin interactions can predict visco-elastic behavior of muscle, but cannot account for the negative viscous modulus measured at low frequencies (Fig. 1 A) or the force redevelopment in phase 3 (Fig. 1 C) (19,20). Some striated muscles, most notably insect flight muscles and cardiac muscles, can additionally exhibit several oscillations in force during phases 3 and 4 (21–25). The frequency of these oscillations is temperature dependent with a Q₁₀ > 3, which suggests that myosin ATPase underlies the observed oscillations (22–24). Interestingly, the frequency of force oscillations that occur with a discrete length change mimics the frequency at which a negative viscous modulus arises during sinusoidal length perturbations (23–25). These data suggest that myosin heads can be recruited, synchronized, or biased to a common non-force-producing state during muscle stretch and are therefore collectively poised to generate force once stretching has ceased (13,24–26).

Some hypotheses considered to explain this recruitment or synchronization of myosin heads include stretch-induced changes in 1), the degree of thin filament activation (27–30); 2), the positions and availability of actin binding sites relative to myosin heads (31); and/or 3), the rates of myosin head attachment and detachment (32). Experimental evidence continues to mount, suggesting that acto-myosin cross-bridge cycling kinetics are influenced by cross-bridge strain (1,14,32–37), and that the force responses in both the frequency and time domains reflect these strain dependencies of cross-bridge kinetics and subsequently the number of cross-bridges attached at any given time. Recent reports using single myosin molecules indeed suggest that strain due to a resistive or extensible load prolongs the time of cross-bridge attachment (38,39).

Two of the earliest mathematical models to describe the influence of strain on the number of attached cross-bridges were three- and four-state models, which prohibited reversal of the cross-bridge cycle within an attached or detached state but permitted the reversal of myosin-actin interactions in a phosphate-dependent manner (24,40). Subsequently, a seven-state model proposed by Kawai and Brandt (1,4,5) attempted to link the mechanical perturbation of each biochemical state in the cross-bridge cycle to the observed force response of muscle and offered to provide a biochemical context within which one may interpret the results of length-perturbation analysis. The predictive power of the model proposed by Kawai and Brandt (1,4,5) relied in part on the observance of a limited number of so-called exponential processes (A-, B-, and C-processes) plus a parallel elastic element (H) as underlying the complex modulus of the force response in the frequency domain. The C-process appears to represent a mechanical work-absorbing exponential process, which the authors attributed to the strain-dependence on the rate of cross-bridge detachment after ATP binding (1,4,5). In support of this interpretation are several reports from Dr. Kawai's laboratory demonstrating that the characteristic rate of the C-process, i.e., 2πc of Eq. 1A, is monotonically proportional to ATP concentration and asymptotically approaches a maximum value at high ATP concentrations in a variety of vertebrate striated muscles (3,9,41–43). A similar response to ATP is observed in invertebrate muscle (11,44).

Further consideration by our laboratory of the passive visco-elastic elements in the muscle has led to the replacement of Kawai and Brandt's A-process and H element (1,4,5) with a single expression for the visco-elastic response of the passive constituents in muscle (6–8,10,11,45). Equations 1A and 1B present the frequency domain expression for the complex modulus (6–8,10,11,45) and the time domain expression for the stress response (σ(t)) per instantaneous fractional length change, i.e., strain (ɛ), modifying the approach pioneered by Kawai and Brandt (1,4,5):

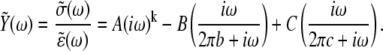(1A)

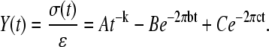(1B)

In this study we revisit the two-state model as a basis for explaining the C-process alone. We considered the molecular mechanisms underlying the C-process and a portion of phases 1 and 2 of the step response to be 1), the intermittent attachment of myosin to actin, i.e., cycling acto-myosin cross-bridges; and 2), the mechanical result of displacing the elastic element associated with the attached acto-myosin cross-bridge. We demonstrate in this study that these two assumptions alone, which appear sufficient to explain isometric force development due to the myosin power stroke, also lead to analytical expressions in the frequency and time domains that represent well the C-process and phases 1 and 2, respectively, that arise due to externally applied length perturbations. We find that the characteristic rate of the C-process, 2πc, is equal to the reciprocal of the mean time of cross-bridge attachment. A computer simulation of the two-state model is used to validate the analytical expressions. The results of the simulation are consistent with experimental data from activated cardiac muscle containing different myosin heavy chain isoforms and examined at different temperatures.

ANALYTICAL SOLUTIONS

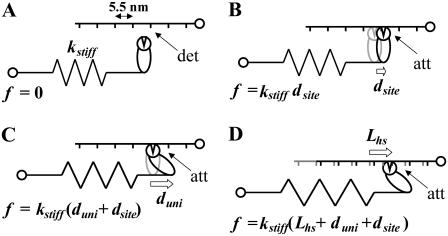
We have assumed that the total force produced by a half-sarcomere, F_hs(t), is given as the sum of the forces produced by the individual acto-myosin cross-bridges, f_(i)(t), i.e., 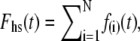where N = the number of individual cross-bridges in the half-sarcomere. All myosin heads are assumed independent of each other and can be described as being in one of two states, attached or detached to actin. The time periods of attachment, t_att, and detachment, t_det, are considered here to be random variables whose values are governed by stochastic processes independent of force, stress, strain, length, velocity, and each other. The total time period for a myosin head to undergo a complete attached-detached cycle is also a random variable, t_cycle = t_att + t_det. During t_det, force produced by an individual myosin head is zero (Fig. 2 A), and during t_att, force is proportional to the length displacement of a Hookian elastic element in series with the cross-bridge (Fig. 2, B–D). It is noteworthy that the modeled elastic element in series with the cross-bridge, as depicted in Fig. 2, represents the most compliant structures between the M- and Z-lines of the sarcomere in series with the attached cross-bridge. Previous work by others has identified the most compliant structures as that portion of the myosin molecule not incorporated into the thick filament backbone, namely 1), the head and neck regions of the S1 segment; 2), the lever arm including the essential and regulatory light chains; and 3), the myosin S2 segment (46–48).

FIGURE 2.

Strains on the acto-myosin cross-bridge. (A) Myosin binding sites, indicated by short vertical lines, occur at 5.5 nm spacings along the actin filament (49). No force, f = 0, results when myosin is detached (det) from actin. (B) An extension or compression of the elastic element may be required for the myosin head to bind to actin. The resultant force, f, is proportional to the stiffness of the elastic element, k_stiff, and the displacement undergone by the myosin head to find to an actin binding site, d_site. (C) Force is generated when the myosin power stroke imposes unitary displacement, d_uni, on the elastic element and is additive to that force resulting from d_site. (D) An additional cross-bridge-dependent force is transmitted through the half-sarcomere when the elastic element undergoes an externally applied length change, L_hs.

In this section, we develop two analytically derived expressions: 1), the isometric force of the half-sarcomere that arises due to an internally generated length displacement, i.e., the myosin power stroke; and 2), the force response of the half-sarcomere that arises due to an externally applied length perturbation. Both of these expressions rely upon the same two-state model of acto-myosin cross-bridge kinetics and are developed in part by employing the probability density functions for the named random variables.

Isometric force

We will first describe F_hs(t) for the case where each acto-myosin cross-bridge can be characterized by 1), a stiffness coefficient of the elastic element (k_stiff), as illustrated in Fig. 2 A; 2), a displacement that the myosin head undergoes to reach an available actin binding site (d_site), as illustrated in Fig. 2 B; and 3), a unitary displacement generated by the myosin power stroke (d_uni), as illustrated in Fig. 2 C. The case where an externally driven length perturbation is applied to the half-sarcomere, as illustrated in Fig. 2 D, will be considered later. The force developed by the i^th cross-bridge over a complete cycle is given as the stiffness-displacement product (Fig. 2 C) during t_att, namely: f_(i)(t) = k_stiff(i)(d_uni(i) + d_site(i)) for t_ini < t < t_ini + t_att, where t_ini = a random variable for the instant of initial attachment. The force-time integral over a complete cycle (left side of Eq. 2) is equal to the force-time integral over the time period attached (right side of Eq. 2):

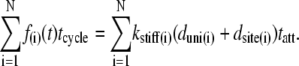(2)

The probability density functions (PDF) for the random variables t_att and t_cycle can now be employed to describe the expected value of the force-time integral:

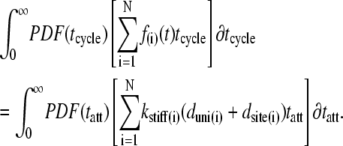(3)

The integrations over the PDFs in Eq. 3 reduce to the mean values for the respective random variables independent of the specific PDFs,

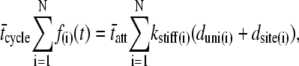(4)

where the bars indicate mean value.

Recalling the definition for F_hs(t),

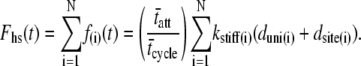(5)

For a large number of cross-bridges, the summation term can be replaced with N multiplied by the integrations over the PDFs for three newly defined random variables, namely k_stiff, d_site, and d_uni. Noting again that the result of integrating over the product of a PDF and its respective abscissa, as was done in Eq. 3, is the mean value of the PDFs, we find

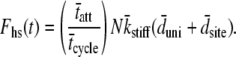(6)

For a large number of myosin molecules the mean displacement to reach an actin-binding site is zero (49), i.e., 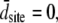we are left with the result for the force of the half-sarcomere:

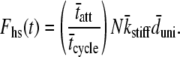(7)

According to the two-state model the force produced by a half-sarcomere at any given time is proportional to the fraction of cross-bridges attached, the total number of acto-myosin cross-bridges available, the mean cross-bridge stiffness and the mean unitary displacement produced by the myosin power stroke (13,50,51). This is a relatively well-accepted result for muscle force arising due to internally generated strains, and we present its development as a demonstration of the methodology we employ below for the case of externally generated strains. It should be noted that the expression above does not rely upon the history of the system or upon the specific probability density functions for t_att or t_det.

Force response due to length perturbation

In the above expressions (Eqs. 2–5), the stiffness-displacement product, i.e., the k_stiff(i) d_uni(i) term, represents the unitary force associated with an individual myosin power stroke. If, instead of considering the power stroke as providing the length displacement of the elastic element responsible for the unitary force, we consider an externally driven length perturbation of the half-sarcomere, L_hs(t), as illustrated in Fig. 2 D, then we would find that the length displacement affecting an individual acto-myosin cross-bridge is proportional to the length change that has occurred relative to the most recent instant of initial attachment, t_ini, which is another random variable:

(8)

In this case, the force response does rely upon the history of the system.

If we use the inverse Fourier transform definitions for F_hs(t) and L_hs(t), namely

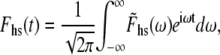(9A)

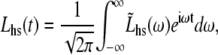(9B)

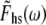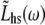where and are the Fourier transforms of F_hs(t) and L_hs(t), respectively, we then obtain from Eq. 8,

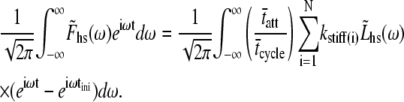(10)

If we now define another random variable, τ = t−t_ini, as the time period from any given time to the instant of the most recent attachment, then the term 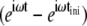becomes 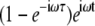and we can remove the Inverse Fourier Transforms of Eq. 10:

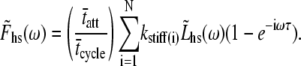(11)

The complex modulus is then given by

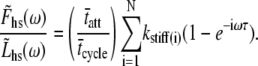(12)

The summation over a large number of cross-bridges, N, can be replaced as the product of N and the expected value of the summed terms,

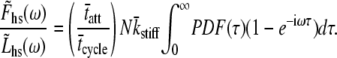(13)

Note that we have adopted the result of the integration over PDF(k_stiff), namely 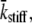in writing Eq. 13. The expression for the complex modulus given by Eq. 13 is dependent upon the particular distribution of values for the random variable, τ, described by PDF(τ).

If we recognize that the cross-bridges attached at any given time have been attached for a time period given by the distribution of the random variable t_att, and we assume that PDF(t_att) and therefore PDF(τ) are well characterized by a single-exponential distribution, as has been detected using laser trap techniques (52),

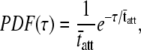(14)

then the complex modulus becomes

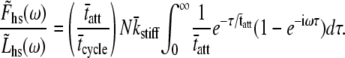(15)

The solution of the above integral gives

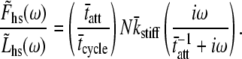(16)

The result provided in Eq. 16 is recognizable as having the same sign and form as the C-process of Eq. 1A used historically and effectively to describe the higher frequency range of the complex modulus resulting from sinusoidal length perturbation analysis. According to the above expression, the magnitude of the complex modulus C-process is proportional to the fraction of cross-bridges attached, the total number of acto-myosin cross-bridges available and the mean cross-bridge stiffness. The frequency-dependent term of Eq. 16 suggests that the parameter 2πc of Eq. 1A is equal to the reciprocal of the mean time attached.

By inverse Fourier transform, Eq. 16 furthermore leads to an expression in the time domain for the force response due to an instantaneous length change,

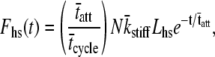(17)

where L_hs = amplitude of the step change in length of the half-sarcomere at time zero. The expression provided in Eq. 17 is similar in sign and form to the C-term in Eq. 1B and suggests the single-exponential representation of a portion of Phases 1 and 2 of a step response. The amplitude of Phase 1 is proportional to the fraction of cross-bridges attached at the instant of length change, the total number of acto-myosin cross-bridges available, the cross-bridge stiffness, and the amplitude of the step change in length of the half-sarcomere. An exponential decay, which describes well a portion of Phase 2, has a time constant equal to the mean time of cross-bridge attachments. It is noteworthy that the force response described by Eq. 17 reflects the distribution of t_att.

METHODS

Computer simulations

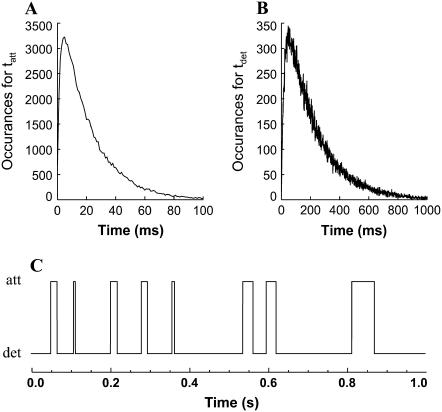
The force response of a virtual half-sarcomere was constructed assuming many (20,000) independent myosin heads alternately attaching and detaching to actin according to independent stochastic processes governing the random variables t_att and t_det. For any one computer simulation, the PDF for each random variable was constructed as the summation of two single-exponential PDFs; the mean values of the first single-exponential PDF were varied between 10 and 60 ms and 140–300 ms for t_att and t_det, respectively, and the mean values of the second single-exponential PDF was 1 ms and 10 ms for t_att and t_det, respectively. This strategy ensured that the resulting PDFs for the random variables avoided the complication of time periods near or at zero value and were still comparable to a single-exponential PDF (Fig. 3, A and B), which was necessary to test the validity of Eq. 16. An example of the attachment-detachment states for a single myosin head over a 1-s time period is shown in Fig. 3 C.

FIGURE 3.

Examples of the number of occurrences generated for the random variables t_att and t_det. (A) The probability density function for t_att with a mean value of 21 ms was constructed by summing two random numbers generated from two independent single-exponential probability density functions having mean values of 20 ms and 1 ms. (B) The probability density function for t_det with a mean value of 210 ms was generated in a similar fashion from two independent single-exponential probability density functions having mean values of 200 ms and 10 ms. (C) Alternating attached and detached states were constructed over a 1-s time period for each of 20,000 acto-myosin cross-bridges. One such second for one such cross-bridge is illustrated here.

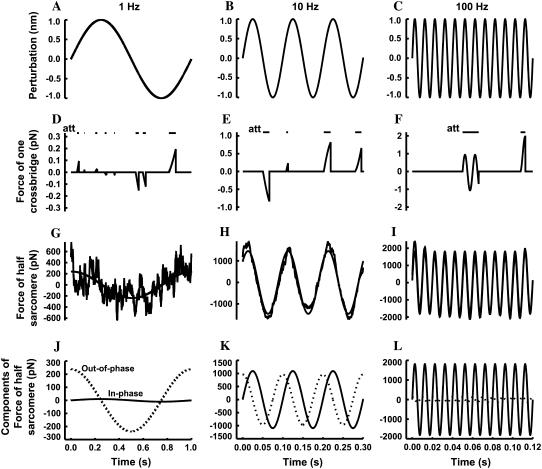
Sinusoidal length perturbations of the virtual half-sarcomere were simulated as having amplitude 1 nm and frequencies over the range 1–250 Hz (Fig. 4, A–C). Each cross-bridge was assigned a stiffness constant of 1 pN/nm (53). The change in length of the cross-bridge relative to the time of initial attachment was multiplied by the stiffness constant to simulate the force resulting from the strain on the elastic element of the cross-bridge (Fig. 4, D–F).

FIGURE 4.

The simulation of individual cross-bridge force responses to length perturbations. Sinusoidal length perturbations of the half-sarcomere at 1 Hz (A), 10 Hz (B), and 100 Hz (C) were simulated with amplitude 1 nm and no phase relative to time zero. The force response of a single cross-bridge occurred only during the time of attachment (att) as indicated by the horizontal bars in panels D–F. At 1 Hz (D), the time of attachment is relatively short such that the deflection in force effectively reflects the instantaneous velocity of the perturbation during the time of attachment. At 10 Hz (E) the time attached is long enough to display some curvature in the force deflection, and at 100 Hz (F) the time attached is so long that the several cycles of the length perturbation are displayed in the force deflection. The sum of 20,000 individual force responses give an ensemble response at 1 Hz (G), 10 Hz (H), and 100 Hz (I), which can be fit with a sine wave (solid line) to provide amplitude and phase of the force response of the ensemble for the virtual half-sarcomere. The fitted sine waves at 1 Hz (J), 10 Hz (K), and 100 Hz (L) can be partitioned into two components that are in-phase (solid line) and out-of-phase (dotted line) with respect to the length perturbation, and the respective magnitudes represent the elastic and viscous moduli.

The resulting force over each second was summed to provide an equivalent second for the 20,000 independent cross-bridges in the virtual half-sarcomere (Fig. 4, G–I). This simulated force of the half-sarcomere, F_hs(t), was fitted using a simplex method to a sine function, whose amplitude (Amp) and phase (φ) permitted the calculation of two components that were in-phase and out-of-phase with respect to the length perturbation: elastic modulus = Amp cos(φ) and viscous modulus = Amp sin(φ) (Fig. 4, J–L). The resulting frequency dependences of the elastic and viscous moduli were fit simultaneously to Eq. 16 using a nonweighted Levenburg-Marquardt nonlinear, least-squares routine. An example of a fitted curve to simulated data is provided in Fig. 5.

FIGURE 5.

The Nyquist plot, i.e., viscous versus elastic moduli, of simulated data (+) at several frequencies of perturbation between 1 and 250 Hz conform to the expression given by Eq. 16.

All computer simulations, random number generations, curve-fittings, and parameter estimation routines were performed using IDL Version 5.5 (Research Systems, Boulder, CO).

Muscle length perturbations

All reagents were purchased from Sigma (St. Louis, MO). Solutions were formulated by solving equations describing ionic equilibria (54). Concentrations are expressed in mmol/L unless otherwise noted. Relaxing solution: pCa 8.0, 5.0 ethylene glycol-tetra-acetic acid, 5.0 ATP, 1.0 Mg²⁺, 0.25 P_i, 20 hydroxyethyl-aminoethanesulfonic acid, 35 phosphocreatine, 300 U/mL creatine kinase, ionic strength 200, pH 7.0. Activating solution: same as relaxing solution with pCa 4.0. Storage solution: same as relaxing with 10 μg/mL leupeptin and 50% wt/vol glycerol. Skinning solution: same as storage with 30 mM butanedione monoxime and 1% wt/vol Triton X-100.

Human and mouse left ventricular skinned myocardial strips were prepared using methods similar to those described previously to yield thin strips (∼140-μm diameter, ∼800-μm length) with longitudinally oriented parallel fibers (45). These strips were chemically skinned for 2 h at 22°C, and stored at −20°C for no more than five days. At the time of study, aluminum T-clips were attached to the ends of a strip ∼150-μm apart. The strip was mounted between a piezoelectric motor (Physik Instrumente, Auburn, MA) and a strain gauge (SensorNor, Horten, Norway), lowered into a 30-μL droplet of relaxing solution maintained at either 17° or 37°C, and incrementally stretched to and maintained at 2.2-μm sarcomere length detected by videography and digital Fourier transform techniques (IonOptix, Milton, MA).

Strips were calcium-activated, and sinusoidal perturbations of amplitude 0.125% strip length were applied over the frequency range 0.125–250 Hz. The elastic and viscous moduli were calculated from the recorded tension transient as the relative magnitudes of the in-phase and out-of-phase components with respect to the imposed sinusoidal length perturbations (1–3). The measured complex modulus was fit to Eq. 1A using a nonweighted Levenburg-Marquardt nonlinear, least-squares routine.

RESULTS

Computer simulations

Fig. 5 illustrates the Nyquist plot, i.e., viscous versus elastic moduli, which resulted from one computer simulation using 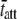= 21 ms and 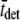= 210 ms. The solid line represents the best fit of Eq. 16 to the data at each frequency. For this example, the best-fit estimates of the two independent parameters in Eq. 16, namely 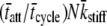and 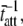were 1828 pN/nm and 47.1 s⁻¹, respectively (Table 1). According to the values used in the simulation, these values would have been expected to be 1818 pN/nm and 47.6 s⁻¹, respectively (Table 1).

TABLE 1.

Parameter values used in computer simulations and then estimated from the computer simulations

Simulation	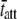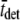(ms)	(ms)	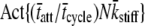(p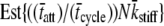N/nm)	(pN/nm)	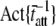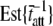(s−1)	(s−1)
1	11	150	1366	1387	90.9	89.7
2	21	210	1818	1828	47.6	47.1
3	31	310	1818	1809	32.3	33.6
4	41	210	3267	3269	24.4	24.5
5	51	210	3908	3905	19.6	20.3
6	61	150	5782	5776	16.4	16.2

The actual parameter values were consistently closely approximated by estimates using a nonlinear least-squares fit of Eq. 16 to the simulated data. For all simulations N = 20,000 and k̄_stiff = 1 pN/nm. Act{} = actual value of bracketed term, Est{} = estimated value of bracketed parameter.

Table 1 provides a comparison of parameter values and parameter estimates from several different computer simulations. For each of these two independent parameter the correlation coefficients between values used for the simulation and values estimated from the simulation were >0.999. These computer simulations therefore corroborate the analytical expression for the C-process provided in Eq. 16, when the probability density function for t_att can be approximated well by a single-exponential function like that given in Eq. 14.

Muscle length perturbations

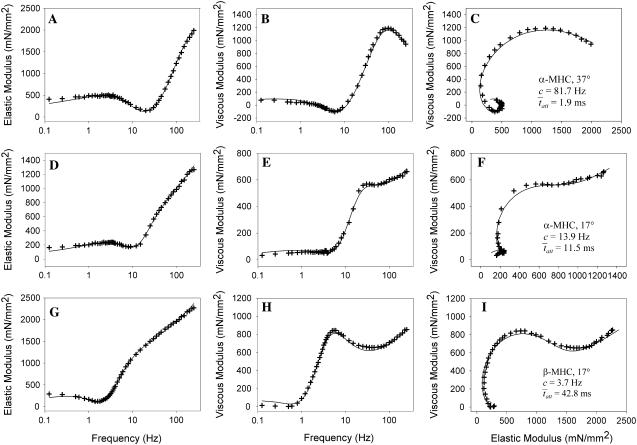
Fig. 6 illustrates the Bode plots (i.e., moduli versus frequency) and Nyquist plots of three different measured examples from mouse cardiac muscle containing different myosin heavy chain isoforms and or examined at different temperatures. Fig. 6, A–C, illustrate the results of wild-type mouse cardiac muscle containing exclusively α-myosin heavy chain (α-MHC) and examined at 37°C. The fit of Eq. 1A to these data is shown in the Bode and Nyquist plots of Fig. 6, A–C. The estimate for the parameter c = 81.7 Hz corresponded to an estimate for 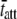= 1.9 ms. Fig. 6, D–F, illustrate the raw data from the same wild-type mouse cardiac muscle (α-MHC) examined at 17°C. Under these conditions, the estimates for the parameters c = 13.9 Hz and 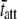= 11.45 ms. We would expect acto-myosin cross-bridge kinetics to be temperature-dependent with a Q₁₀ normally observed for enzyme kinetics, i.e., between 2.0 and 3.0 (55,56). With a temperature difference of 20°C between the two examples presented in Fig. 6, A–F, we would expect the ratio of the actual values for 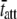to be in the range of 4.0–9.0. In this example, the ratio of the calculated values for 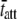at 17°C versus 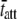at 37°C was found to be 5.88, which is consistent with the expected range for temperature-dependent changes in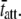

FIGURE 6.

Examples of mouse cardiac muscle undergoing sinusoidal length perturbation analysis. (A–C) Plots of elastic modulus versus frequency (A), viscous modulus versus frequency (B) and viscous versus elastic moduli (C) of data recorded from myofilaments containing α-MHC and examined at 37°C. (D–F) Plots of data from myofilaments containing α-MHC and examined at 17°C. The characteristic dips in elastic and viscous moduli occurred at lower frequencies at 17°C compared to 37°C, which reflects slower cross-bridge kinetics at the lower temperature. (G–I) Plots of data from myofilaments containing β-MHC and examined at 17°C. The characteristic dips in elastic and viscous moduli occurred at lower frequencies with β-MHC compared to α-MHC, which reflects the slower cross-bridge kinetics associated with the β-MHC.

Fig. 6, G–I, illustrate the raw data from wild-type mouse cardiac muscle containing >90% β-MHC examined at 17°C. This mouse expressed cardiac β-MHC due to being hypothyroid (57). The fit of Eq. 1A to these data resulted in estimates for the parameters c = 3.7 Hz and 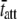= 42.8 ms. Interestingly, the results for 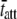for α-MHC and for β-MHC at 17°C are qualitatively consistent with the expected differences in the time attached for α-MHC and β-MHC, which have been reported to be 11 ± 2 ms and 19 ± 3 ms for rabbit cardiac isoforms, respectively, examined in the laser trap at high ATP concentrations and at 25°C (58).

DISCUSSION

The complex modulus, like that shown in Fig. 1 A, arises from sinusoidal (1,3–8,43,45) or random (2,18,59) length perturbation analysis and provides the frequency domain representation of the force response to small length perturbations. It has been postulated that cross-bridge kinetics are sensitive to strain or load, and therefore the recorded complex modulus represents the perturbation-induced redistribution of acto-myosin cross-bridges among force-producing and non-force-producing biochemical states (1,5,32–35). The C-process has specifically been attributed to arise due to a strain dependence of the rate of cross-bridge detachment after ATP has bound to the actin-myosin cross-bridge in its rigor state (1,3–5). The present study does not refute or preclude a strain-dependence of cross-bridge kinetics. Indeed, there is direct evidence for significant changes in the probability density function for t_att due to an externally applied strain (38,39). We have nevertheless demonstrated that a portion of the force response to length perturbation, specifically the C-process, is adequately described as a mechanical outcome of acto-myosin cross bridges cycling through attached and detached states without requiring a strain-dependence of cross-bridge kinetics. We find that the characteristic rate of the C-process, 2πc, provides a direct measure of the rate of cross-bridge detachment, i.e., g or g_app (50,51), whose reciprocal gives the mean time of acto-myosin cross-bridge attachment.

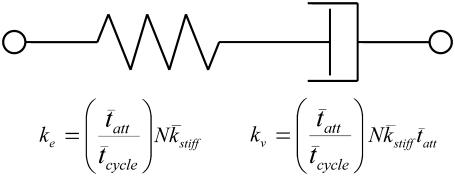
Our result of Eq. 16 suggests that the half-sarcomere can be attributed to a visco-elastic property similar to that provided by a spring and dashpot in series (Fig. 7) with a mechanical transfer function, effective stiffness (k_e), and viscosity (k_v) given as follows:

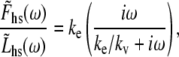(18A)

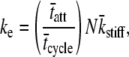(18B)

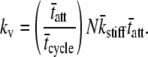(18C)

According to Eq. 18A, the mechanical transfer function at very high frequencies reduces to the effective stiffness, k_e. Intuition suggests that the effective stiffness at very high frequencies of perturbation should be proportional to the fraction of myosin heads attached, the total number of heads, and the mean stiffness associated with each cross-bridge as indicated by the expression for k_e in Eq. 18B. In addition, the relaxation rate constant, k_e/k_v, in Eq. 18A is equivalent to the reciprocal of the mean time attached and is consistent with the interpretation that the exponential rate of force relaxation, due to cross-bridge cycling, mirrors the rate of cross-bridge detachment (12,50,51,60). The equivalent spring-dashpot (Fig. 7) furthermore predicts a symmetry in phases 1 and 2 between stretch and release step perturbations, as has been reported in several muscle types perturbed at small amplitudes (7,25,61). The notion that phases 1 and 2 arise from an equivalent spring-dashpot contrasts with the interpretation of Huxley and Simmons (13), who observed in frog skeletal muscle that phase 2 after a release is much more rapid than that after a stretch and is not exponential in form. Huxley and Simmons and others (13–15) argue that phase 2 after a release reflects the rate of force regeneration by cross-bridges transitioning from weakly to strongly bound states, and that the rate of cross-bridge detachment is too slow to contribute to the observed time course of phase 2 (13). The current analysis and that of others (12,60) conversely suggest that cross-bridge detachment constitutes a significant portion of the force response under normal experimental conditions.

FIGURE 7.

A visco-elastic equivalent of two-state model of acto-myosin cross-bridge kinetics with a single-exponential distribution for t_att. The effective elastic stiffness, k_e, of the half-sarcomere is proportional to the fraction of myosin heads attached, the total number of heads, and the mean stiffness of the cross-bridge elastic elements. The effective viscosity, k_v, due to the intermittent binding of myosin to actin is additionally proportional to the mean time of cross-bridge attachment.

Our interpretation that 2πc of the C-process reflects the rate of cross-bridge detachment is supported by the results of previous studies. Several studies using sinusoidal length perturbation analysis have demonstrated that 2πc rises monotonically with ATP concentration and asymptotically approaches a maximum value (1,3–5,9,11,41–44). The observed dependency of 2πc on ATP is consistent with the interpretation that 2πc is reciprocally related to the mean time of cross-bridge attachment, which is prolonged with ATP deprivation (52,58). Based on our interpretation, the maximum value for 2πc as a function of ATP concentration would reflect the rate of ADP release, which is considered the rate-limiting step of the cross-bridge cycle at high ATP concentrations (62,63). The different values for 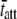we calculated due to different temperatures and MHC isoforms (Fig. 6) are consistent with the expected differences in 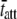under these conditions and lend further evidence to support our interpretation that the characteristic rate of the C-process reflects the rate of cross-bridge detachment (48,60,64).

One consequence of our result is perhaps best recognized in the context of those predictions of the two-state model expressed using the apparent rate constants for myosin attachment and detachment, f_app and g_app, respectively (50,51). The two-state model predicts ATPase = N f_app g_app/(f_app + g_app) and Force = N f_app/(f_app + g_app). Therefore, the ratio of ATPase/Force provides the value for g_app (50,51,60,65). Using indirect methods to infer g_app, the rate of cross-bridge detachment has been reported to remain constant (50) or to asymptotically approach a minimum value (65) as calcium activation is increased. Our current study suggests that g_app can be measured directly in intact myofilaments as the value of 2πc. We and others have reported previously that 2πc, and therefore g_app, is reduced with increasing calcium activation (8,66), which corroborates the findings of Kerrick and colleagues (30,65).

Our results further imply that the mean time of cross-bridge attachment can be measured in an intact myofilament lattice and without the examination of single myosin molecules as done with the laser trap. We believe there would be significant experimental value in providing this direct measurement to compare with results from single molecule experiments. This view is akin to examining the behavior of an ensemble of individuals over a short period of time versus examining a single individual over a long period of time. We recognize that this direct measurement relies upon the assumption that a single-exponential describes accurately the probability density function for t_att (Eq. 14). Results from single myosin molecules in the laser trap do favor a single-exponential distribution (52,58). However, the strongly bound cross-bridge comprises at least three (ADP, rigor, and ATP) biochemical states (52,58), and the probability density function for t_att may therefore be more realistically represented by a multiexponential or γ-distribution rather than by a single-exponential distribution. By applying Eq. 13 to the recorded data and t_att, it is theoretically possible to derive the true form of the probability density function using our analytical approach once analogous stochastic models for the A- and B-processes are developed and integrated with the current model underlying process C. We anticipate that the application of length perturbation analysis to a large population of independent acto-myosin cross-bridges will reveal the strain-dependency of cross-bridge kinetics in the form of the B-process or similar phenomena.